Three-Dimensional Numerical Simulation of Flow Around a Spur Dike in a Meandering Channel Bend
Abstract
1. Introduction
2. Two-Equation Turbulence Closure Models
2.1. Standard Model
2.2. Model
2.3. RNG Model
2.4. Nonlinear Model
3. Methodology and Study Area
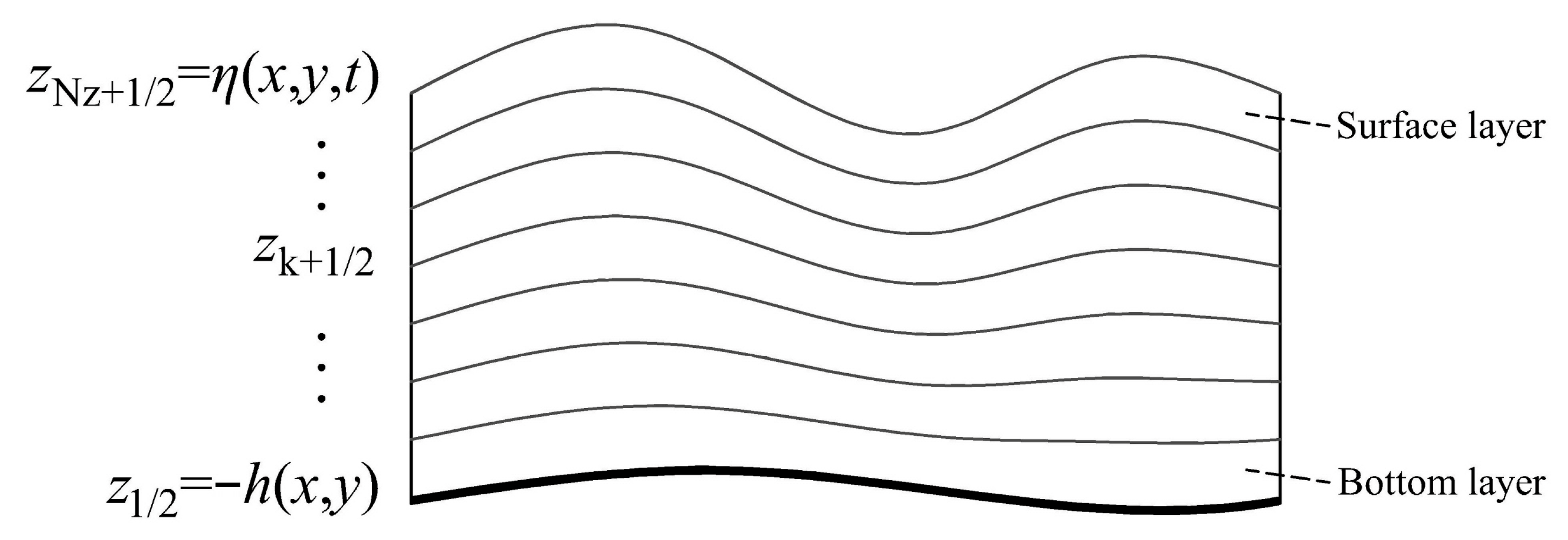
3.1. Methodology
3.2. Study Area
4. Results and Discussion
4.1. Flow Around a Spur Dike Located at the Left Bank (Case 2 and Case 3)
4.2. Flow Around a Spur Dike Located at the Right Bank (Case 2R and Case 3R)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Reynolds-Averaged Navier–Stokes (RANS) Equations
Appendix A.2. Boundary Conditions
References
- Ettema, R.; Muste, M. Scale effects in flume experiments on flow around a spur dike in flatbed channel. J. Hydraul. Eng. 2004, 130, 635–646. [Google Scholar] [CrossRef]
- Sohail, I.; Tanaka, N. An experimental investigation on Dike stabilization against floods. Geosciences 2023, 13, 307. [Google Scholar] [CrossRef]
- Kuhnle, R.A.; Jia, Y.; Alonso, C.V. Measured simulated flow near a submerged spur dike. J. Hydraul. Eng. 2008, 134, 916–924. [Google Scholar] [CrossRef]
- Rajaratnam, N.; Nwachukwa, B.A. Flow near groin-like structures. J. Hydraul. Eng. 1983, 109, 463–480. [Google Scholar] [CrossRef]
- Iqbal, S.; Dissanayaka, K.D.C.R.; Tanaka, N. Numerical modeling and validation of dike-induced water flow dynamics using OpenFOAM. ISH J. Hydraul. Eng. 2024, 30, 559–573. [Google Scholar] [CrossRef]
- Iqbal, S.; Tanaka, N. Numerical modeling of flow dynamics around L-shaped and T-shaped dikes with varying geometric configurations and wing arrangements. Model. Earth Syst. Environ. 2024, 10, 5953–5968. [Google Scholar] [CrossRef]
- Koken, M. Coherent structures around isolated spur dykes at various approach flow angles. J. Hydraul. Res. 2011, 49, 736–743. [Google Scholar] [CrossRef]
- Koken, M.; Gogus, M. Effect of spur dike length on the horseshoe vortex system the bed shear stress distribution. J. Hydraul. Res. 2015, 53, 196–206. [Google Scholar] [CrossRef]
- Mayerle, R.; Wang, S.S.Y.; Toro, F.M. Verification of a three-dimensional numerical model simulation of the flow in the vicinity of spur dikes. J. Hydraul. Res. 1995, 33, 243–256. [Google Scholar] [CrossRef]
- Nagata, N.; Hosoda, T.; Nakato, T.; Muramoto, Y. Three-dimensional numerical model for flow bed deformation around river hydraulic structures. J. Hydraul. Eng. 2005, 131, 1074–1087. [Google Scholar] [CrossRef]
- Ouillon, S.; Dartus, D. Three-dimensional computation of flow around groyne. J. Hydraul. Eng. 1997, 123, 962–970. [Google Scholar] [CrossRef]
- de Vriend, H.J. Velocity redistribution in curved rectangular channels. J. Fluid Mech. 1980, 107, 423–439. [Google Scholar] [CrossRef]
- Ferguson, R.I.; Parsons, D.R.; Lane, S.N.; Hardy, R.J. Flow in meander bends with recirculation at the inner bank. Water Resour. Res. 2003, 39, 1322. [Google Scholar] [CrossRef]
- Nanson, R.A. Flow fields in tightly curving meander bends of low width-depth ratio. Earth Surf. Process. Landf. 2010, 35, 119–135. [Google Scholar] [CrossRef]
- Ghodsian, M.; Vaghefi, M. Experimental study on scour flow field in a scour hole around a T-shape spur dike in a 90 degrees bend. Int. J. Sediment Res. 2009, 24, 145–158. [Google Scholar] [CrossRef]
- Giri, S.; Shimizu, Y.; Surajate, B. Laboratory measurement and numerical simulation of flow and turbulence in a meandering-like flume with spurs. Flow Meas. Instrum. 2004, 15, 301–309. [Google Scholar] [CrossRef]
- Sharma, K.; Mohapatra, P.K. Separation zone in flow past a spur dyke on rigid bed meandering channel. J. Hydraul. Eng. 2012, 138, 897–901. [Google Scholar] [CrossRef]
- Tripathi, R.P.; Pandey, K.K. Numerical Investigation of Flow Field Around T-Shaped Spur Dyke in a Reverse-Meandering Channel (Online). Water Supply 2022, 22, 574–588. [Google Scholar] [CrossRef]
- Vaghefi, M.; Radan, P.; Akbari, M. Flow Pattern Around Attractive Vertical Repelling T-Shaped Spur Dikes in a Mild Bend Using CFDModeling. Int. J. Civ. Eng. 2019, 17, 607–617. [Google Scholar] [CrossRef]
- Vaghefi, M.; Safarpoor, Y.; Akbari, M. Numerical investigation of flow pattern components of three-dimensional velocity around a submerged T-shaped spur dike in a 90° bend. J. Cent. South Univ. 2016, 23, 2984–2998. [Google Scholar] [CrossRef]
- Ai, C.; Ding, W.; Jin, S. A general boundary-fitted 3D non-hydrostatic model for nonlinear focusing wave groups. Ocean Eng. 2014, 89, 134–145. [Google Scholar] [CrossRef]
- Ai, C.; Jin, S. Non-hydrostatic finite volume model for non-linear waves interacting with structures. Comput. Fluids 2010, 39, 2090–2100. [Google Scholar] [CrossRef]
- Ai, C.; Jin, S. A multi-layer non-hydrostatic model for wave breaking and run-up. Coast. Eng. 2012, 62, 1–8. [Google Scholar] [CrossRef]
- Ai, C.; Jin, S.; Lv, B. A new fully non-hydrostatic 3D free surface flow model for water wave motions. Int. J. Numer. Methods Fluids 2011, 66, 1354–1370. [Google Scholar] [CrossRef]
- Ai, C.; Jin, S.; Xing, Y. Influence of suspended load on 3Dnumerical simulation of flow bed evolution in a meandering channel bend. J. Hydraul. Eng. 2013, 139, 450–455. [Google Scholar] [CrossRef]
- Craft, T.J.; Launder, B.E.; Suga, K. Development application of a cubic eddy-viscosity model of turbulence. Int. J. Heat Fluid Flow 1996, 17, 108–115. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Engrg. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Wilcox, D.C. Reassessment of the scale-determining equation for advanced turbulence models. AIAA J. 1988, 26, 1299–1310. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A.; Thangam, S.; Gatski, T.B.; Speziale, C.G. Development of turbulence models for shear flows by a double expansion technique. Phys. Fluids A 1992, 4, 1510–1520. [Google Scholar] [CrossRef]
- Klein, T.S.; Craft, T.J.; Iacovides, H. Assessment of the performance of different classes of turbulence models in a wide range of non-equilibrium flows. Int. J. Heat Fluid Flow 2015, 51, 229–256. [Google Scholar] [CrossRef]













| −0.1 | 0.1 | 0.26 | −10 | 0 | −5 | 5 |
| Test Cases | Spur Dike Location | Flow Depth (m) | Approach Velocity (m/s) |
|---|---|---|---|
| Case 2 | Left bank, = 15° | 0.096 | 0.21 |
| Case 3 | Left bank, = 29° | 0.096 | 0.21 |
| Case 2R | Right bank, = 15° | 0.096 | 0.21 |
| Case 3R | Right bank, = 29° | 0.096 | 0.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, Y.; Ai, C.; Cui, H.; Xiao, Z. Three-Dimensional Numerical Simulation of Flow Around a Spur Dike in a Meandering Channel Bend. Fluids 2025, 10, 198. https://doi.org/10.3390/fluids10080198
Xing Y, Ai C, Cui H, Xiao Z. Three-Dimensional Numerical Simulation of Flow Around a Spur Dike in a Meandering Channel Bend. Fluids. 2025; 10(8):198. https://doi.org/10.3390/fluids10080198
Chicago/Turabian StyleXing, Yan, Congfang Ai, Hailong Cui, and Zhangling Xiao. 2025. "Three-Dimensional Numerical Simulation of Flow Around a Spur Dike in a Meandering Channel Bend" Fluids 10, no. 8: 198. https://doi.org/10.3390/fluids10080198
APA StyleXing, Y., Ai, C., Cui, H., & Xiao, Z. (2025). Three-Dimensional Numerical Simulation of Flow Around a Spur Dike in a Meandering Channel Bend. Fluids, 10(8), 198. https://doi.org/10.3390/fluids10080198






