Numerical Study of Gas Dynamics and Condensate Removal in Energy-Efficient Recirculation Modes in Train Cabins
Abstract
1. Introduction
2. Materials and Methods
2.1. Basic Equations
2.2. Experimental Method
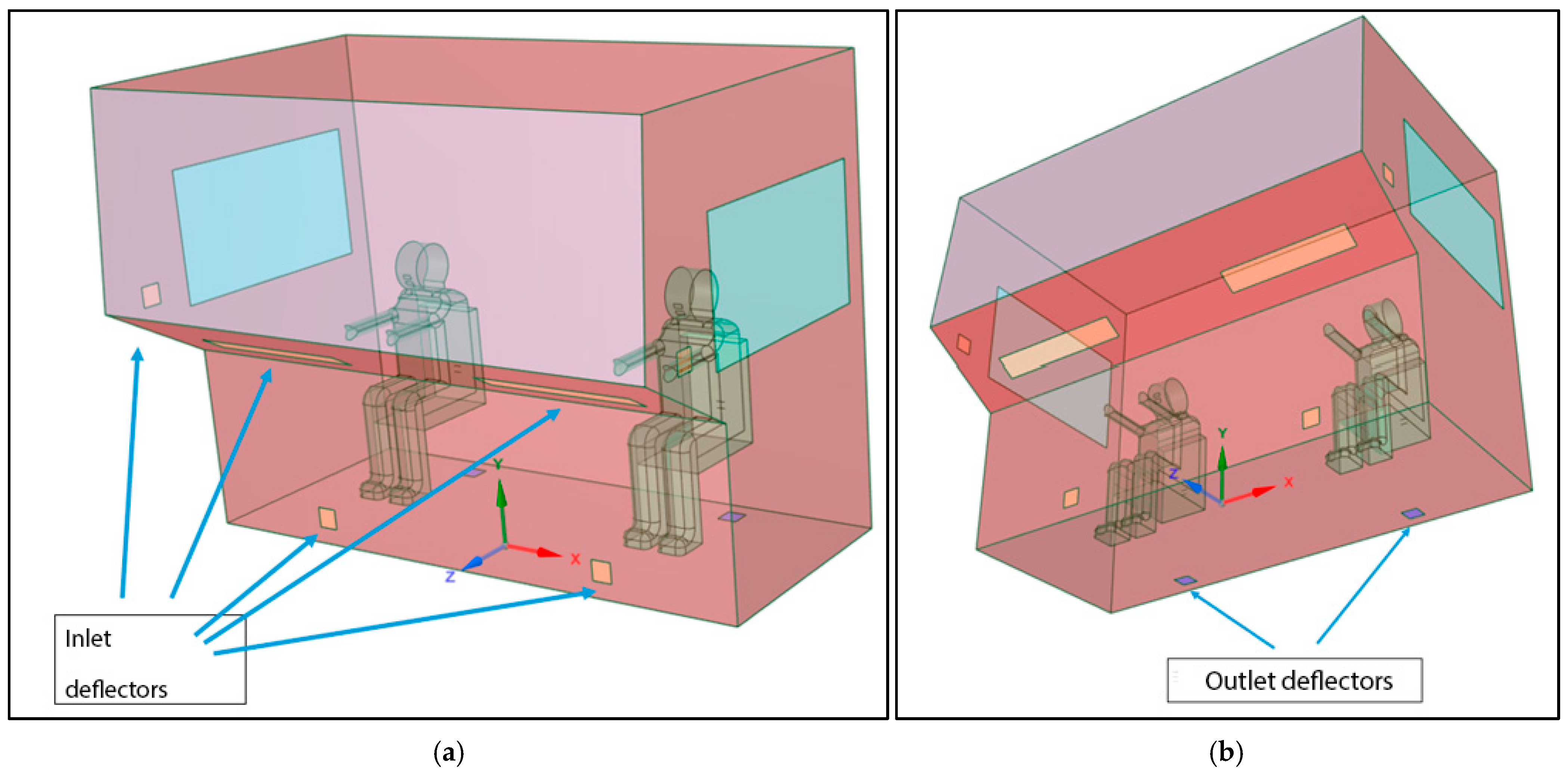
2.3. Geometry Model
3. Results and Discussion
3.1. Numerical Analysis
3.2. Task Parameters
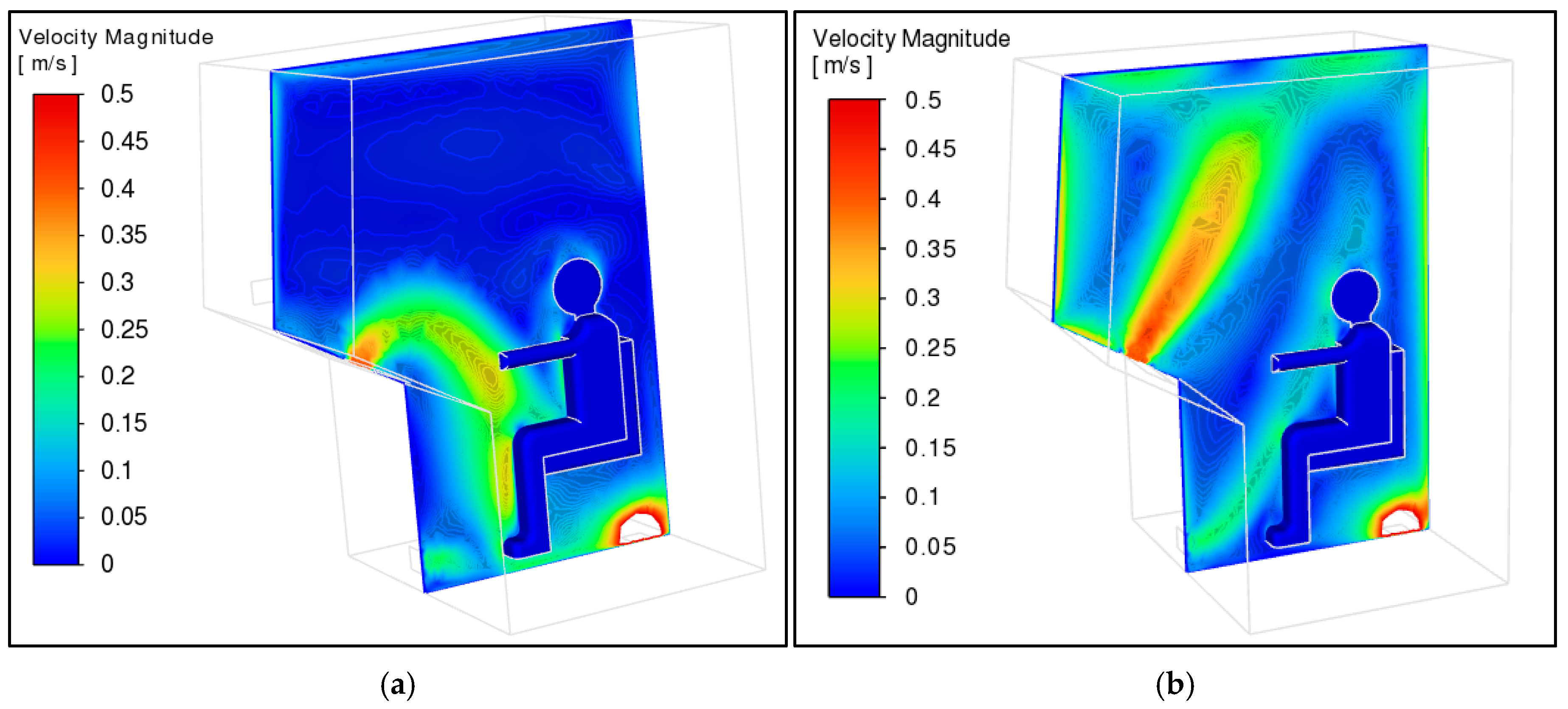
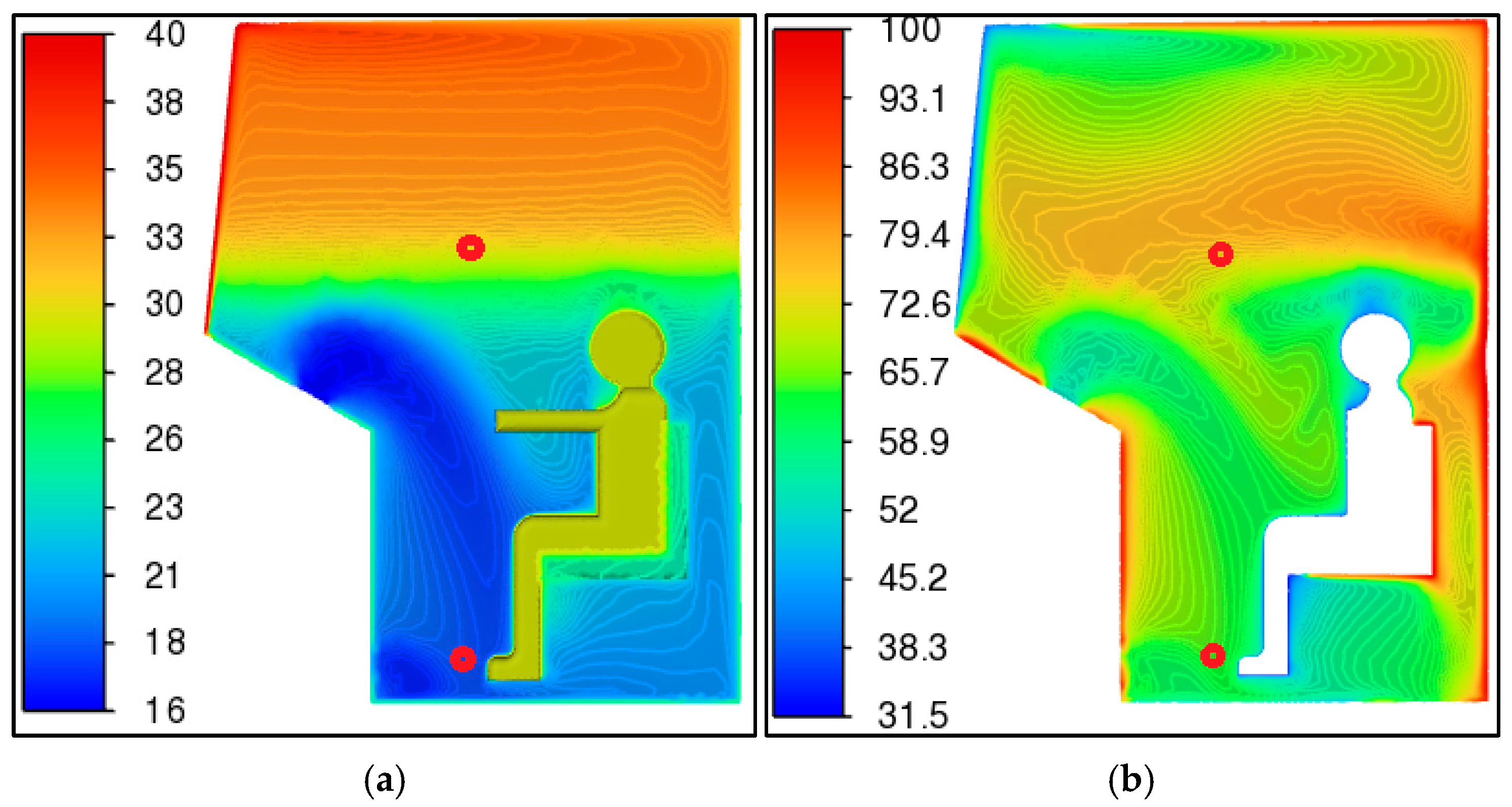
3.3. Numerical Results for Temperature and Air Speed and Verification of Results
3.4. Verification and Comparison with Experimental Data
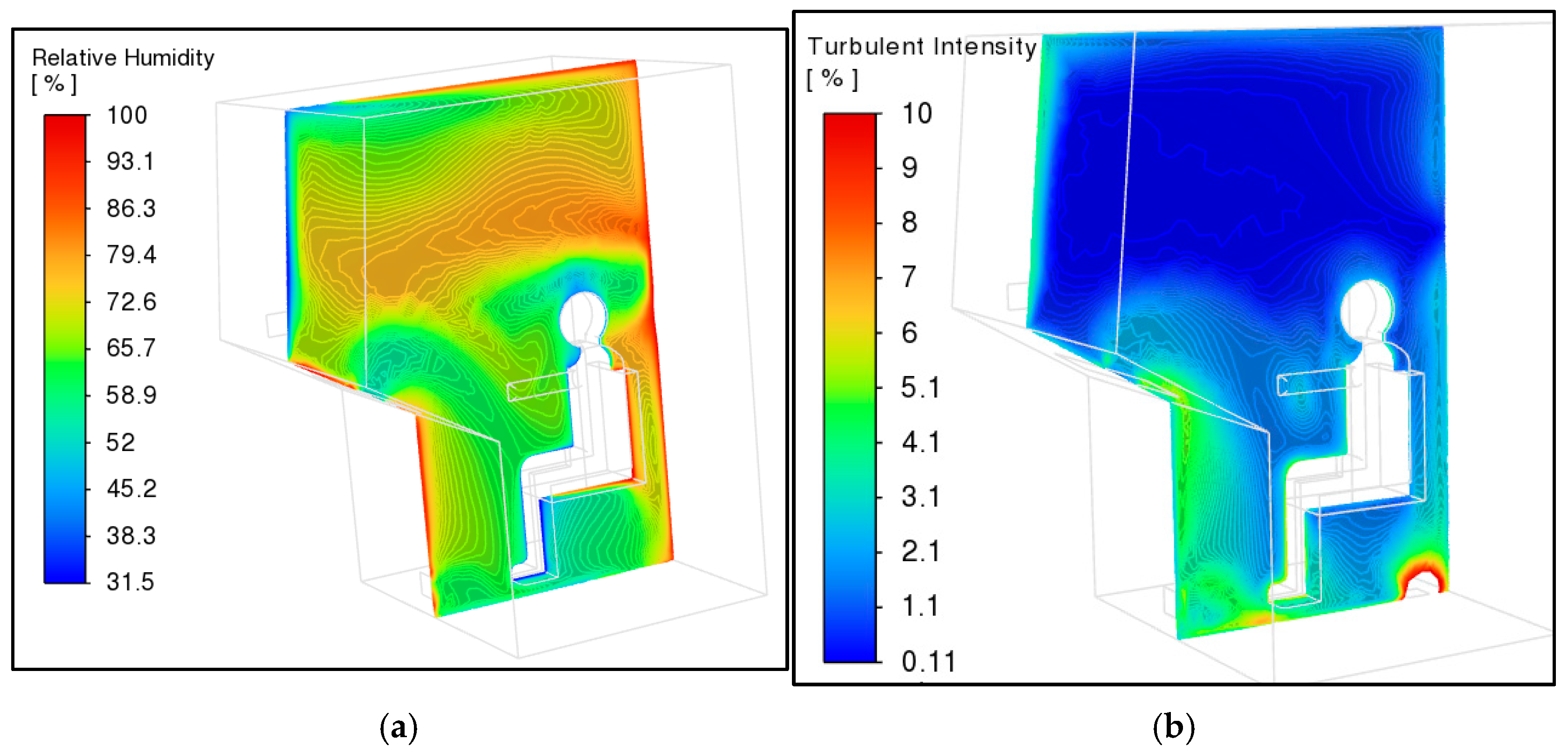
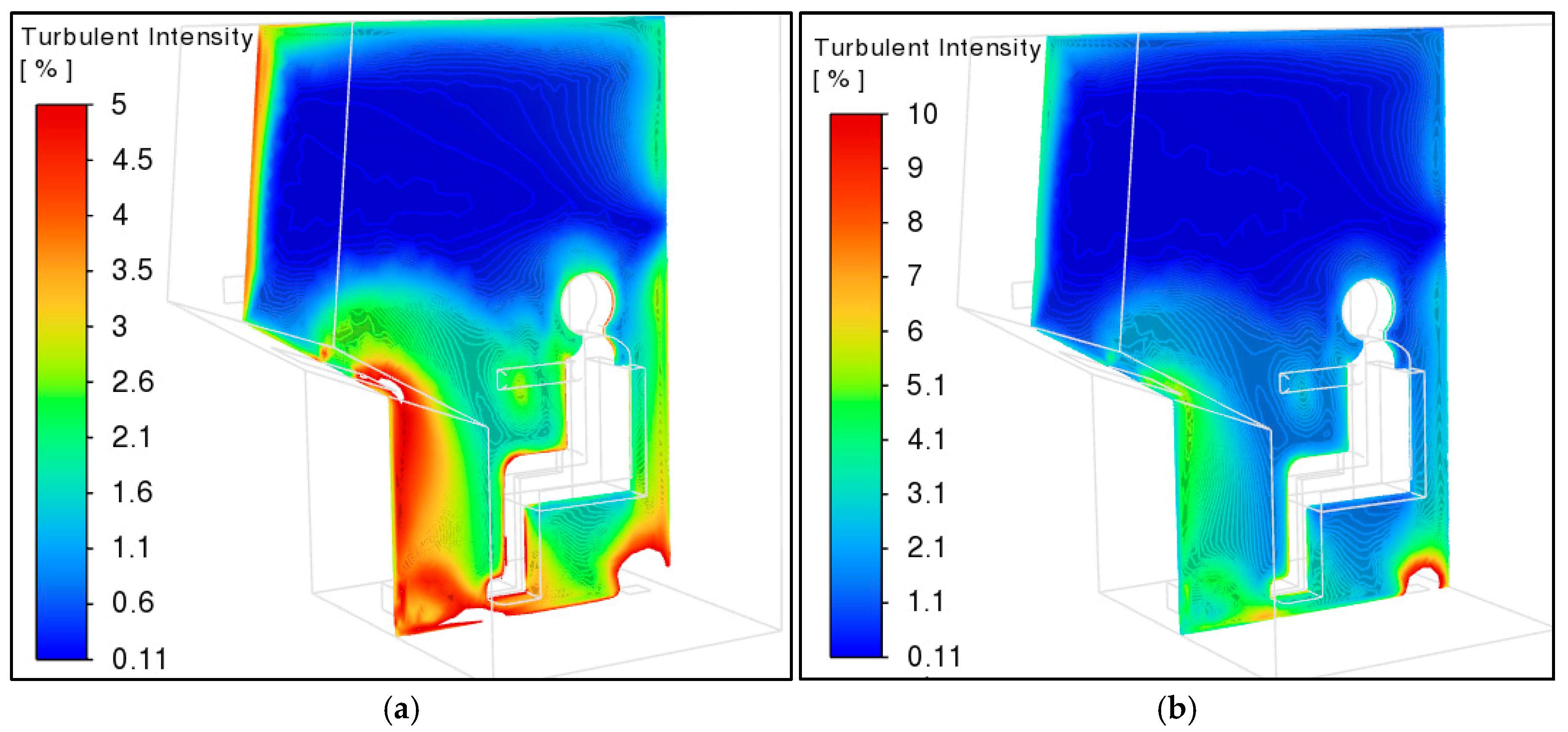
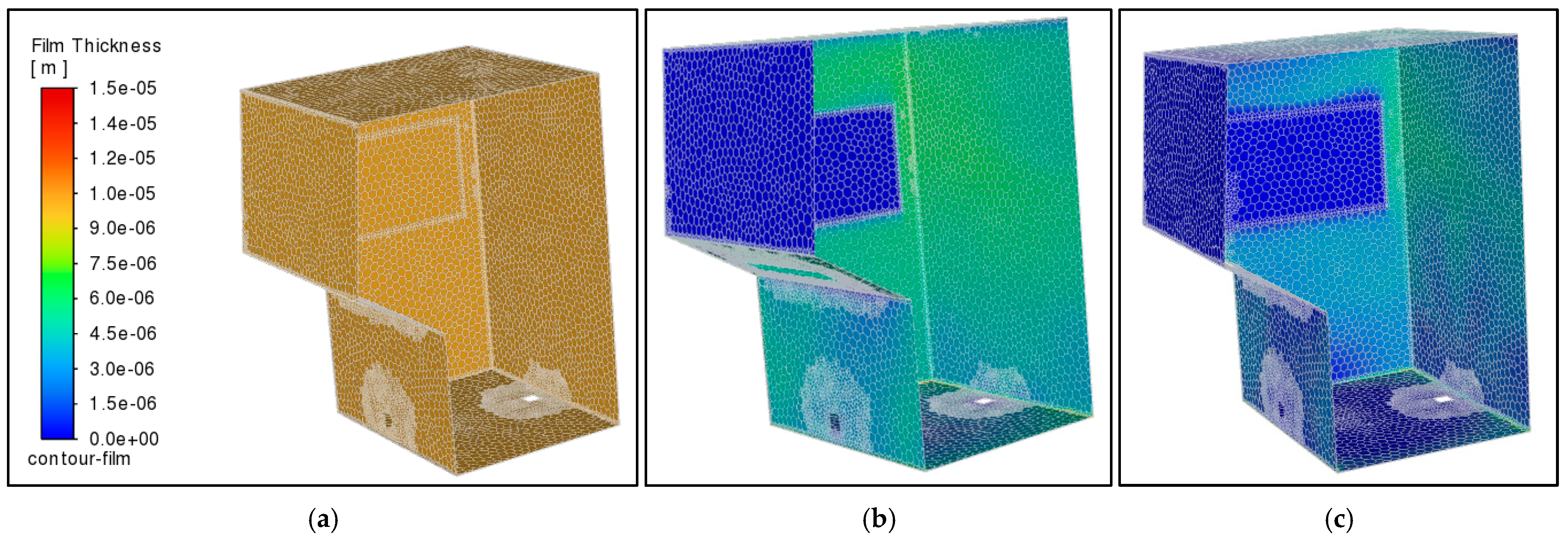
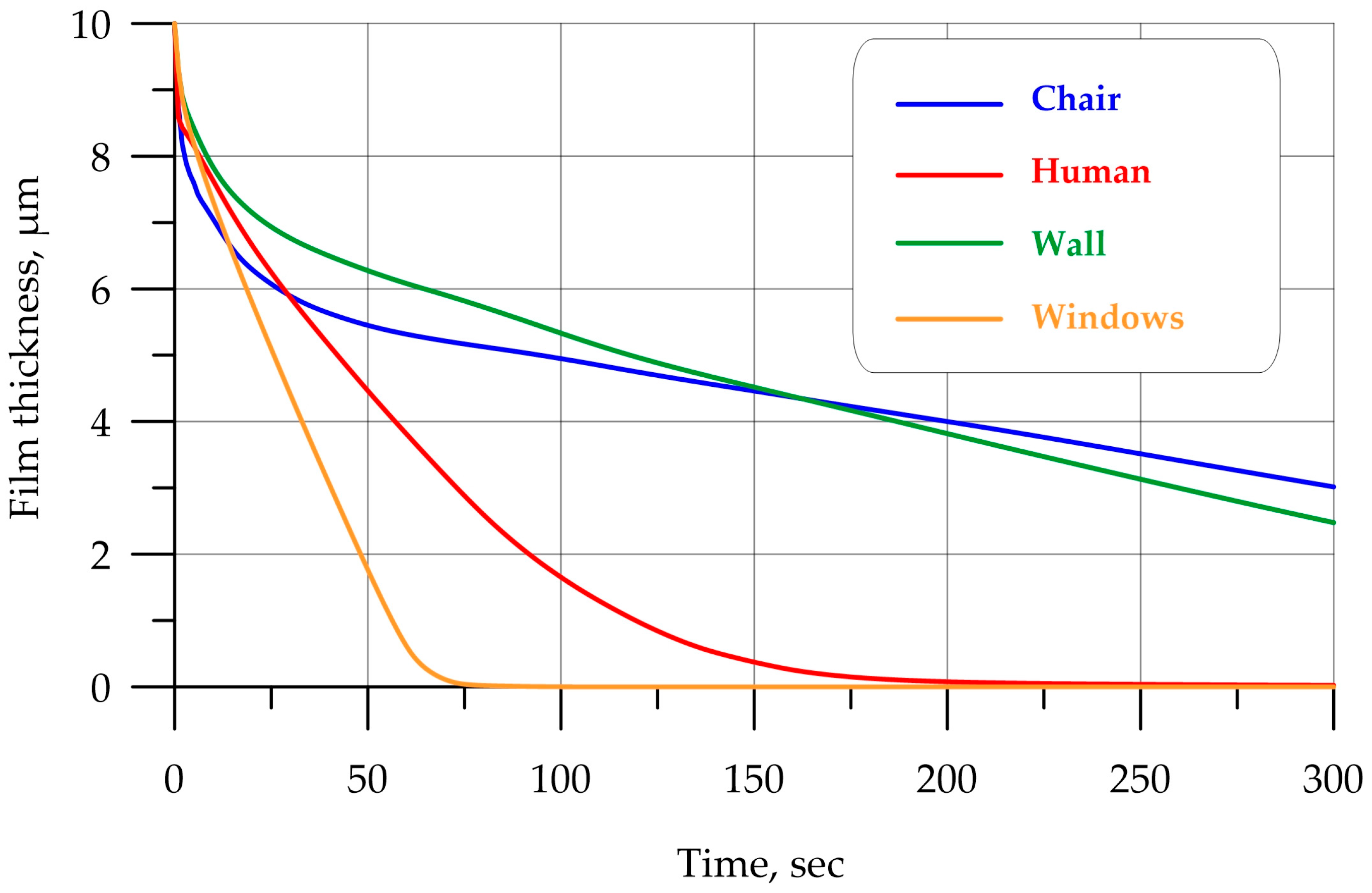
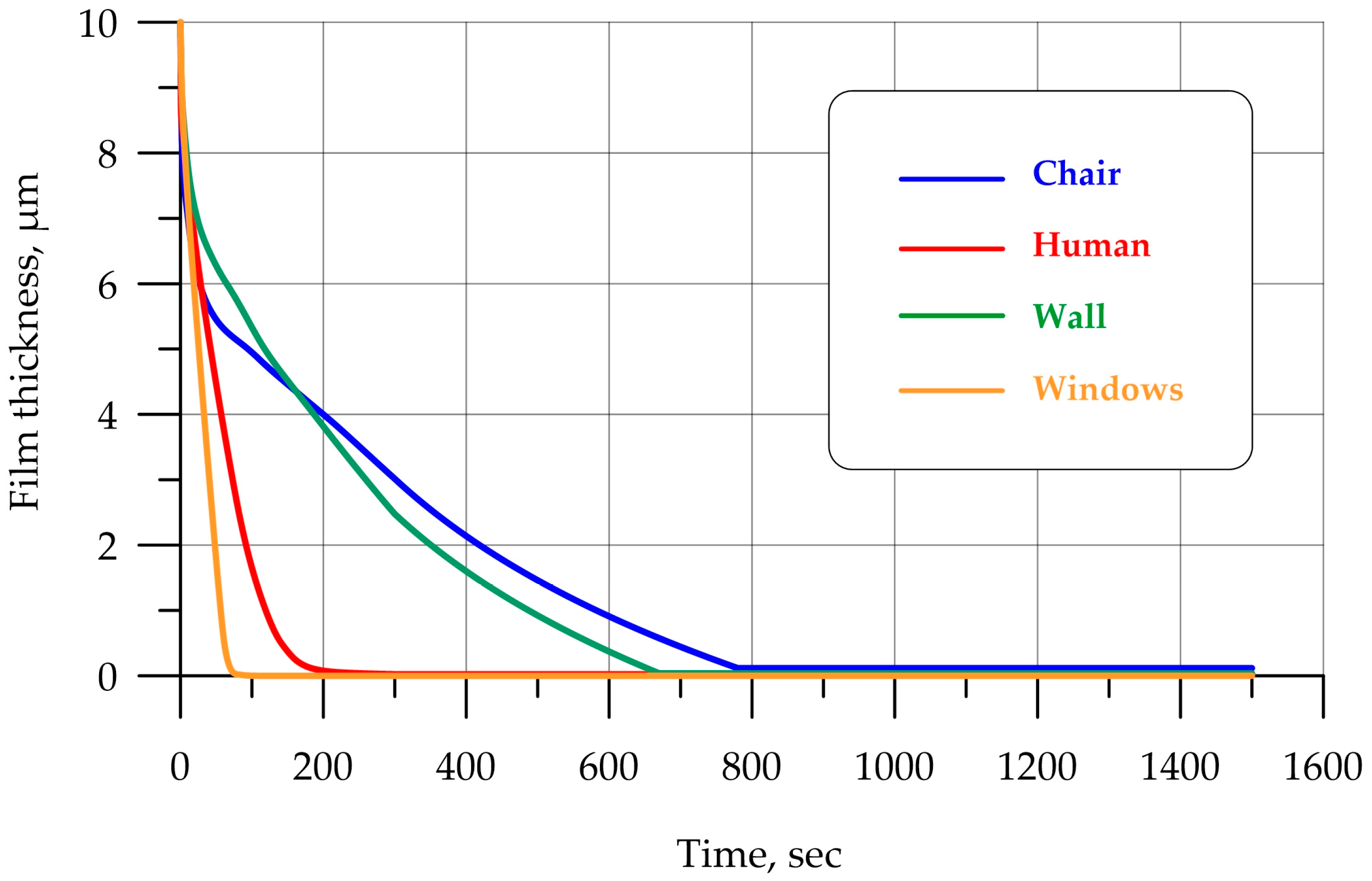
3.5. Numerical Results for Humidity and Condensation for Different Circulation Regimes: Discussion of Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Transport in Russia. 2022: Stat. Collection/Rosstat.—T65 M., 2022—101p. Available online: https://mintrans.gov.ru/file/504718 (accessed on 11 March 2025).
- Federal State Statistics Service. [Electronic Resource]. Available online: https://rosstat.gov.ru/statistics/transport (accessed on 11 March 2025).
- Li, X.; Patel, M.J.; Cole, I.S. Portable Air Purifiers’ Predicted Efficacy in Mitigating Airborne Pathogen Transmission in an Office Room Featuring Mixing Ventilation. Fluids 2023, 8, 307. [Google Scholar] [CrossRef]
- Pozevalkin, V.V.; Polyakov, A.N. Implementation of a Digital Model of Thermal Characteristics Based on the Temperature Field. Adv. Eng. Res. 2024, 24, 178–189. [Google Scholar] [CrossRef]
- Yao, J.; Yao, Y. Transient CFD Modelling of Air–Water Two-Phase Annular Flow Characteristics in a Small Horizontal Circular Pipe. Fluids 2022, 7, 191. [Google Scholar] [CrossRef]
- Moveh, S.; Merchán-Cruz, E.A.; Ibrahim, A.O.; Elhassan, Z.A.M.; Ramadan Abdelhai, N.M.; Abdelrazig, M.D. Thermodynamic Optimization of Building HVAC Systems Through Dynamic Modeling and Advanced Machine Learning. Sustainability 2025, 17, 1955. [Google Scholar] [CrossRef]
- ANSI ANSI/ASHRAE Standard 62.1-2010, Ventilation for Acceptable Indoor Air Quality. Available online: https://www.ashrae.org/technical-resources/bookstore/standards-62-1-62-2 (accessed on 11 March 2025).
- ANSI/ASHRAE Standard 55-2017 Thermal Environmental Conditions for Human Occupancy. Approved by ASHRAE and the American National Standards Institute on 31 July 2020. Available online: https://clck.ru/3ESQGh (accessed on 11 March 2025).
- Safety Standards for Railway Transport Electric Locomotives. NB ZhT CT 04-98 Electric Locomotives. Safety Standards. - M.: 1998. -123p. Available online: https://files.stroyinf.ru/Data2/1/4293756/4293756801.pdf (accessed on 11 March 2025).
- Resolution of the Chief State Sanitary Doctor of the Russian Federation dated 28 January 2021 No. 2 On Approval of Sanitary Rules and Regulations SANPIN 1.2.3685-21 "Hygienic Standards and Requirements for Ensuring the Safety and (or) Harmlessness of Environmental Factors for Humans". [Electronic Resource]. Available online: https://base.garant.ru/400274954/ (accessed on 25 July 2025).
- Mikheev, M.A.; Mikheeva, I.M. Fundamentals of Heat Transfer, 2nd ed.; Energia: Moscow, Russia, 1977; 344p. [Google Scholar]
- Sapozhnikov, S.Z.; Kitanin, E.L. Engineering Thermodynamics and Heat Transfer; Publishing House: St. Petersburg, Russia, 2001; 317p. [Google Scholar]
- Saghir, M.Z.; Rahman, M.M. Effectiveness in Cooling a Heat Sink in the Presence of a TPMS Porous Structure Comparing Two Different Flow Directions. Fluids 2024, 9, 297. [Google Scholar] [CrossRef]
- Panfilov, I.A. Study of heat transfer in shell-and-tube heat exchangers using stored refrigerant. XXI Century: Results Past Probl. Present Plus 2024, 13, 181–188. [Google Scholar]
- Mokrane, M.; Bourouis, M. Heat Transfer and Fluid Flow Characteristics in a Micro Heat Exchanger Employing Warm Nanofluids for Cooling of Electronic Components. Energies 2024, 17, 2383. [Google Scholar] [CrossRef]
- Beskopylny, A.N.; Panfilov, I.; Meskhi, B. Modeling of Flow Heat Transfer Processes and Aerodynamics in the Cabins of Vehicles. Fluids 2022, 7, 226. [Google Scholar] [CrossRef]
- Taebi, A. Deep Learning for Computational Hemodynamics: A Brief Review of Recent Advances. Fluids 2022, 7, 197. [Google Scholar] [CrossRef]
- Pioch, F.; Harmening, J.H.; Müller, A.M.; Peitzmann, F.-J.; Schramm, D.; el Moctar, O. Turbulence Modeling for Physics-Informed Neural Networks: Comparison of Different RANS Models for the Backward-Facing Step Flow. Fluids 2023, 8, 43. [Google Scholar] [CrossRef]
- Drikakis, D.; Sofos, F. Can Artificial Intelligence Accelerate Fluid Mechanics Research? Fluids 2023, 8, 212. [Google Scholar] [CrossRef]
- Zhou, X.-W.; Liu, F.-T.; Jin, Y.-F.; Yin, Z.-Y.; Zhang, C.-B. A volumetric locking-free stable node-based smoothed finite element method for geomechanics. Comput. Geotech. 2022, 149, 104856, ISSN 0266-352X. [Google Scholar] [CrossRef]
- Quaresma, A.L.; Romão, F.; Pinheiro, A.N. A Comparative Assessment of Reynolds Averaged Navier–Stokes and Large-Eddy Simulation Models: Choosing the Best for Pool-Type Fishway Flow Simulations. Water 2025, 17, 686. [Google Scholar] [CrossRef]
- Andrew, S. Kowalski, Jesús Abril-Gago, Exploring unresolved inquiries regarding the meaning of Reynolds averaging and decomposition: A review. Agric. For. Meteorol. 2025, 362, 110364, ISSN 0168-1923. [Google Scholar] [CrossRef]
- Chen, X.; Ishihara, T. Numerical study of turbulent flows over complex terrain using an unsteady Reynolds-averaged Navier-Stokes model with a new method for turbulent inflow generation. J. Wind. Eng. Ind. Aerodyn. 2025, 257, 105991, ISSN 0167-6105. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, T.; Lu, W.; Yang, H.; Li, Y.; Liu, Y.; Zhang, M. Computational Fluid Dynamics (CFD) Technology Methodology and Analysis of Waste Heat Recovery from High-Temperature Solid Granule: A Review. Sustainability 2025, 17, 480. [Google Scholar] [CrossRef]
- Yee, H.C.; Sweby, P.K.; Sjögreen, B.; Kotov, D.V. A Nonlinear Approach in the Quantification of Numerical Uncertainty by High-Order Methods for Compressible Turbulence with Shocks. Fluids 2024, 9, 250. [Google Scholar] [CrossRef]
- Tong, K.; Yang, L.; Du, X.; Yang, Y. Review of modeling and simulation strategies for unstructured packing bed photoreactors with CFD method. Renew. Sustain. Energy Rev. 2020, 131, 109986, ISSN 1364-0321. [Google Scholar] [CrossRef]
- Panfilov, I.; Beskopylny, A.N.; Meskhi, B. Improving the Energy Efficiency of Vehicles by Ensuring the Optimal Value of Excess Pressure in the Cabin Depending on the Travel Speed. Fluids 2024, 9, 130. [Google Scholar] [CrossRef]
- Ogundiran, J.O.; Nyembwe, J.-P.K.B.; Ogundiran, J.; Ribeiro, A.S.N.; Gameiro da Silva, M. A Systematic Review of Indoor Environmental Quality in Passenger Transport Vehicles of Tropical and Subtropical Regions. Atmosphere 2025, 16, 140. [Google Scholar] [CrossRef]
- Luger, C.; Kallinovsky, J.; Rieberer, R. Identification of representative operating conditions of HVAC systems in passenger rail vehicles based on sampling virtual train trips. Adv. Eng. Inform. 2016, 30, 157–167, ISSN 1474-0346. [Google Scholar] [CrossRef]
- Pan, D.; Wen, D.; Guo, X.; Song, H.; Bai, S. Factors Influencing the Sterilization of E. coli in a High-Voltage Electric Field: Electric Field Strength, Temperature and Humidity. Processes 2025, 13, 551. [Google Scholar] [CrossRef]
- Yang, Y.; Shi, N.; Zhang, R.; Zhou, H.; Ding, L.; Tao, J.; Zhang, N.; Cao, B. Study on the Effect of Local Heating Devices on Human Thermal Comfort in Low-Temperature Built Environment. Buildings 2024, 14, 3996. [Google Scholar] [CrossRef]
- Dixit, S.; Kumar, A.; Kumar, S.; Waghmare, N.; Harish; Thakur, C.; Khan, S. CFD analysis of biodiesel blends and combustion using Ansys Fluent. Mater. Today Proc. 2020, 26, 665–670, ISSN 2214-7853. [Google Scholar] [CrossRef]
- 33. Ansys Fluent Tutorial Guide 2023 R1. 2023. Canonsburg, PA. Available online: https://www.ansys.com/content/dam/amp/2023/december/quick-request/ansys-education-resources-23q4-part-1/intro-to-fluent-tutorial-tutiafflen24.pdf (accessed on 9 December 2024).
- Soloviev, A.N.; Panfilov, I.A.; Lesnyak, O.N.; Lee, C.Y.J.; Liu, Y.M. Numerical Simulation of Relative Humidity in a Vehicle Cabin. In Physics and Mechanics of New Materials and Their Applications; Parinov, I.A., Chang, S.H., Soloviev, A.N., Eds.; Springer Proceedings in Materials; Springer: Cham, Switzerland, 2023; Volume 20. [Google Scholar] [CrossRef]
- Lesage, M.; Chalet, D.; Migaud, J. Optimising Ventilation Strategies for Improved Driving Range and Comfort in Electric Vehicles. World Electr. Veh. J. 2025, 16, 98. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhu, S.; Xu, Q.; Yang, B.; Guan, X. Hybrid modeling-based temperature and humidity adaptive control for a multi-zone HVAC system. Appl. Energy 2023, 334, 120622, ISSN 0306-2619. [Google Scholar] [CrossRef]
- Raman, N.S.; Devaprasad, K.; Chen, B.; Ingley, H.A.; Barooah, P. Model predictive control for energy-efficient HVAC operation with humidity and latent heat considerations. Appl. Energy 2020, 279, 115765, ISSN 0306-2619. [Google Scholar] [CrossRef]
- Panfilov, I.; Beskopylny, A.N.; Meskhi, B. Numerical Simulation of Heat Transfer and Spread of Virus Particles in the Car Interior. Mathematics 2023, 11, 784. [Google Scholar] [CrossRef]
- Annapeh, H.F.; Kurushina, V.A. Analysis of the Drag-Reduction Ability of the Layout and Cross-Sectional Shapes of Subsea Structures in the Critical Flow Mode. Adv. Eng. Res. 2024, 24, 135–147. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, Q.; Liu, J.; Wang, Y.; Zhou, H.; Yang, F.; Ru, Y. Experiments and CFD simulation of downwash airflow and fog distribution discharged from a single-rotor UAV fitted with a pulse-jet thermal fogging machine. Biosyst. Eng. 2024, 240, 142–151, ISSN 1537-5110. [Google Scholar] [CrossRef]
- George, A.; Kelm, S.; Cheng, X.; Allelein, H.-J. Efficient CFD modelling of bulk condensation, fog transport and re-evaporation for application to containment scale. Nucl. Eng. Des. 2023, 401, 112067, ISSN 0029-5493. [Google Scholar] [CrossRef]
- Kim, J.; Kang, J. AI based temperature reduction effect model of fog cooling for human thermal comfort: Climate adaptation technology. Sustain. Cities Soc. 2023, 95, 104574, ISSN 2210-6707. [Google Scholar] [CrossRef]
- Nisa, E.C.; Lee, Y.; Kuan, Y.-D. Machine learning-based modeling and fogging prevention strategies for ice rink environments. Build. Environ. 2024, 258, 111553, ISSN 0360-1323. [Google Scholar] [CrossRef]
- Babu, A.R.; Sebben, S.; Chronéer, Z.; Etemad, S. An adaptive cabin air recirculation strategy for an electric truck using a coupled CFD-thermoregulation approach. Int. J. Heat Mass Transf. 2024, 221, 125056, ISSN 0017-9310. [Google Scholar] [CrossRef]
- Hou, J.; Li, S.; Pan, W.; Yang, L. Co-Simulation Modeling and Multi-Objective Optimization of Dynamic Characteristics of Flow Balancing Valve. Machines 2023, 11, 337. [Google Scholar] [CrossRef]
- D’Agaro, P.; Croce, G.; Cortella, G. Numerical simulation of glass doors fogging and defogging in refrigerated display cabinets. Appl. Therm. Eng. 2006, 26, 1927–1934, ISSN 1359-4311. [Google Scholar] [CrossRef]
- Panfilov, I.; Beskopylny, A.N.; Meskhi, B. Improving the Fuel Economy and Energy Efficiency of Train Cab Climate Systems, Considering Air Recirculation Modes. Energies 2024, 17, 2224. [Google Scholar] [CrossRef]
- JSC Transmashholding. Main-Line Freight Diesel Locomotive 2TE25K: [Electronic Resource]. Available online: https://tmholding.ru/products/gruzovye/teplovozy-2te25km-3te25k2m/ (accessed on 3 March 2025).
- Pope, S. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000; 771p. [Google Scholar]
- Landau, L.D.; Lifshits, E.M. Course of Theoretical Physics; Hydrodynamics. M.: Nauka, Mexico, 1988; Volume 6, 736p. [Google Scholar]
- Kuzovlev, V.A. Technical Thermodynamics and Fundamentals of Heat Transfer, 2nd ed.; Vysshaya Shkola: Moscow, Russia, 1983; 335p. [Google Scholar]
- Kutateladze, S.S. Heat Transfer and Hydrodynamic Resistance: Reference Manual; Energoatomizdat: Moscow, Russia, 1990; 367p. [Google Scholar]
- Yang, Y.; Huang, Y.; Zhao, J. Optimization of the automotive air conditioning strategy based on the study of dewing phenomenon and defogging progress. Appl. Therm. Eng. 2020, 169, 114932, ISSN 1359-4311. [Google Scholar] [CrossRef]
- METEOSCOP-M Meter of Microclimate Parameters. [Electronic Resource]. Available online: https://ntm.ru/products/70/7774 (accessed on 25 July 2025).







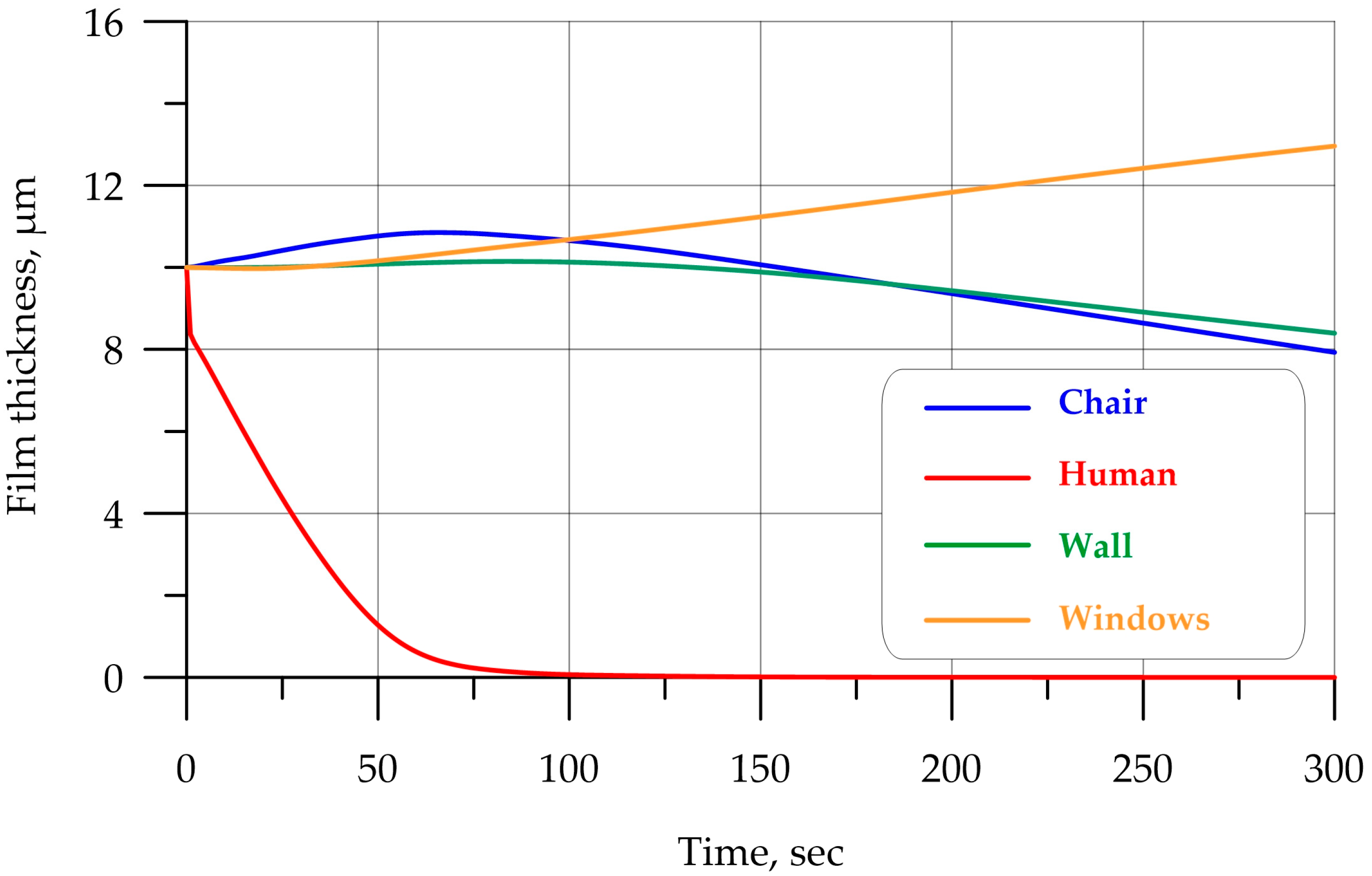
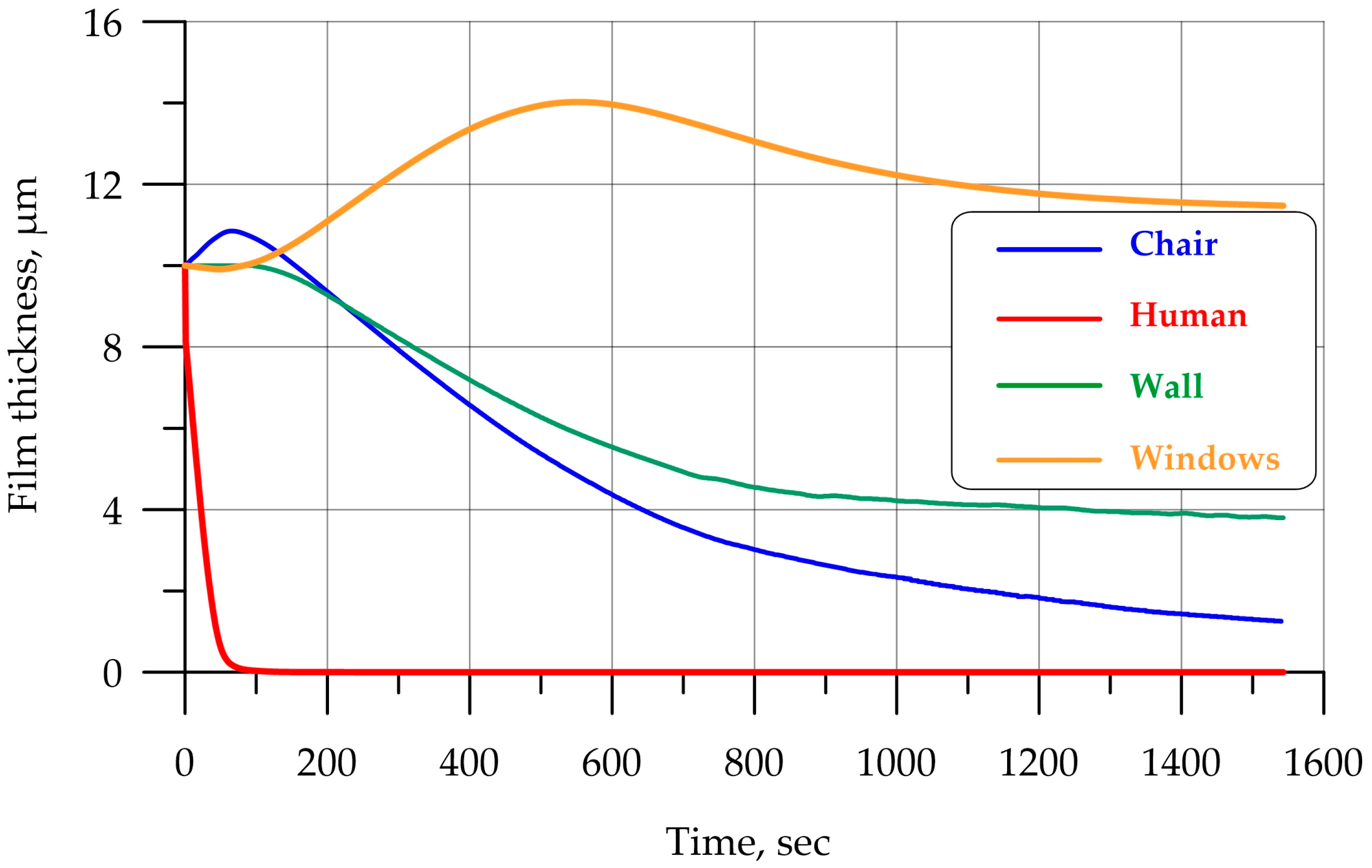
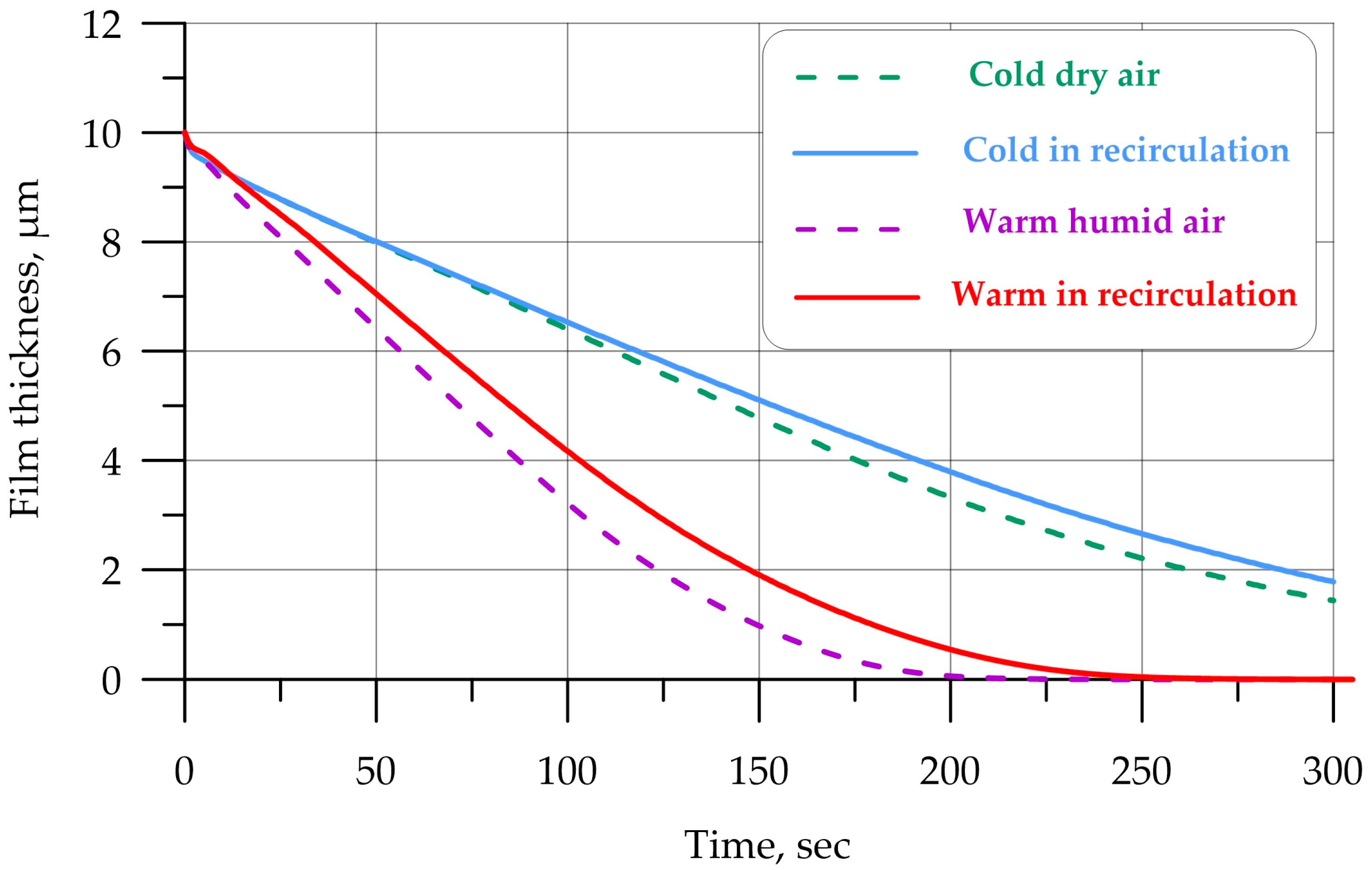
| Num | Title | Value for Tetragonal Mesh | Value for Polygonal Mesh |
|---|---|---|---|
| Grid Settings | |||
| 1 | Number of cells | 523,094 | 246,855 |
| 2 | Number of nodes | 151,094 | 688,375 |
| 3 | Number of wall layers | 6 | 6 |
| 4 | Minimum cell area, m2 | 4.1 × 10−8 | 4.3 × 10−8 |
| 5 | Maximum cell area, m2 | 6.1 × 10−3 | 6.1 × 10−3 |
| 6 | Mesh orthogonality | 7.73 × 10−2 | 2.21 × 10−2 |
| Num | Title | Value 1 | Value 2 (Adopted for Calculation) | Value 3 |
|---|---|---|---|---|
| 1 | Number of cells | 197,728 | 246,855 | 353,841 |
| 2 | Number of nodes | 537,035 | 688,375 | 1,052,085 |
| 3 | Number of wall layers | 6 | 6 | 6 |
| 4 | Minimum cell area, m2 | 3.3 × 10−8 | 4.3 × 10−8 | 3.3 × 10−8 |
| 5 | Maximum cell area, m2 | 1.3 × 10−2 | 6.1 × 10−3 | 2.7 × 10−3 |
| 6 | Mesh orthogonality | 7.7 × 10−2 | 2.2 × 10−2 | 2.4 × 10−2 |
| 7 | Temperature at point 1 | 1 | 1.015 (+1.5%) | 1.022 (+2.2%) |
| 8 | Temperature at point 2 | 1 | 1.024 (+2.4%) | 1.033 (+3.3%) |
| 9 | Temperature at point 3 | 1 | 1.016 (+1.6%) | 1.021 (+2.1%) |
| 10 | Temperature at point 4 | 1 | 1.026 (+2.6%) | 1.025 (+2.5%) |
| 11 | Temperature at point 5 | 1 | 1.017 (+1.7%) | 1.027 (+2.7%) |
| Num | Title | Value |
|---|---|---|
| The numerical method setting | ||
| 1 | Variable residual values | 1 × 10−4 |
| The numerical method setting | ||
| 2 | Solver | Pressure-based |
| 3 | Solution methods | Coupled |
| 4 | Turbulence model | k-ε |
| 5 | Diffusion model | Species transport |
| Euler Film Model | ||
| 6 | Equations | Solve momentum, energy, phase coupling |
| 7 | Maximum thickness, m | 0.005 |
| 8 | Phase change | Diffusion-balance |
| Material of Wall Layers | Coefficient of Thermal Conductivity, | Thickness of Each Layer, m |
|---|---|---|
| Cabin wall | ||
| Carbon steel | 58.1 | 0.002 |
| Bituminous mastic anti-noise layer | 0.272 | 0.004 |
| Foamed polyethylene | 0.0321 | 0.03 |
| Aluminum | 202.2 | 0.003 |
| Wall | 0.039 | |
| Windows | ||
| Glass | 1.1 | 0.012 |
| Num | Title | Value of Summer Mode | Value of Cool Mode |
|---|---|---|---|
| 1 | Flow temperature in inlet deflectors, °C | 16 | 30 |
| 2 | Flow velocity in the inlet deflectors, m/s | 0.41 | 0.41 |
| 3 | Air temperature in the cabin|t=0, °C | 40 | 0 |
| 4 | External air temperature, °C | 45 | 0 |
| 5 | Temperature on the driver’s body, °C | 30 | 30 |
| 6 | Mass fraction of water vapor in air conditioner air | 0.006 | 0.006 |
| 7 | Relative humidity of water vapor in air conditioner air, % | 51.1 | 24.2 |
| 8 | Mass fraction of water vapor in the cabin |t=0 | 0.006 | 0.0035 |
| 9 | Relative humidity in the cabin |t=0, % | 13.2 | 93.1 |
| 10 | Heat transfer coefficient for a multilayer wall, | 1.04 | 1.04 |
| 11 | Heat transfer coefficient for a multilayer wall of the windows, | 45.34 | 45.34 |
| 12 | Heat flux for chair surface, | 0 | 0 |
| 13 | Mixture parameters | ||
| 14 | Density model | Ideal gas | |
| 15 | Model of specific heat | Mixing law | |
| 16 | Model of thermal conductivity | Mass weighted mixing law | |
| 17 | Model of viscosity | Mass weighted mixing law | |
| 18 | Model of diffusivity | Kinetic theory | |
| 19 | Film condensation model | Euler Film Model | |
| 20 | Initial condensate film thickness for all surfaces |t=0, м | 1 × 10−5 | 1 × 10−5 |
| 21 | Initial temperature film thickness for all surfaces |t=0, °C | 40 | 40 |
| 22 | Coeff. mass diffusion H2O, [m2/s] | 2.37 × 10−5 | 2.35 × 10−5 |
| 23 | Coeff. mass diffusion Air, [m2/s] | 2.32 × 10−5 | 2.31 × 10−5 |
| 24 | Coeff. thermo diffusion H2O, [kg/(m s)] | −1.83 × 10−8 | −1.97 × 10−8 |
| 25 | Coeff. thermo diffusion Air, [kg/(m s)] | 1.68 × 10−8 | 1.87 × 10−8 |
| Num | Title | Numerical Without Condensation | Numerical with Condensation | Experiment | Error without Condensation, % | Error with Condensation, % | Allowable Values According to [10] |
|---|---|---|---|---|---|---|---|
| Temperature | |||||||
| 1 | Temperature in 0.15 m, °C | 21.9 | 23.8 | - | - | - | - |
| 2 | Temperature in 1.5 m, °C | 30.3 | 32.8 | - | - | - | - |
| 3 | Average temperature, °C | 26.1 | 28.3 | 31.8 | 18 | 11 | 20–28 |
| Relative humidity | |||||||
| 1 | Relative humidity in 0.15 m, % | 47.6 | 64.3 | ||||
| 2 | Relative humidity in 1.5 m, % | 70.2 | 75.8 | ||||
| 3 | Average Relative humidity, % | 58.9 | 70.1 | 83.1 | 29 | 16 | 15–75 |
| Num | Title | Value 1 (Cool Dry Air) | Value 2 (Hot Humid Air) |
|---|---|---|---|
| 1 | Flow temperature in inlet deflectors, °C | 16 | 45 |
| 2 | Flow velocity in the inlet deflectors, m/s | 0.41 | 0.41 |
| 3 | Air temperature in the cabin|t=0, °C | 25 | 25 |
| 4 | External air temperature, °C | 25 | 25 |
| 5 | Mass fraction of water vapor in air conditioner air | 0.0001 | 0.01 |
| 6 | Relative humidity of water vapor in air conditioner air, % | 1.1 | 16.99 |
| 7 | Mass fraction of water vapor in the cabin |t=0 | 0.006 | 0.006 |
| 8 | Relative humidity in the cabin |t=0, % | 30.7 | 30.7 |
| Euler Film Model | |||
| 9 | Initial condensate film thickness for all surfaces |t=0, м | 1 × 10−5 | 1 × 10−5 |
| 10 | Initial temperature of condensate film for all surfaces |t=0, °C | 25 | 25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panfilov, I.; Beskopylny, A.N.; Meskhi, B.; Podust, S.F. Numerical Study of Gas Dynamics and Condensate Removal in Energy-Efficient Recirculation Modes in Train Cabins. Fluids 2025, 10, 197. https://doi.org/10.3390/fluids10080197
Panfilov I, Beskopylny AN, Meskhi B, Podust SF. Numerical Study of Gas Dynamics and Condensate Removal in Energy-Efficient Recirculation Modes in Train Cabins. Fluids. 2025; 10(8):197. https://doi.org/10.3390/fluids10080197
Chicago/Turabian StylePanfilov, Ivan, Alexey N. Beskopylny, Besarion Meskhi, and Sergei F. Podust. 2025. "Numerical Study of Gas Dynamics and Condensate Removal in Energy-Efficient Recirculation Modes in Train Cabins" Fluids 10, no. 8: 197. https://doi.org/10.3390/fluids10080197
APA StylePanfilov, I., Beskopylny, A. N., Meskhi, B., & Podust, S. F. (2025). Numerical Study of Gas Dynamics and Condensate Removal in Energy-Efficient Recirculation Modes in Train Cabins. Fluids, 10(8), 197. https://doi.org/10.3390/fluids10080197








