Computational Modeling of Droplet-Based Printing Using Multiphase Volume of Fluid (VOF) Method: Prediction of Flow, Spread Behavior, and Printability
Abstract
1. Introduction
- Applications:
2. Numerical Method
2.1. Governing Equations
2.2. Computational Domain
3. Results
3.1. Flow and Spreading Behavior Method Validation: Impact of a Water Droplet on a Hydrophilic Surface
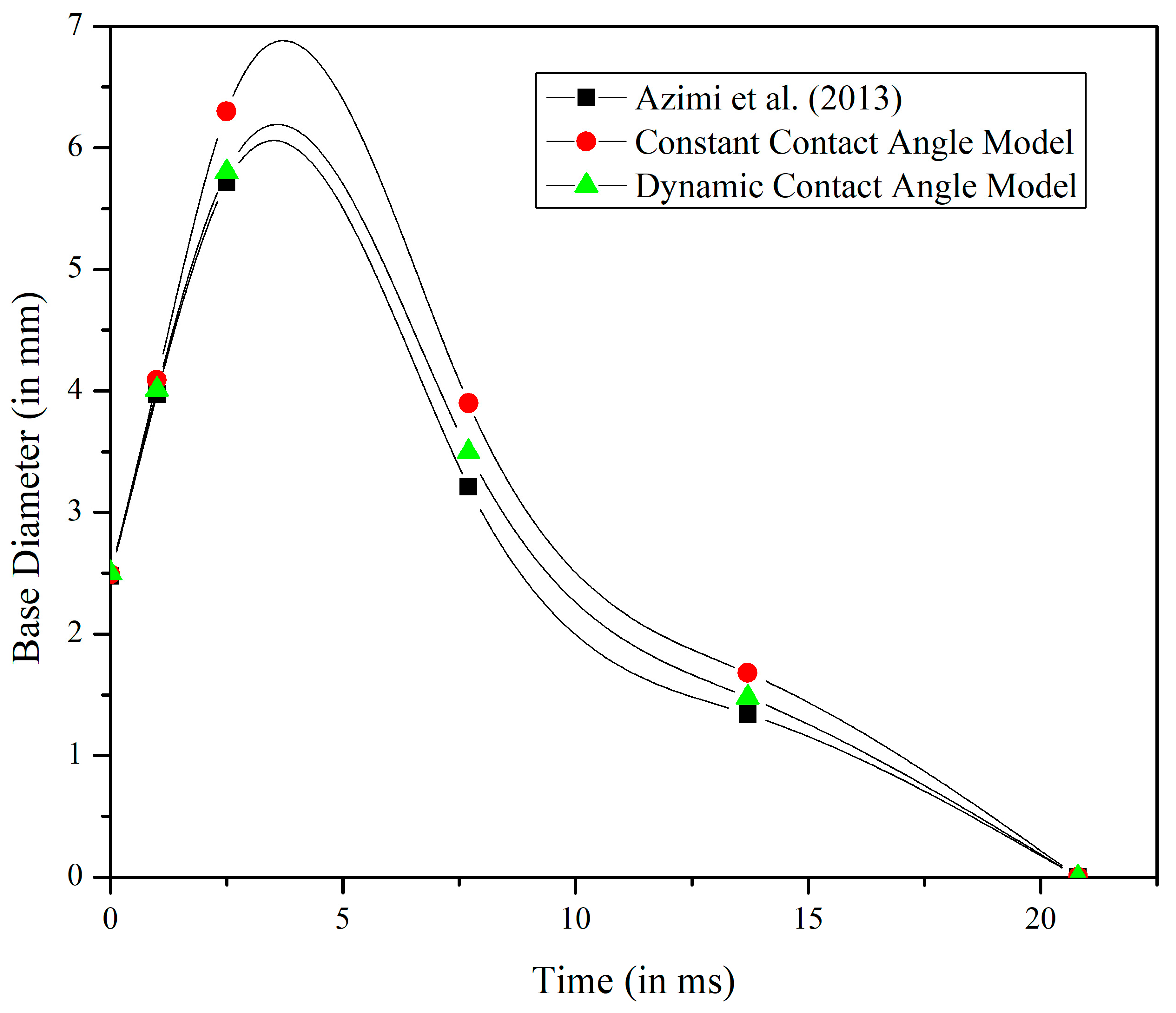
3.1.1. Method Validation: Impact of a Water Droplet on a Hydrophilic Surface
3.1.2. Method Validation: Impact of a Water Droplet on a Hydrophobic Surface
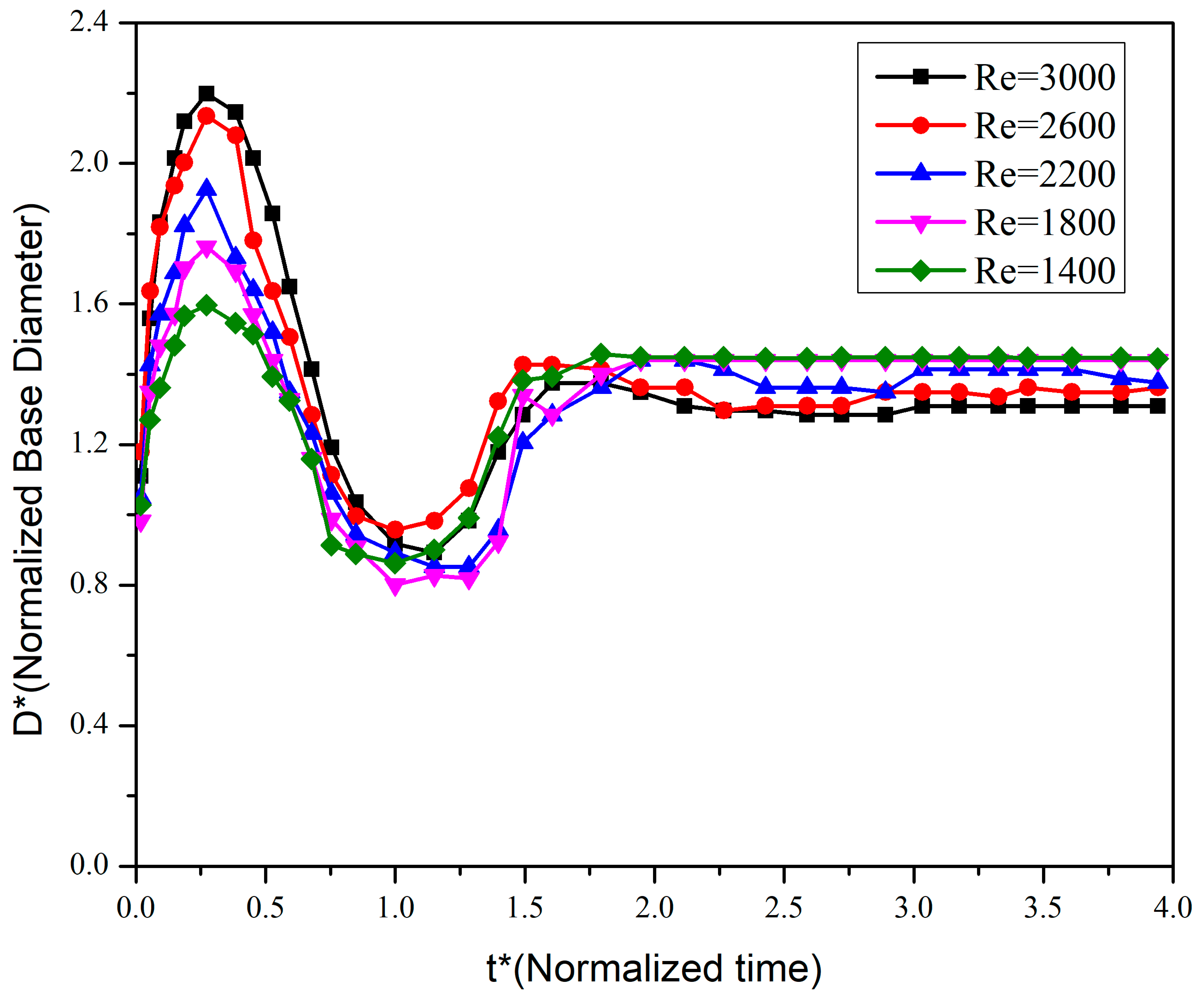
3.2. Effect of Non-Dimensional Reynolds (Re), Weber (We), and Ohnesorge (Oh) Numbers
3.3. Fluid–Fluid Interaction (Droplet Coalescence) and Prediction of Final Print Resolution in Droplet-Based Printing
3.3.1. Flow and Spreading Behavior of Two Coalescing Droplets
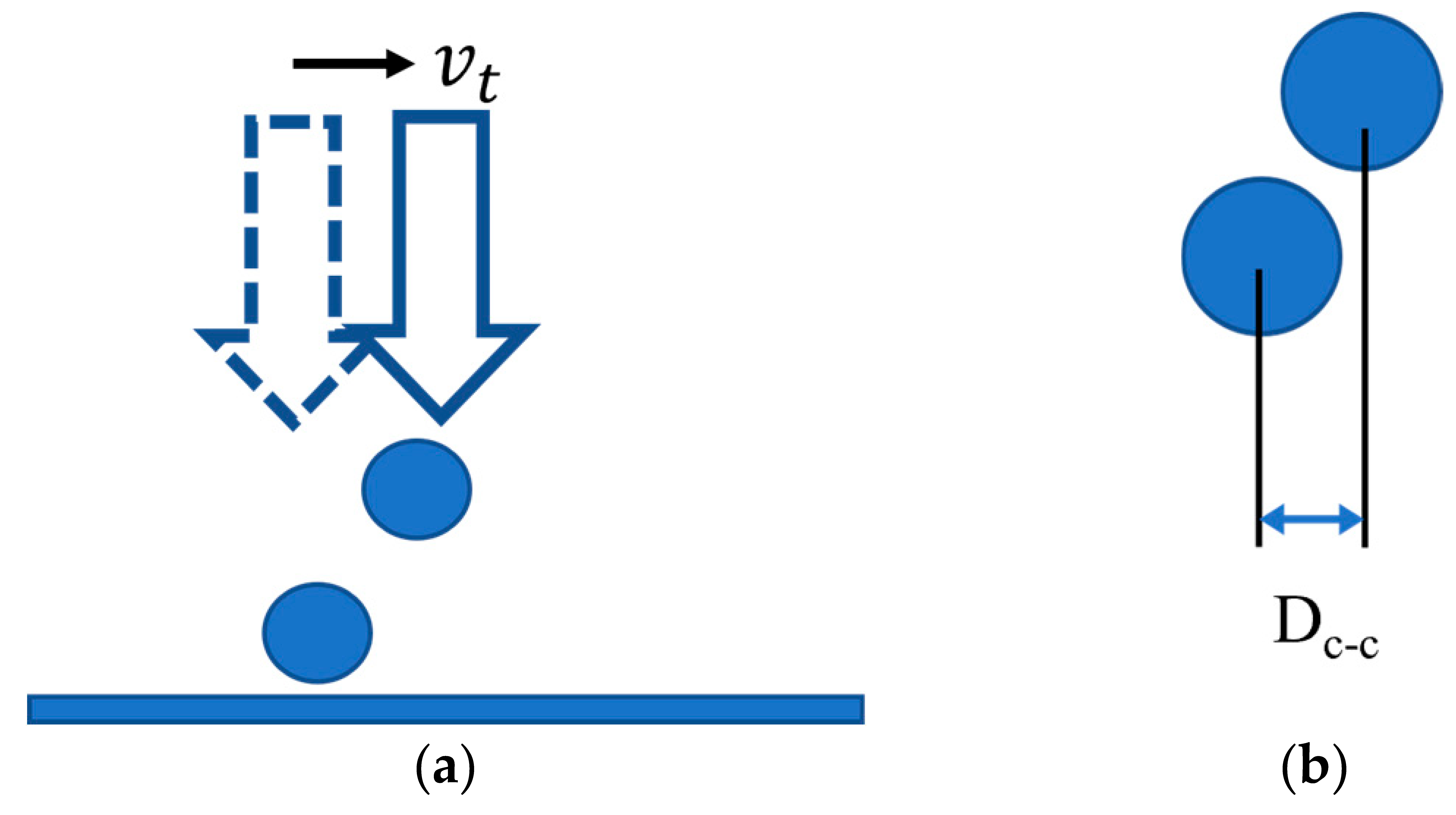
3.3.2. Prediction of the Flow Dynamics with Relevance to Droplet-Based Printing
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| VOF | Volume of Fluid |
| CFD | Computational Fluid Dynamics |
| CFL | Courant–Friedrichs–Lewy |
| PISO | Pressure Implicit with Splitting of Operators |
| SIMPLE | Semi-Implicit Method for Pressure-Linked Equations |
| MULES | Multidimensional Universal Limiter for Explicit Solution |
| Re | Reynolds number |
| We | Weber number |
| Oh | Ohnesorge number |
Appendix A. Grid Independence Study Results
| Mesh Resolution | Cells | Computational Time (Approx Hours) | Key Parameter (Droplet Spread Diameter in mm) |
|---|---|---|---|
| Coarse | 50 × 50 × 35 | 1.0 | 6.532 |
| Medium | 80 × 80 × 45 | 1.5 | 6.010 |
| Fine | 100 × 100 × 60 | 2.0 | 5.791 |
| Finer | 125 × 125 × 75 | 3.5 | 5.767 |
| Finest | 150 × 150 × 90 | 5.0 | 5.720 |
References
- Yarin, A.L. DROP IMPACT DYNAMICS: Splashing, Spreading, Receding, Bouncing. Annu. Rev. Fluid Mech. 2006, 38, 159–192. [Google Scholar] [CrossRef]
- Elliot, T.A.; Ford, D.M. Dynamic contact angles. J. Chem. Soc. 1972, 68, 1814–1823. [Google Scholar] [CrossRef]
- Fukai, J.; Shiiba, Y.; Yamamoto, T.; Miyatake, O.; Poulikakos, D.; Megaridis, C.M.; Zhao, Z. Wetting effects on the spreading of a liquid droplet colliding with a flat surface: Experiment and modeling. Phys. Fluids 1995, 7, 236–247. [Google Scholar] [CrossRef]
- Asai, A.; Shioya, M.; Hirasawa, S.; Okazaki, T. Impact of an Ink Drop on Paper. J. Imaging Sci. Technol. 1993, 37, 205. [Google Scholar]
- Bayer, I.S.; Megaridis, C.M. Contact angle dynamics in droplets impacting on flat surfaces with different wetting characteristics. J. Fluid Mech. 2006, 558, 415–449. [Google Scholar] [CrossRef]
- Scheller, B.; Bousfield, W. Newtonian Drop Impact with a Solid Surface. AIChE J. 1995, 41, 1357–1367. [Google Scholar] [CrossRef]
- Roisman, I. Inertia Dominated Drop Collisions. II. An Analytical Solution of the Navier–Stokes Equations for a Spreading Viscous Film. Phys. Fluids 2009, 21, 052104. [Google Scholar] [CrossRef]
- Toivakka, M. Numerical Investigation of Droplet Impact Spreading in Spray Coating of Paper. In Proceedings of the 2003 TAPPI 8th Advanced Coating Fundamentals Symposium, Chicago, IL, USA, 8–10 May 2003. [Google Scholar]
- Pasandideh-Fard, M.; Qiao, Y.M.; Chandra, S.; Mostaghimi, J. Capillary Effects During Droplet Impact on a Solid Surface. Phys. Fluids 1996, 8, 650–659. [Google Scholar] [CrossRef]
- Feng, J.Q. A Computational Study of High-Speed Microdroplet Impact onto a Smooth Solid Surface. J. Appl. Fluid Mech. 2017, 10, 243–256. [Google Scholar] [CrossRef]
- Adeniyi, A.A.; Morvan, H.P.; Simmons, K.A. A coupled Euler-Lagrange CFD modeling of droplets-to-film. Aeronaut. J. 2017, 121, 1897–1918. [Google Scholar] [CrossRef]
- Yokoi, K.; Vadillo, D.; Hinch, J.; Hutchings, I. Numerical Studies of the Influence of the Dynamic Contact Angle on a Droplet Impacting on a Dry Surface. Phys. Fluids 2009, 21, 072102. [Google Scholar] [CrossRef]
- Gujjula, S. Numerical Investigation of Droplet Spread: Effect of Contact Angle Models. Master’s Thesis, University of Cincinnati, Cincinnati, OH, USA, 2015. [Google Scholar]
- Wang, L.S.; Krull, B.; Lucas, D.; Meller, R.; Schlegel, F.; Tekavcic, M.; Xu, J.Y. Simulation of droplet entrainment in annular flow with a morphology adaptive multifield two-fluid model. Phys. Fluids 2023, 35, 103312. [Google Scholar] [CrossRef]
- Shah, R.G.; Mohan, R.V. Multiphase Modeling of Droplet-Based 3D Printing: Predicting Printability, Resolution and Shape Fidelity in Additive Manufacturing Processes. In Proceedings of the ASME 2023 International Mechanical Engineering Congress and Exposition, New Orleans, LA, USA, 29 October–2 November 2023. [Google Scholar]
- Vontas, K. Enhanced VOF-based CFD simulations of droplet impact. Bachelor’s Thesis, Piraeus University of Applied Sciences, University of Brighton, Brighton, UK, 2016. [Google Scholar]
- Teng, T.; Joralmon, D.; Anyigbo, T.; Li, X. Acoustic Levitation-Assisted Contactless Printing of Microdroplets for Biomedical Applications. J. Manuf. Sci. Eng. 2024, 146, 011002. [Google Scholar] [CrossRef]
- Wu, D.; Xu, C. Predictive Modeling of Droplet Formation Processes in Inkjet-Based Bioprinting. Trans. ASME. 2018, 140, 101007. [Google Scholar] [CrossRef]
- Aladese, A.; Jeong, H. Recent Developments in 3D Printing of Droplet-Based Microfluidics. BioChip J. 2021, 15, 313–333. [Google Scholar] [CrossRef]
- Britel, A.; Tomagra, G.; Apra, P.; Varzi, V.; Sturari, S.; Amine, N.; Olivero, P.; Picollo, F. 3D printing in microfluidics: Experimental optimization of droplet size and generation time through flow focusing, phase, and geometry variation. RSC Adv. 2024, 14, 7770–7778. [Google Scholar] [CrossRef]
- Jiang, J.; Chen, X.; Mei, Z.; Chen, H.; Chen, J.; Wang, X.; Li, S.; Zhang, R.; Zheng, G.; Li, W. Review of droplet printing technologies for flexible electronic devices: Materials, control, and applications. Micromachines 2024, 15, 333. [Google Scholar] [CrossRef]
- Abdolmaleki, H.; Kidmose, P.; Agarwala, S. Droplet-based techniques for printing of functional inks for flexible physical sensors. Adv. Mater. 2021, 33, 2006792. [Google Scholar] [CrossRef]
- Zhang, H.; Cui, L.; Lee, P.-H.; Kim, Y.; Moon, S.K.; Choi, J.P. Data-Driven autonomous printing process optimization and real-time abnormality identification in aerosol jet-deposited droplet morphology. Virtual Phys. Prototyp. 2024, 19, e2429530. [Google Scholar] [CrossRef]
- Tofan, T.; Borodinas, S.; Kačianauskas, R.; Jasevičius, R. Modeling 3D droplet movement using a drop-on-demand inkjet printhead model. Processes 2022, 10, 1467. [Google Scholar] [CrossRef]
- Jia, Y.; Cheng, X.; Song, W.; Zhou, Y.; Zhao, H. A droplet state prediction method for inkjet printing under small sample conditions based on the two-stage TrAdaBoost.R2 algorithm. AIP Adv. 2025, 15, 015120. [Google Scholar] [CrossRef]
- The OpenFOAM Foundation. OpenFOAM v2021 User Guide. Available online: https://cfd.direct/openfoam/user-guide (accessed on 10 January 2023).
- Fujimoto, H.; Shiotani, Y.; Tong, A.Y.; Hama, T.; Takuda, H. Three-Dimensional Numerical Analysis of the Deformation Behavior of Droplets Impinging onto a Solid Substrate. Int. J. Multiph. Flow 2007, 33, 317–332. [Google Scholar] [CrossRef]
- Kim, H.-Y.; Chun, J.-H. The recoiling of liquid droplets upon collision with solid surfaces. Phys. Fluids 2001, 13, 643–659. [Google Scholar] [CrossRef]
- Azimi, G.; Dhiman, R.; Kwon, H.-M.; Paxson, A.T.; Varanasi, K.K. Hydrophobicity of rare-earth oxide ceramics. Nat. Mater. 2013, 12, 315–320. [Google Scholar] [CrossRef] [PubMed]
- Hsu, A.S.; Roy, A.; Leal, L.G. Drop-size effects on coalescence of two equal-sized drops in a head-on collision. J. Rheol. 2008, 52, 1291–1310. [Google Scholar] [CrossRef]
- Acevedo-Malavé, A.; García-Sucre, M. Coalescence collision of liquid drops I: Off-center collisions of equal-size drops. AIP Adv. 2011, 1, 032117. [Google Scholar] [CrossRef]
- Tang, C.; Zhang, P.; Law, C.K. Bouncing, coalescence, and separation in head-on collision of unequal-size droplets. Phys. Fluids 2012, 24, 022101. [Google Scholar] [CrossRef]
- Josserand, C.; Thoroddsen, S.T. Drop impact on a solid surface. Annu. Rev. Fluid Mech. 2016, 48, 365–391. [Google Scholar] [CrossRef]
- Antonini, C.; Amirfazli, A.; Marengo, M. Drop impact and wettability: From hydrophilic to superhydrophobic surfaces. Phys. Fluids 2012, 24, 102104. [Google Scholar] [CrossRef]
- Rein, M. The transitional regime between coalescing and splashing drops. J. Fluid Mech. 1996, 306, 145–165. [Google Scholar] [CrossRef]
- Thoroddsen, S.T.; Etoh, T.G.; Takehara, K. Air entrapment under an impacting drop. J. Fluid Mech. 2003, 478, 125–134. [Google Scholar] [CrossRef]
- Thoroddsen, S.T.; Takehara, K. The coalescence cascade of a drop. Phys. Fluids 2000, 12, 1265–1267. [Google Scholar] [CrossRef]
- Mohamed-Kassim, Z.; Longmire, E.K. Drop coalescence through a liquid/liquid interface. Phys. Fluids 2004, 16, 2170–2181. [Google Scholar] [CrossRef]
- Chen, Y.; Shen, C.; Peterson, G.P. Hydrodynamics and morphologies of droplet coalescence. Ind. Eng. Chem. Res. 2015, 54, 9257–9262. [Google Scholar] [CrossRef]
- Shen, C.; Chen, Y.; Yu, C.; Liu, X. Numerical study on the liquid-liquid interface evolution during droplet coalescence. Microgravity Sci. Technol. 2020, 32, 737–748. [Google Scholar] [CrossRef]
- Zimmermann, P.; Mawbey, A.; Zeiner, T. Calculation of droplet coalescence in binary liquid-liquid systems: An incompressible Cahn–Hilliard/Navier–Stokes approach using the non-random two-liquid model. J. Chem. Eng. 2020, 65, 1083–1094. [Google Scholar] [CrossRef]
- Baroudi, L.; Kawaji, M.; Lee, T. Effects of initial conditions on the simulation of inertial coalescence of two drops. Comput. Math. Appl. 2014, 67, 282–289. [Google Scholar] [CrossRef]
- Lim, S.J.; Choi, M.C.; Weon, B.M.; Gim, B. Lattice Boltzmann simulations for water coalescence. Appl. Phys. Lett. 2017, 111, 101602. [Google Scholar] [CrossRef]
- Gross, M.; Steinbach, I.; Raabe, D.; Varnik, F. Viscous coalescence of droplets: A lattice Boltzmann study. Phys. Fluids. 2013, 25, 052101. [Google Scholar] [CrossRef]
- Perumanath, S.; Borg, M.K.; Chubynsky, M.V.; Sprittles, J.E.; Reese, J.M. Droplet coalescence is initiated by thermal motion. Phys. Rev. Lett. 2019, 122, 104501. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, R.; Mohan, R.V. Computational Modeling of Droplet-Based Printing Using Multiphase Volume of Fluid (VOF) Method: Prediction of Flow, Spread Behavior, and Printability. Fluids 2025, 10, 123. https://doi.org/10.3390/fluids10050123
Shah R, Mohan RV. Computational Modeling of Droplet-Based Printing Using Multiphase Volume of Fluid (VOF) Method: Prediction of Flow, Spread Behavior, and Printability. Fluids. 2025; 10(5):123. https://doi.org/10.3390/fluids10050123
Chicago/Turabian StyleShah, Rauf, and Ram V. Mohan. 2025. "Computational Modeling of Droplet-Based Printing Using Multiphase Volume of Fluid (VOF) Method: Prediction of Flow, Spread Behavior, and Printability" Fluids 10, no. 5: 123. https://doi.org/10.3390/fluids10050123
APA StyleShah, R., & Mohan, R. V. (2025). Computational Modeling of Droplet-Based Printing Using Multiphase Volume of Fluid (VOF) Method: Prediction of Flow, Spread Behavior, and Printability. Fluids, 10(5), 123. https://doi.org/10.3390/fluids10050123








