Abstract
In this paper, a theory for constructing quasi-neutral density variables γ directly in thermodynamic space is formulated, which is based on minimising the absolute value of a purely thermodynamic quantity . Physically, has a dual dynamic/thermodynamic interpretation as the quantity controlling the energy cost of adiabatic and isohaline parcel exchanges on material surfaces, as well as the dependence of in-situ density on spiciness, in a description of water masses based on γ, spiciness and pressure. Mathematically, minimising in thermodynamic space is showed to be equivalent to maximising neutrality in physical space. The physics of epineutral dispersion is also reviewed and discussed. It is argued, in particular, that epineutral dispersion is best understood as the aggregate effect of many individual non-neutral stirring events (being understood here as adiabatic and isohaline events with non-zero buoyancy), so that it is only the net displacement aggregated over many events that is approximately neutral. This new view resolves an apparent paradox between the focus in neutral density theory on zero-buoyancy motions and the overwhelming evidence that lateral dispersion in the ocean is primarily caused by non-zero buoyancy processes such as tides, residual currents and sheared internal waves. The efficiency by which a physical process contributes to lateral dispersion can be characterised by its energy signature, with those processes releasing available potential energy (negative energy cost) being more efficient than purely neutral processes with zero energy cost. The latter mechanism occurs in the wedge of instability, and its source of energy is the coupling between baroclinicity, thermobaricity, and density compensated temperature/salinity anomalies. Such a mechanism, which can only exist in a salty ocean, is speculated to be important for dissipating spiciness anomalies and neutral helicity. The paper also discusses potential conceptual difficulties with the use of neutral rotated diffusion tensors in numerical ocean models, as well as with the construction of neutral density variables in physical space. It also emphasises the irreducible character of thermobaric forces in the ocean. These are argued to be the cause for adiabatic thermobaric dianeutral dispersion, and to forbid the existence of density surfaces along which fluid parcels can be exchanged without experiencing buoyancy forces, in contrast to what is assumed in the theory of neutral surfaces.
1. Introduction
The concepts of neutral surface and neutral density popularised by [1,2]—following earlier attempts by [3,4]—have been influential in shaping up thinking about the preferred directions for mixing and stirring in the ocean, thus extending Montgomery’s [5] ideas for tracking ocean water masses. So far, the main theoretical background for discussing these issues has revolved around the neutral tangent plane equation
where is the so-called neutral vector
and an adiabatic and isohaline displacement, with and the thermal expansion and haline contraction coefficients respectively (defined relative to potential temperature θ and salinity S), with the reference Boussinesq density, is the squared speed of sound, ρ is in-situ density, p is pressure, and g is the acceleration of gravity. Here, the local neutral vector is defined so that its vertical component is equal to the squared buoyancy frequency , a key measure of ocean stability,
where is the normal unit vector pointing in the upward vertical direction.
Because (1) plays a central role in the theory of density variables in the ocean, as well as in current formulations of ocean mixing parameterisations, it appears essential to understand its physical justification and possible limitations. So far, however, how to obtain (1) rigorously and deductively from the equations of motion has remained elusive. In fact, our state of ignorance about (1) is so large that no consensus yet exists about whether (1) is best interpreted as a dynamical concept, and hence connected to the momentum equations, or as a thermodynamic concept linked to the equation of state for density and tracer equations for potential temperature and salinity.
In the neutral density literature, (1) is usually presented as being linked to the momentum equations and hence as a dynamical concept. Indeed, such studies as [1,6] usually interpret (1) as locally defining a surface along which fluid parcels can be exchanged without experiencing restoring buoyancy forces b, defined as
where and , while and denote the densities of the fluid parcel and that of the environment respectively, while , and denote the slowly-varying (relative to parcels’ displacements ) background salinity, potential temperature and pressure fields.
The thermodynamic foundation of (1), on the other hand, takes as its starting point the density equation
where denotes diabatic modifcations of density by heat and salt sources/sinks, and consists in making the approximation and , while also neglecting . After simplifying by , this yields
In the thermodynamic approach, Equation (1) is most commonly interpreted as a statement that fluid parcels conserve their locally referenced potential density (LRPD), where LRPD is envisioned as a density variable whose value is everywhere equal to that of in-situ density (which is non-material and strongly pressure dependent), but which for all practical purposes related to the study of stirring and mixing can be regarded locally as behaving quasi-materially. Regardless of how it is justified, the construction of and of the neutral tangent plane Equation (1) entail a number of unclear approximations and justifications. Among these are the use of the single-parcel argument for defining buoyancy whose validity is not necessarily obvious, e.g., [7,8], or of the seemingly impossible concept of LRPD.
Perhaps one of the most important conceptual difficulty in the dynamical interpretation of (1), however, is how to justify the focus on zero buoyancy motions as having more importance than non-zero buoyancy motions in the study of lateral dispersion in the ocean? Indeed, as far as the adiabatic form of the density Equation (5) is concerned, the buoyancy of fluid parcels experiencing adiabatic and isohaline lateral displacements is—without approximation—given by
and therefore differs from zero more often than not. Moreover, a survey of the literature reveals that the key physical processes responsible for lateral dispersion in the ocean are all non-zero buoyancy processes; indeed, these include tidal and residual currents, as well as internal waves in presence of shear, e.g., [9,10,11]. If so, in order to accept (1) as a meaningful model of epineutral dispersion, one has to interpret it as some averaged form of the adiabatic density equation. However, because traditional Eulerian averages necessarily give rise to eddy correlation terms, which in the present case would lead to an equation of the form , (1) can only makes sense if interpreted in terms of a Lagrangian or quasi-Lagrangian averaging process, such as those considered in Generalised Lagrangian Mean (GLM) theory, e.g., [12,13,14] or the thickness-weighted average (TWA) formalism, e.g., [15,16], which are the only known form of averaging capable of not giving rise to eddy-correlation terms. (Alternatively, one could also directly regard in (1) as a Lagrangian displacement, but doing so destroys the interpretation of (1) in terms of buoyancy—as in (4) must necessarily be an Eulerian displacement—while requiring the definition of a suitable Lagrangian density variable γ, raising precisely the same kind of issues as discussed below.)
This poses a dilemma, because from a practical viewpoint, the task of performing a Lagrangian or quasi-Lagrangian averaging of the equations of motion requires first identifying a suitable Lagrangian density coordinate γ with which to recast the equations of motion, e.g., [17] prior to averaging. How to identify γ, however, is precisely the issue that the theories of neutral density and quasi-neutral density variables aim to solve, which is still open. Moreover, it has always been assumed so far that the construction of γ should proceed from the knowledge of ; for instance, Jackett and McDougall’s [2] empirical neutral density is constructed so that is as parallel to as feasible, which requires that can be known and computed independently of . However, if one accepts that the vector appearing in (1) should be interpreted as a Lagrangian or quasi-Lagrangian averaged quantity, γ needs to be known before can be meaningfully defined and computed. In the neutral density literature, this conceptual difficulty is usually overlooked, as it is simply assumed that can be computed from existing climatologies of temperature and salinity without bothering about the kind of average underlying the construction of such climatologies (i.e., via a depth, isobaric, or isopycnal averaging of individual soundings). Another important conceptual difficulty that tends to be overlooked arises from the nonlinearities of the equation of state, as this complicates the definition of ‘mean’ quantities, since that . Although the latter issue is traditionally ignored in the neutral density literature as well as in ocean modelling, Brankart [18] recently demonstrated the potential importance of subgridscale variability of θ and S on the estimation of the ‘mean’ pressure gradient and momentum balance. The key implication of the above considerations is that the ‘mean’ neutral vector entering (1) cannot be known accurately in physical space, and that its computation is necessarily associated with an error bar arising both from the subgridscale variability of θ and S, as well as from error bars in the mean climatological values of S and θ themselves, the importance of which for the accurate determination of is unknown.
Since the construction of any quasi-neutral density variable in physical space from ‘mean’ climatological values of S and θ entails so many conceptual and practical difficulties, one may wonder why a purely thermodynamic density variable should not be able do the job (the job itself being arguably not entirely clear and not entirely well defined)? Although [2] chose to construct their density variable to be a function of both geographic and thermodynamic coordinates, the need for a density variable—usually regarded as a thermodynamic concept—to depend on spatial position is by no means obvious and difficult to justify from first-principles alone. Because the principles underlying the construction of purely thermodynamic quasi-neutral density variables have not been addressed so far in full generality, it is the issue that is tackled here. Based on the form of the instantaneous neutral vector (2), the most natural choices of purely thermodynamic density variables are either purely material functions or functions of in-situ density and pressure, of which De Szoeke and Springer’s [19] orthobaric density represents the most important example. McDougall and Jackett [20] have postulated that both orthobaric density and material functions are intrinsically limited in their ability to be globally neutral, which has represented so far the main justification for assuming that neutral density should depend on spatial position as well as on thermodynamic properties. It is generally agreed, however, that purely thermodynamic density variables can be constructed to be quite neutral if restricted to regional ocean basins, see [21,22,23], which provides sufficient motivation to elucidate how best to construct them.
From a conceptual viewpoint, the construction of purely thermodynamic quasi-neutral density variables is most naturally done in thermodynamic space and should not require any knowledge of neutral vectors. It therefore requires that one be able to define the concept of ‘neutrality’ in thermodynamic space, which so far has been exclusively defined in physical space. One of the main result of this paper is to demonstrate that the degree of neutrality of material density variables should be measured by the smallness of the absolute value of the Jacobian term
where is the specific volume. Interestingly, it appears possible to justify the introduction of from a dual dynamic/thermodynamic perspective, either via the consideration of the energy cost of parcel exchanges on an iso-γ surface (the dynamical perspective) or via the minimising the dependence of in-situ density on spiciness (the thermodynamic perspective), as explained in Section 5. In other words, the present paper argues that the equation should be regarded as the direct counterpart in thermodynamic space of the neutral tangent plane Equation (1) in physical space.
The main objectives of this paper are to expand upon the above considerations, and to examine some of their consequences for subgridscale ocean mixing parameterisations. The paper is organised as follows. Section 2 first provides a critical discussion of McDougall, et al.’s [6] arguments, which perhaps represent the most elaborate attempt at physically justifying the neutral tangent plane Equation (1) and the use of neutral rotated diffusion tensors in numerical ocean models. One of its main aim is to challenge the conventional interpretation of (1) in terms of momentum and to argue that (1) is in fact best justified in terms of the energetics of adiabatic and isohaline parcel exchanges along material surfaces. In contrast to Nycander [24], who unsuccessfully attempted to identify the ’right’ mixing surfaces from energetics considerations, our approach focuses on the energetics of adiabatic and isohaline stirring on an a priori given (and well-defined) material density surface. This is taken up in Section 3, which also introduces and analyses a new approach to the construction of a material density variable , based on minimising the absolute value of defined by (8). A key point of this paper is to emphasise that adiabatic and isohaline parcel exchanges can only be meaningfully defined on material surfaces of the form . Section 4 discusses the issues arising from attempting to describe adiabatic and isohaline parcel exchanges on non-material density surfaces of the form , and of the need to introduce a new term that is analogous to the so-called thermobaric dianeutral dispersion in the neutral density literature. Section 5 provides an alternative way to justify the energetics-based thermodynamic construction of γ by means of a first-principles density/spiciness/pressure representation of ocean water masses. Section 6 summarises the results and discusses some of their implications. Appendix B provides an alternative treatment of the energetics of adiabatic and isohaline exchanges in physical space, which in textbooks (see pages 280–282 of [25], pages 262–263 of [26], or [27]) is usually discussed in the context of baroclinic instability theory.
2. A Critical Assessment of McDougall et al. (2014)
2.1. Objectives of This Section
Although mixing and stirring are widely believed to take place preferentially in local neutral tangent planes, the first physical principles basis for such a belief remains unclear. Perhaps the most elaborate physical justification for it is that outlined in [6] (see also [20,28]). Interestingly, this justification is meant to provide a reductio ad absurdum that the directions of mixing in rotated diffusion tensors should be based on locally defined neutral tangent planes. Indirect proofs, however, while they have a well established place in abstract Mathematics, are generally regarded as being of lesser value than direct or constructive proofs in Physics, which by its very nature tends to deal with concrete objects. For this reason, it is therefore important to critically review McDougall, et al.’s [6] arguments.
Such critical analysis demonstrates that McDougall, et al.’s [6] arguments do not prove what the authors think it proves. In fact, it is argued that McDougall, et al.’s [6] arguments imply that epineutral dispersion is best understood as being made up of non-neutral stirring events, thus calling for a re-interpretation of neutral surfaces as notional equilibrium surfaces rather than stirring surfaces. It is also argued that the interpretation of the neutral tangent plane Equation (1) in terms of momentum cannot be correct, for lacking a dependence on the horizontal pressure gradient, and hence that (1) should be justified in terms of energetics instead. Finally, the idea that the use of the neutral directions in rotated diffusion tensors is required to avoid spurious diapycnal mixing is argued to be non self-evident, since it can be shown to imply that the effective diapycnal diffusivity for all conceivable material density variables must always exceed the value of turbulent diapycnal mixing used in such tensors.
2.2. Summary of McDougall et al. (2014)’s Arguments
As far as we understand them, McDougall, et al.’s [6] arguments rely on a thought experiment and a number of qualitative arguments whose connection to the real ocean is not necessarily obvious. In essence, these arguments appear to rely on:
- the definition of the buoyancy force acting on a single fluid parcel entering the dynamical interpretation of the neutral tangent plane Equation (1),
- the assumption that it is physically meaningful to parameterise isopycnal and diapycnal dispersion in terms of second-rank diffusion tensor as proposed by [29],
- the observation that lateral dispersion is about 7 orders of magnitude larger than quasi-vertical dispersion,
- the observed smallness of viscous dissipation in the ocean,
- the assumption that it is legitimate to regard the displacement entering the neutral tangent plane Equation (1) as an actual fluid parcel displacement.
McDougall, et al.’s [6] arguments appear to centre on the thought experiment illustrated in Figure 1 that is adapted from their Figure 1. In this thought experiment, a fluid parcel (assumed to characterise meso-scale dispersion) is assumed to be stirred away from its level of neutral buoyancy by means of an adiabatic and isohaline displacement. Presumably, this causes it to become positively or negatively buoyant relative to its environment. As a result, the parcel must feel a vertical restoring buoyancy force that will drive it back to its original neutral surface where its closest level of neutral buoyancy lies. To quote [6] (page 2165 below their Figure 1), the authors state: The vertical motion would either
- (i)
- involve no small-scale turbulent mixing, in which case the combined (two-step) process is adiabatic and isohaline and so is equivalent to epineutral dispersion (meaning along a neutral tangent plane), or
- (ii)
- the sinking and rising parcels would mix and entrain in a plumelike fashion with the ocean environment, and therefore experience irreversible mixing.
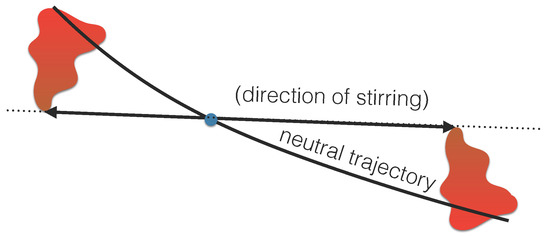
Figure 1.
Schematics adapted and modified from Figure 1 of [6], intended to be a: “Sketch of a central seawater parcel being moved adiabatically and without change in its salinity to either the right or the left of its original position in a direction that is not neutral. When the parcel is then released it feels a vertical buoyant force and begins to move vertically (upward on the left and downward on the right) toward its original “isopycnal”". The sentence (direction of stirring) was added to the original figure.
2.3. A Critical Discussion of McDougall et al. (2014)
Arguably, McDougall, et al.’s [6] arguments are too qualitative and imprecise to “prove” that rotated diffusion tensors should necessarily be based on neutral directions. Most importantly, McDougall, et al. [6] do not explain how their “proof” could be falsified, in Popper’s sense, e.g., [30], or tested.
On the other hand, the idea expressed by (i) that epineutral dispersion should be regarded as made up of non-neutral stirring events is interesting and potentially important for clarifying the nature of lateral dispersion: we find it surprising that McDougall, et al. [6] do not seem make much of it.
2.3.1. Expanding on Point (i) of McDougall et al. (2014)
In order to appreciate the potential importance of point (i) of [6] for clarifying the nature of epineutral dispersion, let us return to the details and interpretation of the thought experiment illustrated in Figure 1. To that end, we find useful to formalise this thought experiment as involving fundamentally two distinct processes, namely:
- First, a non-neutral stirring event associated with the displacement , which as it takes the parcel away from its equilibrium position, must entail a non-zero energy cost and some finite buoyancy force, implying ;
- second, a re-laminarisation process during which the fluid parcel seeks to find its closest level of neutral buoyancy, which is also associated with a displacement experiencing a nonzero buoyancy force and finite energy cost.
Because each of the displacements is individually non neutral, it is only the aggregate displacement that is approximately neutral and solution of . As mentioned in the introduction, it is important to emphasise that a non-zero buoyancy force does not imply diapycnal mixing—contrary to what seems to be often assumed (as point (ii) of [6] seems to imply)—just transience as attested by Equation (7).
Obviously, this two-event view of epineutral dispersion is an idealisation; in reality, epineutral dispersion presumably involves many more non-neutral events, so that we must assume that it is actually the net displacement aggregated over N non-neutral stirring events, with N large, that is approximately neutral and solution of . In this new view, the fact that epineutral dispersion is seemingly a zero-energy cost process obscures the fact that all of the stirring events that cause it may either release available potential energy or require an external source of energy, and be in all cases associated with a non-zero buoyancy . This is consistent with the fact that in the literature about lateral dispersion, lateral dispersion is usually associated with stirring processes with non-zero buoyancy, such as tides [9] or waves [10,11].
2.3.2. Are Neutral Trajectories Really Neutral?
Let us now turn to the issue of what determines the vertical equilibrium position of a fluid parcel being displaced laterally, which plays a key role in McDougall, et al.’s [6] arguments. So far, it has generally been speculated in the neutral density literature that represents the vertical force exerted on a fluid parcel experiencing an adiabatic and isohaline lateral displacement . If so, a fluid parcel displacement satisfying (1) must be in vertical equilibrium with its environment at all times, as assumed by [6]. What is odd with such an argument, however, it that the vertical force experienced by the fluid parcel should not depend on the horizontal pressure gradient. Indeed, the latter must a priori be involved in either opposing or promoting any lateral displacement. This can be established rigorously by considering the expression for the energy cost of a two-parcel exchange, a classical result of the literature, e.g., [25,26,27], also established in the next section for a fully compressible fluid,
where is the full pressure gradient. By invoking energy conservation (neglecting kinetic energy changes, a classical assumption in the present context), the change in potential energy must be balanced by minus twice the work done by the force acting on the fluid parcels times the displacement , that is , where the factor two comes from the system being composed of two parcels. This defines the force as
whose vertical component is easily verified to be given by
where we used the fact that and assumed the pressure to be hydrostatic in order to write ; also , and denote the horizontal components of , of the pressure gradient and of the total displacement respectively.
For purely vertical displacements , both classical and new expressions predict , in agreement with the standard derivation of the buoyancy frequency, but they differ for lateral displacements, with only correctly accounting for the dependence on the horizontal pressure gradient. As a result, the correct expression determining the vertical equilibrium position of a laterally displaced fluid parcels imposes that satisfy
rather than , in contrast to what has been postulated so far in the neutral density literature. We call the solutions of (12) “dynamical neutral paths” to distinguish them from McDougall “static neutral paths”. Figure 2 illustrates the relative positions of McDougall “static neutral surfaces”, “dynamic neutral surfaces”, and “isobaric surfaces”. This shows that dynamical neutral surfaces are actually located in the so-called “wedge of instability”, which plays a central role in the theory of baroclinic instability, e.g., [31,32]. By combining (12) with (9), it is easily showed that the energy cost of “dynamic neutral displacements” is given by
which is negative, and hence associated with a release of available potential energy, as is well known. Again, it is crucial to recognise that displacements in the wedge of instability do not imply diapycnal mixing, just transience, as shown by Equation (7) and as previously recognised by [33].
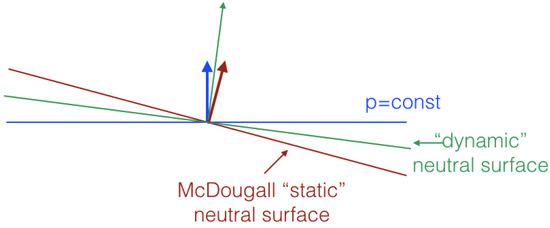
Figure 2.
Relative positions of isobaric surface (blue), McDougall neutral surface (red), and "dynamic" neutral surface (green).
The key implication of the above results is that do not represent the vertical force experienced by an adiabatic and isohaline lateral displacement, and hence that the neutral tangent plane Equation (1) cannot be justified from the consideration of the full momentum balance. On the other hand, (9) shows that displacements satisfying (1) have no energy cost. This suggests therefore that only energetics—rather than momentum—can serve to justify (1) in terms of the displacements minimising the energy cost , as explored in the next section. To that end, it is necessary to exclude isobaric displacements, which represent another class of displacements also minimising , but which do not in general define Lagrangian displacements conserving θ and S. In the following, isobaric displacements are excluded by imposing the displacements considered to take place on material surfaces of the form .
Whether it is possible to meaningfully define a vertical equilibrium position for fluid parcels experiencing adiabatic and isohaline lateral displacements is unclear, because such displacements are intrinsically unstable in presence of non-zero baroclinicity, and therefore bound to become transient.
2.3.3. Are Neutral Trajectories Really Adiabatic and Isohaline?
Because the neutral tangent plane Equation (1) is constructed by assuming to represent an adiabatic and isohaline displacement, it is tempting to believe that a fluid parcel following a neutral trajectory obtained by integrating (1) must also conserve its potential temperature and salinity. As it turns out, this is not the case because of the non-zero helicity of the neutral vector. Indeed, it is well known that a fluid parcel following a neutral trajectory obtained by integrating (1) along a closed loop around the main gyre in the Atlantic ocean ends up about 10 meters above or below its initial position, as discussed by [1]. It is obvious, however, that had the fluid parcel conserved its original potential temperature and salinity, it should have returned exactly to its initial position, assuming the ocean to be stably stratified. This proves therefore that neutral trajectories can never describe actual adiabatic and isohaline fluid parcel trajectories; for a fluid parcel to follow a neutral trajectory, diabatic changes in its potential temperature and salinity are required.
Of course, the problem arises because the quantity describes the buoyancy of fluid parcel displaced laterally from some initial position only for infinitesimal adiabatic and isohaline displacements . As shown by [34] (see also [35]), finite adiabatic and isohaline displacements of a fluid parcel with potential temperature and salinity are solutions of
which states that the density of a fluid parcel is equal to that of the environment (of salinity and potential temperature ). Differentiating while keeping and constant yields
(assuming and ). In other words, the partial differential equation satisfied by an adiabatic and isohaline neutral trajectory (referred to as the trajectory of submesoscale coherent structures in [34]) is actually given by
which differs from (1) whenever the compressibility of a fluid parcel differs from that of the environment. Thus, whatever the neutral trajectories obtained by integrating (1) are meant to represent, they have nothing to do with actual fluid parcel trajectories. As far as we are aware, this is rarely if ever acknowledged in the neutral density literature.
2.3.4. Do Neutral Rotated Diffusion Tensors Really Minimise Spurious Diapycnal Mixing?
Despite their non-rigorous character, McDougall, et al.’s [6] arguments are nevertheless regarded as the main basis for assuming that the isopycnal and diapycnal directions underlying Redi’s [29] rotated diffusion tensor should be based on the neutral vector, and that this is required to avoid spurious diapycnal mixing, e.g., [33,36,37]. As a result, rotated diffusion tensors in coarse numerical ocean general circulation models are usually defined as , e.g., [28], where and represent the values of isopycnal and diapycnal mixing, where is a normalised neutral vector.
Previously, diffusion tensors had been based on using different mixing coefficients in the horizontal and vertical directions, but such a practice was criticised for causing spurious diapycnal mixing owing to what is generally known as the Veronis effect, after George Veronis first described it in [38]. This is because for a model using horizontal and vertical diffusivities and , the diapycnal diffusivity experienced by a material density variable can be shown to be given by
where is the unit normal vector pointing upwards, and the angle made between and . For typical values and , Equation (17) shows that whenever the angle in the sin term exceeds 10−4, the effective diapycnal diffusivity exceeds 10−5 m2/s and becomes dominated by horizontal mixing. Details of the derivations needed to arrive at Equation (17) are given in Appendix A.
Although neutral rotated diffusion tensors are widely thought to eliminate the Veronis effect and the creation of spurious diapycnal mixing, following [33] for instance, one may wonder whether this can ever be true in a thermobaric ocean in presence of density-compensated anomalies. Indeed, because no density variable can be exactly neutral in the ocean, it follows that all conceivable material density variables of the form must all be affected by a Veronis-like effect, since their effective diapycnal diffusivity must be given by
using the same kind of derivation as that leading to (17), where is the angle made between and the neutral vector . Physically, Equation (18) states that the effective diapycnal diffusivity of all conceivable material density variables must always exceed the diapycnal diffusivity specified in the neutral rotated diffusion tensor, possibly by several orders of magnitude depending on their degree of non-neutrality. This seems hard to reconcile with McDougall et al.’s [36,37] assertions that using a direction other than in rotated diffusion tensors will necessarily cause spurious diapycnal mixing, especially as the above arguments clearly establish that cannot represent the diapycnal diffusivity of any mathematically well defined density variable. If does not even relate to the diffusivity of any actual density variable, how is it possible to assume that it relates to the values of diapycnal dispersion measured from tracer release experiments, as assumed by [36,37]? So far, the idea that using a different direction than in rotated neutral diffusion tensors would cause spurious diapycnal mixing has relied exclusively on calling “fictitious mixing” a quantity similar to that underlined in Equation (18), but as far as we are aware, no studies has ever attempted to test whether different forms of rotated diffusion tensors would actually be detrimental to ocean model simulations. In other words, the idea that not using a neutral rotated diffusion tensor in a numerical ocean model would necessarily cause spurious diapycnal mixing is currently purely speculative, its validity having yet to be established in practice by means of actual ocean model experiments. The fact that the diapycnal diffusivity of any actual density variables must necessarily exceed suggests that the validity of such an idea is far less obvious than generally assumed, and that the use of neutral rotated diffusion tensors might actually cause numerical ocean models to be potentially significantly more diffusive than usually assumed.
3. Neutrality and the Energetics Cost of Adiabatic and Isohaline Stirring on Isopycnal Surfaces
3.1. Objectives of This Section
In the introduction, we postulated that the most plausible way to justify the neutral tangent plane Equation (1) from first principles was as the Lagrangian or quasi-Lagrangian averaging of the adiabatic form of the density Equation (5). If so, this would mean that (1) is actually an approximation of an equation of the form , provided that is assumed to be a purely material density variable function of θ and S only, and hence that is an approximation to (up to a multiplicative constant) (using a non-material density variable is also a priori possible, but the resulting equation would only approximately equate to zero ). This would also mean that the justification of (1) is primarily thermodynamic in nature, rather than dynamical. This is supported by the result of the previous section, which challenges the classical justification of (1) in terms of momentum, as it shows that the quantity cannot be a correct expression for the force acting on a fluid parcel experiencing an adiabatic and isohaline lateral displacement, contrary to what had been assumed in the neutral density literature so far, because of its lack of dependence on the horizontal pressure gradient.
Because the number of possible material density variables is infinite in a thermobaric and salty ocean, a selection principle is needed to categorise all such variables. Since solutions of (1) have no energy cost, it is postulated that such a selection principle can be played by the energy cost of fluid parcel exchanges restricted to occur on isopycnal surfaces , see Figure 3. The purpose of this section is to expand upon such an idea, and to show that it leads to a simple mathematical approach for constructing γ directly in thermodynamic space .
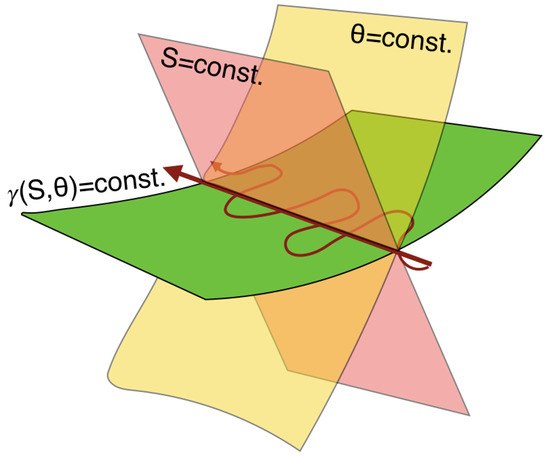
Figure 3.
Fluid parcel trajectories, depicted as the red arrows, must lie at the intersection of surfaces of constant potential temperature and salinity for adiabatic and isohaline displacements caused by stirring. Due to the turbulent character of the ocean, fluid parcel trajectories are expected to undergo large lateral displacements responsible for isopycnal mixing being much larger than diapycnal mixing.
3.2. Link between the Energy Cost of Parcel Exchanges and Lateral Dispersion
Before discussing the details of the energy cost of parcel exchanges on material surfaces, let us first establish qualitatively that the energetics of adiabatic and isohaline dispersion must have a direct bearing on the understanding of the physics of epineutral or isopycnal dispersion. From an energetics viewpoint, there are physically three possible types of parcel exchanges—illustrated in Figure 4—which are respectively associated with the unstable regime (top panel), neutral regime (middle panel) and stable regime (bottom panel).
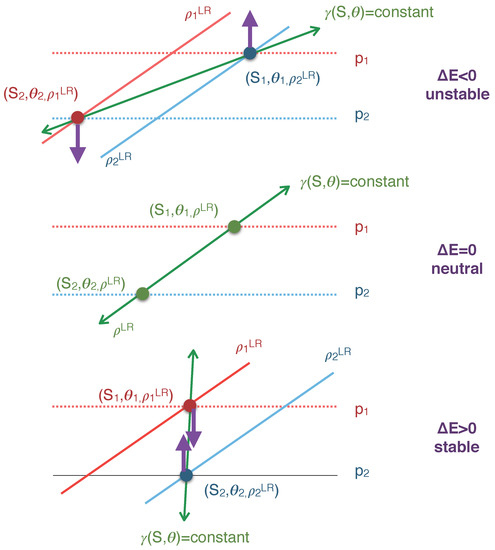
Figure 4.
Schematics of the three main physical situations characterising the two-parcels exchange studied in this paper. (Top panel) Spontaneous exchange taking place on a thermodynamic surface going through the “wedge of instability” thus releasing available potential energy. Following the exchange, the fluid parcels become statically unstable and attracted back to their original neutral surfaces; as they do so, they move further apart from each other, causing enhanced lateral dispersion, while also possibly undergoing some irreversible diffusive mixing through entraining some of the surrounding fluid in the process (not considered in this paper). (Middle panel) Energy neutral parcels exchange associated with regular lateral dispersion. (Bottom panel) Forced exchange on a non-neutral thermodynamic surface not going through the wedge of instability thus requiring an external energy input. Following the exchange, parcels are attracted back to their original surfaces, with a possible reduction of the distance separating them, thus with no or little lateral dispersion, while also possibly undergoing some irreversible diffusive mixing as in the unstable case (not considered in this paper).
In all three panels, two fluid parcels are considered before they exchange position on a locally defined material surface (depicted as the green line). The other surfaces important for understanding the physics of the problem are the locally defined neutral planes and (depicted in red and blue respectively for light and heavy respectively) and isobaric surfaces and . The two fluid parcels are initially assumed to be in equilibrium with their environment, but this is in general no longer the case after they exchange position; the two purple arrows in the top and bottom panels indicate the direction of the buoyancy force experienced by each parcel after the exchange.
As shown in the next paragraph, the energy cost of the parcel exchange is given by , assuming , where is the difference in potential density referenced to the mid pressure between parcel 2 and parcel 1. By assumption, is all three cases but is either negative (top panel), zero (middle panel) or positive (bottom panel), corresponding respectively to the unstable , neutral and stable regimes. The unstable case (top panel) is associated with the spontaneous release of available potential energy and is well known in the parcel theory of baroclinic instability as corresponding to fluid parcels being moved in the wedge of instability, e.g., [25,26,31,32,33]. In the present treatment, there are two wedges of instability, the first one that is comprised between the neutral surface and isobar, and the second one between the neutral surface and isobar.
It is easily seen from even a cursory examination of Figure 4 that only the unstable and neutral cases agree with our physical intuition of lateral dispersion. Indeed, in the stable case , the distance between the two fluid parcels appears to be reduced following the exchange, which suggests that lateral dispersion is suppressed. In contrast, the distance between the two parcels appears to increase in the unstable case , whereas it is unaltered in the neutral case ; this suggests that the unstable case is super-dispersive compared to the neutral case.
It is important to recognise here that the case of a thermobaric and salty ocean is very different from that of a salt-less ocean; indeed, in a salt-less ocean, lateral dispersion can only occur in relation to the energy neutral case , for which the distance between the two fluid parcels remains unaltered following the exchange. In other words, a thermobaric salty ocean possesses an additional physical process causing enhanced lateral dispersion that does not exist in a salt-less ocean. As shown in the next paragraph, the source of energy for this enhanced lateral dispersion stems from the coupling between γ-compensated anomalies and thermobaricity. Since according to Le Chatelier’s principle, instabilities tend to remove what cause them, we speculate that the lateral dispersion occurring in the unstable case represents a mechanism for destroying density compensated (spiciness) anomalies in the ocean. Since the coupling between thermobaricity and density-compensated anomalies is the primary cause for the non-zero helicity of the neutral vector, it follows that the lateral dispersion occurring in the unstable case must also represent a destruction mechanism for the neutral helicity. We speculate that this may explain the relatively small values of neutral helicity observed by [39], which the authors associate with the “thinness” of the ocean in space.
Finally, Figure 4 clearly illustrates the superiority of two-parcel arguments over one-parcel arguments, which make it possible to discuss the physics of lateral dispersion in terms of how the distance between the two parcels is affected by the exchange depending on the particular energetics regime considered.
3.3. Theory of the Energetics of Two-Parcel Exchanges on Material Isopycnal Surfaces
The building block of the theory developed here is the toy model for adiabatic and isohaline stirring previously considered by [23], restricted to occur on a well defined material surface . Specifically, this model predicts the change in available potential energy resulting from two fluid parcels with well defined thermodynamic properties and exchanging their positions (pressures). The physical ingredients of the problem are illustrated in Figure 4. By assumption, the two fluid parcels have equal values of γ, i.e., , but their respective potential density referenced to the mid-pressure may be different, so that depending on the particular case considered, parcel 1 may be more or less buoyant than parcel 2. In line with [1]’s buoyancy argument that neglects the role of kinetic energy, only changes in available potential energy (APE) are retained. For hydrostatic, adiabatic and isohaline displacements, these can be evaluated in terms of enthalpy changes, e.g., [40] (or equivalently in terms of changes in dynamic enthalpy, as considered by [24]), leading to
where is the specific enthalpy, and ν is the specific volume. Before showing how to restrict this result to lateral exchanges on material surfaces of the form , let us first manipulate this expression into a more manageable form. Using a Taylor series expansion around mean salinity and temperature values and , the terms making up the integrand (19) can be approximated as
Inserting the result into (19) yields, after some manipulation,
where it can be verified that the term vanishes by virtue of the definition of . The energy cost function (21) is a purely thermodynamic function that depends uniquely on the six parameters , . At leading order, the expression for the energy cost function reduces to
where . Equation (22) is a well known result previously obtained in the context of the Boussinesq approximation, e.g., [25,26,27]. It is here extended to retain compressibility effects the contribution of internal energy. The exact expression (21) shows that higher-order terms in could in principle be retained if needed, but for the present purposes, the leading order expression is sufficient.
The classical textbook treatment so far has been to move the problem in physical space by expressing the specific volume and pressure differences entering (22) in terms of the mean gradients of these properties times some displacement ,
thus leading to
Pages 280–284 of [25], for instance, offer a detailed mathematical treatment of the Boussinesq version of (24), for which an alternative is also given in Appendix B, and to which the interested reader is referred to. In this paper, we depart from previous approaches by analysing (22) entirely in thermodynamic space, which proves beneficial for clarifying how the neutrality of well defined thermodynamic variables might be optimised.
Having developed some a priori physical intuition for the different cases of interest, we now turn to the problem of quantifying the energetic cost of parcel exchanges taking place on a well defined thermodynamic surface of the form . This imposes the following constraint
which removes one degree of freedom from the problem, thus reducing the dependence of the energy cost function to 5 parameters instead of 6, e.g., and either or . Using a Taylor series expansion around mean values of salinity and temperature and transforms (25) at leading order into a constraint linking the salinity and temperature differences and , namely
Next, using the same technique yields the following approximation for the specific volume difference entering the thermodynamic energy cost function (21)
where the Jacobian term is defined so that
and proceeding similarly with the difference term, (21) becomes
where the function is defined by
with is an arbitrary function of the pressure . Equation (29) is an important new result, which establishes that the energy cost of parcels exchanges on an iso-γ surface depends on the tilt of the γ-isolines relative to those of the in-situ density viewed at constant pressure in thermohaline space. Since thermobaricity causes the isolines of in-situ density to rotate with pressure in space, whereas the γ-isolines are pressure-independent, Equation (29) clearly illustrates the difficulties encountered by a function of alone to minimise . This rationalises a posteriori the use of patched potential density used by [41]. The problem can be formalised in the case where , where is a fixed referenced pressure.
in which case the above formula becomes at leading order
Note that the latter parameter is related to the thermobaric parameter, e.g., [42],
so another way to rewrite Equations (32) and (33) is as
As expected, the above results show that the energy cost of parcels exchange on material surfaces can be either positive (forced exchange) or negative (spontaneous exchange release APE). A typical value of (°C)−1(dbar)−1, using , °C, and Pa yields
In order to get a sense for what these numbers mean, one may for instance compare with the kinetic energy per unit mass of a parcel with typical velocity , that is , which is significantly smaller than the scaling estimate for . As regards to the estimate for , it is somewhat large, and suggests that potential density can only be regarded as sufficiently neutral within perhaps less than 500 dbars away from the reference pressure that serves to define it. This result therefore vindicates the construction of patched potential density used by [41], while also explaining why thermodynamic neutral density , which uses a reference pressure that varies with the thermohaline properties of fluid parcel, appears to be significantly more neutral than any other material density variables, as shown in [23].
3.4. Energy-Based Definition of Global Neutral Surfaces
As discussed in Section 2, there appears to be important and previously overlooked conceptual difficulties in justifying the neutral tangent plane Equation (1) in terms of momentum considerations, which have been the main approach to justifying neutral density so far. However, because displacements satisfying (1) can be characterised as having a zero energy cost , a justification of (1) in terms of energetics—as shown below—appears to be possible and preferable.
As regards to identifying the particular material density variables maximising neutrality in [1]’s sense—a problem previously investigated by [21]—the present energetics approach suggests that γ should be defined to minimise and hence satisfy
Although vanishes for and , these correspond to special cases controlled by the geographical details of water masses properties unrelated to γ itself. Indeed, the functional form of γ affects only via the Jacobian term
so that it is the condition that should be regarded as defining approximately material neutral density surfaces in the present energetics framework. In contrast to the problem considered by [21], which was formulated in physical space, the equation formulates the problem of finding the material density variables maximising neutrality directly in thermodynamic space .
From a mathematical viewpoint, the general solution of in thermodynamic space are the particular functions of the form , of which De Szoeke and Springer’s [17] orthobaric density represents a special case. Because functions of the form are not material in general, it follows that material functions cannot be solution of , but rather of an equation of the form
with ε small in some sense (note that the fact that orthobaric density makes vanish does not imply that the energy cost of parcel exchanges on orthobaric density surfaces is zero, because as discussed in next section, adiabatic and isohaline parcel exchanges on a non-material density surface is impossible). How to formulate an appropriate optimisation problem for γ is not obvious, however. Although [21] succeeded in constructing a material density variable with good neutrality properties over the North Atlantic, attempts at constructing a material density variable with uniformly small neutrality for the global ocean, e.g., [23,36], have proved unsuccessful so far, with [20,36] speculating that this quest might be impossible to achieve for a purely material density variable. None of the arguments given by the latter studies, however, appear to be definitive. As a result, whether a material density variable exists that solves , with ε uniformly small over the whole range of water masses properties encountered in the ocean, must be regarded as an open question until a rigorous mathematical proof is found. The following mathematical analysis aims to make progress in clarifying the types of questions that need to be answered to achieve a definitive understanding of the issue.
In order to understand the nature of the mathematical difficulties associated with solving , with ε a uniformly small number over the range of water masses properties of interest, let us regard the total pressure as the sum of a reference pressure field that is a material function of S and θ plus a perturbation. To fix idea, one may regard as the reference pressure of a fluid parcel in Lorenz reference state, which precisely has such a form, e.g., [23,40], or more simply as a constant. Using a Taylor series expansion of the specific volume around thus yields
By inserting this result into (40) and re-organising the terms, the corresponding Taylor series expansion for is obtained:
where the notations , , and were used.
Equation (43) is an important result, for it naturally explains why the degree of neutrality of all material density variables discussed so far in the literature fails to be uniformly small over the range of ocean water masses. Indeed, all standard potential density variables as well as Lorenz reference density turn out to satisfy but , where and are the terms defined in Equation (43) (presumably, the material density variables discussed by [20,21] are such that and ). In other words, existing material density variables are generally such that they remove the leading order term of ’s Taylor series expansion, but not the second term. The problem with the second term, however, is that it is proportional to , which in general cannot be kept uniformly small over the range of water masses encountered in the ocean, whether is assumed constant, as for standard potential density variables, or a function of S and θ, as in the case of Lorenz reference density discussed by [23]: Even in the latter case, there always exist regions of the ocean where becomes very large, such as the polar regions, and where the neutrality properties of γ deteriorate, possibly significantly. In the case where and for instance, can be written as
Because β and do not vary much in the range of space encountered in the ocean, it follows that increases linearly with the distance from the reference pressure , which is consistent with the widely held view that potential density variables are only useful relatively close to their reference pressure, thus vindicating the use of Lynn and Reid’s [41] “patched potential density”.
Whether one should give up any hope of finding a “good” neutral material density variable is unclear, however. Indeed, because the poor neutrality properties of a material density variable appear to stem from the term in (43), the key question is whether good neutrality properties could be obtained by imposing to γ that it be a solution of instead. If solutions to could be demonstrated to have a small bounded value of , as well as small higher-order terms (those proportional to and above), one would arguably have constructed a material density variable satisfying , with ε uniformly small over the range of water masses of interest, and hence with uniformly good neutrality properties. The problem of how to solve appears to be somewhat complex, however, and is currently under investigation; hopefully, progress will be reported in a subsequent study.
4. Neutrality and Energetics of Parcels Exchanges Using a Non-Material Density Variable
4.1. Objectives of This Section
The focus so far has been on purely material density variables . Such variables play a fundamental role in the study of stirring, for they define the surfaces along which adiabatic and isohaline parcel exchanges take place. Thermodynamic density variables are also of theoretical interest, for they can be made quite neutral, e.g., [36,43]; they also have the advantage of defining an exact geostrophic streamfunction when used as a generalised vertical coordinate [17].
This section focuses on the particular case of orthobaric density [19]. Like , orthobaric density is not conserved during an adiabatic and isohaline parcel exchange. An important consequence of non-materiality is illustrated in Figure 5. This shows that two parcels initially located on the same non-material surface must leave it as soon as the parcel exchange is initiated. As a result, what is meant by “the energy cost of a parcel exchange on a non-material density surface” is really the energy cost of the parcel exchange on the material surface that best approximates the non-material density surface before the parcel exchange. This is also illustrated in Figure 5. This is an important point that needs to be kept in mind in the following. Indeed, it is important to recognise that even though orthobaric density is a function of ρ and p alone, and therefore an exact solution of the equation , the energy cost of adiabatic and isohaline parcel exchanges on a thermobaric surface is not zero, because the parcel exchange actually takes place on the surface that initially coincide with the othobaric density surface considered, not on the thermobaric density surface itself. The consequences is that parcels experience a thermobaric buoyancy force during the parcel exchange, which is the force expelling the fluid parcels out of the thermobaric surface, and hence the cause for the adiabatic dispersion through thermobaric density surfaces.
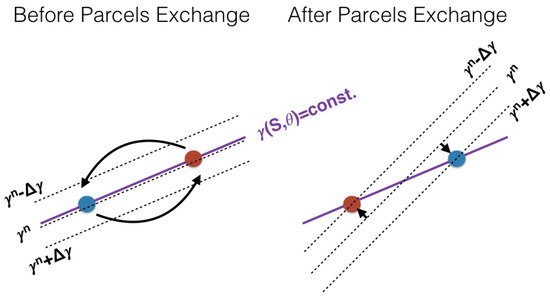
Figure 5.
Schematics illustrating the adiabatic vertical dispersion associated with the exchange of two fluid parcels being initially on the same non-material density surface (such as orthobaric density or neutral density for instance, whose iso-surfaces are depicted by the dotted lines). Before the parcel exchange, the non-material density surface coincides with a material density surface , indicated by the purple solid line, on which the adiabatic and isohaline parcel exchange actually takes place. As the result of the parcels exchange, the density of each parcel changes by , resulting in a net mass loss for the original orthobatic or neutral density density class, and a mass gain for the two orthobaric or neutral density surfaces below and above. Since in physical space, the two fluid parcels are supposed to exchange their position, adiabatic and isohaline stirring on orthobaric or neutral density surfaces must result in the latter moving relative to the material iso-γ surface.
After the parcel exchange, the material surface initially approximating an orthobaric density surface must have moved relative to the orthobaric surface. From the viewpoint of the non-material density variable, the parcel exchange results in a form of diapycnal diffusion that is analogous to the vertical dispersion characterising diabatic diapycnal dispersion, e.g., [44], except that it conserves θ and S. In the context of the neutral surfaces literature, this form of dispersion is usually referred to as thermobaric dianeutral dispersion, e.g., [42,45]. Adiabatic thermobaric diapycnal dispersion is an essential component of the description of adiabatic and isohaline stirring by means of a non-material density variable; this is another key point that needs to be kept in mind in the following. The above arguments indicate that thermobaric buoyancy forces are the cause for thermobaric dianeutral dispersion.
4.2. Description of Adiabatic and Isohaline Stirring Using Orthobaric Density
Keeping in mind the above caveats, let us consider two fluid parcels assumed to belong to the same orthobaric density surface before they exchange position. Mathematically, this imposes the following constraint:
In order to understand the constraint that this imposes between and , let us recall that the total differential of orthobaric density is defined to be
where has the dimension of a squared speed of sound and is empirically constructed from climatological data [19]. As a result,
Using as before a Taylor series expansion around mean values of temperature and salinity, it is easy to show that the constraint satisfied by is now given by
which in turn implies for ,
which in turn yields at leading order
In order to facilitate the comparison with the results obtained for a quasi-material density variable , we need to elucidate the role played by the thermobaric parameter in the above formula. To that end, let us regard as a function of in-situ density, pressure, and salinity, and regard the empirical function as being obtained from the speed of sound evaluated at some empirically determined characteristic salinity function
Using a Taylor series expansion around , the following approximation is obtained for the difference ,
where it is shown in Appendix B that
which is consistent with previous similar results obtained by [19,36,46,47]. Apart when , which occurs only rarely in the ocean, this term is expected to be positive almost everywhere, and shows that in general, the speed of sound increases with salinity at constant p and ρ. Using some algebra yields
where , while we assumed in simplifying the above expression. Now, by defining as a suitable temperature anomaly compensating in density the salinity anomaly , we arrive at the result
A key property of Equation (56) is that it is proportional to , which is much better than the dependence of the energy cost of parcels exchanges on potential density surfaces. Indeed, because is the pressure difference between the two parcels exchanged, it can be assumed to be relatively small, say O(10 dbar) at most. In contrast, is the difference between the actual and reference pressures; hence can potentially be very large (> 1000 dbar), even for thermodynamic neutral density especially in the polar regions.
Since in the ocean does not vary significantly while is bounded, the distribution of is expected to remain quite uniform in comparison to . Moreover, since is proportional to , its values are also expected to be statistically more compatible with the amounts of energy available for stirring in the ocean in comparison to those associated with . This suggests that stirring along orthobaric density surfaces is actually realisable, at least from an energetic perspective.
In order to get a sense for the degree of neutrality of orthobaric density (as measured by the value of ), let us use the typical values (°C)(dbar)−1, °C, and dbar. This yields . This is significantly smaller than the estimate for potential density away from its reference pressure. This clearly establishes the superior neutrality properties of orthobaric density over potential density variables when assessed in terms of the present energy-based neutrality criterion. This is in contrast to [36], who has claimed that the neutrality of orthobaric density is not superior to that of ; McDougall and Jackett’s [36] conclusion, however, derives from the use of a somewhat idiosyncratic definition of neutrality that tends to favour over other density variables. Specifically, McDougall and Jackett’s [36] approach is based on evaluating the fraction of the ocean over which what they call “the spurious diapycnal mixing” associated with a given variable is greater than . They find that this fraction is not smaller for orthobaric density compared to . Whether this is a valid or fair way to assess neutrality is unclear, however, as other criteria exist according to which orthobaric density is clearly more neutral than .
An important advantage of orthobaric density is that it can a priori be constructed to correctly represent ocean stability whenever . Indeed, it is easily shown that
(using the hydrostatic approximation ). Therefore, provided that is defined so that
it is possible to guarantee that whenever . As discussed by [36], defining orthobaric density in such a way deteriorates [1]’s static neutrality (as defined in Section 2). However, Equation (50) shows that imposing makes the energy cost negative, and hence that constructing orthobaric density in such a way makes it dynamically neutral as defined in Section 2. As far as we are aware, orthobaric density is the only density variable that can in principle be constructed to correctly predict ocean stability everywhere, as all other density variables, including Jackett and McDougall’s [2] empirical neutral density , are known to exhibit inversions.
In summary, the fact that orthobaric density can in principle be constructed to be associated with a uniformly small and negative energy cost—making it dynamically neutral—as well as to correctly predict ocean stability everywhere, makes it stand out as a density variable for use in theoretical studies and as a vertical thermodynamic coordinate. These advantageous properties stand in sharp contrast with [36] very negative assessment of orthobaric density.
5. A posteriori Thermodynamic Justification for Computing from the Minimisation of
5.1. Objectives of This Section
In Section 3, we suggested that the criterion quantifying the degree of neutrality of a material density variable in thermodynamic space was the smallness of the absolute value of the Jacobian term , which is the term controlling the energy cost of parcel exchanges on material surfaces . One could argue, however, that the equation is no more rooted in first principles than the neutral tangent plane Equation (1), since the energetics of two-parcel exchanges is in some sense no less artificial or ad-hoc than the focus on the buoyancy force of a single parcel, each approach representing only a partial and incomplete description of the energetics and vertical momentum balance of lateral dispersion respectively.
As it turns out, a rigorous first-principles justification for minimising exists, and naturally arises in the context of a description of water masses in terms of two independent material functions and , as well as pressure p. In that case, is the quantity that needs to be minimised to minimise the dependence of in-situ density on the spiciness variable ξ. As a result, minimising in thermodynamic space also maximises the alignment between and the local neutral vector in physical space, thus maximising the neutrality of γ. The main aim of this section is to formalise this idea mathematically.
5.2. Density/Spiciness Representation of Water Masses
Although the properties of water masses are most naturally described in terms of θ and S, which are the variables that are most directly observable, the study of ocean mixing and ocean dynamics most naturally calls for a density/spiciness representation, e.g., [48], in terms of two independent material functions —the density—and —the spiciness, e.g., see [49] for a recent review of related ideas and concepts. From a mathematical viewpoint, can a priori be chosen arbitrarily so long as the Jacobian associated with the change of variables differs from zero everywhere in the part of space of interest.
The density/spiciness representation of ocean water masses naturally leads one to regard in-situ density as a function of γ, ξ and pressure p. This allows one to write the differential form in the following equivalent forms
where it can be verified that the partial derivatives of relative to γ and ξ are related to the partial derivatives of ρ, γ and ξ relative to S and θ via the following relations
Note here that
which makes it clear that minimising is equivalent to minimising the dependence of in-situ density on spiciness ξ.
In order to establish the link between minimising and maximising the neutral character of γ, let us switch to physical space. From (60), the following expression for the instantaneous neutral vector is easily obtained
Depending on how is defined, and might be strongly correlated in physical space. For this reason, it is useful to introduce a modified spiciness variable , where is a function of γ only, in order to rewrite the instantaneous neutral vector (63) as follows
In practice, the most logical would be to try to construct so as to make and as orthogonal as possible in physical space, a procedure whose details we intend to describe in a forthcoming study. Equation (64) makes it clear that minimising (hence ) is required to maximise the alignment between and , hence to maximise the neutral character of γ. This definitely establishes that minimising in space is equivalent to maximising the neutrality of in physical space.
6. Summary and Conclusions
In this paper, we have revisited the theoretical foundations for quasi-neutral density variables in the ocean. The main points are:
- Elementary but rigorous physical considerations clearly indicate that the physical processes for lateral dispersion in the ocean must in general have a non-zero buoyancy, which is confirmed by a survey of the literature on the topic. The concept of epineutral dispersion, therefore, only makes sense if viewed as the aggregate result of many individual non-neutral (i.e., having non-zero buoyancy) stirring events, so that it is only the net displacement aggregated over N individual stirring events that is approximately neutral and solution of the neutral tangent plane equation ;
- It is not true that neutral trajectories obtained as solutions of the neutral tangent plane Equation (1) can describe actual trajectories, contrary to what is usually assumed, because such trajectories implicitly require the existence of non-material sources of heat and salt. It is also not true that neutral tangent planes represent surfaces along which fluid parcels can be exchanged without experiencing (restoring or otherwise) buoyancy forces. Indeed, irreducible thermobaric forces always accompany adiabatic and isohaline parcels exchanges, and will force any pair of fluid parcels out of their original neutral tangent plane as soon as the parcel exchange takes place. If parcel exchanges on neutral tangent planes truly occurred without experiencing buoyancy forces, they would not experience thermobaric dianeutral dispersion;
- The widespread idea that the neutral tangent plane Equation (1) can be justified in terms of momentum considerations appears to be invalid since the quantity cannot represent the full vertical force acting on a fluid parcel experiencing an adiabatic and isohaline lateral displacement owing to its lack of dependence on the horizontal pressure gradient. The new concept of ‘dynamic neutrality’ is introduced to describe lateral displacements satisfying to distinguish it from Mcdougall buoyancy-based ‘statistic neutrality’. In contrast to McDougall’s neutral displacements, ‘dynamic’ neutral displacements occur in the wedge of instability, have a non-zero buoyancy, a negative energy cost (they release available potential energy) and are necessarily transient;
- Since the stirring events making up epineutral/isopycnal/lateral dispersion are usually individually non-neutral, it is argued that the neutral tangent plane Equation (1) can only be a valid model for epineutral dispersion if interpreted in an averaged sense; however, because traditional Eulerian averages give rise to eddy-correlation terms—absent from (1)—it is postulated that (1) can only be justified from first principles as a Lagrangian or quasi-Lagrangian average of the density Equation (5). This requires that the sought-for Lagrangian or quasi-Lagrangian density variable γ whose identification is the ultimate goal of the neutral density theory should be identified prior to the computation of the mean neutral vector appearing in (1); this suggests that γ can only be meaningfully constructed in thermodynamic space, and cast doubt on the possibility to provide a rigorous justification for density variables also varying geographically;
- We established, using both energetics and thermodynamics arguments, that the criterion measuring the degree of neutrality of a material density variable is the smallness of the absolute value of the Jacobian termPhysically, has both a dynamical and thermodynamic interpretations, as it controls the energy cost of parcel exchanges on material surfaces, as well as the dependence of in-situ density on spiciness. Minimising in thermodynamic space was shown to be equivalent to maximising the neutral character of γ in physical space.
- The present theory naturally explains why most material density variables fail to be uniformly neutral in the ocean, because they are such that in the following Taylor series expansion for :It is speculated that a material density variable constructed to be solution of might be uniformly satisfactorily neutral, a resarch topic left for further research.
- It was demonstrated that the neutral and non-neutral stirring events contributing to epineutral dispersion could be characterised in terms of their energy signature, and suggested that the events with negative energy cost —that is, releasing available potential energy—are associated with enhanced lateral dispersion.
- A new mechanism for enhanced lateral dispersion was identified whose source of energy stems from the coupling between thermobaricity and density-compensated temperature/salinity anomalies. Such a mechanism does not exist in a salt-less ocean, and is speculated to act as a physical process for the removal of density-compensated anomalies and neutral helicity in the ocean;
- It was established that the use of a neutral rotated diffusion tensor, as is the current practice in numerical ocean modelling, implies that the effective diapycnal diffusivity of all conceivable material density variables is potentially much larger than the value of dianeutral diffusivity used in such tensors, raising the issue of whether the use of such tensors avoids or causes spurious diapycnal diffusion;
- It was established that orthobaric density appears to significantly more neutral based on the present energy-based definition of neutrality than suggested by McDougall and Jackett’s [36] evaluation.
We believe that our results are important, because:
- They connect for the first time epineutral dispersion with the actual stirring events that cause it; moreover, the realisation that epineutral dispersion is actually made up of non-neutral stirring events resolves some longstanding apparent paradoxes and inconsistencies between “neutral thinking”, “turbulence thinking” and “baroclinic instability thinking” that have caused much confusion and controversy in the field;
- They clearly establish the relevance of energetics for categorising the different possible dispersion regimes in the ocean, with epineutral dispersion being associated with energy neutral and unstable processes, whereas diapycnal dispersion is associated with positive energy consumption;
- They dispel the widespread misconception, e.g., [1], that the buoyancy forces involved in parcel exchanges in potential density surfaces are necessarily restoring;
- They clearly indicate that the systematic study of density-compensated (spiciness) salinity/ temperature anomalies, e.g., [48], will be essential to progress our understanding of epineutral dispersion, of the observed smallness of helicity, and of the ocean ”thinness” in space established by [39];
- They provide a potential unifying framework for discussing a number of widely disparate results all connected to the thermobaric instability identified here, such as the thermobaric instability sustaining solitary Rossby waves discussed by [50], the existence of a spiciness mode [46], the thermobaric production of potential vorticity [47], thermobaric numerical instabilities in isopycnic numerical ocean circulation models [51], the possibility for thermobaricity to cause a form of conditional instability akin to that at the origin of thunderstorms in the atmosphere [52], that [53] speculated might be responsible for past climate change.
- They provide for the first time concrete ways to test the validity of neutral diffusion tensors; for instance if we could establish on the basis of direct numerical simulations or observations that the diapycnal diffusivity of , , and Lorenz reference density was comparable to observed values of diapycnal mixing, it would unambiguously invalidate the idea that neutral rotated diffusion tensors are necessarily the best possible practice. Until now, to paraphrase Stommel [54], our ideas about neutral density and neutral rotated diffusion have had so far a peculiarly dreamlike quality, and it has been unclear whether any of the premises on which neutral density thinking relies are actually testable or falsifiable. The present results suggest that they might be.
Acknowledgments
The author acknowledges discussions with Stephen Griffies, George Nurser, Kevin Oliver, Anne-Marie Treguier, Antoine Hochet, Marie-Jose Messias, David Ferreira, Alex Megann, Sjoerd Groeskamp and Trevor McDougall as contributing clarifying the physical meaning of our results. John Methven pointed out the paper by [32], while Trevor McDougall pointed out the references in the books by Olbers et al. (2012) and Vallis (2006). This work was supported NERC Grant NE/K016083/1, “Improving simple climate models through a traceable and process-based analysis of ocean heat uptake (INSPECT)”.
Conflicts of Interest
The author declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Appendix A
In numerical ocean models, the evolution equations of potential temperature and salinity are generally assumed to be of the form
where is a neutral rotated diffusion tensor, with a normalised neutral vector. As a result, the evolution equation for any given material density variable must obey
and be the sum of a diffusive conservative and nonlinear production/destruction terms. By definition, the projection of —the diffusive flux of γ—through a iso-γ surface is given by
where is the effective diapycnal diffusivity of γ. Using the fact that , can alternatively rewritten as
where is the angle between the normalised neutral vector and . Provided that , which is usually the case, must always exceed the diapycnal diffusivity used in the definition of neutral diffusion tensors.
Appendix B
The analysis of the cost function (24) is a classical exercise whose analysis can be found in textbooks such as [25,26]. Here, we show that such a cost function naturally defines three natural eigen-directions for stirring. Before we do this, some qualitative remarks are useful. It is easy upon simple inspection to remark that vanishes not only for neutral displacements (i.e., in the case as noted previously), but also for isobaric displacements (such that ). Moreover, one may also remark that for purely vertical displacements , the cost function (24) reduces to
which can be recognised as twice the well-known small amplitude formula for the increase of available potential energy associated with the work done by the two parcels against the restoring buoyancy force due to the stable stratification of buoyancy frequency N, e.g., [55].
The energy cost of more general displacements is most easily understood by noting that (24) is quadratic in , and that it can be written as
in terms of the following symmetric matrix
Since S is real and symmetric, it possesses a set of real orthonormal eigenvectors that forms the natural basis for describing the energy cost of any arbitrary displacement. The eigensystem is straightforward to compute, and one may verify through direct substitution that the eigenvectors are given by
where and are the unit vectors associated with and , while is the cosine of the angle between and . In order to simplify the expression for the associated eigenvalues, it is useful to write down the norm of the pressure gradient and vector in terms of the vertical displacements and of an isobaric surface and local neutral tangent plane as follows
By successively computing for all eigenvectors, one finds that the corresponding eigenvalues are given by
where .
The first eigendirection (72,77) has a vanishing eigenvalue and is directed along the line defined by the intersection of the local neutral tangent plane and isobaric surface; it therefore defines displacements that have zero energy cost. The second eigendirection (73,78) has a negative eigenvalue and is directed in the wedge of baroclinic instability depicted schematically in Figure B1. Physically, such eigendirection defines displacements that release available potential energy associated with the baroclinicity of the stratification, which was first discussed by [31] (see also [32]) in the context of baroclinic instability theory. To the extent that such displacements are realisable, such a direction corresponds to ‘spontaneous stirring’, which can occurs without the need for any external source of energy. Such a situation has been primarily discussed in relation to the conversion of mean available potential energy into eddy available potential energy and the development of meso-scale ocean eddies, but not in relation to the possible development of small-scale turbulence, probably because classical models of baroclinic instability are generally characterised by the existence of a short-wave cut-off that prevents the release of APE for too-small wavelengths. Such a short-wave cut-off does not necessarily exists for the unstable solutions of the linearised QG equations when using realistic mean flow, however, suggesting that such direction might also be relevant for small-scale stirring and mixing. Finally, the third eigendirection (74,79) has a positive eigenvalue and is perpendicular to the second eigendirection. In the general case where then angle between the isobaric surface and local neutral tangent plane is small, and that both surfaces are close to horizontal, the third eigendirection can be regarded as quasi-vertical, it corresponds to displacements—primarily associated with internal gravity waves—requiring an external source of energy.
The above results imply that the energy cost of any arbitrary displacement of amplitude is given by
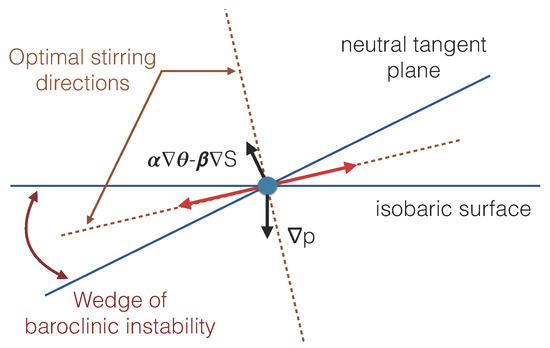
Figure B1.
Schematics illustrating the key directions controlling the energy cost of adiabatic stirring. The red arrows define the optimal direction for stirring and is located in the so-called wedge of baroclinic instability whose origin can be traced back to [31]. The neutral direction associated with zero energy cost is indicated by the big blue dot and is perpendicular to the page.
The eigendirections defined by the eigenvectors of S are illustrated in Figure B1, while a possible way to construct a material surface along which adiabatic and isohaline stirring releases available potential energy—relative to a neutral surface—is illustrated in Figure B2.
Figure B2.
Schematics illustrating approximate neutral surfaces and approximate optimal stirring surface obtained by making a continuous surface to be tangent at all points to the neutral tangent plane and to the optimal stirring direction.
Appendix C
In this Appendix, expressions for the derivatives of the speed of sound with respect to salinity and potential temperature at constant p and ρ are derived. To that end, use the expression for the total differential of in-situ density, viz.,
to obtain the following expression for the total differential of potential temperature viewed as a function of ρ, S and p,
Combining the above results, using the definition of the thermobaric parameter (34), yields
Using the same technique but for potential temperature, it is easily established that
Equations (84) and (85) show that increases with both θ and S in general when , which is the typical behaviour of a spiciness variable. Moreover, note that the derivatives of with respect to S and θ satisfy
where S and θ are regarded as function of ρ, p, and . The derivatives and are density-compensated.
References
- McDougall, T.J. Neutral surfaces. J. Phys. Oceanogr. 1987, 17, 1950–1964. [Google Scholar] [CrossRef]
- Jackett, D.R.; McDougall, T.J. A neutral density variable for the world’s oceans. J. Phys. Oceanogr. 1997, 27, 237–263. [Google Scholar] [CrossRef]
- Pingree, R.D. Mixing in the deep stratified ocean. Deep Sea Res. 1972, 19, 549–561. [Google Scholar] [CrossRef]
- Ivers, W.D. The Deep Circulation in the Northern North Atlantic, with Especial Reference to the Labrador Sea. Ph.D. Thesis, Scripps Institute of Oceanography, University of California, San Diego, CA, USA, 1975. [Google Scholar]
- Montgomery, R.B. Circulation in the upper layers of the southern North Atlantic, deduced with the use of isentropic analysis. Pap. Phys. Oceanogr. Meteor 1938, 6, 55. [Google Scholar]
- McDougall, T.J.; Groeskamp, S.; Griffies, S.M. On geometrical aspects of interior ocean mixing. J. Phys. Oceanogr. 2014, 44, 2164–2175. [Google Scholar] [CrossRef]
- Thorpe, A.J.; Hoskins, B.J.; Innocenti, V. The parcel method in a baroclinic atmosphere. J. Atmos. Sci. 1989, 46, 1274–1284. [Google Scholar] [CrossRef]
- Tailleux, R. On the validity of single-parcel energetics to assess the importance of internal energy and compressibility effects in stratified fluids. J. Fluid Mech. 2015, 767, R2. [Google Scholar] [CrossRef]
- Zimmerman, J.T.F. The tidal whirlpool: A review of horizontal dispersion by tidal and residual currents. Neth. J. Sea Res. 1986, 20, 133–154. [Google Scholar] [CrossRef]
- Young, W.R.; Rhines, P.B.; Garrett, C.J.R. Shear-flow dispersion, internal waves and horizontal mixing in the ocean. J. Phys. Oceanogr. 1982, 12, 515–527. [Google Scholar] [CrossRef]
- Steinbuck, J.V.; Koseff, J.R.; Genin, A.; Stacey, M.T. Horizontal dispersion of ocean tracers in internal wave shear. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Andrews, D.G.; McIntyre, M.E. An exact theory of nonlinear waves on a Lagrangian mean flow. J. Fluid Mech. 1978, 89, 609–646. [Google Scholar] [CrossRef]
- Andrews, D.G.; McIntyre, M.E. On wave action and its relatives. J. Fluid Mech. 1978, 89, 647–664. [Google Scholar] [CrossRef]
- Salmon, R. An alternative view of generalized Lagrangian mean theory. J. Fluid Mech. 2013, 719, 165–182. [Google Scholar] [CrossRef]
- De Szoeke, R.A.; Bennett, A.F. Microstructure fluxes across density surfaces. J. Phys. Oceanogr. 1993, 23, 2254–2264. [Google Scholar] [CrossRef]
- Young, W.R. An exact thickness-weighted average formulation of the Boussinesq equations. J. Phys. Oceanogr. 2012, 42, 692–707. [Google Scholar] [CrossRef]
- De Szoeke, R.A. Equations of motion using thermodynamic coordinates. J. Phys. Oceanogr. 2000, 30, 2184–2829. [Google Scholar] [CrossRef]
- Brankart, J.M. Impact of uncertainties in the horizontal density gradient upon low resolution global ocean modelling. Ocean Model. 2013, 66, 64–76. [Google Scholar] [CrossRef]
- De Szoeke, R.A.; Springer, S.R. Orthobaric density: A thermodynamic variable for ocean circulation studies. J. Phys. Oceanogr. 2000, 30, 2830–2852. [Google Scholar] [CrossRef]
- McDougall, T.J.; Jackett, D.R. The material derivative of neutral density. J. Mar. Res. 2005, 63, 159–185. [Google Scholar] [CrossRef]
- Eden, C.; Willebrand, J. Neutral density revisited. Deep Sea Res. Part II 1999, 46, 33–54. [Google Scholar] [CrossRef]
- Serazin, G. An Approximate Neutral Density Variable for the World’s Oceans. Master’s Thesis, Ecole Centrale Lyon, Écully, France, 2011. [Google Scholar]
- Tailleux, R. Generalised patched potential density and thermodynamic neutral density: Two new physically-based quasi-neutral density variables for ocean water masses analyses and circulation studies. J. Phys. Oceanogr. 2016, in press. [Google Scholar]
- Nycander, J. Energy conversion, mixing energy, and neutral surfaces with a nonlinear equation of state. J. Phys. Oceanogr. 2011, 41, 28–41. [Google Scholar] [CrossRef]
- Olbers, D.; Willebrand, J.; Eden, C. Ocean Dynamics; Springer: Berlin, Germany, 2012; p. 704. [Google Scholar]
- Vallis, G. Atmospheric and Oceanic Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2006; p. 745. [Google Scholar]
- Haine, T.; Marshall, J. Gravitational, symmetric and baroclinic instability of the ocean mixed layer. J. Phys. Oceanogr. 1998, 28, 634–658. [Google Scholar] [CrossRef]
- Griffies, S.M. Fundamentals of Ocean Models; Princeton University Press: Princeton, NJ, USA, 2004; p. 424. [Google Scholar]
- Redi, M.H. Oceanic isopycnal mixing by coordinate rotation. J. Phys. Oceanogr. 1982, 12, 1154–1158. [Google Scholar] [CrossRef]
- Popper, K. The Logic of Scientific Discovery; Routledge: New York, NY, USA, 1959. [Google Scholar]
- Eady, E.T. Long waves and cyclone waves. Tellus 1949, 1, 33–52. [Google Scholar] [CrossRef]
- Heifetz, E.; Alpert, P.; da Silva, A. On the parcel method and the baroclinic wedge of instability. J. Atmos. Sci. 1998, 55, 788–795. [Google Scholar] [CrossRef]
- McDougall, T.J.; Church, J.A. Pitfalls with the numerical representation of isopycnal and diapycnal mixing. J. Phys. Oceanogr. 1986, 16, 196–199. [Google Scholar] [CrossRef]
- McDougall, T.J. The vertical motion of submesocale coherent vortices across neutral surfaces. J. Phys. Oceanogr. 1987, 17, 2334–2342. [Google Scholar] [CrossRef]
- Huang, R.X. Adiabatic density surface, neutral density surface, potential density surface, and mixing path. J. Trop. Oceanogr. 2014, 33, 1–19. [Google Scholar]
- McDougall, T.J.; Jackett, D.R. An assessment of orthobaric density in the global ocean. J. Phys. Oceanogr. 2005, 35, 2054–2075. [Google Scholar] [CrossRef]
- Klocker, A.; McDougall, T.J.; Jackett, D.R. A new method for forming approximately neutral surfaces. Ocean Sci. 2009, 5, 155–172. [Google Scholar] [CrossRef]
- Veronis, G. The role of models in tracer studies. In Numerical Models of Ocean Circulation; National Academy of Science: Washington, DC, USA, 2007; pp. 133–146. [Google Scholar]
- McDougall, T.J.; Jackett, D.R. The thinness of the ocean in S-Θ-p space and the implication for mean diapycnal advection. J. Phys. Oceanogr. 2007, 37, 1715–1732. [Google Scholar] [CrossRef]
- Saenz, J.A.; Tailleux, R.; Butler, E.D.; Hughes, G.O.; Oliver, K.I.C. Estimating Lorenz’s reference state in an ocean with a nonlinear equation of state for seawater. J. Phys. Oceanogr. 2015, 45, 1242–1257. [Google Scholar] [CrossRef]
- Lynn, R.J.; Reid, J.L. Characteristics and circulation of deep and abyssal waters. Deep Sea Res. 1968, 15, 577–598. [Google Scholar] [CrossRef]
- McDougall, T.J. Thermobaricity, cabelling, and water-mass conversion. J. Geophys. Res. 1987, 92, 5448–5464. [Google Scholar] [CrossRef]
- De Szoeke, R.A.; Springer, S.R. The materiality and neutrality of neutral density and orthobaric density. J. Phys. Oceanogr. 2009, 39, 1779–1799. [Google Scholar] [CrossRef]
- Pearson, H.J.; Puttock, J.S.; Hunt, J.C.R. A statistical model of fluid-element motions and vertical diffusion in a homogeneous stratified turbulent flow. J. Fluid Mech. 1983, 129, 219–249. [Google Scholar] [CrossRef]
- McDougall, T.J. The relative roles of diapycnal and isopycnal mixing on subsurface water mass convsersion. J. Phys. Oceanogr. 1984, 14, 1577–1589. [Google Scholar] [CrossRef]
- Muller, P.; Willebrand, J. Compressibility effects in the thermohaline circulation: A manifestation of the temperature-salinity mode. Deep Sea Res. 1986, 33, 559–571. [Google Scholar] [CrossRef]
- Straub, D.N. On thermobaric production of potential vorticity in the ocean. Tellus 1999, 51A, 314–325. [Google Scholar] [CrossRef]
- Tailleux, R.; Lazar, A.; Reason, C. Physics and dynamics of density-compensated temperature and salinity anomalies. Part I: Theory. J. Phys. Oceanogr. 2005, 35, 849–864. [Google Scholar] [CrossRef]
- Huang, R.X. Defining the spicity. J. Mar. Res. 2011, 69, 545–559. [Google Scholar] [CrossRef]
- De Szoeke, R.A. An effect of the thermobaric nonlinearity of the equation of state: A mechanism for sustaining solitary Rossby waves. J. Phys. Oceanogr. 2004, 34, 2042–2056. [Google Scholar] [CrossRef]
- Hallberg, R. A thermobaric instability of Lagrangian vertical coordinate ocean models. Ocean Model. 2004, 8, 279–300. [Google Scholar] [CrossRef]
- Ingersoll, A.P. Boussinesq and anelastic approximations revisited: Potential energy release during thermobaric instability. J. Phys. Oceanogr. 2005, 35, 1359–1369. [Google Scholar] [CrossRef]
- Adkins, J.F.; Ingersoll, A.P.; Pasquero, C. Rapid climate change and conditional instability of the glacial deep ocean from the thermobaric effect and geothermal heating. Quat. Sci. Rev. 2005, 24, 581–594. [Google Scholar] [CrossRef]
- Stommel, H.K. Why do our ideas about the ocean circulation have such a peculiarly dream-like quality? In Collected Works of Henry Stommel; Hogg, N.G., Huang, R.X., Eds.; American Meteorological Society: Boston, MA, USA, 1954; Volume 1, pp. 124–134. [Google Scholar]
- Tailleux, R. Available potential energy and exergy in stratified fluids. Ann. Rev. Fluid Mech. 2013, 45, 35–58. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).