Meridional and Zonal Wavenumber Dependence in Tracer Flux in Rossby Waves
Abstract
:1. Introduction
2. Materials and Methods
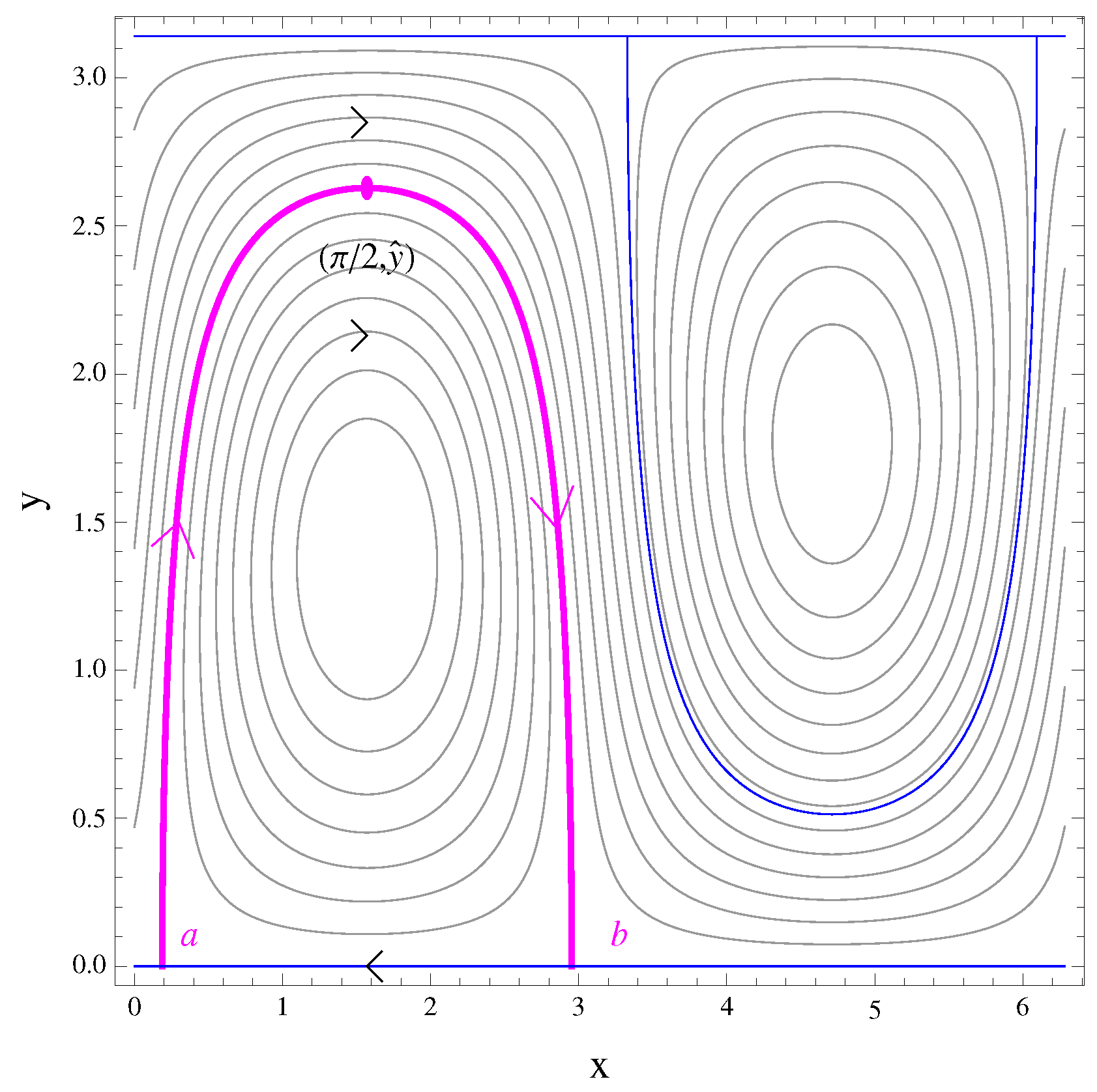
2.1. Rossby Waves
2.2. Fluid and Tracer Flux
- allows for the disturbance to have any time-variation;
- explicitly quantifies the flux as a function of time;
- does not care whether manifolds intersect zero times, a finite number of times, or an infinite number of times;
- captures both simple and complicated (chaotic) forms of transport; and
- works for compressible two-dimensional flows (geophysical fluid might need to satisfy volume preservation, and so when observing behavior on two-dimensional sheets (e.g., isopycnals), area-preservation need not be satisfied since the isopycnals can compress towards one another).
3. Results
3.1. Formulas for Flux
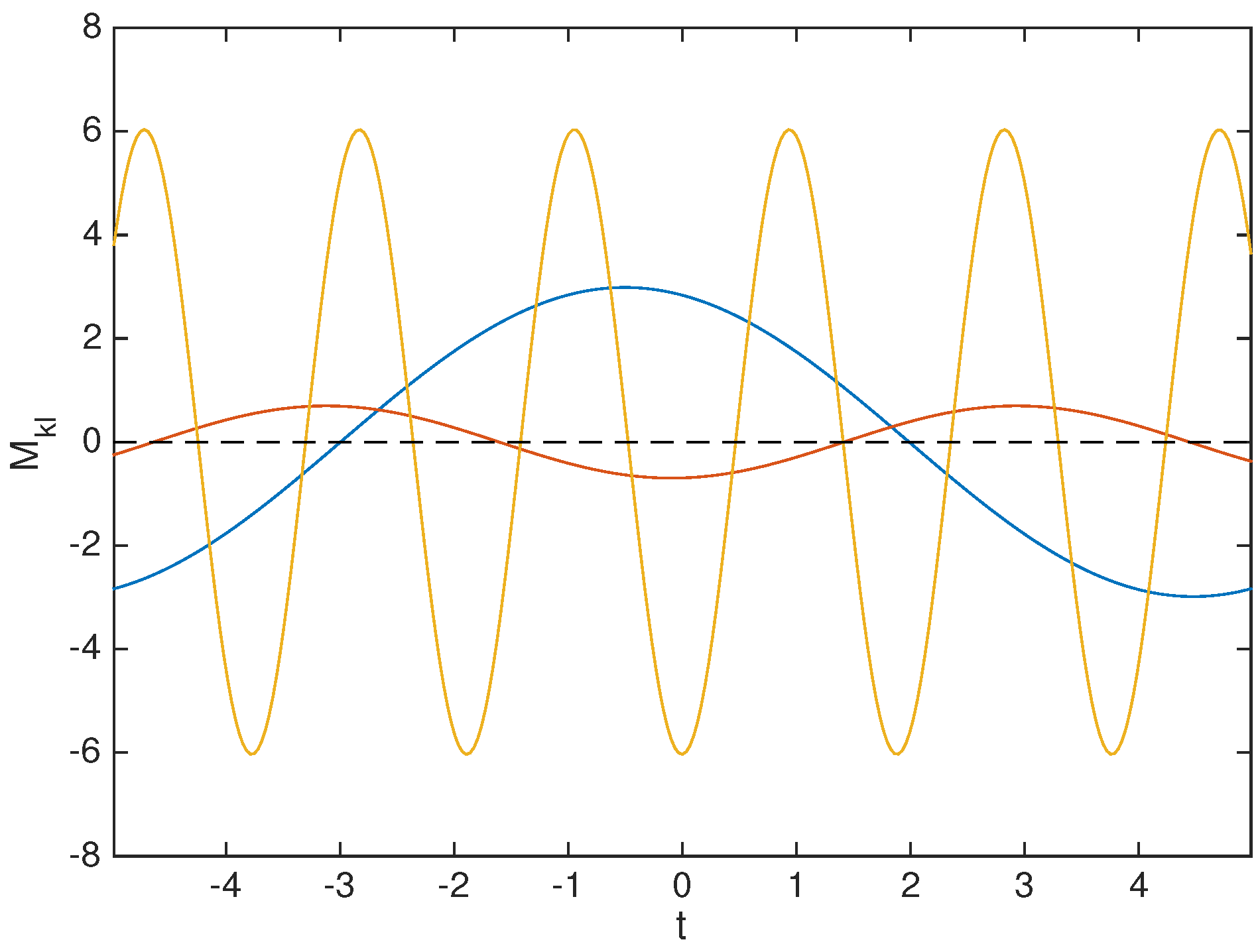
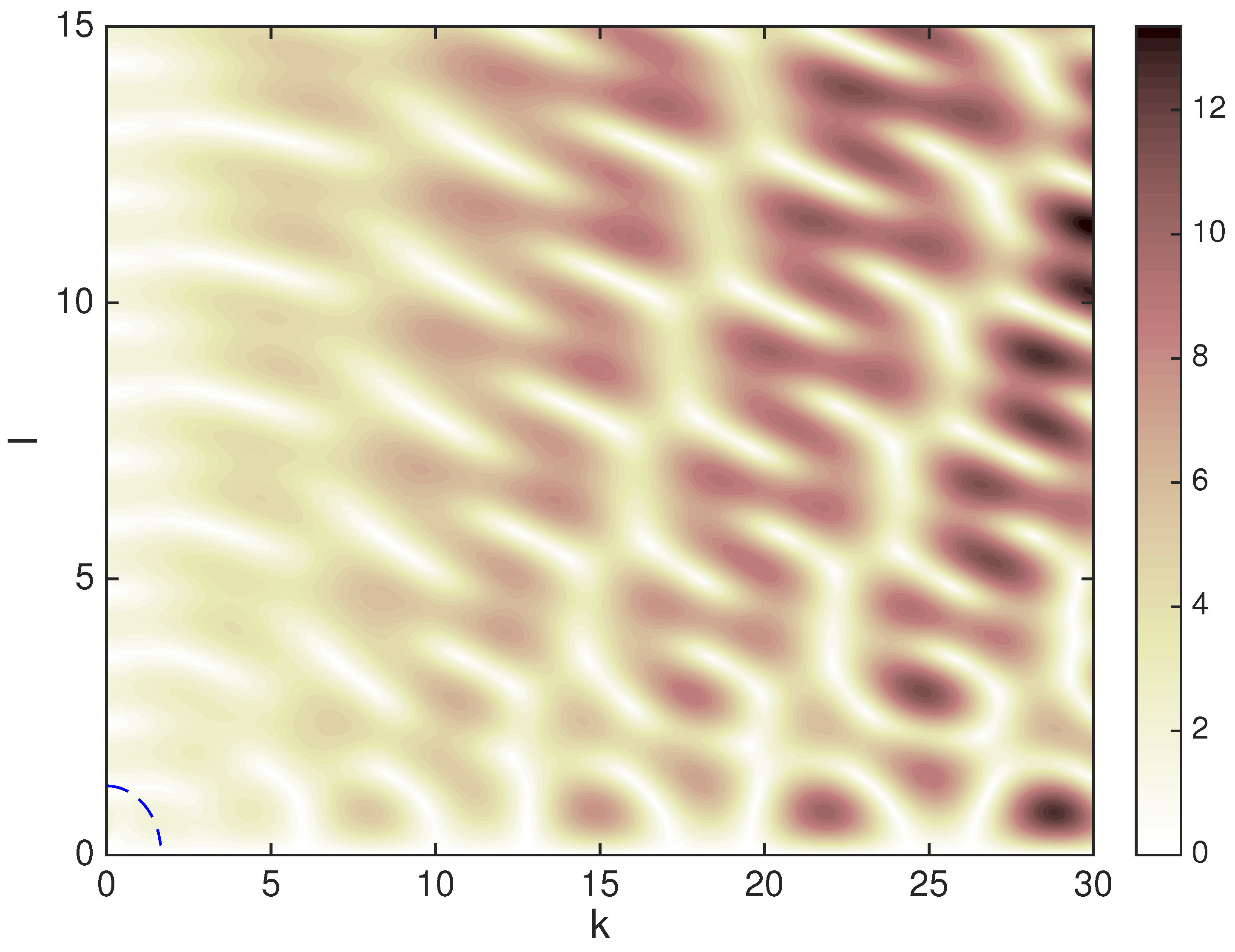
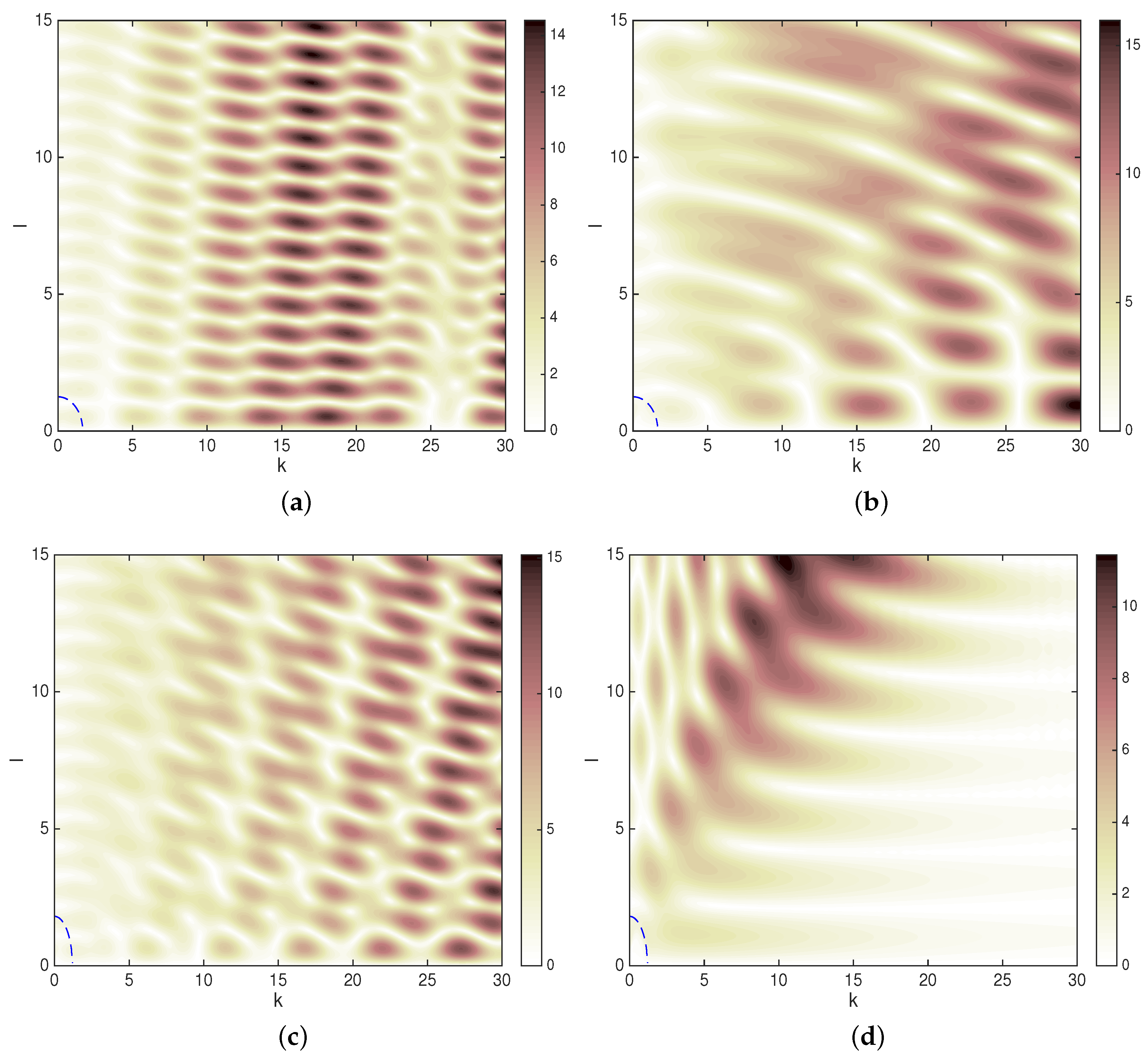
3.2. Optimal Wavenumbers
3.3. Flux for Wave Packets
4. Discussion and Conclusions
Acknowledgments
Conflicts of Interest
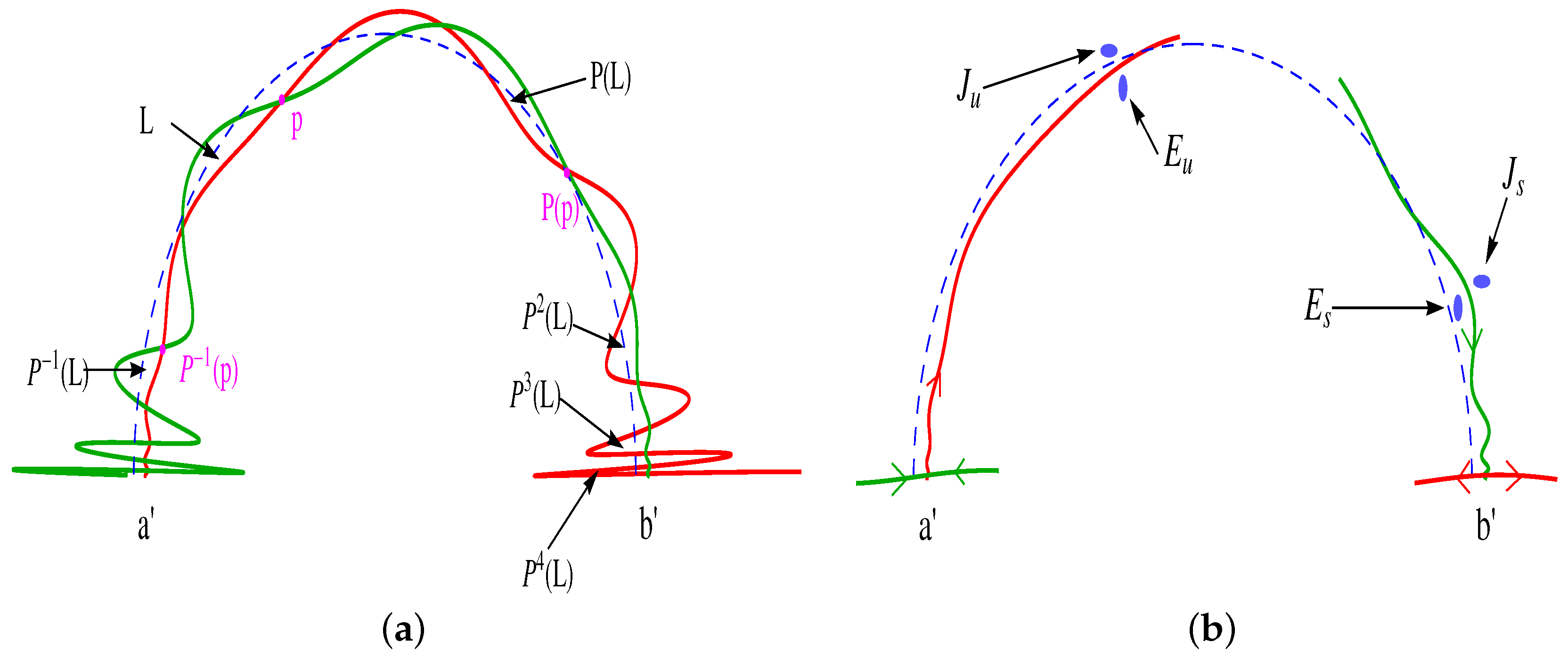
Appendix A. Relationship of Flux Definition to Other Methods
Appendix B. Derivation of the Formula for A kl
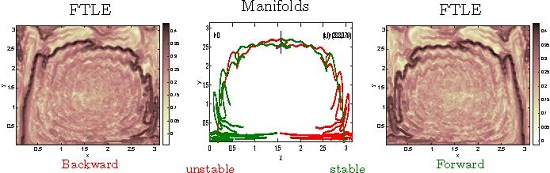
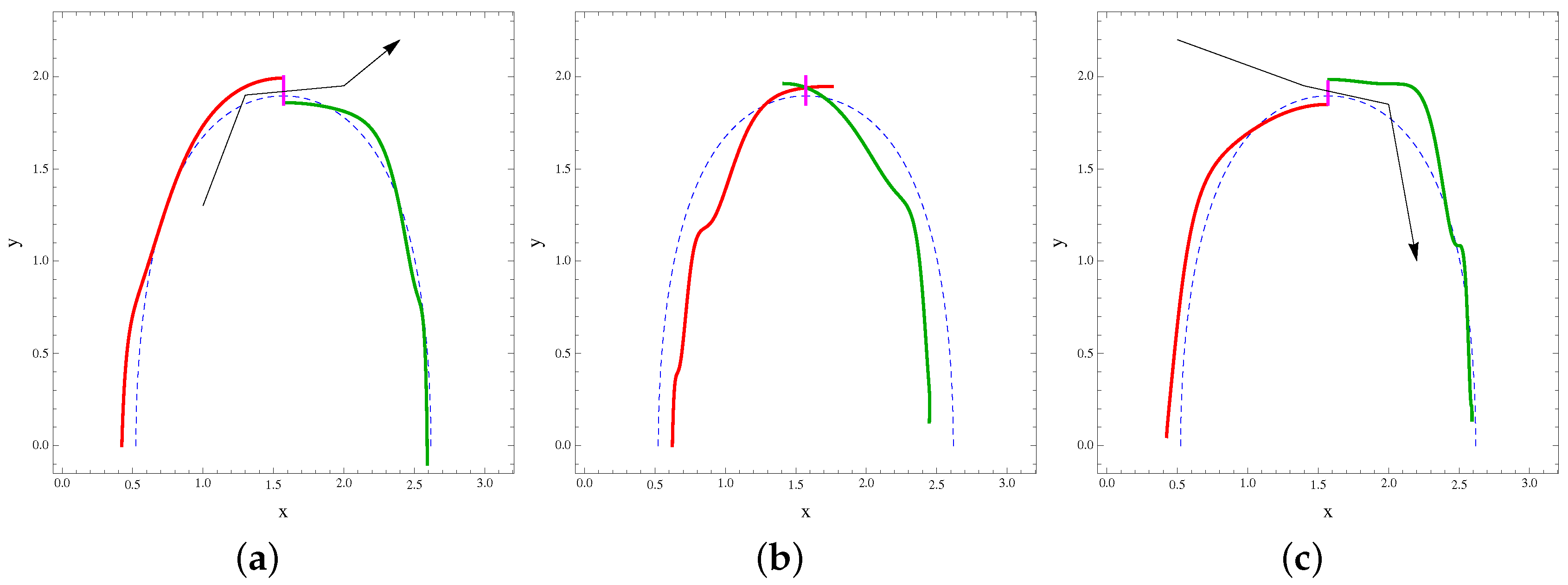
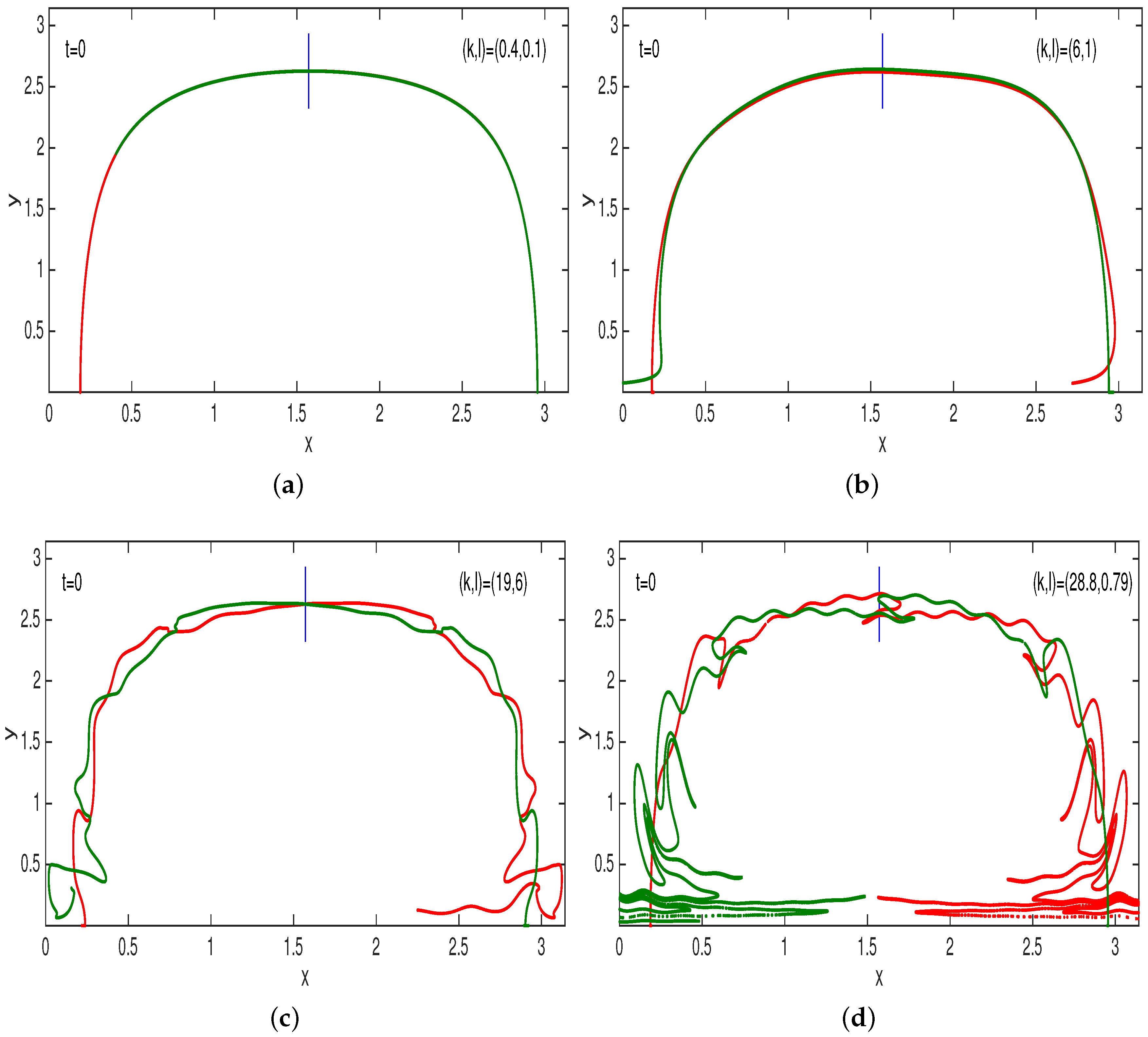
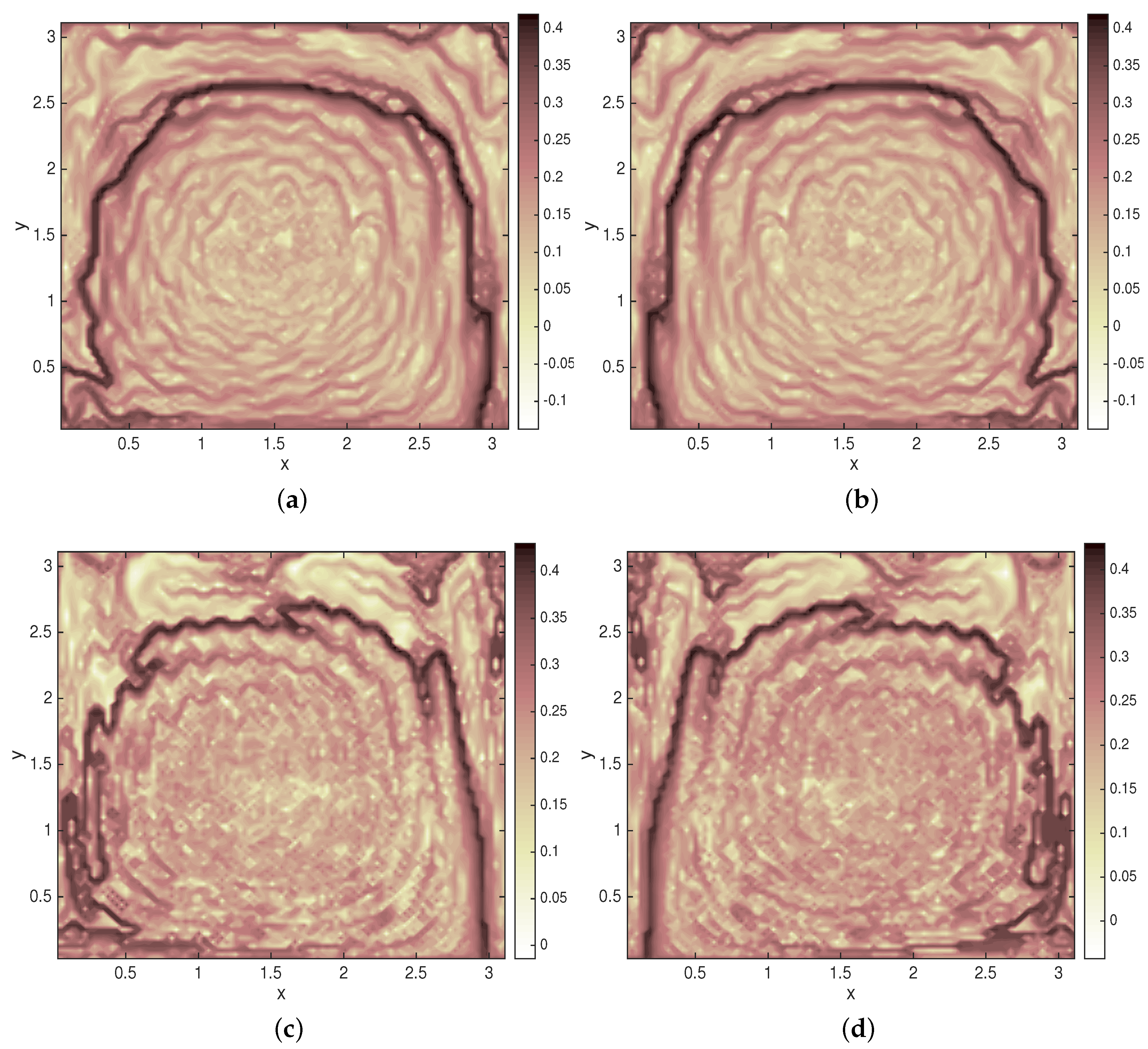
Appendix C. Numerical Scheme for Obtaining Stable and Unstable Manifolds
References
- Randall, D. An Introduction to the Global Circulation of the Atmosphere; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Pedlosky, J. Geophysical Fluids Dynamics; Springer: New York, NY, USA, 1979. [Google Scholar]
- Pierrehumbert, R. Chaotic mixing of tracer and vorticity by modulated travelling Rossby waves. Geophys. Astrophys. Fluid Dyn. 1991, 58, 285–319. [Google Scholar] [CrossRef]
- Mizuta, G. Role of Rossby waves in the broadening of an eastward jet. J. Phys. Oceanogr. 2012, 42, 476–494. [Google Scholar] [CrossRef]
- Graef, F. Free and forced Rossby normal modes in a rectangular gulf of arbitrary orientation. Dyn. Atmos. Oceans 2016, 75, 46–57. [Google Scholar] [CrossRef] [Green Version]
- Kiladis, G. Observations of Rossby waves linked to convection over the eastern tropical Pacific. J. Atmos. Sci. 1998, 55, 321–339. [Google Scholar] [CrossRef]
- Barnes, E.; Hartmann, D. Rossby wave scales, propagation, and variability of eddy-driven jets. J. Atmos. Sci. 2011, 68, 2893–2908. [Google Scholar] [CrossRef]
- Oruba, L.; Lapeyre, G.; Riviere, G. On the northward motion of mid-latitude cyclones in a barotropic meadering jet. J. Atmos. Sci. 2012, 69, 1793–1810. [Google Scholar] [CrossRef]
- Oruba, L.; Lapeyre, G.; Riviere, G. On the poleward motion of mid-latitude cyclones in a baroclinic meandering jet. J. Atmos. Sci. 2013, 70, 2629–2649. [Google Scholar] [CrossRef]
- O’Rourke, A.; Vallis, G. Jet interaction and the influence of a minimum phase speed bound on the propagation of eddies. J. Atmos. Sci. 2013, 70, 2614–2628. [Google Scholar] [CrossRef]
- Haller, G. Lagrangian Coherent Structures. Ann. Rev. Fluid Mech. 2015, 47, 137–162. [Google Scholar] [CrossRef]
- Samelson, R. Lagrangian motion, coherent structures, and lines of persistent material strain. Ann. Rev. Mar. Sci. 2013, 5, 137–163. [Google Scholar] [CrossRef] [PubMed]
- Rypina, I.; Pratt, L.; Pullen, J.; Levin, J.; Gordon, A. Chaotic advection in an archipelago. J. Phys. Oceanogr. 2010, 40, 1988–2006. [Google Scholar] [CrossRef]
- Tew Kai, E.; Rossi, V.; Sudre, J.; Weirmerskirch, H.; Lopez, C.; Hernandez-Garcia, E.; Marsac, F.; Garcon, V. Top marine predators track Lagrangian coherent structures. Proc. Nat. Acad. Sci. USA 2009, 106, 8245–8250. [Google Scholar] [CrossRef] [PubMed]
- Levy, M.; Jahn, O.; Dutkiewicz, S.; Follows, M.; d’Ovidio, F. The dynamical landscape of marine phytoplankton diversity. J. R. Soc. Interface 2015, 12, 20150481. [Google Scholar] [CrossRef] [PubMed]
- BozorgMagham, A.; Ross, S.; Schmale, D. Local finite-time Lyapunov exponent, local sampling and probabilistic source and destination regions. Nonlinear Proc. Geophys. 2015, 22, 663–677. [Google Scholar] [CrossRef]
- d’Ovidio, F.; Fernandez, V.; Hernandez-Garcia, E.; Lopez, C. Mixing structures in the Mediterranean sea from finite-size Lyapunov exponents. Geophys. Res. Lett. 2004, 31, L17203. [Google Scholar] [CrossRef]
- d’Ovidio, F.; Isern, J.; López, C.; Hernández-García, C.; García-Ladona, E. Comparison between Eulerian diagnostics and finite-size Lyapunov exponents computed from the altimetry in the Algerian basin. Deep Sea Res. 2009, 56, 15–31. [Google Scholar] [CrossRef]
- Allshouse, M.; Peacock, T. Refining finite-time Lyapunov ridges and the challenges of classifying them. Chaos 2015, 25, 087410. [Google Scholar] [CrossRef] [PubMed]
- Ngan, K.; Shepherd, T. Chaotic mixing and transport in Rossby-wave critical layers. J. Fluid Mech. 1997, 334, 315–351. [Google Scholar] [CrossRef]
- Joseph, B.; Legras, B. Relation between kinematic boundaries, stirring and barriers for the Antarctic polar vortex. J. Atmos. Sci. 2002, 59, 1198–1212. [Google Scholar] [CrossRef]
- Prants, S.; Budyansky, M.; Ponomarev, V.; Uleysky, M. Lagrangian study of transport and mixing in a mesoscale eddy street. Ocean Model. 2011, 38, 114–125. [Google Scholar] [CrossRef]
- Pratt, L.; Barkan, R.; Rypina, I. Scalar flux kinematics. Fluids 2016, in press. [Google Scholar] [CrossRef]
- Rypina, I.; Kamenkovich, I.; Berloff, P.; Pratt, L. Eddy-induced particle dispersion in the near-surface north Atlantic. J. Phys. Oceanogr. 2012, 42, 2206–2227. [Google Scholar] [CrossRef]
- Mezić, I.; Loire, S.; Fonoberov, V.; Hogan, P. A new mixing diagnostic and Gulf oil spill movement. Science 2010, 330, 486–489. [Google Scholar] [CrossRef] [PubMed]
- Mancho, A.; Small, D.; Wiggins, S.; Ide, K. Computation of stable and unstable manifolds of hyperbolic trajectories in two-dimensional, aperiodically time-dependent vector fields. Physica D 2003, 182, 188–222. [Google Scholar] [CrossRef]
- Haller, G.; Hadjighasem, A.; Farazmand, M.; Huhn, F. Defining coherent vortices objectively from the vorticity. J. Fluid Mech. 2016, 795, 136–173. [Google Scholar] [CrossRef]
- Rypina, I.; Scott, S.; Pratt, L.; Brown, M. Investigating the connection between complexity of isolated trajectories and Lagrangian coherent structures. Nonlinear Proc. Geophys. 2011, 18, 977–987. [Google Scholar] [CrossRef]
- Allshouse, M.; Thiffeault, J.L. Detecting coherent structures using braids. Physica D 2012, 241, 95–105. [Google Scholar] [CrossRef]
- Budis̆ić, M.; Thiffeault, J.L. Finite-time braiding exponents. Chaos 2015, 25, 087407. [Google Scholar] [CrossRef] [PubMed]
- Ma, T.; Bollt, E. Differential geometry perspective of shape coherence and curvature evolution by finite-time nonhyperbolic splitting. SIAM J. Appl. Dyn. Syst. 2014, 13, 1106–1136. [Google Scholar] [CrossRef] [Green Version]
- Balasuriya, S.; Kalampattel, R.; Ouellette, N. Hyperbolic neighborhoods as organizers of finite-time exponential stretching. J. Fluid Mech. 2016. submitted. [Google Scholar]
- Froyland, G.; Horenkamp, C.; Rossi, V.; van Sebille, E. Studying an Agulhas ring’s long-term pathway and decay with finite-time coherent sets. Chaos 2015, 25, 083119. [Google Scholar] [CrossRef] [PubMed]
- Froyland, G.; Stuart, R.; van Sebille, E. How well-connected is the surface of the ocean? Chaos 2014, 24, 0333126. [Google Scholar] [CrossRef] [PubMed]
- Froyland, G.; Padberg, K. Almost-invariant sets and invariant manifolds – connecting probabilistic and geometric descriptions of coherent structures in flows. Physica D 2009, 238, 1507–1523. [Google Scholar] [CrossRef]
- Ser-Giacomi, E.; Rossi, V.; López, C.; Hernández-García, E. Flow networks: A characterization of geophysical fluid transport. Chaos 2015, 25, 036404. [Google Scholar] [CrossRef] [PubMed]
- Balasuriya, S.; Jones, C.; Sandstede, B. Viscous perturbations of vorticity-conserving flows and separatrix splitting. Nonlinearity 1998, 11, 47–77. [Google Scholar] [CrossRef]
- Balasuriya, S.; Jones, C. Diffusive draining and growth of eddies. Nonlinear. Proc. Geophys. 2001, 8, 241–251. [Google Scholar] [CrossRef]
- Balasuriya, S. Nonautonomous flows as open dynamical systems: Characterising escape rates and time-varying boundaries. In Ergodic Theory, Open Dynamics, and Coherent Structures; Bahsoun, W., Bose, C., Froyland, G., Eds.; Springer: Berlin, Germany, 2014; pp. 1–30. [Google Scholar]
- Balasuriya, S. Local stable and unstable manifolds and their control in nonautonomous finite-time flows. J. Nonlinear Sci. 2016, 26, 895–927. [Google Scholar] [CrossRef]
- Balasuriya, S. Melnikov Methods for Flow Barriers and Transport in Unsteady Flows; SIAM Press: Philadelphia, PA, USA, 2016; in press. [Google Scholar]
- Brown, M.; Samelson, R. Particle motion in vorticity-conserving two-dimensional incompressible flows. Phys. Fluids 1994, 6, 2875–2876. [Google Scholar] [CrossRef]
- Balasuriya, S. Gradient evolution for potential vorticity flows. Nonlinear Proc. Geophys. 2001, 8, 253–263. [Google Scholar] [CrossRef] [Green Version]
- Samelson, R. Fluid exchange across a meandering jet. J. Phys. Oceanogr. 1992, 22, 431–442. [Google Scholar] [CrossRef]
- del Castillo Negrete, D.; Morrison, P. Chaotic transport by Rossby waves in shear flow. Phys. Fluids A 1993, 5, 948–965. [Google Scholar] [CrossRef]
- Weiss, J.; Knobloch, E. Mass transport by modulated traveling waves. Phys. Rev. A 1989, 40, 2579–2589. [Google Scholar] [CrossRef]
- Knobloch, E.; Weiss, J. Chaotic advection by modulated traveling waves. Phys. Rev. A 1987, 36, 1522–1524. [Google Scholar] [CrossRef]
- Pratt, L.; Lozier, M.; Beliakova, N. Parcel trajectories in quasigeostrophic jets: Neutral modes. J. Phys. Oceanogr. 1995, 25, 1451–1466. [Google Scholar] [CrossRef]
- Rom-Kedar, V.; Leonard, A.; Wiggins, S. An analytical study of transport, mixing and chaos in an unsteady vortical flow. J. Fluid Mech. 1990, 214, 347–394. [Google Scholar] [CrossRef]
- Rom-Kedar, V.; Poje, A. Universal properties of chaotic transport in the presence of diffusion. Phys. Fluids 1999, 11, 2044–2057. [Google Scholar] [CrossRef] [Green Version]
- Wiggins, S. Chaotic Transport in Dynamical Systems; Springer-Verlag: New York, NY, USA, 1992. [Google Scholar]
- Balasuriya, S. Direct chaotic flux quantification in perturbed planar flows: General time-periodicity. SIAM J. Appl. Dyn. Syst. 2005, 4, 282–311. [Google Scholar] [CrossRef]
- Rypina, I.; Brown, M.; Kocak, H. Transport in an idealized three-gyre system with application to the Adriatic sea. J. Phys. Oceanogr. 2009, 39, 675–690. [Google Scholar] [CrossRef]
- Rypina, I.; Brown, M.; Beron-Vera, F.; Koak, H.; Olascoaga, M.; Udovydchenkov, I. On the Lagrangian dynamics of atmospheric zonal jets and the permeability of the stratospheric polar vortex. J. Atmos. Sci. 2007, 64, 3595–3610. [Google Scholar] [CrossRef]
- Prants, S.; Budyansky, M.; Uleysky, M. Chaotic mixing and transport in a meandering jet flow. Chaos 2006, 16, 033117. [Google Scholar] [CrossRef] [PubMed]
- Miller, P.; Pratt, L.; Helfrich, K.; Jones, C. Chaotic transport of mass and potential vorticity for an island recirculation. J. Phys. Oceanogr. 2002, 32, 80–102. [Google Scholar] [CrossRef]
- Malhotra, N.; Wiggins, S. Geometric structures, lobe dynamics, and Lagrangian transport in flows with aperiodic time-dependence, with applications to Rossby wave flow. J. Nonlinear Sci. 1998, 8, 401–456. [Google Scholar] [CrossRef]
- Mancho, A.; Hernández-Garcia, E.; Small, D.; Wiggins, S.; Fernández, V. Lagrangian transport through an ocean front in the northwestern Mediterranean sea. J. Phys. Oceanogr. 2008, 28, 1222–1237. [Google Scholar] [CrossRef]
- Ide, K.; Wiggins, S. Transport induced by mean-eddy interaction: I. Theory, and relation to Lagrangian lobe dynamics. Commun. Nonlinear Sci. Numer. Simul. 2015, 20, 516–535. [Google Scholar] [CrossRef]
- Kamenkovich, V.; Kamenkovich, I. On the evolution of Rossby waves, generated by wind stress in a closed basin, incoporating total mass conservation. Dyn. Atmos. Oceans 1993, 18, 67–103. [Google Scholar] [CrossRef]
- Peacock, T.; Dabiri, J. Introduction to focus issue: Lagrangian Coherent Structures. Chaos 2010, 20, 017501. [Google Scholar] [CrossRef] [PubMed]
- Peacock, T.; Haller, G. Lagrangian coherent structures: The hidden skeleton of fluid flows. Phys. Today 2013, 66, 41. [Google Scholar] [CrossRef]
- Berloff, P. Dynamically consistent parametrization of mesoscale eddies-Part II eddy fluxes and diffusivity from transient impulses. Fluids 2016, 1, 22. [Google Scholar] [CrossRef]
- Rogerson, A.; Miller, P.; Pratt, L.; Jones, C. Lagrangian motion and fluid exchange in a barotropic meandering jet. J. Phys. Oceanogr. 1999, 29, 2635–2655. [Google Scholar] [CrossRef]
- Shevchencko, I.; Berloff, P. Multi-layer quasi-geostrophic dynamics in eddy-resolving regimes. Ocean Model. 2015, 94, 1–14. [Google Scholar] [CrossRef]
- Maddison, J.; Marshall, D.; Shipton, J. On the dynamical influence of ocean eddy potential vorticity fluxes. Ocean Model. 2015, 92, 169–182. [Google Scholar] [CrossRef]
- Yang, H.; Wu, L.; Shantong, S.; Zhaohui, C. Low-frequency variability of monsoon-driven circulation with application to the South China sea. J. Phys. Oceanogr. 2015, 45, 1632–1650. [Google Scholar] [CrossRef]
- Enomoto, T.; Matsuda, Y. Rossby wavepacket propagation in a zonally-varying basic flow. Tellus 1999, 51A, 588–602. [Google Scholar] [CrossRef]
- Farrell, B. Optimal excitation of neutral Rossby waves. J. Atmos. Sci. 1988, 45, 163–180. [Google Scholar] [CrossRef]
- Balmforth, N.; Piccolo, C. The onset of meandering in a barotropic jet. J. Fluid Mech. 2001, 449, 85–114. [Google Scholar] [CrossRef]
- Shadden, S.; Lekien, F.; Marsden, J. Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional aperiodic flows. Physica D 2005, 212, 271–304. [Google Scholar] [CrossRef]
- Mathew, G.; Mezić, I.; Petzold, L. A multiscale measure for mixing. Physica D 2005, 211, 23–46. [Google Scholar] [CrossRef]
- Nakamura, N. Two-dimensional mixing, edge formation, and permeability diagnosed in area coordinates. J. Atmos. Sci. 1996, 53, 1524–1537. [Google Scholar] [CrossRef]
- Shuckburgh, E.; Haynes, P. Diagnosing transport and mixing using a tracer-based coordinate system. Phys. Fluids 2003, 15, 3342–3357. [Google Scholar] [CrossRef]
- Hendricks, E.; Schubert, W. Transport and mixing in idealized barotropic hurricane-like vortices. Q. J. R. Meteorol. Soc. 2009, 135, 1456–1470. [Google Scholar] [CrossRef]
- Rowe, S.; Hitchman, M. On the relationship between inertial instability, poleward momentum surges, and jet intensifications near mid-latitude cyclones. J. Atmos. Sci. 2016, 73, 2299–2315. [Google Scholar] [CrossRef]
- Held, I.; Pierrehumbert, R.; Garner, S.; Swanson, K. Surface quasi-geostrophic dynamics. J. Fluid Mech. 1995, 282, 1–20. [Google Scholar] [CrossRef]
- Bower, A. A simple kinematic mechanism for mixing fluid across a meandering jet. J. Phys. Oceanogr. 1991, 21, 173–180. [Google Scholar] [CrossRef]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields; Springer: New York, NY, USA, 1983. [Google Scholar]
- Samelson, R.; Wiggins, S. Lagrangian Transport in Geophysical Jets and Waves; Interdisciplinary Applied Mathematics; Springer: Berlin, Germany, 2006. [Google Scholar]
- Balasuriya, S. Cross-separatrix flux in time-aperiodic and time-impulsive flows. Nonlinearity 2006, 19, 282–311. [Google Scholar] [CrossRef]
- Haller, G.; Poje, A. Finite time transport in aperiodic flows. Physica D 1998, 119, 352–380. [Google Scholar] [CrossRef]
- Chelton, D.; Gaube, P.; Schlax, M.; Early, J.; Samelson, R. The influence of nonlinear mesoscale eddies on oceanic chlorophyll. Science 2011, 334, 328–332. [Google Scholar] [CrossRef] [PubMed]
- Gaultier, L.; Djath, B.; Verron, J.; Brankart, J.M.; Brasseur, P.; Melet, A. Inversion of submesoscale patterns from a high-resolution Solomon Sea model: Feasibility assessment. J. Geophys. Res. Oceans 2014, 119, 4520–4541. [Google Scholar] [CrossRef]
- McIntyre, M. Potential vorticity. In Encyclopedia of Atmospheric Science, 2nd ed.; North, G., Zhang, F., Pyle, J., Eds.; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Hadjighasem, A.; Karrasch, D.; Teramoto, H.; Haller, G. Spectral clustering approach to Lagrangian vortex detection. Phys. Rev. E 2016, 93, 063107. [Google Scholar] [CrossRef] [PubMed]
- Balasuriya, S. A tangential displacement theory for locating perturbed saddles and their manifolds. SIAM J. Appl. Dyn. Syst. 2011, 10, 1100–1126. [Google Scholar] [CrossRef] [Green Version]
- Melnikov, V.K. On the stability of the centre for time-periodic perturbations. Trans. Mosc. Math. Soc. 1963, 12, 1–56. [Google Scholar]
- Coppel, W.A. Dichotomies in Stability Theory; Number 629 in Lecture Notes in Mathematics; Springer-Verlag: Berlin, Germany, 1978. [Google Scholar]
- Balasuriya, S.; Padberg-Gehle, K. Controlling the unsteady analogue of saddle stagnation points. SIAM J. Appl. Math. 2013, 73, 1038–1057. [Google Scholar] [CrossRef]
- Balasuriya, S. A numerical scheme for computing stable and unstable manifolds in nonautonomous flows. Int. J. Bifurc. Chaos 2016. submitted. [Google Scholar]

© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balasuriya, S. Meridional and Zonal Wavenumber Dependence in Tracer Flux in Rossby Waves. Fluids 2016, 1, 30. https://doi.org/10.3390/fluids1030030
Balasuriya S. Meridional and Zonal Wavenumber Dependence in Tracer Flux in Rossby Waves. Fluids. 2016; 1(3):30. https://doi.org/10.3390/fluids1030030
Chicago/Turabian StyleBalasuriya, Sanjeeva. 2016. "Meridional and Zonal Wavenumber Dependence in Tracer Flux in Rossby Waves" Fluids 1, no. 3: 30. https://doi.org/10.3390/fluids1030030
APA StyleBalasuriya, S. (2016). Meridional and Zonal Wavenumber Dependence in Tracer Flux in Rossby Waves. Fluids, 1(3), 30. https://doi.org/10.3390/fluids1030030