Comment on Tailleux, R. Neutrality versus Materiality: A Thermodynamic Theory of Neutral Surfaces. Fluids 2016, 1, 32
Abstract
:1. Overarching Comments on Tailleux
- Tailleux [7] misunderstands or misinterprets the justification, as published by Griffies [4], McDougall and Jackett [5], and McDougall et al. [6], that the energetic lateral mixing of mesoscale eddies occurs in the locally-referenced potential density surface. For example, Tailleux [7] quotes McDougall et al. [6] as implying that the individual fluid motions in mesoscale eddies move across the locally-referenced potential density surface. In contrast, McDougall et al. [6] discuss these motions only as part of a reductio ad absurdum proof. That is, McDougall et al. [6] specifically conclude, based on ocean measurements, that this dianeutral motion is NOT what occurs in the ocean. Moreover, inexplicably, Tailleux [7] asserts that while individual motions are diabatic, their average is adiabatic. This is incorrect. Rather, if individual motions are diabatic, then the average of many such motions exhibits dianeutral diffusion.
- Tailleux [7] states that, (1) in order for an adiabatic and isohaline displacement of a fluid parcel over a distance to be neutral, then (his Equation (1), where is the normal vector to the neutral tangent plane); and (2) then goes on to state that (his Equation (7)) is the buoyant force experienced by fluid parcels after such an adiabatic and isohaline displacement. Both of these statements are generally incorrect. Indeed, we consider these two incorrect equations to be at the core of the errors that permeate Tailleux [7]. The reason these equations are generally incorrect is that they ignore the unsteady nature of baroclinic motion. These two equations are only correct if the ocean hydrography is in a steady state. This is the case for a hydrographic atlas, but is it not appropriate for discussions of the underlying physics and energetics of epineutral mixing. For such discussions, it is crucial to properly account for unsteadiness of the flow during baroclinic instability and the associated release of available potential energy.
- Tailleux [7] asserts that “adiabatic and isohaline parcel exchanges can only be meaningfully defined on material surfaces of the form ”. We disagree with this statement. There is no fundamental reason that the ocean should oblige in this regard. Rather, we oceanographers should examine ocean mixing in terms of known physical processes that occur at the in situ pressure of the mixing. (Tailleux [7] uses potential temperature and an undefined type of salinity. Since Absolute Salinity and Conservative Temperature are the recommended salinity and temperature variables for use in oceanographic publications (see Valladares et al. [9] and Intergovernmental Oceanographic Commission (IOC) et al. [10]), we have adopted these variables in this paper).
2. Comments on Section 1 of Tailleux
3. Comments on Section 2 of Tailleux
4. Comments on Section 3 of Tailleux
5. Comments on Section 6 of Tailleux
5.1. Tailleux’s First Conclusion
5.2. Tailleux’s Second Conclusion
5.3. Tailleux’s Third Conclusion
5.4. Tailleux’s Fourth Conclusion
5.5. Tailleux’s Seventh Conclusion
5.6. Tailleux’s Eighth Conclusion
5.7. Tailleux’s Ninth Conclusion
5.8. Tailleux’s Eleventh Conclusion
5.9. Tailleux’s Twelfth Conclusion
5.10. Tailleux’s Thirteenth Conclusion
6. Conclusions
Acknowledgments
Conflicts of Interest
Appendix A
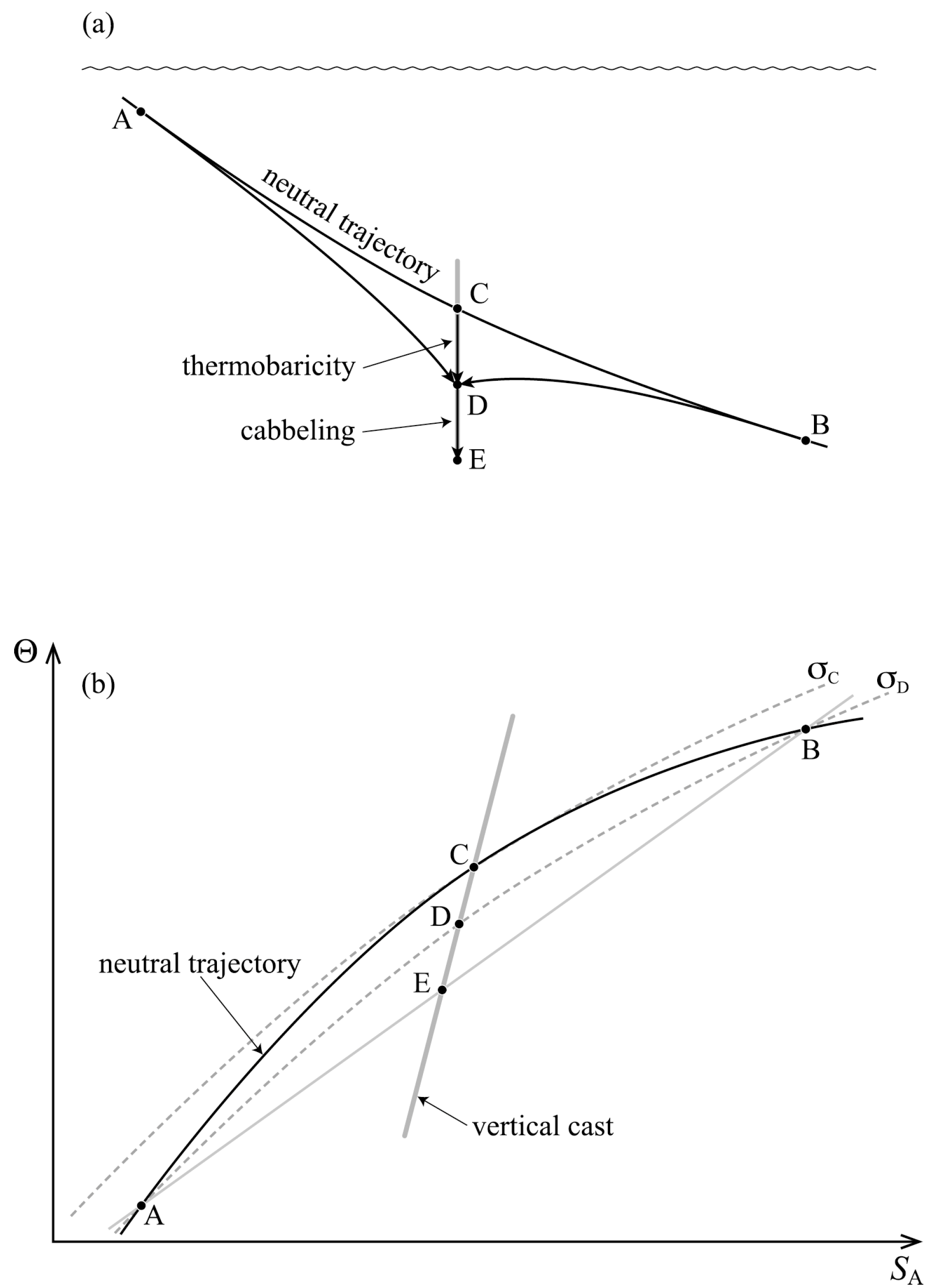
Neutral Trajectories at Finite Amplitude
References
- Iselin, C.O’.D. The influence of vertical and lateral turbulence on the characteristics of the waters at mid-depths. EOS Trans. Am. Geophys. Union 1939, 20, 414–417. [Google Scholar] [CrossRef]
- McDougall, T.J. Neutral surfaces. J. Phys. Oceanogr. 1987, 17, 1950–1964. [Google Scholar] [CrossRef]
- McDougall, T.J. Thermobaricity, cabbeling, and water-mass conversion. J. Geophys. Res. 1987, 92, 5448–5464. [Google Scholar] [CrossRef]
- Griffies, S.M. Fundamentals of Ocean Climate Models; Princeton University Press: Princeton, NJ, USA, 2004; 518 pp + xxxiv. [Google Scholar]
- McDougall, J.T.; Jackett, D.R. The material derivative of neutral density. J. Mar. Res. 2005, 63, 159–185. [Google Scholar] [CrossRef]
- McDougall, T.J.; Groeskamp, S.; Griffies, S.M. On geometrical aspects of interior ocean mixing. J. Phys. Oceanogr. 2014, 44, 2164–2175. [Google Scholar] [CrossRef]
- Tailleux, R. Neutrality versus materiality: A thermodynamic theory of neutral surfaces. Fluids 2016, 1, 32. [Google Scholar] [CrossRef]
- McDougall, T.J.; Griffies, S.M.; Groeskamp, S. The direction of mesoscale eddy-induced lateral mixing in the ocean. J. Phys. Oceanogr 2017. submitted for publication. [Google Scholar]
- Valladares, J.; Fennel, W.; Morozov, E.G. Replacement of EOS-80 with the International Thermodynamic Equation of Seawater-2010 (TEOS-10). Deep-Sea Res. I 2011, 58, 978. [Google Scholar]
- IOC (International Olympic Committee), SCOR and IAPSO. The International Thermodynamic Equation of Seawater—2010: Calculation and Use of Thermodynamic Properties. Available online: http://www.TEOS-10.org (accessed on 25 April 2017).
- Turner, J.S. Buoyancy Effects in Fluids; Cambridge University Press: Cambridge, UK, 1973; 368p. [Google Scholar]
- Groeskamp, S.; Zika, J.D.; McDougall, T.J.; Sloyan, B.M.; Laliberté, F. The representation of ocean circulation and variability in thermodynamic coordinates. J. Phys. Oceanogr. 2014, 44, 1735–1750. [Google Scholar] [CrossRef]
- Veronis, G. The role of models in tracer studies. In Numerical Models of Ocean Circulation; National Academy of Science: Washington, DC, USA, 1975; pp. 133–146. [Google Scholar]
- Gargett, E.A.; Osborn, T.R.; Nasymyth, P.W. Local isotropy and the decay of turbulence in a stratified fluid. J. Fluid Mech. 1984, 144, 231–280. [Google Scholar] [CrossRef]
- Gregg, M.C.; Sanford, T.B. The dependence of turbulent dissipation on stratification in a diffusively stable thermocline. J. Geophys. Res. 1988, 93, 12381–12392. [Google Scholar] [CrossRef]
- McDougall, T.J. The vertical motion of submesoscale coherent vortices across neutral surfaces. J. Phys. Oceanogr. 1987, 17, 2334–2342. [Google Scholar] [CrossRef]
- McDougall, T.J. Neutral-surface potential vorticity. Prog. Oceanogr. 1988, 20, 185–221. [Google Scholar] [CrossRef]
- McDougall, J.T.; Jackett, D.R. On the helical nature of neutral trajectories in the ocean. Prog. Oceanogr. 1988, 20, 153–183. [Google Scholar] [CrossRef]
- McDougall, J.T.; Jackett, D.R. The thinness of the ocean in space and the implications for mean diapycnal advection. J. Phys. Oceanogr. 2007, 37, 1714–1732. [Google Scholar] [CrossRef]
- Klocker, A.; McDougall, T.J. Influence of the nonlinear equation of state on global estimates of dianeutral advection and diffusion. J. Phys. Oceanogr. 2010, 40, 1690–1709. [Google Scholar] [CrossRef]
- Klocker, A.; McDougall, T.J. Quantifying the consequences of the ill-defined nature of neutral surfaces. J. Phys. Oceanogr. 2010, 40, 1866–1880. [Google Scholar] [CrossRef]
- Iudicone, D.; Madec, G.; McDougall, T.J. Water-mass transformations in a neutral density framework and the key role of light penetration. J. Phys. Oceanogr. 2008, 38, 1357–1376. [Google Scholar] [CrossRef]
- Groeskamp, S.; Abernathey, R.P.; Klocker, A. Water mass transformation by cabbeling and thermobaricity. Geophys. Res. Lett. 2016, 43, 10835–10845. [Google Scholar] [CrossRef]
- Klocker, A.; McDougall, T.J.; Jackett, D.R. A new method for forming approximately neutral surfaces. Ocean Sci. 2009, 5, 155–172. [Google Scholar] [CrossRef]
- McDougall, J.T.; Klocker, A. An approximate geostrophic streamfunction for use in density surfaces. Ocean Model. 2010, 32, 105–117. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
McDougall, T.J.; Groeskamp, S.; Griffies, S.M. Comment on Tailleux, R. Neutrality versus Materiality: A Thermodynamic Theory of Neutral Surfaces. Fluids 2016, 1, 32. Fluids 2017, 2, 19. https://doi.org/10.3390/fluids2020019
McDougall TJ, Groeskamp S, Griffies SM. Comment on Tailleux, R. Neutrality versus Materiality: A Thermodynamic Theory of Neutral Surfaces. Fluids 2016, 1, 32. Fluids. 2017; 2(2):19. https://doi.org/10.3390/fluids2020019
Chicago/Turabian StyleMcDougall, Trevor J., Sjoerd Groeskamp, and Stephen M. Griffies. 2017. "Comment on Tailleux, R. Neutrality versus Materiality: A Thermodynamic Theory of Neutral Surfaces. Fluids 2016, 1, 32" Fluids 2, no. 2: 19. https://doi.org/10.3390/fluids2020019
APA StyleMcDougall, T. J., Groeskamp, S., & Griffies, S. M. (2017). Comment on Tailleux, R. Neutrality versus Materiality: A Thermodynamic Theory of Neutral Surfaces. Fluids 2016, 1, 32. Fluids, 2(2), 19. https://doi.org/10.3390/fluids2020019




