Mathematical Modeling and Computer Simulations of Nanofluid Flow with Applications to Cooling and Lubrication
Abstract
:1. Introduction
2. Use of Nanofluids in Cooling and Lubrication
2.1. Experimental Evidence
2.1.1. Cooling with Nanofluids
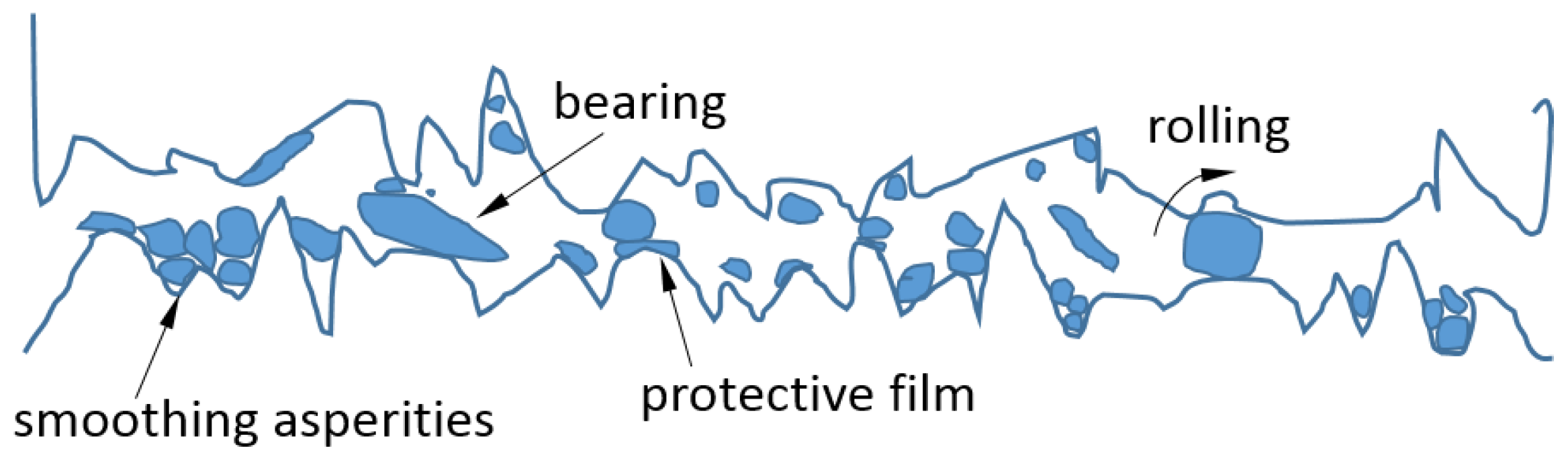
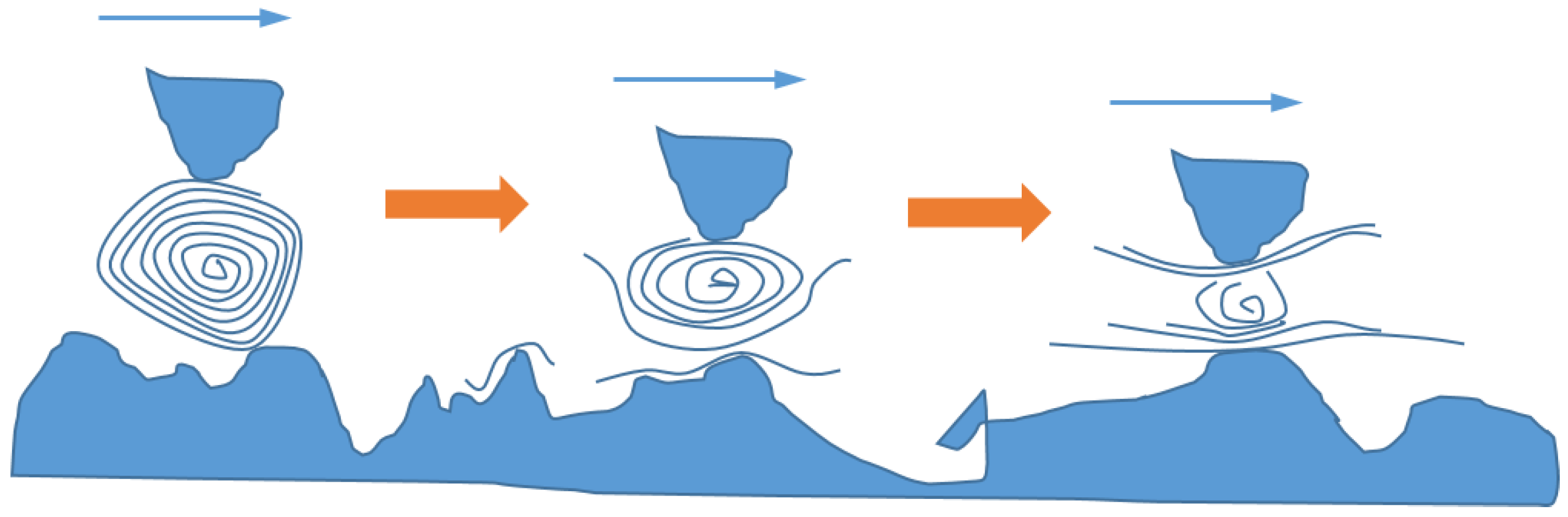
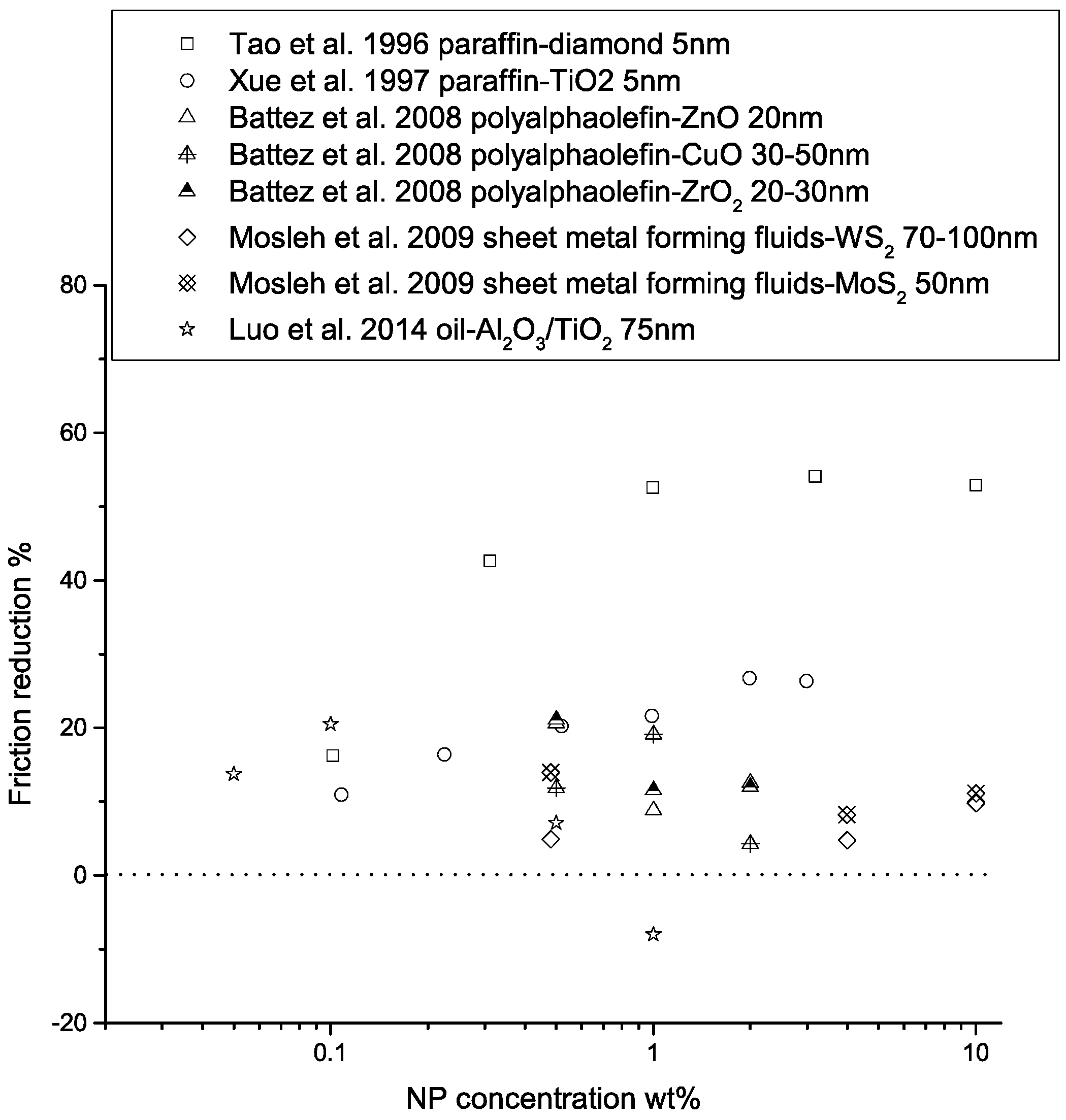
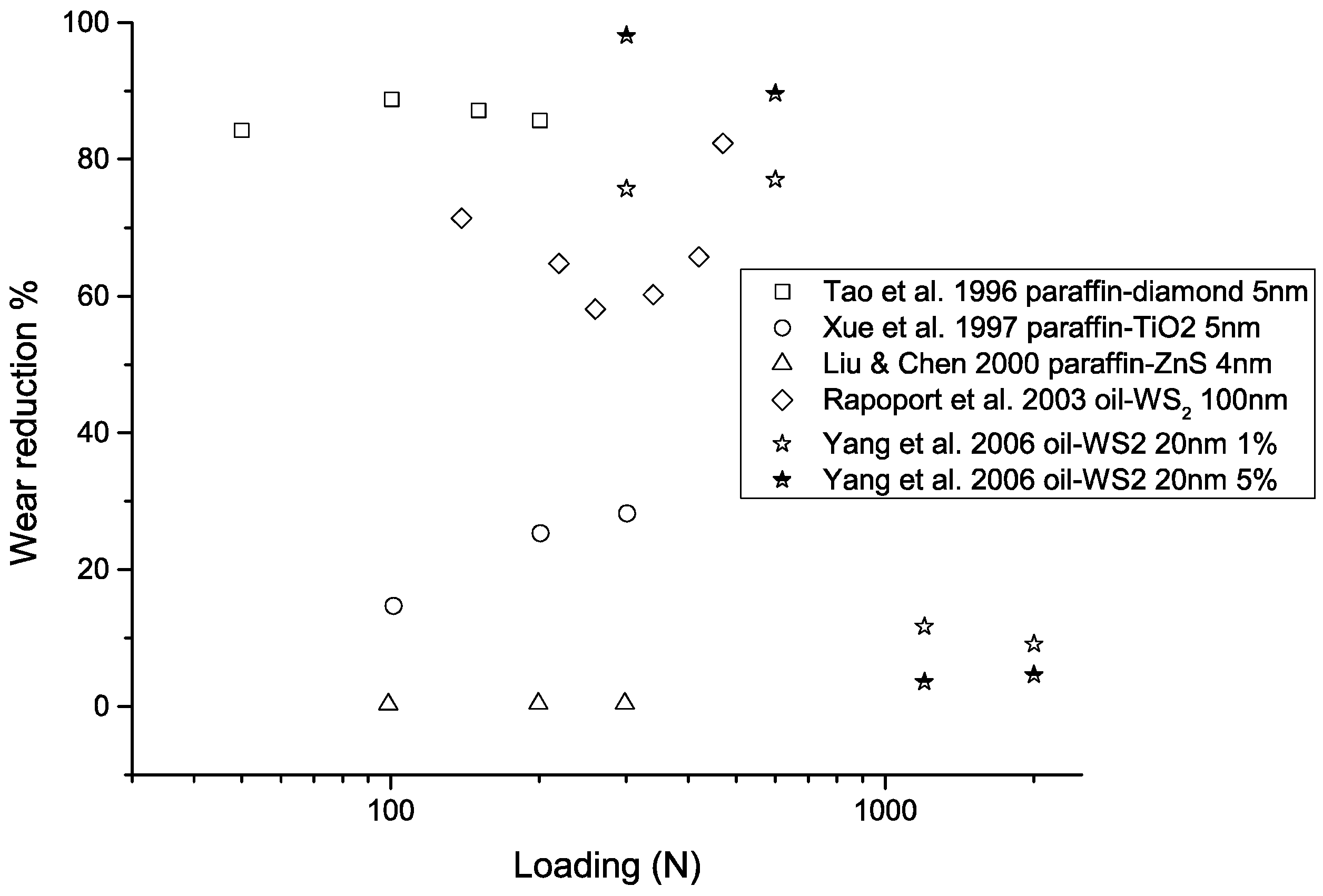
2.1.2. Nanoparticles in Lubrication
2.2. Theoretical Background
2.2.1. Forces Acting on Nanoparticles
2.2.2. Nanoparticle Aggregation
2.2.3. Thermo-Physical Properties of Nanofluids
2.3. Transport Equations and Modeling Approaches
2.3.1. Single-Phase Approach
- (Laminar flow)
- (Turbulent flow)
- (Laminar flow)
- (Turbulent flow)
2.3.2. Two-Phase Approach
2.3.3. Nanofluid Transport in Porous Media
2.3.4. Magnetic Nanofluids
2.3.5. Nanofluid Transport in Thin Films
3. Nanofluid Flow Applications
3.1. Entropy Generation
3.2. Nanodroplet-Vapor-Air Mixture Dynamics
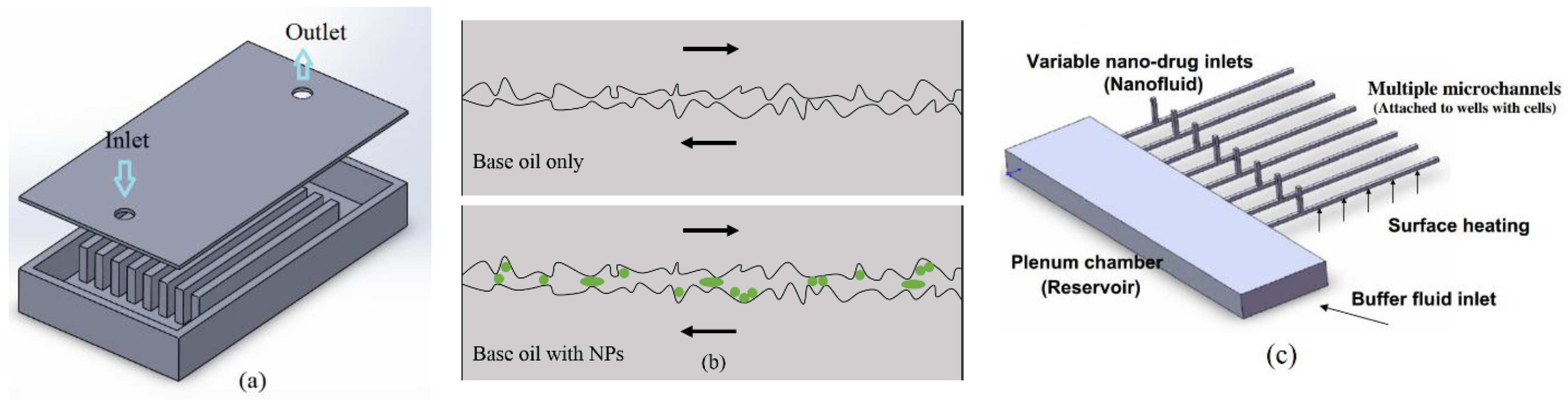
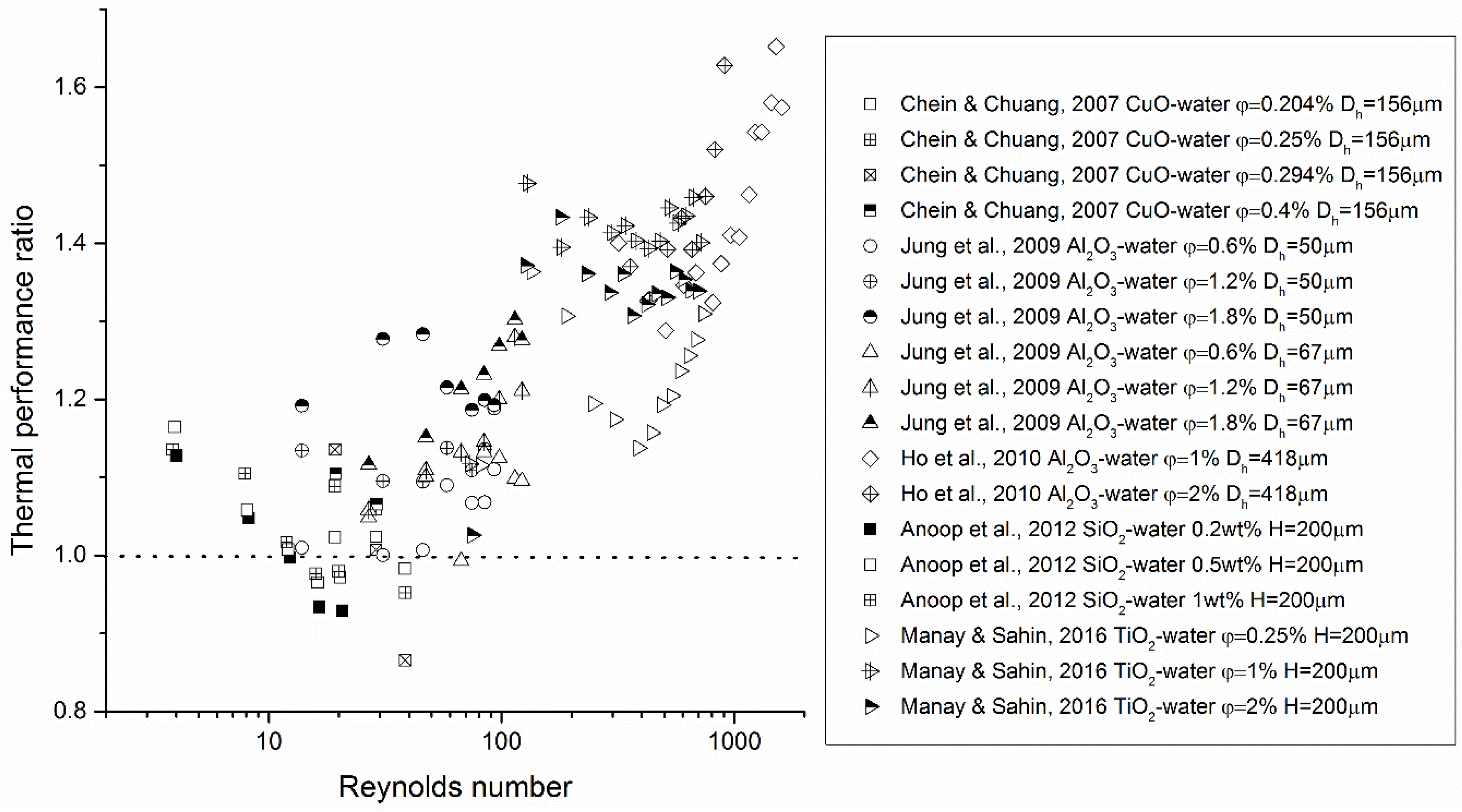
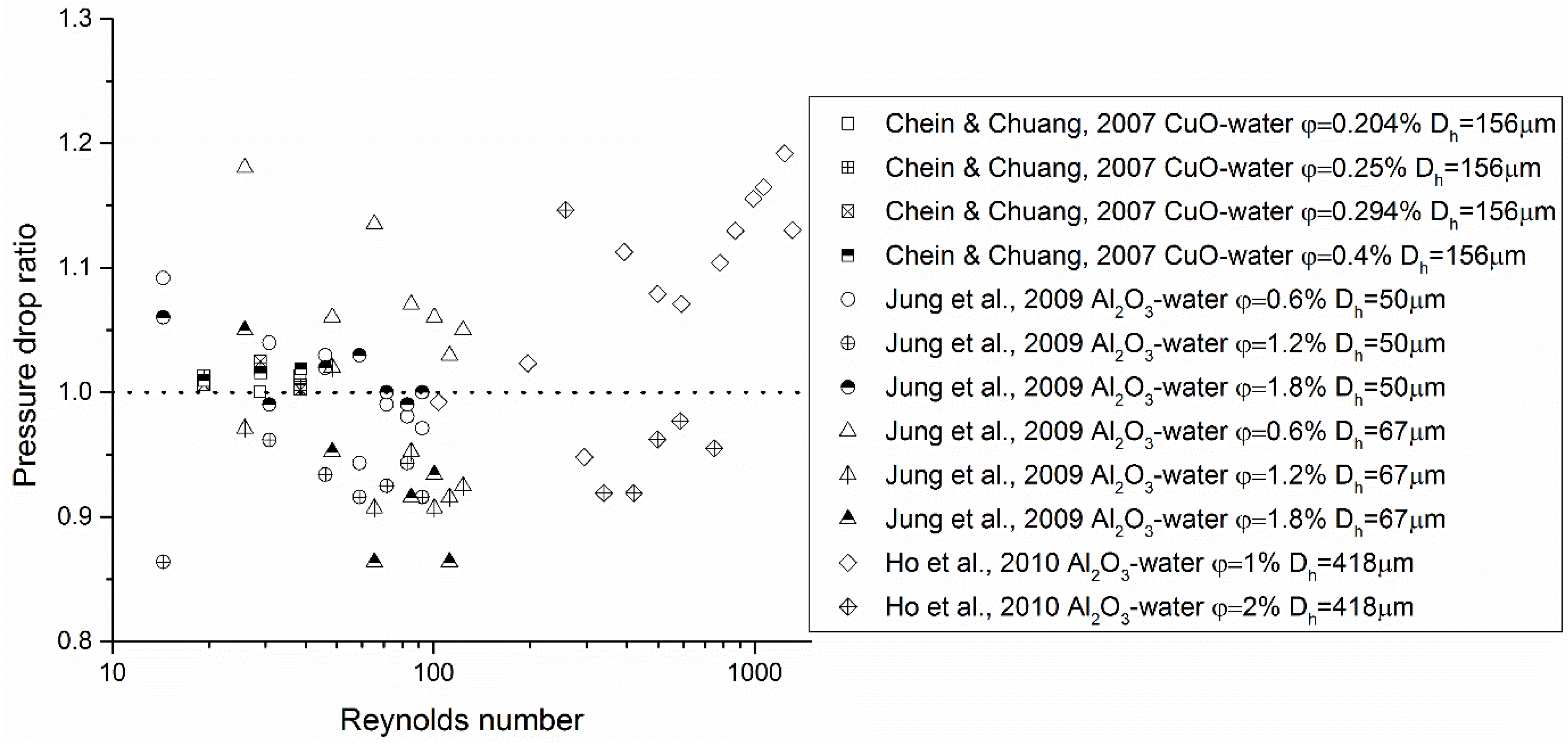
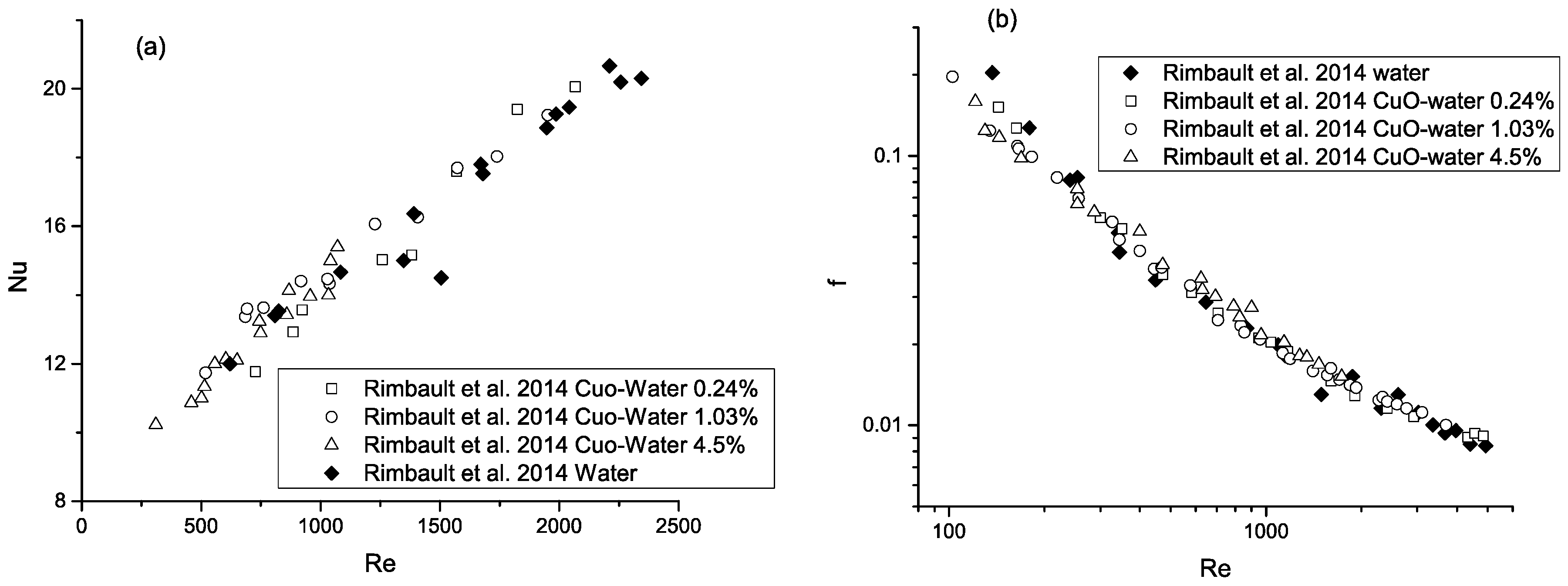
3.3. Nanofluids for Microsystem Cooling
3.4. Nanoparticles for Enhanced Lubrication
4. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| MCHS | microchannel heat sink |
| MD | molecular dynamics |
| NP | nanoparticle |
References
- Kleinstreuer, C.; Xu, Z. Thermal nanofluid flow in microchannels with applications. In Heat Transfer Enhancement with Nanofluids; Bianco, V., Manca, O., Nardini, S., Vafai, K., Eds.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Kleinstreuer, C.; Xu, Z. Convection heat transfer in conduits with nanofluids. In CRC Handbook of Thermal Engineering, 2nd ed.; Chhabra, R.P., Ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Kleinstreuer, C. Computational nanofluid flow and heat transfer in microchannels. In CRC Handbook of Fluid Dynamics, 2nd ed.; Johnson, R.W., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 1–8. [Google Scholar]
- Kleinstreuer, C.; Childress, E.M. Nanodrug delivery for tumor treatment. In Encyclopedia of Microfluidics and Nanofluidics; Li, D., Ed.; Springer: New York, NY, USA, 2015. [Google Scholar]
- Kleinstreuer, C.; Childress, E.M.; Kennedy, A.S. Targeted drug delivery: Multifunctional nanoparticles and direct micro-drug delivery to tumors. In Transport in Biological Media; Becker, S.M., Kuznetsov, A.V., Eds.; Academic Press: Cambridge, MA, USA, 2013; pp. 391–416. [Google Scholar]
- Kleinstreuer, C.; Feng, Y.; Childress, E.M. Drug-targeting methodologies with applications: A review. World J. Clin. Cases 2014, 2, 742–756. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Jernigan, S.; Kleinstreuer, C.; Buckner, G.D. Solid tumor embolotherapy in hepatic arteries with an anti-reflux catheter system. Ann. Biomed. Eng. 2016, 44, 1036–1046. [Google Scholar] [CrossRef] [PubMed]
- Fang, X.; Xuan, Y.; Li, Q. Experimental investigation on enhanced mass transfer in nanofluids. Appl. Phys. Lett. 2009, 95. [Google Scholar] [CrossRef]
- Veilleux, J.; Coulombe, S. A dispersion model of enhanced mass diffusion in nanofluids. Chem. Eng. Sci. 2011, 66, 2377–2384. [Google Scholar] [CrossRef]
- Kim, S.J.; Bang, I.C.; Buongiorno, J.; Hu, L.W. Surface wettability change during pool boiling of nanofluids and its effect on critical heat flux. Int. J. Heat Mass Transf. 2007, 50, 4105–4116. [Google Scholar] [CrossRef]
- Kwark, S.M.; Kumar, R.; Moreno, G.; Yoo, J.; You, S.M. Pool boiling characteristics of low concentration nanofluids. Int. J. Heat Mass Transf. 2010, 53, 972–981. [Google Scholar] [CrossRef]
- Michael, J.J.; Iniyan, S. Performance analysis of a copper sheet laminated photovoltaic thermal collector using copper oxide-water nanofluid. Sol. Energy 2015, 119, 439–451. [Google Scholar] [CrossRef]
- Wu, Y.Y.; Wu, S.Y.; Xiao, L. Performance analysis of photovoltaic-thermoelectric hybrid system with and without glass cover. Energy Convers. Manag. 2015, 93, 151–159. [Google Scholar] [CrossRef]
- Xu, Z.; Kleinstreuer, C. Concentration photovoltaic-thermal energy co-generation system using nanofluids for cooling and heating. Energy Convers. Manag. 2014, 87, 504–512. [Google Scholar] [CrossRef]
- Xu, Z.; Kleinstreuer, C. Computational analysis of nanofluid cooling of high concentration photovoltaic cells. J. Therm. Sci. Eng. Appl. 2014, 6. [Google Scholar] [CrossRef]
- Liu, G.L.; Kim, J.; Lu, Y.U.; Lee, L.P. Optofluidic control using photothermal nanoparticles. Nat. Mater. 2006, 5, 27–32. [Google Scholar] [CrossRef] [PubMed]
- Taylor, R.A.; Phelan, P.E.; Otanicar, T.P.; Adrian, R.; Prasher, R. Nanofluid optical property characterization: Towards efficient direct absorption solar collectors. Nanoscale Res. Lett. 2011, 6, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Taylor, R.; Coulombe, S.; Otanicar, T.; Phelan, P.; Gunawan, A.; Lv, W.; Rosengarten, G.; Prasher, R.; Tyagi, H. Small particles, big impacts: A review of the diverse applications of nanofluids. J. Appl. Phys. 2013, 113. [Google Scholar] [CrossRef]
- Ogihara, H.; Xie, J.; Okagaki, J.; Saji, T. Simple method for preparing superhydrophobic paper: Spray-deposited hydrophobic silica nanoparticle coatings exhibit high water-repellency and transparency. Langmuir 2012, 28, 4605–4608. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Wu, R.; Jing, Z.; Yan, L.; Zha, F.; Lei, Z. One-step spray-coating process for the fabrication of colorful superhydrophobic coatings with excellent corrosion resistance. Langmuir 2015, 31, 10702–10707. [Google Scholar] [CrossRef] [PubMed]
- Tao, X.; Jiazheng, Z.; Kang, X. The ball-bearing effect of diamond nanoparticles as an oil additive. J. Phys. D Appl. Phys. 1996, 29, 2932. [Google Scholar] [CrossRef]
- Hu, C.; Bai, M.; Lv, J.; Wang, P.; Li, X. Molecular dynamics simulation on the friction properties of nanofluids confined by idealized surfaces. Tribol. Int. 2014, 78, 152–159. [Google Scholar] [CrossRef]
- Spikes, H. Friction modifier additives. Tribol. Lett. 2015, 60, 1–26. [Google Scholar] [CrossRef]
- Akbulut, M. Nanoparticle-based lubrication systems. J. Powder Metall. Min. 2012, 1. [Google Scholar] [CrossRef]
- Choi, U.S. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the International Mechanical Engineering Congress and Exposition on Developments and Applications of Non-Newtonian Flows, San Francisco, CA, USA, 12–17 November 1995; Siginer, D.A., Wang, H.P., Eds.; ASME: New York, NY, USA FED-Vol. 231/MD-Vol. 66. ; pp. 99–105.
- Kleinstreuer, C.; Li, J.; Koo, J. Microfluidics of nano-drug delivery. Int. J. Heat Mass Transf. 2008, 51, 5590–5597. [Google Scholar] [CrossRef]
- Kandlikar, S.G. History, advances, and challenges in liquid flow and flow boiling heat transfer in microchannels: A critical review. J. Heat Transf. 2012, 134. [Google Scholar] [CrossRef]
- Salman, B.H.; Mohammed, H.A.; Munisamy, K.M.; Kherbeet, A.S. Characteristics of heat transfer and fluid flow in microtube and microchannel using conventional fluids and nanofluids: A review. Renew. Sustain. Energy Rev. 2013, 28, 848–880. [Google Scholar] [CrossRef]
- Chein, R.; Chuang, J. Experimental microchannel heat sink performance studies using nanofluids. Int. J. Therm. Sci. 2007, 46, 57–66. [Google Scholar] [CrossRef]
- Jung, J.Y.; Oh, H.S.; Kwak, H.Y. Forced convective heat transfer of nanofluids in microchannels. Int. J. Heat Mass Transf. 2009, 52, 466–472. [Google Scholar] [CrossRef]
- Ho, C.J.; Wei, L.C.; Li, Z.W. An experimental investigation of forced convective cooling performance of a microchannel heat sink with Al2O3/water nanofluid. Appl. Therm. Eng. 2010, 30, 96–103. [Google Scholar] [CrossRef]
- Anoop, K.; Sadr, R.; Yu, J.; Kang, S.; Jeon, S.; Banerjee, D. Experimental study of forced convective heat transfer of nanofluids in a microchannel. Int. Commun. Heat Mass Transf. 2012, 39, 1325–1330. [Google Scholar] [CrossRef]
- Byrne, M.D.; Hart, R.A.; da Silva, A.K. Experimental thermal–hydraulic evaluation of CuO nanofluids in microchannels at various concentrations with and without suspension enhancers. Int. J. Heat Mass Transf. 2012, 55, 2684–2691. [Google Scholar] [CrossRef]
- Rimbault, B.; Nguyen, C.T.; Galanis, N. Experimental investigation of CuO-water nanofluid flow and heat transfer inside a microchannel heat sink. Int. J. Therm. Sci. 2014, 84, 275–292. [Google Scholar] [CrossRef]
- Liu, D.; Yu, L. Single-phase thermal transport of nanofluids in a mini-channel. J. Heat Transf. 2011, 133. [Google Scholar] [CrossRef]
- Manay, E.; Sahin, B. The effect of microchannel height on performance of nanofluids. Int. J. Heat Mass Transf. 2016, 95, 307–320. [Google Scholar] [CrossRef]
- Azizi, Z.; Alamdari, A.; Malayeri, M.R. Thermal performance and friction factor of a cylindrical microchannel heat sink cooled by cu-water nanofluid. Appl. Therm. Eng. 2016, 99, 970–978. [Google Scholar] [CrossRef]
- Chevalier, J.; Tillement, O.; Ayela, F. Rheological properties of nanofluids flowing through microchannels. Appl. Phys. Lett. 2007, 91. [Google Scholar] [CrossRef]
- Hu, C.; Bai, M.; Lv, J.; Liu, H.; Li, X. Molecular dynamics investigation of the effect of copper nanoparticle on the solid contact between friction surfaces. Appl. Surf. Sci. 2014, 321, 302–309. [Google Scholar] [CrossRef]
- Zhang, Z.; Xue, Q.; Zhang, J. Synthesis, structure and lubricating properties of dialkyldithiophosphate-modified Mo-S compound nanoclusters. Wear 1997, 209, 8–12. [Google Scholar] [CrossRef]
- Xue, Q.; Liu, W.; Zhang, Z. Friction and wear properties of a surface-modified TiO2 nanoparticle as an additive in liquid paraffin. Wear 1997, 213, 29–32. [Google Scholar] [CrossRef]
- Liu, W.; Chen, S. An investigation of the tribological behaviour of surface-modified ZnS nanoparticles in liquid paraffin. Wear 2000, 238, 120–124. [Google Scholar] [CrossRef]
- Gao, Y.; Chen, G.; Oli, Y.; Zhang, Z.; Xue, Q. Study on tribological properties of oleic acid-modified TiO2 nanoparticle in water. Wear 2002, 252, 454–458. [Google Scholar] [CrossRef]
- Radice, S.; Mischler, S. Effect of electrochemical and mechanical parameters on the lubrication behaviour of Al2O3 nanoparticles in aqueous suspensions. Wear 2006, 261, 1032–1041. [Google Scholar] [CrossRef]
- Battez, A.H.; González, R.; Viesca, J.L.; Fernández, J.E.; Fernández, J.D.; Machado, A.; Chou, R.; Riba, J. CuO, ZrO2 and ZnO nanoparticles as antiwear additive in oil lubricants. Wear 2008, 265, 422–428. [Google Scholar] [CrossRef]
- Tevet, O.; Von-Huth, P.; Popovitz-Biro, R.; Rosentsveig, R.; Wagner, H.D.; Tenne, R. Friction mechanism of individual multilayered nanoparticles. Proc. Natl. Acad. Sci. USA 2011, 108, 19901–19906. [Google Scholar] [CrossRef] [PubMed]
- Tannous, J.; Dassenoy, F.; Lahouij, I.; le Mogne, T.; Vacher, B.; Bruhács, A.; Tremel, W. Understanding the tribochemical mechanisms of IF-MoS2 nanoparticles under boundary lubrication. Tribol. Lett. 2011, 41, 55–64. [Google Scholar] [CrossRef]
- Rapoport, L.; Moshkovich, A.; Perfilyev, V.; Laikhtman, A.; Lapsker, I.; Yadgarov, L.; Rosentsveig, R.; Tenne, R. High lubricity of re-doped fullerene-like MoS2 nanoparticles. Tribol. Lett. 2012, 45, 257–264. [Google Scholar] [CrossRef]
- Yadgarov, L.; Petrone, V.; Rosentsveig, R.; Feldman, Y.; Tenne, R.; Senatore, A. Tribological studies of rhenium doped fullerene-like MoS2 nanoparticles in boundary, mixed and elasto-hydrodynamic lubrication conditions. Wear 2013, 297, 1103–1110. [Google Scholar] [CrossRef]
- Shahnazar, S.; Bagheri, S.; Hamid, S.B.A. Enhancing lubricant properties by nanoparticle additives. Int. J. Hydrog. Energy 2016, 41, 3153–3170. [Google Scholar] [CrossRef]
- Rapoport, L.; Leshchinsky, V.; Lapsker, I.; Volovik, Y.; Nepomnyashchy, O.; Lvovsky, M.; Popovitz-Biro, R.; Feldman, Y.; Tenne, R. Tribological properties of WS2 nanoparticles under mixed lubrication. Wear 2003, 255, 785–793. [Google Scholar] [CrossRef]
- Kalin, M.; Kogovšek, J.; Remškar, M. Mechanisms and improvements in the friction and wear behavior using MoS2 nanotubes as potential oil additives. Wear 2012, 280, 36–45. [Google Scholar] [CrossRef]
- Bartz, W.J. Some investigations on the influence of particle size on the lubricating effectiveness of molybdenum disulfide. ASLE Trans. 1972, 15, 207–215. [Google Scholar] [CrossRef]
- Cusano, C.; Sliney, H.E. Dynamics of solid dispersions in oil during the lubrication of point contacts, Part I—Graphite. ASLE Trans. 1982, 25, 183–189. [Google Scholar] [CrossRef]
- Cusano, C.; Sliney, H.E. Dynamics of solid dispersions in oil during the lubrication of point contacts, Part II—molybdenum disulfide. ASLE Trans. 1982, 25, 190–197. [Google Scholar] [CrossRef]
- Zhou, J.; Yang, J.; Zhang, Z.; Liu, W.; Xue, Q. Study on the structure and tribological properties of surface-modified Cu nanoparticles. Mater. Res. Bull. 1999, 34, 1361–1367. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Shan, L.; Chen, J.; Xue, Q. Tribological performances of the graphite like carbon films deposited with different target powers in ambient air and distilled water. Tribol. Int. 2014, 73, 17–24. [Google Scholar] [CrossRef]
- Qiu, S.; Dong, J.; Cheng, G. A review of ultrafine particles as antiwear additives and friction modifiers in lubricating oils. Lubr. Sci. 1999, 11, 217–226. [Google Scholar]
- Liu, G.; Li, X.; Qin, B.; Xing, D.; Guo, Y.; Fan, R. Investigation of the mending effect and mechanism of copper nano-particles on a tribologically stressed surface. Tribol. Lett. 2004, 17, 961–966. [Google Scholar] [CrossRef]
- Mosleh, M.; Atnafu, N.D.; Belk, J.H.; Nobles, O.M. Modification of sheet metal forming fluids with dispersed nanoparticles for improved lubrication. Wear 2009, 267, 1220–1225. [Google Scholar] [CrossRef]
- Hisakado, T.; Tsukizoe, T.; Yoshikawa, H. Lubrication mechanism of solid lubricants in oils. J. Lubr. Technol. 1983, 105, 245–252. [Google Scholar] [CrossRef]
- Tenne, R. Inorganic nanotubes and fullerene-like nanoparticles. Nat. Nanotechnol. 2006, 1, 103–111. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Qin, L.; Zeng, Q.; Dong, G. Understanding the physical adsorption action mechanism of MoS2 nanoparticles in boundary lubrication with different Polyisobutyleneamine Succinimide (PIBS) concentrations. Tribol. Lett. 2015, 60, 1–12. [Google Scholar] [CrossRef]
- Liang, S.; Shen, Z.; Yi, M.; Liu, L.; Zhang, X.; Ma, S. In-situ exfoliated graphene for high-performance water-based lubricants. Carbon 2016, 96, 1181–1190. [Google Scholar] [CrossRef]
- Xie, H.; Jiang, B.; He, J.; Xia, X.; Pan, F. Lubrication performance of MoS2 and SiO2 nanoparticles as lubricant additives in magnesium alloy-steel contacts. Tribol. Int. 2016, 93, 63–70. [Google Scholar] [CrossRef]
- Rosentsveig, R.; Gorodnev, A.; Feuerstein, N.; Friedman, H.; Zak, A.; Fleischer, N.; Tannous, J.; Dassenoy, F.; Tenne, R. Fullerene-like MoS2 nanoparticles and their tribological behavior. Tribol. Lett. 2009, 36, 175–182. [Google Scholar] [CrossRef]
- Paskvale, S.; Remškar, M.; Čekada, M. Tribological performance of TiN, TiAlN and CrN hard coatings lubricated by MoS2 nanotubes in Polyalphaolefin oil. Wear 2016, 352, 72–78. [Google Scholar] [CrossRef]
- Luo, J.; Wen, S.; Huang, P. Thin film lubrication. Part I. Study on the transition between EHL and thin film lubrication using a relative optical interference intensity technique. Wear 1996, 194, 107–115. [Google Scholar] [CrossRef]
- Shen, M.; Luo, J.; Wen, S. The tribological properties of oils added with diamond nano-particles. Tribol. Trans. 2001, 44, 494–498. [Google Scholar] [CrossRef]
- Peng, D.X.; Kang, Y.; Hwang, R.M.; Shyr, S.S.; Chang, Y.P. Tribological properties of diamond and SiO2 nanoparticles added in paraffin. Tribol. Int. 2009, 42, 911–917. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, C.; Jia, D.; Zhang, D.; Zhang, X. Experimental evaluation of the lubrication performance of MoS2/CNT nanofluid for minimal quantity lubrication in Ni-based alloy grinding. Int. J. Mach. Tools Manuf. 2015, 99, 19–33. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, C.; Jia, D.; Li, B.; Wang, Y.; Yang, M.; Hou, Y.; Zhang, X. Experimental study on the effect of nanoparticle concentration on the lubricating property of nanofluids for MQL grinding of Ni-based alloy. J. Mater. Process. Technol. 2016, 232, 100–115. [Google Scholar] [CrossRef]
- Jia, D.; Li, C.; Zhang, Y.; Zhang, D.; Zhang, X. Experimental research on the influence of the jet parameters of minimum quantity lubrication on the lubricating property of Ni-based alloy grinding. Int. J. Adv. Manuf. Technol. 2016, 82, 617–630. [Google Scholar] [CrossRef]
- Nam, J.S.; Kim, D.H.; Chung, H.; Lee, S.W. Optimization of environmentally benign micro-drilling process with nanofluid minimum quantity lubrication using response surface methodology and genetic algorithm. J. Clean. Prod. 2015, 102, 428–436. [Google Scholar] [CrossRef]
- Yu, X.; Jiang, Z.; Zhao, J.; Wei, D.; Zhou, C.; Huang, Q. Effects of grain boundaries in oxide scale on tribological properties of nanoparticles lubrication. Wear 2015, 332, 1286–1292. [Google Scholar] [CrossRef]
- Yu, X.; Jiang, Z.; Zhao, J.; Wei, D.; Zhou, J.; Zhou, C.; Huang, Q. The role of oxide-scale microtexture on tribological behaviour in the nanoparticle lubrication of hot rolling. Tribol. Int. 2016, 93, 190–201. [Google Scholar] [CrossRef]
- Zareh-Desari, B.; Abaszadeh-Yakhforvazani, M.; Khalilpourazary, S. The effect of nanoparticle additives on lubrication performance in deep drawing process: Evaluation of forming load, friction coefficient and surface quality. Int. J. Precis. Eng. Manuf. 2015, 16, 929–936. [Google Scholar] [CrossRef]
- Wang, L.; Gao, Y.; Li, Z.; Zhou, A.; Li, P. Preparation and tribological properties of surface-modified ZnS nanoparticles. Lubr. Sci. 2015, 27, 241–250. [Google Scholar] [CrossRef]
- Alves, S.M.; Mello, V.S.; Faria, E.A.; Camargo, A.P.P. Nanolubricants developed from tiny CuO nanoparticles. Tribol. Int. 2016, in press. [Google Scholar] [CrossRef]
- Sui, T.; Song, B.; Wen, Y.H.; Zhang, F. Bifunctional hairy silica nanoparticles as high-performance additives for lubricant. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Hou, X.; Li, Z.; Li, X.; Yu, L.; Zhang, Z. Preparation of surface-modified lanthanum fluoride-graphene oxide nanohybrids and evaluation of their tribological properties as lubricant additive in liquid paraffin. Appl. Surf. Sci. 2015, in press. [Google Scholar] [CrossRef]
- Verma, A.; Jiang, W.; Abu Safe, H.H.; Brown, W.D.; Malshe, A.P. Tribological behavior of deagglomerated active inorganic nanoparticles for advanced lubrication. Tribol. Trans. 2008, 51, 673–678. [Google Scholar] [CrossRef]
- Battez, A.H.; Viesca, J.L.; González, R.; Blanco, D.; Asedegbega, E.; Osorio, A. Friction reduction properties of a CuO nanolubricant used as lubricant for a NiCrBSi coating. Wear 2010, 268, 325–328. [Google Scholar] [CrossRef]
- Jiao, D.; Zheng, S.; Wang, Y.; Guan, R.; Cao, B. The tribology properties of alumina/silica composite nanoparticles as lubricant additives. Appl. Surf. Sci. 2011, 257, 5720–5725. [Google Scholar] [CrossRef]
- Zhang, B.S.; Xu, B.S.; Xu, Y.; Gao, F.; Shi, P.J.; Wu, Y.X. Cu nanoparticles effect on the tribological properties of hydrosilicate powders as lubricant additive for steel-steel contacts. Tribol. Int. 2011, 44, 878–886. [Google Scholar] [CrossRef]
- Lahouij, I.; Vacher, B.; Martin, J.M.; Dassenoy, F. IF-MoS2 based lubricants: Influence of size, shape and crystal structure. Wear 2012, 296, 558–567. [Google Scholar] [CrossRef]
- Luo, T.; Wei, X.; Zhao, H.; Cai, G.; Zheng, X. Tribology properties of Al2O3/TiO2 nanocomposites as lubricant additives. Ceram. Int. 2014, 40, 10103–10109. [Google Scholar] [CrossRef]
- Rabaso, P.; Ville, F.; Dassenoy, F.; Diaby, M.; Afanasiev, P.; Cavoret, J.; Vacher, B.; le Mogne, T. Boundary lubrication: Influence of the size and structure of inorganic fullerene-like MoS2 nanoparticles on friction and wear reduction. Wear 2014, 320, 161–178. [Google Scholar] [CrossRef]
- Bogunovic, L.; Zuenkeler, S.; Toensing, K.; Anselmetti, D. An oil-based lubrication system based on nanoparticular TiO2 with superior friction and wear properties. Tribol. Lett. 2015, 59, 1–12. [Google Scholar] [CrossRef]
- Ghaednia, H.; Hossain, M.S.; Jackson, R.L. Tribological performance of silver nanoparticle-enhanced polyethylene glycol lubricants. Tribol. Trans. 2015. [Google Scholar] [CrossRef]
- Xu, Z. An Improved Thermal Conductivity Model for Nanofluids with Applications to Concentration Photovoltaic-Thermal Systems. Master’s Thesis, North Carolina State University, Raleigh, NC, USA, 2014. [Google Scholar]
- Michaelides, E.E. Transport properties of nanofluids. A critical review. J. Non-Equilib. Thermodyn. 2013, 38, 1–79. [Google Scholar] [CrossRef]
- McNab, G.S.; Meisen, A. Thermophoresis in liquids. J. Colloid Interface Sci. 1973, 44, 339–346. [Google Scholar] [CrossRef]
- Hunter, R.J. Foundations of Colloid Science; Oxford University Press: New York, NY, USA, 2001. [Google Scholar]
- Shukla, R.K.; Dhir, V.K. Effect of Brownian motion on thermal conductivity of nanofluids. J. Heat Transf. 2008, 130. [Google Scholar] [CrossRef]
- Kleinstreuer, C.; Feng, Y. Thermal nanofluid property model with application to nanofluid flow in a parallel-disk System—Part I: A new thermal conductivity model for nanofluid flow. J. Heat Transf. 2012, 134. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Ghadimi, A.; Saidur, R.; Metselaar, H.S.C. A review of nanofluid stability properties and characterization in stationary conditions. Int. J. Heat Mass Transf. 2011, 54, 4051–4068. [Google Scholar] [CrossRef]
- Saidur, R.; Leong, K.Y.; Mohammad, H.A. A review on applications and challenges of nanofluids. Renew. Sustain. Energy Rev. 2011, 15, 1646–1668. [Google Scholar] [CrossRef]
- Nan, C.W.; Birringer, R.; Clarke, D.R.; Gleiter, H. Effective thermal conductivity of particulate composites with interfacial thermal resistance. J. Appl. Phys. 1997, 81, 6692–6699. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism; Clarendon Press: Oxford, UK, 1881. [Google Scholar]
- Yu, W.; Choi, S.U.S. The role of interfacial layers in the enhanced thermal conductivity of nanofluids: A renovated Maxwell model. J. Nanopart. Res. 2003, 5, 167–171. [Google Scholar] [CrossRef]
- Kleinstreuer, C. Microfluidic and Nanofluidics: Theory and Selected Applications; John Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Mahbubul, I.M.; Saidur, R.; Amalina, M.A. Latest developments on the viscosity of nanofluids. Int. J. Heat Mass Transf. 2012, 55, 874–885. [Google Scholar] [CrossRef]
- Prasher, R.; Song, D.; Wang, J.; Phelan, P. Measurements of nanofluid viscosity and its implications for thermal applications. App. Phys. Lett. 2006, 89. [Google Scholar] [CrossRef]
- Timofeeva, E.V.; Routbort, J.L.; Singh, D. Particle shape effect on thermophysical properties of alumina nanofluids. J. Appl. Phys. 2009, 106. [Google Scholar] [CrossRef]
- Halelfadl, S.; Maré, T.; Estellé, P. Efficiency of carbon nanotubes water based nanofluids as coolants. Exp. Therm. Fluid Sci. 2014, 53, 104–110. [Google Scholar] [CrossRef]
- Einstein, A. Eine neue bestimmung der moleküldimensionen. Ann. Phys. 1906, 324, 289–306. [Google Scholar] [CrossRef]
- Brinkman, H.C. The viscosity of concentrated suspensions and solutions. J. Chem. Phys. 1952, 20, 571–571. [Google Scholar] [CrossRef]
- Corcione, M. Empirical correlating equations for predicting the effective thermal conductivity and dynamic viscosity of nanofluids. Energy Convers. Manag. 2011, 52, 789–793. [Google Scholar] [CrossRef]
- Sarkar, J. A critical review on convective heat transfer correlations of nanofluids. Renew. Sustain. Energy Rev. 2011, 15, 3271–3277. [Google Scholar] [CrossRef]
- Sundar, L.S.; Singh, M.K. Convective heat transfer and friction factor correlations of nanofluid in a tube and with inserts: A review. Renew. Sustain. Energy Rev. 2013, 20, 23–35. [Google Scholar] [CrossRef]
- Yu, W.; France, D.M.; Timofeeva, E.V.; Singh, D.; Routbort, J.L. Comparative review of turbulent heat transfer of nanofluids. Int. J. Heat Mass Transf. 2012, 55, 5380–5396. [Google Scholar] [CrossRef]
- Karimipour, A.; Nezhad, A.H.; D’Orazio, A.; Esfe, M.H.; Safaei, M.R.; Shirani, E. Simulation of copper-water nanofluid in a microchannel in slip flow regime using the lattice Boltzmann method. Eur. J. Mech. B Fluids 2015, 49, 89–99. [Google Scholar] [CrossRef]
- Sun, C.; Lu, W.Q.; Liu, J.; Bai, B. Molecular dynamics simulation of nanofluid’s effective thermal conductivity in high-shear-rate Couette flow. Int. J. Heat Mass Transf. 2011, 54, 2560–2567. [Google Scholar] [CrossRef]
- Yang, J.C.; Li, F.C.; Cai, W.H.; Zhang, H.N.; Yu, B. On the mechanism of convective heat transfer enhancement in a turbulent flow of nanofluid investigated by DNS and analyses of POD and FSP. Int. J. Heat Mass Transf. 2014, 78, 277–288. [Google Scholar] [CrossRef]
- Abu-Nada, E. Dissipative particle dynamics simulation of natural convection using variable thermal properties. Int. Commun. Heat Mass Transf. 2015, 69, 84–93. [Google Scholar] [CrossRef]
- Mokmeli, A.; Saffar-Avval, M. Prediction of nanofluid convective heat transfer using the dispersion model. Int. J. Therm. Sci. 2010, 49, 471–478. [Google Scholar] [CrossRef]
- Kamyar, A.; Saidur, R.; Hasanuzzaman, M. Application of computational fluid dynamics (CFD) for nanofluids. Int. J. Heat Mass Transf. 2012, 55, 4104–4115. [Google Scholar] [CrossRef]
- Bahiraei, M.; Hosseinalipour, S.M. Thermal dispersion model compared with Euler-Lagrange approach in simulation of convective heat transfer for nanoparticle suspensions. J. Dispers. Sci. Technol. 2013, 34, 1778–1789. [Google Scholar] [CrossRef]
- Behroyan, I.; Vanaki, S.M.; Ganesan, P.; Saidur, R. A comprehensive comparison of various CFD models for convective heat transfer of Al2O3 nanofluid inside a heated tube. Int. Commun. Heat Mass Transf. 2016, 70, 27–37. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. Thermal instability in a porous medium layer saturated by a nanofluid. Int. J. Heat Mass Transf. 2009, 52, 5796–5801. [Google Scholar] [CrossRef]
- Mahdi, R.A.; Mohammed, H.A.; Munisamy, K.M.; Saeid, N.H. Review of convection heat transfer and fluid flow in porous media with nanofluid. Renew. Sustain. Energy Rev. 2015, 41, 715–734. [Google Scholar] [CrossRef]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- Tzou, D.Y. Thermal instability of nanofluids in natural convection. Int. J. Heat Mass Transf. 2008, 51, 2967–2979. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Schmid, S.R.; Jacobson, B.O. Fundamentals of Fluid Film Lubrication, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Shenoy, B.S.; Binu, K.G.; Pai, R.; Rao, D.S.; Pai, R.S. Effect of nanoparticles additives on the performance of an externally adjustable fluid film bearing. Tribol. Lett. 2012, 45, 38–42. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization: The Method of Thermodynamic Optimization of Finite-Size Systems and Finite-Time Processes; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Li, J.; Kleinstreuer, C. Entropy generation analysis for nanofluid flow in microchannels. J. Heat Transf. 2010, 132. [Google Scholar] [CrossRef]
- Feng, Y.; Kleinstreuer, C. Nanofluid convective heat transfer in a parallel-disk system. Int. J. Heat Mass Transf. 2010, 53, 4619–4628. [Google Scholar] [CrossRef]
- Mahian, O.; Kianifar, A.; Kleinstreuer, C.; Al-Nimr, M.A.; Pop, I.; Sahin, A.Z.; Wongwises, S. A review of entropy generation in nanofluid flow. Int. J. Heat Mass Transf. 2013, 65, 514–532. [Google Scholar]
- Feng, Y.; Kleinstreuer, C.; Castro, N.; Rostami, A. Computational transport, phase change and deposition analysis of inhaled multicomponent droplet-vapor mixtures in an idealized human upper lung model. J. Aerosol Sci. 2016, 96, 96–123. [Google Scholar] [CrossRef]
- Turns, S.R. An Introduction to Combustion; McGraw-Hill: New York, NY, USA, 1996; Volume 287. [Google Scholar]
- Hinds, W.C. Aerosol Technology: Properties, Behavior, and Measurement of Airborne Particles, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- Tu, H.H.; Ray, A.K. Measurement of activity coefficients from unsteady state evaporation and growth of microdroplets. Chem. Eng. Commun. 2005, 192, 474–498. [Google Scholar] [CrossRef]
- Lee, S.; Choi, S.U.S. Application of Metallic Nanoparticle Suspensions in Advanced Cooling Systems; No. ANL/ET/CP-90558; CONF-961105-20; Argonne National Lab.: Argonne, IL, USA, 1996.
- Chein, R.; Huang, G. Analysis of microchannel heat sink performance using nanofluids. Appl. Therm. Eng. 2005, 25, 3104–3114. [Google Scholar] [CrossRef]
- Koo, J.; Kleinstreuer, C. Laminar nanofluid flow in microheat-sinks. Int. J. Heat Mass Transf. 2005, 48, 2652–2661. [Google Scholar] [CrossRef]
- Jang, S.P.; Choi, S.U. Cooling performance of a microchannel heat sink with nanofluids. Appl. Therm. Eng. 2006, 26, 2457–2463. [Google Scholar] [CrossRef]
- Li, J.; Kleinstreuer, C. Thermal performance of nanofluid flow in microchannels. Int. J. Heat Fluid Flow 2008, 29, 1221–1232. [Google Scholar] [CrossRef]
- Lelea, D. The performance evaluation of Al2O3/water nanofluid flow and heat transfer in microchannel heat sink. Int. J. Heat Mass Transf. 2011, 54, 3891–3899. [Google Scholar] [CrossRef]
- Lelea, D.; Nisulescu, C. The micro-tube heat transfer and fluid flow of water based Al2O3 nanofluid with viscous dissipation. Int. Commun. Heat Mass Transf. 2011, 38, 704–710. [Google Scholar] [CrossRef]
- Ting, T.W.; Hung, Y.M.; Guo, N. Entropy generation of nanofluid flow with streamwise conduction in microchannels. Energy 2014, 64, 979–990. [Google Scholar] [CrossRef]
- Tsai, T.H.; Chein, R. Performance analysis of nanofluid-cooled microchannel heat sinks. Int. J. Heat Fluid Flow 2007, 28, 1013–1026. [Google Scholar] [CrossRef]
- Chen, C.H.; Ding, C.Y. Study on the thermal behavior and cooling performance of a nanofluid-cooled microchannel heat sink. Int. J. Therm. Sci. 2011, 50, 378–384. [Google Scholar] [CrossRef]
- Hatami, M.; Ganji, D.D. Thermal and flow analysis of microchannel heat sink (MCHS) cooled by Cu-water nanofluid using porous media approach and least square method. Energy Convers. Manag. 2014, 78, 347–358. [Google Scholar] [CrossRef]
- Kalteh, M.; Abbassi, A.; Saffar-Avval, M.; Harting, J. Eulerian–Eulerian two-phase numerical simulation of nanofluid laminar forced convection in a microchannel. Int. J. Heat Fluid Flow 2011, 32, 107–116. [Google Scholar] [CrossRef]
- Kalteh, M.; Abbassi, A.; Saffar-Avval, M.; Frijns, A.; Darhuber, A.; Harting, J. Experimental and numerical investigation of nanofluid forced convection inside a wide microchannel heat sink. Appl. Therm. Eng. 2012, 36, 260–268. [Google Scholar] [CrossRef]
- Fani, B.; Abbassi, A.; Kalteh, M. Effect of nanoparticles size on thermal performance of nanofluid in a trapezoidal microchannel-heat-sink. Int. Commun. Heat Mass Transf. 2013, 45, 155–161. [Google Scholar] [CrossRef]
- Ghale, Z.Y.; Haghshenasfard, M.; Esfahany, M.N. Investigation of nanofluids heat transfer in a ribbed microchannel heat sink using single-phase and multiphase CFD models. Int. Commun. Heat Mass Transf. 2015, 68, 122–129. [Google Scholar] [CrossRef]
- Ahmed, M.; Eslamian, M. Laminar forced convection of a nanofluid in a microchannel: Effect of flow inertia and external forces on heat transfer and fluid flow characteristics. Appl. Therm. Eng. 2015, 78, 326–338. [Google Scholar] [CrossRef]
- Shalchi-Tabrizi, A.; Seyf, H.R. Analysis of entropy generation and convective heat transfer of Al2O3 nanofluid flow in a tangential micro heat sink. Int. J. Heat Mass Transf. 2012, 55, 4366–4375. [Google Scholar] [CrossRef]
- Ting, T.W.; Hung, Y.M.; Guo, N. Effects of streamwise conduction on thermal performance of nanofluid flow in microchannel heat sinks. Energy Convers. Manag. 2014, 78, 14–23. [Google Scholar] [CrossRef]
- Ting, T.W.; Hung, Y.M.; Guo, N. Entropy generation of viscous dissipative nanofluid flow in thermal non-equilibrium porous media embedded in microchannels. Int. J. Heat Mass Transf. 2015, 81, 862–877. [Google Scholar] [CrossRef]
- Cruz-Duarte, J.M.; Garcia-Perez, A.; Amaya-Contreras, I.M.; Correa-Cely, C.R. Designing a microchannel heat sink with colloidal coolants through the entropy generation minimisation criterion and global optimisation algorithms. Appl. Therm. Eng. 2016, 100, 1052–1062. [Google Scholar] [CrossRef]
- Sabaghan, A.; Edalatpour, M.; Moghadam, M.C.; Roohi, E.; Niazmand, H. Nanofluid flow and heat transfer in a microchannel with longitudinal vortex generators: Two-phase numerical simulation. Appl. Therm. Eng. 2016, 100, 179–189. [Google Scholar] [CrossRef]
- Mohammed, H.A.; Bhaskaran, G.; Shuaib, N.H.; Abu-Mulaweh, H.I. Influence of nanofluids on parallel flow square microchannel heat exchanger performance. Int. Commun. Heat Mass Transf. 2011, 38, 1–9. [Google Scholar] [CrossRef]
- Mohammed, H.A.; Bhaskaran, G.; Shuaib, N.H.; Saidur, R. Numerical study of heat transfer enhancement of counter nanofluids flow in rectangular microchannel heat exchanger. Superlattices Microstruct. 2011, 50, 215–233. [Google Scholar] [CrossRef]
- Mohammadian, S.K.; Seyf, H.R.; Zhang, Y. Performance augmentation and optimization of aluminum oxide-water nanofluid flow in a two-fluid microchannel heat exchanger. J. Heat Transf. 2014, 136. [Google Scholar] [CrossRef]
- Islami, S.B.; Dastvareh, B.; Gharraei, R. Numerical study of hydrodynamic and heat transfer of nanofluid flow in microchannels containing micromixer. Int. Commun. Heat Mass Transf. 2013, 43, 146–154. [Google Scholar] [CrossRef]
- Islami, S.B.; Dastvareh, B.; Gharraei, R. An investigation on the hydrodynamic and heat transfer of nanofluid flow, with non-Newtonian base fluid, in micromixers. Int. J. Heat Mass Transf. 2014, 78, 917–929. [Google Scholar] [CrossRef]
- Lelea, D.; Laza, I. The water based Al2O3 nanofluid flow and heat transfer in tangential microtube heat sink with multiple inlets. Int. J. Heat Mass Transf. 2014, 69, 264–275. [Google Scholar] [CrossRef]
- Wang, X.D.; An, B.; Lin, L.; Lee, D.J. Inverse geometric optimization for geometry of nanofluid-cooled microchannel heat sink. Appl. Therm. Eng. 2013, 55, 87–94. [Google Scholar] [CrossRef]
- Wang, X.D.; An, B.; Xu, J.L. Optimal geometric structure for nanofluid-cooled microchannel heat sink under various constraint conditions. Energy Convers. Manag. 2013, 65, 528–538. [Google Scholar] [CrossRef]
- Halelfadl, S.; Adham, A.M.; Mohd-Ghazali, N.; Maré, T.; Estellé, P.; Ahmad, R. Optimization of thermal performances and pressure drop of rectangular microchannel heat sink using aqueous carbon nanotubes based nanofluid. Appl. Therm. Eng. 2014, 62, 492–499. [Google Scholar] [CrossRef]
- Yang, Y.T.; Tang, H.W.; Ding, W.P. Optimization design of micro-channel heat sink using nanofluid by numerical simulation coupled with genetic algorithm. Int. Commun. Heat Mass Transf. 2016, 72, 29–38. [Google Scholar] [CrossRef]
- Mital, M. Analytical analysis of heat transfer and pumping power of laminar nanofluid developing flow in microchannels. Appl. Therm. Eng. 2013, 50, 429–436. [Google Scholar] [CrossRef]
- Alvariño, P.F.; Jabardo, J.S.; Agras, J.P.; del Valle, J.G. Self-diffusion assessment in laminar developed flow of nanofluids in microchannels. Int. J. Therm. Sci. 2015, 98, 113–123. [Google Scholar] [CrossRef]
- Hedayati, F.; Domairry, G. Nanoparticle migration effects on fully developed forced convection of TiO2-water nanofluid in a parallel plate microchannel. Particuology 2016, 24, 96–107. [Google Scholar] [CrossRef]
- Nikkhah, Z.; Karimipour, A.; Safaei, M.R.; Forghani-Tehrani, P.; Goodarzi, M.; Dahari, M.; Wongwises, S. Forced convective heat transfer of water/functionalized multi-walled carbon nanotube nanofluids in a microchannel with oscillating heat flux and slip boundary condition. Int. Commun. Heat Mass Transf. 2015, 68, 69–77. [Google Scholar] [CrossRef]
- Zhao, G.; Jian, Y.; Li, F. Streaming potential and heat transfer of nanofluids in microchannels in the presence of magnetic field. J. Magn. Magn. Mater. 2016, 407, 75–82. [Google Scholar] [CrossRef]
- Bahiraei, M.; Hangi, M. Flow and heat transfer characteristics of magnetic nanofluids: A review. J. Magn. Magn. Mater. 2015, 374, 125–138. [Google Scholar] [CrossRef]
- Malvandi, A.; Ganji, D.D. Effects of nanoparticle migration and asymmetric heating on magnetohydrodynamic forced convection of alumina/water nanofluid in microchannels. Eur. J. Mech. B Fluids 2015, 52, 169–184. [Google Scholar] [CrossRef]
- Malvandi, A.; Kaffash, M.H.; Ganji, D.D. Nanoparticles migration effects on magnetohydrodynamic (MHD) laminar mixed convection of alumina/water nanofluid inside microchannels. J. Taiwan Inst. Chem. Eng. 2015, 52, 40–56. [Google Scholar] [CrossRef]
- Hajialigol, N.; Fattahi, A.; Ahmadi, M.H.; Qomi, M.E.; Kakoli, E. MHD mixed convection and entropy generation in a 3-D microchannel using Al2O3-water nanofluid. J. Taiwan Inst. Chem. Eng. 2015, 46, 30–42. [Google Scholar] [CrossRef]
- Lv, J.; Bai, M.; Cui, W.; Li, X. The molecular dynamic simulation on impact and friction characters of nanofluids with many nanoparticles system. Nanoscale Res. Lett. 2011, 6. [Google Scholar] [CrossRef] [PubMed]
- Hu, C.; Bai, M.; Lv, J.; Kou, Z.; Li, X. Molecular dynamics simulation on the tribology properties of two hard nanoparticles (diamond and silicon dioxide) confined by two iron blocks. Tribol. Int. 2015, 90, 297–305. [Google Scholar] [CrossRef]
- Hu, C.; Bai, M.; Lv, J.; Li, X. Molecular dynamics simulation of mechanism of nanoparticle in improving load-carrying capacity of lubricant film. Comput. Mater. Sci. 2015, 109, 97–103. [Google Scholar] [CrossRef]
- Binu, K.G.; Shenoy, B.S.; Rao, D.S.; Pai, R. Static characteristics of a fluid film bearing with TiO2 based nanolubricant using the modified Krieger-Dougherty viscosity model and couple stress model. Tribol. Lett. 2014, 75, 69–79. [Google Scholar] [CrossRef]
- Nicoletti, R. The importance of the heat capacity of lubricants with nanoparticles in the static behavior of journal bearings. J. Tribol. 2014, 136, 044502. [Google Scholar] [CrossRef]
- Österle, W.; Dmitriev, A.I.; Kloß, H. Possible impacts of third body nanostructure on friction performance during dry sliding determined by computer simulation based on the method of movable cellular automata. Tribol. Int. 2012, 48, 128–136. [Google Scholar] [CrossRef]
- Österle, W.; Dmitriev, A.I.; Kloß, H. Assessment of sliding friction of a nanostructured solid lubricant film by numerical simulation with the method of movable cellular automata (MCA). Tribol. Lett. 2014, 54, 257–262. [Google Scholar] [CrossRef]
- Dmitriev, A.I.; Österle, W.; Wetzel, B.; Zhang, G. Mesoscale modeling of the mechanical and tribological behavior of a polymer matrix composite based on epoxy and 6 vol % silica nanoparticles. Comput. Mater. Sci. 2015, 110, 204–214. [Google Scholar] [CrossRef]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kleinstreuer, C.; Xu, Z. Mathematical Modeling and Computer Simulations of Nanofluid Flow with Applications to Cooling and Lubrication. Fluids 2016, 1, 16. https://doi.org/10.3390/fluids1020016
Kleinstreuer C, Xu Z. Mathematical Modeling and Computer Simulations of Nanofluid Flow with Applications to Cooling and Lubrication. Fluids. 2016; 1(2):16. https://doi.org/10.3390/fluids1020016
Chicago/Turabian StyleKleinstreuer, Clement, and Zelin Xu. 2016. "Mathematical Modeling and Computer Simulations of Nanofluid Flow with Applications to Cooling and Lubrication" Fluids 1, no. 2: 16. https://doi.org/10.3390/fluids1020016
APA StyleKleinstreuer, C., & Xu, Z. (2016). Mathematical Modeling and Computer Simulations of Nanofluid Flow with Applications to Cooling and Lubrication. Fluids, 1(2), 16. https://doi.org/10.3390/fluids1020016





