Estimating the Size of Dog Populations in Tanzania to Inform Rabies Control
Abstract
1. Introduction
2. Methods
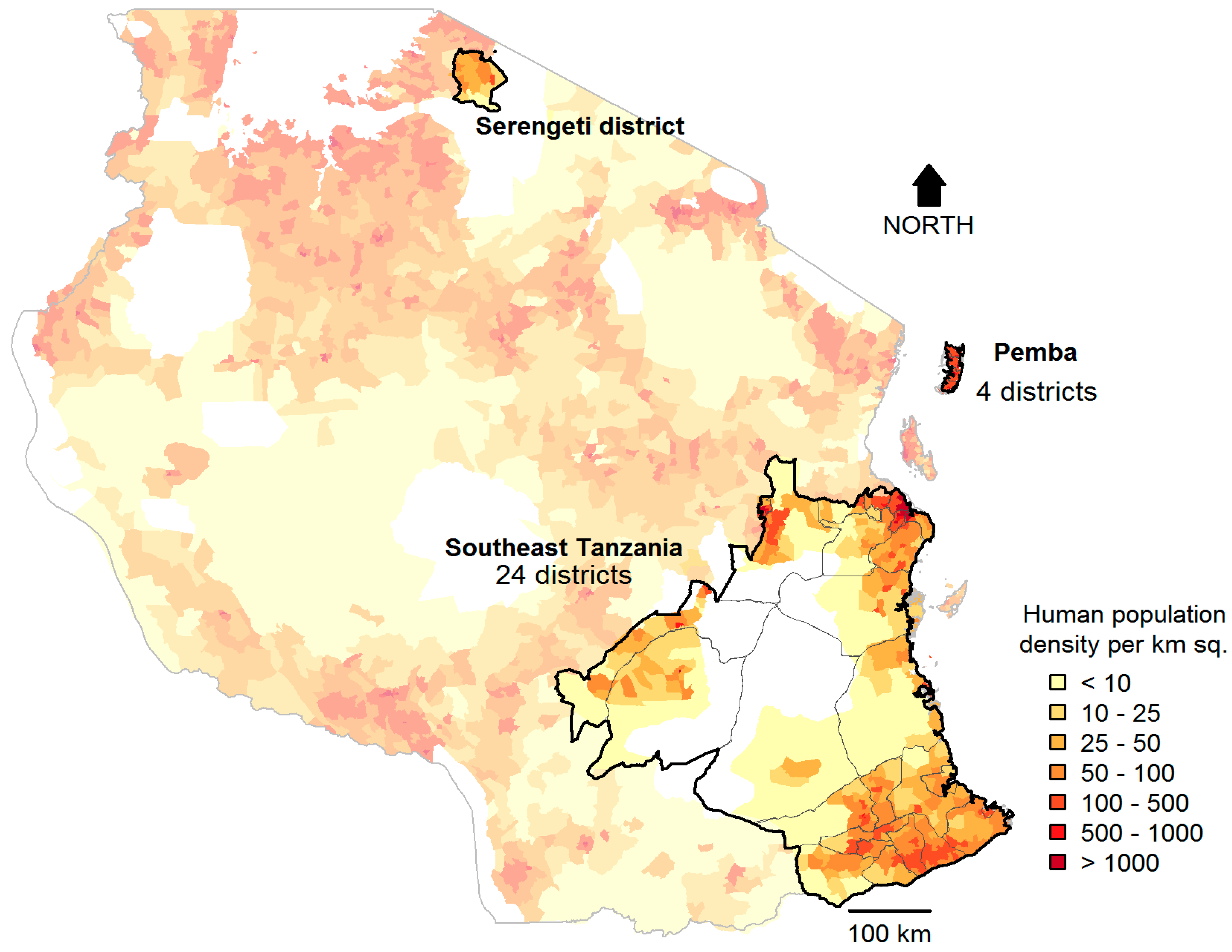
2.1. Study Sites
2.2. Data Collection
2.3. Characteristics of Study Districts
2.4. Statistical Analysis
2.5. Ethics
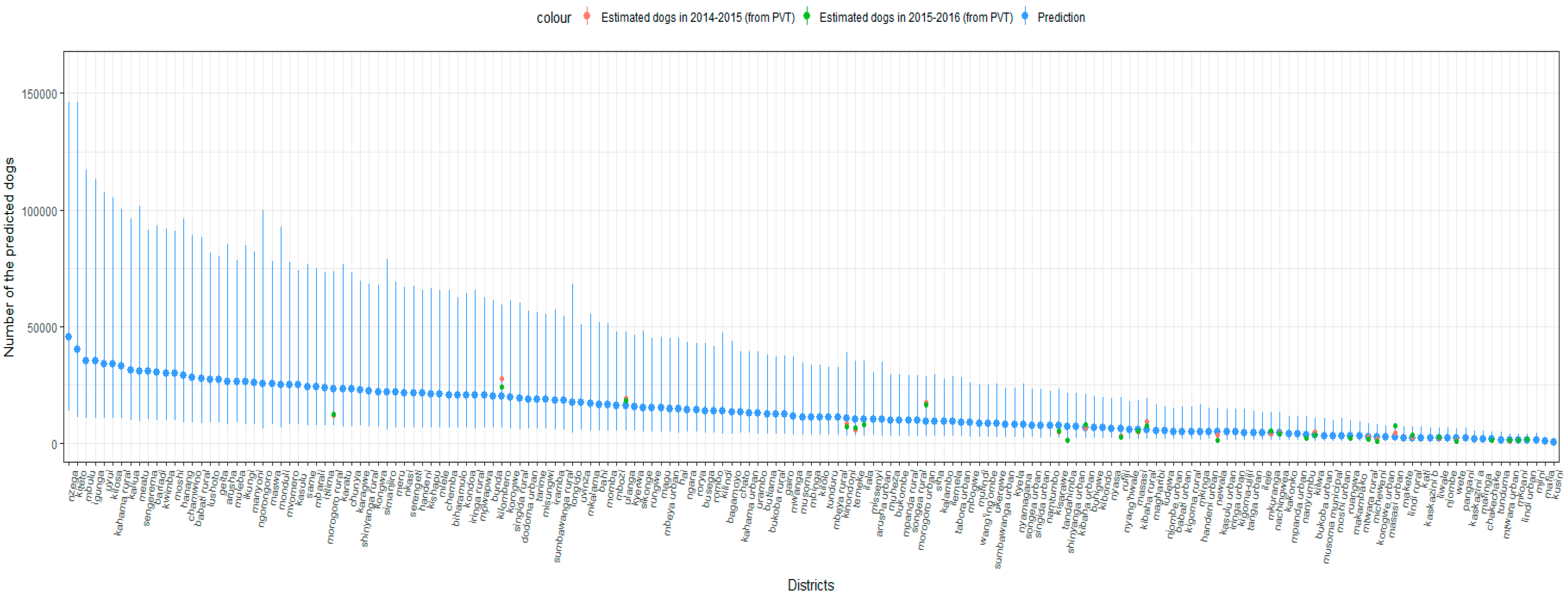
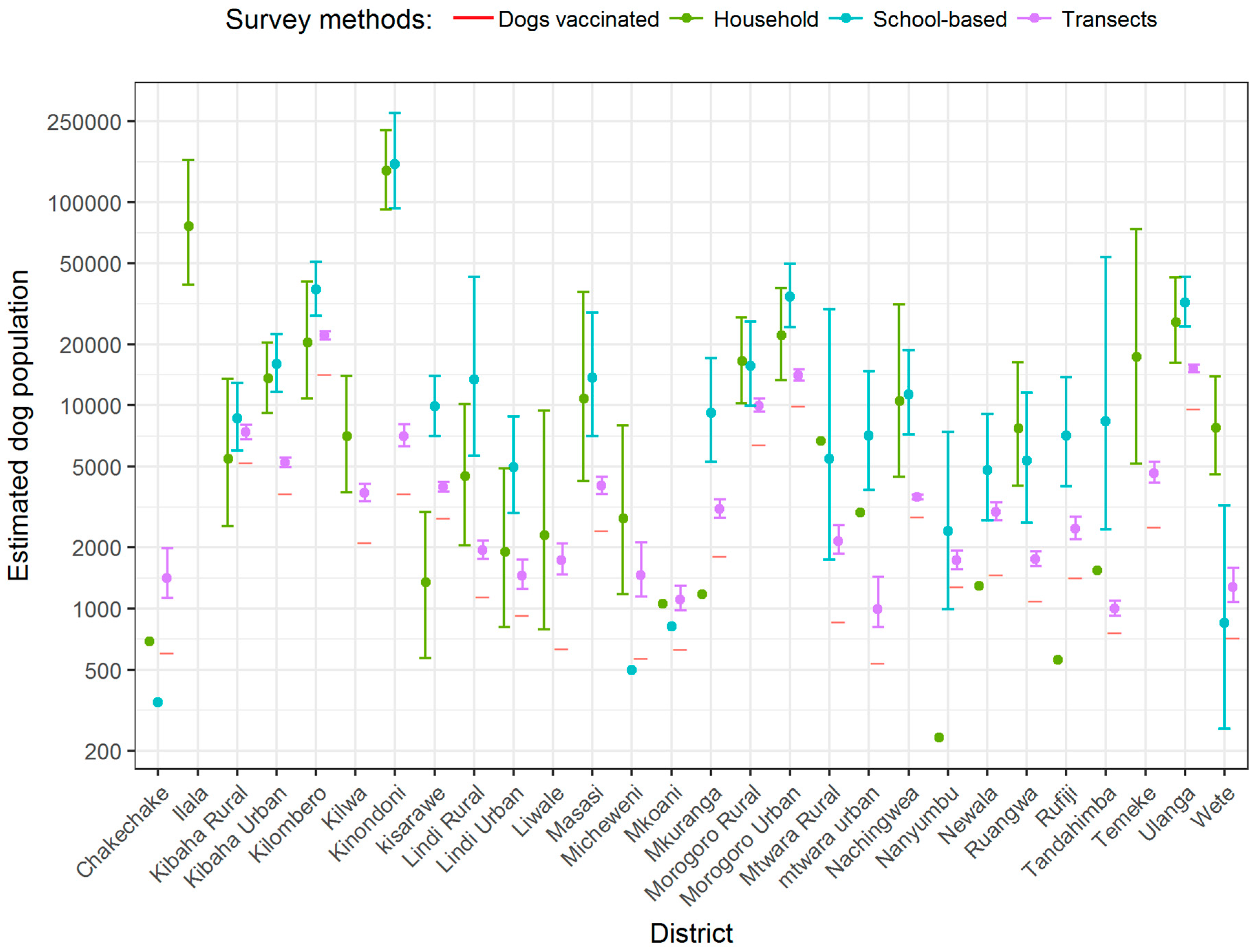
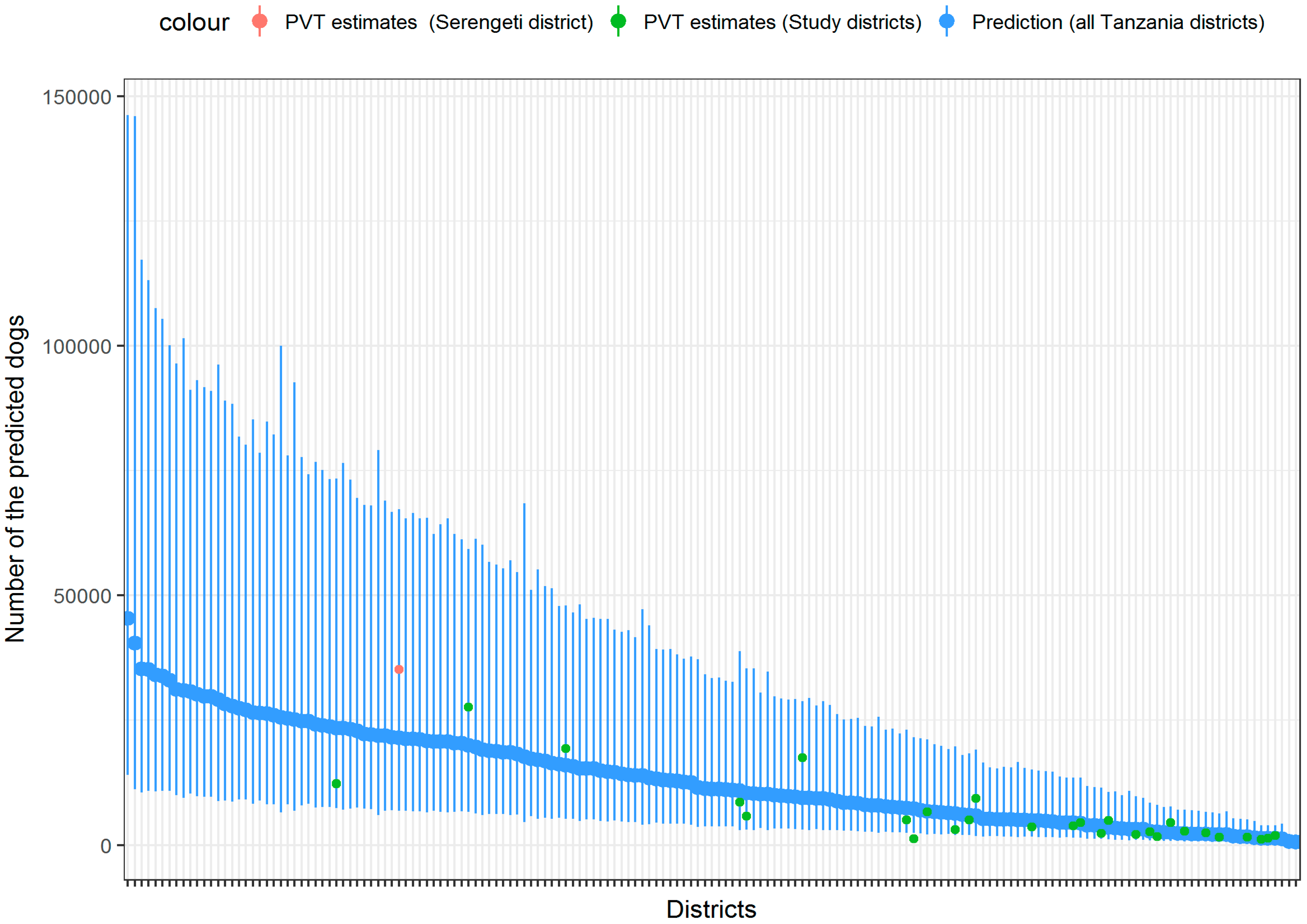
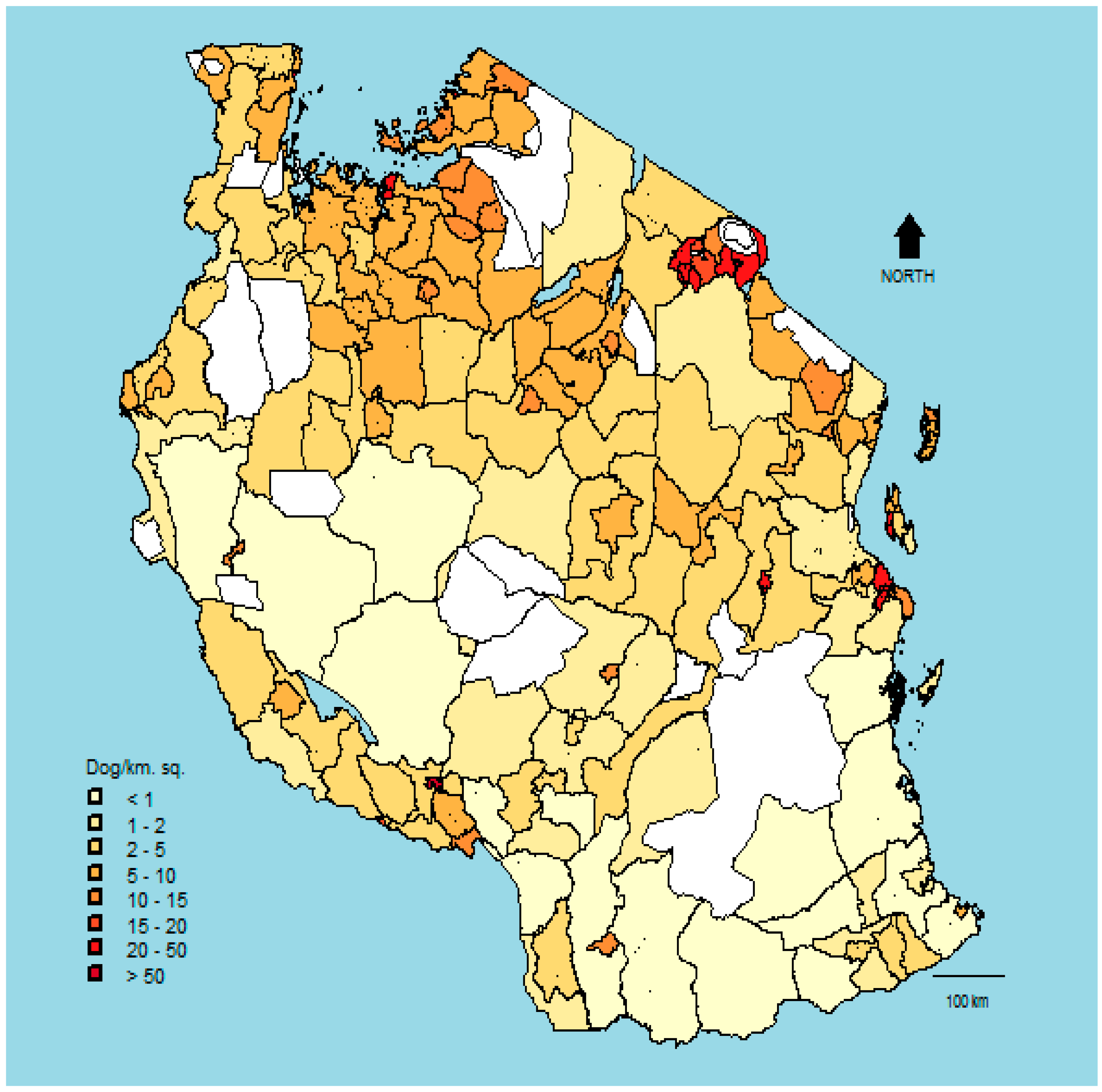
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
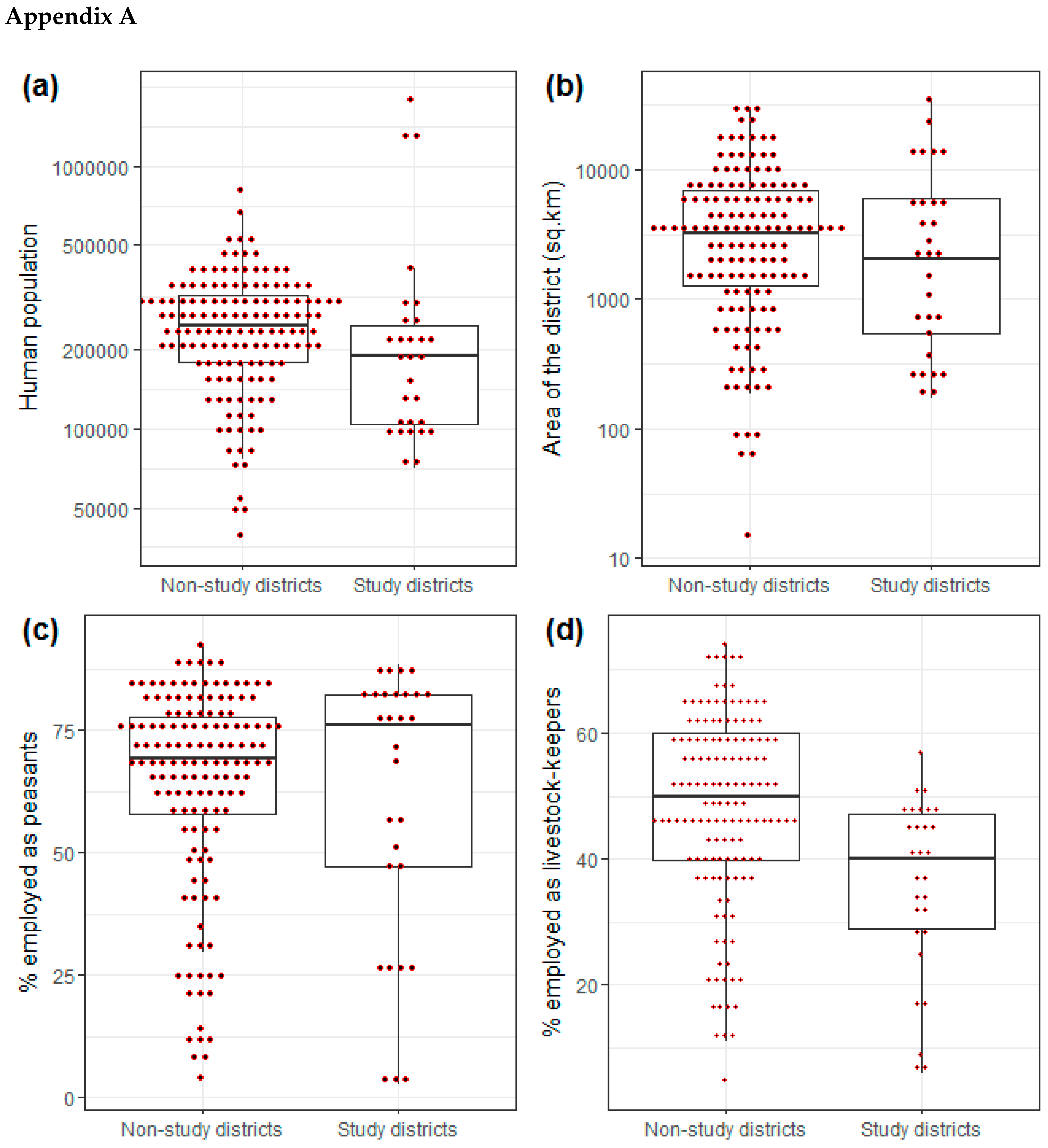
Appendix A
| Variables | VIF After Step | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| Human population in 2014 | 972.8 | 9.5 | 2.4 | 2.9 |
| Number of households | 9.5 | NA | NA | NA |
| Proportion of livestock keeping households | 8.8 | 7.8 | 5.4 | NA |
| Number of people living in rural areas | 948.9 | 2.9 | NA | NA |
| Proportion of persons employed as livestock keepers | 1.6 | 1.6 | 1.4 | 1.3 |
| Setting (inland vs coastal) | 1.9 | 1.9 | 1.8 | 1.5 |
| Setting (mainland vs island) | 9.2 | 5.3 | 4.7 | 2.1 |
| Proportion of persons employed as peasant | 9.4 | 8.8 | 5.4 | 4.7 |
| Area | 8.2 | 4.3 | 4.1 | 3.1 |
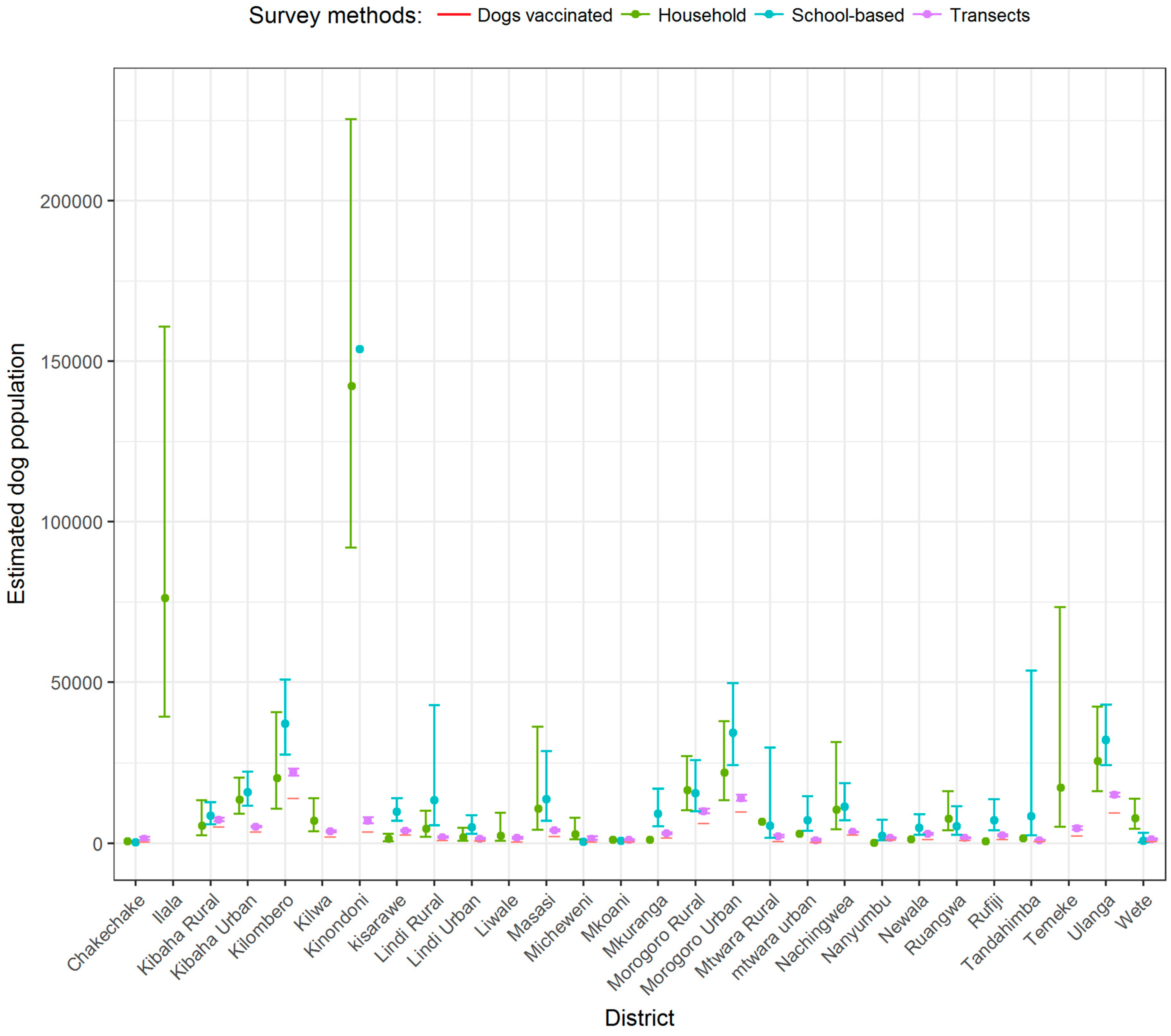
| District | Setting | Number of Households (% Rural) | Employment Status in Percentage | HHS | SBS | HDR (CI) * | Vaccinated Dogs ** | Estimated Dogs | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Peasants | Livestock Keepers | Others | Dogs (Mean Dogs/HH) | Coverage (%) | Dogs (Mean Dogs/Pupil) | Coverage (%) | HHS | SBS | |||||
| Chakechake | Coastal | 17,551 (47) | 51.1 | 0.5 | 48.4 | 7 (0.04) | 0 | 3 (0.02) | 100 | 59 (20, 177) | 608 | 702 | 351 |
| Ilala | Coastal | 297,750 (9) | 4.0 | 1.2 | 94.8 | 34 (0.26.) | 50 | NA | NA | NA | 4218 | 77,415 | NA |
| Kibaha Rural | Inland | 16,892 (28) | 47.2 | 5.8 | 47.0 | 30 (0.32) | 23 | 199 (0.50) | 59 | 13 (4, 40) | 5226 | 5405 | 8446 |
| Kibaha Urban | Inland | 31,092 (25) | 27.7 | 2.7 | 69.6 | 66 (0.44) | 44 | 237 (0.51) | 59 | 21 (7, 65) | 3684 | 13,680 | 15,857 |
| Kilombero | Inland | 93,331 (37) | 78.7 | 0.7 | 20.6 | 32 (0.22) | 47 | 218 (0.40) | 66 | 21 (7, 63) | 14,208 | 20,533 | 37,332 |
| Kilwa | Coastal | 42,596 (48) | 71.6 | 0.4 | 28.0 | 26 (0.16) | 15 | NA | NA | 55 (18, 166) | 2120 | 6815 | NA |
| Kinondoni | Coastal | 441,240 (8) | 2.9 | 0.8 | 96.3 | 59 (0.32) | 44 | 163 (0.35) | 52 | 181(50, 648) | 3696 | 141,197 | 154,434 |
| Kisarawe | Inland | 25,475 (48) | 78.7 | 2.3 | 19.0 | 9 (0.05) | 89 | 109 (0.39) | 80 | 14 (4, 43) | 2787 | 1274 | 9935 |
| Lindi Rural | Coastal | 52,821 (42) | 87.2 | 0.1 | 12.7 | 15 (0.08) | 60 | 60 (0.24) | 55 | 83 (27, 257) | 1148 | 4226 | 12,677 |
| Lindi Urban | Coastal | 22,344 (29) | 55.8 | 0.3 | 43.9 | 17 (0.10) | 41 | 70 (0.20) | 50 | 68 (23, 205) | 930 | 2234 | 4469 |
| Liwale | Inland | 21,084 (50) | 76.2 | 0.1 | 23.7 | 19 (0.11) | 16 | NA | NA | 43 (14, 132) | 637 | 2319 | NA |
| Masasi | Inland | 67,872 (45) | 82.2 | 0.1 | 17.7 | 27 (0.15) | 30 | 32 (0.20) | 69 | 42 (14, 127) | 4558 | 10,181 | 13,574 |
| Micheweni | Coastal | 19,257 (52) | 57.3 | 1.2 | 41.5 | 25 (0.14) | 0 | 4 (0.03) | 25 | 41 (14, 125) | 569 | 2696 | 578 |
| Mkoani | Coastal | 18,067 (57) | 26.0 | 0.6 | 73.4 | 9 (0.06) | 100 | 8 (0.05) | 100 | 75 (25, 224) | 631 | 1084 | 903 |
| Mkuranga | Coastal | 51,101 (34) | 68.5 | 0.5 | 31.0 | 4 (0.02) | 100 | 58 (0.18) | 62 | 52 (17, 157) | 1811 | 1022 | 9198 |
| Morogoro Rural | Inland | 67,671 (46) | 81.0 | 3.0 | 16.0 | 41 (0.24) | 56 | 103 (0.25) | 65 | 12 (4, 39) | 6434 | 16,241 | 16,918 |
| Morogoro Urban | Inland | 76,039 (16) | 25.2 | 0.7 | 74.1 | 49 (0.29) | 76 | 225 (0.40) | 67 | 35 (12, 108) | 9968 | 22,051 | 30,416 |
| Mtwara Rural | Inland | 58,602 (37) | 83.2 | 0.1 | 16.7 | 16 (0.11) | 50 | 31 (0.09) | 61 | 85 (27, 262) | 860 | 6446 | 5274 |
| Mtwara Urban | Coastal | 27,968 (18) | 27.7 | 0.4 | 71.9 | 14 (0.09) | 64 | 69 (0.24) | 35 | 84 (28, 252) | 540 | 2517 | 6712 |
| Nachingwea | Inland | 48,145 (45) | 85.7 | 0.1 | 14.2 | 37 (0.22) | 32 | 84 (0.25) | 8 | 41 (12, 125) | 2823 | 10,592 | 12,036 |
| Nanyumbu | Inland | 40,746 (33) | 88.4 | 0.1 | 11.5 | 1 (0.01) | 100 | 28 (0.06) | 18 | 41 (13, 123) | 1281 | 407 | 2445 |
| Newala | Inland | 58,035 (49) | 81.2 | 0.1 | 18.7 | 4 (0.02) | 100 | 55 (0.09) | 53 | 42 (14, 128) | 1465 | 1161 | 5223 |
| Ruangwa | Inland | 37,326 (47) | 83.7 | 0.1 | 16.2 | 37 (0.21) | 35 | 24 (0.14) | 50 | 42 (14, 126) | 1090 | 7838 | 5226 |
| Rufiji | Coastal | 48,164 (31) | 77.1 | 1.3 | 21.6 | 2 (0.01) | 100 | 61 (0.14) | 49 | 35 (11, 109) | 1423 | 482 | 6743 |
| Tandahimba | Inland | 60,872 (44) | 86.2 | 0.2 | 13.6 | 2 (0.03) | 100 | 24 (0.14) | 8 | 32 (11, 95) | 762 | 1826 | 8522 |
| Temeke | Coastal | 344,391 (6) | 4.6 | 0.8 | 94.6 | 8 (0.05) | 88 | NA | NA | 147 (44, 496) | 2521 | 17,220 | NA |
| Ulanga | Inland | 53,290 (42) | 83.2 | 1.1 | 15.7 | 85 (0.48) | 45 | 326 (0.58) | 61 | 18 (6, 53) | 9645 | 25,579 | 30,908 |
| Wete | Coastal | 20,151 (40) | 47.2 | 0.8 | 52.0 | 56 (0.38) | 57 | 7 (0.04) | 100 | 52 (17, 155) | 718 | 7657 | 806 |
| Overall | 731 (0.6) | 56 | 2,198 (0.7) | 56 | 86,321 | 410,800 | 398,983 | ||||||
References
- Hampson, K.; Coudeville, L.; Lembo, T.; Sambo, M.; Kieffer, A.; Attlan, M.; Barrat, J.; Blanton, J.D.; Briggs, D.J.; Cleaveland, S.; et al. Estimating the global burden of endemic canine rabies. PLoS Negl. Trop. Dis. 2015, 9, e0003709. [Google Scholar] [CrossRef]
- Coleman, P.G.; Dye, C. Immunization coverage required to prevent outbreaks of dog rabies. Vaccine 1996, 14, 185–186. [Google Scholar] [CrossRef]
- Hampson, K.; Dushoff, J.; Cleaveland, S.; Haydon, D.T.; Kaare, M.; Packer, C.; Dobson, A. Transmission dynamics and prospects for the elimination of canine Rabies. PLoS Biol. 2009, 7, 462–471. [Google Scholar] [CrossRef] [PubMed]
- Abela-Ridder, B.; Knopf, L.; Martin, S.; Taylor, L.; Torres, G.; De Balogh, K. 2016: The beginning of the end of rabies? Lancet Glob. Health 2018, 4, e780–e781. [Google Scholar] [CrossRef]
- Mpolya, E.A.; Lembo, T.; Lushasi, K.; Mancy, R.; Mbunda, E.M.; Makungu, S.; Maziku, M.; Sikana, L.; Jaswant, G.; Townsend, S.; et al. Toward Elimination of Dog-Mediated Human Rabies: Experiences from Implementing a Large-scale Demonstration Project in Southern Tanzania. Front. Vet. Sci. 2017, 4, 21. [Google Scholar] [CrossRef] [PubMed]
- Lembo, T.; Hampson, K.; Kaare, M.T.; Ernest, E.; Knobel, D.; Kazwala, R.R.; Haydon, D.T.; Cleaveland, S. The Feasibility of Canine Rabies Elimination in Africa: Dispelling Doubts with Data. PLoS Negl. Trop. Dis. 2010, 4, e626. [Google Scholar] [CrossRef] [PubMed]
- Downes, M.J.; Dean, R.S.; Stavisky, J.H.; Adams, V.J.; Grindlay, D.J.; Brennan, M.L. Methods used to estimate the size of the owned cat and dog population: A systematic review. BMC Vet. Res. 2013, 9, 121. [Google Scholar] [CrossRef] [PubMed]
- Gsell, A.S.; Knobel, D.L.; Kazwala, R.R.; Vounatsou, P.; Zinsstag, J. Domestic dog demographic structure and dynamics relevant to rabies control planning in urban areas in Africa: The case of Iringa, Tanzania. BMC Vet. Res. 2012, 8, 236–245. [Google Scholar] [CrossRef] [PubMed]
- Knobel, D.L.; Laurenson, M.K.; Kazwala, R.R.; Boden, L.A.; Cleaveland, S. A cross-sectional study of factors associated with dog ownership in Tanzania. BMC Vet. Res. 2008, 4, 5. [Google Scholar] [CrossRef] [PubMed]
- Kongkaew, W.; Coleman, P.; Pfeiffer, D.U.; Antarasena, C.; Thiptara, A. Vaccination coverage and epidemiological parameters of the owned-dog population in Thungsong District, Thailand. Prev. Vet. Med. 2004, 65, 105–115. [Google Scholar] [CrossRef] [PubMed]
- Tenzin, T.; McKenzie, J.S.; Vanderstichel, R.; Rai, B.D.; Rinzin, K.; Tshering, Y.; Pem, R.; Tshering, C.; Dahal, N.; Dukpa, K.; et al. Comparison of mark-resight methods to estimate abundance and rabies vaccination coverage of free-roaming dogs in two urban areas of south Bhutan. Prev. Vet. Med. 2015, 118, 436–448. [Google Scholar] [CrossRef] [PubMed]
- Tenzin, T.; Ahmed, R.; Debnath, N.C.; Ahmed, G.; Yamage, M. Free-roaming dog population estimation and status of the dog population management and rabies control program in Dhaka City, Bangladesh. PLoS Negl. Trop. Dis. 2015, 9, e0003784. [Google Scholar] [CrossRef] [PubMed]
- Sambo, M.; Johnson, P.C.; Hotopp, K.; Changalucha, J.; Cleaveland, S.; Kazwala, R.; Lembo, T.; Lugelo, A.; Lushasi, K.; Maziku, M.; et al. Comparing Methods of Assessing Dog Rabies Vaccination Coverage in Rural and Urban Communities in Tanzania. Front. Vet. Sci. 2017, 4, 33. [Google Scholar] [CrossRef] [PubMed]
- Sambo, M.; Lembo, T.; Cleaveland, S.; Ferguson, H.M.; Sikana, L.; Simon, C.; Urassa, H.; Hampson, K. Knowledge, Attitudes and Practices (KAP) about Rabies Prevention and Control: A Community Survey in Tanzania. PLoS Negl. Trop. Dis. 2014, 8, 12. [Google Scholar] [CrossRef] [PubMed]
- Bardosh, K.; Sambo, M.; Sikana, L.; Hampson, K.; Welburn, S.C. Eliminating Rabies in Tanzania? Local Understandings and Responses to Mass Dog Vaccination in Kilombero and Ulanga Districts. PLoS Negl. Trop. Dis. 2014, 8, e2935. [Google Scholar] [CrossRef] [PubMed]
- NBS. Tanzania Housing and Population Census. In Planning Office; NBS: Dar Es Salaam, Tanzania, 2012. [Google Scholar]
- Kaare, M.; Lembo, T.; Hampson, K.; Ernest, E.; Estes, A.; Mentzel, C.; Cleaveland, S. Rabies control in rural Africa: Evaluating strategies for effective domestic dog vaccination. Vaccine 2009, 27, 152–160. [Google Scholar] [CrossRef] [PubMed]
- Teddlie, C.; Yu, F. Mixed Methods Sampling: A Typology with Examples. J. Mixed Methods Res. 2007, 1. [Google Scholar] [CrossRef]
- NBS. Tanzania GIS Shapefiles. Available online: http://www.nbs.go.tz/nbstz/index.php/english/statistics-by-subject/population-and-housing-census/258-2012-phc-shapefiles-level-one-and-two (accessed on 16 August 2018).
- Bivand, R.; Lewin-Koh, N. Maptools: Tools for reading and handling spatial objects. R Package Version 2013, 27, 8–29. [Google Scholar]
- Durr, S.; Mindekem, R.; Kaninga, Y.; Moto, D.D.; Melter, M.I.; Vounatsou, P.; Zinsstag, J. Effectiveness of dog rabies vaccination programmes: Comparison of owner-charged and free vaccination campaigns. Epidemiol. Infect. 2009, 137, 1558–1567. [Google Scholar] [CrossRef] [PubMed]
- Minyoo, A.B.; Steinmetz, M.; Czupryna, A.; Bigambo, M.; Mzimbiri, I.; Powell, G.; Gwakisa, P.; Lankester, F. Incentives increase participation in mass dog rabies vaccination clinics and methods of coverage estimation are assessed to be accurate. PLoS Negl. Trop. Dis. 2015, 9, e0004221. [Google Scholar] [CrossRef] [PubMed]
- Arief, R.A.; Hampson, K.; Jatikusumah, A.; Widyastuti, M.D.W.; Basri, C.; Putra, A.G.; Willyanto, I.; Estoepangestie, A.T.; Mardiana, I.W.; Kesuma, I.K.G.N.; et al. Determinants of vaccination coverage and consequences for rabies control in Bali, Indonesia. Front. Vet. Sci. 2017, 3, 123. [Google Scholar] [CrossRef] [PubMed]
- Zuur, A.F.; Ieno, E.N.; Elphick, C.S. A protocol for data exploration to avoid common statistical problems. Methods Ecol. Evol. 2010, 1, 3–14. [Google Scholar] [CrossRef]
- Wagenmakers, E.J.; Farrell, S. AIC model selection using Akaike weights. Psychon. Bull. Rev. 2004, 11, 192–196. [Google Scholar] [CrossRef] [PubMed]
- Rousson, V.; Goşoniu, N.F. An R-square coefficient based on final prediction error. Stat. Methodol. 2007, 4, 331–340. [Google Scholar] [CrossRef]
- Efron, B. Large-Scale Simultaneous Hypothesis Testing. J. Am. Stat. Assoc. 2004, 99, 96–104. [Google Scholar] [CrossRef]
- Nakagawa, S.; Johnson, P.C.D.; Schielzeth, H. The coefficient of determination R2 and intra-class correlation coefficient from generalized linear mixed-effects models revisited and expanded. J. R. Soc. Interface 2017, 14, 20170213. [Google Scholar] [CrossRef] [PubMed]
- Von Tress, M. Generalized, Linear, and Mixed Models. Technometrics 2003, 4, 99. [Google Scholar] [CrossRef]
- R Core Team. R: A language and environment for statistical computing. In R Foundation for Statistical Computing; R Core Team: Vienna, Austria, 2017; ISBN 3-900051-07-0. Available online: http://www.R-project.org (accessed on 4 September 2018).
- Bates, D.; Maechler, M.; Bolker, B.; Walker, S. lme4: Linear mixed-effects models using Eigen and S4. R Package Version 2013, 1, 1–23. [Google Scholar]
- Magnusson, A.; Skaug, H.; Nielsen, A.; Berg, C.; Kristensen, K.; Maechler, M.; van Bentham, K.J.; Bolker, B.M.; Brooks, M.E. glmmTMB: Generalized Linear Mixed Models using Template Model Builder. R Package Version 2016. Available online: https://github.com/glmmTMB (accessed on 4 September 2018).
- Bartoń, K. MuMIn: Multi-Model Inference. R Package Version 2014, 1. Available online: http//CRAN R-project org/package= MuMIn (accessed on 4 September 2018).
- Davlin, S.L.; Vonville, H.M. Canine rabies vaccination and domestic dog population characteristics in the developing world: A systematic review. Vaccine 2012, 30, 3492–3502. [Google Scholar] [CrossRef] [PubMed]
- Maas, C.J.; Hox, J. Sufficient Sample Sizes for Multilevel Modeling. J. Res. Methods Behav. Soc. Sci. 2005, 78, 217–230. [Google Scholar] [CrossRef]
- Snijders, T.A.B. Power and Sample Size in Multilevel Linear Models. Encycl. Stat. Behav. Sci. 2005, 1, 86. [Google Scholar] [CrossRef]
- Kitala, P.; McDermott, J.; Kyule, M.; Gathuma, J.; Perry, B.; Wandeler, A. Dog ecology and demography information to support the planning of rabies control in Machakos District, Kenya. Acta Trop. 2001, 78, 217–230. [Google Scholar] [CrossRef]
- Acosta-Jamett, G.; Cleaveland, S.; Cunningham, A.A.; Bronsvoort, B.M. Demography of domestic dogs in rural and urban areas of the Coquimbo region of Chile and implications for disease transmission. Prev. Vet. Med. 2010, 94, 272–281. [Google Scholar] [CrossRef] [PubMed]
- Awoyomi, O.J.; Adeyemi, I.G.; Awoyomi, F.S. Socioeconomic Factors Associated With Non-Vaccination of Dogs Against Rabies In Ibadan, Nigeria. Niger. Vet. J. 2008, 2, 59–63. [Google Scholar] [CrossRef]
- El-Yuguda, A.; Baba, A.A.; Baba, S.S.A. Dog population structure and cases of rabies among dog bite victims in urban and rural areas of Borno state, Nigeria. Trop. Vet. 2007, 25, 34–40. [Google Scholar]
- Mbilo, C.; Léchenne, M.; Hattendorf, J.; Madjadinan, S.; Anyiam, F. Rabies awareness and dog ownership among rural northern and southern Chadian communities—Analysis of a community-based, cross-sectional household survey. Acta Trop. 2017, 175, 100–111. [Google Scholar] [CrossRef] [PubMed]
- Hatch, B.; Anderson, A.; Sambo, M.; Maziku, M.; Mchau, G.; Mbunda, E.; Mtema, Z.; Rupprecht, C.E.; Shwiff, S.A.; Nel, L. Towards Canine Rabies Elimination in South-Eastern Tanzania: Assessment of Health Economic Data. Transbound. Emerg. Dis. 2017, 64, 951–958. [Google Scholar] [CrossRef] [PubMed]
- Wallace, R.M.; Mehal, J.; Nakazawa, Y.; Recuenco, S.; Bakamutumaho, B.; Osinubi, M.; Tugumizemu, V.; Blanton, J.D.; Gilbert, A.; Wamala, J. The impact of poverty on dog ownership and access to canine rabies vaccination: Results from a knowledge, attitudes and practices survey, Uganda 201. Infect. Dis. Poverty 2017, 6, 97. [Google Scholar] [CrossRef] [PubMed]
- Malele, I.; Nyingilili, H.; Msangi, A. Factors defining the distribution limit of tsetse infestation and the implication for livestock sector in Tanzania. Afr. J. Agric. Res. 2011, 6, 2341–2347. [Google Scholar] [CrossRef]
- Knobel, D.L.; Cleaveland, S.; Coleman, P.G.; Fevre, E.M.; Meltzer, M.I.; Miranda, M.E.; Shaw, A.; Zinsstag, J.; Meslin, F.X. Re-evaluating the burden of rabies in Africa and Asia. Bull. World Health Organ. 2005, 83, 360–368. [Google Scholar] [PubMed]
- Brooks, R. Survey of the dog population of Zimbabwe and its level of rabies vaccination. Vet. Rec. 1990, 127, 592–596. [Google Scholar] [CrossRef] [PubMed]
- Dye, C.; Cleaveland, S. Maintenance of a Microparasite Infecting Several Host Species Rabies in the Serengeti. Parasitology 1995, 111, S33–S47. [Google Scholar] [CrossRef]
- Kitala, P.M.; McDermott, J.J.; Coleman, P.G.; Dye, C. Comparison of vaccination strategies for the control of dog rabies in Machakos District, Kenya. Epidemiol. Infect. 2002, 129, 215–222. [Google Scholar] [CrossRef] [PubMed]
- Cleaveland, S.; Kaare, M.; Tiringa, P.; Mlengeya, T.; Barrat, J. A dog rabies vaccination campaign in rural Africa: Impact on the incidence of dog rabies and human dog-bite injuries. Vaccine 2003, 21, 1965–1973. [Google Scholar] [CrossRef]
- Lembo, T.; Hampson, K.; Haydon, D.T.; Craft, M.; Dobson, A.; Dushoff, J.; Ernest, E.; Hoare, R.; Kaare, M.; Mlengeya, T.; et al. Exploring reservoir dynamics: A case study of rabies in the Serengeti ecosystem. J. Appl. Ecol. 2008, 45, 1246–1257. [Google Scholar] [CrossRef] [PubMed]
- Rinzin, K.; Tenzin, T.; Robertson, I. Size and demography pattern of the domestic dog population in Bhutan: Implications for dog population management and disease control. Prev. Vet. Med. 2016, 126, 39–47. [Google Scholar] [CrossRef] [PubMed]
- Matter, H.C.; Wandeler, A.I.; Neuenschwander, B.E.; Harischandra, L.P.; Meslin, F.X. Study of the dog population and the rabies control activities in the Mirigama area of Sri Lanka. Acta Trop. 2000, 75, 95–108. [Google Scholar] [CrossRef]
- Mazeri, S.; Gibson, A.D.; Meunier, N.; Barend, M.; Handel, I.G.; Mellanby, R.J.; Gamble, L. Barriers of attendance to dog rabies static point vaccination clinics in Blantyre, Malawi. PLoS Negl. Trop. Dis. 2018, 12, e0006159. [Google Scholar] [CrossRef] [PubMed]
| Variable | Study Districts (n = 28) | Non-Study District (n = 140) |
|---|---|---|
| Human population size | 307,676 (70,209, 1,775,049) | 257,188 (39,242, 807,619) |
| Annual human population growth rate (%) | 2.3 (−1.0, 7.0) | 2.6 (−3, 7) |
| Number of households | 75,452 (16,892, 441,240) | 50,636 (9027, 134,608) |
| Average household size (persons per household) | 4.2 (3.5, 5.5) | 5.1 (3.8, 7.8) |
| Area (km2) ¥ | 4375 (15, 28,000) | 4375 (18.6, 28,244) |
| Setting: | ||
| Inland | 14 (50%) | 128 (91%) |
| Coastal ‡ [Island] | 14 (50%) [4 (14%)] | 12 (9%) [6 (4.7%)] |
| Number of livestock-keeping households | 18,317 (4771, 35,829) | 24,168 (2258, 71,335) |
| Proportion (%) of persons employed * as: | ||
| Peasants | 60 (3, 88) | 64 (4, 93) |
| Livestock keepers | 1 (0, 6) | 1 (0, 65) |
| Regression Coefficient Estimates | Model Fit Statistics | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Intercept | Area (km2) | Inland vs Coastal & Island | Mainland vs. Island | Number of People | Employed as Livestock Keepers | Employed as Peasants | Partial R2FPE | R2FPE | Adjusted R2 | df | LL | δAICC | Aikakeweight |
| 5.60 | −0.708 | 0.358 | 0.448 | 57.6% | 61.6% | 72.4 | 5 | −18.65 | 0.00 | 26.0% | |||
| 9.51 | 0.124 | −0.758 | −0.447 | 0.303 | 57.9% | 63.1% | 76.3 | 6 | −17.49 | 0.94 | 16.2% | ||
| 8.07 | −0.760 | −0.219 | 0.335 | 0.300 | 57.5% | 62.7% | 76.0 | 6 | −17.65 | 1.27 | 13.8% | ||
| 9.99 | −0.907 | −0.412 | 0.281 | 55.3% | 59.5% | 75.7 | 5 | −19.39 | 1.48 | 12.4% | |||
| 11.03 | −0.767 | −0.422 | −0.489 | 0.302 | 54.7% | 60.2% | 70.3 | 6 | −18.54 | 3.05 | 5.7% | ||
| Variable robustness | 33% | 91% | 13% | 51% | 97% | 49% | |||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sambo, M.; Hampson, K.; Changalucha, J.; Cleaveland, S.; Lembo, T.; Lushasi, K.; Mbunda, E.; Mtema, Z.; Sikana, L.; Johnson, P.C.D. Estimating the Size of Dog Populations in Tanzania to Inform Rabies Control. Vet. Sci. 2018, 5, 77. https://doi.org/10.3390/vetsci5030077
Sambo M, Hampson K, Changalucha J, Cleaveland S, Lembo T, Lushasi K, Mbunda E, Mtema Z, Sikana L, Johnson PCD. Estimating the Size of Dog Populations in Tanzania to Inform Rabies Control. Veterinary Sciences. 2018; 5(3):77. https://doi.org/10.3390/vetsci5030077
Chicago/Turabian StyleSambo, Maganga, Katie Hampson, Joel Changalucha, Sarah Cleaveland, Tiziana Lembo, Kennedy Lushasi, Eberhard Mbunda, Zacharia Mtema, Lwitiko Sikana, and Paul C.D. Johnson. 2018. "Estimating the Size of Dog Populations in Tanzania to Inform Rabies Control" Veterinary Sciences 5, no. 3: 77. https://doi.org/10.3390/vetsci5030077
APA StyleSambo, M., Hampson, K., Changalucha, J., Cleaveland, S., Lembo, T., Lushasi, K., Mbunda, E., Mtema, Z., Sikana, L., & Johnson, P. C. D. (2018). Estimating the Size of Dog Populations in Tanzania to Inform Rabies Control. Veterinary Sciences, 5(3), 77. https://doi.org/10.3390/vetsci5030077





