Development of Artificial Neural Network Models to Assess Beer Acceptability Based on Sensory Properties Using a Robotic Pourer: A Comparative Model Approach to Achieve an Artificial Intelligence System
Abstract
:1. Introduction
2. Materials and Methods
2.1. Beer Samples Description
2.2. Color and Foam-Related Parameters
2.3. Sensory Session
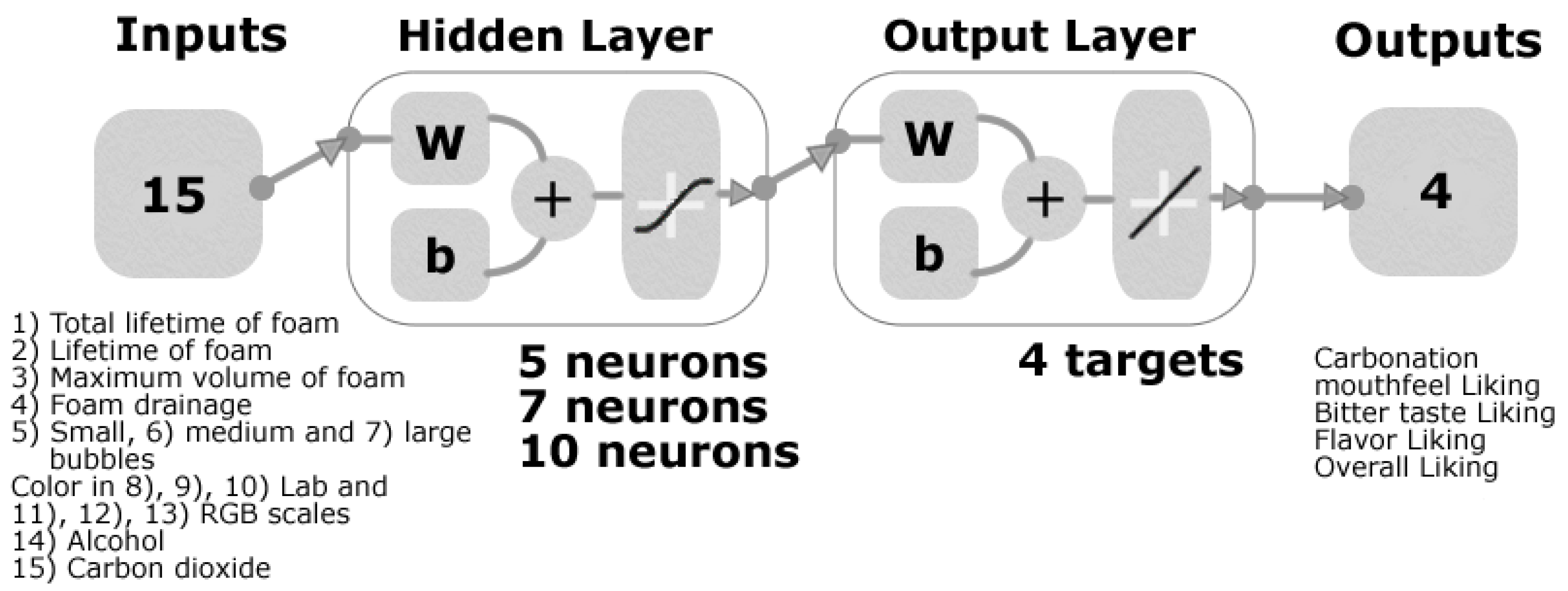
2.4. Machine Learning Modelling
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Michalski, R.S.; Carbonell, J.G.; Mitchell, T.M. Machine Learning: An Artificial Intelligence Approach; Elsevier Science: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Bell, J. Machine Learning: Hands-On for Developers and Technical Professionals; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene selection for cancer classification using support vector machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Polat, K.; Güneş, S. Breast cancer diagnosis using least square support vector machine. Digit. Signal Process. 2007, 17, 694–701. [Google Scholar] [CrossRef]
- Gonzalez Viejo, C.; Fuentes, S.; Li, G.; Collmann, R.; Condé, B.; Torrico, D. Development of a robotic pourer constructed with ubiquitous materials, open hardware and sensors to assess beer foam quality using computer vision and pattern recognition algorithms: RoboBEER. Food Res. Int. 2016, 89, 504–513. [Google Scholar] [CrossRef]
- Gonzalez Viejo, C.; Fuentes, S.; Torrico, D.; Howell, K.; Dunshea, F.R. Assessment of beer quality based on foamability and chemical composition using computer vision algorithms, near infrared spectroscopy and machine learning algorithms. J. Sci. Food Agric. 2018, 98, 618–627. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez Viejo, C.; Fuentes, S.; Howell, K.; Torrico, D.D.; Dunshea, F.R. Integration of non-invasive biometrics with sensory analysis techniques to assess acceptability of beer by consumers. Physiol. Behav. 2019, 200, 139–147. [Google Scholar] [CrossRef]
- Gonzalez Viejo, C.; Fuentes, S.; Howell, K.; Torrico, D.; Dunshea, F.R. Robotics and computer vision techniques combined with non-invasive consumer biometrics to assess quality traits from beer foamability using machine learning: A potential for artificial intelligence applications. Food Control 2018, 92, 72–79. [Google Scholar] [CrossRef]
- Fuentes, S.; Hernández-Montes, E.; Escalona, J.; Bota, J.; Gonzalez Viejo, C.; Poblete-Echeverría, C.; Tongson, E.; Medrano, H. Automated grapevine cultivar classification based on machine learning using leaf morpho-colorimetry, fractal dimension and near-infrared spectroscopy parameters. Comput. Electron. Agric. 2018, 151, 311–318. [Google Scholar] [CrossRef]
- Romero, M.; Luo, Y.; Su, B.; Fuentes, S. Vineyard water status estimation using multispectral imagery from an UAV platform and machine learning algorithms for irrigation scheduling management. Comput. Electron. Agric. 2018, 147, 109–117. [Google Scholar] [CrossRef]
- Yu, H.Y.; Niu, X.Y.; Lin, H.J.; Ying, Y.B.; Li, B.B.; Pan, X.X. A feasibility study on on-line determination of rice wine composition by Vis–NIR spectroscopy and least-squares support vector machines. Food Chem. 2009, 113, 291–296. [Google Scholar] [CrossRef]
- Gonzalez Viejo, C.; Fuentes, S.; Torrico, D.D.; Howell, K.; Dunshea, F.R. Assessment of Beer Quality Based on a Robotic Pourer, Computer Vision, and Machine Learning Algorithms Using Commercial Beers. J. Food Sci. 2018, 83, 1381–1388. [Google Scholar] [CrossRef] [PubMed]
- Ellis, D.I.; Broadhurst, D.; Kell, D.B.; Rowland, J.J.; Goodacre, R. Rapid and quantitative detection of the microbial spoilage of meat by Fourier transform infrared spectroscopy and machine learning. Appl. Environ. Microbiol. 2002, 68, 2822–2828. [Google Scholar] [CrossRef]
- Mathworks Inc. Mastering Machine Learning: A Step-by-Step Guide with MATLAB; Mathworks Inc.: Sherborn, MA, USA, 2018. [Google Scholar]
- Lin, M.-I.B.; Groves, W.A.; Freivalds, A.; Lee, E.G.; Harper, M. Comparison of artificial neural network (ANN) and partial least squares (PLS) regression models for predicting respiratory ventilation: An exploratory study. Eur. J. Appl. Physiol. 2012, 112, 1603–1611. [Google Scholar] [CrossRef] [PubMed]
- Amini, M.; Abbaspour, K.C.; Khademi, H.; Fathianpour, N.; Afyuni, M.; Schulin, R. Neural network models to predict cation exchange capacity in arid regions of Iran. Eur. J. Soil Sci. 2005, 56, 551–559. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J.; Van Genuchten, M.T. Neural network analysis for hierarchical prediction of soil hydraulic properties. Soil Sci. Soc. Am. J. 1998, 62, 847–855. [Google Scholar] [CrossRef]
- Ogunoiki, A.; Olatunbosun, O. Artificial Road Load Generation Using Artificial Neural Networks; 0148-7191; SAE Technical Paper; SAE: Warrendale, PA, USA, 2015. [Google Scholar]
- Buss, D. Food Companies Get Smart About Artificial Intelligence. Food Technol. 2018, 72, 26–41. [Google Scholar]
- Cajka, T.; Riddellova, K.; Tomaniova, M.; Hajslova, J. Recognition of beer brand based on multivariate analysis of volatile fingerprint. J. Chromatogr. A 2010, 1217, 4195–4203. [Google Scholar] [CrossRef]
- Iñón, F.A.; Garrigues, S.; de la Guardia, M. Combination of mid-and near-infrared spectroscopy for the determination of the quality properties of beers. Anal. Chim. Acta 2006, 571, 167–174. [Google Scholar] [CrossRef]
- Gonzalez Viejo, C.; Fuentes, S.; Torrico, D.; Lee, M.; Hu, Y.; Chakraborty, S.; Dunshea, F. The Effect of Soundwaves on Foamability Properties and Sensory of Beers with a Machine Learning Modeling Approach. Beverages 2018, 4, 53. [Google Scholar] [CrossRef]
- Beale, M.H.; Hagan, M.T.; Demuth, H.B. Deep Learning Toolbox User’s Guide; Mathworks Inc.: Sherborn, MA, USA, 2018. [Google Scholar]
- Markopoulos, A.P.; Georgiopoulos, S.; Manolakos, D.E. On the use of back propagation and radial basis function neural networks in surface roughness prediction. J. Ind. Eng. Int. 2016, 12, 389–400. [Google Scholar] [CrossRef]
- Saduf, M.A.W. Comparative study of back propagation learning algorithms for neural networks. Int. J. Adv. Res. Comput. Sci. Softw. Eng. 2013, 3, 1151–1156. [Google Scholar]
- Kayri, M. Predictive abilities of bayesian regularization and Levenberg–Marquardt algorithms in artificial neural networks: A comparative empirical study on social data. Math. Comput. Appl. 2016, 21, 20. [Google Scholar] [CrossRef]
- Riedmiller, M.; Braun, H. A Direct Adaptive Method for Faster Backpropagation Learning: The RPROP Algorithm. In Proceedings of the IEEE International Conference on Neural Networks, San Francisco, CA, USA, 28 March–1 April 1993; pp. 586–591. [Google Scholar]
- Mathworks Inc. Resilient Backpropagation. Available online: https://au.mathworks.com/help/deeplearning/ref/trainrp.html (accessed on 1 October 2018).
- Patnaik, L.M.; Rajan, K. Target detection through image processing and resilient propagation algorithms. Neurocomputing 2000, 35, 123–135. [Google Scholar] [CrossRef]
- Pajchrowski, T.; Zawirski, K.; Nowopolski, K. Neural speed controller trained online by means of modified RPROP algorithm. IEEE Trans. Ind. Inform. 2015, 11, 560–568. [Google Scholar] [CrossRef]
- Bamforth, C. Perceptions of beer foam. J. Inst. Brew. 2000, 106, 229–238. [Google Scholar] [CrossRef]
- De Keukeleire, D. Fundamentals of beer and hop chemistry. Quim. Nova 2000, 23, 108–112. [Google Scholar] [CrossRef]
- Liger-Belair, G.; Cilindre, C.; Gougeon, R.D.; Lucio, M.; Gebefügi, I.; Jeandet, P.; Schmitt-Kopplin, P. Unraveling different chemical fingerprints between a champagne wine and its aerosols. Proc. Natl. Acad. Sci. USA 2009, 106, 16545–16549. [Google Scholar] [CrossRef]


| Beer Style | Country of Origin | Type of Fermentation |
|---|---|---|
| Kolsch | Australia | Top |
| Porter | Poland | Top |
| Steam Ale | Australia | Top |
| Sparkling Ale | Australia | Top |
| Blonde Ale | Belgium | Top |
| Red Ale | USA | Top |
| American Lager | Mexico | Bottom |
| American Lager | Mexico | Bottom |
| Lager | The Netherlands | Bottom |
| Pilsner | Czech Republic | Bottom |
| American Lager | USA | Bottom |
| Pilsner | Czech Republic | Bottom |
| Lambic Gueuze | Belgium | Spontaneous |
| Lambic Cassis | Belgium | Spontaneous |
| Lambic Kriek | Belgium | Spontaneous |
| Lambic Framboise | Belgium | Spontaneous |
| Main Function Type | Algorithm | Abbreviation |
|---|---|---|
| Backpropagation with Jacobian derivatives | Levenberg Marquardt | LM |
| Bayesian Regularization | BR | |
| Backpropagation with gradient derivatives | Broyden, Fletcher, Goldfarb, and Shanno quasi-Newton | BFGS |
| Conjugate gradient with Powell-Beale restarts | PB | |
| Conjugate gradient with Fletcher-Reeves updates | FR | |
| Conjugate gradient with Polak-Ribiere updates | PR | |
| Gradient descent backpropagation | GD | |
| Gradient descent with adaptive learning rate | GDLR | |
| Gradient descent with momentum | GDM | |
| Gradient descent with momentum and adaptive learning rate | GDMLR | |
| One step secant | OSS | |
| Resilient backpropagation | RPROP | |
| Scaled conjugate gradient | SCG | |
| Supervised weight and bias training functions | Batch training with weight and bias learning rate | BLR |
| Cyclical order weight and bias | CO | |
| Random order weight and bias | RO | |
| Sequential order weight and bias | SO |
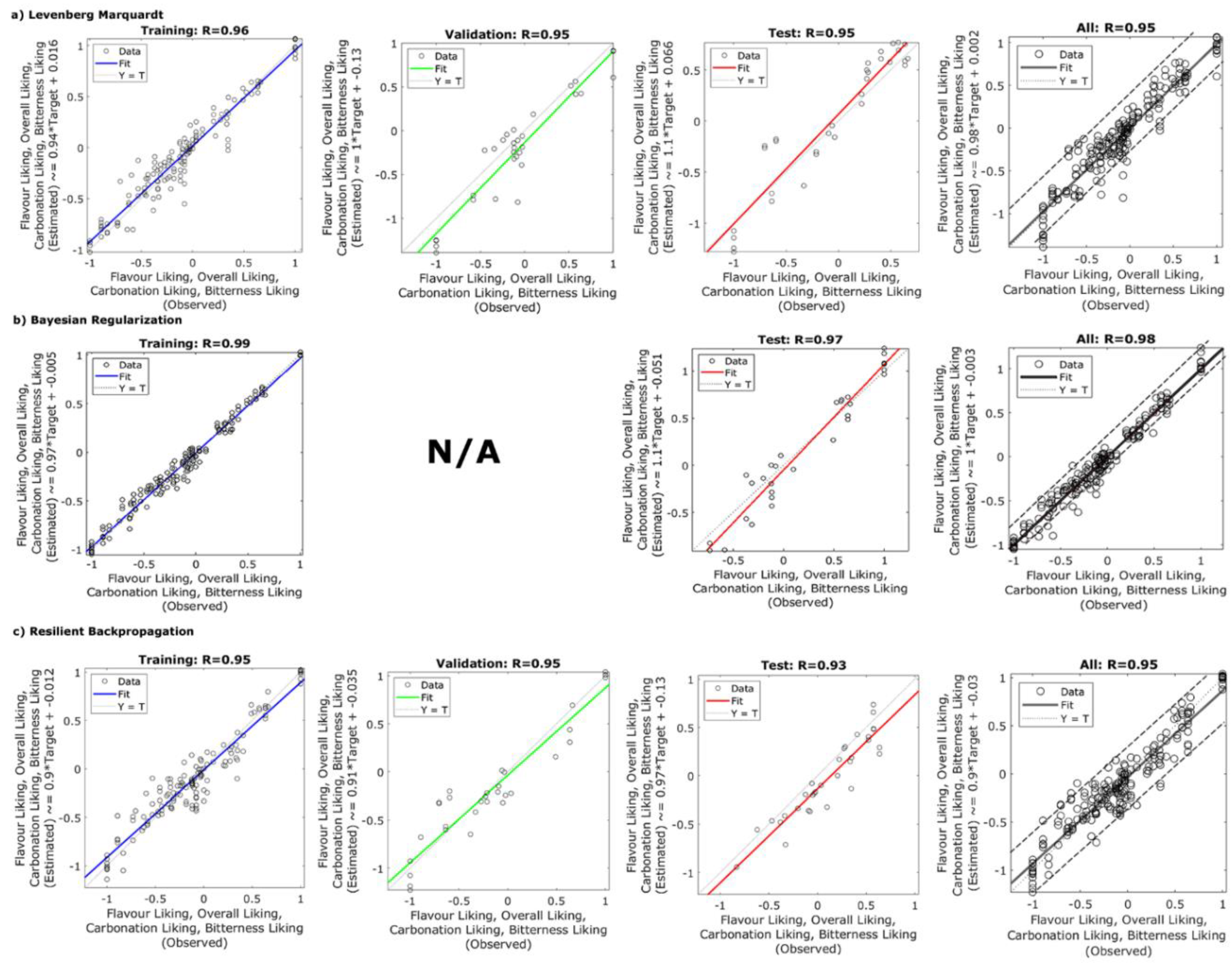
| Algorithm | Neurons | Stage | R | R2 | b | MSE |
|---|---|---|---|---|---|---|
| Backpropagation with Jacobian derivatives algorithm | ||||||
| Levenberg Marquardt | 7 | Training | 0.96 | 0.92 | 0.94 | 0.02 |
| Validation | 0.95 | 0.90 | 1.00 | 0.06 | ||
| Testing | 0.95 | 0.90 | 1.10 | 0.05 | ||
| Overall | 0.95 | 0.90 | 0.98 | 0.03 | ||
| Bayesian Regularization | 7 | Training | 0.99 | 0.98 | 0.97 | 0.01 |
| Validation | - | - | - | - | ||
| Testing | 0.97 | 0.94 | 1.1 | 0.03 | ||
| Overall | 0.98 | 0.96 | 1.0 | 0.01 | ||
| Backpropagation with gradient derivative algorithms | ||||||
| Gradient descent backpropagation | 5 | Training | 0.83 | 0.69 | 0.60 | 0.04 |
| Validation | 0.67 | 0.45 | 0.39 | 0.07 | ||
| Testing | 0.65 | 0.42 | 0.57 | 0.11 | ||
| Overall | 0.77 | 0.59 | 0.56 | 0.06 | ||
| Resilient backpropagation | 7 | Training | 0.95 | 0.90 | 0.90 | 0.02 |
| Validation | 0.95 | 0.90 | 0.91 | 0.04 | ||
| Testing | 0.93 | 0.86 | 0.97 | 0.04 | ||
| Overall | 0.95 | 0.90 | 0.90 | 0.03 | ||
| Supervised weight and bias algorithms | ||||||
| Batch training with weight and bias learning rate | 7 | Training | 0.80 | 0.64 | 0.59 | 0.10 |
| Validation | 0.67 | 0.45 | 0.49 | 0.13 | ||
| Testing | 0.76 | 0.58 | 0.57 | 0.11 | ||
| Overall | 0.76 | 0.58 | 0.57 | 0.06 | ||
| Random order weight and bias | 10 | Training | 0.89 | 0.79 | 0.82 | 0.06 |
| Validation | 0.84 | 0.71 | 0.74 | 0.10 | ||
| Testing | 0.88 | 0.77 | 1.10 | 0.06 | ||
| Overall | 0.87 | 0.76 | 0.83 | 0.06 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzalez Viejo, C.; Torrico, D.D.; Dunshea, F.R.; Fuentes, S. Development of Artificial Neural Network Models to Assess Beer Acceptability Based on Sensory Properties Using a Robotic Pourer: A Comparative Model Approach to Achieve an Artificial Intelligence System. Beverages 2019, 5, 33. https://doi.org/10.3390/beverages5020033
Gonzalez Viejo C, Torrico DD, Dunshea FR, Fuentes S. Development of Artificial Neural Network Models to Assess Beer Acceptability Based on Sensory Properties Using a Robotic Pourer: A Comparative Model Approach to Achieve an Artificial Intelligence System. Beverages. 2019; 5(2):33. https://doi.org/10.3390/beverages5020033
Chicago/Turabian StyleGonzalez Viejo, Claudia, Damir D. Torrico, Frank R. Dunshea, and Sigfredo Fuentes. 2019. "Development of Artificial Neural Network Models to Assess Beer Acceptability Based on Sensory Properties Using a Robotic Pourer: A Comparative Model Approach to Achieve an Artificial Intelligence System" Beverages 5, no. 2: 33. https://doi.org/10.3390/beverages5020033
APA StyleGonzalez Viejo, C., Torrico, D. D., Dunshea, F. R., & Fuentes, S. (2019). Development of Artificial Neural Network Models to Assess Beer Acceptability Based on Sensory Properties Using a Robotic Pourer: A Comparative Model Approach to Achieve an Artificial Intelligence System. Beverages, 5(2), 33. https://doi.org/10.3390/beverages5020033








