Geographical Classification of Tannat Wines Based on Support Vector Machines and Feature Selection
Abstract
1. Introduction
2. Materials and Methods
2.1. Wine Samples
2.2. Chemical Compounds Determination
2.3. Color Determination
2.4. Total Polyphenols
2.5. Total Monomeric Anthocyanins
2.6. Individual Anthocyanins
2.6.1. HPLC–DAD
2.6.2. HPLC–DAD–MS
2.7. Antioxidant Activity
2.7.1. Free Radical Scavenging Capacity (DPPH)
2.7.2. Oxygen Radical Absorbance Capacity (ORAC)
2.8. Data Mining
2.9. Support Vector Machines
2.10. Variable Selection
2.11. Performance Analysis
3. Results and Discussion
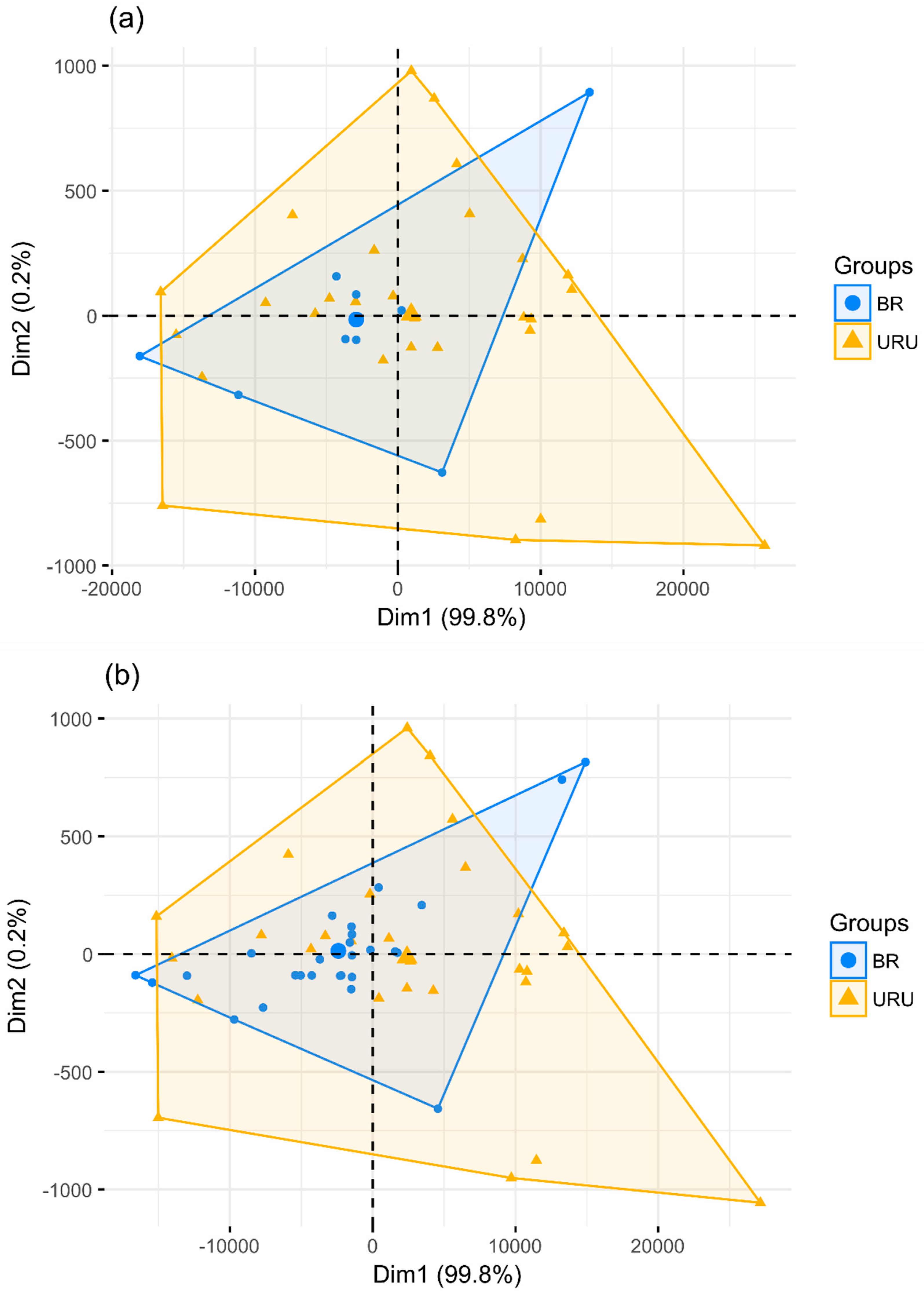
3.1. Classification Analysis
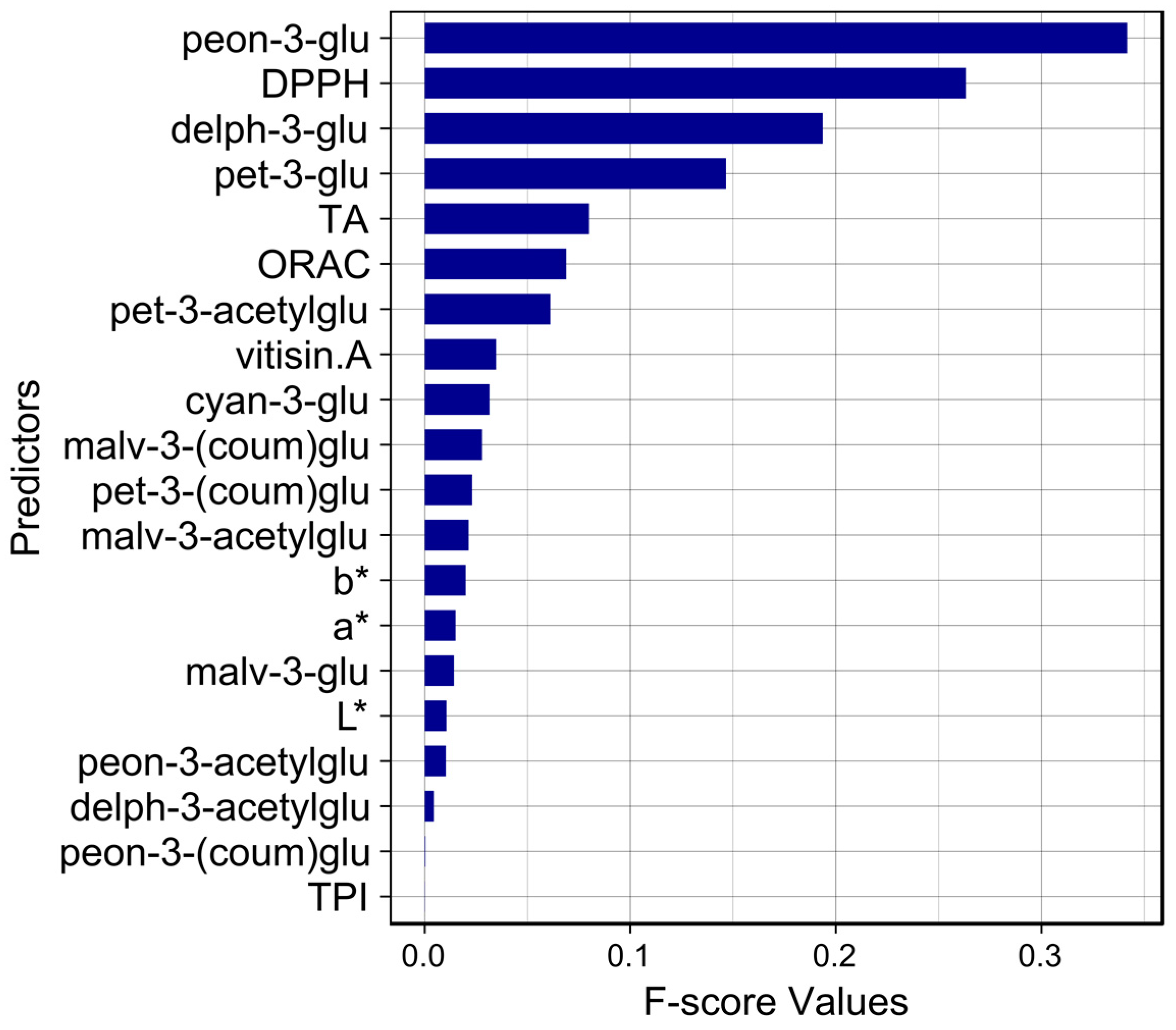
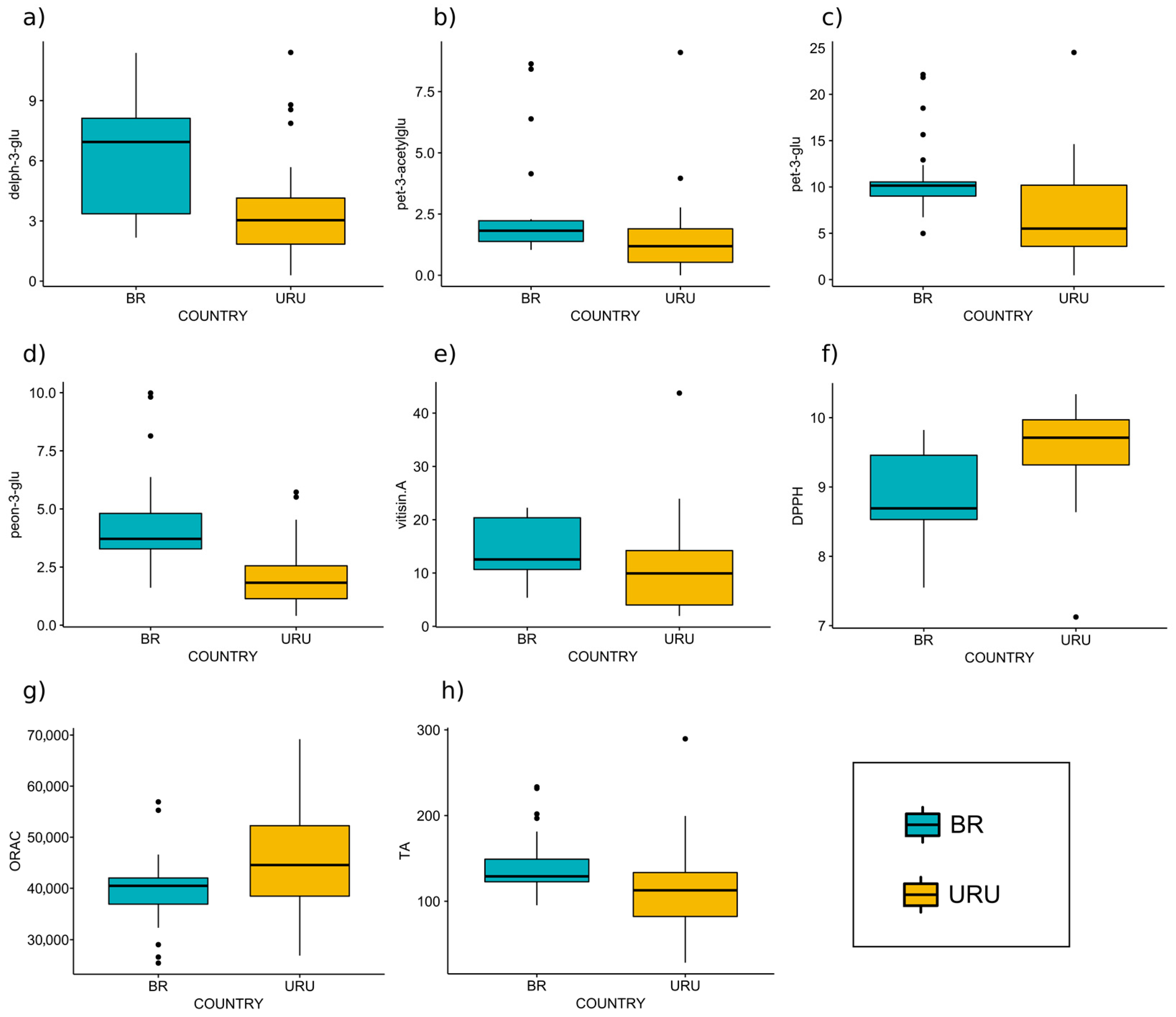
3.2. Analysis of Variable Importance
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gómez-Meire, S.; Campos, C.; Falqué, E.; Díaz, F.; Fdez-Riverola, F. Assuring the authenticity of northwest Spain white wine varieties using machine learning techniques. Food Res. Int. 2014, 60, 230–240. [Google Scholar] [CrossRef]
- Luykx, D.M.A.M.; van Ruth, S.M. An overview of analytical methods for determining the geographical origin of food products. Food Chem. 2008, 107, 897–911. [Google Scholar] [CrossRef]
- Geana, E.I.; Popescu, R.; Costinel, D.; Dinca, O.R.; Stefanescu, I.; Ionete, R.E.; Bala, C. Verifying the red wines adulteration through isotopic and chromatographic investigations coupled with multivariate statistic interpretation of the data. Food Control 2016, 62, 1–9. [Google Scholar] [CrossRef]
- Versari, A.; Laurie, V.F.; Ricci, A.; Laghi, L.; Parpinello, G.P. Progress in authentication, typification and traceability of grapes and wines by chemometric approaches. Food Res. Int. 2014, 60, 2–18. [Google Scholar] [CrossRef]
- Juan Gennari, A. A letter by the Regional Editor for South America: From varietals to terroir. Wine Econ. Policy 2014, 3, 69–70. [Google Scholar] [CrossRef]
- González-Neves, G.; Gil, G.; Barreiro, L.; Favre, G. Pigment profile of red wines cv. Tannat made with alternative winemaking techniques. J. Food Compos. Anal. 2010, 23, 447–454. [Google Scholar] [CrossRef]
- González-Neves, G.; Franco, J.; Barreiro, L.; Gil, G.; Moutounet, M.; Carbonneau, A. Varietal differentiation of Tannat, Cabernet-Sauvignon and Merlot grapes and wines according to their anthocyanic composition. Eur. Food Res. Technol. 2007, 225, 111–117. [Google Scholar] [CrossRef]
- Welke, J.E.; Manfroi, V.; Zanus, M.; Lazzarotto, M.; Zini, C.A. Differentiation of wines according to grape variety using multivariate analysis of comprehensive two-dimensional gas chromatography with time-of-flight mass spectrometric detection data. Food Chem. 2013, 141, 3897–3905. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Z.; Liu, S.; Gu, Y.; Xu, N.; Shang, Y.; Zhu, J. Discrimination of cherry wines based on their sensory properties and aromatic fingerprinting using HS-SPME-GC-MS and multivariate analysis. J. Food Sci. 2014, 79, C284–C294. [Google Scholar] [CrossRef] [PubMed]
- Rešetar, D.; Marchetti-Deschmann, M.; Allmaier, G.; Katalinić, J.P.; Pavelić, S.K. Matrix assisted laser desorption ionization mass spectrometry linear time-of-flight method for white wine fingerprinting and classification. Food Control 2016, 64, 157–164. [Google Scholar] [CrossRef]
- Płotka-Wasylka, J.; Simeonov, V.; Morrison, C.; Namieśnik, J. Impact of selected parameters of the fermentation process of wine and wine itself on the biogenic amines content: Evaluation by application of chemometric tools. Microchem. J. 2018, 142, 187–194. [Google Scholar] [CrossRef]
- Bonello, F.; Cravero, M.; Dell’Oro, V.; Tsolakis, C.; Ciambotti, A. Wine Traceability Using Chemical Analysis, Isotopic Parameters, and Sensory Profiles. Beverages 2018, 4, 54. [Google Scholar] [CrossRef]
- Aceto, M.; Bonello, F.; Musso, D.; Tsolakis, C.; Cassino, C.; Osella, D. Wine Traceability with Rare Earth Elements. Beverages 2018, 4, 23. [Google Scholar] [CrossRef]
- Zielinski, A.A.F.; Haminiuk, C.W.I.; Nunes, C.A.; Schnitzler, E.; Ruth, S.M.; Granato, D. Chemical composition, sensory properties, provenance, and bioactivity of fruit juices as assessed by chemometrics: A critical review and guideline. Compre. Rev. Food Sci. food Saf. 2014, 13, 300–316. [Google Scholar] [CrossRef]
- Callao, M.P.; Ruisánchez, I. An overview of multivariate qualitative methods for food fraud detection. Food Control 2018, 86, 283–293. [Google Scholar] [CrossRef]
- Condurso, C.; Cincotta, F.; Tripodi, G.; Verzera, A. Characterization and ageing monitoring of Marsala dessert wines by a rapid FTIR-ATR method coupled with multivariate analysis. Eur. Food Res. Technol. 2018, 244, 1073–1081. [Google Scholar] [CrossRef]
- Ríos-Reina, R.; García-González, D.L.; Callejón, R.M.; Amigo, J.M. NIR spectroscopy and chemometrics for the typification of Spanish wine vinegars with a protected designation of origin. Food Control 2018, 89, 108–116. [Google Scholar] [CrossRef]
- Ioannou-Papayianni, E.; Kokkinofta, R.I.; Theocharis, C.R. Authenticity of Cypriot sweet wine commandaria using FT-IR and chemometrics. J. Food Sci. 2011, 76, C420–C427. [Google Scholar] [CrossRef] [PubMed]
- Ropodi, A.I.; Panagou, E.Z.; Nychas, G.-J. Data mining derived from food analyses using non-invasive/non-destructive analytical techniques; determination of food authenticity, quality & safety in tandem with computer science disciplines. Trends Food Sci. Technol. 2016, 50, 11–25. [Google Scholar] [CrossRef]
- Guo, H.; Li, Y.; Jennifer, S.; Gu, M.; Huang, Y.; Gong, B. Learning from class-imbalanced data: Review of methods and applications. Expert Syst. Appl. 2017, 73, 220–239. [Google Scholar] [CrossRef]
- Majchrzak, T.; Wojnowski, W.; Płotka-Wasylka, J. Classification of Polish wines by application of ultra-fast gas chromatography. Eur. Food Res. Technol. 2018, 1–9. [Google Scholar] [CrossRef]
- Capron, X.; Massart, D.L.; Smeyers-Verbeke, J. Multivariate authentication of the geographical origin of wines: A kernel SVM approach. Eur. Food Res. Technol. 2007, 225, 559–568. [Google Scholar] [CrossRef]
- Ríos-Reina, R.; Elcoroaristizabal, S.; Ocaña-González, J.A.; García-González, D.L.; Amigo, J.M.; Callejón, R.M. Characterization and authentication of Spanish PDO wine vinegars using multidimensional fluorescence and chemometrics. Food Chem. 2017, 230, 108–116. [Google Scholar] [CrossRef] [PubMed]
- Jurado, J.M.; Alcázar, Á.; Palacios-Morillo, A.; De Pablos, F. Classification of Spanish DO white wines according to their elemental profile by means of support vector machines. Food Chem. 2012, 135, 898–903. [Google Scholar] [CrossRef] [PubMed]
- da Costa, N.L.; Castro, I.A.; Barbosa, R. Classification of Cabernet Sauvignon from Two Different Countries in South America by Chemical Compounds and Support Vector Machines. Appl. Artif. Intell. 2016, 30, 679–689. [Google Scholar] [CrossRef]
- Soares, F.; Anzanello, M.J.; Fogliatto, F.S.; Marcelo, M.C.A.; Ferrão, M.F.; Manfroi, V.; Pozebon, D. Element selection and concentration analysis for classifying South America wine samples according to the country of origin. Comput. Electron. Agric. 2018, 150, 33–40. [Google Scholar] [CrossRef]
- Singleton, V.L.; Rossi, J.A. Colorimetry of total phenolics with phosphomolybdic-phosphotungstic acid reagents. Am. J. Enol. Vitic. 1965, 16, 144–158. [Google Scholar]
- Fuleki, T.; Francis, F.J. Determination of total anthocyanin and degradation index for cranberry juice. Food Sci. 1968, 33, 78–83. [Google Scholar] [CrossRef]
- Boido, E.; Alcalde-Eon, C.; Carrau, F.; Dellacassa, E.; Rivas-Gonzalo, J.C. Aging effect on the pigment composition and color of Vitis vinifera L. cv. Tannat wines. Contribution of the main pigment families to wine color. J. Agric. Food Chem. 2006, 54, 6692–6704. [Google Scholar] [CrossRef] [PubMed]
- Arnous, A.; Makris, D.P.; Kefalas, P. Effect of principal polyphenolic components in relation to antioxidant characteristics of aged red wines. J. Agric. Food Chem. 2001, 49, 5736–5742. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.; Ou, B.; Hampsch-Woodill, M.; Flanagan, J.A.; Prior, R.L. High-throughput assay of oxygen radical absorbance capacity (ORAC) using a multichannel liquid handling system coupled with a microplate fluorescence reader in 96-well format. J. Agric. Food Chem. 2002, 50, 4437–4444. [Google Scholar] [CrossRef] [PubMed]
- Witten, I.H.; Frank, E.; Hall, M.A. Data Mining: Practical Machine Learning Tools and Techniques; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Team, the R.C. R: A language and environment for statistical computing. R Foundation for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 30 November 2018).
- Kuhn, M. The caret package. Available online: http://caret.r-forge.r-project.org/ (accessed on 30 November 2018).
- Wickham, H. Ggplot2: Elegant Graphics for Data Analysis; Springer-Verlag New York: New York, NY, USA, 2009. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Xue, H.; Yang, Q.; Chen, S. SVM: Support vector machines. In The Top Ten Algorithms in Data Mining; Taylor & Francis Group: Abingdon-on-Thames, UK, 2009; pp. 37–59. [Google Scholar]
- Noori, R.; Abdoli, M.A.; Ghasrodashti, A.A.; Jalili Ghazizade, M. Prediction of municipal solid waste generation with combination of support vector machine and principal component analysis: A case study of Mashhad. Environ. Prog. Sustain. Energy 2009, 28, 249–258. [Google Scholar] [CrossRef]
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Chen, Y.-W.; Lin, C.-J. Combining SVMs with various feature selection strategies. In Feature Extraction; Springer: Berlin, Germany, 2006; pp. 315–324. [Google Scholar]
- Liu, F.; Guo, W.; Fouche, J.-P.; Wang, Y.; Wang, W.; Ding, J.; Zeng, L.; Qiu, C.; Gong, Q.; Zhang, W.; et al. Multivariate classification of social anxiety disorder using whole brain functional connectivity. Brain Struct. Funct. 2015, 220, 101–115. [Google Scholar] [CrossRef] [PubMed]
- Turra, C.; de Lima, M.D.; Fernandes, E.A.D.N.; Bacchi, M.A.; Barbosa, F.; Barbosa, R. Multielement determination in orange juice by ICP-MS associated with data mining for the classification of organic samples. Inf. Process. Agric. 2017, 4, 199–205. [Google Scholar] [CrossRef]
- Marin, G.; Dominio, F.; Zanuttigh, P. Hand gesture recognition with jointly calibrated leap motion and depth sensor. Multimed. Tools Appl. 2016, 75, 14991–15015. [Google Scholar] [CrossRef]
- Adnane, M.; Belouchrani, A. Heartbeats classification using QRS and T waves autoregressive features and RR interval features. Expert Syst. 2017, 34, e12219. [Google Scholar] [CrossRef]
- Gutiérrez, L.; Quintana, F.A.; Baer, D.; von Mardones, C. Multivariate Bayesian discrimination for varietal authentication of Chilean red wine. J. Appl. 2011, 4763, 1–28. [Google Scholar] [CrossRef]
- Río Segade, S.; Orriols, I.; Gerbi, V.; Rolle, L. Phenolic characterization of thirteen red grape cultivars from galicia by anthocyanin profile and flavanol composition. J. Int. Sci. Vigne Vin 2009, 43, 189–198. [Google Scholar] [CrossRef]

| Reference | Prediction | |
|---|---|---|
| Positive | Negative | |
| Positive | TP | FN |
| Negative | FP | TN |
| Variable | Brazil (n = 28) | Uruguay (n = 28) |
|---|---|---|
| L * | 16.02 ± 5.91 (3.84–31.02) | 17.48 ± 6.25 (4.7–32.43) |
| a * | 45.47 ± 6.74 (25.7–54.17) | 47.24 ± 5.84 (29.43–54.51) |
| b * | 26.35 ± 8.63 (6.37–42.87) | 28.95 ± 9.59 (7.61–48.6) |
| TPI | 1924.45 ± 352.61 (1365.36–2999.55) | 1973.45 ± 454.56 (1015.98–2946.75) |
| TA | 143.41 ± 35.32 (95.35–233.45) | 117.02 ± 52.93 (28.72–289.56) |
| ORAC | 39,623.59 ± 6942.55 (25,423.23–56,914.9) | 44,431.93 ± 9938.45 (26,883.63–69,192.46) |
| DPPH | 8.88 ± 0.58 (7.55–9.82) | 9.56 ± 0.67 (7.12–10.34) |
| cyan-3-glu | 0.22 ± 0.12 (0.1–0.62) | 0.18 ± 0.07 (0.07–0.36) |
| delph-3-acetylglu | 1.15 ± 0.81 (0.48–3.61) | 0.98 ± 0.7 (0.33–3.83) |
| delph-3-glu | 6.19 ± 2.71 (2.17–11.38) | 3.65 ± 2.63 (0.29–11.4) |
| malv-3-(coum)glu | 6.36 ± 2.89 (2.97–11.84) | 5.04 ± 3.53 (0.41–14.18) |
| malv-3-acetylglu | 13.05 ± 5.69 (4.55–27.78) | 11.01 ± 7.35 (1.04–30.79) |
| malv-3-glu | 42.58 ± 22.03 (26.03–95.19) | 36.89 ± 22.79 (3.86–89.98) |
| peon-3-(coum)glu | 1.48 ± 1.98 (0.57–4.71) | 1.76 ± 2.07 (0.27–11.11) |
| peon-3-acetylglu | 1.57 ± 0.74 (0.89–3.25) | 1.41 ± 0.61 (0.51–2.9) |
| peon-3-glu | 4.27 ± 2.12 (1.61–9.99) | 2.11 ± 1.46 (0.4–5.72) |
| pet-3-(coum)glu | 0.45 ± 0.56 (0.1–2.14) | 0.28 ± 0.29 (0.1–1.64) |
| pet-3-acetylglu | 2.43 ± 2.02 (1.04–8.63) | 1.57 ± 1.74 (0–9.1) |
| pet-3-glu | 11.02 ± 3.97 (4.98–22.14) | 7.16 ± 5.21 (0.46–24.52) |
| vitisin A | 14.37 ± 5.2 (5.37–22.25) | 11.32 ± 8.89 (1.95–43.75) |
| # | Compounds | Acc | MCC | Sens | Spec |
|---|---|---|---|---|---|
| #1 | peon-3-glu | 91.07 | 0.82 | 89.66 | 92.59 |
| #2 | peon-3-glu, DPPH | 94.64 | 0.90 | 90.32 | 100 |
| #3 | peon-3-glu, DPPH, delph-3-glu | 85.71 | 0.71 | 85.71 | 85.71 |
| #4 | peon-3-glu, DPPH, delph-3-glu, pet-3-glu | 92.86 | 0.86 | 90.00 | 96.15 |
| #5 | peon-3-glu, DPPH, delph-3-glu, pet-3-glu, TA | 91.07 | 0.82 | 89.66 | 92.59 |
| #6 | peon-3-glu, DPPH, delph-3-glu, pet-3-glu, TA, ORAC | 94.64 | 0.90 | 90.32 | 100 |
| #7 | peon-3-glu, DPPH, delph-3-glu, pet-3-glu, TA, ORAC, pet-3-acetylglu | 91.07 | 0.83 | 87.10 | 96.00 |
| #8 | peon-3-glu, DPPH, delph-3-glu, pet-3-glu, TA, ORAC, pet-3-acetylglu, vitisin A | 94.64 | 0.90 | 90.32 | 100 |
| #9 | peon-3-glu, DPPH, delph-3-glu, pet-3-glu, TA, ORAC, pet-3-acetylglu, vitisin A, cyan-3-glu | 91.07 | 0.83 | 87.10 | 96.00 |
| #10 | peon-3-glu, DPPH, delph-3-glu, pet-3-glu, TA, ORAC, pet-3-acetylglu, vitisin A, cyan-3-glu, malv-3-(coum)glu | 91.07 | 0.83 | 87.10 | 96.00 |
| #11 | peon-3-glu, DPPH, delph-3-glu, pet-3-glu, TA, ORAC, pet-3-acetylglu, vitisin A, cyan-3-glu, malv-3-(coum)glu, pet-3-(coum)glu | 85.71 | 0.72 | 83.33 | 88.46 |
| #12 | peon-3-glu, DPPH, delph-3-glu, pet-3-glu, TA, ORAC, pet-3-acetylglu, vitisin A, cyan-3-glu, malv-3-(coum)glu, pet-3-(coum)glu, malv-3-acetylglu | 92.86 | 0.87 | 87.50 | 100 |
| #13 | peon-3-glu, DPPH, delph-3-glu, pet-3-glu, TA, ORAC, pet-3-acetylglu, vitisin A, cyan-3-glu, malv-3-(coum)glu, pet-3-(coum)glu, malv-3-acetylglu, b * | 89.29 | 0.79 | 86.67 | 92.31 |
| #14 | peon-3-glu, DPPH, delph-3-glu, pet-3-glu, TA, ORAC, pet-3-acetylglu, vitisin A, cyan-3-glu, malv-3-(coum)glu, pet-3-(coum)glu, malv-3-acetylglu, b *, a * | 91.07 | 0.83 | 87.10 | 96.00 |
| #15 | peon-3-glu, DPPH, delph-3-glu, pet-3-glu, TA, ORAC, pet-3-acetylglu, vitisin A, cyan-3-glu, malv-3-(coum)glu, pet-3-(coum)glu, malv-3-acetylglu, b *, a *, malv-3-glu | 89.29 | 0.79 | 86.67 | 92.31 |
| #16 | peon-3-glu, DPPH, delph-3-glu, pet-3-glu, TA, ORAC, pet-3-acetylglu, vitisin A, cyan-3-glu, malv-3-(coum)glu, pet-3-(coum)glu, malv-3-acetylglu, b *, a *, malv-3-glu, L * | 92.86 | 0.87 | 87.50 | 100 |
| #17 | peon-3-glu, DPPH, delph-3-glu, pet-3-glu, TA, ORAC, pet-3-acetylglu, vitisin A, cyan-3-glu, malv-3-(coum)glu, pet-3-(coum)glu, malv-3-acetylglu, b *, a *, malv-3-glu, L *, peon-3-acetylglu | 91.07 | 0.83 | 87.10 | 96.00 |
| #18 | peon-3-glu, DPPH, delph-3-glu, pet-3-glu, TA, ORAC pet-3-acetylglu, vitisin A, cyan-3-glu, malv-3-(coum)glu, pet-3-(coum)glu, malv-3-acetylglu, b *, a *, malv-3-glu, L *, peon-3-acetylglu, delph-3-acetylglu | 91.07 | 0.83 | 87.10 | 96.00 |
| #19 | peon-3-glu, DPPH, delph-3-glu, pet-3-glu, TA, ORAC, pet-3-acetylglu, vitisin A, cyan-3-glu, malv-3-(coum)glu, pet-3-(coum)glu, malv-3-acetylglu, b *, a *, malv-3-glu, L *, peon-3-acetylglu, delph-3-acetylglu, peon-3-(coum)glu | 92.86 | 0.87 | 87.50 | 100 |
| #20 | peon-3-glu, DPPH, delph-3-glu, pet-3-glu, TA, ORAC, pet-3-acetylglu, vitisin A, cyan-3-glu, malv-3-(coum)glu, pet-3-(coum)glu, malv-3-acetylglu, b *, a *, malv-3-glu, L *, peon-3-acetylglu, delph-3-acetylglu, peon-3-(coum)glu, TPI | 92.86 | 0.87 | 87.50 | 100 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa, N.L.; Llobodanin, L.A.G.; Castro, I.A.; Barbosa, R. Geographical Classification of Tannat Wines Based on Support Vector Machines and Feature Selection. Beverages 2018, 4, 97. https://doi.org/10.3390/beverages4040097
Costa NL, Llobodanin LAG, Castro IA, Barbosa R. Geographical Classification of Tannat Wines Based on Support Vector Machines and Feature Selection. Beverages. 2018; 4(4):97. https://doi.org/10.3390/beverages4040097
Chicago/Turabian StyleCosta, Nattane Luíza, Laura Andrea García Llobodanin, Inar Alves Castro, and Rommel Barbosa. 2018. "Geographical Classification of Tannat Wines Based on Support Vector Machines and Feature Selection" Beverages 4, no. 4: 97. https://doi.org/10.3390/beverages4040097
APA StyleCosta, N. L., Llobodanin, L. A. G., Castro, I. A., & Barbosa, R. (2018). Geographical Classification of Tannat Wines Based on Support Vector Machines and Feature Selection. Beverages, 4(4), 97. https://doi.org/10.3390/beverages4040097





