Determination of Total Anthocyanin Concentration in Barbera Red Wines by Raman Spectroscopy and Multivariate Statistical Methods
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Design
2.2. Materials
2.3. Spectrophotometric Acquisition of Barbera Wine Sample
2.4. Raman Spectrum Acquisition of Barbera Wine Sample
- Spectrometer: Exemplar Pro (B&W Tek, Plainsboro, NJ, USA) featuring a highly sensitive deep cooled (−25 °C) with a wavelength range of 190–1100 nm and a spectral resolution of 0.6 nm. Also equipped with a CCD back-illuminated (BT) detector that is highly sensitive and cooled (−25 °C);
- Optical fiber coupled to a BAC102 Raman Trigger probe (B&W Tek, Plainsboro, NJ, USA): the latter has a working distance of 5.5 mm, while the fiber is characterized by a numerical aperture of 0.22;
- Laser: BRM-785E (B&W Tek, Plainsboro, NJ, USA) with a wavelength of 785 nm and an output power of 300 mW;
- Raman shift range for acquisition: [50, 3400] ;
- Raman spectral resolution average: 11 ;
- Number of scans: 3;
- Acquisition time for each scan: 10 s.
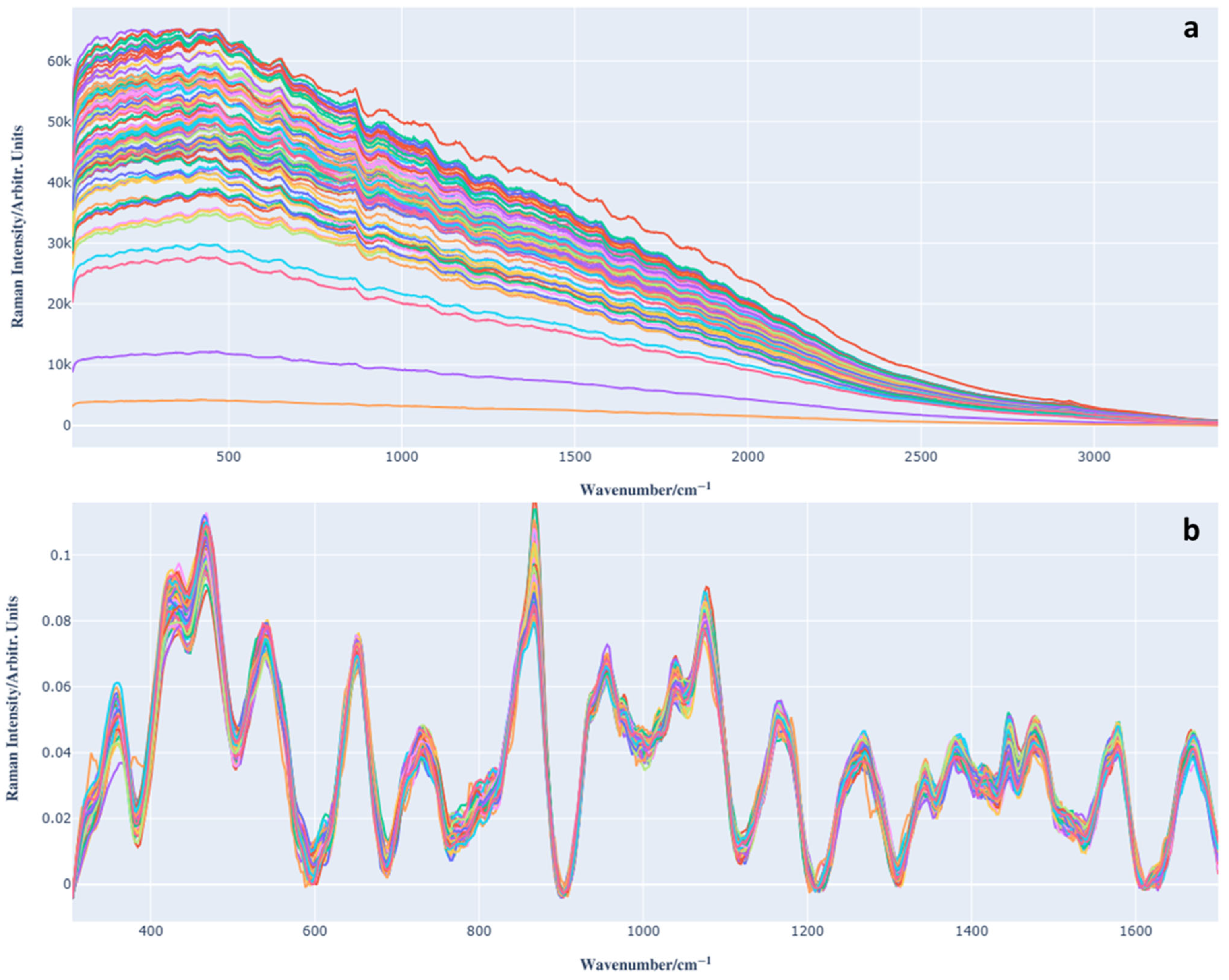
2.5. Data Preprocessing
- Removal of the Rayleigh peak tail (the spectral region with the lowest Raman shift) that does not contain information on the samples under examination
- Noise reduction by applying the Savitzky–Golay algorithm from the SciPy library [32] (9 points window and second-order polynomial);
- Baseline removal using asymmetric least squares (AsLS) fitting (, ). A function of the Python (version 3.12) library “pybaselines.whittaker” that provides several Whittaker-smoothing-based algorithms for fitting the baseline [33];
- l2 normalization of the spectral intensities, in order to have spectra with the same scale (the “preprocessing.normalize” function of the scikit-learn package was used).
2.6. Application of PLS Regression
2.7. Best PLS Regression Model and Evaluation of Performance
3. Results and Discussion
3.1. Raman Spectrum Analysis of Barbera Wine and Preprocessing
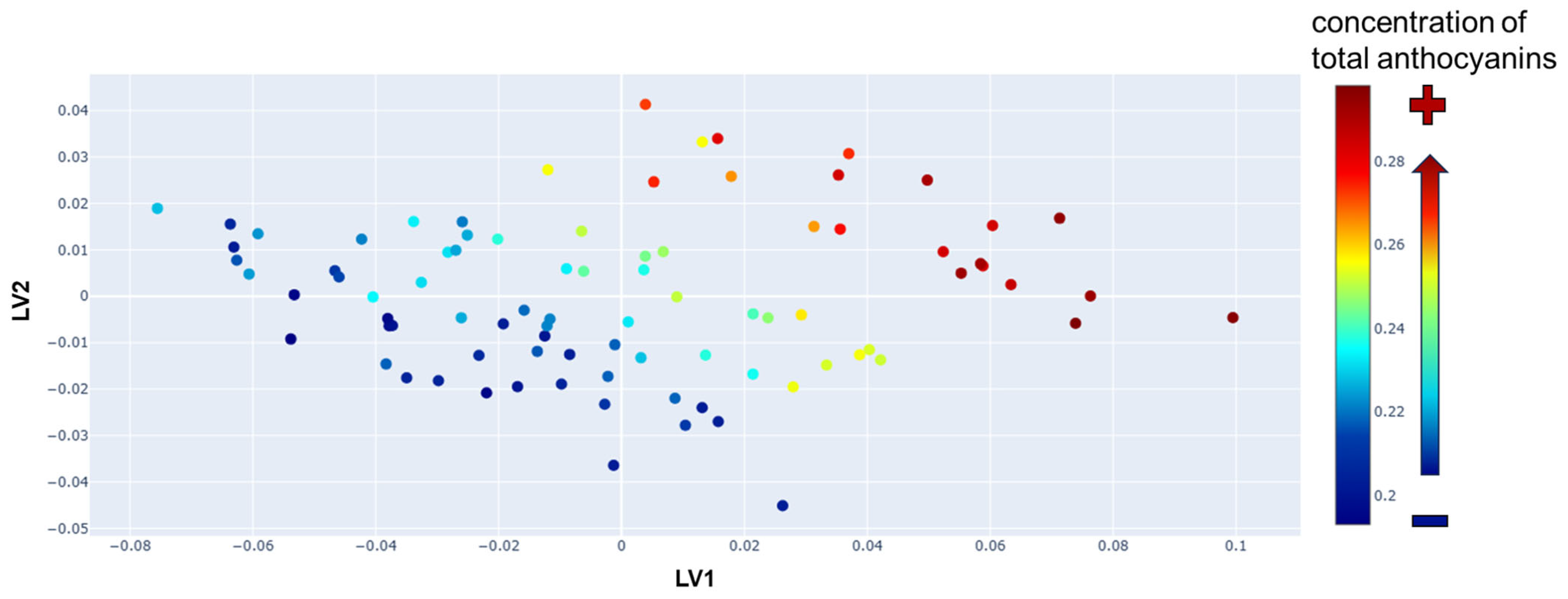
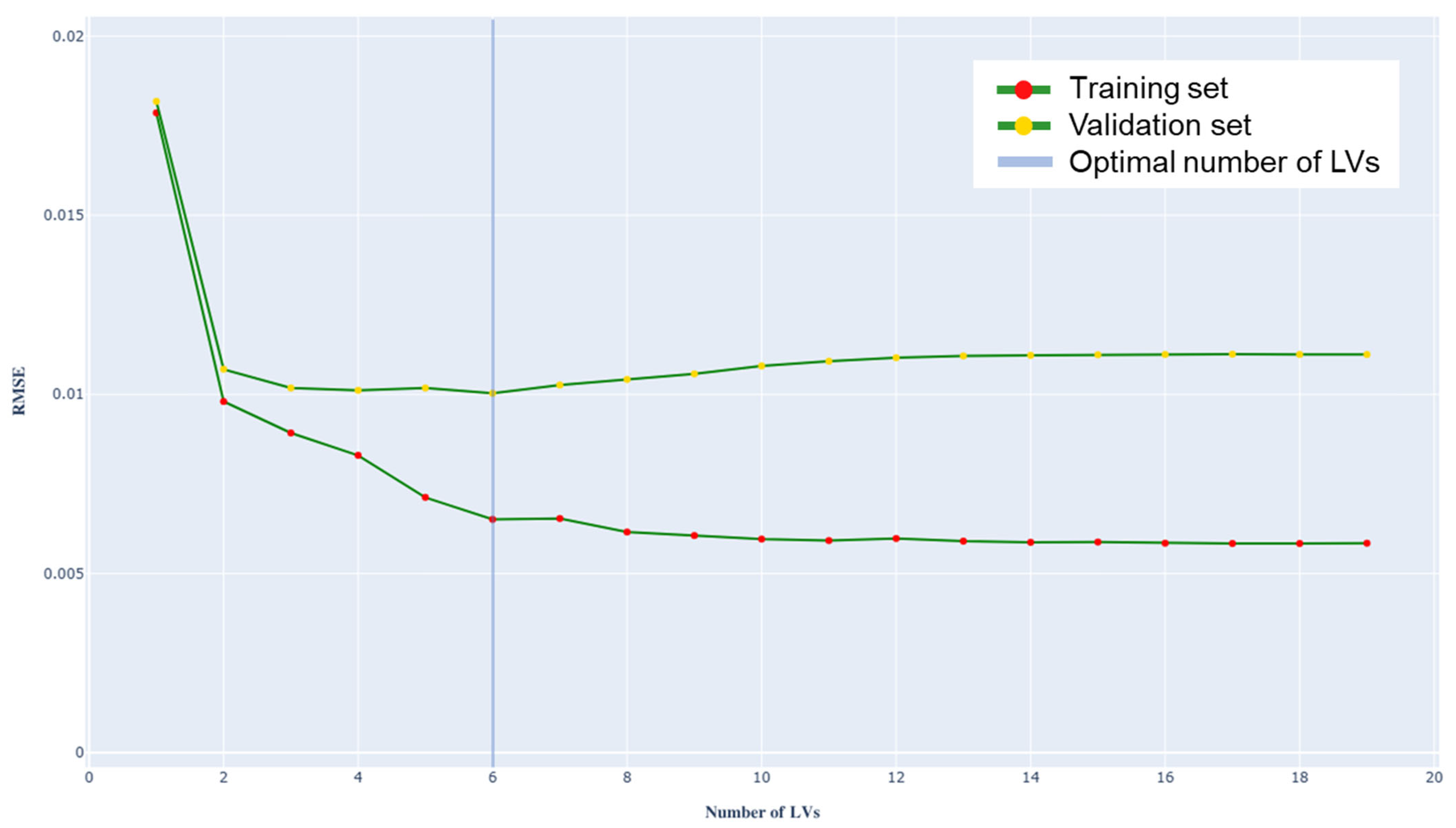
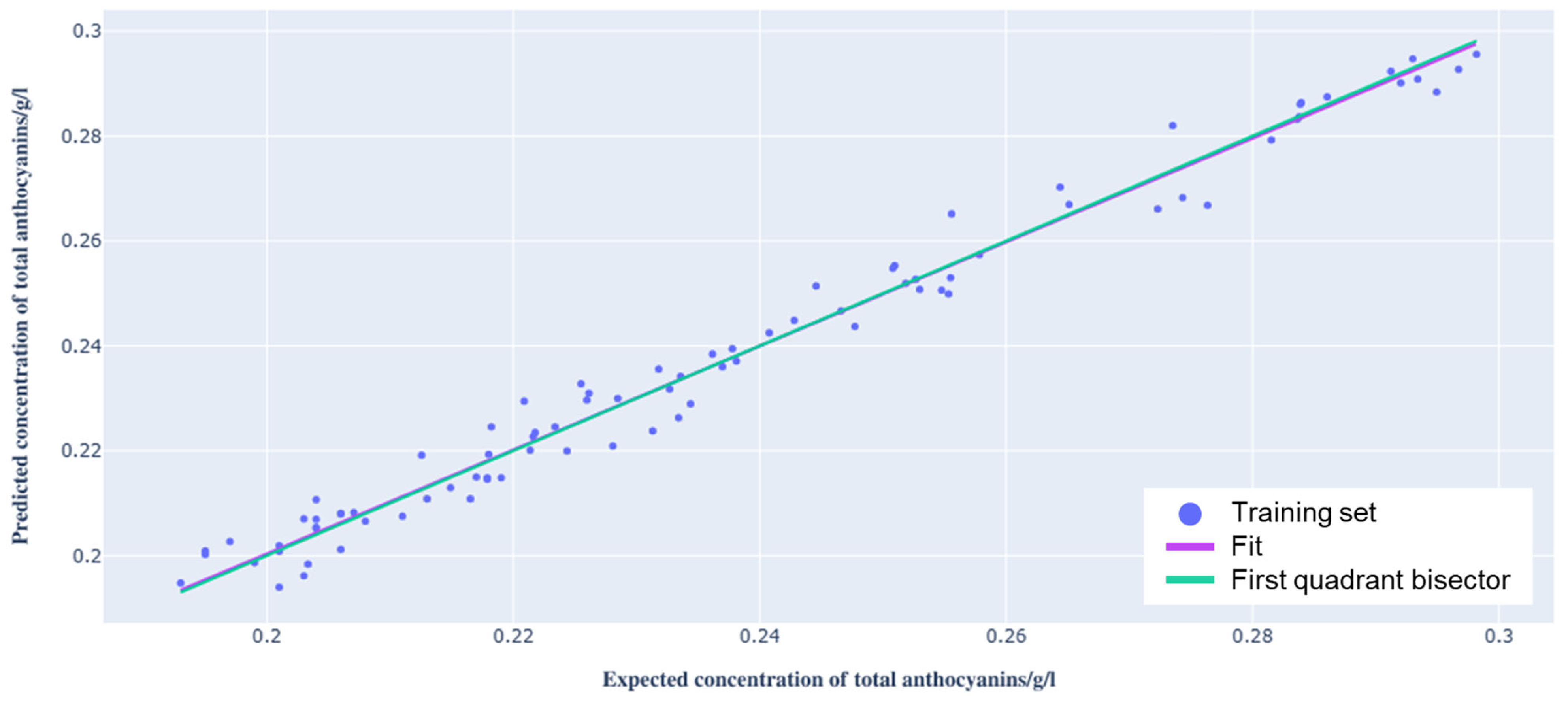
3.2. PLS Regression Model
- RMSE = 0.010 g/L,
- Optimal number of LVs = 6.
3.3. Testing New Data
3.4. Comparison of Spectrophotometry and Raman Spectroscopy
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AsLS | Asymmetric least squares |
| BT | Back-thinned |
| CCD | Charge-coupled device |
| CV | Cross validation |
| HPLC | High-performance liquid chromatography |
| LV | Latent variable |
| ML | Machine learning |
| MSE | Mean square error |
| MST | Mean total sum |
| OIV | International organization of vine and wine |
| PCR | Principal component regression |
| PLS | Partial least square |
| RMSE | Root mean square error |
| RPD | Relative predictive determinant |
| UV | Ultraviolet |
| VIS | Visible |
References
- Chen, H.; Wang, M.; Zhang, L.; Ren, F.; Li, Y.; Chen, Y.; Liu, Y.; Zhang, Z.; Zeng, Q. Anthocyanin Profiles and Color Parameters of Fourteen Grapes and Wines from the Eastern Foot of Helan Mountain in Ningxia. Food Chem. X 2024, 24, 102034. [Google Scholar] [CrossRef] [PubMed]
- Mazza, G.; Fukumoto, L.; Delaquis, P.; Girard, B.; Ewert, B. Anthocyanins, Phenolics, and Color of Cabernet Franc, Merlot, and Pinot Noir Wines from British Columbia. J. Agric. Food Chem. 1999, 47, 4009–4017. [Google Scholar] [CrossRef]
- Ofoedu, C.E.; Ofoedu, E.O.; Chacha, J.S.; Owuamanam, C.I.; Efekalam, I.S.; Awuchi, C.G. Comparative Evaluation of Physicochemical, Antioxidant, and Sensory Properties of Red Wine as Markers of Its Quality and Authenticity. Int. J. Food Sci. 2022, 2022, 8368992. [Google Scholar] [CrossRef]
- Lorrain, B.; Ky, I.; Pechamat, L.; Teissedre, P.-L. Evolution of Analysis of Polyhenols from Grapes, Wines, and Extracts. Molecules 2013, 18, 1076–1100. [Google Scholar] [CrossRef]
- Sanna, R.; Piras, C.; Marincola, F.C.; Lecca, V.; Maurichi, S.; Scano, P. Multivariate Statistical Analysis of the UV-Vis Profiles of Wine Polyphenolic Extracts during Vinification. J. Agric. Sci. 2014, 6, 152. [Google Scholar] [CrossRef]
- Gierschner, J.; Duroux, J.-L.; Trouillas, P. UV/Visible Spectra of Natural Polyphenols: A Time-Dependent Density Functional Theory Study. Food Chem. 2012, 131, 79–89. [Google Scholar]
- Aleixandre-Tudo, J.L.; Buica, A.; Nieuwoudt, H.; Aleixandre, J.L.; du Toit, W. Spectrophotometric Analysis of Phenolic Compounds in Grapes and Wines. J. Agric. Food Chem. 2017, 65, 4009–4026. [Google Scholar] [CrossRef] [PubMed]
- Harbertson, J.F.; Spayd, S. Measuring Phenolics in the Winery. Am. J. Enol. Vitic. 2006, 57, 280–288. [Google Scholar] [CrossRef]
- de Andrade, R.H.S.; do Nascimento, L.S.; Pereira, G.E.; Hallwass, F.; Paim, A.P.S. Anthocyanic Composition of Brazilian Red Wines and Use of HPLC-UV–Vis Associated to Chemometrics to Distinguish Wines from Different Regions. Microchem. J. 2013, 110, 256–262. [Google Scholar] [CrossRef]
- Gallego, Á.L.; Guesalaga, A.R.; Bordeu, E.; Gonzalez, Á.S. Rapid Measurement of Phenolics Compounds in Red Wine Using Raman Spectroscopy. IEEE Trans. Instrum. Meas. 2011, 60, 507–512. [Google Scholar] [CrossRef]
- Gao, Z.; Yang, G.; Zhao, X.; Jiao, L.; Wen, X.; Liu, Y.; Xia, X.; Zhao, C.; Dong, D. Rapid Measurement of Anthocyanin Content in Grape and Grape Juice: Raman Spectroscopy Provides Non-Destructive, Rapid Methods. Comput. Electron. Agric. 2024, 222, 109048. [Google Scholar] [CrossRef]
- Duan, C.; Xiao, X.; Yu, Y.; Xu, M.; Zhang, Y.; Liu, X.; Dai, H.; Pi, F.; Wang, J. In Situ Raman Characterization of the Stability of Blueberry Anthocyanins in Aqueous Solutions under Perturbations in Temperature, UV, pH. Food Chem. 2024, 431, 137155. [Google Scholar] [CrossRef]
- Liu, H.; Cao, L.; Sui, J.; Lin, H.; Wang, X.; Wang, K. Unveiling Anthocyanins Structural Basis with Multiplexed Colorimetric and SERS Responses for Smart Monitoring of Seafood Freshness. Food Chem. 2025, 488, 144841. [Google Scholar] [CrossRef]
- Fuller, H.; Beaver, C.; Harbertson, J. Alcoholic Fermentation Monitoring and pH Prediction in Red and White Wine by Combining Spontaneous Raman Spectroscopy and Machine Learning Algorithms. Beverages 2021, 7, 78. [Google Scholar] [CrossRef]
- Lu, B.; Tian, F.; Chen, C.; Wu, W.; Tian, X.; Chen, C.; Lv, X. Identification of Chinese Red Wine Origins Based on Raman Spectroscopy and Deep Learning. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2023, 291, 122355. [Google Scholar] [CrossRef] [PubMed]
- Ezenarro, J.; Schorn-García, D. How Are Chemometric Models Validated? A Systematic Review of Linear Regression Models for NIRS Data in Food Analysis. J. Chemom. 2025, 39, e70036. [Google Scholar] [CrossRef]
- Htet, T.T.M.; Cruz, J.; Khongkaew, P.; Suwanvecho, C.; Suntornsuk, L.; Nuchtavorn, N.; Limwikrant, W.; Phechkrajang, C. PLS-Regression-Model-Assisted Raman Spectroscopy for Vegetable Oil Classification and Non-Destructive Analysis of Alpha-Tocopherol Contents of Vegetable Oils. J. Food Compos. Anal. 2021, 103, 104119. [Google Scholar] [CrossRef]
- Xiao, L.; Liu, J.; Hua, M.Z.; Lu, X. Rapid Determination of Total Phenolic Content and Antioxidant Capacity of Maple Syrup Using Raman Spectroscopy and Deep Learning. Food Chem. 2025, 463, 141289. [Google Scholar] [CrossRef]
- dos Santos, I.; Bosman, G.; Aleixandre-Tudo, J.L.; du Toit, W. Direct Quantification of Red Wine Phenolics Using Fluorescence Spectroscopy with Chemometrics. Talanta 2022, 236, 122857. [Google Scholar] [CrossRef]
- Wang, T.; Xie, C.; You, Q.; Tian, X.; Xu, X. Qualitative and Quantitative Analysis of Four Benzimidazole Residues in Food by Surface-Enhanced Raman Spectroscopy Combined with Chemometrics. Food Chem. 2023, 424, 136479. [Google Scholar] [CrossRef]
- Wen, Y.; Li, Z.; Ning, Y.; Yan, Y.; Li, Z.; Wang, N.; Wang, H. Portable Raman Spectroscopy Coupled with PLSR Analysis for Monitoring and Predicting of the Quality of Fresh-Cut Chinese Yam at Different Storage Temperatures. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2024, 310, 123956. [Google Scholar] [CrossRef] [PubMed]
- Castro, R.C.; Ribeiro, D.S.M.; Santos, J.L.M.; Páscoa, R.N.M.J. The Use of In-Situ Raman Spectroscopy to Monitor at Real Time the Quality of Different Types of Edible Oils under Frying Conditions. Food Control 2022, 136, 108879. [Google Scholar] [CrossRef]
- Ewing-Mulligan, M.; McCarthy, E. Italian Wine for Dummies; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Torchio, F.; Cagnasso, E.; Gerbi, V.; Rolle, L. Mechanical Properties, Phenolic Composition and Extractability Indices of Barbera Grapes of Different Soluble Solids Contents from Several Growing Areas. Anal. Chim. Acta 2010, 660, 183–189. [Google Scholar] [CrossRef]
- Gilioli, A.L.; Sacco, A.; Giovannozzi, A.M.; Giacosa, S.; Bosso, A.; Panero, L.; Barera, S.R.; Messina, S.; Lagori, M.; Motta, S.; et al. Raman Spectroscopy as a Rapid Tool for Monitoring Lactic Acid Concentration during Wine Malolactic Fermentation Directly in the Winery. Talanta Open 2025, 12, 100494. [Google Scholar] [CrossRef]
- OIV HPLC-Determination of Nine Major Anthocyanins in Red and Rosé Wine. Available online: https://www.oiv.int/standards/annex-a-methods-of-analysis-of-wines-and-musts/section-3-chemical-analysis/section-3-1-organic-compounds/section-3-1-5-other-organic-compounds/hplc-determination-of-nine-major-anthocyanins-in-red-and-rose-wines-%28type-ii%29 (accessed on 10 November 2025).
- Petrozziello, M.; Torchio, F.; Piano, F.; Giacosa, S.; Ugliano, M.; Bosso, A.; Rolle, L. Impact of Increasing Levels of Oxygen Consumption on the Evolution of Color, Phenolic, and Volatile Compounds of Nebbiolo Wines. Front. Chem. 2018, 6, 137. [Google Scholar] [CrossRef]
- Comuzzo, P.; Battistutta, F. Chapter 2—Acidification and pH Control in Red Wines. In Red Wine Technology; Morata, A., Ed.; Academic Press: Cambridge, MA, USA, 2019; pp. 17–34. ISBN 978-0-12-814399-5. [Google Scholar]
- Di Stefano, R.; Genfilini, N. Per Lo Studio Dei Polifenoli. L’enotecnico 1989, 5, 83–90. [Google Scholar]
- Bruni, S.; Longoni, M.; Minzoni, C.; Basili, M.; Zocca, I.; Pieraccini, S.; Sironi, M. Resonance Raman and Visible Micro-Spectroscopy for the In-Vivo and In-Vitro Characterization of Anthocyanin-Based Pigments in Blue and Violet Flowers: A Comparison with HPLC-ESI- MS Analysis of the Extracts. Molecules 2023, 28, 1709. [Google Scholar] [CrossRef]
- Zaffino, C.; Russo, B.; Bruni, S. Surface-Enhanced Raman Scattering (SERS) Study of Anthocyanidins. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2015, 149, 41–47. [Google Scholar] [CrossRef] [PubMed]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Peng, S.; Jiang, A.; Wei, J.; Li, C.; Tan, J. Asymmetric Least Squares for Multiple Spectra Baseline Correction. Anal. Chim. Acta 2010, 683, 63–68. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Dumancas, G.G.; Ramasahayam, S.; Bello, G.; Hughes, J.; Kramer, R. Chemometric Regression Techniques as Emerging, Powerful Tools in Genetic Association Studies. TrAC Trends Anal. Chem. 2015, 74, 79–88. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-Regression: A Basic Tool of Chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Nti, I.K.; Nyarko-Boateng, O.; Aning, J. Performance of Machine Learning Algorithms with Different K Values in K-Fold Cross-Validation. Int. J. Inf. Technol. Comput. Sci. 2021, 13, 61–71. [Google Scholar]
- Chicco, D.; Warrens, M.J.; Jurman, G. The Coefficient of Determination R-Squared Is More Informative than SMAPE, MAE, MAPE, MSE and RMSE in Regression Analysis Evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Moncunill, X.C. Laser-Induced Breakdown Spectroscopy (LIBS): A Potential Quality Tool for Infant Formula Manufacture. Ph.D. Thesis, Technological University Dublin, Dublin, Ireland, 2019. [Google Scholar]
- Matese, A.; Di Gennaro, S.F.; Orlandi, G.; Gatti, M.; Poni, S. Assessing Grapevine Biophysical Parameters From Unmanned Aerial Vehicles Hyperspectral Imagery. Front. Plant Sci. 2022, 13, 898722. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Xie, J.; Han, J.; Wang, H.; Sun, J.; Li, R.; Li, S. Visible and Near-Infrared Spectroscopy with Chemometrics Are Able to Predict Soil Physical and Chemical Properties. J. Soils Sediments 2020, 20, 2749–2760. [Google Scholar] [CrossRef]
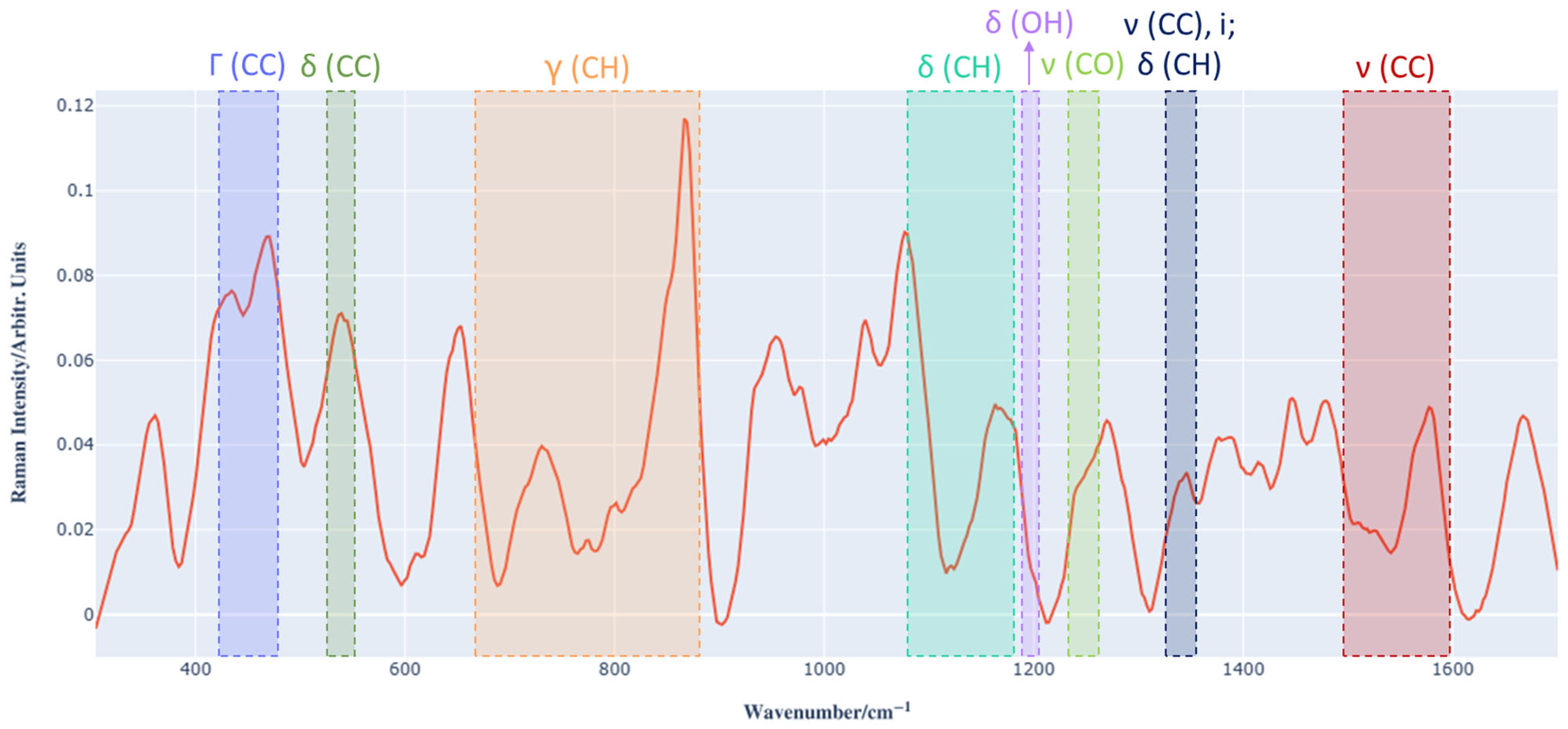

| Assigned Vibrational Mode | |
|---|---|
| Γ (CC) | 424–483 |
| δ (CC) | 535–545 |
| γ (CH) | 670–875 |
| δ (CH) | 1081–1172 |
| δ (OH) | 1190–1197 |
| ν (CO) | 1243–1254 |
| ν (CC), i; δ (CH) | 1325–1346 |
| ν (CC) | 1496–1645 |
| Fit Parameters | Measurements | Expected Values | Z Test | p-Value |
|---|---|---|---|---|
| m | 0.99 ± 0.02 | 1 | −0.66 | 0.51 |
| q | 0.002 ± 0.004 g/L | 0 g/L | 0.65 | 0.52 |
| Sample | Total Anthocyanin Concentration by Spectrophotometry (g/L) | Total Anthocyanin Concentration by Raman Spectroscopy (g/L) | Z-Test | p-Value |
|---|---|---|---|---|
| 1 | 0.238 ± 0.001 | 0.233 ± 0.008 | −0.64 | 0.52218 |
| 2 | 0.267 ± 0.010 | 0.256 ± 0.008 | −1.41 | 0.15854 |
| 3 | 0.195 ± 0.001 | 0.192 ± 0.008 | −0.40 | 0.68916 |
| 4 | 0.268 ± 0.002 | 0.270 ± 0.008 | 0.26 | 0.79486 |
| 5 | 0.246 ± 0.004 | 0.232 ± 0.008 | −1.80 | 0.07186 |
| 6 | 0.273 ± 0.002 | 0.269 ± 0.008 | −0.44 | 0.65994 |
| 7 | 0.206 ± 0.001 | 0.203 ± 0.008 | −0.42 | 0.67448 |
| 8 | 0.224 ± 0.001 | 0.216 ± 0.008 | −1.08 | 0.28014 |
| 9 | 0.207 ± 0.002 | 0.205 ± 0.008 | −0.17 | 0.86502 |
| 10 | 0.230 ± 0.002 | 0.224 ± 0.008 | −0.77 | 0.4413 |
| Set\Parameters | RMSE (g/L) | RPD | |
|---|---|---|---|
| Training | 0.004 | 7.04 | 0.98 |
| Validation | 0.010 | 2.94 | 0.88 |
| Test | 0.007 | 3.86 | 0.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gilioli, A.L.; Sacco, A.; Giovannozzi, A.M.; Giacosa, S.; Bosso, A.; Panero, L.; Ferrero, L.; Barera, S.R.; Messina, S.; Lagori, M.; et al. Determination of Total Anthocyanin Concentration in Barbera Red Wines by Raman Spectroscopy and Multivariate Statistical Methods. Beverages 2025, 11, 161. https://doi.org/10.3390/beverages11060161
Gilioli AL, Sacco A, Giovannozzi AM, Giacosa S, Bosso A, Panero L, Ferrero L, Barera SR, Messina S, Lagori M, et al. Determination of Total Anthocyanin Concentration in Barbera Red Wines by Raman Spectroscopy and Multivariate Statistical Methods. Beverages. 2025; 11(6):161. https://doi.org/10.3390/beverages11060161
Chicago/Turabian StyleGilioli, Anna Lisa, Alessio Sacco, Andrea Mario Giovannozzi, Simone Giacosa, Antonella Bosso, Loretta Panero, Lorenzo Ferrero, Silvia Raffaela Barera, Stefano Messina, Marco Lagori, and et al. 2025. "Determination of Total Anthocyanin Concentration in Barbera Red Wines by Raman Spectroscopy and Multivariate Statistical Methods" Beverages 11, no. 6: 161. https://doi.org/10.3390/beverages11060161
APA StyleGilioli, A. L., Sacco, A., Giovannozzi, A. M., Giacosa, S., Bosso, A., Panero, L., Ferrero, L., Barera, S. R., Messina, S., Lagori, M., Motta, S., Guaita, M., Vittone, E., & Rossi, A. M. (2025). Determination of Total Anthocyanin Concentration in Barbera Red Wines by Raman Spectroscopy and Multivariate Statistical Methods. Beverages, 11(6), 161. https://doi.org/10.3390/beverages11060161











