A Procedure for Estimating Drought Duration and Magnitude at the Uniform Cutoff Level of Streamflow: A Case of the Weekly Flows of Canadian Rivers
Abstract
:1. Introduction
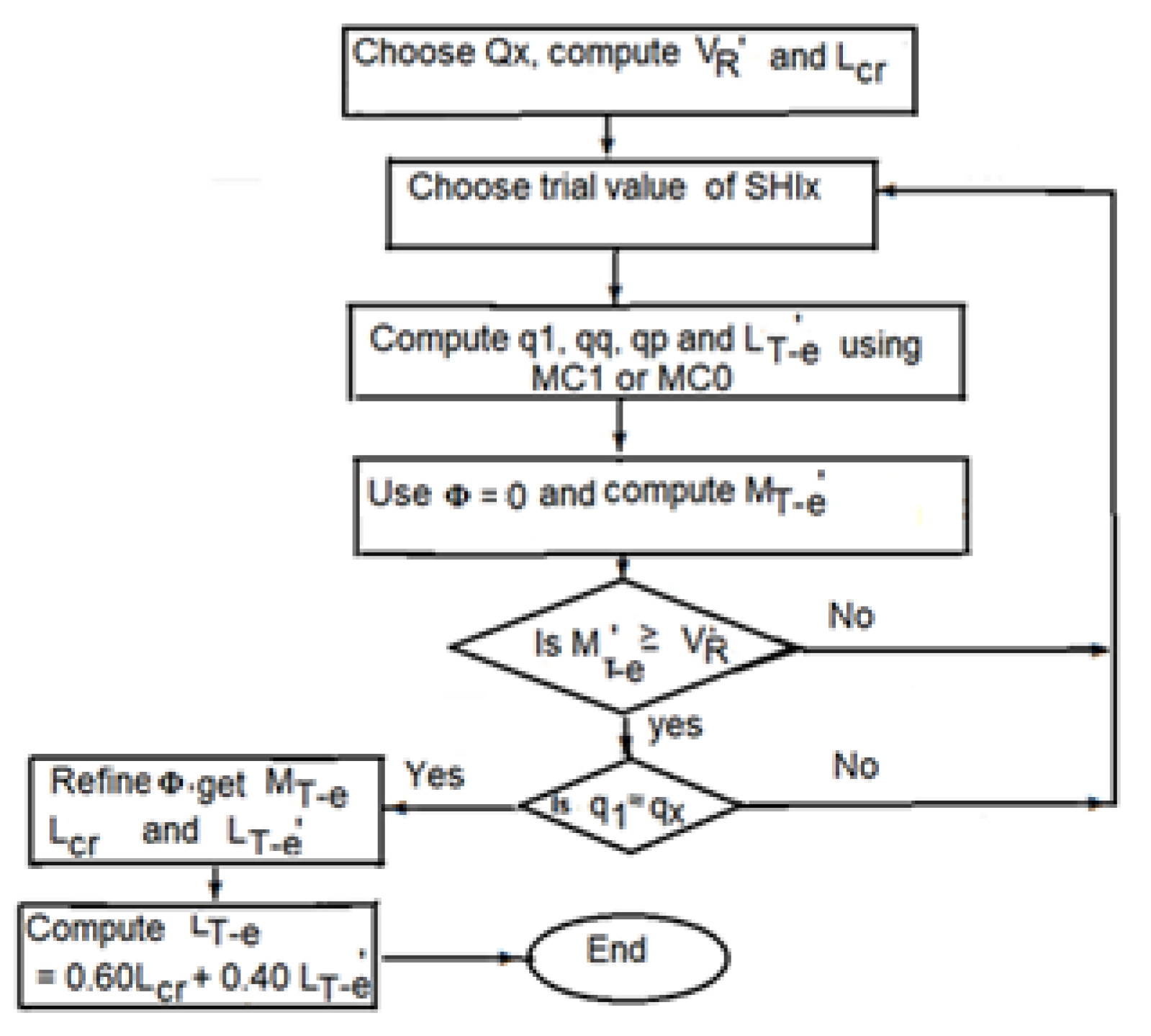
2. Background of the Model
Estimation of Drought Length, LT-e
3. Data and Methods of Analysis
3.1. Data Acquisition
3.2. Computation of Flow Statistics and Probabilities
3.3. Identification of Cutoff Level
4. Results and Discussion
4.1. Estimation of MT-e and LT-e: Fitting the Model Structure
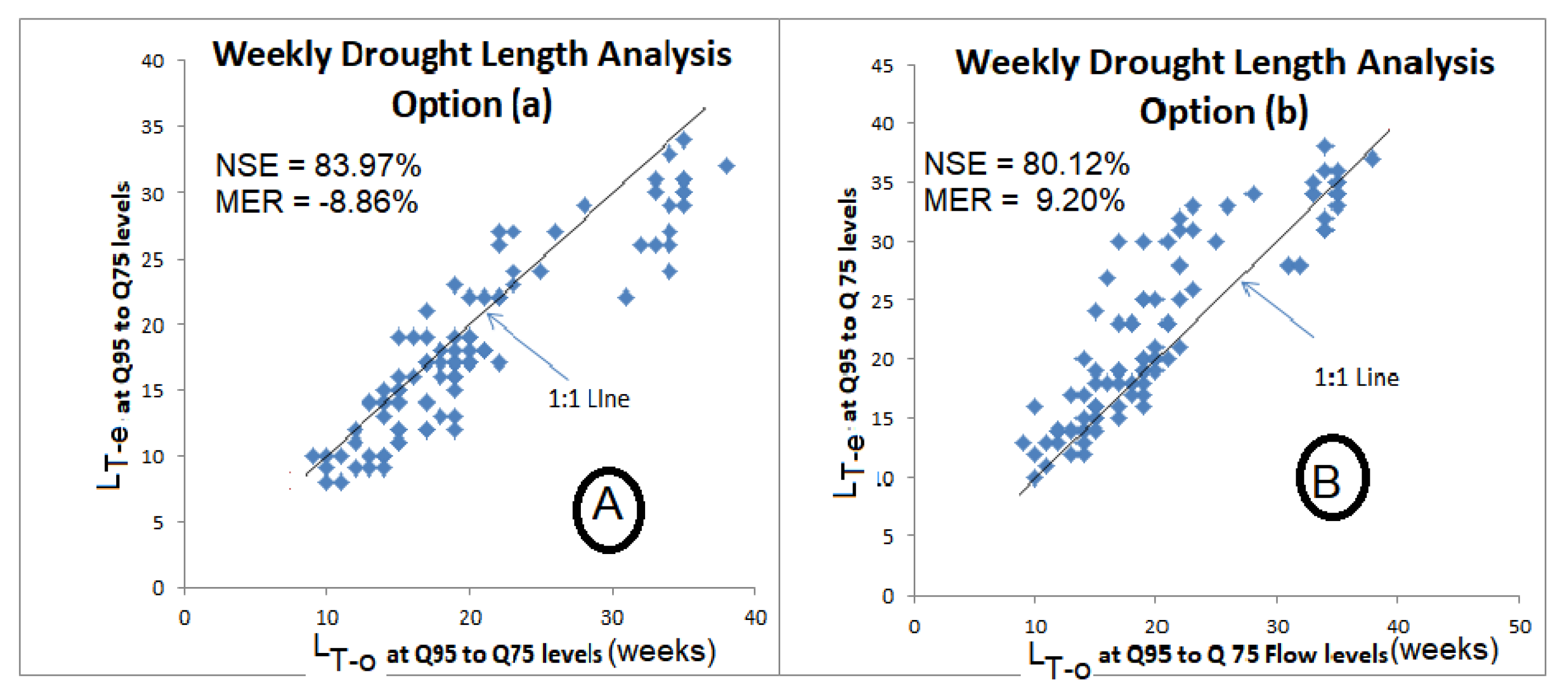
4.2. Validation of the Model Structure
4.3. An Illustrative Example for the Estimation of MT-e and LT-e
4.4. A Comment on the Present State of Drought Magnitude Assessment and Cutoff Levels at the Uniform Flow Levels
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zelenhasic, E.; Salvai, A. A method of streamflow drought analysis. Water Resour. Res. 1987, 23, 156–168. [Google Scholar] [CrossRef]
- Tallaksen, L.M.; Madsen, H.; Clausen, B. On definition and modeling of streamflow drought duration and deficit volume. Hydrol. Sci. J. 1997, 42, 15–33. [Google Scholar] [CrossRef]
- Tallaksen, L.M.; Van Lanen, H.A. Hydrological Drought: Processes and Estimation Methods for Streamflow and Groundwater, Developments in Water Science; Elsevier: Amsterdam, The Netherlands, 2004; Volume 48. [Google Scholar]
- Laaha, G. Hydrological drought severity explained by climate and catchment characteristics. J. Hydrol. 2015, 526, 3–14. [Google Scholar] [CrossRef] [Green Version]
- Clausen, B.; Pearson, C.P. Regional frequency analysis of annual maximum streamflow drought. J. Hydrol. 1995, 173, 111–130. [Google Scholar] [CrossRef]
- Sharma, T.C.; Panu, U.S. Analytical procedures for weekly hydrological droughts: A case of Canadian rivers. Hydrol. Sci. J. 2010, 55, 79–92. [Google Scholar] [CrossRef]
- Sharma, T.C.; Panu, U.S. Predicting drought durations and magnitudes at weekly time scale: Constant flow as a truncation level. Open J. Atmos. Clim. Chang. 2014, 1, 1–16. [Google Scholar] [CrossRef]
- TCLFE (Task Committee on Low Flow Evaluation). Characteristics of low flows. ASCE J. Hydraulic Div. 1980, 106, 717–731. [Google Scholar] [CrossRef]
- Gustard, A.; Bullock, A.; Dixon, J.M. Low Flow Estimation in the United Kingdom; Report no.108; Institute of Hydrology: Wallingford, UK, 1992. [Google Scholar]
- Dracup, J.A.; Lee, K.S.; Paulson, E.G., Jr. On identification of droughts. Water Resour. Res. 1980, 16, 289–296. [Google Scholar] [CrossRef]
- Yevjevich, V. Methods for determining statistical properties of droughts. In Coping with Droughts; Yevjevich, V., da Cunha, L., Vlachos, E., Eds.; Water Resources Publications: Littleton, CO, USA, 1983; pp. 22–43. [Google Scholar]
- Kjeldsen, T.R.; Lundorf, A.; Rosbjerg, D. Use of a two-component exponential distribution in partial duration modeling of hydrological droughts in Zimbabwean rivers. Hydrol. Sci. J. 2000, 45, 285–298. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesen, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–184. [Google Scholar]
- Hayes, M. Drought Indices. Available online: www.drought.unl.edu/whatis/indices.pdf.lastaccesed (accessed on 15 May 2022).
- Wu, J.; Chen, X.; Love, C.A.; Yao, H.; Chen, X.; AghaKouchak, A. Determination of water required to recover from hydrological drought: Perspective for drought propagation and non-standardized indices. J. Hydrol. 2020, 590, 125227. [Google Scholar] [CrossRef]
- Borgomeo, E.; Pflug, G.; Hall, J.W.; Hochrainer-Stigler, S. Assessing water resources system vulnerability to understand hydrological drought using copulas to characterize drought duration and deficit. Water Resour. Res. 2015, 51, 8927–8948. [Google Scholar] [CrossRef] [Green Version]
- Rad, A.M.; Ghahraman, B.; Khalili, D.; Ghabremani, Z.; Ardakani, S.A. Integrated meteorological and hydrological drought model: A management tool for proactive water resources planning in semi-arid regions. Adv. Water Resour. 2017, 107, 336–353. [Google Scholar] [CrossRef]
- McMahon, T.A.; Adeloye, A.J. Water Resources Yield; Water Resources Publications: Littleton, CO, USA, 2005; pp. 80–88. [Google Scholar]
- McMahon, T.A.; Pegram, G.G.S.; Vogel, R.M.; Peel, M.C. Revisiting Reservoir Storage–Yield Relationships using a Global Streamflow Database. Adv. Water Resour. 2007, 30, 1858–1872. [Google Scholar] [CrossRef]
- Sharma, T.C.; Panu, U.S. Reservoir sizing at the draft level of 75% of mean annual flow using drought magnitude method on Canadian rivers. Hydrology 2021, 8, 79. [Google Scholar] [CrossRef]
- Sharma, T.C.; Panu, U.S. Compatibility of drought magnitude based method with SPA for assessing reservoir volume: Analysis using Canadian river flows. J. Water Resour. Protection 2022, 14, 1–20. [Google Scholar] [CrossRef]
- Adamowski, K. Plotting formula for flood frequency. Water Resour. Bull. 1981, 17, 197–202. [Google Scholar] [CrossRef]
- Sen, Z. Statistical analysis of hydrological critical droughts. ASCE J. Hydraul. Eng. 1980, 106, 99–115. [Google Scholar]
- Sen, Z. Applied Drought Modeling, Prediction and Mitigation; Elsevier Inc.: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988; p. 367. [Google Scholar]
- Environment Canada. HYDAT CD-ROM Version 96-1.04 and HYDAT CD-ROM User’s Manual. In Surface Water and Sediment Data; Water Survey of Canada: Gatineau, QC, Canada, 2020. [Google Scholar]
- Lorenzo-Lacruz, J.; Vicente-Serrano, S.M.; Gonzalez-Hidalgo, J.C.; Lopez-Moreno, J.I.; Cortesi, N. Hydrological drought response to meteorological drought in the Iberian Peninsula. Clim. Res. 2013, 58, 117–131. [Google Scholar] [CrossRef] [Green Version]
- Lopez-Moreno, J.I.; Vicente-Serrano, S.M.; Beguria, S.; Garcia-Ruiz, J.M.; Portela, M.M.; Almeida, A.B. Dam effect on drought magnitude and duration in a transboundary basin: The lower River Tagus, Spain and Portugal. Water Resour. Res. 2009, 45, W02405. [Google Scholar] [CrossRef] [Green Version]


| Numeric Identifier of the River in Figure 1 with Name and Gauging Station Identity | Data Size (Years) | Area (km2) | μo | cvo | cvmx | cvav | cvgm | ρ |
|---|---|---|---|---|---|---|---|---|
| [1] Fraser at Shelley, BC08KB001 | 70 (1951–2020) | 32,400 | 817.34 | 0.90 | 0.82 | 0.36 | 0.28 | 0.75 |
| [2] Athabasca River at Athabasca, AB07BE001 | 69 (1952–2020) | 74,600 | 429.19 | 0.98 | 1.32 | 0.43 | 0.26 | 0.81 |
| [3] Bow River at Banff, AB05BB001 | 110 (1911–2020) | 2210 | 39.24 | 1.11 | 1.22 | 0.31 | 0.14 | 0.72 |
| [4] pipestone River at Karl lake, ON04DA001 | 54 (1967–2020) | 5960 | 59.05 | 1.04 | 1.56 | 0.63 | 0.41 | 0.89 |
| [5] Neebing at Thunder Bay, ON02AB008 | 66 (1954–2019) | 187 | 1.62 | 1.87 | 3.84 | 1.10 | 0.68 | 0.63 |
| [6] Pic River near Marathon, ON02BB003 | 50 (1971–2020) | 4270 | 50.10 | 1.24 | 2.16 | 0.71 | 0.48 | 0.74 |
| [7] Pagwachaun at highway#11, ON04JD005 | 53 (1968–2020) | 2020 | 53.08 | 1.45 | 2.77 | 0.79 | 0.48 | 0.74 |
| [8] Nagamgami at highway#11, ON04JC002 | 70 (1951–2020) | 2410 | 24.56 | 1.11 | 1.66 | 0.55 | 0.40 | 0.87 |
| [9] Batchawana at Batchawana, ONBF001 | 50 ((1971–2020) | 1190 | 22.38 | 1.38 | 2.75 | 0.74 | 0.52 | 0.62 |
| [10] Goulis near Searchmont, ON02FB002 | 53 (1968–2020) | 1160 | 18.37 | 1.32 | 2.69 | 0.75 | 0.55 | 0.69 |
| [11] Whitson at Chemsford, ON02CF007 | 60 (1961–2020) | 243 | 3.06 | 1.50 | 3.62 | 0.78 | 0.57 | 0.68 |
| [12] North French near Mouth, ON04MF001 | 54 (1967–2020) | 1190 | 95.72 | 1.29 | 2.44 | 0.71 | 0.46 | 0.72 |
| [13] Labase River at North Bay, ON02DD013 | 54 (1975–2018) | 70.4 | 0.91 | 1.49 | 3.24 | 0.96 | 0.79 | 0.44 |
| [14] Chippewa Creek at North Bay, ON02DD014 | 54 (1975–2018) | 37.3 | 0.62 | 1.11 | 2.10 | 0.81 | 0.67 | 0.43 |
| [15] Commanda at Commanda, ON02DD015 | 46 (1975–2020) | 106 | 1.76 | 1.22 | 2.31 | 0.77 | 0.66 | 0.58 |
| [16] N. Magnetwan at Pickerel Lake, ON02EA010 | 52 (1969–2020) | 149 | 2.86 | 1.26 | 2.54 | 0.82 | 0.70 | 0.51 |
| [17] Becancour A Lyster, QC02PL001 | 46 (1923–1968) | 1410 | 30.62 | 1.32 | 2.46 | 0.82 | 0.69 | 0.62 |
| [18] Beaurivage A. Sainte Entiene, QC02PJ007 | 75 (1926–2000) | 709 | 14.21 | 1.47 | 2.67 | 0.90 | 0.77 | 0.49 |
| [19] Lepreau River at Lepreau, NB01AQ001 | 101 (1919–2019) | 239 | 7.43 | 1.08 | 2.01 | 0.87 | 0.80 | 0.49 |
| [20] Carruther at Saint Anthony, PE01CA003 | 59 (1962–2020) | 46.8 | 0.97 | 1.33 | 2.89 | 0.82 | 0.62 | 0.48 |
| [21] Bevearbank River at Kinsac, NS01DG003 | 88 (1922–2019) | 97 | 3.04 | 1.09 | 1.53 | 0.90 | 0.84 | 0.43 |
| [22] N. Margaree at Margaree valley, NS01FB001 | 90 (1929–2020) | 368 | 17.01 | 0.96 | 1.60 | 0.68 | 0.59 | 0.46 |
| [23] Upper Humber at Reidville, NF02YL001 | 68 ((1953–2020) | 2210 | 80.29 | 1.07 | 1.57 | 0.66 | 0.60 | 0.48 |
| [24] Torrent River at Bristol Pool, NF02YC001 | 61 (1960–2020) | 624 | 24.90 | 1.07 | 2.21 | 0.62 | 0.53 | 0.57 |
| River Identity | Qx, (q), VR′, Lcr | Cutoff SHIx = Z0 | q1 *, qq, qp | LT-e′, µd, MT-e′ | Decision | Model Φ, MT-e | LT-e |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Upper Humber (#23, Table 1) T = 3536 σav = 53.10 ρ = 0.48 | Q75 = 24.16, (q = 0.25), 4.18, 21 LT-o = 17 | (iii) = −1. 06 (iiia) = −0.86 (i) = −0.66 | 0.046, 0.389, 0.030 0.117, 0.528, 0.063 0.242, 0.575, 0.136 | 6, 0.51, 2.84 9, 0.55, 4.87 11, 0.60, 6.68 | MT-e < VR′, next MT-e > VR′, q1 is low, next cutoff (i) is fine | MC1 0.47, 4.20 | A = 16 b = 19 c = 17 |
| Q80 = 20.47, (q = 0.20), 3.06, 20 LT-o = 16 | (iii) = −1.13 (iiia) = −0.91 (i) = −0.70 | 0.030, 0.358, 0.020 0.091, 0.497, 0.051 0.210, 0.552, 0.119 | 5, 0.50, 2.41 8, 0.54, 4.25 10, 0.59, 6.06 | MT-e < VR′, next MT-e > VR′, q1 is low, next cutoff (i) fine | MC1 0.63, 3.07 | a = 15 b = 18 c = 16 | |
| Q85 = 16.78 (q = 0.15), 2.02, 17 LT-o = 15 | (i) = −0.74 | 0.185, 0.530, 0.107 At cutoff levels (iiia) and (iii) q = 0.071 and 0.02, very low | 10, 0.58,5.54 | Cutoff(i) fine, Level (iii) and (iiia) were rejected due to low q1 values | MC1 0.82, 2.01 | a = 13 b = 15 c = 14 | |
| Q90 = 13.57 (q = 0.10), 1.27, 16 LT-o = 14 | (i) = −0.78 | 0.158, 0.538, 0.087 At cutoff levels (iiia) and (iii) q = 0.056 and 0.014, very low. | 9, 0.57, 5.42 | Cutoff Level (i) is fine. Cutoff (iiia) and (iii) resulted in very low values of q1, so were rejected | MC1 0.99, 1.27 | a = 13 b = 14 c = 13 | |
| Q95 * = 10.48 (q = 0.05), 0.70, 15 LT-o = 9 | (i) = −0.81 (iiia) = −1.06 | 0.138, 0.518, 0.077 0.043, 0.379, 0.028 | 4, 0.51, 2.20 (9, 0.56, 4.99) 3, 0.51, 1.27 (5, 0.51, 2.75) | Cutoff level (i) is too high—so next lower cutoff level (iiia) is fine | MC0 0.97, 0.70 | a = 9 b = 11 c = 10 |
| River Identity | VR′ | MT-o | LT-o | Qx * | q1 * | qp | Cutoff | MT-e′ | Φ | MT-e | Lcr | LT-e′ | MC type | LT-e ** | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | |||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||||||||||||
| Athabasca (#2, Table 1) T = 3588 σav = 183.97 ρ = 0.81 | 0.93 | 0.93 | 15 | 69.73 | 0.022 | 0.500 | 0.011 | iiia | 0.93 | 0.00 | 0.93 | 20 | 2 | MC0 | 11 | 16 | 13 |
| 1.99 | 1.90 | 19 | 79.77 | 0.025 | 0.538 | 0.012 | iiia | 3.00 | 0.50 | 1.99 | 24 | 17 | MC1 | 15 | 20 | 17 | |
| 3.37 | 3.37 | 21 | 91.92 | 0.202 | 0.727 | 0.069 | i | 3.58 | 0.09 | 3.36 | 28 | 17 | MC1 | 18 | 23 | 20 | |
| 4.56 | 4.56 | 22 | 102.32 | 0.211 | 0.728 | 0.073 | i | 9.58 | 0.67 | 4.57 | 28 | 17 | MC1 | 22 | 25 | 24 | |
| 5.70 | 5.70 | 23 | 112.35 | 0.224 | 0.738 | 0.076 | i | 10.13 | 0.56 | 5.69 | 29 | 18 | MC1 | 23 | 26 | 24 | |
| Goulis (#11, Table 1) T = 2756 σav = 13.84 ρ = 0.69 | 1.50 | 1.50 | 31 | 2.204 | 0.079 | 0.647 | 0.031 | iiia | 5.92 | 1.00 | 1.53 | 34 | 11 | MC1 | 22 | 28 | 25 |
| 4.10 | 4.10 | 34 | 3.288 | 0.095 | 0.654 | 0.037 | iiia | 6.39 | 0.48 | 4.09 | 37 | 12 | MC1 | 24 | 31 | 27 | |
| 5.90 | 5.90 | 35 | 4.010 | 0.259 | 0.770 | 0.081 | i | 12.92 | 0.68 | 5.86 | 39 | 20 | MC1 | 30 | 34 | 32 | |
| 7.36 | 7.36 | 35 | 4.587 | 0.275 | 0.782 | 0.083 | i | 13.75 | 0.59 | 7.33 | 39 | 22 | MC1 | 31 | 35 | 32 | |
| 8.89 | 8.89 | 35 | 5.190 | 0.292 | 0.785 | 0.089 | i | 13.97 | 0.47 | 8.86 | 39 | 22 | MC1 | 31 | 35 | 32 | |
| Bevearbank (#21, Table 1) T = 5096 σav = 2.74 ρ = 0.43 | 0.24 | 0.24 | 12 | 0.065 | 0.065 | 0.413 | 0.041 | i | 1.55 | 1.00 | 0.58 | 16 | 3 | MC0 | 9 | 13 | 11 |
| 0.80 | 0.80 | 19 | 0.174 | 0.145 | 0.515 | 0.082 | ia | 2.31 | 0.93 | 0.79 | 21 | 4 | MC0 | 12 | 17 | 14 | |
| 1.79 | 1.79 | 19 | 0.324 | 0.168 | 0.518 | 0.097 | ia | 5.38 | 0.87 | 1.77 | 24 | 9 | MC1 | 17 | 20 | 18 | |
| 3.20 | 3.20 | 21 | 0.511 | 0.203 | 0.541 | 0.117 | ia | 5.97 | 0.59 | 3.22 | 27 | 10 | MC1 | 18 | 23 | 20 | |
| 4.63 | 4.63 | 22 | 0.696 | 0.255 | 0.566 | 0.148 | ia | 6.71 | 0.40 | 4.59 | 34 | 11 | MC1 | 22 | 28 | 25 | |
| River Identity | Qx * | VR | MT-0 | Lcr | LT-0 | Cutoff | Φ | MT-e | Model order | LT-e | LT-e | LT-e | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (a) Ϯ | (%) ҂ | (b) ϮϮ | (%)҂ | (c) ϮϮϮ | (%) ҂ | ||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||||
| Lepreau River (#19, Table 1) T = 3588 σav = 183.97, ρ = 0.49 | 0.58 | 0.78 | 0.57 | 18 | 12 | iii | 0.78 | 0.78 | MC0 | 10 | −16.67 | 14 | 16.67 | 12 | 0.00 |
| 1.03 | 1.78 | 1.78 | 24 | 15 | iiia | 0.55 | 1.78 | MC1 | 15 | 0.00 | 19 | 26.67 | 17 | 13.33 | |
| 1.40 | 2.70 | 2.70 | 27 | 19 | i | 0.56 | 2.72 | MC1 | 18 | −5.26 | 22 | 15.79 | 19 | 0.00 | |
| 1.78 | 3.75 | 3.68 | 32 | 19 | i | 0.42 | 3.78 | MC1 | 21 | 10.53 | 26 | 36.84 | 23 | 21.05 | |
| 2.19 | 5.17 | 5.17 | 34 | 23 | i | 0.27 | 5.20 | MC1 | 22 | −4.35 | 28 | 21.74 | 25 | 8.70 | |
| Pipestone River (#4,Table 1), T = 2808 σav = 37.31 ρ = 0.89 | 9.20 | 0.91 | 0.91 | 16 | 13 | iiia | 0.60 | 0.91 | MC0 | 9 | −30.77 | 13 | 0.00 | 11 | −15.38 |
| 10.84 | 1.52 | 1.52 | 17 | 16 | iiia | 0.02 | 1.52 | MC1 | 17 | 18.75 | 17 | 18.75 | 17 | 18.75 | |
| 12.67 | 2.28 | 2.28 | 20 | 18 | iiia | 1.00 | 2.54 | MC1 | 19 | 5.56 | 19 | 5.56 | 19 | 5.56 | |
| 14.46 | 3.08 | 3.08 | 22 | 20 | iiia | 0.93 | 3.04 | MC1 | 20 | 0.00 | 21 | 5.00 | 20 | 0.00 | |
| 16.66 | 4.16 | 4.16 | 24 | 22 | i | 0.96 | 4.22 | MC1 | 26 | 0.00 | 25 | 4.55 | 25 | 0.00 | |
| Chippewa River (#14, Table 1) T = 2288 σav = 0.48, ρ = 0.43 | 0.12 | 0.45 | 0.43 | 9 | 7 | iiia | 1 | 0.59 | MC0 | 6 | −14.29 | 7 | 0.00 | 7 | 0.00 |
| 0.14 | 0.86 | 0.72 | 11 | 10 | iiia | 1 | 0.98 | MC1 | 9 | −10.00 | 10 | 0.00 | 9 | −10.00 | |
| 0.16 | 1.23 | 1.23 | 16 | 11 | iiia | 0.95 | 1.24 | MC1 | 12 | 9.09 | 14 | 27.27 | 13 | 18.18 | |
| 0.19 | 1.62 | 1.62 | 18 | 13 | iiia | 0.87 | 1.63 | MC1 | 13 | 0.00 | 16 | 23.08 | 14 | 7.69 | |
| 0.21 | 2.27 | 2.27 | 20 | 14 | iiia | 0.74 | 2.27 | MC1 | 15 | 7.14 | 17 | 21.43 | 16 | 14.29 | |
| Bow River (#3, Table 1) T = 5720 σav = 12.05 ρ = 0.72 | 7.11 | 1.77 | 1.77 | 20 | 18 | i | 0.99 | 1.77 | MC1 | 17 | −5.56 | 19 | 5.56 | 18 | 0.00 |
| 7.67 | 2.67 | 2.67 | 22 | 20 | i | 0.86 | 2.69 | MC1 | 18 | −10.00 | 20 | 0.00 | 19 | −5.00 | |
| 8.18 | 3.55 | 3.55 | 24 | 21 | i | 0.74 | 3.56 | MC1 | 19 | −9.52 | 22 | 4.76 | 20 | −4.47 | |
| 8.63 | 4.34 | 4.34 | 26 | 22 | i | 0.63 | 4.37 | MC1 | 20 | −9.09 | 23 | 4.55 | 21 | −4.55 | |
| 9.16 | 5.27 | 5.27 | 26 | 24 | i | 0.50 | 5.28 | MC1 | 20 | −10.67 | 23 | −4.17 | 21 | −12.56 | |
| Mean Stan. error | −4.0% 11.4% | 12.0% 11.9% | 3% 10.4% | ||||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, T.C.; Panu, U.S. A Procedure for Estimating Drought Duration and Magnitude at the Uniform Cutoff Level of Streamflow: A Case of the Weekly Flows of Canadian Rivers. Hydrology 2022, 9, 109. https://doi.org/10.3390/hydrology9060109
Sharma TC, Panu US. A Procedure for Estimating Drought Duration and Magnitude at the Uniform Cutoff Level of Streamflow: A Case of the Weekly Flows of Canadian Rivers. Hydrology. 2022; 9(6):109. https://doi.org/10.3390/hydrology9060109
Chicago/Turabian StyleSharma, Tribeni C., and Umed S. Panu. 2022. "A Procedure for Estimating Drought Duration and Magnitude at the Uniform Cutoff Level of Streamflow: A Case of the Weekly Flows of Canadian Rivers" Hydrology 9, no. 6: 109. https://doi.org/10.3390/hydrology9060109
APA StyleSharma, T. C., & Panu, U. S. (2022). A Procedure for Estimating Drought Duration and Magnitude at the Uniform Cutoff Level of Streamflow: A Case of the Weekly Flows of Canadian Rivers. Hydrology, 9(6), 109. https://doi.org/10.3390/hydrology9060109






