Abstract
The agricultural sector is vulnerable to extreme phenomena such as droughts, particularly in arid and semi-arid environments and in regions where water infrastructure is limited. Devising preparedness plans, including means for efficient monitoring and timely identification of drought events, is essential for informed decision making on drought mitigation and water management, especially for the water-dependant agricultural sector. This paper presents the incorporation of two new drought indices, designed for agricultural drought identification, in Drought Indices Calculator (DrinC) software. These indices, namely the Agricultural Standardized Precipitation Index (aSPI) and the Effective Reconnaissance Drought Index (eRDI), require commonly available meteorological data, while they employ the concept of effective precipitation, taking into account the amount of water that contributes productively to plant development. The design principles of DrinC software leading to the proper use of the indices for agricultural drought assessment, including the selection of appropriate reference periods, calculation time steps and other related issues, are presented and discussed. The incorporation of aSPI and eRDI in DrinC enhances the applicability of the software towards timely agricultural drought characterisation and analysis, through a straightforward and comprehensible approach, particularly useful for operational purposes.
1. Introduction
Drought is a natural hazard with direct and significant impacts on agriculture. Especially under arid or semi-arid conditions, drought effects are more intense [1], while prolonged droughts can cause serious food security issues [2,3,4]. Drought is typically classified into types, which are based on specific attributes of the phenomenon. Meteorological drought is related to the physical drivers, i.e., the variation of meteorological parameters such as precipitation and temperature, leading to a drought episode. Other types of droughts are the hydrological drought, expressing the effects of drought on water resources, and the agricultural (or vegetation-agricultural) drought, describing the impacts of the phenomenon on plant development. Due to the slow onset of drought, its characteristics (severity, duration and areal extent) cannot be easily assessed. Nonetheless, the accurate and timely identification of a drought event is essential for implementing efficiently drought management plans and relief measures.
Agricultural drought characterisation is not a simple task, considering the complexity of vegetation types, including the diverse susceptibility and tolerance of plants to drought events under different climates, soil types, cultivation techniques, etc. Agricultural drought severity can be assessed by quantifying the impact of the phenomenon on vegetation, taking into account parameters related to plant development, crop yield and others. However, the direct implementation of the above is practically difficult, due to the complexity of the analysis, the involved uncertainties and the variety of factors, apart from drought, that may also affect the soil-plant-atmosphere system. Therefore, the most common approach is to aggregate hydroclimatic fluxes and/or land surface characteristics, for quantifying the triggering variables of agricultural drought [5]. This can be achieved by employing drought indices, commonly used for drought characterisation, which can provide a quantitative measure of drought intensity [6,7,8,9].
Currently, there are several indices suitable for agricultural drought identification [10]. Many of them are based on soil moisture, since this is one of the key parameters directly associated to vegetation stress due to water deficiency, such as the widely used Palmer Drought Severity Index, PDSI [11] and many others, e.g., [12,13,14,15]. During the recent years, several satellite-based indices have also been developed, using vegetation properties, soil moisture measurements through remote sensing approaches, etc. [16,17]. However, many of the above indices may be complex and/or data demanding, thus their use in operational applications may be limited.
On the other hand, indices based on meteorological data (precipitation, evapotranspiration) have been proven to be efficient in agricultural drought identification, e.g., [18,19,20,21]. Furthermore, such indices are usually preferred due to their simple structure and to the fact that the required input data are easily obtainable.
The calculation of drought indices can be facilitated by software tools currently available, e.g., [22,23,24]. The design and the available modules in such software may vary, though it is important to be customizable to fit the specific needs of different case studies, while the outcomes must be clearly interpretable for allowing objective and transparent decision making.
The Drought Indices Calculator (DrinC) software was developed towards the above principles, providing means for drought analysis based on drought indices for research and operational purposes [25,26]. DrinC is a stand-alone software, freely available online (https://drought-software.com, accessed on 29 April 2022) and it is currently used in more than 145 countries in a wide range of drought-related studies and applications, e.g., [27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52].
Two drought indices specifically developed for agricultural drought identification have been incorporated in DrinC software (version 1.7), aiming at enhancing its potential for agricultural drought analyses. These indices, namely the Agricultural Standardized Precipitation Index (aSPI) [53] and the Effective Reconnaissance Drought Index (eRDI) [54,55], are modifications of two broadly used drought indices, the Standardized Precipitation Index (SPI) [56] and the Reconnaissance Drought Index (RDI) [57], respectively. Both aforementioned modifications aimed at retaining the simple structure and low data requirements of the original indices, while providing more robust conceptual base towards the characterisation of agricultural drought conditions and the assessment of drought impacts on vegetation.
As already mentioned, agricultural drought characterization has different goals and principles than meteorological drought. However, the similarities that aSPI and eRDI share with their corresponding original indices, including the fact that they use only meteorological input data, might create confusion regarding their proper assessment approach for agricultural drought identification. Therefore, it is crucial for DrinC software to include distinguishable components, which can be suitably adjusted according to the objectives of each drought characterisation study. Furthermore, it is important to identify the reasons leading to the selection of these adjustments in order to avoid misconducted analyses and consequent misinterpretations of the outcomes.
To this end, the paper presents the aforementioned design principles that have been used for incorporating aSPI and eRDI in DrinC software including the adjustable components which emphasise the key points of agricultural drought analysis. The major issues which are illustrated in detail are the selection of suitable reference periods and calculation steps, while specific justifications are presented regarding their proper use in agricultural drought characterisation and monitoring. The presented update of the software aims at providing researchers and stakeholders with means for conducting straightforward, transparent and sound analyses for timely agricultural drought identification, towards informed decision making and efficient water resources management for mitigating the anticipated drought impacts.
2. Basic Notions
The characterization of agricultural drought is focusing on the conditions affecting the development of vegetation, which is linked to the specific system under study. For instance, drought impacts may vary, depending on the considered plant species, the water deficits during critical growth stages, etc. Therefore, agricultural drought analysis should be based on properly adjustable tools, according to the properties of the system of interest.
The aSPI and eRDI indices intend to build on the advantages of the SPI and RDI, while being customizable and more sensitive to the factors affecting agricultural drought [53,54,55]. To this end, the parameter of total precipitation has been replaced in both indices with the effective precipitation, i.e., the portion of total precipitation that can be used productively by the plants. This is achieved by employing empirical methods, which are solely using monthly precipitation data to estimate the corresponding effective precipitation.
Additionally, eRDI is also using potential evapotranspiration, formulating its initial value αe as the ratio of the cumulative effective precipitation (Pe) to the cumulative potential evapotranspiration (PET), for a specified reference period of k months:
The calculation of the indices is based on a standardisation process, in which the initial timeseries (Pe and αe for aSPI and eRDI, respectively) is fitted into a suitable distribution which is then transformed into normal distribution, producing the final standardised values of each index. Details regarding the theoretical base of the indices can be found at Tigkas et al. [53,55].
The main advantages of the indices, apart from the simple structure and the low data requirements, are their ability to provide comprehensible outcomes even for non-experts, that correspond to specific drought classes (Table 1), while they are not location-specific, since their results can be spatially comparable.

Table 1.
Drought classes based on aSPI or eRDI values.
The aSPI and the eRDI can be used to study the impacts of drought on farming crops, but also natural ecosystems, in order to investigate the response of vegetation growth to drought. Recent studies have shown that these indices are suitable for such purposes, providing similar or more accurate outcomes regarding agricultural drought characterisation compared to the original indices [53,55,58,59,60,61,62]. To this end, the reference periods can be adjusted according to the vegetation type under investigation, for interpreting efficiently its response to drought.
3. Implementation of aSPI and eRDI in DrinC Software
3.1. Software Design for Assessing Agricultural Drought
The agricultural drought characterisation process in DrinC software includes three main stages: (a) data management and input parameters; (b) selection of appropriate reference periods and time step; (c) drought indices calculation. The design of the software aims at producing, through a straightforward approach with customizable options, concrete and clearly interpretable outcomes regarding agricultural drought conditions. The above are performed through the graphical user interface of the software (Figure 1).
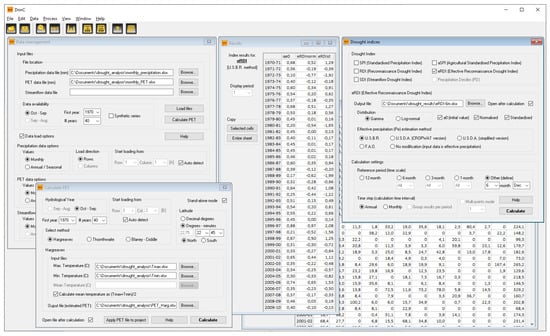
Figure 1.
The graphical user interface of DrinC software.
In the next sections, each of the above stages is described in detail, along with the principles for the suitable adjustments to fit the objectives of drought analysis cases. In brief, in the first stage the required input data for each index are presented, along with the description of the available effective precipitation estimation methods and the module for assessing potential evapotranspiration with temperature-based methods. The second stage presents the principles for selecting the appropriate reference period and time step, depending on the aims of the agricultural drought characterisation or monitoring study. The third stage describes the calculation procedure for both indices and the interpretation of their outcomes. A schematic representation of the overall process is shown in Figure 2.

Figure 2.
Schematic overview of the assessment process of aSPI and eRDI in DrinC software.
3.2. Data Management and Input Parameters
The required data for both aSPI and eRDI is monthly precipitation, while eRDI requires also monthly PET. Annual or seasonal data (cumulative values of precipitation and/or PET) can be also used; however, in such a case, the results will refer only to the specific accumulated input periods. Data may be imported using various file formats (MS Excel files, delimited text files, etc.).
The estimation of Pe based on precipitation data is performed through empirical methods. Four alternative methods are incorporated in DrinC:
- U.S. Bureau of Reclamation (USBR) method: In this method, Pe is estimated through the use of precipitation classes, as presented in Table 2 [63].
 Table 2. Effective precipitation estimates, based on total monthly precipitation classes.
Table 2. Effective precipitation estimates, based on total monthly precipitation classes.
- Soil Conservation Service/U.S. Department of Agriculture–CROPWAT version (USDA-SCS CROPWAT) method: This is an approach used in CROPWAT software, based on the USDA SCS [64] method, using only total precipitation (P) for estimating Pe according to the following formulae [64]:
- Soil Conservation Service/U.S. Department of Agriculture–simplified version (USDA-SCS simp.) method: A simplified version of the USDA SCS [64] method, using only precipitation data and assuming constant the other parameters of the model [53].
- U.N. Food and Agriculture Organization (FAO) method: A simple empirical approach that has been proposed by FAO, using the following equations [65]:
It is noted that the first three methods have very similar response for total monthly precipitation up to 110 mm, which is the usual case for arid and semi-arid regions. The FAO method follows a different pattern, with lower effective precipitation estimates for the same amount of total monthly precipitation. Overall, the aforementioned methods are mostly considered suitable for arid and semi-arid conditions, while their use in humid environments may have limited credibility. Furthermore, the FAO method can be applied mainly in plain areas, with maximum slope of 4–5% [53].
Obviously, the software also includes the option to import directly effective precipitation data, in which case no further processing is performed for this parameter.
Regarding the estimation of PET, a relevant module is available in DrinC incorporating three temperature-based methods (Hargreaves, Blaney-Criddle and Thornthwaite), which are appropriate for RDI calculation [66,67]. The required input for these methods is monthly temperature data and specifically:
- monthly averages of maximum and minimum temperature values for Hargreaves method;
- monthly average of mean temperature values for Blaney-Criddle and Thornthwaite methods (optionally for Hargreaves method).
Additionally, the latitude of the meteorological station must be set (Figure 3). Nevertheless, PET data estimated by other appropriate methods (e.g., FAO Penman-Monteith) can be also imported directly in the software. This is quite useful, considering the uncertainties of PET estimates depending on the adopted method [68,69] and the characteristics of the surface above which the meteorological attributes are measured [70].

Figure 3.
The PET calculation module of DrinC software.
3.3. Selection of Reference Periods and Time Step
An important decision for proper agricultural drought analysis is the selection of the reference period and the calculation time step, which must be suitable for the purpose of each study or application. The reference period (or time scale) determines the time (months) for which the respective input parameters are accumulated, while the index outcome corresponds to the conditions of the specific period. The time step (or calculation time interval; usually monthly or annual) refers to the calculation interval between subsequent reference periods.
The selection of the appropriate reference periods and time step for aSPI and eRDI may be different from what applies to the original indices (SPI and RDI), due to the distinctive nature of vegetation-agricultural drought. For instance, the typical approach for assessing meteorological drought using SPI is by selecting a specific time scale (e.g., 12-month) which is calculated for a monthly time step. This produces a ‘rolling’ timeseries of the index (one value per month), representing the prevailing conditions for the corresponding reference period (e.g., the past 12 months) in the study area.
However, in agricultural drought characterisation, the focus of the investigation is on the potential impacts of drought on agricultural or natural systems. Therefore, depending on the objectives of the analysis, emphasis should be given to cultivation periods of the considered crops, growth periods of vegetation in natural ecosystems (e.g., forests), as well as development stages, during which specific plants may be more susceptible to drought conditions. It is noted that for the dry seasons of the year under arid or semi-arid conditions, a high percentage of zero values is expected in precipitation timeseries, which may cause difficulties in the calculation of the indices, if short reference periods (e.g., 1- or 3-month) are selected.
Indicatively, for a typical winter wheat crop under Mediterranean conditions, the cultivation period initiates in November, while the harvesting usually takes place in June. A suitable reference period to identify drought conditions for such a case would be the entire 8-month cultivation period November–June. In addition, shorter reference periods could be also considered, such as the 3-month February–April period, focusing on critical development stages of the crop (e.g., tillering, anthesis), in which water stress may have considerable effects on yield [71,72,73].
The selection of the appropriate calculation time step is important for focusing on the aim of drought analysis and avoiding the production of excessive information that may be disorientating, especially in decision making process. To this end, the annual time step is recommended for evaluating the vegetation response to drought conditions, while the monthly time step is more appropriate for real time drought monitoring.
Another efficient approach for agricultural drought monitoring, reflecting possible cumulative effects of water deficits during crop development, is the use of progressively incrementing reference periods (e.g., 3-, 4-, 5-month), starting always from the same month (e.g., the sowing month). A graphical example of this approach is presented in Figure 4. As shown by this figure, the cumulative water deficit for each month is illustrated more clearly through the use of progressive reference periods (from the beginning of the cropping season), instead of using a constant (in this case 3-month) reference period.

Figure 4.
Drought monitoring with aSPI during cropping season (winter wheat crop), using constant and progressive reference periods for an indicative drought year (location: Alexandroupolis–Greece; hydrological year: 1984–1985).
3.4. Drought Indices Calculation
The calculation of aSPI and eRDI in DrinC is performed through the interface presented in Figure 5, in which the respective index is selected. The distributions that can be used for each drought index (DI) are log-normal and gamma, both considered suitable for the calculation of the indices.

Figure 5.
Drought indices calculation settings.
The log-normal distribution is based on the logarithmic data transformation:
in which x is the input variable for each DI, i.e., Pe for aSPI and αe for eRDI, for the considered reference period.
y = ln(x), for x > 0
The standardised timeseries of the DI is derived by:
in which is the arithmetic mean and is the standard deviation.
It is noted that the above cannot be applied, if the accumulated effective precipitation for the selected reference period includes zero values (x = 0). This is a usual condition, if a short reference period is selected under arid or semi-arid conditions, in which case gamma distribution can be used, as follows.
In gamma distribution, the probability density function is:
in which γ and β are shape and scale parameters, respectively, with γ > 0 and β > 0, and Γ(γ) is the gamma function: .
The parameters γ and β can be estimated by:
in which and n is the length (years) of the timeseries.
The cumulative probability G(x) is derived from Equation (6) as:
Letting t = x/β, Equation (8) becomes the incomplete gamma function:
As already mentioned, the above is defined for x > 0; if x = 0, i.e., the cumulative effective precipitation for a selected period is zero, to estimate the zero-value probability (q) of x, the cumulative distribution function is:
The cumulative distribution function is transformed to normal distribution for the estimation of DI, using the following approximation [74]:
in which , while the values of the constants are:
c0 = 2.515517, c1 = 0.802853, c2 = 0.010328, d1 = 1.43278, d2 = 0.189269 and d3 = 0.001308.
Due to the probabilistic nature of the indices’ calculation, the sufficient length of input data timeseries plays important role. Typically, a 30-year timeseries is considered adequate for a reliable analysis, while 50 to 60 years of available data would be ideal. However, in real-world applications it may be needed to conduct analyses with limited data availability (shorter timeseries). In such cases, it is critical to acknowledge the level of reliability due to the involved uncertainties of the analysis. To this end, major points that should be taken into account are the actual length of the timeseries, the quality of the available data and possible indications whether the range of the climatic conditions of the area is sufficiently represented by the dataset.
The calculated results can be directly exported from DrinC to MS Excel files, including drawn charts of the selected index. The drought severity level can be categorised according to Table 1, as indicatively presented in Figure 6, providing a direct visualisation of drought conditions.
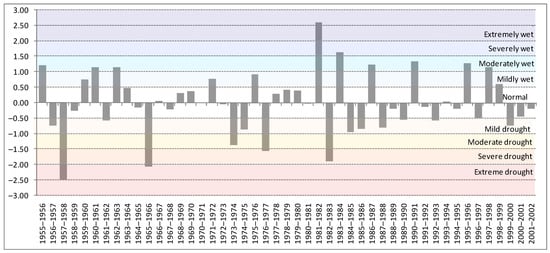
Figure 6.
eRDI values (reference period: 6-month, December–May) with the corresponding drought severity classes (location: Larissa-Greece).
4. Concluding Remarks
In this paper, the incorporation in DrinC software of two new indices for agricultural drought identification, the Agricultural Standardised Precipitation Index (aSPI) and the Effective Reconnaissance Drought Index (eRDI), is presented. Previous studies have shown that the use of these indices provides a robust conceptual base for accurate agricultural drought identification and analysis [53,55,59,60,61]. Furthermore, the data requirements of both indices are low, including commonly available meteorological parameters, allowing their application even in data-scarce locations.
One of the principal goals of the paper is to clarify possible misconceptions and discuss the appropriate approaches regarding agricultural drought characterisation, which can be achieved through the use of DrinC software. Towards this objective, it is illustrated how the design of the software emphasises the key-points that must be properly adjusted for agricultural drought identification, according to the different types of analysis.
Additionally, the software includes modules for transforming input data (precipitation, temperature) to the parameters required for each index (effective precipitation, potential evapotranspiration), using suitable approaches for any study. In addition, the software allows the customisation of the calculation process, using different reference periods and calculation time steps, in order to fit best to any drought characterisation and monitoring purpose. One of the main advantages is the easy interpretation of the outcomes, using drought severity classes that facilitate the understanding of drought phenomenon by stakeholders and decision-makers, enhancing timely and efficient water management and mitigation of the anticipated drought effects on agriculture.
Author Contributions
Conceptualization, D.T.; methodology, D.T.; software, D.T.; validation, D.T., H.V., N.P. and G.T.; formal analysis, D.T. and H.V.; investigation, D.T., H.V., N.P. and G.T.; resources, D.T., H.V., N.P. and G.T.; writing—original draft preparation, D.T.; writing—review and editing, D.T., H.V., N.P. and G.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used in the presented illustrative cases for agricultural drought characterisation and monitoring have been kindly provided by the Hellenic National Meteorological Service (HNMS) (Larissa station: 39.65° N, 22.43° E, alt. 71 m a.s.l.; Alexandroupolis station: 40.85° N, 25.93° E, alt. 3 m a.s.l.). The open data service of HNMS is available at http://www.emy.gr/emy/el/services/paroxi-ipiresion-elefthera-dedomena (accessed on 25 April 2022). Sample data for testing DrinC software are also available at https://drought-software.com/download/file-templates/ (accessed on 25 April 2022).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Peña-Gallardo, M.; Vicente-Serrano, S.M.; Quiring, S.; Svoboda, M.; Hannaford, J.; Tomas-Burguera, M.; Martín-Hernández, N.; Domínguez-Castro, F.; El Kenawy, A. Response of crop yield to different time-scales of drought in the United States: Spatio-temporal patterns and climatic and environmental drivers. Agric. For. Meteorol. 2019, 264, 40–55. [Google Scholar] [CrossRef] [Green Version]
- Lesk, C.; Rowhani, P.; Ramankutty, N. Influence of extreme weather disasters on global crop production. Nature 2016, 529, 84–87. [Google Scholar] [CrossRef] [PubMed]
- Sheffield, J.; Wood, E.F.; Chaney, N.; Guan, K.; Sadri, S.; Yuan, X.; Olang, L.; Amani, A.; Ali, A.; Demuth, S. A drought monitoring and forecasting system for sub-Sahara African water resources and food security. Bull. Am. Meteorol. Soc. 2014, 95, 861–882. [Google Scholar] [CrossRef]
- Zhao, M.; Running, S.W. Drought-induced reduction in global terrestrial net primary production from 2000 through 2009. Science 2010, 329, 940–943. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mishra, A.K.; Ines, A.V.; Das, N.N.; Khedun, C.P.; Singh, V.P.; Sivakumar, B.; Hansen, J.W. Anatomy of a local-scale drought: Application of assimilated remote sensing products, crop model, and statistical methods to an agricultural drought study. J. Hydrol. 2015, 526, 15–29. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Rossi, G.; Cancelliere, A. Managing drought risk in water supply systems in Europe: A review. Int. J. Water Resour. Dev. 2013, 29, 272–289. [Google Scholar] [CrossRef]
- Tsakiris, G.; Loukas, A.; Pangalou, D.; Vangelis, H.; Tigkas, D.; Rossi, G.; Cancelliere, A. Drought characterization. Drought Manag. Guidel. Tech. Annex 2007, 58, 85–102. [Google Scholar]
- Zargar, A.; Sadiq, R.; Naser, B.; Khan, F.I. A review of drought indices. Environ. Rev. 2011, 19, 333–349. [Google Scholar] [CrossRef]
- Sivakumar, M.; Stone, R.; Sentelhas, P.C.; Svoboda, M.; Omondi, P.; Sarkar, J.; Wardlow, B. Agricultural drought indices: Summary and recommendations. In Agricultural Drought Indices Proceedings of an Expert Meeting, Murcia, Spain, 2–4 June 2010; World Meteorological Organization: Geneva, Switzerland, 2011; pp. 172–197. [Google Scholar]
- Palmer, W.C. Meteorological Drought; Research Paper No. 45; US Department of Commerce, Weather Bureau: Washington, DC, USA, 1965.
- Cammalleri, C.; Micale, F.; Vogt, J. A novel soil moisture-based drought severity index (DSI) combining water deficit magnitude and frequency. Hydrol. Processes 2016, 30, 289–301. [Google Scholar] [CrossRef] [Green Version]
- Narasimhan, B.; Srinivasan, R. Development and evaluation of Soil Moisture Deficit Index (SMDI) and Evapotranspiration Deficit Index (ETDI) for agricultural drought monitoring. Agric. For. Meteorol. 2005, 133, 69–88. [Google Scholar] [CrossRef]
- Sohrabi, M.M.; Ryu, J.H.; Abatzoglou, J.; Tracy, J. Development of soil moisture drought index to characterize droughts. J. Hydrol. Eng. 2015, 20, 04015025. [Google Scholar] [CrossRef]
- Yang, H.; Wang, H.; Fu, G.; Yan, H.; Zhao, P.; Ma, M. A modified soil water deficit index (MSWDI) for agricultural drought monitoring: Case study of Songnen Plain, China. Agric. Water Manag. 2017, 194, 125–138. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Farahmand, A.; Melton, F.; Teixeira, J.; Anderson, M.; Wardlow, B.D.; Hain, C. Remote sensing of drought: Progress, challenges and opportunities. Rev. Geophys. 2015, 53, 452–480. [Google Scholar] [CrossRef] [Green Version]
- Dalezios, N.R.; Dercas, N.; Eslamian, S. Water scarcity management: Part 2: Satellite-based composite drought analysis. Int. J. Glob. Environ. Issues 2018, 17, 262–295. [Google Scholar] [CrossRef]
- Chen, T.; Xia, G.; Liu, T.; Chen, W.; Chi, D. Assessment of drought impact on main cereal crops using a standardized precipitation evapotranspiration index in Liaoning Province, China. Sustainability 2016, 8, 1069. [Google Scholar] [CrossRef] [Green Version]
- Popova, Z.; Ivanova, M.; Martins, D.; Pereira, L.; Doneva, K.; Alexandrov, V.; Kercheva, M. Vulnerability of Bulgarian agriculture to drought and climate variability with focus on rainfed maize systems. Nat. Hazards 2014, 74, 865–886. [Google Scholar] [CrossRef]
- Potopová, V.; Štěpánek, P.; Možný, M.; Türkott, L.; Soukup, J. Performance of the standardised precipitation evapotranspiration index at various lags for agricultural drought risk assessment in the Czech Republic. Agric. For. Meteorol. 2015, 202, 26–38. [Google Scholar] [CrossRef]
- Tian, L.; Yuan, S.; Quiring, S.M. Evaluation of six indices for monitoring agricultural drought in the south-central United States. Agric. For. Meteorol. 2018, 249, 107–119. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Stagge, J. Package SCI: Standardized Climate Indices such as SPI, SRI or SPEI (Version 1.0-2). Available online: https://cran.r-project.org/web/packages/SCI/SCI.pdf (accessed on 14 October 2021).
- Hao, Z.; Hao, F.; Singh, V.P.; Ouyang, W.; Cheng, H. An integrated package for drought monitoring, prediction and analysis to aid drought modeling and assessment. Environ. Model. Softw. 2017, 91, 199–209. [Google Scholar] [CrossRef]
- Klein, T.; Samourkasidis, A.; Athanasiadis, I.N.; Bellocchi, G.; Calanca, P. webXTREME: R-based web tool for calculating agroclimatic indices of extreme events. Comput. Electron. Agric. 2017, 136, 111–116. [Google Scholar] [CrossRef]
- Tigkas, D.; Vangelis, H.; Tsakiris, G. The drought indices calculator (DrinC). In Proceedings of the 8th International Conference of EWRA: Water Resources Management in an Interdisciplinary and Changing Context, Porto, Portugal, 26–29 June 2013. [Google Scholar]
- Tigkas, D.; Vangelis, H.; Tsakiris, G. DrinC: A software for drought analysis based on drought indices. Earth Sci. Inform. 2015, 8, 697–709. [Google Scholar] [CrossRef]
- Al-Faraj, F.A.; Tigkas, D. Impacts of multi-year droughts and upstream human-induced activities on the development of a semi-arid transboundary basin. Water Resour. Manag. 2016, 30, 5131–5143. [Google Scholar] [CrossRef]
- Al-Quraishi, A.M.; Gaznayee, H.A.; Crespi, M. Drought trend analysis in a semi-arid area of Iraq based on Normalized Difference Vegetation Index, Normalized Difference Water Index and Standardized Precipitation Index. J. Arid Land 2021, 13, 413–430. [Google Scholar] [CrossRef]
- Ashraf, M.; Ullah, K.; Adnan, S. Satellite based impact assessment of temperature and rainfall variability on drought indices in Southern Pakistan. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102726. [Google Scholar] [CrossRef]
- Babre, A.; Kalvāns, A.; Avotniece, Z.; Retiķe, I.; Bikše, J.; Jemeljanova, K.P.M.; Zelenkevičs, A.; Dēliņa, A. The use of predefined drought indices for the assessment of groundwater drought episodes in the Baltic States over the period 1989–2018. J. Hydrol. Reg. Stud. 2022, 40, 101049. [Google Scholar] [CrossRef]
- Benzougagh, B.; Meshram, S.G.; El Fellah, B.; Mastere, M.; Dridri, A.; Sadkaoui, D.; Mimich, K.; Khedher, K.M. Combined use of Sentinel-2 and Landsat-8 to monitor water surface area and evaluated drought risk severity using Google Earth Engine. Earth Sci. Inform. 2022, 1–12. [Google Scholar] [CrossRef]
- Chisadza, B.; Tumbare, M.J.; Nyabeze, W.R.; Nhapi, I. Linkages between local knowledge drought forecasting indicators and scientific drought forecasting parameters in the Limpopo River Basin in Southern Africa. Int. J. Disaster Risk Reduct. 2015, 12, 226–233. [Google Scholar] [CrossRef]
- Elhoussaoui, A.; Zaagane, M.; Benaabidate, L. Comparison of various drought indices for assessing drought status of the Northern Mekerra watershed, Northwest of Algeria. Arab. J. Geosci. 2021, 14, 915. [Google Scholar] [CrossRef]
- Kopsiaftis, G.; Tigkas, D.; Christelis, V.; Vangelis, H. Assessment of drought impacts on semi-arid coastal aquifers of the Mediterranean. J. Arid Environ. 2017, 137, 7–15. [Google Scholar] [CrossRef]
- Mbiriri, M.; Mukwada, G.; Manatsa, D. Spatiotemporal characteristics of severe dry and wet conditions in the Free State Province, South Africa. Theor. Appl. Climatol. 2019, 135, 693–706. [Google Scholar] [CrossRef]
- Merabti, A.; Martins, D.S.; Meddi, M.; Pereira, L.S. Spatial and time variability of drought based on SPI and RDI with various time scales. Water Resour. Manag. 2018, 32, 1087–1100. [Google Scholar] [CrossRef]
- Mohammed, R.; Scholz, M.; Zounemat-Kermani, M. Temporal hydrologic alterations coupled with climate variability and drought for transboundary river basins. Water Resour. Manag. 2017, 31, 1489–1502. [Google Scholar] [CrossRef] [Green Version]
- Mohammed, Y.; Yimam, A. Analysis of meteorological droughts in the Lake’s Region of Ethiopian Rift Valley using reconnaissance drought index (RDI). Geoenviron. Disasters 2021, 8, 13. [Google Scholar] [CrossRef]
- Mondol, M.; Haque, A.; Ara, I.; Das, S.C. Meteorological drought index mapping in Bangladesh using standardized precipitation index during 1981–2010. Adv. Meteorol. 2017, 2017, 4642060. [Google Scholar] [CrossRef] [Green Version]
- Mustafa, A.; Rahman, G. Assessing the spatio-temporal variability of meteorological drought in Jordan. Earth Syst. Environ. 2018, 2, 247–264. [Google Scholar] [CrossRef]
- Myronidis, D.; Ioannou, K.; Fotakis, D.; Dörflinger, G. Streamflow and hydrological drought trend analysis and forecasting in Cyprus. Water Resour. Manag. 2018, 32, 1759–1776. [Google Scholar] [CrossRef]
- Myronidis, D.; Nikolaos, T. Changes in climatic patterns and tourism and their concomitant effect on drinking water transfers into the region of South Aegean, Greece. Stoch. Environ. Res. Risk Assess. 2021, 35, 1725–1739. [Google Scholar] [CrossRef]
- Rahmani, F.; Fattahi, M.H. A multifractal cross-correlation investigation into sensitivity and dependence of meteorological and hydrological droughts on precipitation and temperature. Nat. Hazards 2021, 109, 2197–2219. [Google Scholar] [CrossRef]
- Shafeeque, M.; Luo, Y. A multi-perspective approach for selecting CMIP6 scenarios to project climate change impacts on glacio-hydrology with a case study in Upper Indus river basin. J. Hydrol. 2021, 599, 126466. [Google Scholar] [CrossRef]
- Sobral, B.S.; Oliveira-Júnior, J.F.; de Gois, G.; Pereira-Júnior, E.R. Spatial variability of SPI and RDIst drought indices applied to intense episodes of drought occurred in Rio de Janeiro State, Brazil. Int. J. Climatol. 2018, 38, 3896–3916. [Google Scholar] [CrossRef]
- Soulsby, C.; Scheliga, B.; Neill, A.; Comte, J.C.; Tetzlaff, D. A longer-term perspective on soil moisture, groundwater and stream flow response to the 2018 drought in an experimental catchment in the Scottish Highlands. Hydrol. Processes 2021, 35, e14206. [Google Scholar] [CrossRef]
- Surendran, U.; Kumar, V.; Ramasubramoniam, S.; Raja, P. Development of drought indices for semi-arid region using drought indices calculator (DrinC)–a case study from Madurai District, a semi-arid region in India. Water Resour. Manag. 2017, 31, 3593–3605. [Google Scholar] [CrossRef]
- Tareke, K.A.; Awoke, A.G. Hydrological Drought Analysis using Streamflow Drought Index (SDI) in Ethiopia. Adv. Meteorol. 2022, 2022, 7067951. [Google Scholar] [CrossRef]
- Tigkas, D.; Vangelis, H.; Tsakiris, G. Implementing crop evapotranspiration in RDI for farm-level drought evaluation and adaptation under climate change conditions. Water Resour. Manag. 2020, 34, 4329–4343. [Google Scholar] [CrossRef]
- Tsakiris, G.; Kordalis, N.; Tigkas, D.; Tsakiris, V.; Vangelis, H. Analysing drought severity and areal extent by 2D Archimedean copulas. Water Resour. Manag. 2016, 30, 5723–5735. [Google Scholar] [CrossRef]
- Yadav, S.M.; Bhagat, S.R.; Yadav, V.G. Temporal analysis of precipitation in Saurashtra, Kutch, and Diu sub-division of Western Indian region. Theor. Appl. Climatol. 2021, 144, 521–533. [Google Scholar] [CrossRef]
- Yisehak, B.; Shiferaw, H.; Abrha, H.; Gebremedhin, A.; Hagos, H.; Adhana, K.; Bezabh, T. Spatio-temporal characteristics of meteorological drought under changing climate in semi-arid region of northern Ethiopia. Environ. Syst. Res. 2021, 10, 21. [Google Scholar] [CrossRef]
- Tigkas, D.; Vangelis, H.; Tsakiris, G. Drought characterisation based on an agriculture-oriented standardised precipitation index. Theor. Appl. Climatol. 2019, 135, 1435–1447. [Google Scholar] [CrossRef]
- Tigkas, D.; Vangelis, H.; Tsakiris, G. Introducing a modified reconnaissance drought index (RDIe) incorporating effective precipitation. Procedia Eng. 2016, 162, 332–339. [Google Scholar] [CrossRef] [Green Version]
- Tigkas, D.; Vangelis, H.; Tsakiris, G. An enhanced effective reconnaissance drought index for the characterisation of agricultural drought. Environ. Processes 2017, 4, 137–148. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–183. [Google Scholar]
- Tsakiris, G.; Pangalou, D.; Vangelis, H. Regional drought assessment based on the Reconnaissance Drought Index (RDI). Water Resour. Manag. 2007, 21, 821–833. [Google Scholar] [CrossRef]
- Durowoju, O.S.; Ologunorisa, T.E.; Akinbobola, A. Characterization of Drought in Kaduna River Basin, Kaduna, Nigeria. J. Meteorol. Clim. Sci. 2021, 19, 43–59. [Google Scholar]
- Llanes-Cárdenas, O.; Norzagaray-Campos, M.; Gaxiola, A.; Pérez-González, E.; Montiel-Montoya, J.; Troyo-Diéguez, E. Sensitivity of Four Indices of Meteorological Drought for Rainfed Maize Yield Prediction in the State of Sinaloa, Mexico. Agriculture 2022, 12, 525. [Google Scholar]
- Proutsos, N.; Tigkas, D. Growth response of endemic black pine trees to meteorological variations and drought episodes in a Mediterranean region. Atmosphere 2020, 11, 554. [Google Scholar] [CrossRef]
- Syed, F.; Adnan, S.; Zamreeq, A.; Ghulam, A. Identification of droughts over Saudi Arabia and global teleconnections. Nat. Hazards 2022, 1–21. [Google Scholar] [CrossRef]
- Vishwakarma, A.; Choudhary, M.K.; Chauhan, M.S. Non-parametric trend and the validity of a newly developed drought indicator for agricultural application over the central India region. Arab. J. Geosci. 2022, 15, 365. [Google Scholar] [CrossRef]
- Stamm, G. Problems and Procedures in Determining Water Supply Requirements for Irrigation Proiects. Irrig. Agric. Lands 1967, 11, 769–785. [Google Scholar] [CrossRef]
- Soil Conservation Service. Irrigation Water Requirements; Technical Release No. 21; United States Department of Agriculture, Soil Conservation Service: Washington, DC, USA, 1970; p. 88.
- Brouwer, C.; Heibloem, M. Irrigation Water Management: Irrigation Water Needs; Technical Manual No. 3; Food and Agriculture Organization of the United Nations: Rome, Italy, 1986. [Google Scholar]
- Vangelis, H.; Tigkas, D.; Tsakiris, G. The effect of PET method on reconnaissance drought index (RDI) calculation. J. Arid Environ. 2013, 88, 130–140. [Google Scholar] [CrossRef]
- Zarei, A.R.; Mahmoudi, M.R. Evaluation of changes in RDI st index effected by different Potential Evapotranspiration calculation methods. Water Resour. Manag. 2017, 31, 4981–4999. [Google Scholar] [CrossRef]
- Bourletsikas, A.; Argyrokastritis, I.; Proutsos, N. Comparative evaluation of 24 reference evapotranspiration equations applied on an evergreen-broadleaved forest. Hydrol. Res. 2018, 49, 1028–1041. [Google Scholar] [CrossRef]
- Proutsos, N.D.; Tsiros, I.X.; Nastos, P.; Tsaousidis, A. A note on some uncertainties associated with Thornthwaite’s aridity index introduced by using different potential evapotranspiration methods. Atmos. Res. 2021, 260, 105727. [Google Scholar] [CrossRef]
- Alexandris, S.; Proutsos, N. How significant is the effect of the surface characteristics on the Reference Evapotranspiration estimates? Agric. Water Manag. 2020, 237, 106181. [Google Scholar] [CrossRef]
- Tigkas, D.; Tsakiris, G. Early Estimation of Drought Impacts on Rainfed Wheat Yield in Mediterranean Climate. Environ. Processes 2015, 2, 97–114. [Google Scholar] [CrossRef] [Green Version]
- Zarei, A.R.; Shabani, A.; Mahmoudi, M.R. Susceptibility Assessment of Winter Wheat, Barley and Rapeseed to Drought Using Generalized Estimating Equations and Cross-Correlation Function. Environ. Processes 2021, 8, 163–197. [Google Scholar] [CrossRef]
- Madhukar, A.; Dashora, K.; Kumar, V. Climate Trends in Temperature and Water Variables during Wheat Growing Season and Impact on Yield. Environ. Processes 2021, 8, 1047–1072. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Applied Mathematics Series No. 55; US Department of Commerce, National Bureau of Standards: Washington, DC, USA, 1964.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).