Assessing the Impact of Land Use and Climate Change on Surface Runoff Response Using Gridded Observations and SWAT+
Abstract
1. Introduction
2. Materials and Methods
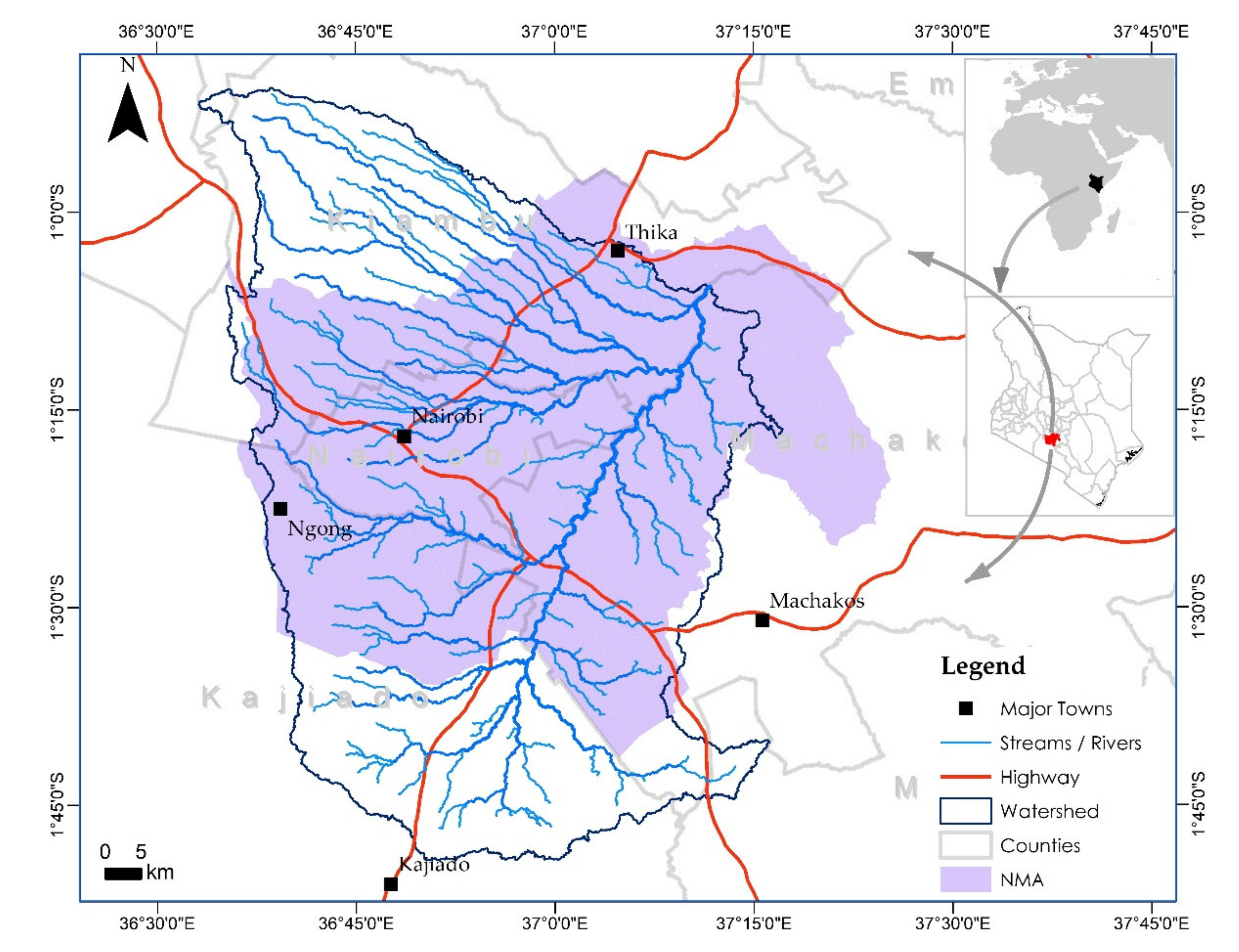
2.1. Study Area
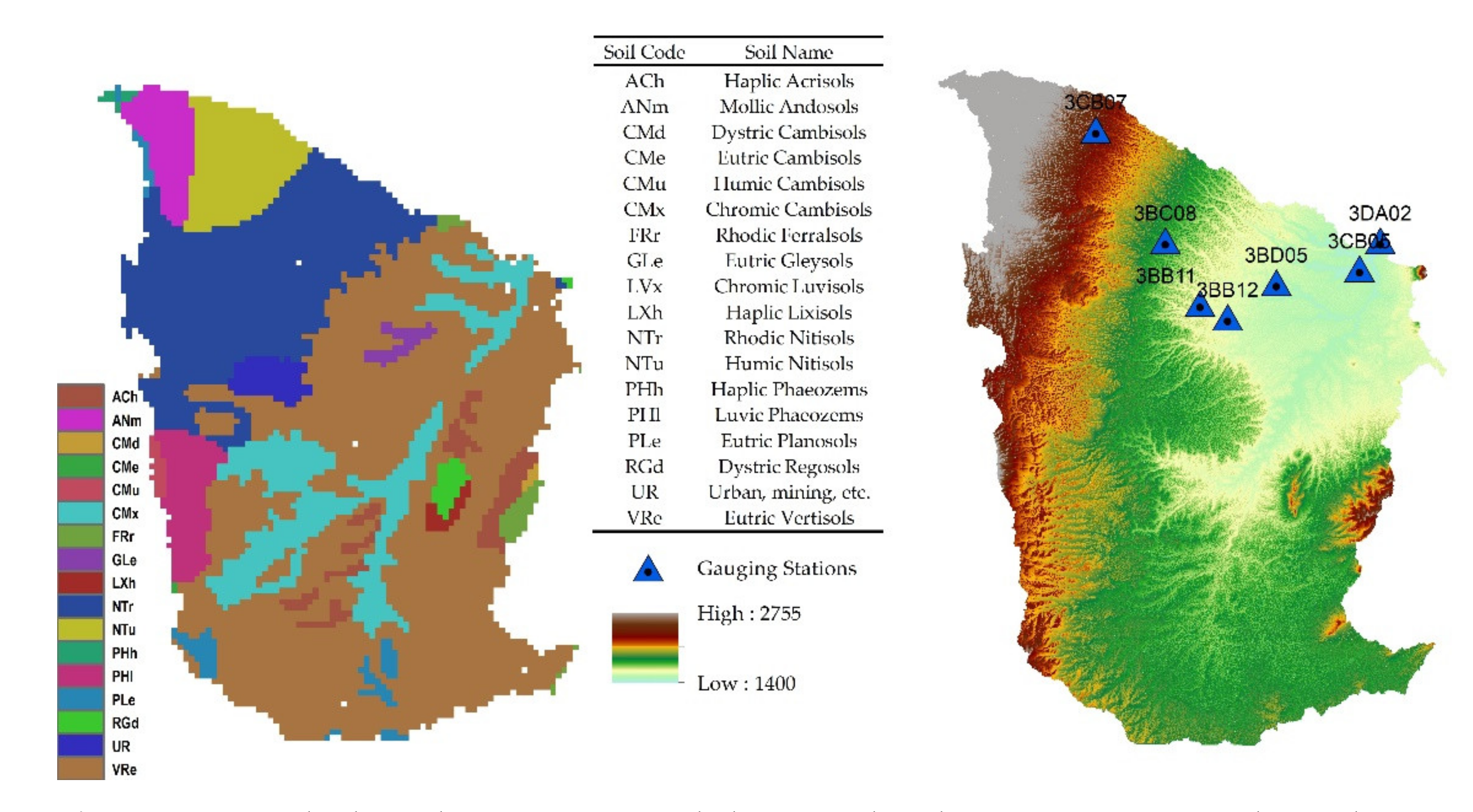
2.2. Datasets
2.3. Land Use Model
2.4. Climate Models
2.5. Bias Correction
2.6. QSWAT Interface
2.7. Model Setup
2.8. Sensitivity Analysis, Calibration and Validation
2.9. Evaluation of the Effects of LULC and Climate Change on Surface Runoff
3. Results and Discussion
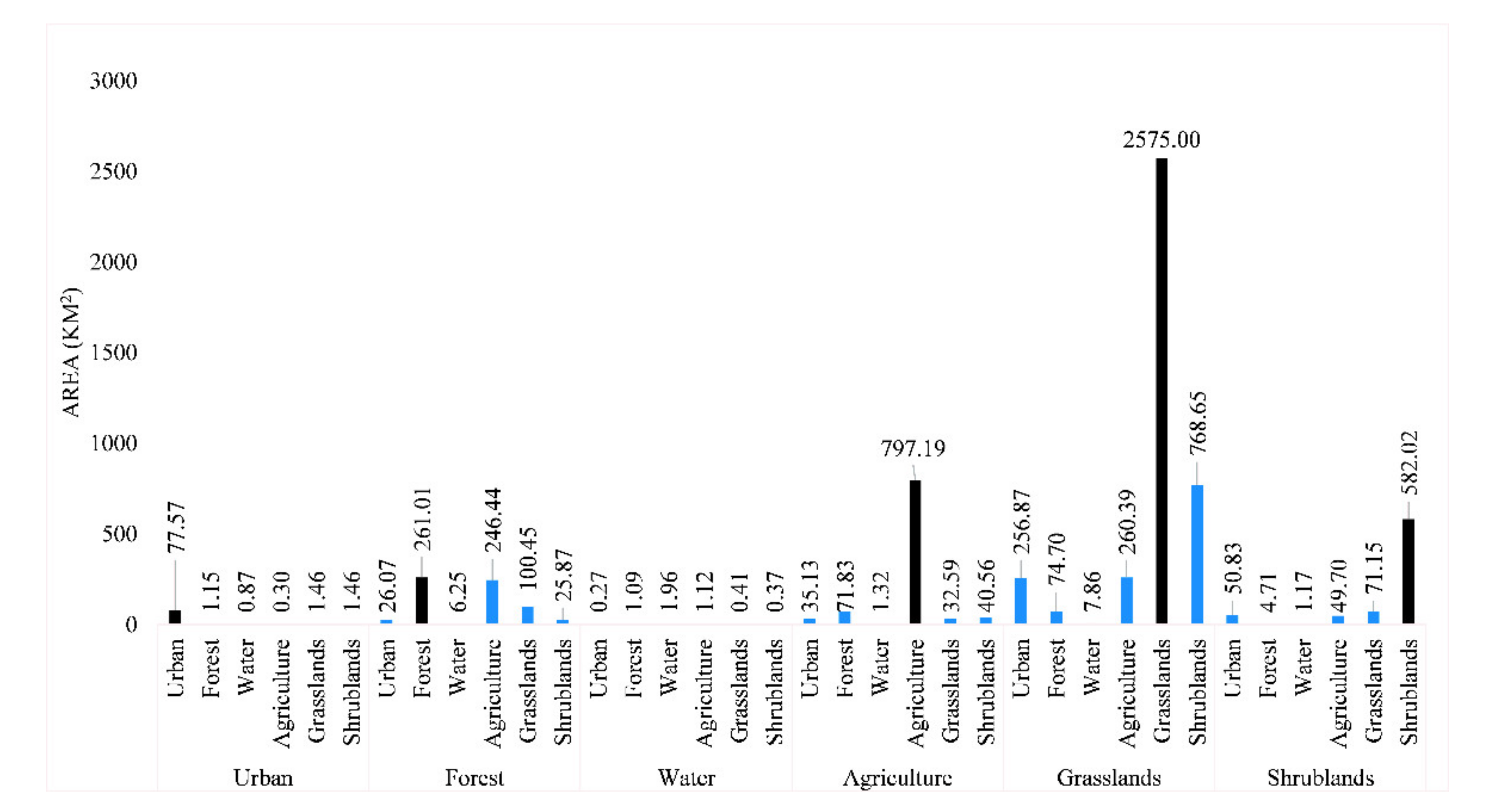
3.1. Land Use/Land Cover Change Analysis
3.2. Climate Data Evaluation
3.2.1. Precipitation
3.2.2. Surface Air Temperature
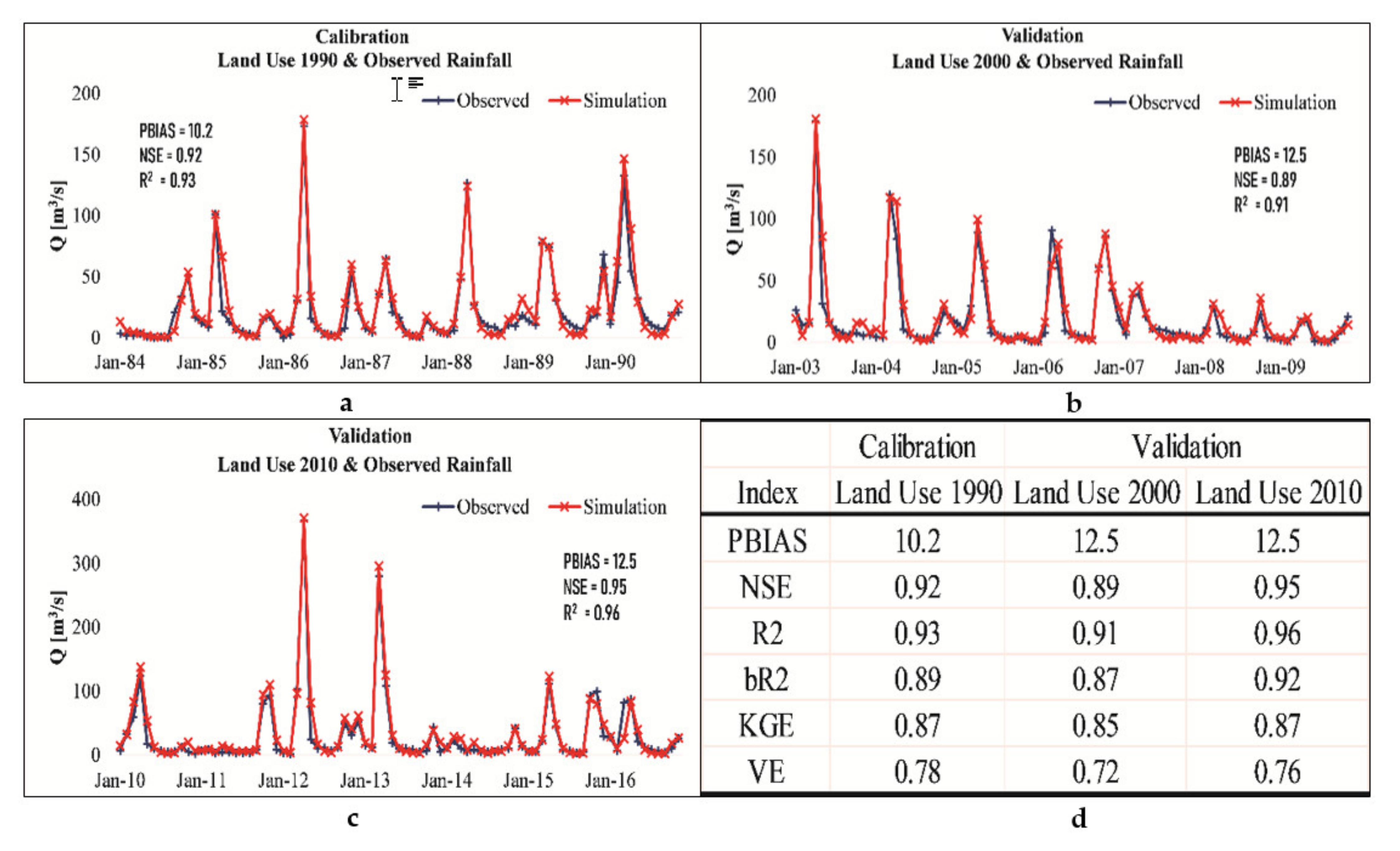
3.3. SWAT + Model Sensitivity Evaluation
3.4. Surface Runoff Response
3.4.1. Due to LULC
3.4.2. Due to Climate Change
3.4.3. Due to Climate and Land Use
3.5. Implications of Surface Runoff Change on Water Balance and Quality
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- is the final soil water content (mm H2O),
- SW0 is the initial soil water content (mm H2O),
- t is time in days,
- is the amount of precipitation on the day i (mm H2O),
- is the amount of surface runoff on the day i (mm H2O),
- is the amount of evapotranspiration on the day i (mm H2O),
- is the amount of percolation and bypass exiting the soil profile bottom on day i (mm H2O),
- is the amount of return flow on the day i (mm H2O).
Appendix B
| 1990 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| URB | FOR | WAT | AGR | GRA | SHR | Total | U_Accuracy | Kappa | |
| URB | 50 | 0 | 0 | 0 | 0 | 0 | 50 | 1 | |
| FOR | 0 | 64 | 1 | 2 | 2 | 0 | 69 | 0.93 | |
| WAT | 0 | 0 | 9 | 0 | 0 | 0 | 9 | 1 | |
| AGR | 0 | 3 | 0 | 51 | 5 | 0 | 59 | 0.86 | |
| GRA | 0 | 1 | 0 | 0 | 46 | 5 | 52 | 0.88 | |
| SHR | 6 | 0 | 0 | 7 | 7 | 42 | 62 | 0.68 | |
| Total | 56 | 68 | 10 | 60 | 60 | 47 | 301 | ||
| P_Accuracy | 0.89 | 0.94 | 0.90 | 0.85 | 0.77 | 0.89 | 0.87 | ||
| Kappa | 0.84 | ||||||||
| 2000 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| URB | FOR | WAT | AGR | GRA | SHR | Total | U_Accuracy | Kappa | |
| URB | 81 | 0 | 0 | 0 | 0 | 0 | 81 | 1.00 | |
| FOR | 0 | 87 | 4 | 5 | 0 | 0 | 96 | 0.91 | |
| WAT | 0 | 0 | 31 | 0 | 0 | 0 | 31 | 1.00 | |
| AGR | 1 | 10 | 0 | 131 | 2 | 0 | 144 | 0.91 | |
| GRA | 9 | 3 | 0 | 10 | 110 | 8 | 140 | 0.79 | |
| SHR | 3 | 0 | 0 | 2 | 7 | 72 | 84 | 0.86 | |
| Total | 94 | 100 | 35 | 148 | 119 | 80 | 576 | ||
| P_Accuracy | 0.86 | 0.87 | 0.89 | 0.89 | 0.92 | 0.90 | 0.89 | ||
| Kappa | 0.86 | ||||||||
| 2010 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| URB | FOR | WAT | AGR | GRA | SHR | Total | U_Accuracy | Kappa | |
| URB | 171 | 0 | 1 | 2 | 2 | 0 | 176 | 0.97 | |
| FOR | 0 | 174 | 2 | 30 | 0 | 0 | 180 | 0.97 | |
| WAT | 3 | 0 | 71 | 0 | 0 | 0 | 74 | 0.96 | |
| AGR | 4 | 3 | 0 | 296 | 0 | 0 | 303 | 0.98 | |
| GRA | 0 | 1 | 2 | 9 | 169 | 7 | 188 | 0.90 | |
| SHR | 6 | 0 | 0 | 1 | 8 | 84 | 99 | 0.85 | |
| Total | 184 | 178 | 76 | 312 | 179 | 91 | 1020 | ||
| P_Accuracy | 0.93 | 0.98 | 0.93 | 0.95 | 0.94 | 0.92 | 0.95 | ||
| Kappa | 0.93 | ||||||||
| 2020 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| URB | FOR | WAT | AGR | GRA | SHR | Total | U_Accuracy | Kappa | |
| URB | 301 | 0 | 0 | 15 | 2 | 0 | 318 | 0.95 | |
| FOR | 0 | 379 | 2 | 3 | 1 | 0 | 385 | 0.98 | |
| WAT | 0 | 0 | 101 | 0 | 0 | 0 | 101 | 1.00 | |
| AGR | 0 | 3 | 5 | 367 | 6 | 3 | 384 | 0.95 | |
| GRA | 1 | 1 | 2 | 6 | 82 | 7 | 99 | 0.83 | |
| SHR | 2 | 0 | 0 | 9 | 5 | 104 | 120 | 0.87 | |
| Total | 304 | 383 | 110 | 400 | 96 | 114 | 1407 | ||
| P_Accuracy | 0.99 | 0.99 | 0.92 | 0.92 | 0.85 | 0.91 | 0.95 | ||
| Kappa | 0.93 | ||||||||
| Land Use Types | Urban | Forest | Water | Agricultural | Grassland | Shrubland | Total |
|---|---|---|---|---|---|---|---|
| Urban | 22563 | 24 | 107 | 1843 | 1265 | 95 | 25897 |
| Forest | 76 | 32402 | 18 | 4468 | 881 | 0 | 37845 |
| Water | 8 | 0 | 409 | 0 | 7 | 0 | 424 |
| Agricultural | 781 | 372 | 77 | 76073 | 22090 | 49 | 99442 |
| Grassland | 3478 | 11 | 108 | 12537 | 176014 | 361 | 192509 |
| Shrubland | 114 | 0 | 0 | 260 | 9323 | 77019 | 86716 |
| Total | 27020 | 32809 | 719 | 95181 | 220324 | 77524 | 453577 |
| Land Use Types | Commission Error | Omission Error | Producer’s Accuracy | User’s Accuracy |
|---|---|---|---|---|
| Urban | 0.13 | 0.16 | 0.84 | 0.87 |
| Forest | 0.14 | 0.01 | 0.99 | 0.86 |
| Water | 0.04 | 0.43 | 0.57 | 0.96 |
| Agricultural | 0.24 | 0.20 | 0.80 | 0.76 |
| Grassland | 0.09 | 0.20 | 0.80 | 0.91 |
| Shrubland | 0.11 | 0.01 | 0.99 | 0.89 |
| Kappa | 0.835048 | Overall | 0.8750 |
References
- Dale, V.H.; Efroymson, R.A.; Kline, K.L. The land use-climate change-energy nexus. Landsc. Ecol. 2011. [Google Scholar] [CrossRef]
- Smith, B.D.; Zeder, M.A. The onset of the Anthropocene. Anthropocene 2013. [Google Scholar] [CrossRef]
- Crutzen, P.J. The Anthropocene. In Earth System Science in the Anthropocene; Springer: Berlin/Heidelberg, Germany, 2006; ISBN 3540265880. [Google Scholar]
- Lewis, S.L.; Maslin, M.A. Defining the Anthropocene. Nature 2015, 519, 171–180. [Google Scholar] [CrossRef]
- Zalasiewicz, J.; Williams, M.; Haywood, A.; Ellis, M. The anthropocene: A new epoch of geological time? Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 835–841. [Google Scholar] [CrossRef]
- Ellis, E.C.; Goldewijk, K.K.; Siebert, S.; Lightman, D.; Ramankutty, N. Anthropogenic transformation of the biomes, 1700 to 2000. Glob. Ecol. Biogeogr. 2010, 19, 589–606. [Google Scholar] [CrossRef]
- Ellis, E.C.; Beusen, A.H.W.; Goldewijk, K.K. Anthropogenic biomes: 10,000 BCE to 2015 CE. Land 2020, 9, 129. [Google Scholar] [CrossRef]
- Fu, B.J.; Wang, Y.F.; Lu, Y.H.; He, C.S.; Chen, L.D.; Song, C.J. The effects of land-use combinations on soil erosion: A case study in the Loess Plateau of China. Prog. Phys. Geogr. 2009, 33, 793–804. [Google Scholar] [CrossRef]
- Lin, Y.P.; Hong, N.M.; Wu, P.J.; Wu, C.F.; Verburg, P.H. Impacts of land use change scenarios on hydrology and land use patterns in the Wu-Tu watershed in Northern Taiwan. Landsc. Urban Plan. 2007, 80, 111–126. [Google Scholar] [CrossRef]
- Pielke, R.A.; Avissar, R. Influence of landscape structure on local and regional climate. Landsc. Ecol. 1990, 4, 133–155. [Google Scholar] [CrossRef]
- Yeh, C.T.; Huang, S.L. Investigating spatiotemporal patterns of landscape diversity in response to urbanization. Landsc. Urban Plan. 2009, 93, 151–162. [Google Scholar] [CrossRef]
- Randhir, T.O.; Tsvetkova, O. Spatiotemporal dynamics of landscape pattern and hydrologic process in watershed systems. J. Hydrol. 2011, 404, 1–12. [Google Scholar] [CrossRef]
- Mohammady, M.; Moradi, H.R.; Zeinivand, H.; Temme, A.J.A.M.; Yazdani, M.R.; Pourghasemi, H.R. Modeling and assessing the effects of land use changes on runoff generation with the CLUE-s and WetSpa models. Theor. Appl. Climatol. 2018, 133, 459–471. [Google Scholar] [CrossRef]
- Huong, H.T.L.; Pathirana, A. Urbanization and climate change impacts on future urban flooding in Can Tho city, Vietnam. Hydrol. Earth Syst. Sci. 2013, 17, 379–394. [Google Scholar] [CrossRef]
- Brath, A.; Montanari, A.; Moretti, G. Assessing the effect on flood frequency of land use change via hydrological simulation (with uncertainty). J. Hydrol. 2006, 324, 141–153. [Google Scholar] [CrossRef]
- IPCC. IPCC Fourth Assessment Report, Climate Change 2007: Impacts, Adaptation and Vulnerability; Working Group II Contribution to the 4th Assessment Report; IPCC: Geneva, Switzerland, 2007; ISBN 0521705975. [Google Scholar]
- IPCC. IPCC—Fifth Assessment Report (AR5) WGII; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- Metz, B.; Meyer, L.; Bosch, P. Climate Change 2007: Mitigation of Climate Change; IPCC: Geneva, Switzerland, 2007; ISBN 9780511546013. [Google Scholar]
- Steele-Dunne, S.; Lynch, P.; McGrath, R.; Semmler, T.; Wang, S.; Hanafin, J.; Nolan, P. The impacts of climate change on hydrology in Ireland. J. Hydrol. 2008, 356, 28–45. [Google Scholar] [CrossRef]
- Boyer, C.; Chaumont, D.; Chartier, I.; Roy, A.G. Impact of climate change on the hydrology of St. Lawrence tributaries. J. Hydrol. 2010, 384, 65–83. [Google Scholar] [CrossRef]
- Yang, N.; Men, B.H.; Lin, C.K. Impact analysis of climate change on water resources. Procedia Eng. 2011, 24, 643–648. [Google Scholar]
- IPCC. Climate Change and Land: An IPCC Special Report on Climate Change, Desertification, Land Degradation, Sustainable Land Management, Food Security, and Greenhouse Gas Fluxes in Terrestrial Ecosystems; IPCC: Geneva, Switzerland, 2019. [Google Scholar]
- Vaze, J.; Post, D.A.; Chiew, F.H.S.; Perraud, J.M.; Viney, N.R.; Teng, J. Climate non-stationarity—Validity of calibrated rainfall-runoff models for use in climate change studies. J. Hydrol. 2010, 394, 447–457. [Google Scholar] [CrossRef]
- Araos, M.; Berrang-Ford, L.; Ford, J.D.; Austin, S.E.; Biesbroek, R.; Lesnikowski, A. Climate change adaptation planning in large cities: A systematic global assessment. Environ. Sci. Policy 2016, 66, 375–382. [Google Scholar] [CrossRef]
- Winsemius, H.C.; Aerts, J.C.J.H.; Van Beek, L.P.H.; Bierkens, M.F.P.; Bouwman, A.; Jongman, B.; Kwadijk, J.C.J.; Ligtvoet, W.; Lucas, P.L.; Van Vuuren, D.P.; et al. Global drivers of future river flood risk. Nat. Clim. Chang. 2016, 6, 381–385. [Google Scholar] [CrossRef]
- Mozumder, P.; Flugman, E.; Randhir, T. Adaptation behavior in the face of global climate change: Survey responses from experts and decision makers serving the Florida Keys. Ocean Coast. Manag. 2011, 54, 37–44. [Google Scholar] [CrossRef]
- Quevauviller, P. Adapting to climate change: Reducing water-related risks in Europe—EU policy and research considerations. Environ. Sci. Policy 2011, 14, 722–729. [Google Scholar] [CrossRef]
- Forsee, W.J.; Ahmad, S. Evaluating Urban Storm-Water Infrastructure Design in Response to Projected Climate Change. J. Hydrol. Eng. 2011, 16, 865–873. [Google Scholar] [CrossRef]
- Bormann, H.; Breuer, L.; Gräff, T.; Huisman, J.A.; Croke, B. Assessing the impact of land use change on hydrology by ensemble modelling (LUCHEM) IV: Model sensitivity to data aggregation and spatial (re-)distribution. Adv. Water Resour. 2009, 32, 171–192. [Google Scholar] [CrossRef]
- Tang, L.; Yang, D.; Hu, H.; Gao, B. Detecting the effect of land-use change on streamflow, sediment and nutrient losses by distributed hydrological simulation. J. Hydrol. 2011, 409, 172–182. [Google Scholar] [CrossRef]
- Li, Z.; Liu, W.Z.; Zhang, X.C.; Zheng, F.L. Impacts of land use change and climate variability on hydrology in an agricultural catchment on the Loess Plateau of China. J. Hydrol. 2009, 377, 35–42. [Google Scholar] [CrossRef]
- Pervez, M.S.; Henebry, G.M. Assessing the impacts of climate and land use and land cover change on the freshwater availability in the Brahmaputra River basin. J. Hydrol. Reg. Stud. 2015, 3, 285–311. [Google Scholar] [CrossRef]
- Karlsson, I.B.; Sonnenborg, T.O.; Refsgaard, J.C.; Trolle, D.; Børgesen, C.D.; Olesen, J.E.; Jeppesen, E.; Jensen, K.H. Combined effects of climate models, hydrological model structures and land use scenarios on hydrological impacts of climate change. J. Hydrol. 2016, 535, 301–317. [Google Scholar] [CrossRef]
- Dibaba, W.T.; Demissie, T.A.; Miegel, K. Watershed hydrological response to combined land use/land cover and climate change in highland ethiopia: Finchaa catchment. Water 2020, 12, 1801. [Google Scholar] [CrossRef]
- Githui, F.; Mutua, F.; Bauwens, W. Estimating the impacts of land-cover change on runoff using the soil and water assessment tool (SWAT): Case study of Nzoia catchment, Kenya/Estimation des impacts du changement d’occupation du sol sur l’écoulement à l’aide de SWAT: Étude du cas du bassi. Hydrol. Sci. J. 2009, 54, 899–908. [Google Scholar] [CrossRef]
- Musau, J.; Sang, J.; Gathenya, J.; Luedeling, E. Hydrological responses to climate change in Mt. Elgon watersheds. J. Hydrol. Reg. Stud. 2015. [Google Scholar] [CrossRef]
- Mango, L.M.; Melesse, A.M.; McClain, M.E.; Gann, D.; Setegn, S.G. Land use and climate change impacts on the hydrology of the upper Mara River Basin, Kenya: Results of a modeling study to support better resource management. Hydrol. Earth Syst. Sci. 2011, 15, 2245–2258. [Google Scholar] [CrossRef]
- Seiller, G.; Anctil, F.; Perrin, C. Multimodel evaluation of twenty lumped hydrological models under contrasted climate conditions. Hydrol. Earth Syst. Sci. 2012, 16, 1171–1189. [Google Scholar] [CrossRef]
- Roy, T.; Gupta, H.V.; Serrat-Capdevila, A.; Valdes, J.B. Using satellite-based evapotranspiration estimates to improve the structure of a simple conceptual rainfall-runoff model. Hydrol. Earth Syst. Sci. 2017, 21, 879–896. [Google Scholar] [CrossRef]
- Rozos, E. A methodology for simple and fast streamflow modelling. Hydrol. Sci. J. 2020, 65, 1084–1095. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, G.H.; Wang, D.; Zhang, X. Multi-period calibration of a semi-distributed hydrological model based on hydroclimatic clustering. Adv. Water Resour. 2011. [Google Scholar] [CrossRef]
- Kim, N.W.; Chung, I.M.; Won, Y.S.; Arnold, J.G. Development and application of the integrated SWAT-MODFLOW model. J. Hydrol. 2008, 356, 1–16. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; Van Griensven, A.; Van Liew, M.W.; et al. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Abbott, M. Distributed Hydrological Modelling; Kluwer Academic: Dordrecht, The Netherlands; Boston, MA, USA, 1996; ISBN 0792340426. [Google Scholar]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Droogers, P. Calibration of a distributed hydrological model based on satellite evapotranspiration. J. Hydrol. 2008, 349, 411–424. [Google Scholar] [CrossRef]
- Francesconi, W.; Srinivasan, R.; Pérez-Miñana, E.; Willcock, S.P.; Quintero, M. Using the Soil and Water Assessment Tool (SWAT) to model ecosystem services: A systematic review. J. Hydrol. 2016, 535, 625–636. [Google Scholar] [CrossRef]
- Jayakrishnan, R.; Srinivasan, R.; Santhi, C.; Arnold, J.G. Advances in the application of the SWAT model for water resources management. Hydrol. Process. 2005, 19, 749–762. [Google Scholar] [CrossRef]
- Radcliffe, D.E.; Reid, D.K.; Blombäck, K.; Bolster, C.H.; Collick, A.S.; Easton, Z.M.; Francesconi, W.; Fuka, D.R.; Johnsson, H.; King, K.; et al. Applicability of Models to Predict Phosphorus Losses in Drained Fields: A Review. J. Environ. Qual. 2015, 44, 614–628. [Google Scholar] [CrossRef]
- Krysanova, V.; White, M. Advances in water resources assessment with SWAT—An overview. Hydrol. Sci. J. 2015. [Google Scholar] [CrossRef]
- Glavan, M.; Pintar, M.; Urbanc, J. Spatial variation of crop rotations and their impacts on provisioning ecosystem services on the river Drava alluvial plain. Sustain. Water Qual. Ecol. 2015, 5, 31–48. [Google Scholar] [CrossRef]
- Arnold, J.G.; Kiniry, J.R.; Srinivasan, R.; Williams, J.R.; Haney, E.B.; Neitsch, S.L. Soil and Water Assessment Tool; Input/Output Documentation, TR-439; Texas Water Resources Institute: Huston, TX, USA, 2012. [Google Scholar]
- Dile, Y.T.; Daggupati, P.; George, C.; Srinivasan, R.; Arnold, J. Introducing a new open source GIS user interface for the SWAT model. Environ. Model. Softw. 2016, 85, 129–138. [Google Scholar] [CrossRef]
- Molina-Navarro, E.; Nielsen, A.; Trolle, D. A QGIS plugin to tailor SWAT watershed delineations to lake and reservoir waterbodies. Environ. Model. Softw. 2018, 108, 67–71. [Google Scholar] [CrossRef]
- Reddy, N.N.; Reddy, K.V.; Vani, J.S.L.S.; Daggupati, P.; Srinivasan, R. Climate change impact analysis on watershed using QSWAT. Spat. Inf. Res. 2018, 26, 253–259. [Google Scholar] [CrossRef]
- Tanksali, A.; Soraganvi, V.S. Assessment of impacts of land use/land cover changes upstream of a dam in a semi-arid watershed using QSWAT. Model. Earth Syst. Environ. 2020. [Google Scholar] [CrossRef]
- Bansode, S.; Patil, K. Water Balance Assessment using Q-SWAT Rheological Properties of Nanoclay Modified Bitumen View project Water Balance Assessment using Q-SWAT. Artic. Int. J. Eng. Res. 2016, 5, 515–518. [Google Scholar]
- Munoth, P.; Goyal, R. Effects of area threshold values and stream burn-in process on runoff and sediment yield using QSWAT model. ISH J. Hydraul. Eng. 2019. [Google Scholar] [CrossRef]
- Ledesma, J.L.J.; Futter, M.N. Gridded climate data products are an alternative to instrumental measurements as inputs to rainfall–runoff models. Hydrol. Process. 2017, 31, 3283–3293. [Google Scholar] [CrossRef]
- Afrifa-Yamoah, E.; Mueller, U.A.; Taylor, S.M.; Fisher, A.J. Missing data imputation of high-resolution temporal climate time series data. Meteorol. Appl. 2020. [Google Scholar] [CrossRef]
- Vu, M.T.; Raghavan, S.V.; Liong, S.Y. SWAT use of gridded observations for simulating runoff—A Vietnam river basin study. Hydrol. Earth Syst. Sci. 2012, 16, 2801–2811. [Google Scholar] [CrossRef]
- Try, S.; Tanaka, S.; Tanaka, K.; Sayama, T.; Oeurng, C.; Uk, S.; Takara, K.; Hu, M.; Han, D. Comparison of gridded precipitation datasets for rainfall-runoff and inundation modeling in the Mekong River Basin. PLoS ONE 2020. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015. [Google Scholar] [CrossRef] [PubMed]
- Funk, C.; Peterson, P.; Peterson, S.; Shukla, S.; Davenport, F.; Michaelsen, J.; Knapp, K.R.; Landsfeld, M.; Husak, G.; Harrison, L.; et al. A high-resolution 1983–2016 TMAX climate data record based on infrared temperatures and stations by the climate hazard center. J. Clim. 2019, 32, 5639–5658. [Google Scholar] [CrossRef]
- Qin, L.; He, Y.; Huang, W.; Ma, G. Analysis of the rainfall and runoff temporal variation of Jialing River during 1955–2006. In Proceedings of the 11th Asian Conference on Chemical Sensors (ACCS2015), Penang, Malaysia, 16–18 November 2015; Volume 1820, p. 80008. [Google Scholar] [CrossRef]
- Liu, X.; Liang, X.; Li, X.; Xu, X.; Ou, J.; Chen, Y.; Li, S.; Wang, S.; Pei, F. A future land use simulation model (FLUS) for simulating multiple land use scenarios by coupling human and natural effects. Landsc. Urban Plan. 2017, 168, 94–116. [Google Scholar] [CrossRef]
- Luo, M.; Li, X. Forest Loss Simulation and Water Yield Assessment Based on GEOSOS-FLUS Model: A Case Study of Yangtze River Delta and Pearl River Delta. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Madrid, Spain, 13–16 September 2019; pp. 6582–6585. [Google Scholar]
- Li, X.; Chen, G.; Liu, X.; Liang, X.; Wang, S.; Chen, Y.; Pei, F.; Xu, X. A New Global Land-Use and Land-Cover Change Product at a 1-km Resolution for 2010 to 2100 Based on Human-Environment Interactions. Ann. Am. Assoc. Geogr. 2017, 107, 1040–1059. [Google Scholar] [CrossRef]
- Wang, Y.; Shen, J.; Yan, W.; Chen, C. Backcasting approach with multi-scenario simulation for assessing effects of land use policy using GeoSOS-FLUS software. MethodsX 2019, 6, 1384–1397. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Waliser, D.E.; Mattmann, C.A.; Goodale, C.E.; Hart, A.F.; Zimdars, P.A.; Crichton, D.J.; Jones, C.; Nikulin, G.; Hewitson, B.; et al. Evaluation of the CORDEX-Africa multi-RCM hindcast: Systematic model errors. Clim. Dyn. 2014, 42, 1189–1202. [Google Scholar] [CrossRef]
- Van Vuuren, D.P.; Edmonds, J.; Kainuma, M.; Riahi, K.; Thomson, A.; Hibbard, K.; Hurtt, G.C.; Kram, T.; Krey, V.; Lamarque, J.F.; et al. The representative concentration pathways: An overview. Clim. Chang. 2011, 109, 5–31. [Google Scholar] [CrossRef]
- Riahi, K.; Grübler, A.; Nakicenovic, N. Scenarios of long-term socio-economic and environmental development under climate stabilization. Technol. Forecast. Soc. Chang. 2007, 74, 887–935. [Google Scholar] [CrossRef]
- Gadissa, T.; Nyadawa, M.; Behulu, F.; Mutua, B. The effect of climate change on loss of lake volume: Case of sedimentation in Central Rift Valley Basin, Ethiopia. Hydrology 2018, 5, 67. [Google Scholar] [CrossRef]
- Rathjens, H.; Bieger, K.; Srinivasan, R.; Arnold, J.G. CMhyd User Manual Documentation for Preparing Simulated Climate Change Data for Hydrologic Impact Studies; SWAT: Huston, TX, USA, 2016. [Google Scholar]
- Fang, G.H.; Yang, J.; Chen, Y.N.; Zammit, C. Comparing bias correction methods in downscaling meteorological variables for a hydrologic impact study in an arid area in China. Hydrol. Earth Syst. Sci. 2015, 19, 2547–2559. [Google Scholar] [CrossRef]
- Zhang, B.; Shrestha, N.K.; Daggupati, P.; Rudra, R.; Shukla, R.; Kaur, B.; Hou, J. Quantifying the impacts of climate change on streamflow dynamics of two major rivers of the Northern Lake Erie basin in Canada. Sustainability 2018, 10, 2897. [Google Scholar] [CrossRef]
- Setegn, S.G.; Srinivasan, R.; Dargahi, B. Hydrological Modelling in the Lake Tana Basin, Ethiopia Using SWAT Model. Open Hydrol. J. 2008, 2, 49–62. [Google Scholar] [CrossRef]
- Soil Conservation Service Engineering Division. Section 4: Hydrology. In National Engineering Handbook; NRCS: Washington, DC, USA, 1972. [Google Scholar]
- Yen, H.; Park, S.; Arnold, J.G.; Srinivasan, R.; Chawanda, C.J.; Wang, R.; Feng, Q.; Wu, J.; Miao, C.; Bieger, K.; et al. IPEAT+: A built-in optimization and automatic calibration tool of SWAT. Water 2019, 11, 1681. [Google Scholar] [CrossRef]
- Haan, C.T. Statistical methods in hydrology. Stat. Methods Hydrol. 1977. [Google Scholar] [CrossRef]
- Lenhart, T.; Eckhardt, K.; Fohrer, N.; Frede, H.G. Comparison of two different approaches of sensitivity analysis. Phys. Chem. Earth 2002, 27, 645–654. [Google Scholar] [CrossRef]
- Feyereisen, G.W.; Strickland, T.C.; Bosch, D.D.; Sullivan, D.G. Evaluation of SWAT Manual Calibration and Input Parameter Sensitivity in the Little River Watershed. Trans. ASABE 2007, 50, 843–855. [Google Scholar] [CrossRef]
- Brouziyne, Y.; Abouabdillah, A.; Bouabid, R.; Benaabidate, L.; Oueslati, O. SWAT manual calibration and parameters sensitivity analysis in a semi-arid watershed in North-western Morocco. Arab. J. Geosci. 2017, 10. [Google Scholar] [CrossRef]
- Zambrano, M.B. Package “hydroGOF”: Goodness-of-Fit Functions for Comparison of Simulated and Observed Hydrological Time Series; SWAT: Huston, TX, USA, 2017. [Google Scholar]
- Yapo, P.O.; Gupta, H.V.; Sorooshian, S. Automatic calibration of conceptual rainfall-runoff models: Sensitivity to calibration data. J. Hydrol. 1996. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009. [Google Scholar] [CrossRef]
- Criss, R.E.; Winston, W.E. Do Nash values have value? Discussion and alternate proposals. Hydrol. Process. 2008, 22, 2723–2725. [Google Scholar] [CrossRef]
- Hu, S.; Fan, Y.; Zhang, T. Assessing the Effect of Land Use Change on Surface Runoff in a Rapidly Urbanized City: A Case Study of the Central Area of Beijing. Land 2020, 9, 17. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Liu, X.; Ai, B. Modeling urban land-use dynamics in a fast developing city using the modified logistic cellular automaton with a patch-based simulation strategy. Int. J. Geogr. Inf. Sci. 2014, 28, 234–255. [Google Scholar] [CrossRef]
- Pontius, R.G.; Boersma, W.; Castella, J.-C.; Clarke, K.; de Nijs, T.; Dietzel, C.; Duan, Z.; Fotsing, E.; Goldstein, N.; Kok, K.; et al. Comparing the input, output, and validation maps for several models of land change. Ann. Reg. Sci. 2008, 42, 11–37. [Google Scholar] [CrossRef]
- Lyon, B.; Vigaud, N. Unraveling East Africa’s Climate Paradox. Clim. Extrem. Patterns Mech. Geophys. Monogr. 2017, 265, 281. [Google Scholar] [CrossRef]
- Williams, A.P.; Funk, C. A westward extension of the warm pool leads to a westward extension of the Walker circulation, drying eastern Africa. Clim. Dyn. 2011, 37, 2417–2435. [Google Scholar] [CrossRef]
- Lyon, B.; Dewitt, D.G. A recent and abrupt decline in the East African long rains. Geophys. Res. Lett. 2012, 39, 1–5. [Google Scholar] [CrossRef]
- Yang, W.; Seager, R.; Cane, M.A.; Lyon, B. The East African long rains in observations and models. J. Clim. 2014, 27, 7185–7202. [Google Scholar] [CrossRef]
- Beyene, T.; Lettenmaier, D.P.; Kabat, P. Hydrologic impacts of climate change on the Nile River Basin: Implications of the 2007 IPCC scenarios. Clim. Chang. 2010. [Google Scholar] [CrossRef]
- Guzha, A.C.; Rufino, M.C.; Okoth, S.; Jacobs, S.; Nóbrega, R.L.B. Impacts of land use and land cover change on surface runoff, discharge and low flows: Evidence from East Africa. J. Hydrol. Reg. Stud. 2018, 15, 49–67. [Google Scholar] [CrossRef]
- Lucas-Borja, M.E.; Carrà, B.G.; Nunes, J.P.; Bernard-Jannin, L.; Zema, D.A.; Zimbone, S.M. Impacts of land-use and climate changes on surface runoff in a tropical forest watershed (Brazil). Hydrol. Sci. J. 2020, 65, 1–18. [Google Scholar] [CrossRef]
- Laothawornkitkul, J.; Taylor, J.E.; Paul, N.D.; Hewitt, C.N. Biogenic volatile organic compounds in the Earth system: Tansley review. New Phytol. 2009, 183, 27–51. [Google Scholar] [CrossRef]
- Nyenzi, B.S.; Kiangi, P.M.R.; Rao, N.N.P. Evaporation values in East Africa. Arch. Meteorol. Geophys. Bioclimatol. Ser. B 1981, 29, 37–55. [Google Scholar] [CrossRef]
- Karongo, S.K.; Sharma, T.C. An evaluation of actual evapotranspiration in tropical East Africa. Hydrol. Process. 1997, 11, 501–510. [Google Scholar] [CrossRef]
- Dagg, M.; Woodhead, T.; Rijks, D.A. Evaporation in East Africa. Int. Assoc. Sci. Hydrol. Bull. 1970, 15, 61–67. [Google Scholar] [CrossRef]
- Alemayehu, T.; van Griensven, A.; Senay, G.B.; Bauwens, W. Evapotranspiration Mapping in a Heterogeneous Landscape Using Remote Sensing and Global Weather Datasets: Application to the Mara Basin, East Africa. Remote Sens. 2017, 9, 390. [Google Scholar] [CrossRef]
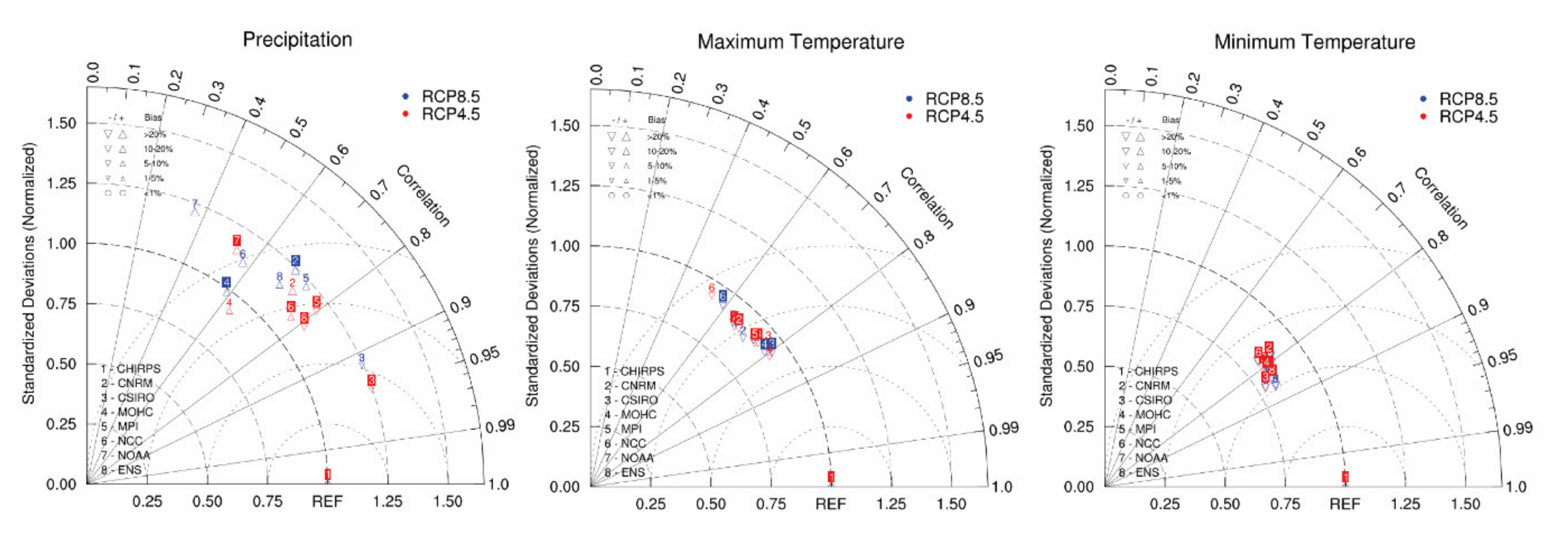


| Institute | RCM | Driving GCM | Historical | RCP4.5 | RCP8.5 |
|---|---|---|---|---|---|
| SHMI | RCA4 | CNRM-CERFACS-CNRM-CM5 | √ | √ | √ |
| SHMI | RCA4 | CSIRO-QCCCE-CSIRO-Mk3-6-0 | √ | √ | √ |
| SHMI | RCA4 | MOHC-HadGEM2-ES | √ | √ | √ |
| SHMI | RCA4 | MPI-M-MPI-ESM-LR | √ | √ | √ |
| SHMI | RCA4 | NCC-NorESM1-M | √ | √ | √ |
| SHMI | RCA4 | NOAA-GFDL-GFDL-ESM2M | √ | √ | √ |
| Parameter | Object Type | Description | Range |
|---|---|---|---|
| cn2 | hru | Initial SCS runoff curve number for moisture condition II. | 28–98 |
| awc | sol | Available water content of the soil layer (mm H2O/mm). | 0.01–1.0 |
| esco | Soil evaporation compensation factor. | 0.01–1.00 | |
| perco | hru | Amount of water percolating out of root zone (mm H2O) | 0–1 |
| gw_lte | hlt | Initial shallow aquifer storage | 0–10 m |
| revap_co | aqu | Groundwater “revap” coefficient. | 0.02–0.2 |
| revap_min | aqu | Minimum depth of water in the shallow aquifer for percolation to the deep aquifer to occur (mm H2O). | 0–10 m |
| alpha_bf | aqu | Baseflow alpha-factor (days). | 0–1 day |
| canmax | hru | Maximum canopy storage (mm H2O) | 0–100 mm/H2O |
| k_ch | rte | Effective hydraulic conductivity in tributary channelalluvium (mm/h). | 0–0.01–500 mm/h |
| flo_min | aqu | Minimum water depth in the shallow aquifer required to return flow (mm H2O). | 0–10 m |
| gwflow | lte | Groundwater contribution to streamflow (mm H2O). | 0–10 m |
| gwdeep | lte | Deep aquifer percolation fraction. | 0–10 m |
| ovn | hru | Manning’s “n” value for overland flow | 0.01–30 |
| Class | Sensitivity Category | |
|---|---|---|
| I | 0.00 ≤ < 0.05 | Small to negligible |
| II | 0.05 ≤ < 0.20 | Medium |
| III | 0.2 ≤ < 1 | High |
| IV | > 1 | Very high |
| Coefficient | Description | Optimal Values |
|---|---|---|
| Percent bias (PBIAS) [85] | measures the average tendency of the simulated channel flow to deviate from the observed flow. | 0—Optimal, Negative—underestimation, Positive—overestimation |
| Nash-Sutcliffe efficiency (NSE) [86] | a normalised statistic that calculates the relative magnitude of the simulated flow variance compared to the observed flow variance. | NSE = 1 perfect match, NSE = 0, model predictions accurate as the mean of the observed data, -Inf < NSE < 0, observed mean is a better predictor than the model |
| Product of coefficient of determination (R2) and the regression line slope between simulation and observation (bR2) [87] | allows measurement for the discrepancy in the magnitude of simulated and observed flows (b) and their dynamics (R2) | 0 ≤ bR2 ≤ 1 1—Optimal, >0.5—good match, <0.5—representative. |
| Kling-Gupta efficiency (KGE) [88] | aids the evaluation of the relative importance of diverse components (correlation, bias, and variability) | -inf < KGE > 1 efficient |
| Volumetric efficiency (VE) [89] | represents the fraction of water reaching the channel at the proper time | -Inf ≤ VE ≤ 1 efficient |
| Urban | Forest | Water | Agriculture | Grasslands | Shrublands | |
|---|---|---|---|---|---|---|
| 1990 | 85.87 | 666.01 | 5.93 | 980.90 | 3162.12 | 785.02 |
| 2000 | 98.73 | 401.99 | 10.78 | 1041.76 | 3097.78 | 1034.78 |
| 2010 | 274.98 | 427.09 | 9.64 | 1083.75 | 2817.02 | 1073.40 |
| 2020 | 428.31 | 410.72 | 19.68 | 1154.78 | 2532.13 | 1140.26 |
| 2050 | 624.58 | 419.05 | 21.03 | 1185.73 | 2244.61 | 1190.17 |
| 2080 | 725.20 | 392.75 | 23.27 | 1194.67 | 2169.12 | 1181.17 |
| Parameter | Water Yield | Baseflow | Surface Runoff | Sr | Sensitivity Category | Final Calibrated Value | Rank |
|---|---|---|---|---|---|---|---|
| cn2 | 1.53 | −1.32 | 5.01 | 1.74 | IV | 20.175–79.086 | 1 |
| awc | −0.31 | −0.55 | −0.67 | 0.51 | III | 0.733 | 2 |
| esco | 0.10 | 0.09 | 0.11 | 0.10 | II | 0.659 | 3 |
| perco | −0.03 | −0.02 | −0.04 | 0.03 | I | 0.128 | 4 |
| gw_lte | 0.00 | 0.00 | 0.00 | 0.00 | I | - | - |
| revap_co | 0.00 | 0.00 | 0.00 | 0.00 | I | - | - |
| revap_min | 0.00 | 0.00 | 0.00 | 0.00 | I | - | - |
| alpha_bf | 0.00 | 0.00 | 0.00 | 0.00 | I | - | - |
| canmax | 0.00 | 0.00 | 0.00 | 0.00 | I | - | - |
| k_ch | 0.00 | 0.00 | 0.00 | 0.00 | I | - | - |
| flo_min | 0.00 | 0.00 | 0.00 | 0.00 | I | - | - |
| gwflow | 0.00 | 0.00 | 0.00 | 0.00 | I | - | - |
| gwdeep | 0.00 | 0.00 | 0.00 | 0.00 | I | - | - |
| ovn | 0.00 | 0.00 | 0.00 | 0.00 | I | - | - |
| Urban | Forest | Water | Agriculture | Grasslands | Shrublands | Q | |
|---|---|---|---|---|---|---|---|
| 1990 | 85.87 | 666.01 | 5.93 | 980.90 | 3162.12 | 785.02 | 18.32 |
| 2000 | 98.73 | 401.99 | 10.78 | 1041.76 | 3097.78 | 1034.78 | 25.32 |
| 2010 | 274.98 | 427.09 | 9.64 | 1083.75 | 2817.02 | 1073.40 | 40.70 |
| t | 3.92 | −0.93 | 0.70 | 3.03 | −7.40 | 1.42 | - |
| p | 0.16 | 0.52 | 0.61 | 0.20 | 0.09 | 0.39 | - |
| R2 | 0.94 | 0.46 | 0.33 | 0.90 | 0.98 | 0.67 | - |
| Land Use | Climate | Climate + Land Use | |||
|---|---|---|---|---|---|
| Baseline | RCP4.5 | RCP8.5 | RCP4.5 | RCP8.5 | |
| 1984–1990 | 18.32 | - | - | - | - |
| 2003–2009 | 25.32 | - | - | - | - |
| 2010–2016 | 40.70 | 45.57 | 39.65 | - | - |
| 2051–2059 | - | 42.70 | 67.78 | 60.72 | 97.36 |
| 2081–2089 | - | 39.13 | 80.52 | 63.17 | 127.33 |
| Land Use | Climate | Climate + Land Use | |||
|---|---|---|---|---|---|
| Baseline | RCP4.5 | RCP8.5 | RCP4.5 | RCP8.5 | |
| 1984–1990 | - | - | - | - | - |
| 2003–2009 | 0.0040 | - | - | - | - |
| 2010–2016 | 0.0208 | - | - | - | - |
| 2051–2059 | - | −0.0185 | 0.0455 | 0.0441 | 0.0838 |
| 2081–2089 | - | −0.0072 | −0.0040 | 0.0004 | 0.0069 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiprotich, P.; Wei, X.; Zhang, Z.; Ngigi, T.; Qiu, F.; Wang, L. Assessing the Impact of Land Use and Climate Change on Surface Runoff Response Using Gridded Observations and SWAT+. Hydrology 2021, 8, 48. https://doi.org/10.3390/hydrology8010048
Kiprotich P, Wei X, Zhang Z, Ngigi T, Qiu F, Wang L. Assessing the Impact of Land Use and Climate Change on Surface Runoff Response Using Gridded Observations and SWAT+. Hydrology. 2021; 8(1):48. https://doi.org/10.3390/hydrology8010048
Chicago/Turabian StyleKiprotich, Paul, Xianhu Wei, Zongke Zhang, Thomas Ngigi, Fengting Qiu, and Liuhao Wang. 2021. "Assessing the Impact of Land Use and Climate Change on Surface Runoff Response Using Gridded Observations and SWAT+" Hydrology 8, no. 1: 48. https://doi.org/10.3390/hydrology8010048
APA StyleKiprotich, P., Wei, X., Zhang, Z., Ngigi, T., Qiu, F., & Wang, L. (2021). Assessing the Impact of Land Use and Climate Change on Surface Runoff Response Using Gridded Observations and SWAT+. Hydrology, 8(1), 48. https://doi.org/10.3390/hydrology8010048








