Copula-Based Bivariate Flood Risk Assessment on Tarbela Dam, Pakistan
Abstract
1. Introduction
2. Methodology
2.1. Copula Theory
2.1.1. Sklar’s Theorem
2.1.2. Copula Function
- ➢
- ,
- ➢
- and
- ➢
- ,
2.2. Dependence and Copula Fitting
2.3. Goodness-of-Fit
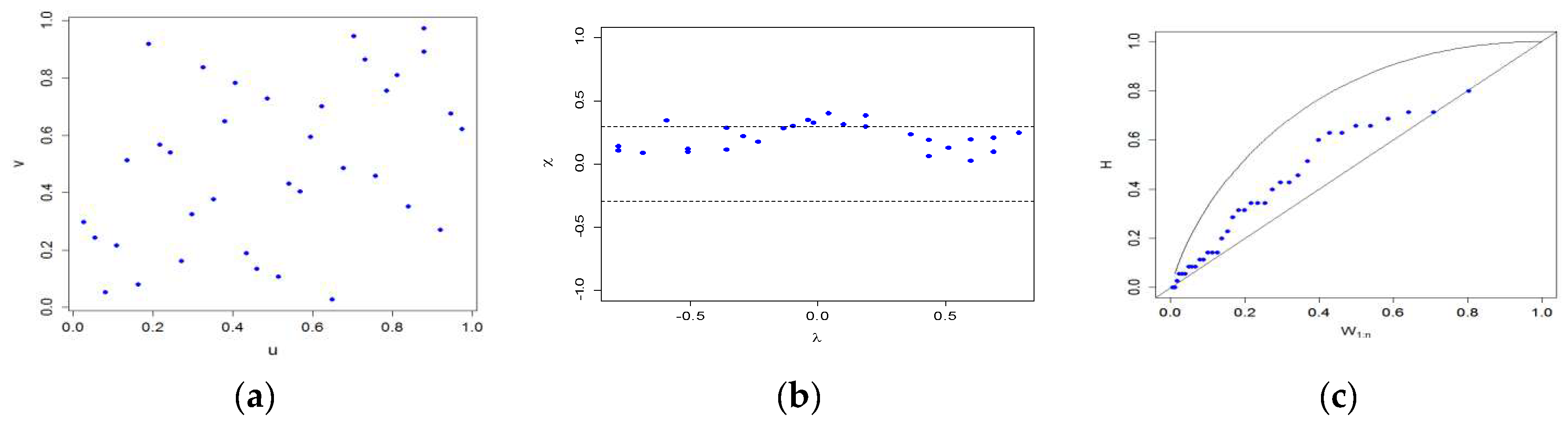
2.4. Tail-Dependence Test
2.5. Return Periods
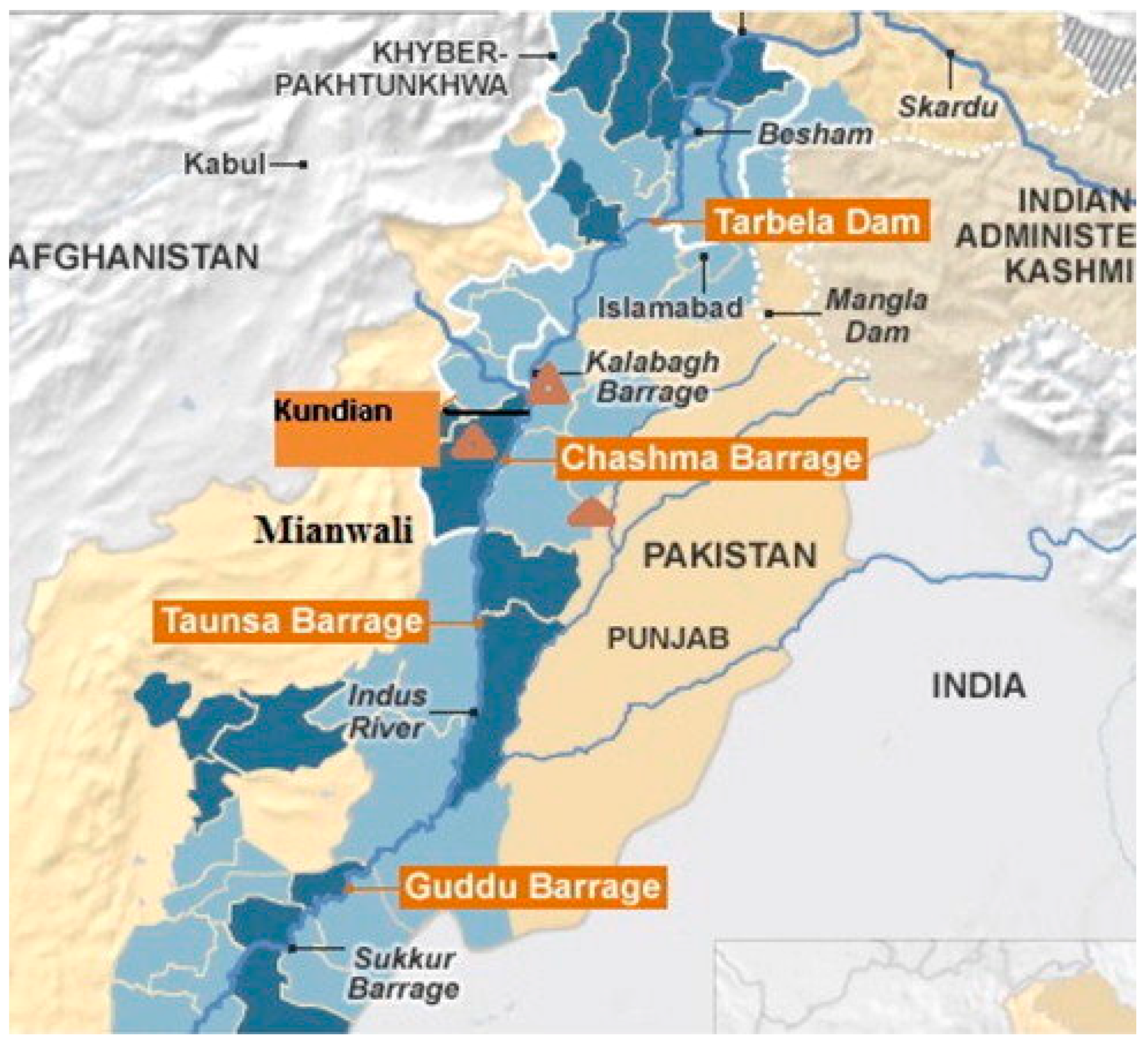
2.6. Description of Study Area
3. Results and Discussion
3.1. Dependence of Flood Variables (Peak and Volume)
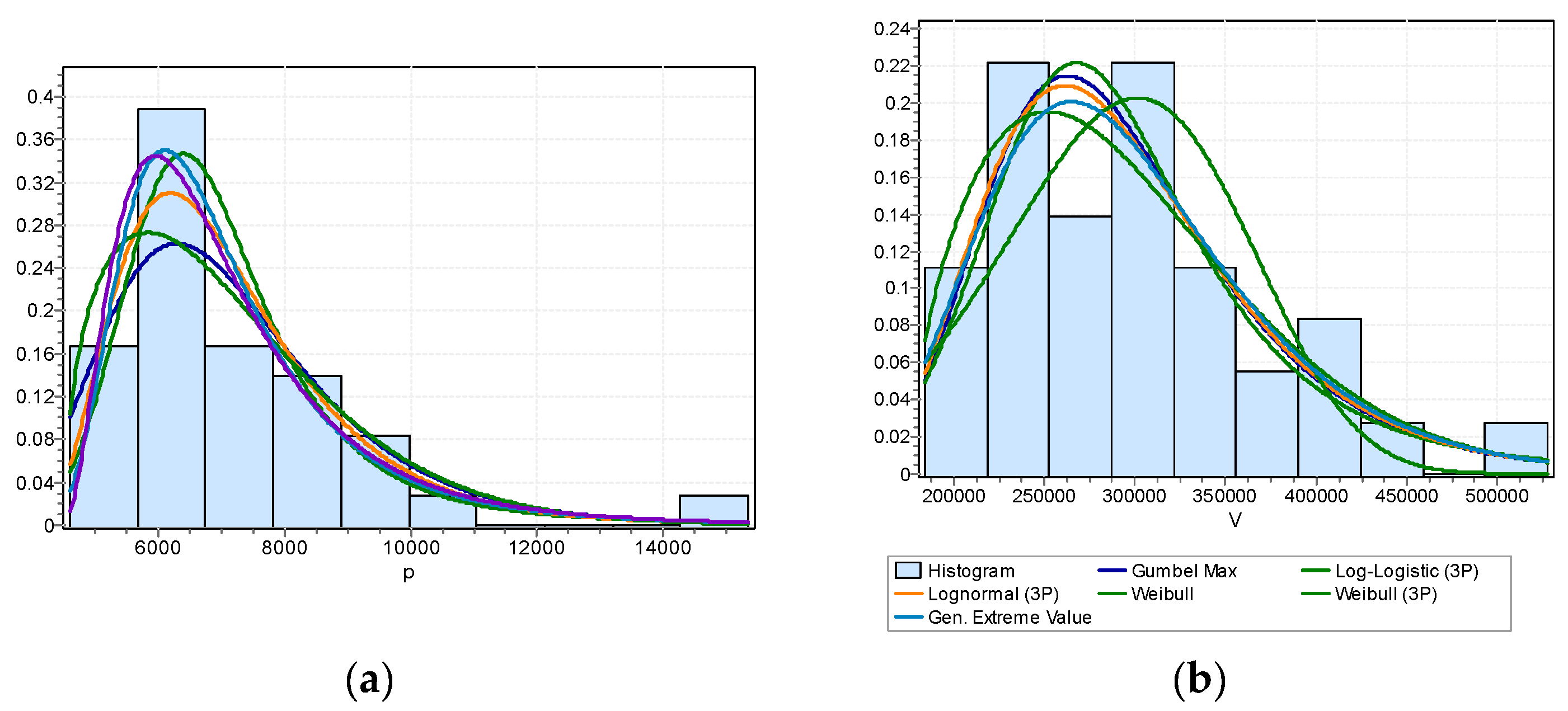
Marginal Distribution Analysis
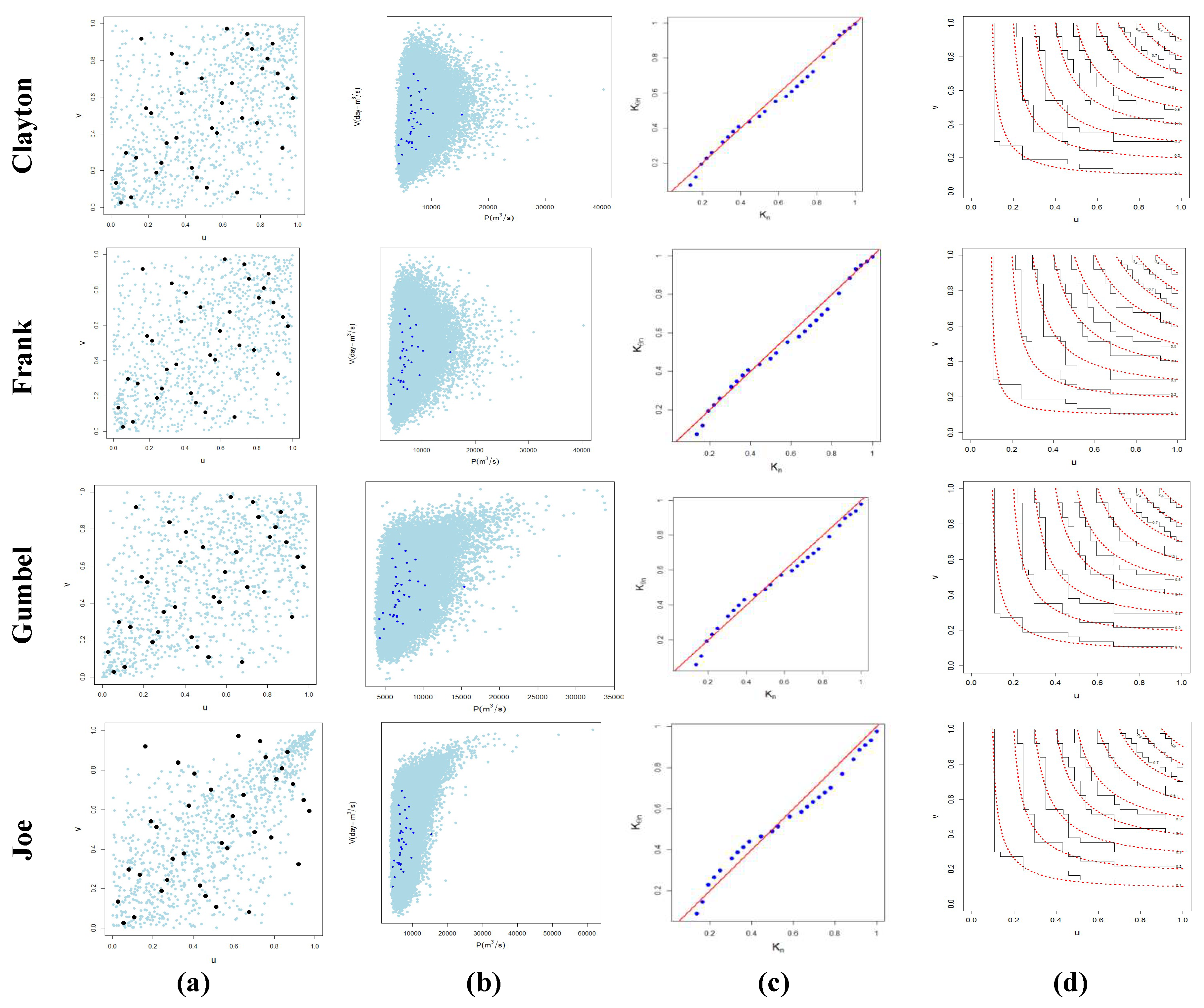
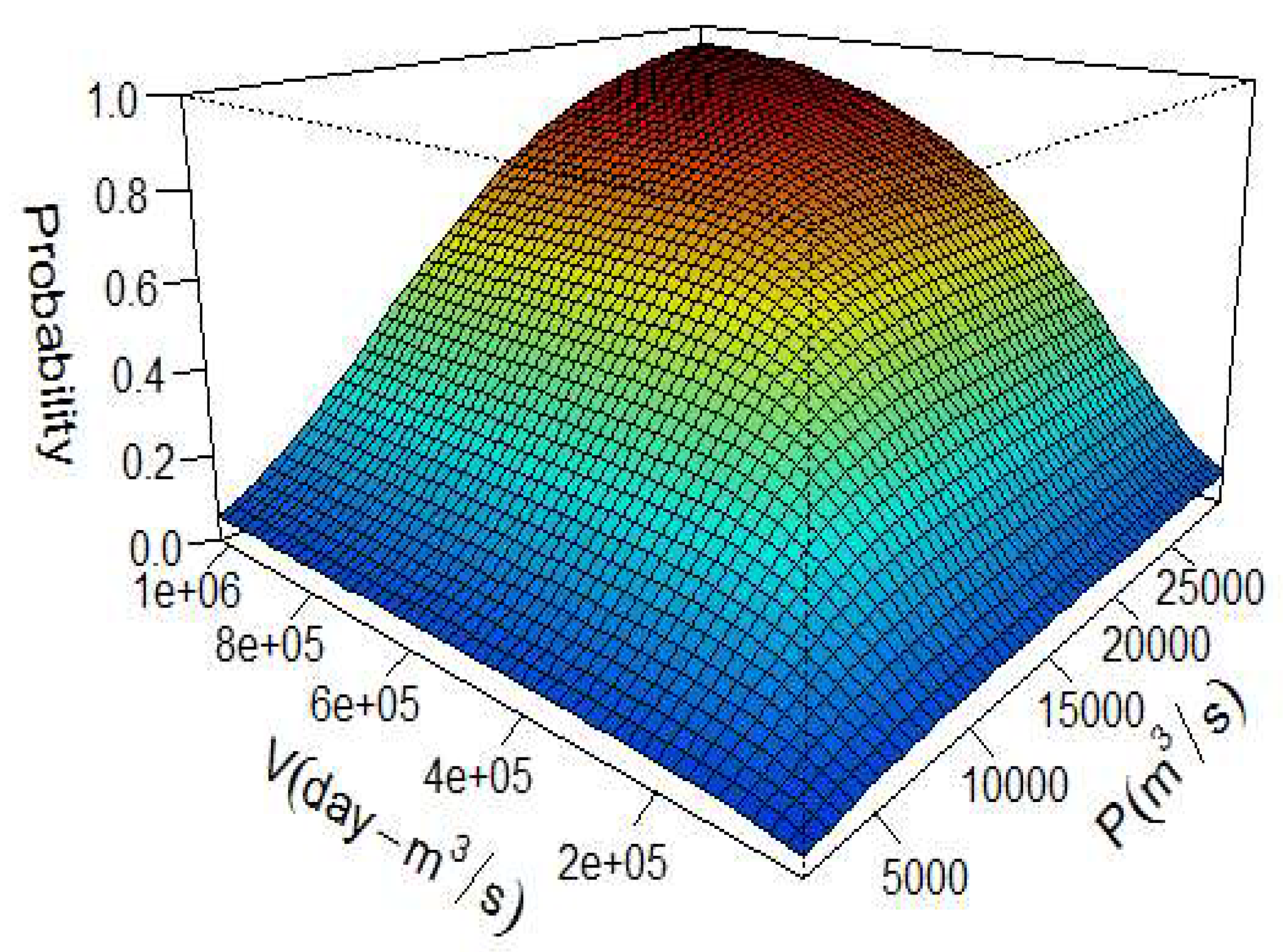
3.2. Dependence Structure between Peak and Volume Using Copula Function
Copula Modeling
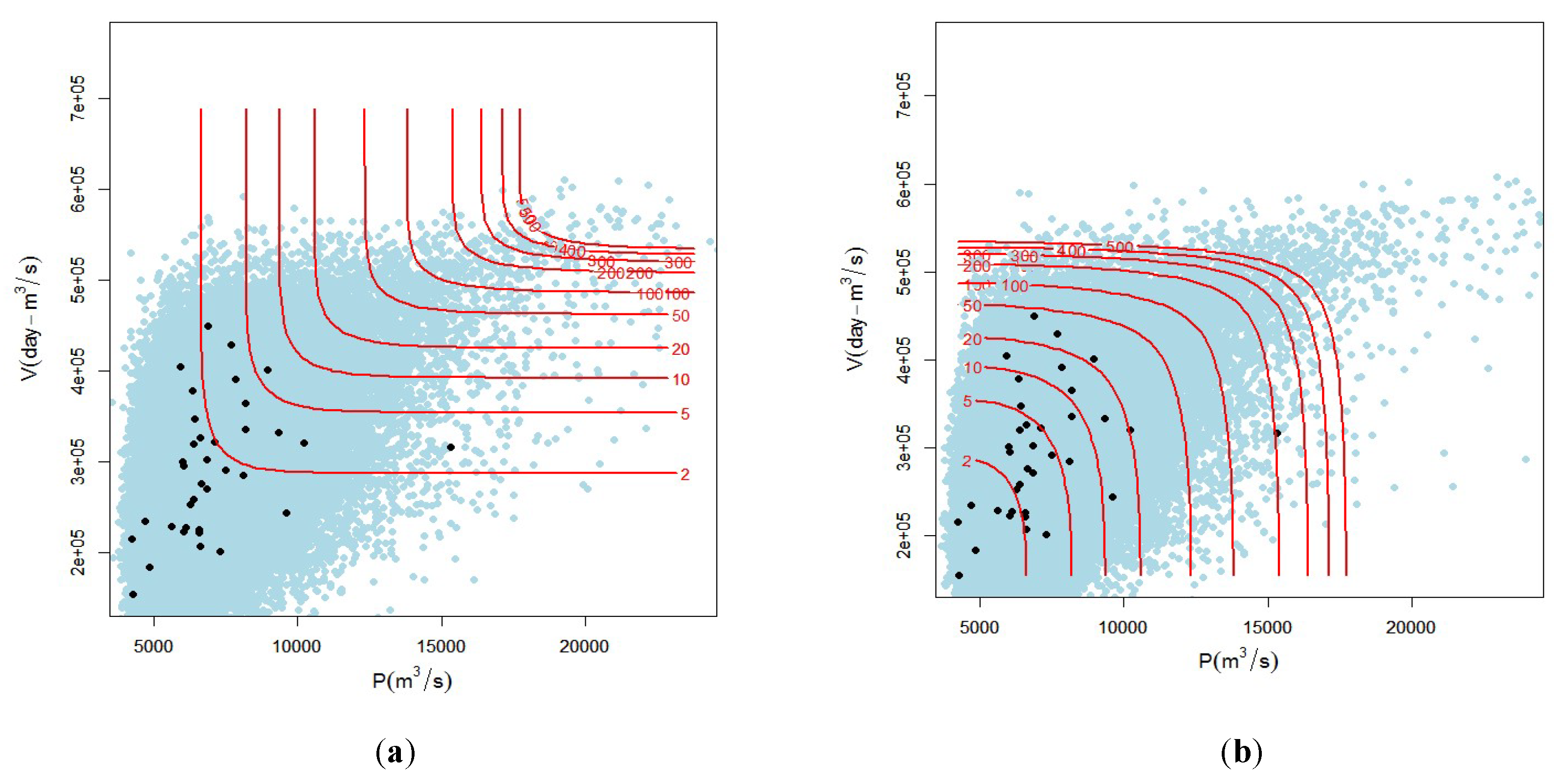
3.3. Analysis Tail Dependence Coefficient
3.4. Primary Return Periods (T AND, TOR)
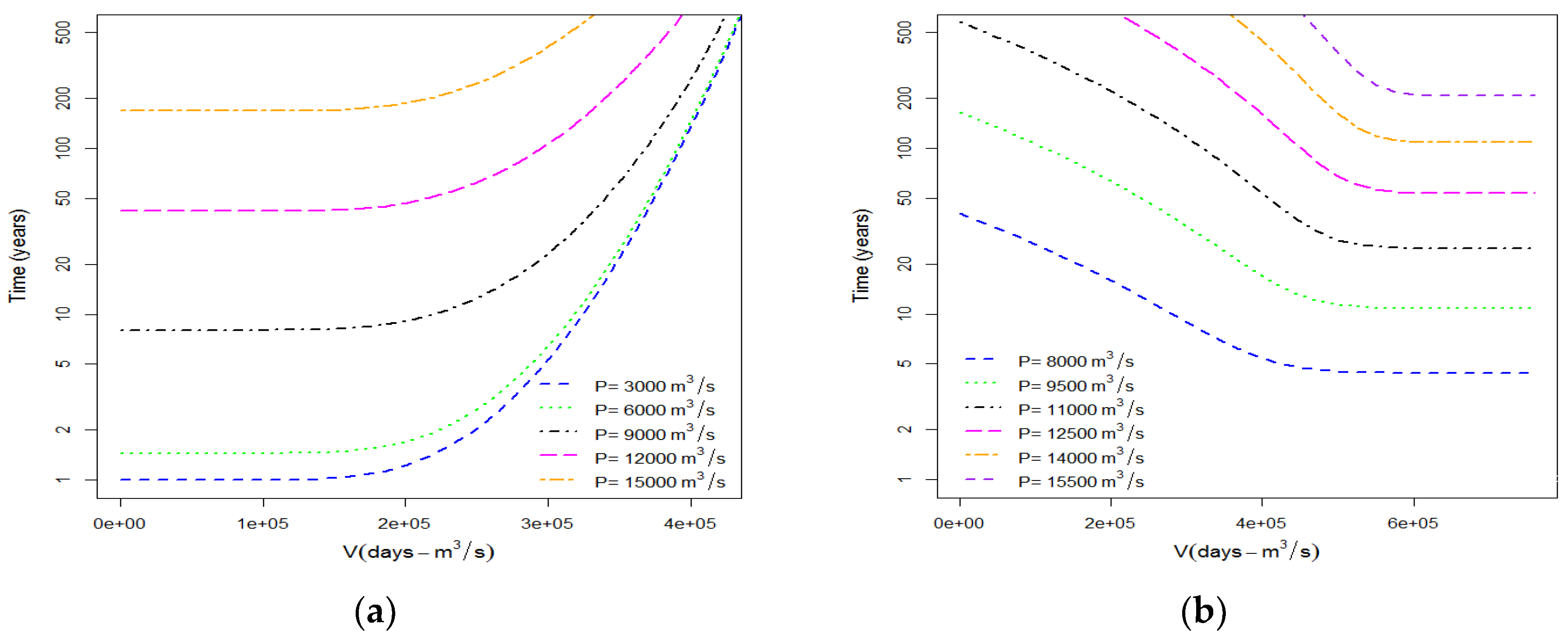
3.5. Conditional Return Period ( and )
3.6. Kendall or Secondary Return Period
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Ashkar, F.; Rousselle, J. A Multivariate Statistical Analysis of Flood Magnitude, Duration and Volume; Water Resource Publication: Reston, VA, USA, 1982; pp. 659–669. [Google Scholar]
- Ashkar, F. Partial Duration Series Models for Flood Analysis; École Polytechnique de Montréal: Montréal, QC, Canada, 1980. [Google Scholar]
- Lee, H.-T. A copula-based regime-switching GARCH model for optimal futures hedging. J. Futures Markets 2009, 29, 946–972. [Google Scholar] [CrossRef]
- Yue, S.; Ouarda, T.B.M.J.; Bobée, B.; Legendre, P.; Bruneau, P. The Gumbel mixed model for flood frequency analysis. J. Hydrol. 1999, 226, 88–100. [Google Scholar] [CrossRef]
- Yue, S. The bivariate lognormal distribution to model a multivariate flood episode. Hydrol. Process. 2000, 14, 2575–2588. [Google Scholar] [CrossRef]
- Shiau, J.-T. Return period of bivariate distributed extreme hydrological events. Stoch. Environ. Res. Risk Assess. 2003, 17, 42–57. [Google Scholar] [CrossRef]
- Yue, S. A bivariate gamma distribution for use in multivariate flood frequency analysis. Hydrol. Process. 2001, 15, 1033–1045. [Google Scholar] [CrossRef]
- Yue, S. A bivariate extreme value distribution applied to flood frequency analysis. Hydrol. Res. 2001, 32, 49–64. [Google Scholar] [CrossRef]
- Yue, S. The Gumbel mixed model applied to storm frequency analysis. Water Resour. Manag. 2000, 14, 377–389. [Google Scholar] [CrossRef]
- Yue, S. Applicability of the Nagao–Kadoya bivariate exponential distribution for modeling two correlated exponentially distributed variates. Stoch. Environ. Res. Risk Assess. 2001, 15, 244–260. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C.Y. A comparison of two bivariate extreme value distributions. Stoch. Environ. Res. Risk Assess. 2004, 18, 61–66. [Google Scholar] [CrossRef]
- Sklar, M. Fonctions de repartition an dimensions et leurs marges. Publ. Inst. Statist. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Chowdhary, H.; Escobar, L.A.; Singh, V.P. Identification of suitable copulas for bivariate frequency analysis of flood peak and flood volume data. Hydrol. Res. 2011, 42, 193–216. [Google Scholar] [CrossRef]
- Favre, A.C.; El Adlouni, S.; Perreault, L.; Thiémonge, N.; Bobée, B. Multivariate hydrological frequency analysis using copulas. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Ganguli, P.; Reddy, M.J. Probabilistic assessment of flood risks using trivariate copulas. Theor. Appl. Climatol. 2013, 111, 341–360. [Google Scholar] [CrossRef]
- Karmakar, S.; Simonovic, S.P. Bivariate flood frequency analysis. Part 2: A copula-based approach with mixed marginal distributions. J. Flood Risk Manag. 2009, 2, 32–44. [Google Scholar] [CrossRef]
- Requena, A.I.; Mediero, L.; Garrote, L. Bivariate return period based on copulas for hydrologic dam design: comparison of theoretical and empirical approach. Hydrol. Earth Syst. Sci. Discuss. 2013, 17, 3023–3038. [Google Scholar] [CrossRef]
- De Michele, C.; Salvadori, G. A generalized Pareto intensity-duration model of storm rainfall exploiting 2-copulas. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- De Michele, C.; Salvadori, G.; Passoni, G.; Vezzoli, R. A multivariate model of sea storms using copulas. Coast.Eng. 2007, 54, 734–751. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C. Frequency analysis via copulas: Theoretical aspects and applications to hydrological events. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Bivariate flood frequency analysis using the copula method. J. Hydrol. Eng. 2006, 11, 150–164. [Google Scholar] [CrossRef]
- Klein, B.; Pahlow, M.; Hundecha, Y.; Schumann, A. Probability analysis of hydrological loads for the design of flood control systems using copulas. J. Hydrol. Eng. 2009, 15, 360–369. [Google Scholar] [CrossRef]
- Ben Aissia, M.A.; Chebana, F.; Ouarda Taha, B.M.J.; Roy, L.; Desrochers, G.; Chartier, I.; Robichaud, É. Multivariate analysis of flood characteristics in a climate change context of the watershed of the Baskatong reservoir, Province of Québec, Canada. Hydrol. Process. 2012, 26, 130–142. [Google Scholar] [CrossRef]
- Sraj, M.; Bezak, N.; Brilly, M. Bivariate flood frequency analysis using the copula function: A case study of the Litija station on the Sava River. Hydrol. Process. 2015, 29, 225–238. [Google Scholar] [CrossRef]
- Li, F.; Zheng, Q. Probabilistic modelling of flood events using the entropy copula. Adv. Water Resour. 2016, 97, 233–240. [Google Scholar] [CrossRef]
- Höffding, W. Masstabinvariante korrelationstheorie. Schriften des Mathematischen Instituts und Instituts fur Angewandte Mathematik der Universitat Berlin 1940, 5, 181–233. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas, 2nd ed.; Springer Science Business Media: New York, NY, USA, 2006. [Google Scholar]
- Fisher, N.I.; Switzer, P. Chi-plots for assessing dependence. Biometrika 1985, 72, 253–265. [Google Scholar] [CrossRef]
- Genest, C.; Boies, J.-C. Detecting dependence with Kendall plots. Am. Stat. 2003, 57, 275–284. [Google Scholar] [CrossRef]
- Genest, C.; Rivest, L.-P. Statistical inference procedures for bivariate Archimedean copulas. J. Am. Stat. Assoc. 1993, 88, 1034–1043. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Bivariate rainfall frequency distributions using Archimedean copulas. J. Hydrol. 2007, 332, 93–109. [Google Scholar] [CrossRef]
- Gringorten, I.I. A plotting rule for extreme probability paper. J. Geophys. Res. 1963, 68, 813–814. [Google Scholar] [CrossRef]
- Karmakar, S.; Simonovic, S.P. Bivariate flood frequency analysis: Part 1. Determination of marginals by parametric and nonparametric techniques. J. Flood Risk Manag. 2008, 1, 190–200. [Google Scholar] [CrossRef]
- Genest, C.; Rémillard, B.; Beaudoin, D. Goodness-of-fit tests for copulas: A review and a power study. Insur. Math. Econ. 2009, 44, 199–213. [Google Scholar] [CrossRef]
- Frahm, G.; Junker, M.; Schmidt, R. Estimating the tail-dependence coefficient: Properties and pitfalls. Insur. Math. Econ. 2005, 37, 80–100. [Google Scholar] [CrossRef]
- Salvadori, G.; Durante, F.; De Michele, C. On the return period and design in a multivariate framework. 2011. [Google Scholar] [CrossRef]
- Naz, S.; Iqbal, M.J.; Akhter, S.M.; Hussain, I. The Gumbel Mixed Model for Flood Frequency Analysis of Tarbela. The Nucleus 2016, 53, 171–179. [Google Scholar]
- Michiels, F.; De Schepper, A. A copula test space model how to avoid the wrong copula choice. Kybernetika 2008, 44, 864–878. [Google Scholar]
- Hofert, M.; Kojadinovic, I.; Maechler, M.; Yan, J. Copula: Multivariate dependence with copulas. 2014. R Package Version 0.999-9. Available online: http://CRAN. R-project. org/package= copula (accessed on 10 June 2019).
- Poulin, A.; Huard, D.; Favre, A.-C.; Pugin, S. Importance of tail dependence in bivariate frequency analysis. J. Hydrol. Eng. 2007, 12, 394–403. [Google Scholar] [CrossRef]

| Copula | Space | |||
|---|---|---|---|---|
| Clayton | ||||
| Frank | (* (θ)-1) | |||
| Gumbel-Hougaard | ||||
| Joe |
| Statistical Measures | Tarbela Dam | |
|---|---|---|
| P(m3/s) | V(Day-m3/s) | |
| Minimum | 4231 | 154,900 |
| Median | 6602 | 293,500 |
| Maximum | 15,340 | 450,000 |
| Mean | 7073 | 293,000 |
| St. Deviation | 1929.8 | 75,594.0 |
| Skewness | 2.3143 | 12,599 |
| Kurtosis | 8.4322 | 1.108 |
| Dependence Measures | Station: Tarbela Dam |
|---|---|
| Pearson’s coefficient (p-value) | 0.358 |
| Kendall’s (p-value) | 0.311 |
| Spearman’s -(p-value) |
| Distribution | Parameters | K-S-Statistic (p-Value) | (p-Value) | |||
|---|---|---|---|---|---|---|
| Peak | Volume | Peak | Volume | Peak | Volume | |
| Gen. Extreme value | 0.964 | 0.924 | ||||
| Gumbel | 0.773 | 0.663 | ||||
| Log-Logistic (3P) | 0.849 | 0.654 | ||||
| Log-Normal (3P) | 0.904 | 0.723 | ||||
| Log-Pearson 3 | 0.937 | 0.097 | 0.723 | |||
| Weibull | 0.333 | 0.963 | 0.224 | 0.978 | ||
| Copula | RMSE | AIC | p-Value | ||
|---|---|---|---|---|---|
| Clayton | |||||
| Frank | |||||
| Gumbel | |||||
| Joe |
| Copulas | Θ | ||
|---|---|---|---|
| Clayton | 0 | 0.9032 | |
| Frank | 0 | 3.044 | |
| Gumbel | 1.452 | ||
| Joe | 1.814 |
| Return Periods | Copula | Gumbel | Frank | Clayton |
|---|---|---|---|---|
| Median | 1.507 | 1.704 | 1.505 | |
| Max. | 34.114 | 30.936 | 30.669 | |
| Median | 3.154 | 2.541 | 3.166 | |
| Max. | 280.48 | 1820.808 | 3737.91 | |
| Median | 6.643 | 3.224 | ||
| Max. | 36.603 | 36.227 | ||
| median | 4.946 | 6.161 | ||
| Max. | 353,889.807 | 726,495.046 |
| t (Levels) | T (Years) | TKEN | |
|---|---|---|---|
| 0.9 | 10 | 0.932 | 28.82 |
| 0.99 | 100 | 0.9932 | 301.84 |
| 0.999 | 1000 | 0.99932 | 3267.97 |
| 0.9999 | 10000 | 0.99932 | 37037.037 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naz, S.; Ahsanuddin, M.; Inayatullah, S.; Siddiqi, T.A.; Imtiaz, M. Copula-Based Bivariate Flood Risk Assessment on Tarbela Dam, Pakistan. Hydrology 2019, 6, 79. https://doi.org/10.3390/hydrology6030079
Naz S, Ahsanuddin M, Inayatullah S, Siddiqi TA, Imtiaz M. Copula-Based Bivariate Flood Risk Assessment on Tarbela Dam, Pakistan. Hydrology. 2019; 6(3):79. https://doi.org/10.3390/hydrology6030079
Chicago/Turabian StyleNaz, Saba, Muhammad Ahsanuddin, Syed Inayatullah, Tanveer Ahmed Siddiqi, and Muhammad Imtiaz. 2019. "Copula-Based Bivariate Flood Risk Assessment on Tarbela Dam, Pakistan" Hydrology 6, no. 3: 79. https://doi.org/10.3390/hydrology6030079
APA StyleNaz, S., Ahsanuddin, M., Inayatullah, S., Siddiqi, T. A., & Imtiaz, M. (2019). Copula-Based Bivariate Flood Risk Assessment on Tarbela Dam, Pakistan. Hydrology, 6(3), 79. https://doi.org/10.3390/hydrology6030079





