Estimating the Sediment Flux and Budget for a Data Limited Rift Valley Lake in Ethiopia
Abstract
:1. Introduction
2. Study Area
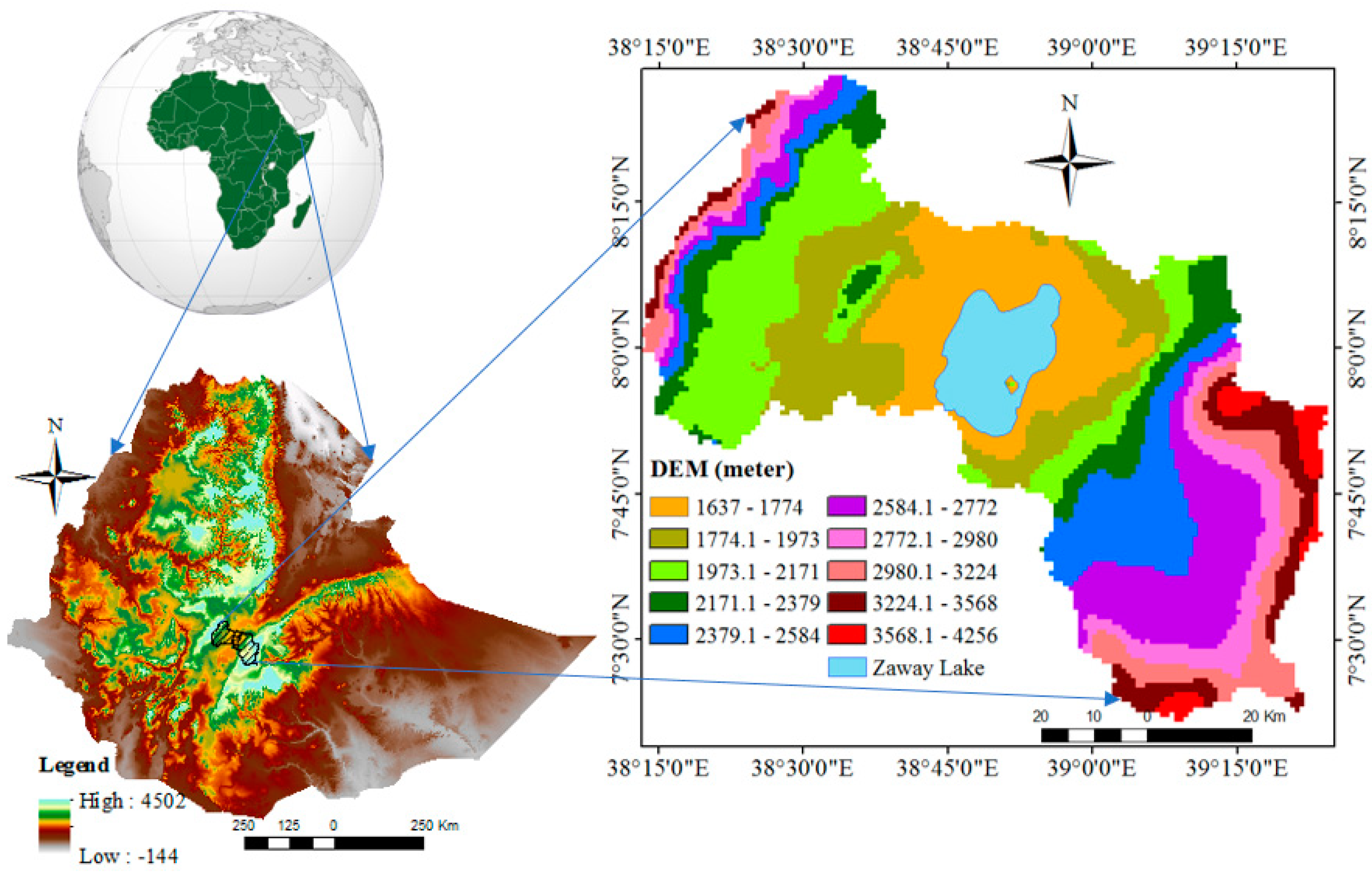
2.1. Location and Topography
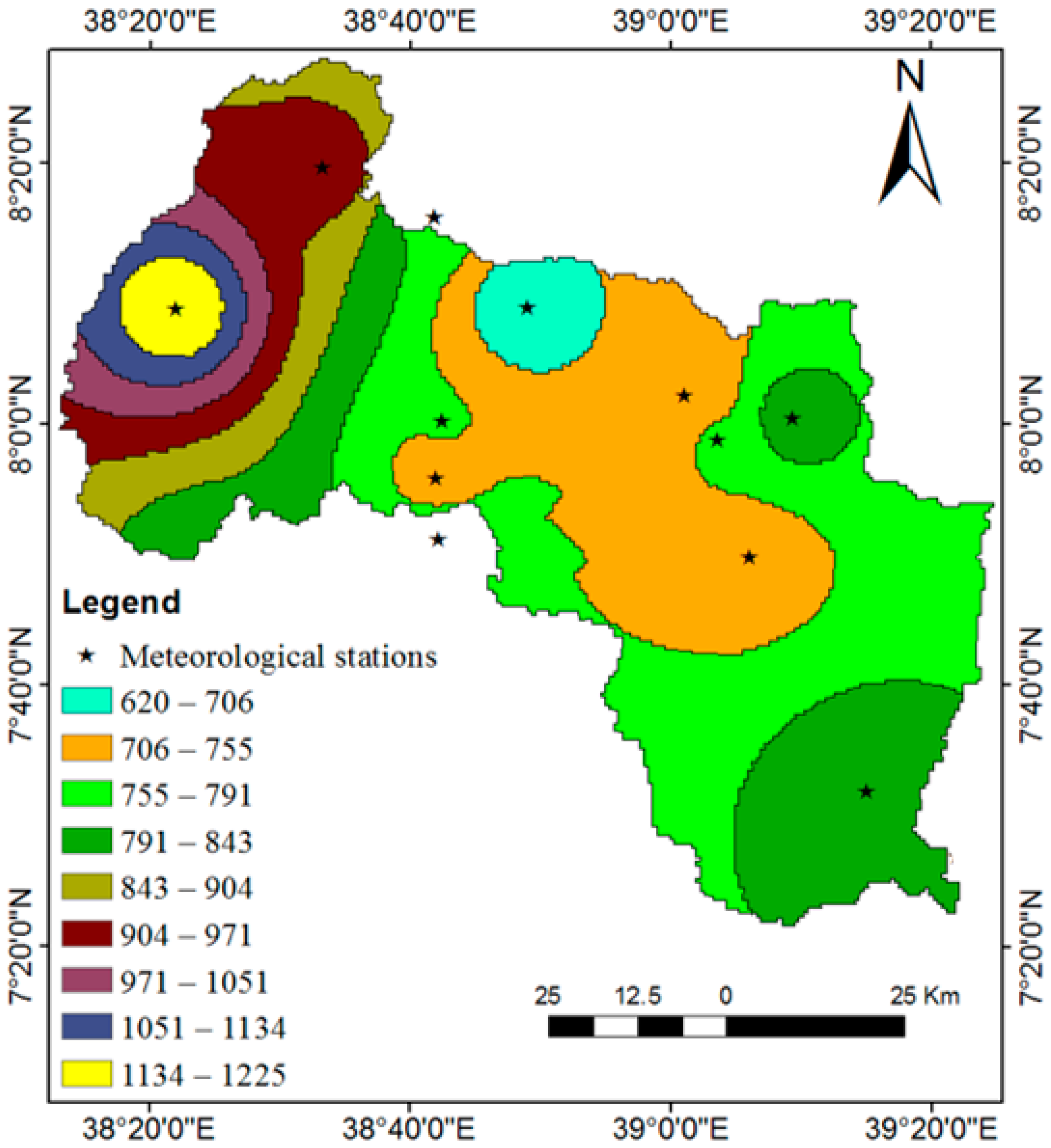
2.2. Climate
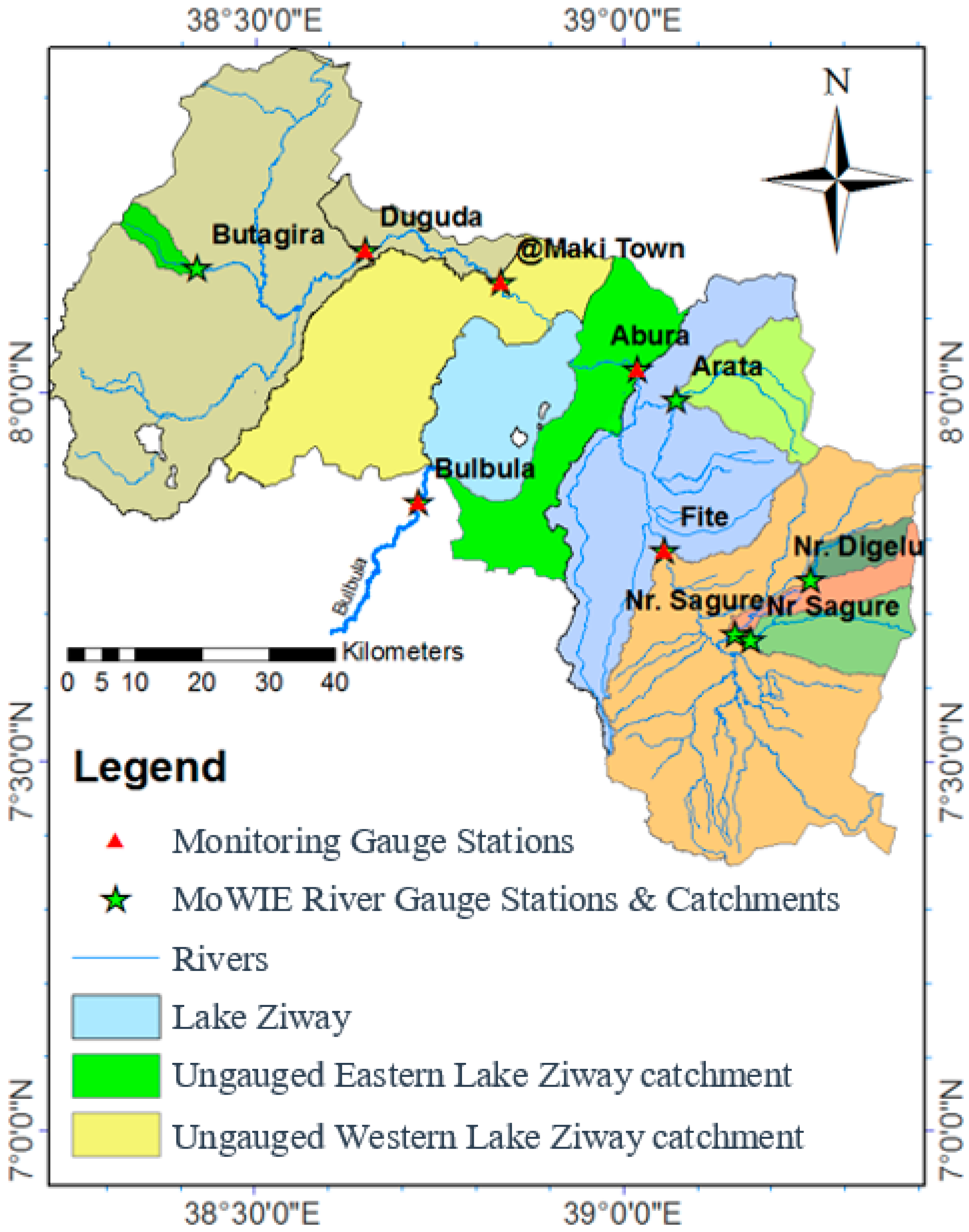
2.3. Hydrology
2.4. Geology, Soil, and Land Use
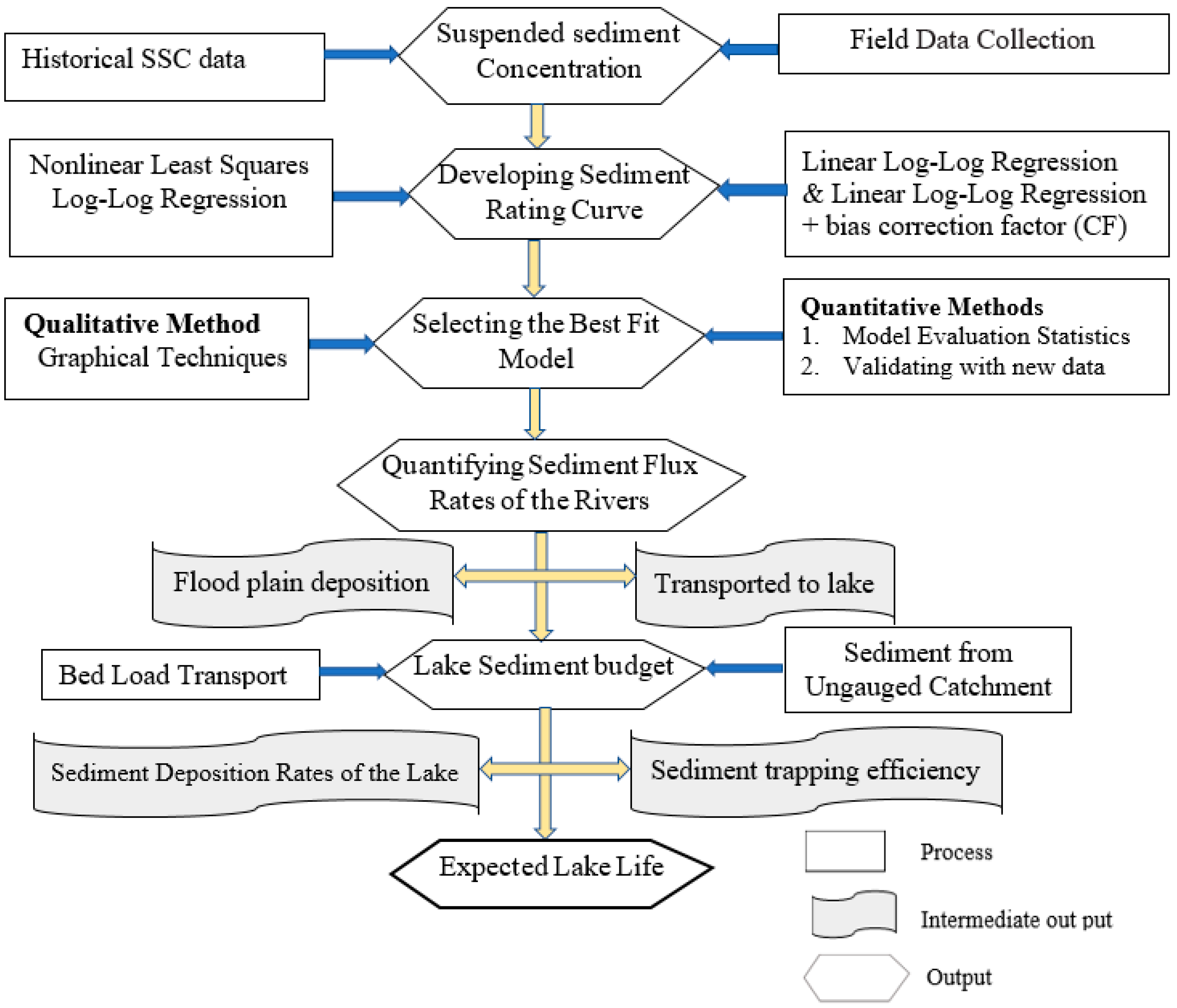
3. Methodology
3.1. Historical Data Collection
3.2. Field Data Collection
3.3. Estimating the Suspended Sediment Yield through Regression Relationship
3.4. Estimating the Sediment Deposition on Rivers Floodplains
3.5. Application of the Regression Relationships to Ungauged Watersheds
3.6. Sediment Trap Efficiency of Lake Ziway
3.7. Bedload Estimation
3.8. Sediment Balances of Lake Ziway
3.9. Sediment Volume and Lake SedimentTrapping Efficiency
4. Result and Discussion
4.1. Suspended Sediment Discharge from Gauged Catchments
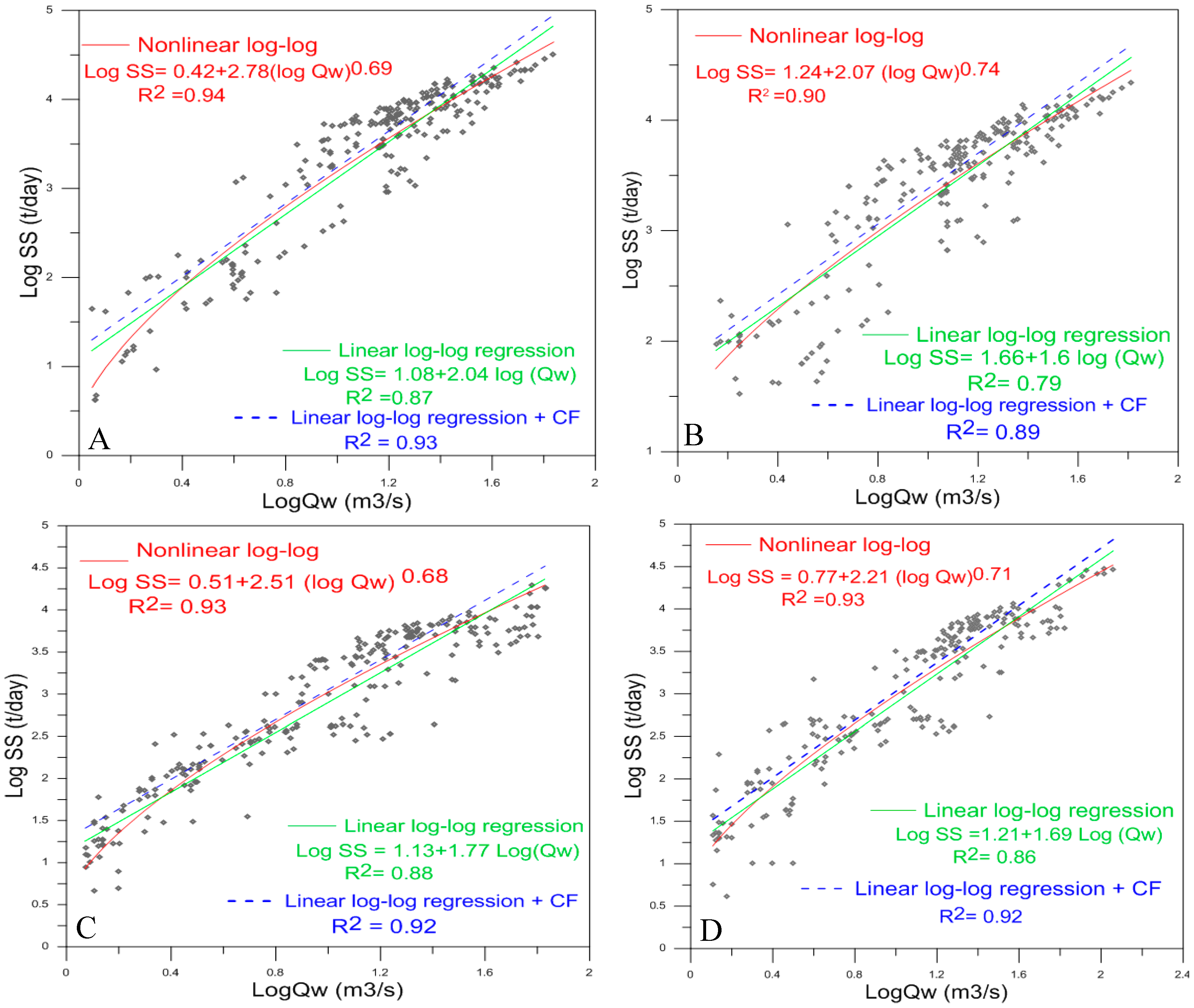
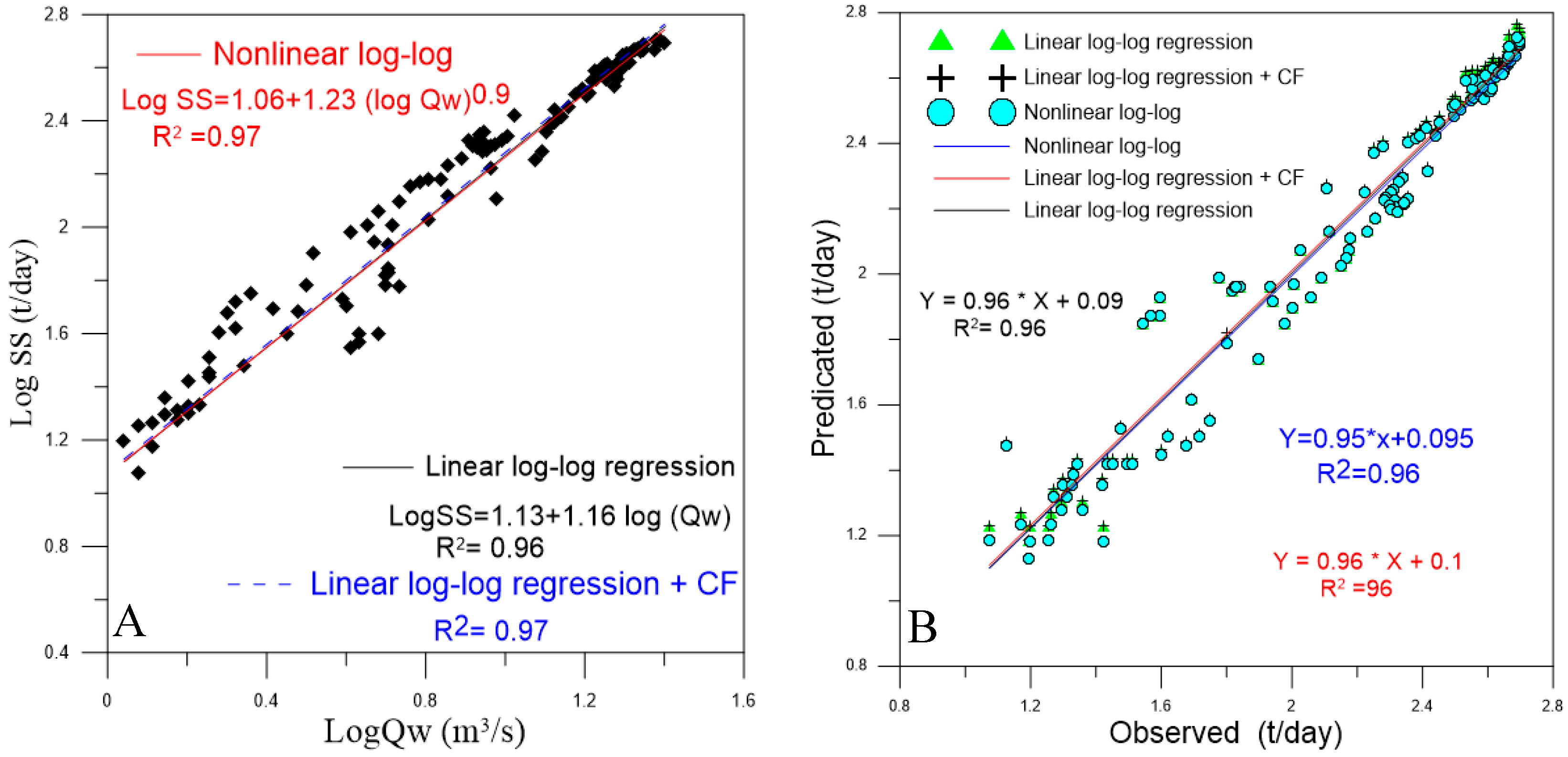
4.1.1. Sediment Rating Curve Development
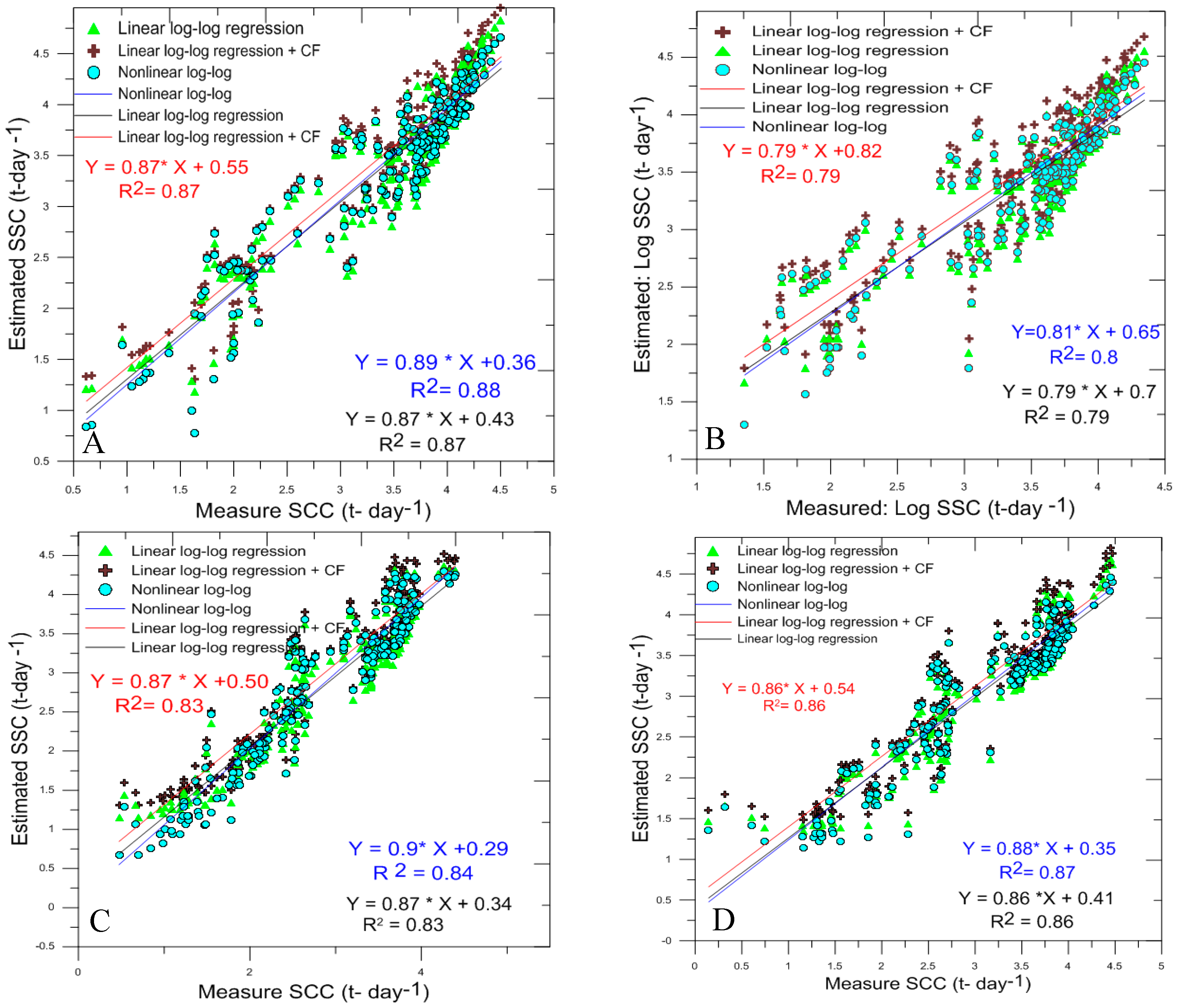
4.1.2. Predicted Sediment Concentrations in Each Monitoring Station
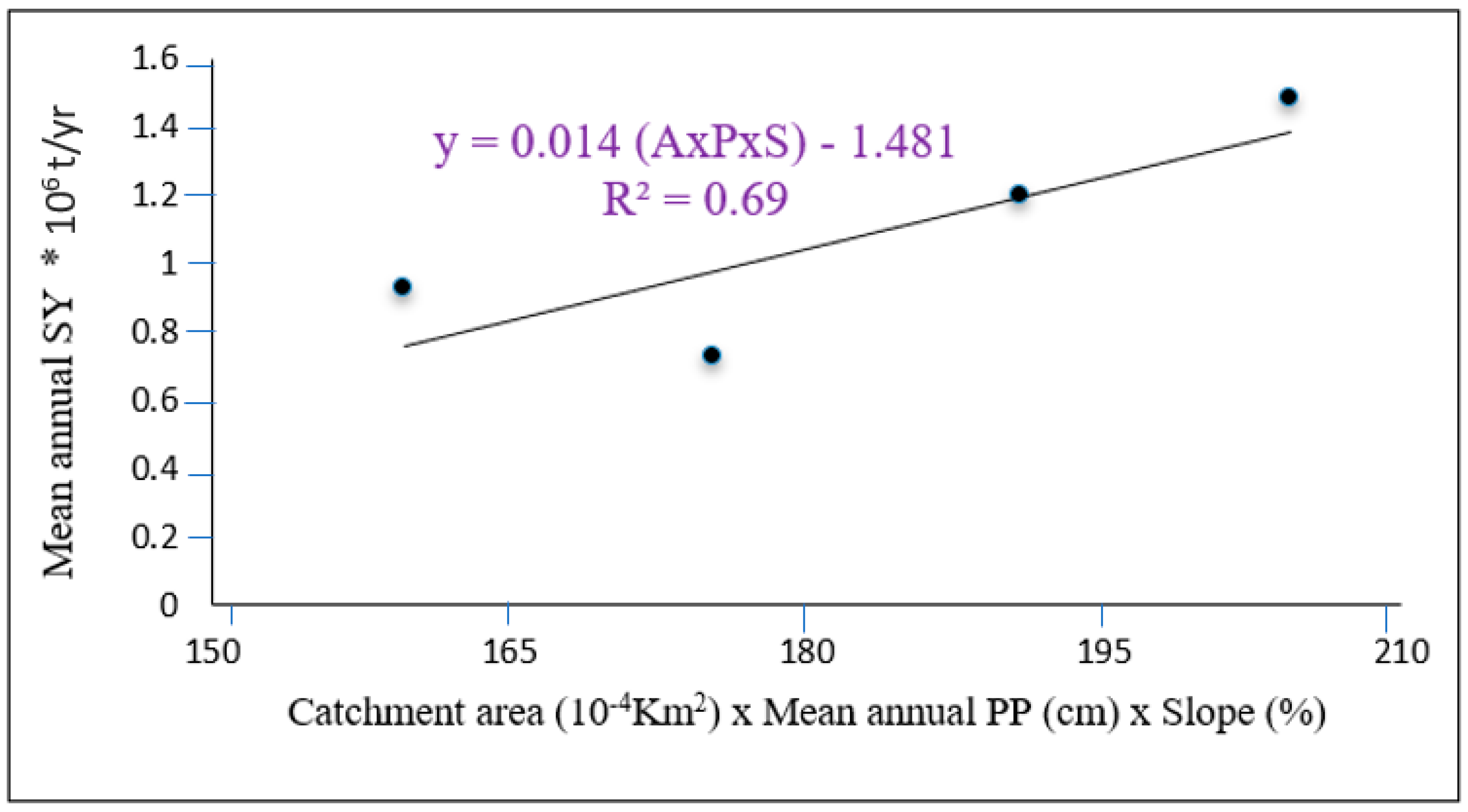
4.2. Suspended Sediment Discharge from the Ungauged Streams
4.3. Suspended Sediment Deposited in Floodplains
4.4. Estimated Bedload
4.5. Suspended Sediment Exported Out of Lake
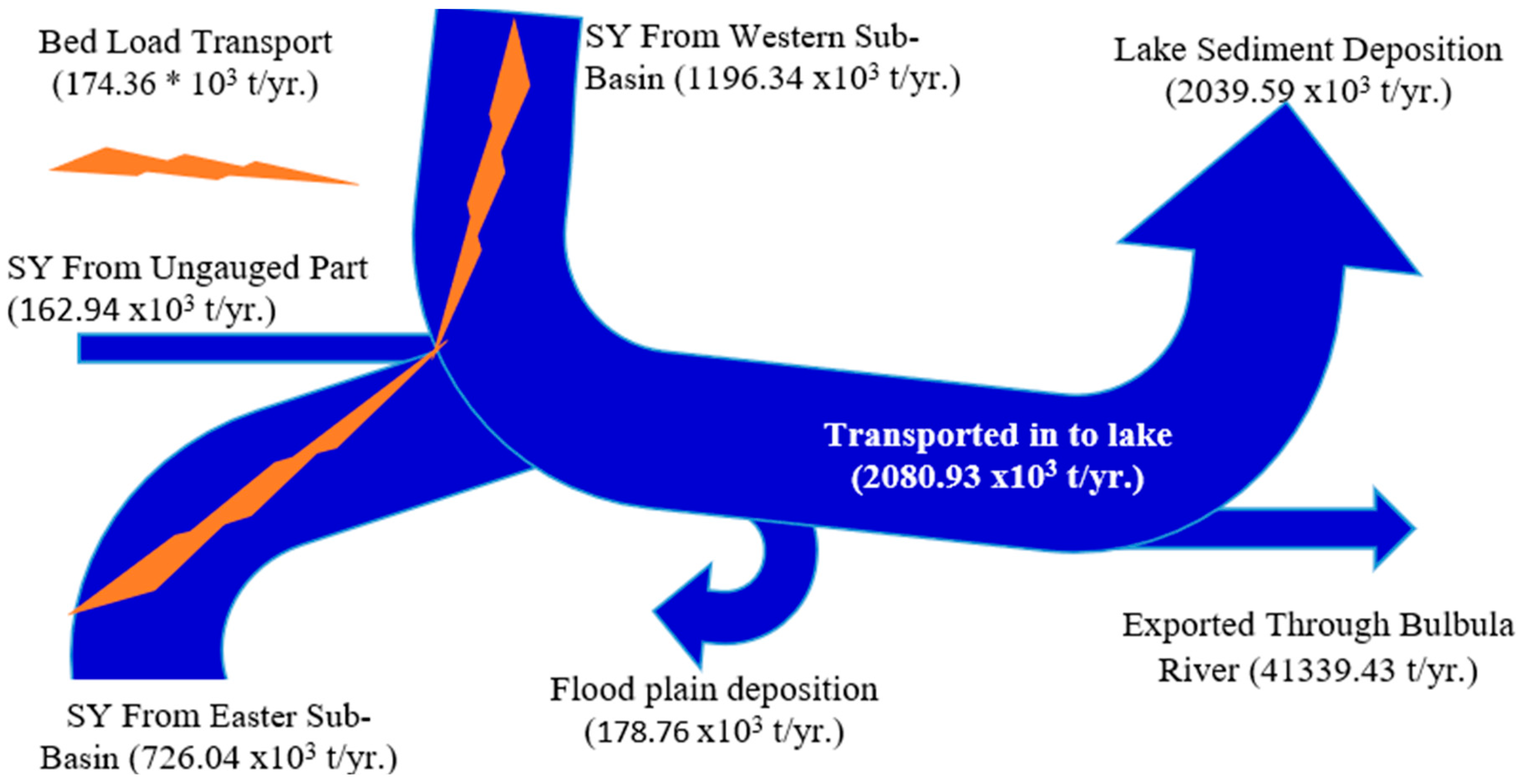
4.6. Sediment Budget and Deposition Rates of the Lake
4.7. Uncertainties in Sediment Budget Calculation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abdallah, M.; Stamm, J. Evaluation of Sudanese Eastern Nile Reservoirs Sedimentation. Dresdner Wasserbaukolloquium 2012, 35, 285–297. [Google Scholar]
- Asselman, N.E.M. Fitting and Interpretation of Sediment Rating Curves. J. Hydrol. 2000, 234, 228–248. [Google Scholar] [CrossRef]
- Wisser, D.; Frolking, S.; Hagen, S.; Bierkens, M.F.P. Beyond peak reservoir storage? A global estimate of declining water storage capacity in large reservoirs. Water Resour. Res. 2013, 49, 5732–5739. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.M.; Jang, T.I.; Kang, M.S.; Im, S.J.; Park, S.W. GIS-based lake sediment budget estimation taking into consideration land use change in an urbanizing catchment area. Environ. Earth Sci. 2014, 71, 2155–2165. [Google Scholar] [CrossRef]
- Walling, D.E.; Collins, A.L. The catchment sediment budget as a management tool. Environ. Sci. Policy 2008, 11, 136–143. [Google Scholar] [CrossRef]
- Hajigholizadeh, M.; Melesse, A.M.; Fuentes, H. Erosion and Sediment Transport Modelling in Shallow Waters: A Review on Approaches, Models and Applications. Int. J. Environ. Res. Public Health 2018, 15, 518. [Google Scholar] [CrossRef] [PubMed]
- Osore, A.; Moges, A. Extent of Gully Erosion and Farmer’s Perception of Soil Erosion in Alalicha Watershed, Southern Ethiopia. J. Environ. Earth Sci. 2014, 4, 74–81. [Google Scholar]
- Sadeghi, S.H.; Saeidi, P. Reliability of sediment rating curves for a deciduous forest watershed in Iran. Hydrol. Sci. J. 2010, 55, 821–831. [Google Scholar] [CrossRef] [Green Version]
- Mhiret, D.; Ayana, E.; S Legesse, E.; Moges, M.; Tilahun, S.; Moges, M. Estimating reservoir sedimentation using bathymetric differencing and hydrologic modeling in data scarce Koga watershed, Upper Blue Nile, Ethiopia. J. Agric. Environ. Int. Dev. 2016, 110, 413–427. [Google Scholar] [CrossRef]
- Defersha, M.B.; Melesse, A.M. Effect of rainfall intensity, slope and antecedent moisture content on sediment concentration and sediment enrichment ratio. CATENA 2012, 90, 47–52. [Google Scholar] [CrossRef]
- Mekonnen, M.; Melesse, A.M. Soil Erosion Mapping and Hotspot Area Identification Using GIS and Remote Sensing in Northwest Ethiopian Highlands, Near Lake Tana. In Nile River Basin; Springer: Dordrecht, The Netherlands, 2011; pp. 207–224. ISBN 978-94-007-0688-0. [Google Scholar]
- Maalim, F.K.; Melesse, A.M. Modelling the impacts of subsurface drainage on surface runoff and sediment yield in the Le Sueur Watershed, Minnesota, USA. Hydrol. Sci. J. 2013, 58, 570–586. [Google Scholar] [CrossRef] [Green Version]
- Melesse, A.M.; Ahmad, S.; McClain, M.E.; Wang, X.; Lim, Y.H. Suspended sediment load prediction of river systems: An artificial neural network approach. Agric. Water Manag. 2011, 98, 855–866. [Google Scholar] [CrossRef]
- Setegn, S.; Dargahi, B.; Srinivasan, R.; Melesse, A.M. Modeling of Sediment Yield from Anjeni-Gauged Watershed, Ethiopia Using SWAT Model1. J. Am. Water Resour. Assoc. 2010, 46, 514–526. [Google Scholar] [CrossRef]
- Abtew, W.; Melesse, A.M. Landscape Changes Impact on Regional Hydrology and Climate. In Landscape Dynamics, Soils and Hydrological Processes in Varied Climates; Springer Geography; Springer: Cham, Switzerland, 2016; pp. 31–50. ISBN 978-3-319-18786-0. [Google Scholar]
- Anwar, A.A.; Seifu, A.T.; Essayas, K.A.; Abeyou, W.W.; Tewodros, T.A.; Shimelis, B.D.; Melesse, A.M. Climate Change Impact on Sediment Yield in the Upper Gilgel Abay Catchment, BlueNile Basin, Ethiopia. In Landscape Dynamics, Soils and Hydrological Processes in Varied Climates; Springer International Publishing: Cham, Switzerland, 2015; Volume 7, pp. 615–644. [Google Scholar]
- Defersha, M.B.; Quraishi, S.; Melesse, A.M. Interrill erosion, runoff and sediment size distribution as affected by slope steepness and antecedent moisture content. Hydrol. Earth Syst. Sci. Discuss. 2010, 7, 6447–6489. [Google Scholar] [CrossRef]
- Dessu, S.; Melesse, A.M. Modelling the rainfall–runoff process ofthe Mara River basin using the soil and water assessment tool. Hydrol. Process. 2012, 26, 4038–4049. [Google Scholar] [CrossRef]
- Dessu, S.; Melesse, A.M.; Bhat, M.; McClain, M.E. Assessment of water resources availability and demand in the Mara River basin. CATENA 2014, 115, 104–114. [Google Scholar] [CrossRef]
- Grey, O.; St, F.; Webber, D.; Setegn, S.; Melesse, A.M. Application of the soil and water assessment tool (SWAT model) on a small tropical island (Great River watershed, Jamaica) as a tool in integrated watershed and coastal zone management. Int. J. Trop. Biol. Conserv. 2014, 62, 293–305. [Google Scholar]
- Melesse, A.M.; Graham, W.D.; Jordan, J.D. Spatially Distributed Watershed Mapping and Modeling: GIS-based Storm Runoff and Hydrograph Analysis: (part 2). J. Spat. Hydrol. 2003, 3, 2–28. [Google Scholar]
- Wang, X.; Garza, J.; Whitney, M.; Melesse, A.; Yang, W. Prediction of Sediment Source Areas within Watersheds as Affected by Soil Data Resolution, In: Environmental Modelling; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2008; pp. 151–185. [Google Scholar]
- Setegn, S.G.; Srinivasan, R.; Dargahi, B.; Melesse, A.M. Spatial delineation of soil erosion vulnerability in the Lake Tana Basin, Ethiopia. Hydrol. Process. 2009, 23, 3738–3750. [Google Scholar] [CrossRef]
- Msaghaa, J.J.; Melesse, A.M.; Ndomba, P.M. Modeling Sediment Dynamics: Effect of Land Use, Topography, and Land Management in the Wami-Ruvu Basin, Tanzania. In Nile River Basin; Springer: Cham, Switzerland, 2014; pp. 165–192. ISBN 978-3-319-02719-7. [Google Scholar]
- De Vente, J.; Poesen, J.; Verstraeten, G.; Govers, G.; Vanmaercke, M.; Van Rompaey, A.; Arabkhedri, M.; Boix-Fayos, C. Predicting soil erosion and sediment yield at regional scales: Where do we stand? Earth-Sci. Rev. 2013, 127, 16–29. [Google Scholar] [CrossRef]
- Tilahun, S.A.; Guzman, C.D.; Zegeye, A.D.; Ayana, E.K.; Collick, A.S.; Yitaferu, B.; Steenhuis, T.S. Spatial and Temporal Patterns of Soil Erosion in the Semi-humid Ethiopian Highlands: A Case Study of Debre Mawi Watershed. In Nile River Basin; Springer: Cham, Swizterland, 2014; pp. 149–163. ISBN 978-3-319-02719-7. [Google Scholar]
- Yesuf, H.; Alamirew, T.; Melesse, A.M.; Assen, M. Bathymetric Mapping for Lake Hardibo in Northeast Ethiopia Using Sonar. Int. J. Water Sci. 2012, 1, 1–9. [Google Scholar] [CrossRef]
- Yesuf, H.; Alamirew, T.; Melesse, A.M.; Assen, M. Bathymetric study of Lake Hayq, Ethiopia. Lakes Reserv. Res. Manag. 2013, 18, 155–165. [Google Scholar] [CrossRef]
- Moges, M.M.; Abay, D.; Engidayehu, H. Investigating reservoir sedimentation and its implications to watershed sediment yield: The case of two small dams in data-scarce upper Blue Nile Basin, Ethiopia. Lakes Reserv. Sci. Policy Manag. Sustain. Use 2018, 23, 217–229. [Google Scholar] [CrossRef]
- Wischmeir, W.H. Predicting Rainfall-erosion Losses from Cropland East of the Rocky Mountain, Guide for Selection of Practices for Soil and Water Conservation. Agric. Handb. 1965, 282, 47. [Google Scholar]
- Steenhuis, S.; Collick, S.; Easton, M.; Leggesse, S.; Bayabil, K.; White, E.D.; Awulachew, S.B.; Adgo, E.; Ahmed, A.A. Predicting discharge and sediment for the Abay (Blue Nile) with a simple model. Hydrol. Process. 2009, 23, 3728–3737. [Google Scholar] [CrossRef]
- Syvitski, J.P.; Morehead, M.D.; Bahr, D.B.; Mulder, T. Estimating fluvial sediment transport: The rating parameters. Water Resour. Res. 2000, 36, 2747–2760. [Google Scholar] [CrossRef] [Green Version]
- Warrick, J.A. Trend analyses with river sediment rating curves. Hydrol. Process. 2015, 29, 936–949. [Google Scholar] [CrossRef]
- Bordbar, A.; Fuladipanah, M. Sediment Rating Curve Modification (Case Study: Marun Dam, Behbahan, Iran). Indian J. Fundam. Appl. Life Sci. 2014, 4, 2345–2351. [Google Scholar]
- Lee, J.-S.; Kim, C.-G.; You, E.-G. Derivation Method of Rating Curve and Relationships for Flow Discharge-Total Sediment at Small-Midium Streams in Agrarian Basin. J. Korea Contents Assoc. 2015, 15, 544–555. [Google Scholar] [CrossRef]
- Costa, A.; Anghileri, D.; Molnar, P. A Process–Based Rating Curve to model suspended sediment concentration in Alpine environments. Hydrol. Earth Syst. Sci. Discuss. 2017, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Moges, M.A.; Zemale, F.A.; Alemu, M.L.; Ayele, G.K.; Dagnew, D.C.; Tilahun, S.A.; Steenhuis, T.S. Sediment concentration rating curves for a monsoonal climate: Upper Blue Nile Basin. SOIL Discuss. 2015, 2, 1419–1448. [Google Scholar] [CrossRef]
- Lemma, H.; Admasu, T.; Dessie, M.; Fentie, D.; Deckers, J.; Frankl, A.; Poesen, J.; Adgo, E.; Nyssen, J. Revisiting lake sediment budgets: How the calculation of lake lifetime is strongly data and method dependent. Earth Surf. Process. Landf. 2017, 43, 593–607. [Google Scholar] [CrossRef]
- Ayele, G.T.; Teshale, E.Z.; Yu, B.; Rutherfurd, I.D.; Jeong, J. Streamflow and Sediment Yield Prediction for Watershed Prioritization in the Upper Blue Nile River Basin, Ethiopia. Water 2017, 9, 782. [Google Scholar] [CrossRef]
- Yesuf, H.M.; Assen, M.; Alamirew, T.; Melesse, A.M. Modeling of sediment yield in Maybar gauged watershed using SWAT; northeast Ethiopia. CATENA 2015, 127, 191–205. [Google Scholar] [CrossRef]
- Setegn, S.G.; Srinivasan, R.; Melesse, A.M.; Dargahi, B. SWAT model application and prediction uncertainty analysis in the Lake Tana Basin, Ethiopia. Hydrol. Process. 2010, 24, 357–367. [Google Scholar] [CrossRef]
- Aga, A.O.; Chane, B.; Melesse, A.M. Soil Erosion Modelling and Risk Assessment in Data Scarce Rift Valley Lake Regions, Ethiopia. Water 2018, 10, 1684. [Google Scholar] [CrossRef]
- Demissie, M.; Renjie, X.; Laura, K.; Nani, B. The Sediment Budget of the Illinois River; Report for Illinois State Water Survey—2204; Griffith Drive: Champaign, IL, USA, 2004; pp. 1–59. [Google Scholar]
- Achitea, M.; Ouillon, S. Suspended sediment transport in a semiarid watershed, Wadi Abd, Algeria (1973–1995). J. Hydrol. 2007, 343, 187–202. [Google Scholar] [CrossRef]
- Ferguson, R.I. River Loads Underestimated by Rating Curves. Water Resour. Res. 1986, 22, 74–76. [Google Scholar] [CrossRef]
- Harrington, S.T.; Harrington, J.R. An assessment of the suspended sediment rating curve approach for load estimation on the Rivers Bandon and Owenabue, Ireland. Geomorphology 2013, 185, 27–38. [Google Scholar] [CrossRef]
- MOWR The Federal Democratic Republic of Ethiopia-Ministry of Water Resources. Rift Valley Lakes Basin Integrated Resources Development Master Plan Study Project. Part 1 and 2, Halcrow Group Limited and Generation Integrated Rural Development Consultants; Unpublished Document; MOWR The Federal Democratic Republic of Ethiopia-Ministry of Water Resources: Addis Ababa, Ethiopia, 2010.
- Legesse, D. Analysis of the Hydrological Response of the Ziway–Shala Lake Basin (Main Ethiopian Rift) to Changes in Climate and Human Activities. Ph.D. Thesis, Univ. d’Aix-Marseille III, Aix-en-Provenece, France, 2002. [Google Scholar]
- Ayenew, T. The Hydrogeological System of the Lake District basin. Central Main Ethiopian Rift. Ph.D. Thesis, Free University of Amsterdam, Amsterdam, The Netherlands, 1998. [Google Scholar]
- Makin, M.J.; Kingham, T.J.; Waddams, A.E.; Birchall, C.J.; Eavis, B.W. Prospects for irrigation development around Lake Zwai, Ethiopia. In Land Resource Study; Land Resources Division, Ministry of Overseas Development: Surbiton, UK, 1976. [Google Scholar]
- Edwards, T.; Glysson, G. Field Methods for Measurement of Fluvial Sediment; Open File Report 86-531; U.S. Geological Survey: Reston, VA, USA, 1988; pp. 1–132.
- ASTM (American Society of Testing and Materials). Standard Methods for Determining Sediment Concentrations in Water Samples; D 3977-97; American Society of Testing and Materials (ASTM): West Conshohocken, PA, USA, 2007; Volume 11.02. [Google Scholar]
- Ongley, E.D.; Nations, F.; A.O. of the U. Control of Water Pollution from Agriculture; Food & Agriculture Org.: Rome, Italy, 1996; ISBN 978-92-5-103875-8. [Google Scholar]
- Zhang, K.; Zhang, W.; Li, J.; Shi, Z.; Pu, S. Relation between precipitation and sediment transport in the Dasha River Watershed. Chin. Geogr. Sci. 2004, 14, 129–134. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Liew, M.W.V.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- EFDR RVLA. The Federal Democratic Republic of Ethiopia—Rift Valley Lakes Basin Authorty: Lake Ziway Basin Integrated Watershed Management Feasibility Study; EFDR RVLA: Hawassa, Ethiopia, 2016.
- Walling, D.; Collins, A.L.; Sichingabula, H.M.; Leeks, G.J.L. Integrated assessment of catchment suspended sediment budgets: A Zambian example. Land Degrad. Dev. 2001, 12, 387–415. [Google Scholar] [CrossRef]
- Delmas, M.; Cerdan, O.; Cheviron, B.; Mouchel, J.-M.; Eyrolle, F. Sediment export from French rivers to the sea. Earth Surf. Process. Landf. 2012, 37, 754–762. [Google Scholar] [CrossRef]
- Engida, A. Hydrological and Suspended Sediment Modeling in the Lake Tana Basin, Ethiopia. Ph.D. Thesis, University of Grenoble, Saint-Martin-d’Hères, France, 2010. [Google Scholar]
- Vanmaercke, M.; Poesen, J.; Broeckx, J.; Nyssen, J. Sediment yield in Africa. Earth-Sci. Rev. 2014, 136, 350–368. [Google Scholar] [CrossRef] [Green Version]
- Church, M. Bed Material Transport and the Morphology of Alluvial River Channels. Annu. Rev. Earth Planet. Sci. 2006, 34, 325–354. [Google Scholar] [CrossRef]
- Sitaula, B.; Garde, M.; Burbank, D.W.; Oskin, M.; Heimsath, A.; Gabet, E. Bedload-to-suspended load ratio and rapid bedrock incision from Himalayan Landslide-dam lake record. Quat. Res. 2007, 68, 111–120. [Google Scholar] [CrossRef]
- Nyssen, J.; Poesen, J.; Moeyersons, J.; Haile, M.; Deckers, J. Dynamics of soil erosion rates and controlling factors in the Northern Ethiopian Highlands—Towards a sediment budget. Earth Surf. Process. Landf. 2008, 33, 695–711. [Google Scholar] [CrossRef]
- Zenebe, A.; Vanmaercke, M.; Poesen, J.; Verstraeten, G.; Haregeweyn, N.; Haile, M.; Amare, K.; Deckers, J.; Nyssen, J. Spatial and temporal variability of river flows in the degraded semi-arid tropical mountains of northern Ethiopia. Z. Geomorphol. 2013, 57, 143–169. [Google Scholar] [CrossRef]
- Ali, Y.; Crosato, A.; Mohamed, Y.; Abdalla, S.; Wright, N. Sediment balances in the Blue Nile River Basin. Int. J. Sedim. Res. 2014, 29, 316–328. [Google Scholar] [CrossRef]
- Lahlou, A. The Silting of Morocaan Dams. In Sediment Budgets: Proceedings of the Symposium, Porto Alegre, Brazil, 11–15 December 1988; Bordas, M.P., Walling, D.E., Eds.; IAHS: Wallingford, UK, 1988; pp. 71–77. [Google Scholar]
- Tamene, L.; Park, S.J.; Dikau, R.; Vlek, P.L.G. Reservoir siltation in the semi-arid highlands of northern Ethiopia: Sediment yield–catchment area relationship and a semi-quantitative approach for predicting sediment yield. Earth Surf. Process. Landf. 2006, 31, 1364–1383. [Google Scholar] [CrossRef]
- Nyssen, J.; Poesen, J.; Moeyersons, J.; Deckers, J.; Haile, M.; Lang, A. Human impact on the environment in the Ethiopian and Eritrean highlands—A state of the art. Earth-Sci. Rev. 2004, 64, 273–320. [Google Scholar] [CrossRef]
- Walling, D.; Horowitz, A. Sediment Budgets: Proccedings of Symposium Held during the Seventh IAHS Scientific Assembly at Foz do Ignaçu, Brazil; IAHS Publ.: Wallingford, UK, 2005; Volume 291. [Google Scholar]
- Belete, M. The Impact of Sedimentation and Climate Variability on the Hydrological Status of Lake Hawassa, South Ethiopia. Ph.D. Thesis, Universität Bonn, Bonn, Germany, 2013. [Google Scholar]
- Rupasingha, R.A. Use of GIS and RS for Assessing Lake Sedimentation Processes. Case Study for Naivasha Lake, Kenya. Master’s Thesis, International Institute for Geo-Information Science and Earth Observation Enschede, Enschede, The Netherlands, 2002. [Google Scholar]
- Zimale, F.A.; Mogus, M.A.; Alemu, M.L.; Ayana, E.K.; Demissie, S.S.; Tilahun, S.A.; Steenhuis, T.S. Calculating the sediment budget of a tropical lake in the Blue Nile basin: Lake Tana. SOIL Discuss. 2016, 1–32. [Google Scholar] [CrossRef] [Green Version]
- Douglas, B.; Michael, S.; Stephen, P. Sea level rise: History and consequences. Int. Geophys. 2001, 75, 1–232. [Google Scholar]

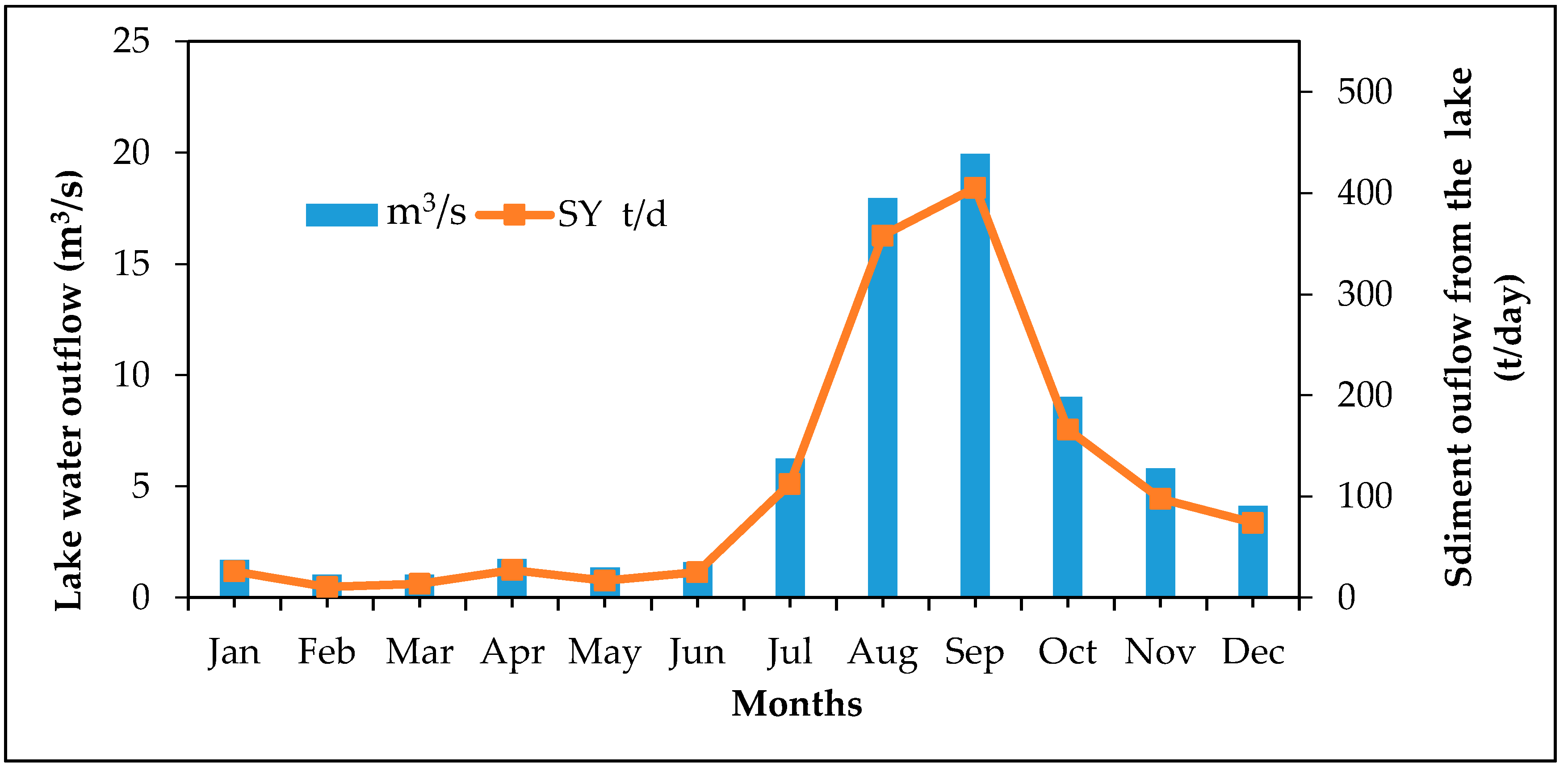
| Statistics | Performance Rating | ||||
|---|---|---|---|---|---|
| Excellent | Very Good | Good | Fair | Unsatisfactory | |
| (0.9–1) | (0.75–0.9) | (0.65–0.75) | (0.5–0.65) | (0–0.5) | |
| (0.9–1) | (0.75–0.9) | 0.65–0.75) | (0.5–0.65) | (−∞–0.5) | |
| (0–0.25) | (0.25–0.5) | (0.5–0.6) | (0.6–0.7) | (0.7–+∞) | |
| (0–0.25) | (0.25–0.5) | (0.5–0.6) | (0.6–0.7) | (0.7–+∞) | |
| (0–±5) | (±5–±15) | (±15–±30) | (±30–±55) | (±55–±∞) | |
| Rating Curve | Stations | |||||
|---|---|---|---|---|---|---|
| Maki | Duguda | Abura | Fite | Bulbula | ||
| Linear log-log Regression Log (SS) = a + b * log (Qw) | R2 | 0.79 | 0.87 | 0.88 | 0.86 | 0.96 |
| NSE | 0.79 | 0.87 | 0.85 | 0.86 | 0.96 | |
| RSR | 0.46 | 0.36 | 0.38 | 0.37 | 0.21 | |
| PBIAS | 0.23 | 0.15 | 0.74 | 0.29 | −0.03 | |
| RMSE | 0.33 | 0.32 | 0.35 | 0.34 | 0.08 | |
| Linear log-log Regression + CF Log (SS) = a + b * log (Qw) + CF | CF | 0.1 | 0.12 | 0.15 | 0.13 | 0.01 |
| R2 | 0.89 | 0.93 | 0.92 | 0.92 | 0.97 | |
| NSE | 0.77 | 0.86 | 0.83 | 0.85 | 0.96 | |
| RSR | 0.48 | 0.38 | 0.41 | 0.39 | 0.21 | |
| PBIAS | −3.33 | −3.42 | −4.23 | −4.06 | −0.49 | |
| RMSE | 0.35 | 0.34 | 0.37 | 0.36 | 0.08 | |
| Non-Linear log-log Regression Log (SS) = a + b * (log Qw)c | R2 | 0.90 | 0.94 | 0.93 | 0.93 | 0.97 |
| NSE | 0.80 | 0.88 | 0.87 | 0.87 | 0.96 | |
| RSR | 0.45 | 0.34 | 0.36 | 0.36 | 0.21 | |
| PBIAS | 0.02 | 0.06 | −0.61 | 0.28 | 0.38 | |
| RMSE | 0.32 | 0.31 | 0.33 | 0.33 | 0.08 | |
| River | Monitoring Station | Annual Sediment Yield (SY) in 103 Tons |
|---|---|---|
| Katar (Upper monitoring station) | Fite | 928.58 |
| Katar (Lower monitoring station) | Abura | 726.04 |
| Maki (Upper monitoring station) | Duguda | 1480.45 |
| Maki (Lower monitoring station) | Maki | 1196.34 |
| Main River (1) | Monitoring Station | SSC 103 ton/year | River Length Km | Rate of Floodplain Aggradation per km Length 103 ton/year (8) = ((4) − (5))/(6) | % of Upper Station SSC in Lower Station (9) = 100 × ((4) − (5))/(4) | Net SY into Lake (103 ton/year) (10) = (5) − ((7) × (8)) | |||
|---|---|---|---|---|---|---|---|---|---|
| Upper (2) | Lower (3) | Upper (4) | Lower (5) | Upper to Lower (6) | Lower to Lake (7) | ||||
| Maki | Duguda | Maki | 1480.45 | 1196.34 | 41.56 | 15.39 | 6.84 | 19.2 | 1091.11 |
| Katar | Fite | Abura | 928.58 | 726.04 | 37.46 | 13.60 | 5.41 | 22.0 | 652.51 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aga, A.O.; Melesse, A.M.; Chane, B. Estimating the Sediment Flux and Budget for a Data Limited Rift Valley Lake in Ethiopia. Hydrology 2019, 6, 1. https://doi.org/10.3390/hydrology6010001
Aga AO, Melesse AM, Chane B. Estimating the Sediment Flux and Budget for a Data Limited Rift Valley Lake in Ethiopia. Hydrology. 2019; 6(1):1. https://doi.org/10.3390/hydrology6010001
Chicago/Turabian StyleAga, Alemu O., Assefa M. Melesse, and Bayou Chane. 2019. "Estimating the Sediment Flux and Budget for a Data Limited Rift Valley Lake in Ethiopia" Hydrology 6, no. 1: 1. https://doi.org/10.3390/hydrology6010001
APA StyleAga, A. O., Melesse, A. M., & Chane, B. (2019). Estimating the Sediment Flux and Budget for a Data Limited Rift Valley Lake in Ethiopia. Hydrology, 6(1), 1. https://doi.org/10.3390/hydrology6010001






