2015 Disastrous Floods in Louisiana, USA, and Assam, India: Groundwater Impact on the Water Balance Estimation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Problem of Water Budget Estimation during the Flood
2.2. Overview of the Basic Water Balance Estimation Approach
- Precipitation
- Evaporation
- Soil permeability
- Calculated water mass
- Observed water mass
2.3. Advanced Water Balance Estimation Approach
- Soil permeability
- Region-to-region transfer of water mass (streamflow)
3. Results
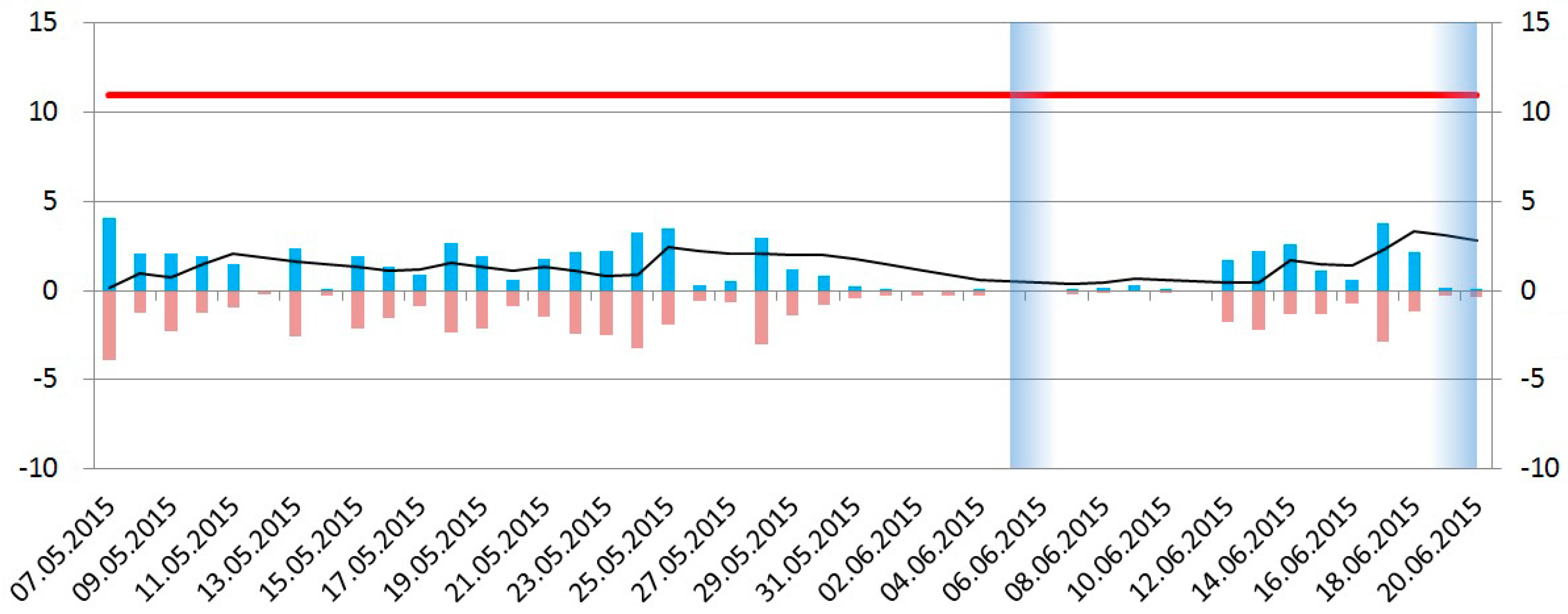
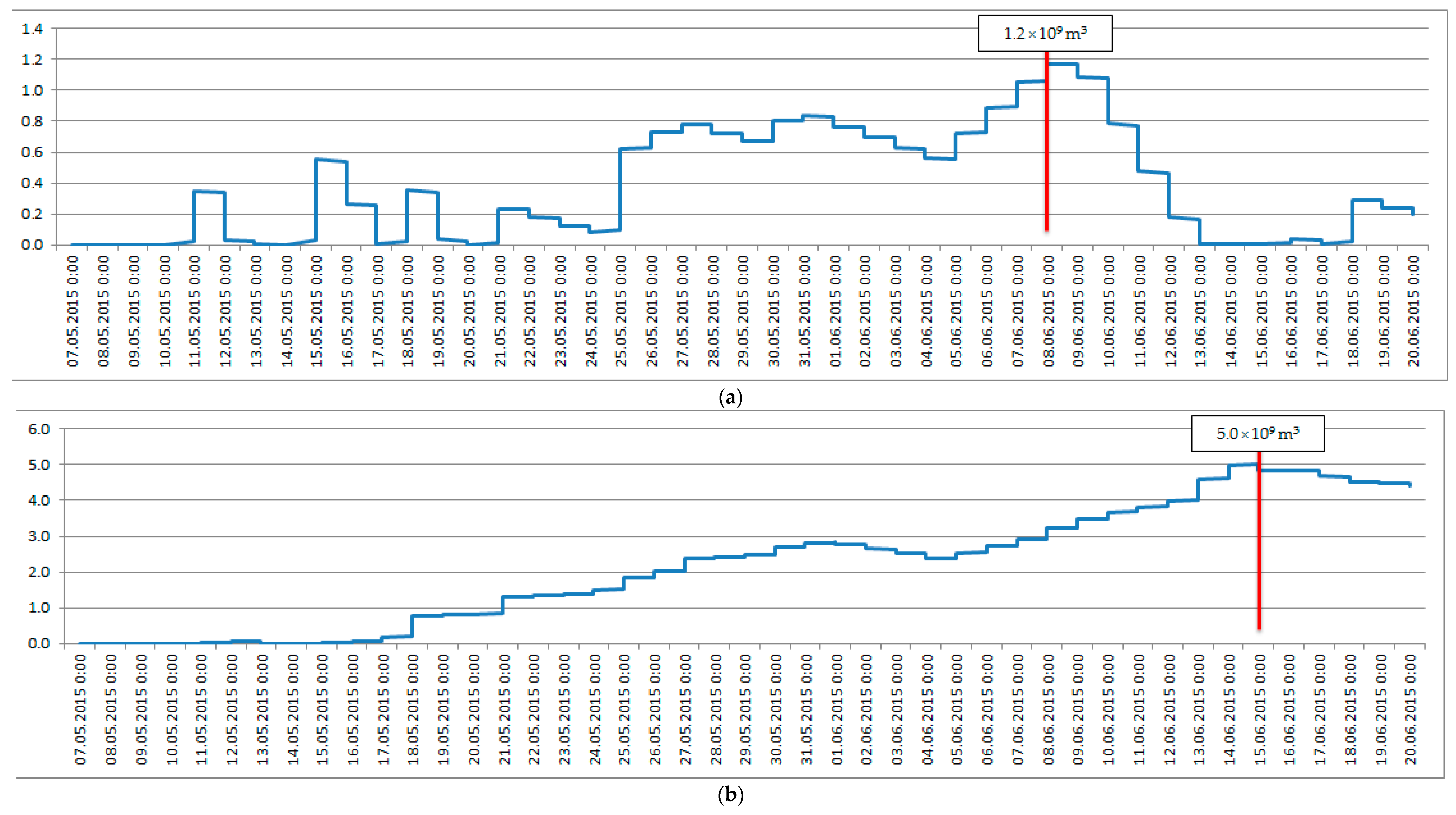
3.1. The Louisiana Flood Analysis
3.2. The Louisiana Flood Advanced Analysis
3.3. The Assam Flood Analysis
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pinneker, E.V.; Howard, D.E.; Harvey, J.C. General Hydrogeology; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Trifonova, T.A.; Tulenev, N.Y.; Trifonov, D.V.; Arakelian, S.M. Surface water, groundwater and unified 3D-crack network as a triple coupling dynamic system for a river watershed functioning—Manifestation in catastrophic floods. In Proceedings of the EGU General Assembly, Vienna, Austria, 27 April–2 May 2014.
- Fleckenstein, J.H.; Krause, S.; Hannah, D.M.; Boano, F. Groundwater-surface water interactions: New methods and models to improve understanding of processes and dynamics. Adv. Water Resour. 2010, 33, 1291–1295. [Google Scholar] [CrossRef]
- Trifonova, T.A.; Trifonov, D.V.; Arakelian, S.M. Catastrophic Floods—Possible Contribution of Groundwater due to Flash Reconstruction of the Rock Mass 3D-Cracknet under Seismic Factors. Mod. Appl. Sci. 2015, 9, 76–86. [Google Scholar] [CrossRef]
- Roeloffs, E.A.; Quilty, E.; Scholtz, C.H. Water level and strain changes preceding and following the August 4, 1985 Kettleman Hills, California, earthquake. Pure Appl. Geophys. 1997, 149, 21–60. [Google Scholar] [CrossRef]
- BGR—Whymap. Available online: http://www.whymap.org/whymap/EN/Home/whymap_node.html (accessed on 7 July 2016).
- Smyth, J.R.; Jacobsen, S.D. Nominally anhydrous minerals and Earth’s deep water cycle. Earth Deep Water Cycle Geophys. Monogr. Ser. 2006, 168. [Google Scholar] [CrossRef]
- Bouwer, H.; Maddock, T. Making sense of the interaction between groundwater and streamflow: Lessons for water masters and adjudicators. Rivers 1997, 6, 19–31. [Google Scholar]
- Carabin, G.; Dassargues, A. Modeling groundwater with ocean and river interaction. Water Resour. Res. 1999, 35, 2347–2358. [Google Scholar] [CrossRef]
- Kurth, A.-M.; Weber, C.; Schirmer, M. How effective is river restoration in re-establishing groundwater—surface water interactions?—A case study. Hydrol. Earth Syst. Sci. 2015, 19, 2663–2672. [Google Scholar] [CrossRef]
- King, A.C.; Raiber, M.; Cendón, D.I.; Cox, M.E.; Hollins, S.E. Identifying flood recharge and inter-aquifer connectivity using multiple isotopes in subtropical Australia. Hydrol. Earth Syst. Sci. 2015, 19, 2315–2335. [Google Scholar] [CrossRef]
- Holden, J. An Introduction to Physical Geography and the Environment; Pearson Education: New York, NY, USA, 2005. [Google Scholar]
- Ward, R.C.; Ward, R.C.; Robinson, M. Principles of Hydrology; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Trifonova, T.A.; Arakelian, S.M. The interconnectedness of surface and groundwater in a single system of river catchment; manifestation of catastrophic events in the conditions of intense rainfall in mountainous areas with sharply dissected mountainous terrain (on mudflow model example). Successes Mod. Sci. 2013, 1, 53–67. [Google Scholar]
- 80 Per Cent of Assam Hit by Flood: ASDMA—Timesofindia-Economictimes. Available online: http://articles.economictimes.indiatimes.com/2015-09-07/news/66297150_1_jia-bharali-goalpara-sonitpur (accessed on 7 July 2016).
- Local Weather from AccuWeather—Superior Accuracy. Available online: http://www.accuweather.com (accessed on 7 July 2016).
- Climate Prediction Center—United States Evaporation Monitoring. Available online: http://www.cpc.ncep.noaa.gov/products/Soilmst_Monitoring/US/US_Evaporation-Monthly.php (accessed on 10 October 2016).
- Evaporation in Average Year—Maps—Evaporation—Evaporation. Available online: http://www.waterandclimatechange.eu/evaporation/average-monthly-1985-1999 (accessed on 7 July 2016).
- Evaporation. Available online: http://nihroorkee.gov.in/rbis/india_information/evaporation.htm (accessed on 7 July 2016).
- FAO/UNESCO Soil Map of the World|FAO|Food and Agriculture Organization of the United Nations. Available online: http://www.fao.org/soils-portal/soil-survey/soil-maps-and-databases/faounesco-soil-map-of-the-world/en/ (accessed on 7 July 2016).
- Kruseman, G.P.; de Ridder, N.A. Analysis and Evaluation of Pumping Test Data, 2nd ed.; International Institute for Land Reclamation and Improvement: Wageningen, The Netherlands, 1994; p. 21. [Google Scholar]
- Google Maps. Available online: https://www.google.com/maps (accessed on 7 July 2016).
- Red River Floods in Louisiana—River at Highest Levels for 70 Years—FloodList. Available online: http://floodlist.com/america/red-river-floods-louisiana-june-2015 (accessed on 7 July 2016).
- Louisiana Topographic Maps by Topo Zone. Available online: http://www.topozone.com/louisiana/ (accessed on 7 July 2016).
- Wu, H.; Adler, R.F.; Tian, Y.; Huffman, G.J.; Li, H.; Wang, J. Real-time global flood estimation using satellite-based precipitation and a coupled land surface and routing model. Water Resour. Res. 2014, 50, 2693–2717. [Google Scholar] [CrossRef]
- Global Flood Monitoring. Available online: http://flood.umd.edu/ (accessed on 10 October 2016).
- USGS Groundwater Daily Data for the Nation. Available online: http://nwis.waterdata.usgs.gov/nwis/dv/?referred_module=gw (accessed on 10 October 2016).
- Alexandru, R.-G.; Vlad, D.; Paisa, M.M. The influence of the pedological factor on the relief dynamics within Săsăuș river catchment. Cinq Cont. 2012, 2, 115–125. [Google Scholar]
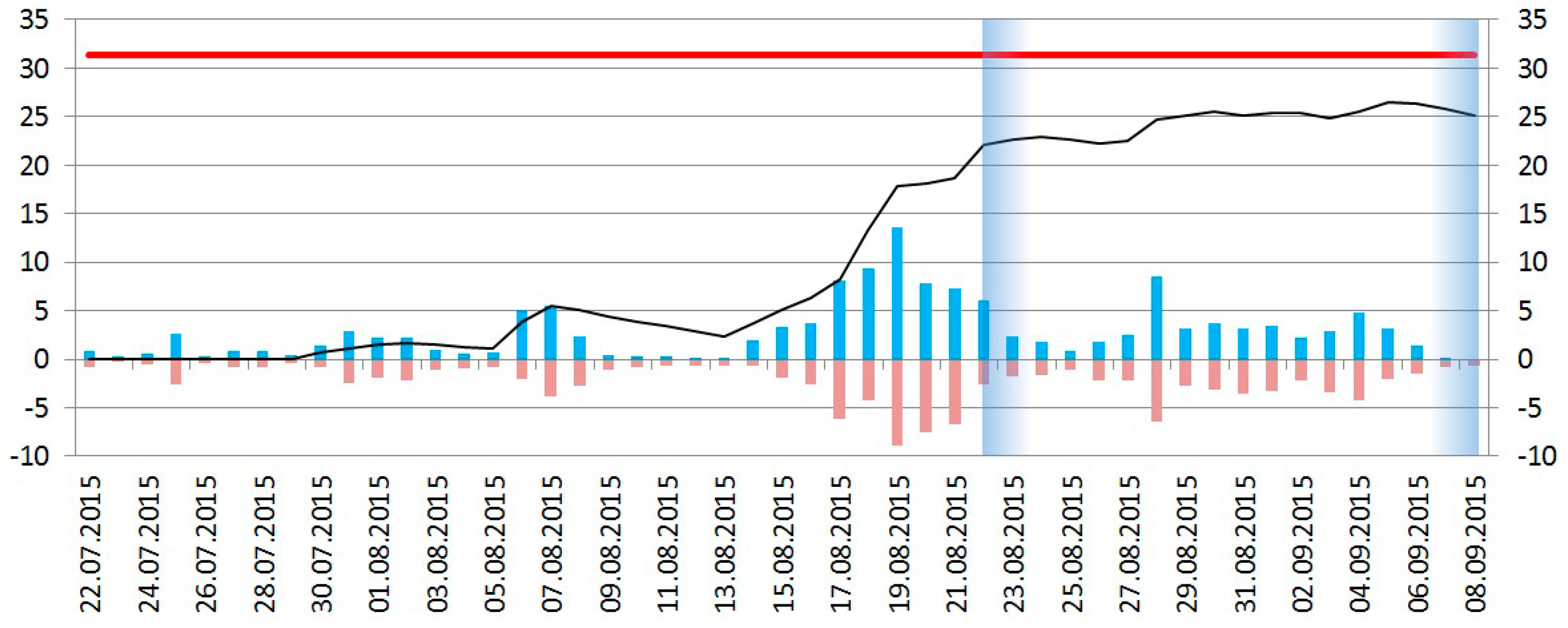
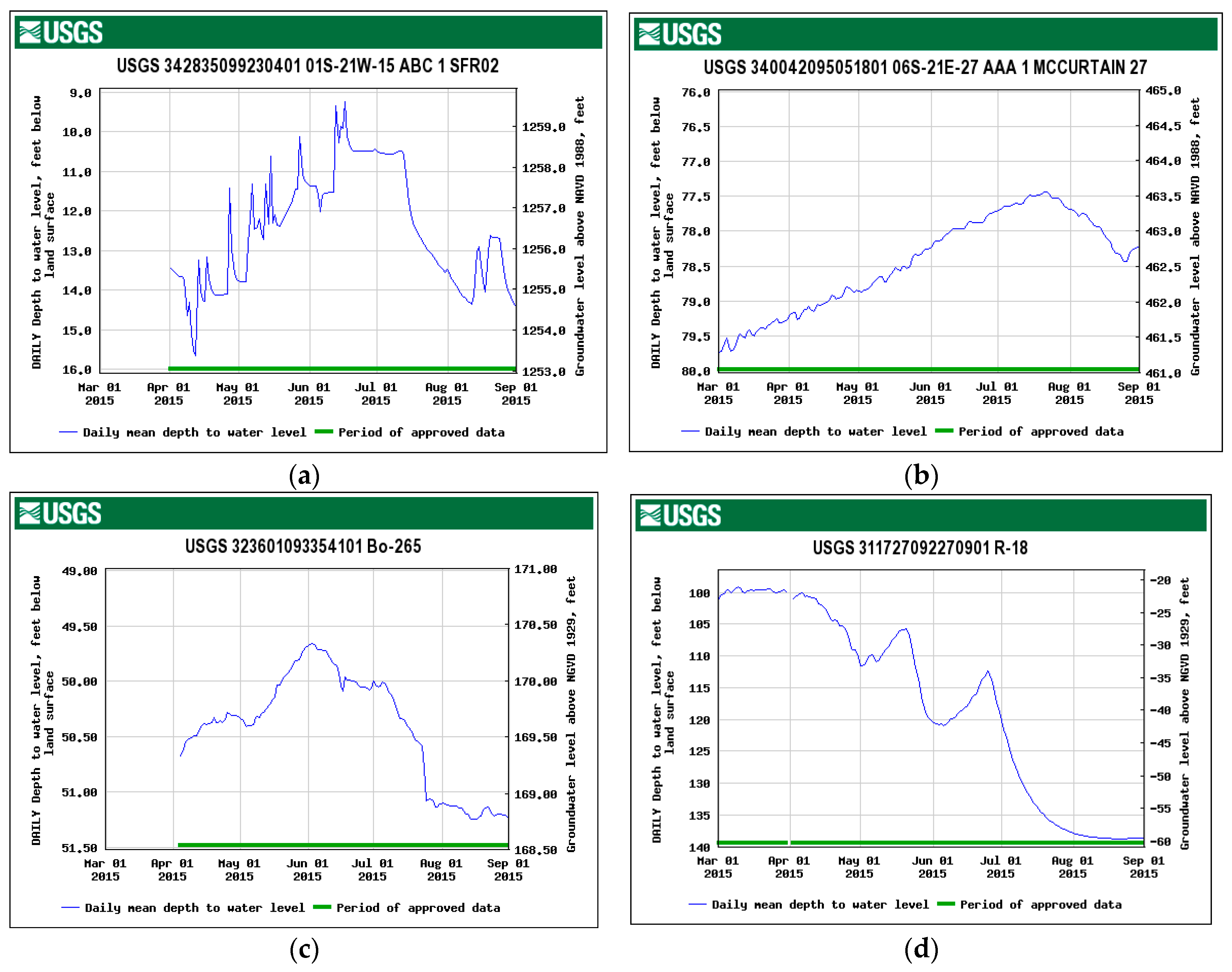
| Argument | Temporal Simplification | Spatial Simplification | Source |
|---|---|---|---|
| precipitation intensity, Pin | exact daily data | precipitation intensity in any relatively large city near the center of a region is extrapolated to a whole region | AccuWeather service [16] |
| evaporation rate, ein | monthly average data | USA states: average evaporation rate of every region is used; China regions: all the regions are considered having the same evaporation rate, characteristic for the riverhead of the Brahmaputra river; India regions: all the regions are considered having the same evaporation rate, mentioned as the evaporation rate of northeast India | USA states: National Oceanic and Atmospheric Administration’s (NOAA) National Weather Service [17]; China regions: Integrated Project Water and Global Change (EU WATCH project) [18]; India regions: National Institute of Hydrology, Roorkee, India [19] |
| soil permeability, pn | no temporal dependence | different soil types of the region surface are distinguished; resulting soil permeability of a region is calculated as weighted average | soil types: Food and Agriculture Organization of the United Nations (FAO)/UNESCO Soil Map of the World [20]; soil permeability: tabular values [21] |
| the area of region, Sn | no temporal dependence | - | Google Maps service [22] |
| Region Name | Area, 103 km2 | Evaporation Rate, mm/Day | Prevailing Soils | Estimated Soil Permeability, mm/Day |
|---|---|---|---|---|
| Amarillo | 24.4 | May: 6.7; June: 8.0 | kastanozems, luvisols | 800.2 |
| Lawton | 34.4 | May: 8.2; June: 10.5 | kastanozems, luvisols, cambisols | 900.1 |
| Sherman | 33.3 | May: 5.9; June: 8.7 | acrisols, cambisols, phaeozems, luvisols, kastanozems | 1450.1 |
| Camden | 35.5 | May: 5.0; June: 5.7 | acrisols, gleysols | 0.1 |
| Shreveport | 16.8 | May: 5.6; June: 6.3 | acrisols, phaeozems, planosols, gleysols | 3000.1 |
| Monroe | 13.1 | May: 5.6; June: 6.3 | acrisols, gleysols, luvisols | 0.7 |
| Alexandria | 12.5 | May: 4.8; June: 5.2 | acrisols, gleysols, phaeozems, luvisols | 500.2 |
| Affected City | Flood Stage, m | Red River Level on 11.06.2015, m | Estimated Observed Water Mass, 109 m3 |
|---|---|---|---|
| Shreveport | 9.1 | 11.2 | 2.9 |
| Coushatta | 9.4 | 11.8 | 3.3 |
| Grand Ecore | 10.1 | 12.6 | 3.6 |
| Alexandria | 9.8 | 10.6 | 1.2 |
| Region Name | Area, 103 km2 | Evaporation Rate, mm/Day | Prevailing Soils | Estimated Soil Permeability, mm/Day |
|---|---|---|---|---|
| Xigazê | 122.9 | July: 1.0; August: 1.0; September: 1.4 | lithosols | 1.0 |
| Lhasa | 56.5 | July: 1.0; August: 1.0; September: 1.4 | lithosols | 1.0 |
| Shannan | 58.0 | July: 1.0; August: 1.0; September: 1.4 | lithosols | 1.0 |
| Nyingchi | 58.7 | July: 1.0; August: 1.0; September: 1.4 | lithosols | 1.0 |
| Ngopok | 50.4 | July 3.9; August: 3.2; September: 1.7 | acrisols, cambisols | 100.0 |
| Dibrugarh | 46.8 | July: 3.9; August: 3.2; September: 1.7 | acrisols, cambisols | 200.0 |
| Gohpur | 36.6 | July: 3.9; August: 3.2; September: 1.7 | acrisols, cambisols | 200.0 |
| Tezpur | 34.7 | July: 3.9; August: 3.2; September: 1.7 | acrisols, nitosols, cambisols, regosols | 100.4 |
| Guwahati | 43.4 | July: 3.9; August: 3.2; September: 1.7 | acrisols, regosols, nitosols, cambisols | 50.2 |
| Alipurduar | 143.3 | July: 3.9; August: 3.2; September: 1.7 | acrisols, cambisols, gleysols, regosols | 300.3 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trifonova, T.; Trifonov, D.; Arakelian, S. 2015 Disastrous Floods in Louisiana, USA, and Assam, India: Groundwater Impact on the Water Balance Estimation. Hydrology 2016, 3, 41. https://doi.org/10.3390/hydrology3040041
Trifonova T, Trifonov D, Arakelian S. 2015 Disastrous Floods in Louisiana, USA, and Assam, India: Groundwater Impact on the Water Balance Estimation. Hydrology. 2016; 3(4):41. https://doi.org/10.3390/hydrology3040041
Chicago/Turabian StyleTrifonova, Tatiana, Dmitriy Trifonov, and Sergey Arakelian. 2016. "2015 Disastrous Floods in Louisiana, USA, and Assam, India: Groundwater Impact on the Water Balance Estimation" Hydrology 3, no. 4: 41. https://doi.org/10.3390/hydrology3040041
APA StyleTrifonova, T., Trifonov, D., & Arakelian, S. (2016). 2015 Disastrous Floods in Louisiana, USA, and Assam, India: Groundwater Impact on the Water Balance Estimation. Hydrology, 3(4), 41. https://doi.org/10.3390/hydrology3040041





