Analysis of the Potential Impacts of Climate Change on the Mean Annual Water Balance and Precipitation Deficits for a Catchment in Southern Ecuador
Abstract
1. Introduction
2. Materials and Methods
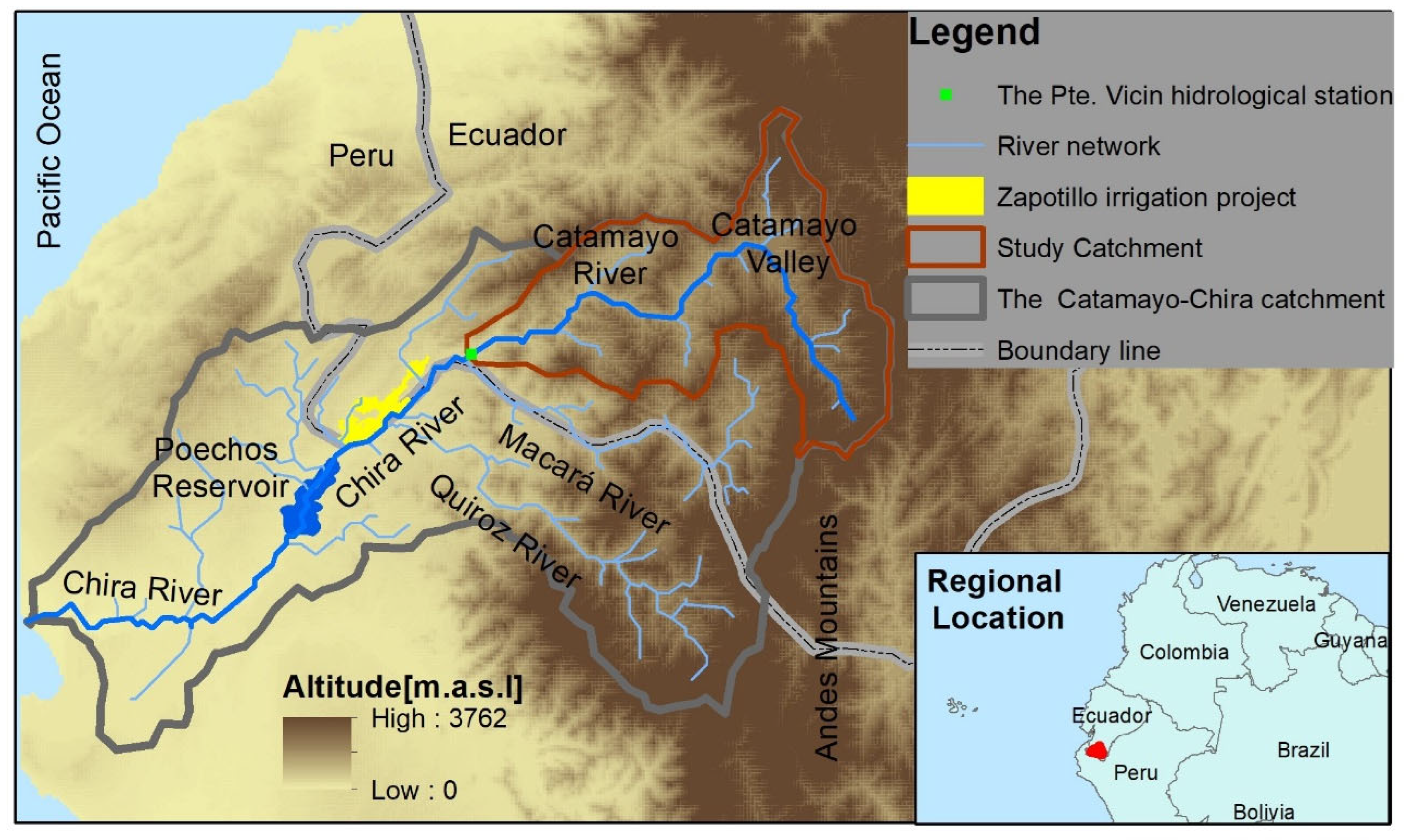
2.1. Study Catchment
2.2. Data Description
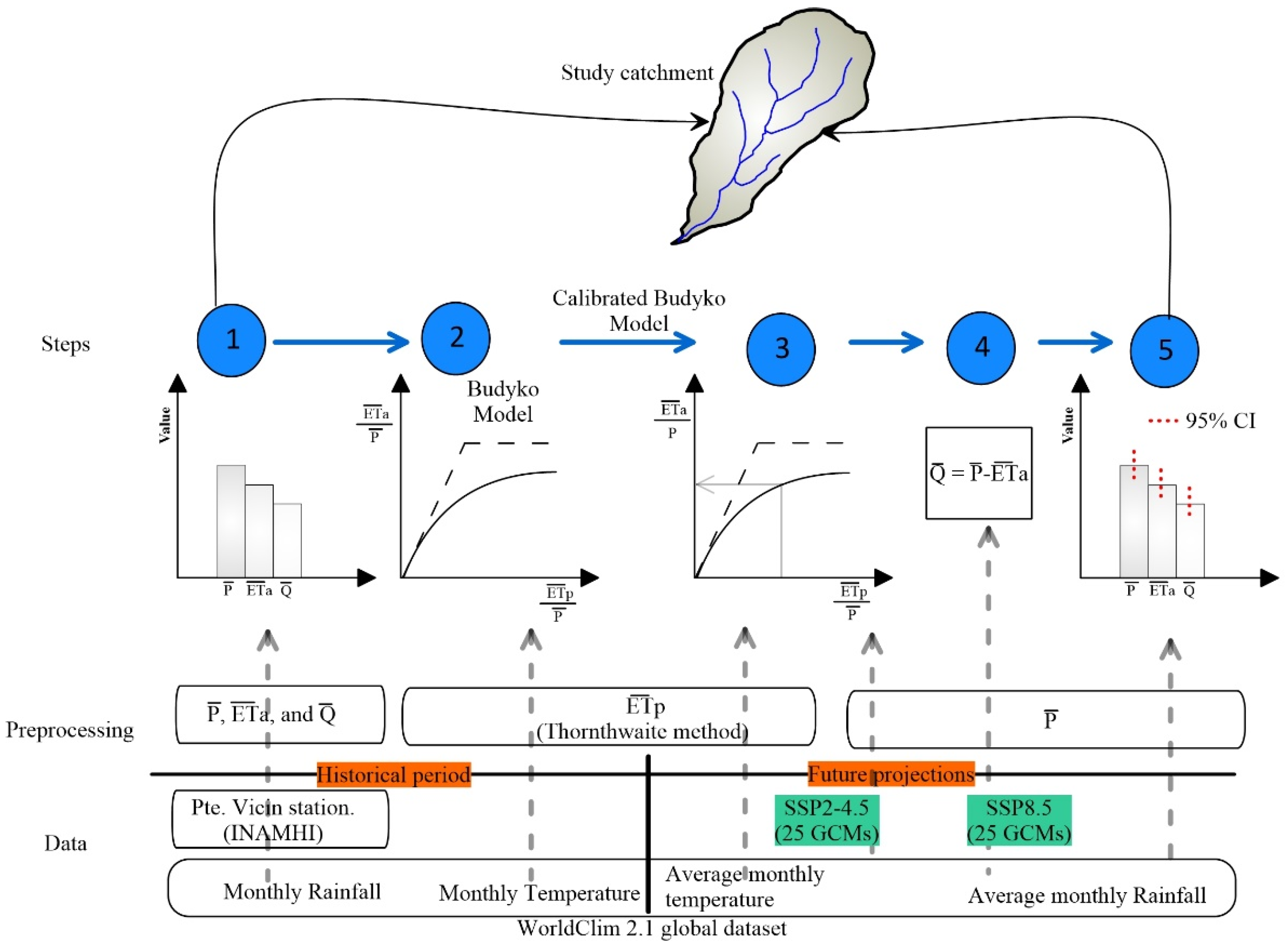
2.3. Methodology
2.3.1. General Description of the Water Balance Framework
2.3.2. Calculation of the Mean Annual Water Balance Variables for the Historical Period
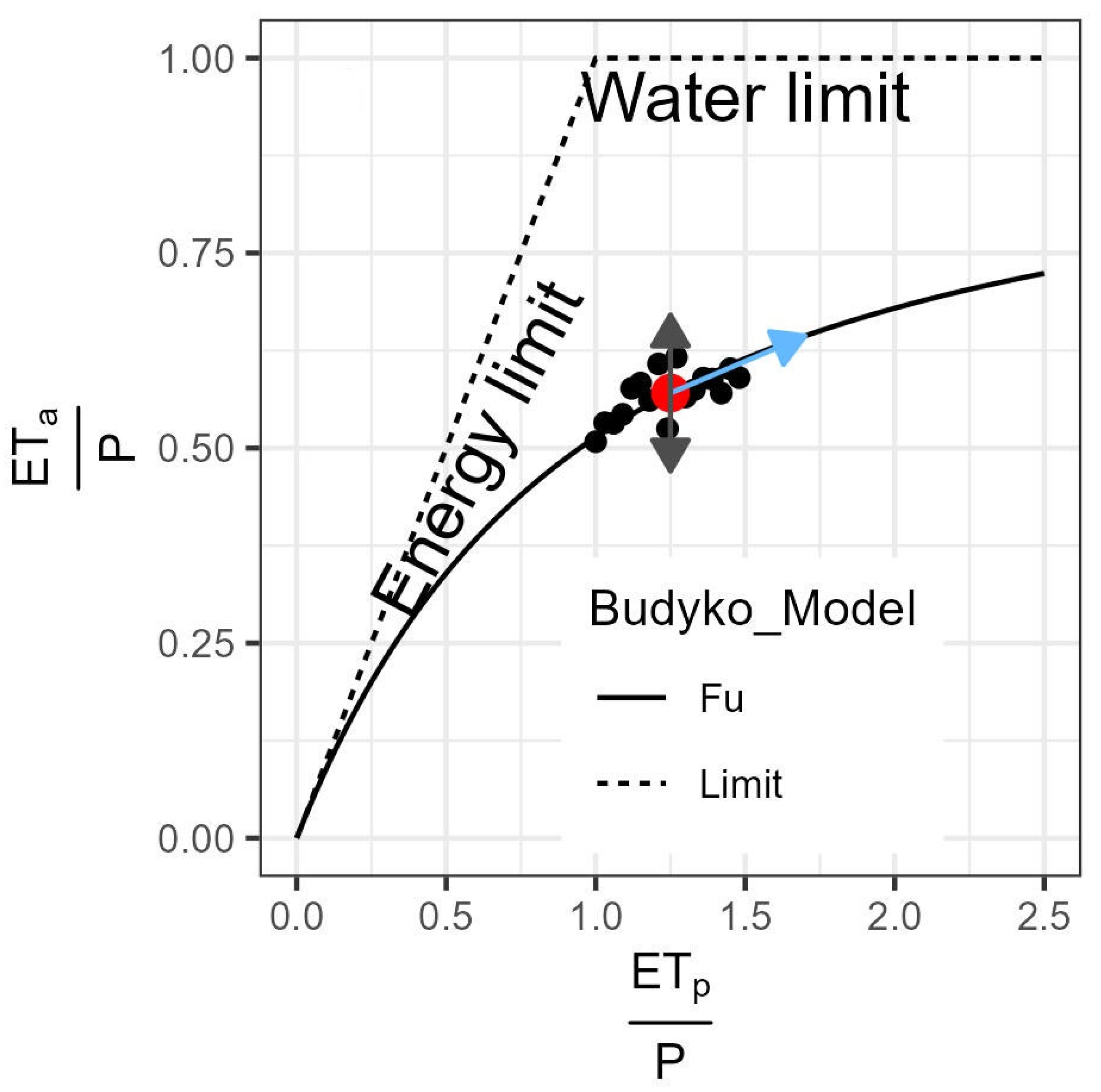
2.3.3. Budyko Framework
2.3.4. Calibration of the Budyko Model for the Study Catchment
- : average potential evapotranspiration for the month [mm/month];
- : average temperature for the month [°C];
- : the annual heat index defined as the sum of 12 monthly value of where
- a:
- : correction factor for the month based on number of daylight hours per day compared to 12 and number of days in a month compared to 30. Therefore, this value depends also on the latitude. Some values of this factor are described in Table 2.
2.3.5. Calculation of the Mean Annual Water Balance Variables for the Future Scenarios
2.3.6. Climate Change Impact Estimate on Water Availability (Significance and 95th Percentile Band)
- : sample mean of the future projections;
- : t-score with area in the right and left tails equal to 0.025;
- : sample standard deviation of the future projections;
- : sample size of the future projections.
2.3.7. Precipitation Deficit Analysis and Future Deficit Projections Under Climate Change
3. Results and Analysis
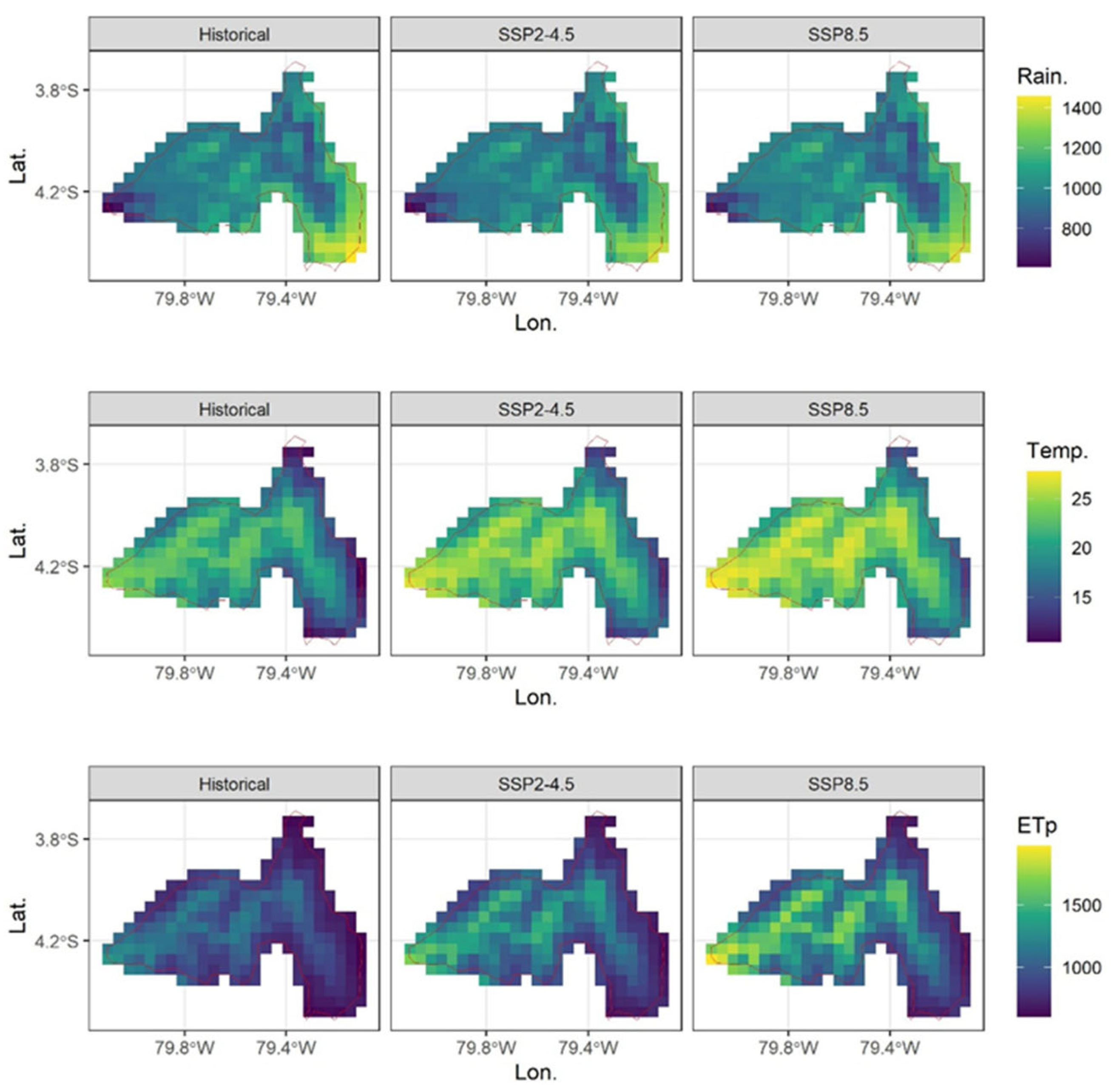
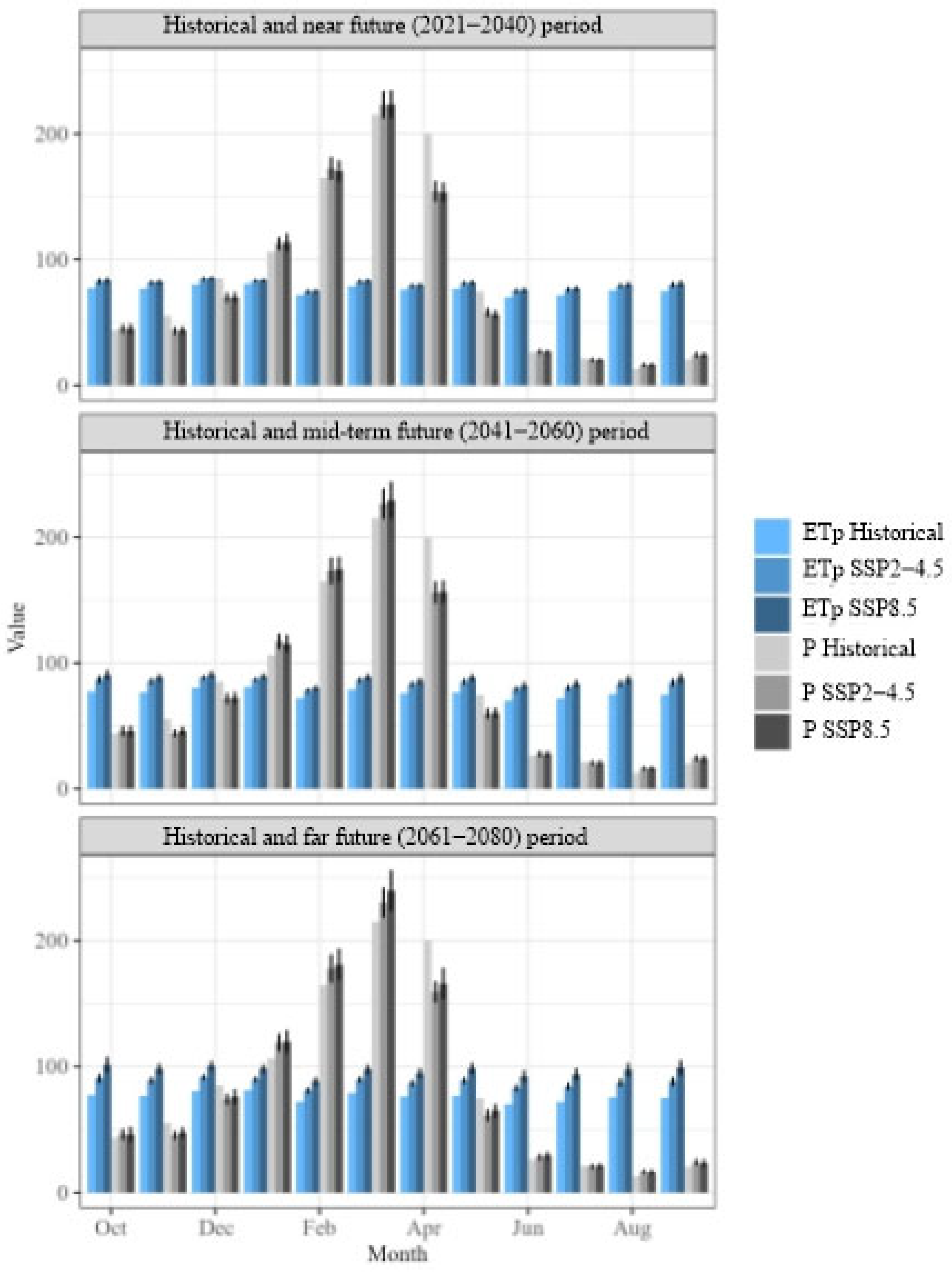
3.1. Historical 5 Km Grid Values of Climate Variables and Future Projections
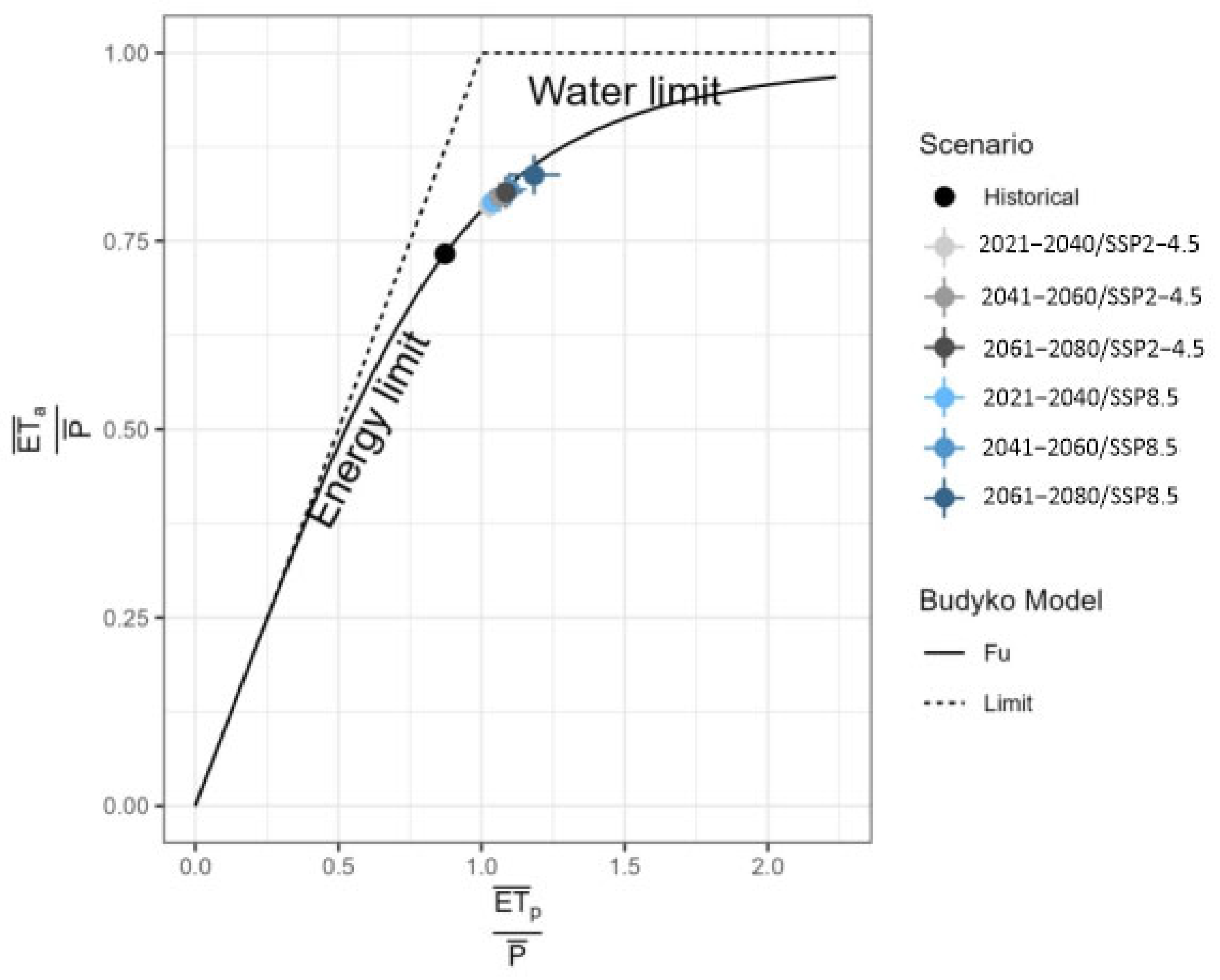
3.2. Budyko Model and Future Projections
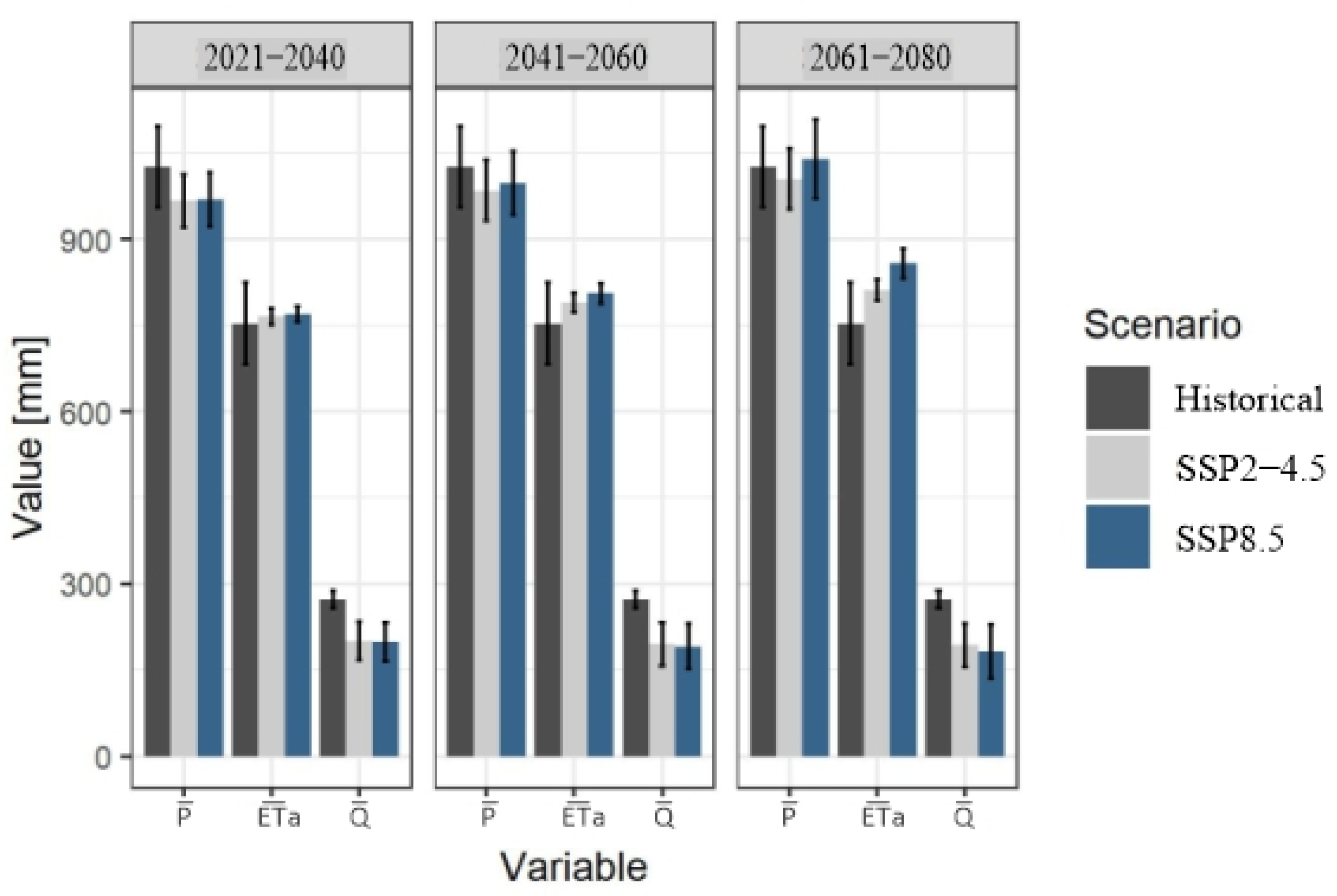
3.3. Climate Change Impact on the Mean Annual Water Balance in the Study Catchment
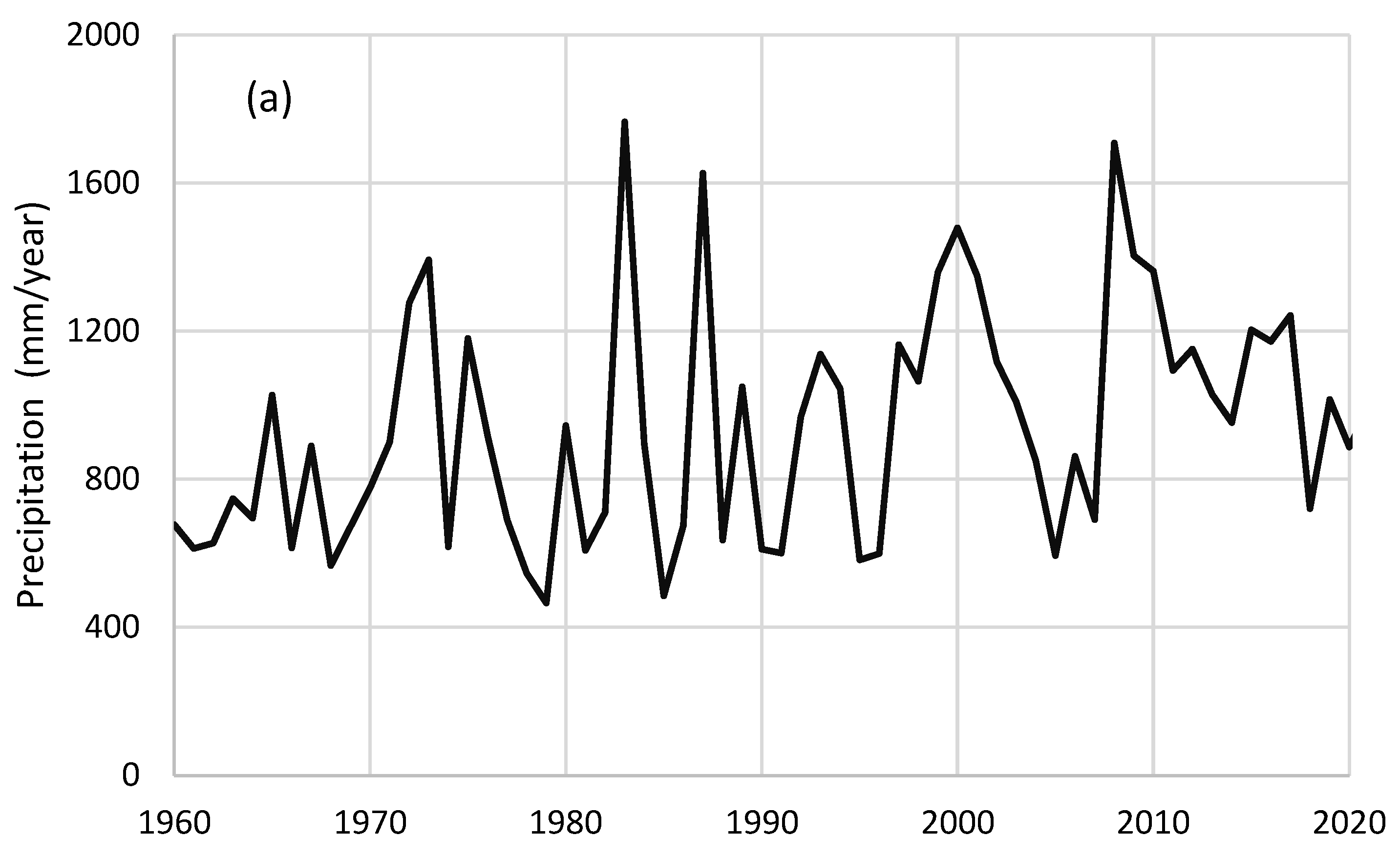
3.4. Annual Precipitation Deficits and Future Projections
3.5. Mitigation and Adaptation Strategies
3.6. Limitations and Future Research
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yao, L.; Libera, D.A.; Kheimi, M.; Sankarasubramanian, A.; Wang, D. The Roles of Climate Forcing and Its Variability on Streamflow at Daily, Monthly, Annual, and Long-Term Scales. Water Resour. Res. 2020, 56, e2020WR027111. [Google Scholar] [CrossRef]
- Austin, J.; Zhang, L.; Jones, R.N.; Durack, P.; Dawes, W.; Hairsine, P. Climate Change Impact on Water and Salt Balances: An Assessment of the Impact of Climate Change on Catchment Salt and Water Balances in the Murray-Darling Basin, Australia. Clim. Change 2010, 100, 607–631. [Google Scholar] [CrossRef]
- Campozano, L.; Ballari, D.; Montenegro, M.; Avilés, A. Future Meteorological Droughts in Ecuador: Decreasing Trends and Associated Spatio-Temporal Features Derived From CMIP5 Models. Front. Earth Sci. 2020, 8, 17. [Google Scholar] [CrossRef]
- Carvajal, P.E.; Li, F.G.N. Challenges for Hydropower-Based Nationally Determined Contributions: A Case Study for Ecuador. Clim. Policy 2019, 19, 974–987. [Google Scholar] [CrossRef]
- Zhang, Y.; Engel, B.; Ahiablame, L.; Liu, J. Impacts of Climate Change on Mean Annual Water Balance for Watersheds in Michigan, USA. Water 2015, 7, 3565–3578. [Google Scholar] [CrossRef]
- Wang, S.; McKenney, D.W.; Shang, J.; Li, J. A National-scale Assessment of Long-term Water Budget Closures for Canada’s Watersheds. J. Geophys. Res. Atmos. 2014, 119, 8712–8725. [Google Scholar] [CrossRef]
- Han, J.; Yang, Y.; Roderick, M.L.; McVicar, T.R.; Yang, D.; Zhang, S.; Beck, H.E. Assessing the Steady-State Assumption in Water Balance Calculation Across Global Catchments. Water Resour. Res. 2020, 56, e2020WR027392. [Google Scholar] [CrossRef]
- Collignan, J.; Polcher, J.; Bastin, S.; Quintana-Segui, P. Budyko Framework Based Analysis of the Effect of Climate Change on Watershed Evaporation Efficiency and Its Impact on Discharge Over Europe. Water Resour. Res. 2023, 59, e2023WR034509. [Google Scholar] [CrossRef]
- Safeeq, M.; Bart, R.R.; Pelak, N.F.; Singh, C.K.; Dralle, D.N.; Hartsough, P.; Wagenbrenner, J.W. How Realistic Are Water-balance Closure Assumptions? A Demonstration from the Southern Sierra Critical Zone Observatory and Kings River Experimental Watersheds. Hydrol. Process. 2021, 35, e14199. [Google Scholar] [CrossRef]
- Wang, D. Evaluating Interannual Water Storage Changes at Watersheds in Illinois Based on Long-term Soil Moisture and Groundwater Level Data. Water Resour. Res. 2012, 48, W03502. [Google Scholar] [CrossRef]
- Li, Z.; Li, Q.; Wang, J.; Feng, Y.; Shao, Q. Impacts of Projected Climate Change on Runoff in Upper Reach of Heihe River Basin Using Climate Elasticity Method and GCMs. Sci. Total Environ. 2020, 716, 137072. [Google Scholar] [CrossRef]
- Osborne, J.M.; Lambert, F.H. A Simple Tool for Refining GCM Water Availability Projections, Applied to Chinese Catchments. Hydrol. Earth Syst. Sci. 2018, 22, 6043–6057. [Google Scholar] [CrossRef]
- Teng, J.; Chiew, F.H.S.; Vaze, J.; Marvanek, S.; Kirono, D.G.C. Estimation of Climate Change Impact on Mean Annual Runoff across Continental Australia Using Budyko and Fu Equations and Hydrological Models. J. Hydrometeorol. 2012, 13, 1094–1106. [Google Scholar] [CrossRef]
- Zaninelli, P.G.; Menéndez, C.G.; Falco, M.; López-Franca, N.; Carril, A.F. Future Hydroclimatological Changes in South America Based on an Ensemble of Regional Climate Models. Clim. Dyn. 2019, 52, 819–830. [Google Scholar] [CrossRef]
- Jaramillo, F.; Piemontese, L.; Berghuijs, W.R.; Wang-Erlandsson, L.; Greve, P.; Wang, Z. Fewer Basins Will Follow Their Budyko Curves Under Global Warming and Fossil-Fueled Development. Water Resour. Res. 2022, 58, e2021WR031825. [Google Scholar] [CrossRef] [PubMed]
- IPCC Synthesis Report of the Sixth Assessment Report. Available online: https://www.ipcc.ch/ar6-syr/ (accessed on 3 December 2022).
- Joslyn, S.; Demnitz, R. Communicating Climate Change: Probabilistic Expressions and Concrete Events. Weather Clim. Soc. 2019, 11, 651–664. [Google Scholar] [CrossRef]
- Fu, B.-P. On the Calculation of the Evaporation from Land Surface. Chin. J. Atmos. Sci. 1981, 5, 23–31. [Google Scholar] [CrossRef]
- Lavado-Casimiro, W.S.; Felipe, O.; Silvestre, E.; Bourrel, L. ENSO Impact on Hydrology in Peru. Adv. Geosci. 2013, 33, 33–39. [Google Scholar] [CrossRef]
- Pacheco, J.; Solera, A.; Avilés, A.; Tonón, M.D. Influence of ENSO on Droughts and Vegetation in a High Mountain Equatorial Climate Basin. Atmosphere 2022, 13, 2123. [Google Scholar] [CrossRef]
- Pineda, L.; Ntegeka, V.; Willems, P. Rainfall Variability Related to Sea Surface Temperature Anomalies in a Pacific–Andean Basin into Ecuador and Peru. Adv. Geosci. 2013, 33, 53–62. [Google Scholar] [CrossRef]
- Tote, C.; Govers, G.; Van Kerckhoven, S.; Filiberto, I.; Verstraeten, G.; Eerens, H. Effect of ENSO Events on Sediment Production in a Large Coastal Basin in Northern Peru. Earth Surf. Process. Landf. 2011, 36, 1776–1788. [Google Scholar] [CrossRef]
- Foucher, A.; Morera, S.; Sanchez, M.; Orrillo, J.; Evrard, O. El Niño–Southern Oscillation (ENSO)-Driven Hypersedimentation in the Poechos Reservoir, Northern Peru. Hydrol. Earth Syst. Sci. 2023, 27, 3191–3204. [Google Scholar] [CrossRef]
- PENUD. Gestión Integrada de Recursos Hídricos de Las Cuencas Transfronterizas y Acuíferos de Puyango-Tumbez, Catamayo-Chira, y Zarumilla; PENUD: Quito, Ecuador, 2015. [Google Scholar]
- Vílchez, S.; Núñez, S. Valenzuela Germán Estudio Geoambiental de La Cuenca Del Río Chira-Catamayo-[Boletín C 31]; INGEMMET: Lima, Peru, 2006. [Google Scholar]
- Fick, S.E.; Hijmans, R.J. WorldClim 2: New 1-km Spatial Resolution Climate Surfaces for Global Land Areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- Newell, F.L.; Ausprey, I.J.; Robinson, S.K. Spatiotemporal Climate Variability in the Andes of Northern Peru: Evaluation of Gridded Datasets to Describe Cloud Forest Microclimate and Local Rainfall. Int. J. Climatol. 2022, 42, 5892–5915. [Google Scholar] [CrossRef]
- Ceccarelli, V.; Fremout, T.; Chavez, E.; Argüello, D.; Loor Solórzano, R.G.; Sotomayor Cantos, I.A.; Thomas, E. Vulnerability to Climate Change of Cultivated and Wild Cacao in Ecuador. Clim. Change 2024, 177, 103. [Google Scholar] [CrossRef]
- Zhang, L.; Hickel, K.; Dawes, W.R.; Chiew, F.H.S.; Western, A.W.; Briggs, P.R. A Rational Function Approach for Estimating Mean Annual Evapotranspiration. Water Resour. Res. 2004, 40, 2502. [Google Scholar] [CrossRef]
- Ruggiu, D.; Viola, F. Linking Climate, Basin Morphology and Vegetation Characteristics to Fu’s Parameter in Data Poor Conditions. Water 2019, 11, 2333. [Google Scholar] [CrossRef]
- Ning, T.; Li, Z.; Feng, Q.; Liu, W.; Li, Z. Comparison of the Effectiveness of Four Budyko-Based Methods in Attributing Long-Term Changes in Actual Evapotranspiration. Sci. Rep. 2018, 8, 12665. [Google Scholar] [CrossRef]
- Aschonitis, V.; Touloumidis, D.; ten Veldhuis, M.-C.; Coenders-Gerrits, M. Correcting Thornthwaite Potential Evapotranspiration Using a Global Grid of Local Coefficients to Support Temperature-Based Estimations of Reference Evapotranspiration and Aridity Indices. Earth Syst. Sci. Data 2022, 14, 163–177. [Google Scholar] [CrossRef]
- Lemaitre-Basset, T.; Oudin, L.; Thirel, G.; Collet, L. Unraveling the Contribution of Potential Evaporation Formulation to Uncertainty under Climate Change. Hydrol. Earth Syst. Sci. 2022, 26, 2147–2159. [Google Scholar] [CrossRef]
- Mather, J.R.; Ambroziak, R.A. A Search for Understanding Potential Evapotranspiration. Geogr. Rev. 1986, 76, 355. [Google Scholar] [CrossRef]
- Almazroui, M.; Ashfaq, M.; Islam, M.N.; Rashid, I.U.; Kamil, S.; Abid, M.A.; O’Brien, E.; Ismail, M.; Reboita, M.S.; Sörensson, A.A.; et al. Assessment of CMIP6 Performance and Projected Temperature and Precipitation Changes Over South America. Earth Syst. Environ. 2021, 5, 155–183. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Rudolf, B.; Ziese, M. GPCC Full Data Reanalysis Version 7.0 at 0.5°: Monthly Land-Surface Precipitation from Rain-Gauges Built on GTS-Based and Historic Data. Available online: https://opendata.dwd.de/climate_environment/GPCC/html/fulldata_v7_doi_download.html (accessed on 5 March 2024).
- O’Connell, E.; O’Donnell, G.; Koutsoyiannis, D. The Spatial Scale Dependence of The Hurst Coefficient in Global Annual Precipitation Data, and Its Role in Characterising Regional Precipitation Deficits within a Naturally Changing Climate. Hydrology 2022, 9, 199. [Google Scholar] [CrossRef]
- Santos, F.; Jara, J.; Acosta, N.; Galeas, R.; de Bièvre, B. Assessing Annual and Monthly Precipitation Anomalies in Ecuador Bioregions Using WorldClim CMIP6 GCM Ensemble Projections and Dynamic Time Warping. Int. J. Climatol. 2024, 45, e8685. [Google Scholar] [CrossRef]
- Ochoa, P.A.; Fries, A.; Mejía, D.; Burneo, J.I.; Ruíz-Sinoga, J.D.; Cerdà, A. Effects of Climate, Land Cover and Topography on Soil Erosion Risk in a Semiarid Basin of the Andes. Catena 2016, 140, 31–42. [Google Scholar] [CrossRef]
- Ekstrand, S.; Mancinelli, C.; Houghton-Carr, H.; Govers, G.; Debels, P.; Camaño, B.; Alcoz, S.; Filiberto, I.; Gámez, S.; Duque, A. TWINLATIN: Twinning European and Latin American River Basins for Research Enabling Sustainable Water Resources Management. Final Report; IVL Swedish Environmental Research Institute: Stockholm, Sweden, 2009. [Google Scholar]
- Zhou, G.; Wei, X.; Chen, X.; Zhou, P.; Liu, X.; Xiao, Y.; Sun, G.; Scott, D.F.; Zhou, S.; Han, L.; et al. Global Pattern for the Effect of Climate and Land Cover on Water Yield. Nat. Commun. 2015, 6, 5918. [Google Scholar] [CrossRef]
- Reaver, N.G.F.; Kaplan, D.A.; Klammler, H.; Jawitz, J.W. Theoretical and Empirical Evidence against the Budyko Catchment Trajectory Conjecture. Hydrol. Earth Syst. Sci. 2022, 26, 1507–1525. [Google Scholar] [CrossRef]
- Ponce, V.M.; Pandey, R.P.; Ercan, S. Characterization of Drought across Climatic Spectrum. J. Hydrol. Eng. 2000, 5, 222–224. [Google Scholar] [CrossRef]
- Hu, K.; Huang, G.; Huang, P.; Kosaka, Y.; Xie, S.-P. Intensification of El Niño-Induced Atmospheric Anomalies under Greenhouse Warming. Nat. Geosci. 2021, 14, 377–382. [Google Scholar] [CrossRef]
- Hou, M.; Tang, Y. Recent Progress in Simulating Two Types of ENSO—From CMIP5 to CMIP6. Front. Mar. Sci. 2022, 9, 986780. [Google Scholar] [CrossRef]
- Shen, M.; Chen, J.; Zhuan, M.; Chen, H.; Xu, C.-Y.; Xiong, L. Estimating Uncertainty and Its Temporal Variation Related to Global Climate Models in Quantifying Climate Change Impacts on Hydrology. J. Hydrol. 2018, 556, 10–24. [Google Scholar] [CrossRef]
- da Costa, J.A.C.; Andreoli, R.V.; Kayano, M.T.; de Souza, I.P.; de Souza, R.A.F.; Cerón, W.L. The South American Precipitation Trends under (or Not) El Niño-Southern Oscillation Influences and Relationship with Large-scale Circulation. Int. J. Climatol. 2024, 44, 3154–3168. [Google Scholar] [CrossRef]
- O’Connell, E.; O’Donnell, G.; Koutsoyiannis, D. On the Spatial Scale Dependence of Long-Term Persistence in Global Annual Precipitation Data and the Hurst Phenomenon. Water Resour. Res. 2023, 59, e2022WR033133. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Poulin, A.; Leconte, R. Overall Uncertainty Study of the Hydrological Impacts of Climate Change for a Canadian Watershed. Water Resour. Res. 2011, 47, W12509. [Google Scholar] [CrossRef]
- Wilby, R.L.; Hassan, H.; Hanaki, K. Statistical Downscaling of Hydrometeorological Variables Using General Circulation Model Output. J. Hydrol. 1998, 205, 1–19. [Google Scholar] [CrossRef]
- Jung, I.-W.; Moradkhani, H.; Chang, H. Uncertainty Assessment of Climate Change Impacts for Hydrologically Distinct River Basins. J. Hydrol. 2012, 466, 73–87. [Google Scholar] [CrossRef]
- Kay, A.L.; Davies, H.N.; Bell, V.A.; Jones, R.G. Comparison of Uncertainty Sources for Climate Change Impacts: Flood Frequency in England. Clim. Change 2009, 92, 41–63. [Google Scholar] [CrossRef]
- Hamel, P.; Guswa, A.J. Uncertainty Analysis of a Spatially Explicit Annual Water-Balance Model: Case Study of the Cape Fear Basin, North Carolina. Hydrol. Earth Syst. Sci. 2015, 19, 839–853. [Google Scholar] [CrossRef]
- Redhead, J.W.; Stratford, C.; Sharps, K.; Jones, L.; Ziv, G.; Clarke, D.; Oliver, T.H.; Bullock, J.M. Empirical Validation of the InVEST Water Yield Ecosystem Service Model at a National Scale. Sci. Total Environ. 2016, 569–570, 1418–1426. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Efstratiadis, A.; Mamassis, N.; Christofides, A. On the Credibility of Climate Predictions. Hydrol. Sci. J. 2008, 53, 671–684. [Google Scholar] [CrossRef]
- Rocheta, E.; Sugiyanto, M.; Johnson, F.; Evans, J.; Sharma, A. How Well Do General Circulation Models Represent Low-frequency Rainfall Variability? Water Resour. Res. 2014, 50, 2108–2123. [Google Scholar] [CrossRef]
- Moon, H.; Gudmundsson, L.; Seneviratne, S.I. Drought Persistence Errors in Global Climate Models. J. Geophys. Res. Atmos. 2018, 123, 3483–3496. [Google Scholar] [CrossRef] [PubMed]
- Ault, T.R.; Cole, J.E.; Overpeck, J.T.; Pederson, G.T.; Meko, D.M. Assessing the Risk of Persistent Drought Using Climate Model Simulations and Paleoclimate Data. J. Clim. 2014, 27, 7529–7549. [Google Scholar] [CrossRef]
- Varuolo-Clarke, A.M.; Williams, A.P.; Smerdon, J.E.; Ting, M.; Bishop, D.A. Influence of the South American Low-Level Jet on the Austral Summer Precipitation Trend in Southeastern South America. Geophys. Res. Lett. 2022, 49, e2021GL096409. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Hurst-Kolmogorov Dynamics and Uncertainty1. JAWRA J. Am. Water Resour. Assoc. 2011, 47, 481–495. [Google Scholar] [CrossRef]
| Variable | Temporal Resolution | Time Period | Spatial Resolution | Source/Description |
|---|---|---|---|---|
| Streamflow [m3/s] | Monthly | 1990–2011 | - | Records of the Pte. Vicin station. (INAMHI) |
| Maximum, minimum, and average * temperature [°C] | ~5 km | WorldClim 2.1 https://www.worldclim.org/data/index.html (accessed on 5 March 2024) | ||
| Precipitation ** [mm] | ||||
| Precipitation [mm] | Average monthly | 2021–2040 2041–2060 2061–2080 | ||
| Maximum, minimum, and average * temperature [°C] |
| Lat. | Jan. | Feb. | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sep. | Oct. | Nov. | Dec. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10° N | 1.00 | 0.91 | 1.03 | 1.03 | 1.08 | 1.05 | 1.08 | 1.07 | 1.02 | 1.02 | 0.98 | 0.99 |
| 5° N | 1.02 | 0.93 | 1.03 | 1.02 | 1.06 | 1.03 | 1.06 | 1.05 | 1.01 | 1.03 | 0.99 | 1.02 |
| Ecuador | 1.04 | 0.94 | 1.04 | 1.01 | 1.04 | 1.01 | 1.04 | 1.04 | 1.01 | 1.04 | 1.01 | 1.04 |
| 5° S | 1.06 | 0.95 | 1.04 | 1.00 | 1.02 | 0.99 | 1.02 | 1.03 | 1.00 | 1.05 | 1.03 | 1.06 |
| 10° S | 1.08 | 0.97 | 1.05 | 0.99 | 1.01 | 0.96 | 1.00 | 1.01 | 1.00 | 1.06 | 1.05 | 1.10 |
| Variable/Scenario | Historical | SPP2-4.5 | SSP8.5 |
|---|---|---|---|
| [mm] | 1023 | 1005 ± 53 −1.8 ± 5.2% | 1040 ± 69 +1.6 ± 6.7% |
| [°C] | 19 | 21.14 ± 0.27 +11.3 ± 0.01% | 22.3 ± 0.38 17.2 ± 0.02% |
| [mm] | 892 | 1075 ± 25 +20.5 ± 0.03% | 1194 ± 45 +33.8 ± 0.05% |
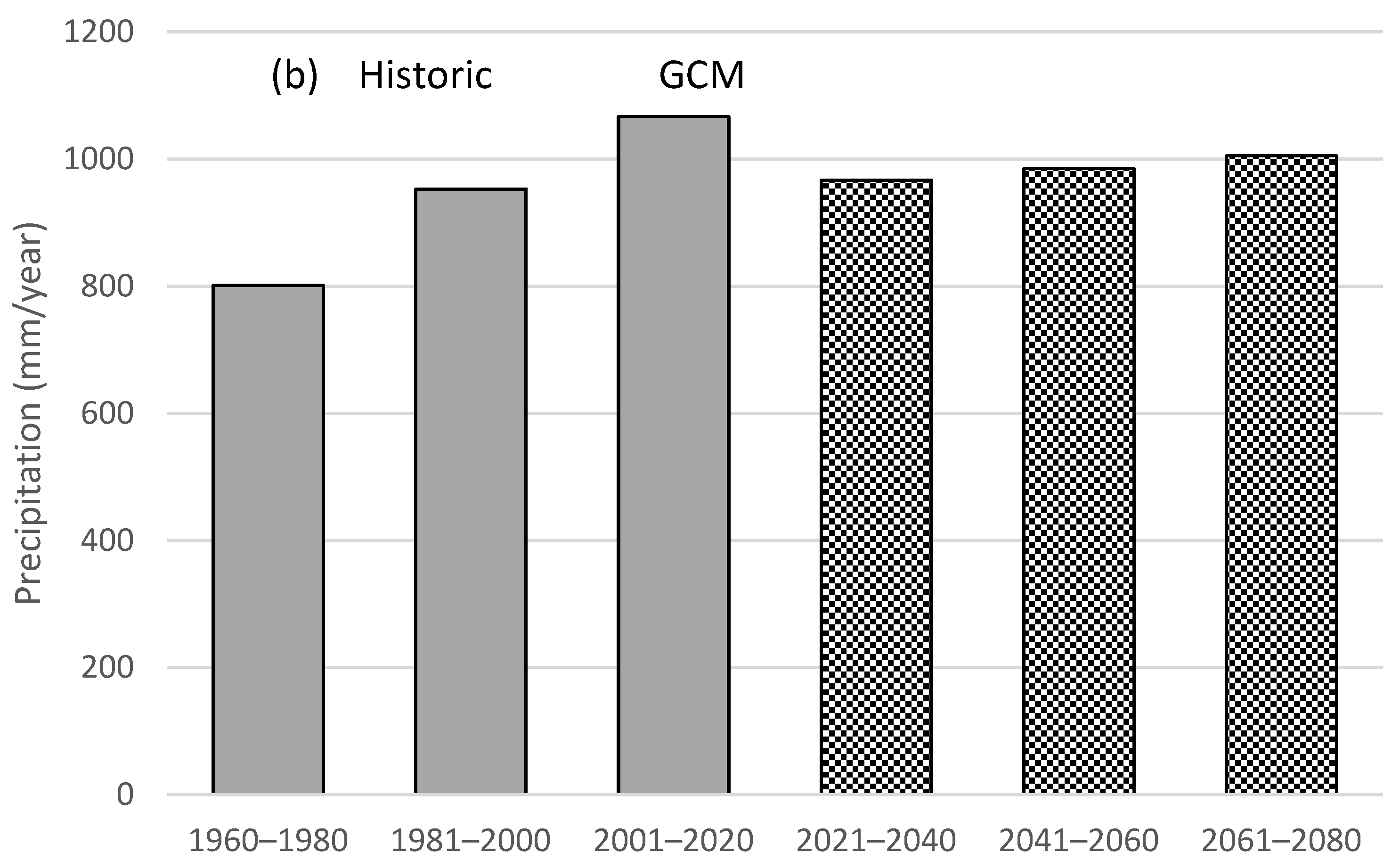
| Variable | Scenario | 1990–2011 | 2021–2040 | 2041–2060 | 2061–2080 |
|---|---|---|---|---|---|
| [mm] | Historical | 1023 | |||
| SPP2-4.5 | 967 ± 47 −5.5 ± 4.6% | 985 ± 52 −3.7 ± 5.1% | 1005 ± 53 −1.8 ± 5.2% | ||
| SSP8.5 | 969 ± 47 −5.3 ± 4.6% | 997 ± 55 −2.5 ± 5.4% | 1040 ± 69 +1.6 ± 6.7% | ||
| [mm] | Historical | 750 | |||
| SPP2-4.5 | 766 ± 15 2.1 ± 1.9% | 790 ± 17 5.3 ± 2.2% | 812 ± 18 8.2 ± 2.4% | ||
| SSP8.5 | 769 ± 14 2.54 ± 1.9% | 806 ± 18 7.4 ± 2.4% | 858 ± 26 14.3 ± 3.5% | ||
| [mm] | Historical | 273 | |||
| SPP2-4.5 | 201 ± 34 −26.3 ± 12.3% | 195 ± 37 −28.5 ± 13.7% | 193 ± 37 −29.2 ± 13.7% | ||
| SSP8.5 | 200 ± 34 −26.8 ± 12.3% | 191 ± 39 −29.9 ± 14.4% | 182 ± 46 −33.3 ± 17.0% | ||
| (a) | |||||||||||
| Period 1 1961–1980 | = 807.71 | ||||||||||
| Start | End | D | SV | SI | |||||||
| 1962 | 1964 | 3 | 43.82 | 14.61 | |||||||
| 1966 | 1966 | 1 | 23.95 | 23.95 | |||||||
| 1968 | 1970 | 3 | 50.72 | 16.91 | |||||||
| 1974 | 1974 | 1 | 23.61 | 23.61 | |||||||
| 1977 | 1979 | 3 | 89.38 | 29.79 | |||||||
| Period 2 1981–2000 | = 952.76 | ||||||||||
| Start | End | D | SV | SI | |||||||
| 1982 | 1982 | 1 | 25.42 | 25.42 | |||||||
| 1984 | 1986 | 3 | 84.43 | 28.14 | |||||||
| 1988 | 1988 | 1 | 33.31 | 33.31 | |||||||
| 1990 | 1991 | 2 | 72.88 | 36.44 | |||||||
| 1995 | 1996 | 2 | 76.08 | 38.04 | |||||||
| Period 3 2001–2020 | = 1070.36 | ||||||||||
| Start | End | D | SV | SI | |||||||
| 2003 | 2007 | 5 | 126.05 | 25.21 | |||||||
| 2013 | 2014 | 2 | 14.91 | 7.46 | |||||||
| 2018 | 2020 | 3 | 54.98 | 18.33 | |||||||
| (b) | |||||||||||
| D | E(D) | E(SV) | E(SI) | ||||||||
| 1 | 4 | 0.27 | 0.27 | 26.57 | 7.09 | 26.57 | 7.09 | ||||
| 2 | 3 | 0.24 | 0.49 | 54.62 | 13.35 | 27.31 | 6.68 | ||||
| 3 | 5 | 0.38 | 1.13 | 64.67 | 24.43 | 21.56 | 8.14 | ||||
| 4 | 0 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||||
| 5 | 1 | 0.11 | 0.56 | 126.05 | 14.01 | 25.21 | 2.80 | ||||
| 13 | 1.00 | 2.44 | 58.87 | 24.71 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duque, L.-F.; O’Donnell, G.; Cordero, J.; Jaramillo, J.; O’Connell, E. Analysis of the Potential Impacts of Climate Change on the Mean Annual Water Balance and Precipitation Deficits for a Catchment in Southern Ecuador. Hydrology 2025, 12, 177. https://doi.org/10.3390/hydrology12070177
Duque L-F, O’Donnell G, Cordero J, Jaramillo J, O’Connell E. Analysis of the Potential Impacts of Climate Change on the Mean Annual Water Balance and Precipitation Deficits for a Catchment in Southern Ecuador. Hydrology. 2025; 12(7):177. https://doi.org/10.3390/hydrology12070177
Chicago/Turabian StyleDuque, Luis-Felipe, Greg O’Donnell, Jimmy Cordero, Jorge Jaramillo, and Enda O’Connell. 2025. "Analysis of the Potential Impacts of Climate Change on the Mean Annual Water Balance and Precipitation Deficits for a Catchment in Southern Ecuador" Hydrology 12, no. 7: 177. https://doi.org/10.3390/hydrology12070177
APA StyleDuque, L.-F., O’Donnell, G., Cordero, J., Jaramillo, J., & O’Connell, E. (2025). Analysis of the Potential Impacts of Climate Change on the Mean Annual Water Balance and Precipitation Deficits for a Catchment in Southern Ecuador. Hydrology, 12(7), 177. https://doi.org/10.3390/hydrology12070177








