Tail-Aware Forecasting of Precipitation Extremes Using STL-GEV and LSTM Neural Networks
Abstract
1. Introduction
2. Materials and Methods
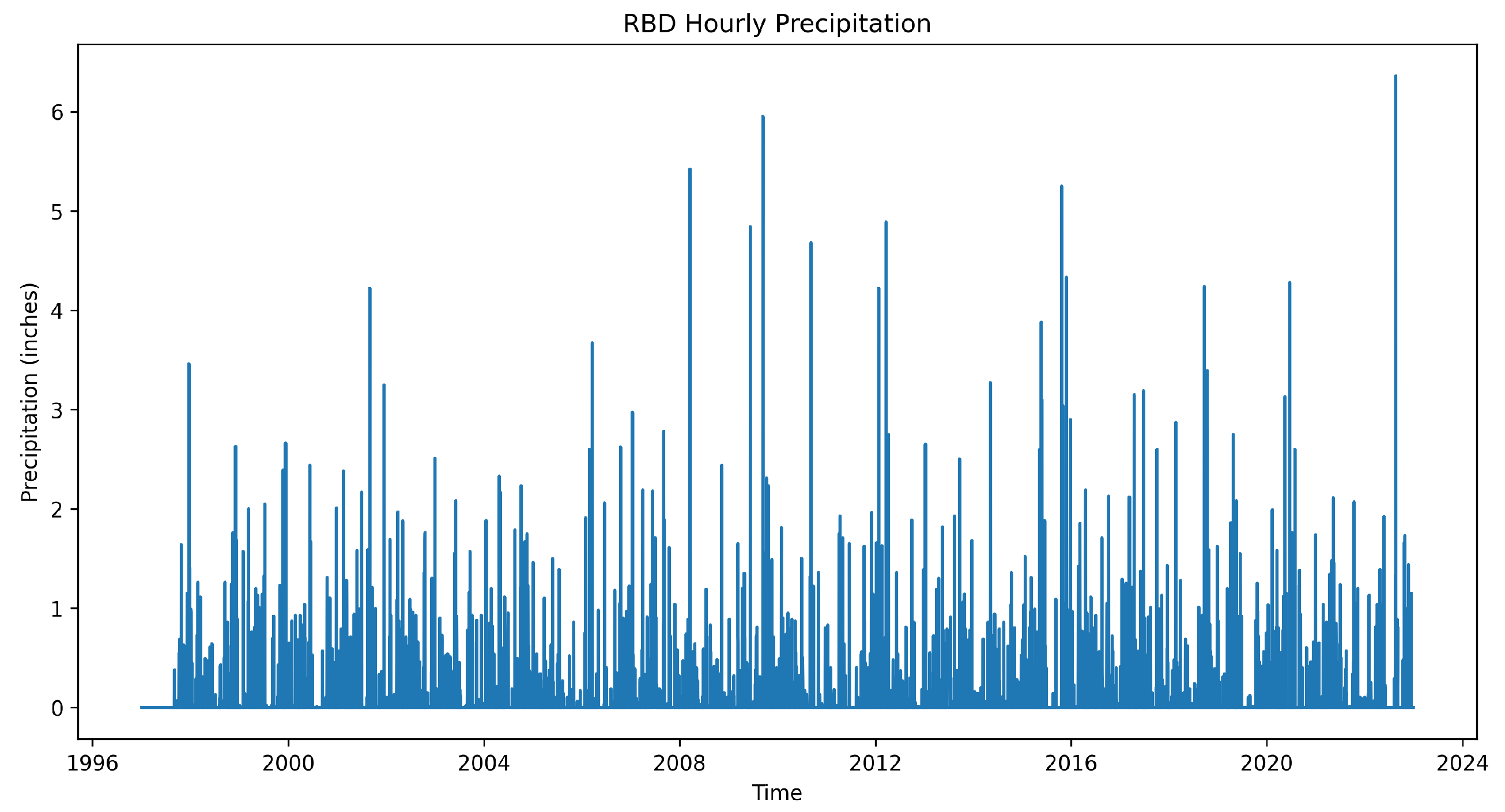
2.1. Data Source
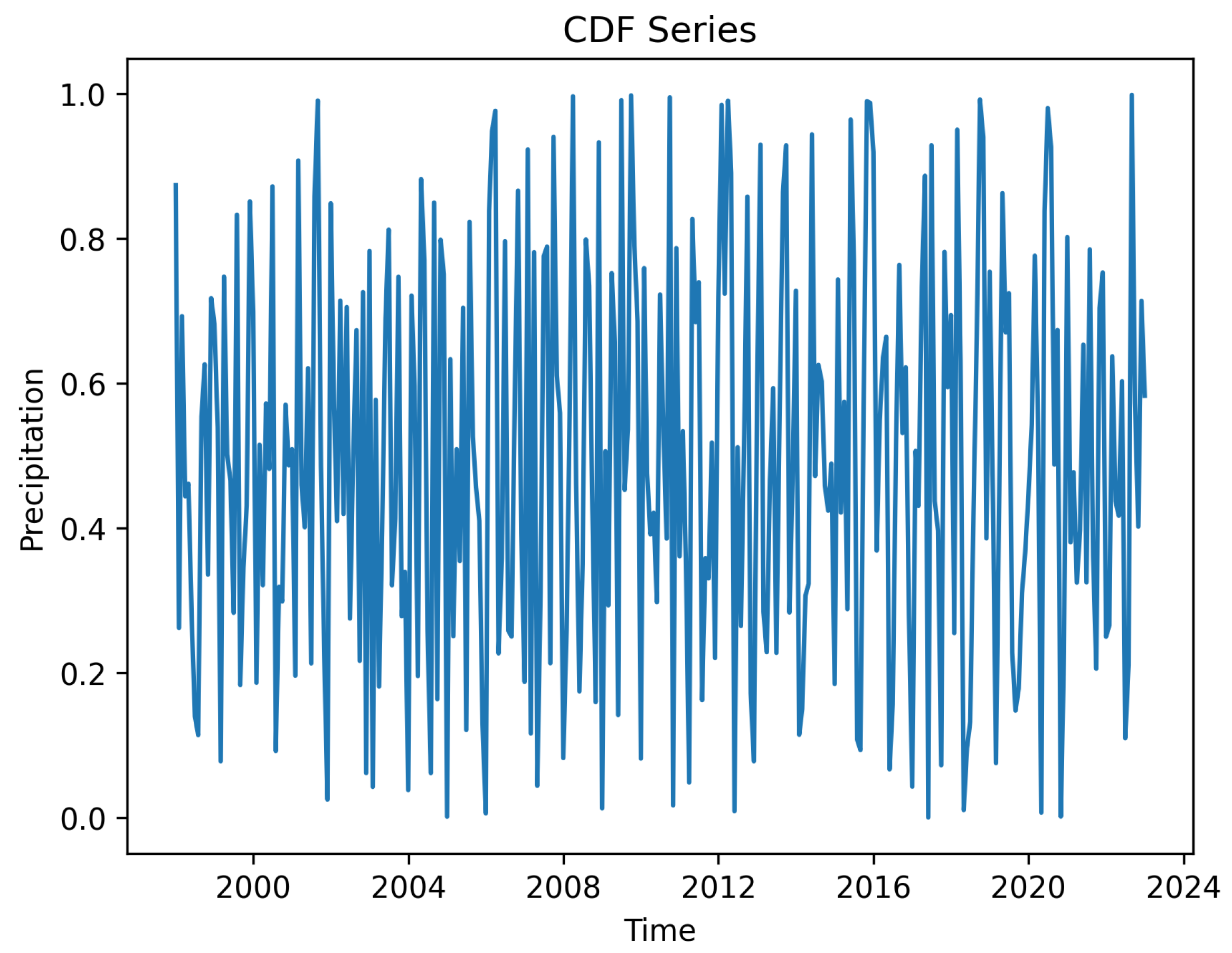
2.2. Data Processing
2.3. The Proposed Methods and Models
2.4. Model Evaluation Metrics
3. Results and Discussion
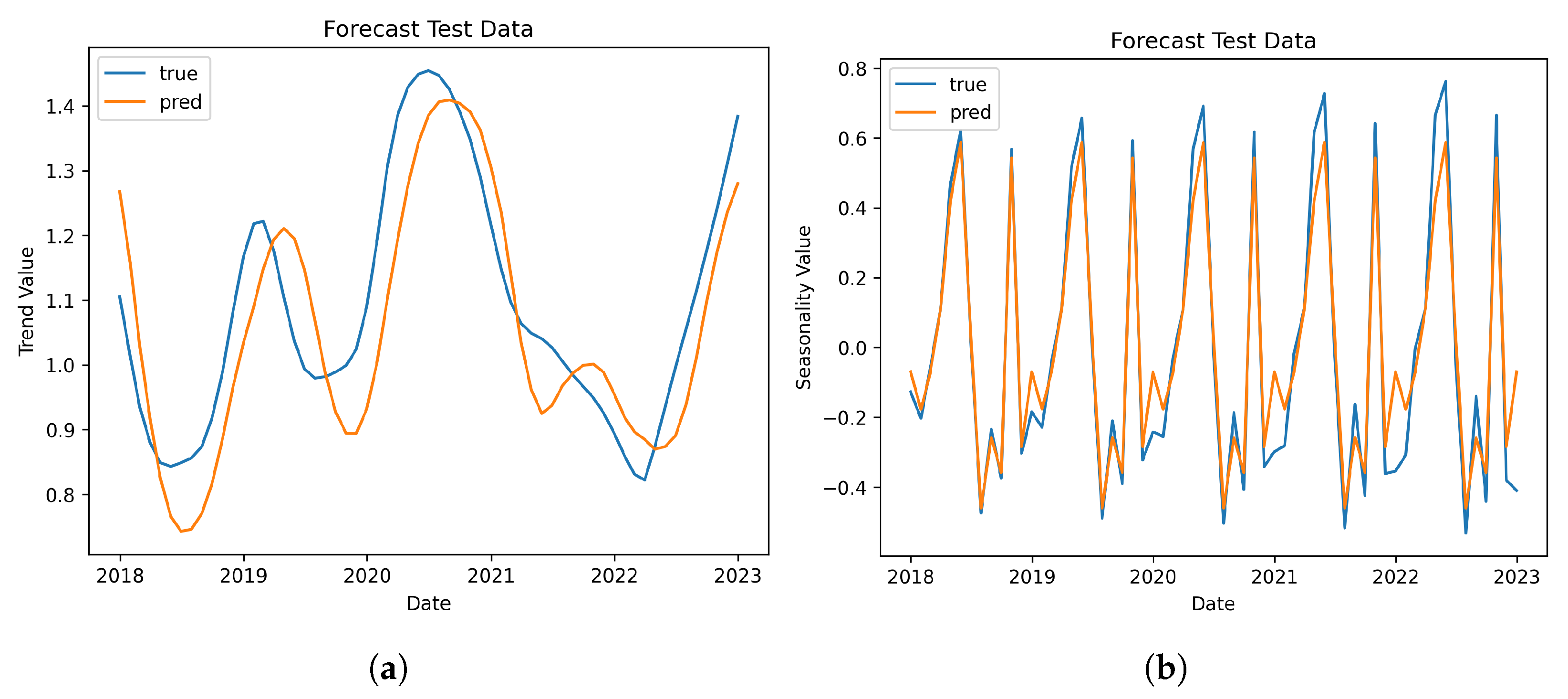
3.1. The STL Decomposition Performance
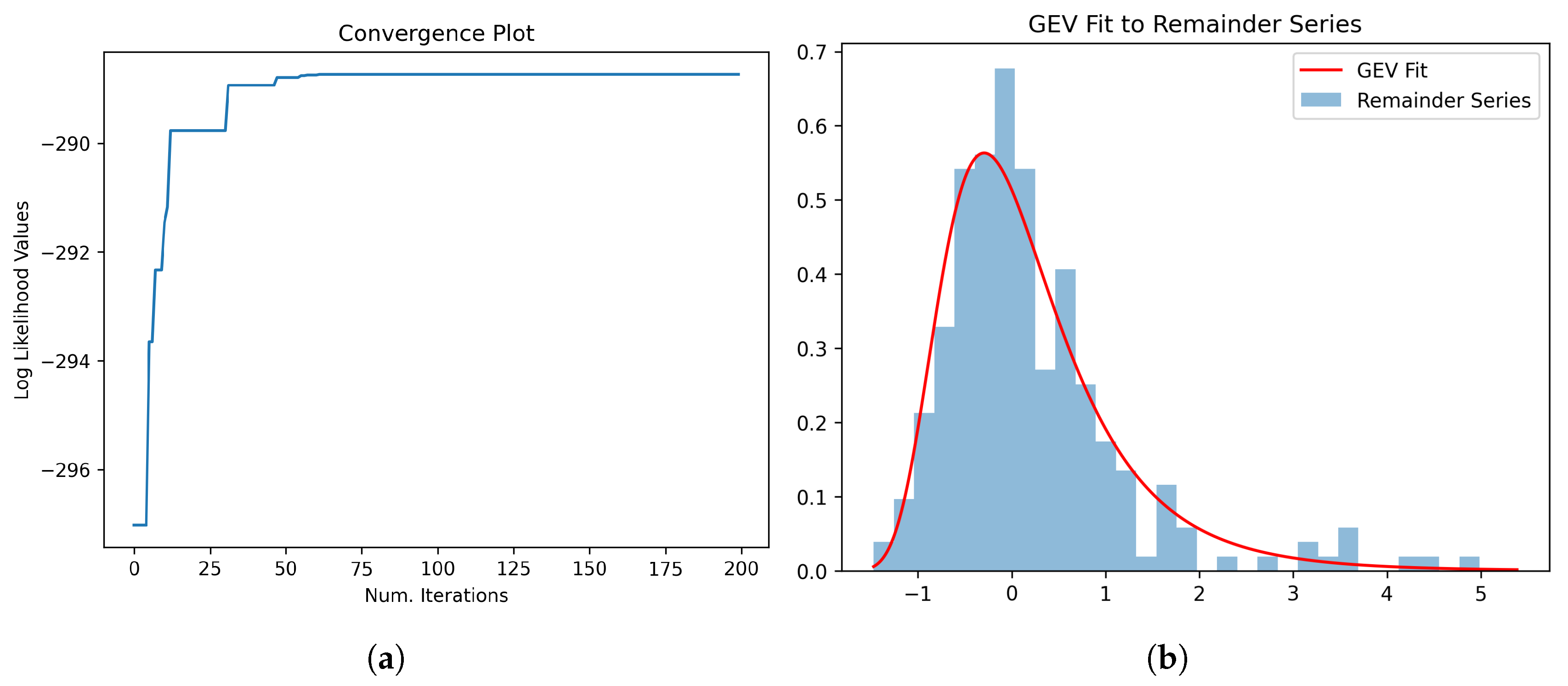
3.2. Parameter Estimation of GEV Fitted to Remainder Series
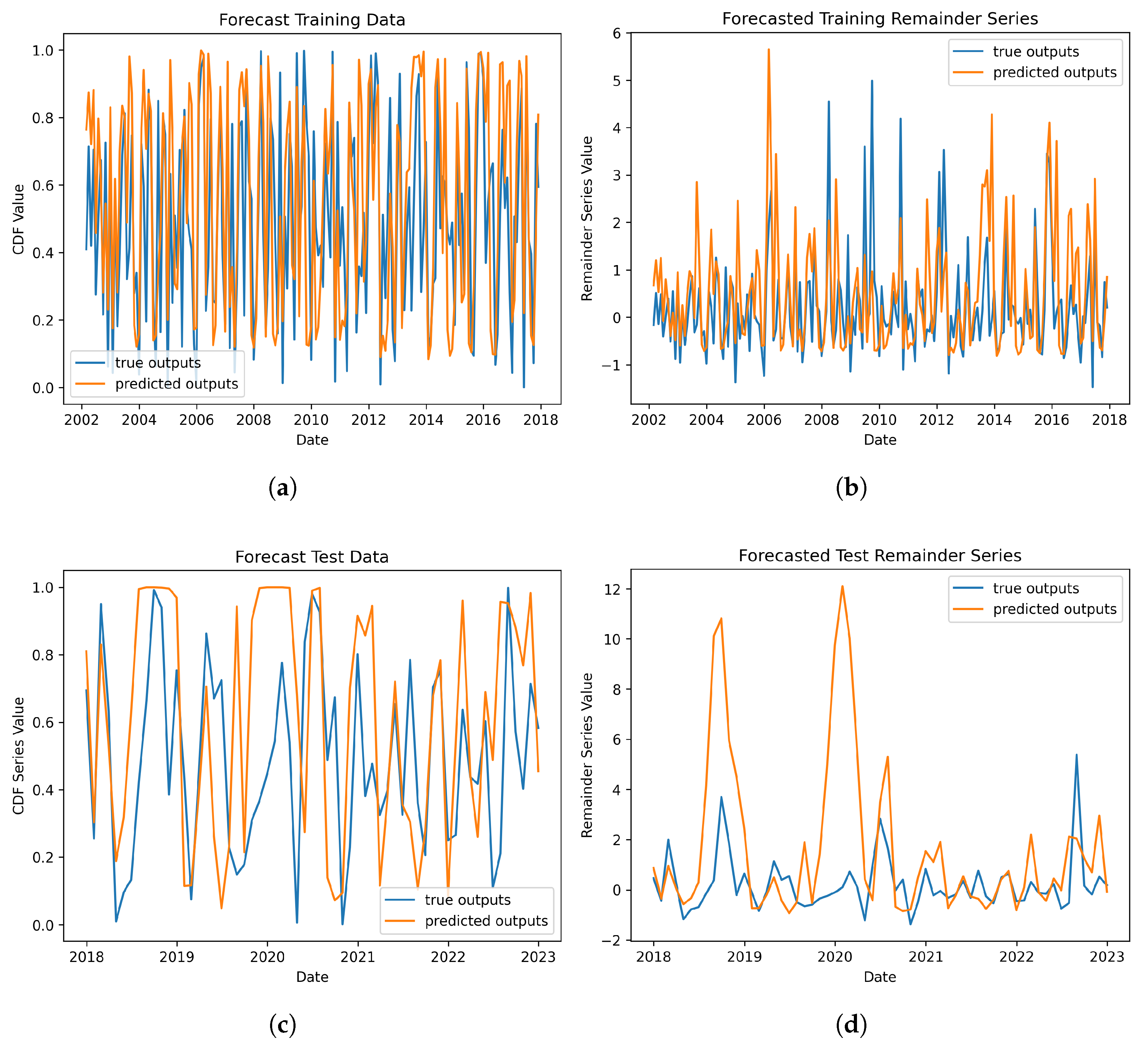
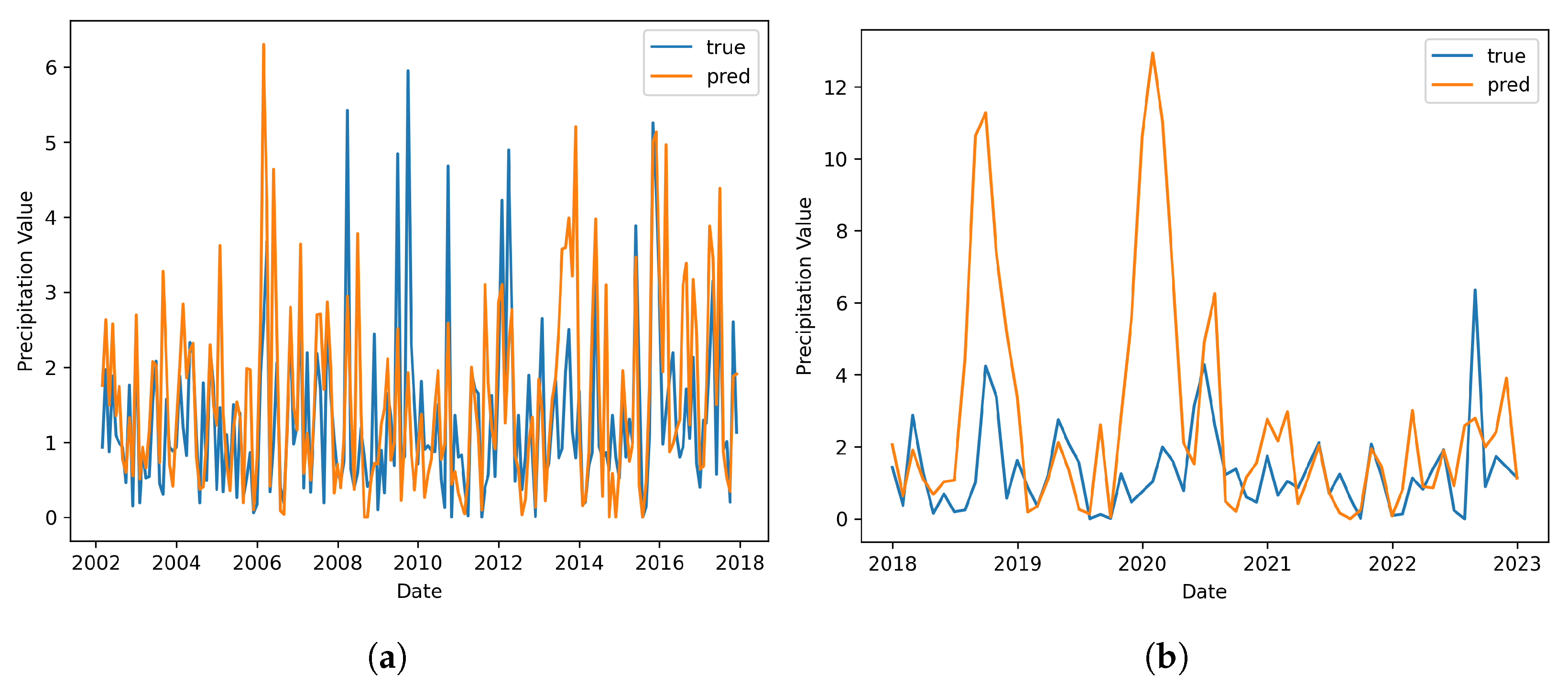
3.3. Model Forecasting Performance
4. Conclusions
5. Research Reproducibility
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADF | Augmented Dickey-Fuller |
| ARIMA | AutoRegressive Integrated Moving Average |
| ASOS | Automated Surface Observing System |
| BiTCN | Bi-directional Temporal Convolutional Network |
| CDF | Cumulative Distribution Function |
| CNN | Convolutional Neural Network |
| EVL | Extreme Value Loss |
| GEV | Generalized Extreme Value |
| K—S | Kolmogorov—Smirnov |
| LSTM | Long Short-term Memory |
| MAE | Mean Absolute Error |
| MSE | Mean Squared Error |
| NWP | Numerical Weather Prediction |
| Probability Density Function | |
| POT | Peak Over Threshold |
| PSO | Particle Swarm Optimization |
| RNN | Recurrent Neural Network |
| SSA | Singular Spectrum Analysis |
| SEATS | Seasonal Extraction in ARIMA Time Series |
| STL | Seasonal Trend Decomposition Based On Loess |
References
- Gleason, K.L.; Lawrimore, J.H.; Levinson, D.H.; Karl, T.R.; Karoly, D.J. A revised US climate extremes index. J. Clim. 2008, 21, 2124–2137. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Kanae, S.; Seneviratne, S.I.; Handmer, J.; Nicholls, N.; Peduzzi, P.; Mechler, R.; Bouwer, L.M.; Arnell, N.; Mach, K.; et al. Flood risk and climate change: Global and regional perspectives. Hydrol. Sci. J. 2014, 59, 1–28. [Google Scholar] [CrossRef]
- Kim, J.; Shu, E.; Lai, K.; Amodeo, M.; Porter, J.; Kearns, E. Assessment of the standard precipitation frequency estimates in the United States. J. Hydrol. Reg. Stud. 2022, 44, 101276. [Google Scholar] [CrossRef]
- Tabari, H. Climate change impact on flood and extreme precipitation increases with water availability. Sci. Rep. 2020, 10, 13768. [Google Scholar] [CrossRef]
- Wing, O.E.; Lehman, W.; Bates, P.D.; Sampson, C.C.; Quinn, N.; Smith, A.M.; Neal, J.C.; Porter, J.R.; Kousky, C. Inequitable patterns of US flood risk in the Anthropocene. Nat. Clim. Chang. 2022, 12, 156–162. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Changes in extreme precipitation in Texas. J. Geophys. Res. Atmos. 2010, 115, D14106. [Google Scholar] [CrossRef]
- Bhatia, N.; Singh, V.P.; Lee, K. Sensitivity of extreme precipitation in Texas to climatic cycles. Theor. Appl. Climatol. 2020, 140, 905–914. [Google Scholar] [CrossRef]
- Gersonius, B.; Ashley, R.; Pathirana, A.; Zevenbergen, C. Climate change uncertainty: Building flexibility into water and flood risk infrastructure. Clim. Chang. 2013, 116, 411–423. [Google Scholar] [CrossRef]
- Arnbjerg-Nielsen, K.; Fleischer, H. Feasible adaptation strategies for increased risk of flooding in cities due to climate change. Water Sci. Technol. 2009, 60, 273–281. [Google Scholar] [CrossRef]
- Moore, T.L.; Gulliver, J.S.; Stack, L.; Simpson, M.H. Stormwater management and climate change: Vulnerability and capacity for adaptation in urban and suburban contexts. Clim. Chang. 2016, 138, 491–504. [Google Scholar] [CrossRef]
- Heidari, B.; Prideaux, V.; Jack, K.; Jaber, F.H. A planning framework to mitigate localized urban stormwater inlet flooding using distributed Green Stormwater Infrastructure at an urban scale: Case study of Dallas, Texas. J. Hydrol. 2023, 621, 129538. [Google Scholar] [CrossRef]
- Kourtis, I.M.; Tsihrintzis, V.A. Adaptation of urban drainage networks to climate change: A review. Sci. Total Environ. 2021, 771, 145431. [Google Scholar] [CrossRef]
- Li, Y.; Xu, J.; Anastasiu, D.C. An extreme-adaptive time series prediction model based on probability-enhanced LSTM neural networks. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 8684–8691. [Google Scholar]
- Sattari, A.; Foroumandi, E.; Gavahi, K.; Moradkhani, H. A probabilistic machine learning framework for daily extreme events forecasting. Expert Syst. Appl. 2025, 265, 126004. [Google Scholar] [CrossRef]
- Najafi, M.S.; Kuchak, V.S. Ensemble-based monthly to seasonal precipitation forecasting for Iran using a regional weather model. Int. J. Climatol. 2024, 44, 4366–4387. [Google Scholar] [CrossRef]
- Li, Y.; Lu, G.; Wu, Z.; He, H.; He, J. High-resolution dynamical downscaling of seasonal precipitation forecasts for the Hanjiang basin in China using the Weather Research and Forecasting Model. J. Appl. Meteorol. Climatol. 2017, 56, 1515–1536. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Wang, S. A hybrid statistical downscaling framework based on nonstationary time series decomposition and machine learning. Earth Space Sci. 2022, 9, e2022EA002221. [Google Scholar] [CrossRef]
- Sha, Y.; Sobash, R.A.; Gagne, D.J. Improving ensemble extreme precipitation forecasts using generative artificial intelligence. Artif. Intell. Earth Syst. 2025, 4, e240063. [Google Scholar] [CrossRef]
- Tran Anh, D.; Van, S.P.; Dang, T.D.; Hoang, L.P. Downscaling rainfall using deep learning long short-term memory and feedforward neural network. Int. J. Climatol. 2019, 39, 4170–4188. [Google Scholar] [CrossRef]
- Ng, K.; Huang, Y.; Koo, C.; Chong, K.; El-Shafie, A.; Ahmed, A.N. A review of hybrid deep learning applications for streamflow forecasting. J. Hydrol. 2023, 625, 130141. [Google Scholar] [CrossRef]
- Ding, D.; Zhang, M.; Pan, X.; Yang, M.; He, X. Modeling extreme events in time series prediction. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 1114–1122. [Google Scholar]
- Sun, W.; Chen, H.; Guan, X.; Shen, X.; Ma, T.; He, Y.; Nie, J. Improved prediction of extreme rainfall using a machine learning approach. Adv. Atmos. Sci. 2025, 42, 1661–1674. [Google Scholar] [CrossRef]
- Sønderby, C.K.; Espeholt, L.; Heek, J.; Dehghani, M.; Oliver, A.; Salimans, T.; Agrawal, S.; Hickey, J.; Kalchbrenner, N. Metnet: A neural weather model for precipitation forecasting. arXiv 2020, arXiv:2003.12140. [Google Scholar] [CrossRef]
- Lin, K.C.; Chen, W.T.; Chang, P.L.; Ye, Z.Y.; Tsai, C.C. Enhancing the rainfall forecasting accuracy of ensemble numerical prediction systems via convolutional neural networks. Artif. Intell. Earth Syst. 2024, 3, 230105. [Google Scholar] [CrossRef]
- Luo, G.; Cao, A.; Ma, X.; Hu, A.; Wang, C. Prediction of extreme precipitation events based on LSTM-self attention model. In Proceedings of the 2024 8th International Conference on Control Engineering and Artificial Intelligence, Shanghai, China, 26–28 January 2024; pp. 91–97. [Google Scholar]
- Liu, X.; Zhao, N.; Guo, J.; Guo, B. Prediction of monthly precipitation over the Tibetan Plateau based on LSTM neural network. J. Geo-Inf. Sci. 2020, 22, 1617–1629. [Google Scholar]
- Wang, W.C.; Ye, F.R.; Wang, Y.Y.; Gu, M. A singular spectrum analysis-enhanced BiTCN-selfattention model for runoff prediction. Earth Sci. Inform. 2025, 18, 31. [Google Scholar] [CrossRef]
- Wang, C.H.; Yuan, J.; Zeng, Y.; Lin, S. A deep learning integrated framework for predicting stock index price and fluctuation via singular spectrum analysis and particle swarm optimization. Appl. Intell. 2024, 54, 1770–1797. [Google Scholar] [CrossRef]
- Xiang, X.; Yuan, T.; Cao, G.; Zheng, Y. Short-term electric load forecasting based on signal decomposition and improved tcn algorithm. Energies 2024, 17, 1815. [Google Scholar] [CrossRef]
- Iowa Environmental Mesonet. Iowa Mesonet: Iowa Environmental Mesonet (IEM) ASOS-AWOS-METAR Data, Iowa State University [data set]. Available online: https://www.mesonet.agron.iastate.edu/request/download.phtml?network=TX_ASOS (accessed on 13 October 2023).
- RB, C. STL: A seasonal-trend decomposition procedure based on Loess. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Dagum, E.B.; Bianconcini, S. Seasonal Adjustment Methods and Real Time Trend-Cycle Estimation; Springer: Berlin/Heidelberg, Germany, 2016; Volume 8. [Google Scholar]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Melbourne, Australia, 2018. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; IEEE: New York, NY, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Solari, S.; Losada, M. A unified statistical model for hydrological variables including the selection of threshold for the peak over threshold method. Water Resour. Res. 2012, 48, W10541. [Google Scholar] [CrossRef]



| Weather Station | POT (Inches/Hour) | Precision | Recall | F1-Score |
|---|---|---|---|---|
| RBD | 1.48 | 0.48 | 0.84 | 0.62 |
| ADS | 0.64 | 0.57 | 0.33 | 0.42 |
| DAL | 1.66 | 0.44 | 0.29 | 0.35 |
| LNC | 1.63 | 0.30 | 0.21 | 0.25 |
| DFW | 1.73 | 0.75 | 0.25 | 0.38 |
| GPM | 0.78 | 0.42 | 0.53 | 0.47 |
| GKY | 1.50 | 0.75 | 0.67 | 0.71 |
| HQZ | 0.94 | 0.44 | 0.57 | 0.50 |
| TKI | 1.70 | 0.62 | 0.56 | 0.59 |
| FTW | 1.51 | 0.32 | 0.36 | 0.34 |
| AFW | 1.25 | 0.62 | 0.53 | 0.57 |
| NFW | 1.20 | 0.60 | 0.45 | 0.51 |
| FWS | 0.72 | 0.53 | 0.67 | 0.59 |
| DTO | 1.49 | 0.45 | 0.74 | 0.56 |
| JWY | 1.20 | 0.53 | 0.53 | 0.53 |
| IAH | 1.87 | 0.34 | 0.32 | 0.33 |
| HOU | 1.81 | 0.46 | 0.65 | 0.54 |
| ELP | 0.46 | 0.63 | 0.54 | 0.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, H.; Murray, S.; Jaber, F.; Heidari, B.; Duffield, N. Tail-Aware Forecasting of Precipitation Extremes Using STL-GEV and LSTM Neural Networks. Hydrology 2025, 12, 284. https://doi.org/10.3390/hydrology12110284
Niu H, Murray S, Jaber F, Heidari B, Duffield N. Tail-Aware Forecasting of Precipitation Extremes Using STL-GEV and LSTM Neural Networks. Hydrology. 2025; 12(11):284. https://doi.org/10.3390/hydrology12110284
Chicago/Turabian StyleNiu, Haoyu, Samantha Murray, Fouad Jaber, Bardia Heidari, and Nick Duffield. 2025. "Tail-Aware Forecasting of Precipitation Extremes Using STL-GEV and LSTM Neural Networks" Hydrology 12, no. 11: 284. https://doi.org/10.3390/hydrology12110284
APA StyleNiu, H., Murray, S., Jaber, F., Heidari, B., & Duffield, N. (2025). Tail-Aware Forecasting of Precipitation Extremes Using STL-GEV and LSTM Neural Networks. Hydrology, 12(11), 284. https://doi.org/10.3390/hydrology12110284







