Figure 1.
Study area and regions of Mexico.
Figure 1.
Study area and regions of Mexico.
Figure 2.
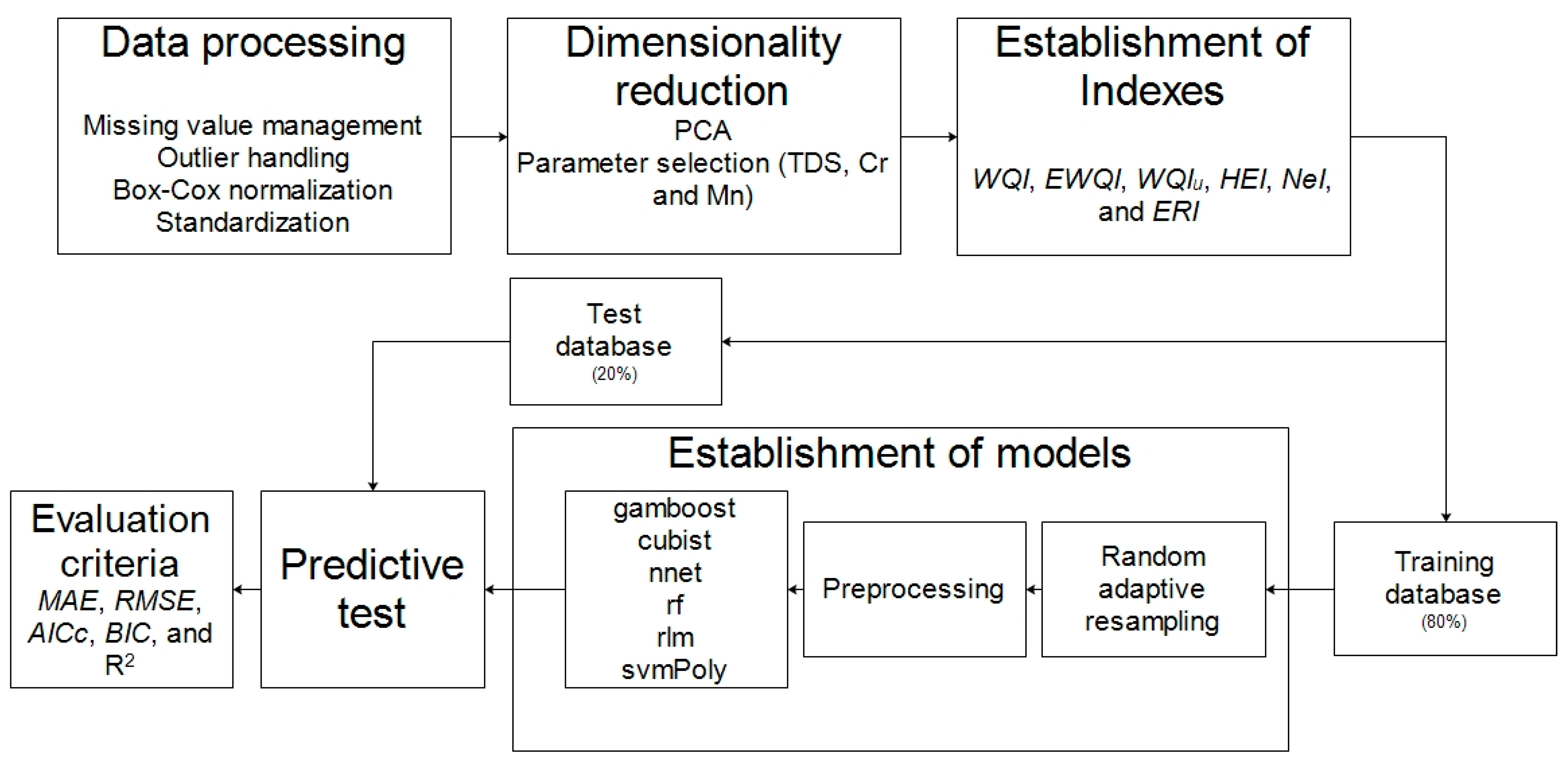
Process diagram. , water quality index; , entropy weighted water quality index; , unified water quality index; , heavy metal evaluation index; , nemerow index; , ecological risks of heavy metals; TDS, total dissolved solids; Cr, crome; Mn, manganese; gamboost, boosted generalized additive model; cubist, decision trees and multiple linear regression methods; rf, random forest; nnet, neural network; rlm, robust linear model; svmPoly, support vector machines with polynomial kernel; , mean absolute error; , root mean square error; , Akaike information criterion corrected; , Bayesian information criterion; R2, coefficient of determination.
Figure 2.
Process diagram. , water quality index; , entropy weighted water quality index; , unified water quality index; , heavy metal evaluation index; , nemerow index; , ecological risks of heavy metals; TDS, total dissolved solids; Cr, crome; Mn, manganese; gamboost, boosted generalized additive model; cubist, decision trees and multiple linear regression methods; rf, random forest; nnet, neural network; rlm, robust linear model; svmPoly, support vector machines with polynomial kernel; , mean absolute error; , root mean square error; , Akaike information criterion corrected; , Bayesian information criterion; R2, coefficient of determination.
Figure 3.
Bi-graph of PCs (A) and Spearman correlation matrix of indicators and PCs (B). PCs, principal components; EC, electrical conductivity; TDSs, total dissolved solids; HRD, hardness; Cr, chromium; Mn, manganese.
Figure 3.
Bi-graph of PCs (A) and Spearman correlation matrix of indicators and PCs (B). PCs, principal components; EC, electrical conductivity; TDSs, total dissolved solids; HRD, hardness; Cr, chromium; Mn, manganese.
Figure 4.
Spatial distribution of indicators resulting from the PCA. TDS (A), total dissolved solids; Cr (B), chromium; Mn (C), manganese.
Figure 4.
Spatial distribution of indicators resulting from the PCA. TDS (A), total dissolved solids; Cr (B), chromium; Mn (C), manganese.
Figure 5.
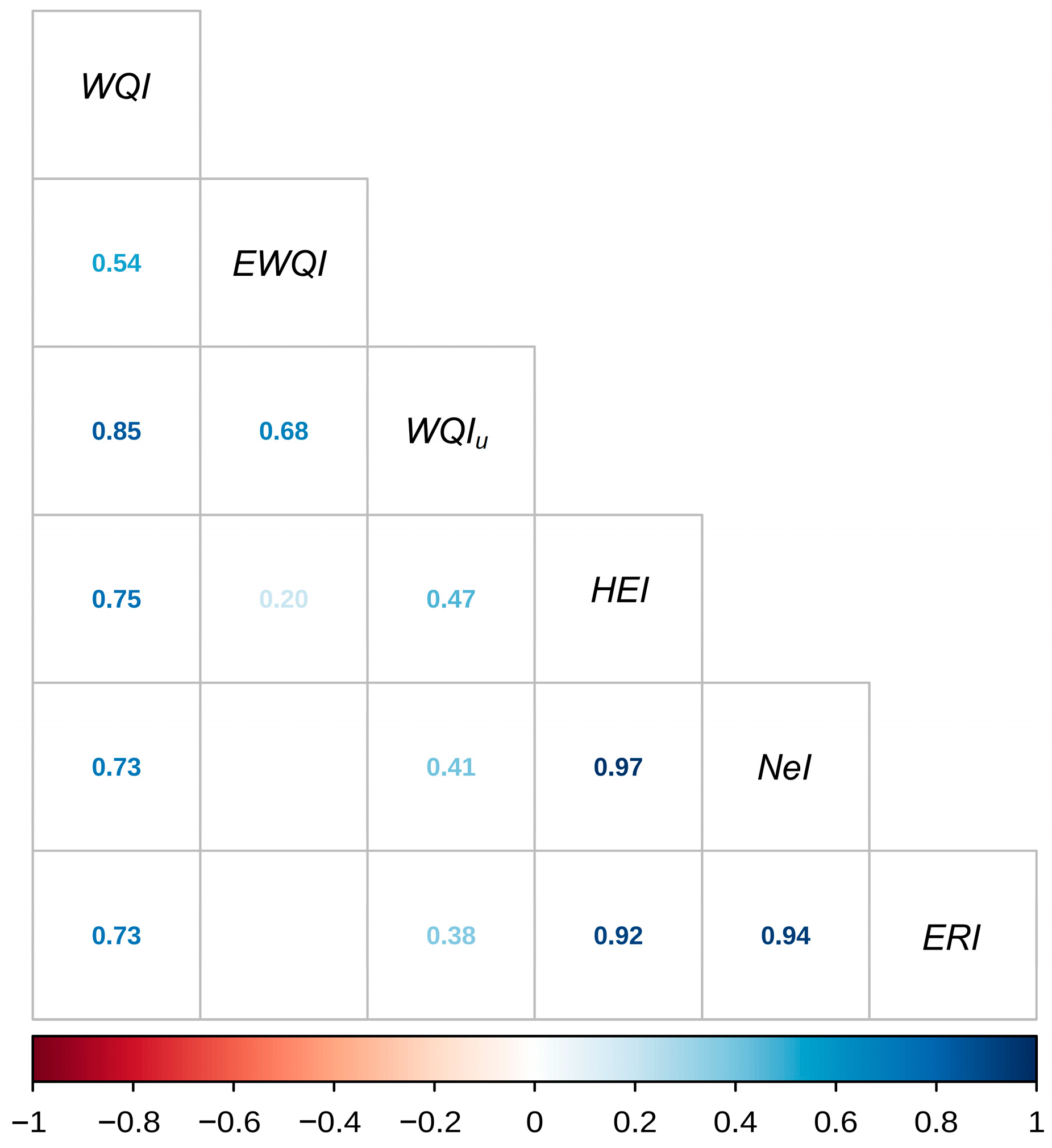
Spearman correlation matrix of analyzed indixes. , water quality index; , entropy weighted water quality index; , unified water quality index; , heavy metal evaluation index; , nemerow index; , ecological risks of heavy metals in groundwater.
Figure 5.
Spearman correlation matrix of analyzed indixes. , water quality index; , entropy weighted water quality index; , unified water quality index; , heavy metal evaluation index; , nemerow index; , ecological risks of heavy metals in groundwater.
Figure 6.
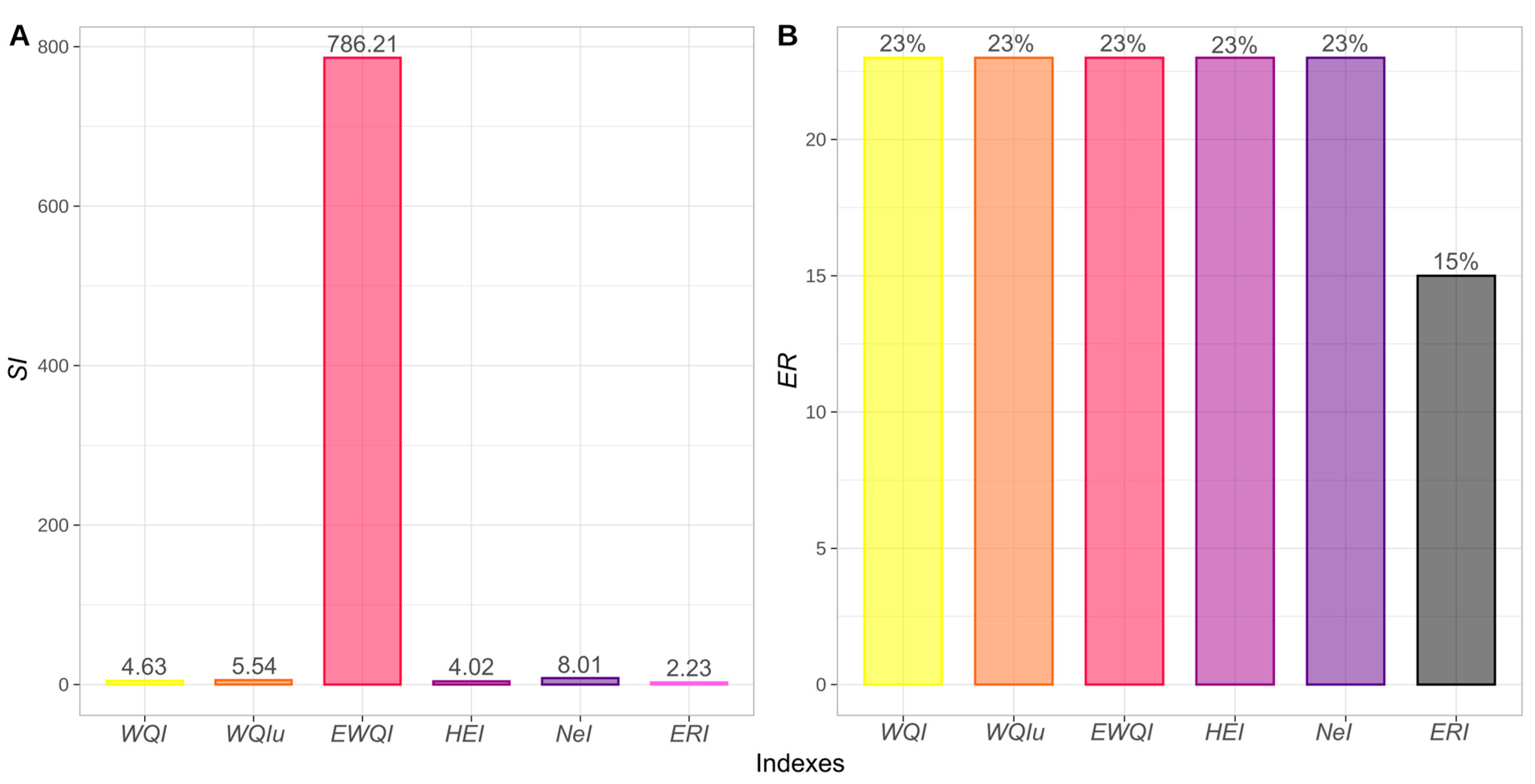
Sensitivity index (A) and efficiency rate index (B) of developed quality indices. , water quality index; , entropy weighted water quality index; , unified water quality index; , heavy metal evaluation index; , nemerow index; , ecological risks of heavy metals in groundwater.
Figure 6.
Sensitivity index (A) and efficiency rate index (B) of developed quality indices. , water quality index; , entropy weighted water quality index; , unified water quality index; , heavy metal evaluation index; , nemerow index; , ecological risks of heavy metals in groundwater.
Figure 7.
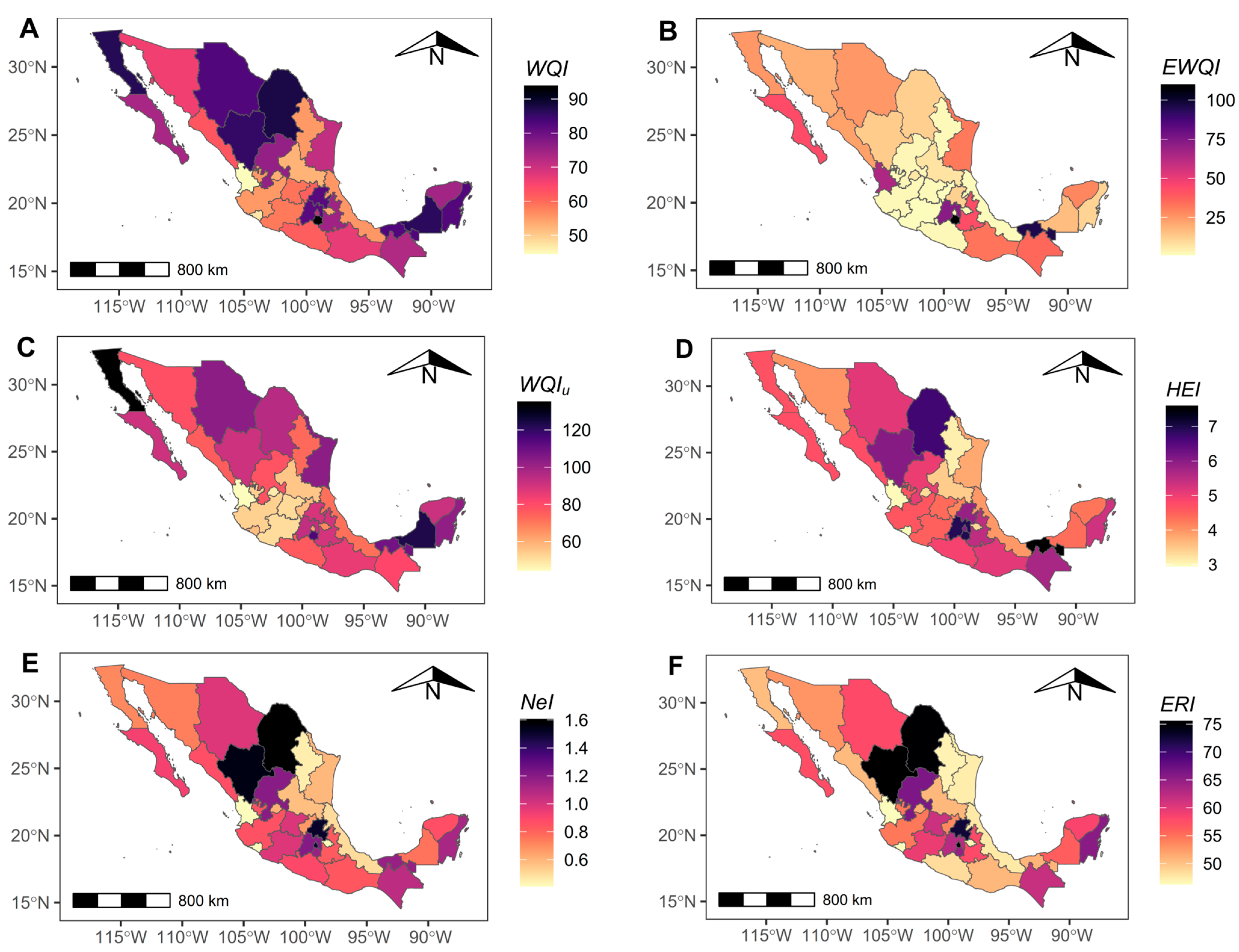
Spatial distribution of quality values of developed quality indices. (A) , water quality index; (B) , entropy-weighted water quality index; (C) , unified water quality index; (D) , heavy metal evaluation index; (E) , nemerow index; (F) , ecological risks of heavy metals in groundwater.
Figure 7.
Spatial distribution of quality values of developed quality indices. (A) , water quality index; (B) , entropy-weighted water quality index; (C) , unified water quality index; (D) , heavy metal evaluation index; (E) , nemerow index; (F) , ecological risks of heavy metals in groundwater.
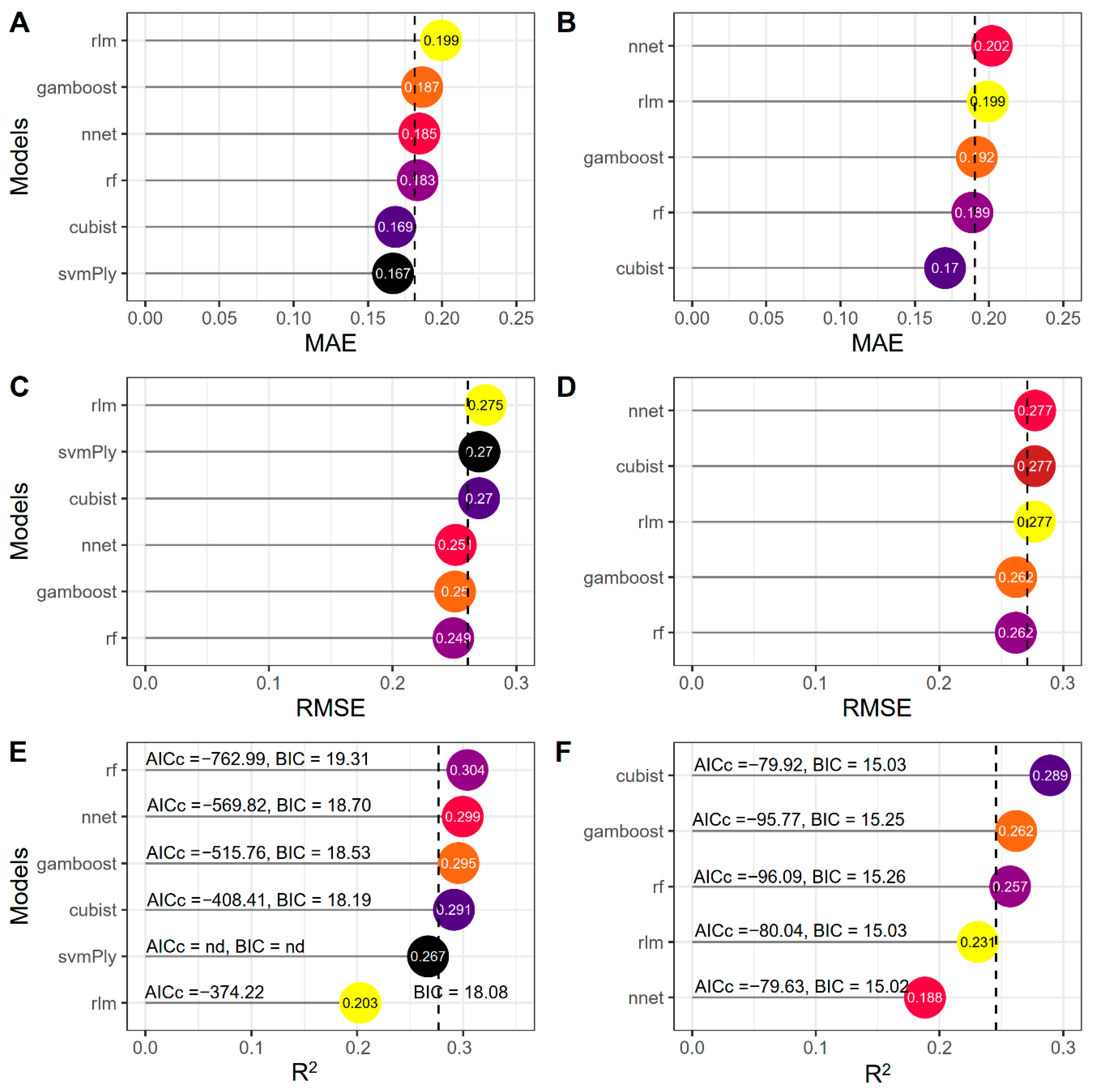
Figure 8.
Evaluation criteria for the ML models developed for the . (A,C,E), training stage criteria. (B,D,F), evaluation stage criteria. , water quality index; gamboost, boosted generalized additive model; cubist, decision trees and multiple linear regression methods; rf, random forest; nnet, neural network; rlm, robust linear model; svmPoly, support vector machines with polynomial kernel; , mean absolute error; , root mean square error; , Corrected Akaike information criterion; , Bayesian information criterion; R2, coefficient of determination; Dotted line, mean value of the criterion.
Figure 8.
Evaluation criteria for the ML models developed for the . (A,C,E), training stage criteria. (B,D,F), evaluation stage criteria. , water quality index; gamboost, boosted generalized additive model; cubist, decision trees and multiple linear regression methods; rf, random forest; nnet, neural network; rlm, robust linear model; svmPoly, support vector machines with polynomial kernel; , mean absolute error; , root mean square error; , Corrected Akaike information criterion; , Bayesian information criterion; R2, coefficient of determination; Dotted line, mean value of the criterion.
Figure 9.
Evaluation criteria for the ML models developed for the . (A,C,E), training stage criteria. (B,D,F), evaluation stage criteria. , unified water quality index; gamboost, boosted generalized additive model; cubist, decision trees and multiple linear regression methods; rf, random forest; nnet, neural network; rlm, robust linear model; svmPoly, support vector machines with polynomial kernel; , mean absolute error; , root mean square error; , Corrected Akaike information criterion; , Bayesian information criterion; R2, coefficient of determination; Dotted line, mean value of the criterion.
Figure 9.
Evaluation criteria for the ML models developed for the . (A,C,E), training stage criteria. (B,D,F), evaluation stage criteria. , unified water quality index; gamboost, boosted generalized additive model; cubist, decision trees and multiple linear regression methods; rf, random forest; nnet, neural network; rlm, robust linear model; svmPoly, support vector machines with polynomial kernel; , mean absolute error; , root mean square error; , Corrected Akaike information criterion; , Bayesian information criterion; R2, coefficient of determination; Dotted line, mean value of the criterion.
Figure 10.
Evaluation criteria for the ML models developed for the . (A,C,E), training stage criteria. (B,D,F), evaluation stage criteria. , heavy metal evaluation index; gamboost, boosted generalized additive model; cubist, decision trees and multiple linear regression methods; rf, random forest; nnet, neural network; rlm, robust linear model; svmPoly, support vector machines with polynomial kernel; , mean absolute error; , root mean square error; , Corrected Akaike information criterion; , Bayesian information criterion; R2, coefficient of determination; Dotted line, mean value of the criterion.
Figure 10.
Evaluation criteria for the ML models developed for the . (A,C,E), training stage criteria. (B,D,F), evaluation stage criteria. , heavy metal evaluation index; gamboost, boosted generalized additive model; cubist, decision trees and multiple linear regression methods; rf, random forest; nnet, neural network; rlm, robust linear model; svmPoly, support vector machines with polynomial kernel; , mean absolute error; , root mean square error; , Corrected Akaike information criterion; , Bayesian information criterion; R2, coefficient of determination; Dotted line, mean value of the criterion.
Table 1.
Indicators analyzed for groundwater.
Table 1.
Indicators analyzed for groundwater.
| Indicator | Levels | Criteria | Indicator | Levels | Criteria |
|---|
| ALK | | Undesirable | FLU | | High |
| Low | | Optimum |
| Medium | | Medium |
| Undesirable | | Low |
| EC | | Excellent for irrigation | TDS | | Excellent for irrigation |
| Good for irrigation | | Use for sensitive crops |
| Permissible for irrigation | | Use for special handling crops |
| Doubtful for irrigation | | Use for tolerant crops |
| Undesirable for irrigation | | Undesirable for irrigation |
| FCL | | Excellent | HRD | | Mild |
| Good | | Moderately mild |
| Acceptable | | Hard |
| Polluted | | Very hard |
| Heavily polluted | | | |
| NO3− | | Excellent | As | | Excellent |
| Good | | Suitable |
| Unsuitable | | Unsuitable |
| Cd | | Excellent | Mn | | Excellent |
| Suitable | | No health effect |
| Unsuitable | | No health effect |
| Hg | | Excellent | Pb | | Excellent |
| Unsuitable | | Unsuitable |
| Fe | | Excellent | Cr | | Excellent |
| No health effect | | Unsuitable |
Table 2.
Standard values and weights of indicators analyzed [
6,
25,
26].
Table 2.
Standard values and weights of indicators analyzed [
6,
25,
26].
| Inticators | Standard Values | | Inticators | Standard Values | |
|---|
| ALK | 400 | 5 | FLU | 1.5 | 4 |
| EC | 1500 | 2 | TDS | 1000 | 2 |
| FCL | 1000 | 4 | HRD | 100 | 2 |
| NO3− | 50 | 5 | As | 0.01 | 5 |
| Cd | 0.003 | 5 | Mn | 0.1 | 2 |
| Hg | 0.006 | 5 | Pb | 0.01 | 5 |
| Fe | 0.3 | 2 | Cr | 0.05 | 5 |
Table 3.
Quality levels of the .
Table 3.
Quality levels of the .
| Level | Quality |
|---|
| Excellent |
| Good |
| Poor |
| Very poor |
| Unsuitable for drinking |
Table 4.
Weights of analyzed parameters of the .
Table 4.
Weights of analyzed parameters of the .
| Indicators | | Indicators | |
|---|
| ALK | 0.235 | FLU | 0.112 |
| EC | 0.235 | TDS | 0.235 |
| FCL | 0.235 | HRD | 0.235 |
| NO3− | 0.235 | As | 0.112 |
| Cd | 0.072 | Mn | 0.103 |
| Hg | 0.189 | Pb | 0.189 |
| Fe | 0.189 | Cr | 0.072 |
Table 5.
Quality levels of the .
Table 5.
Quality levels of the .
| Level | Contamination |
|---|
| Low |
| Moderate |
| High |
Table 6.
Quality levels of .
Table 6.
Quality levels of .
| Level | Contamination |
|---|
| Negligible |
| Slight |
| Moderate |
| Contaminated |
Table 7.
Factors of biological toxicity of heavy metals [
25,
28,
29].
Table 7.
Factors of biological toxicity of heavy metals [
25,
28,
29].
| Heavy Metal | |
|---|
| As | 10 |
| Cd | 30 |
| Cr | 2 |
| Hg | 40 |
| Pb | 5 |
| Mn | 1 |
| Fe | 1 |
Table 8.
Quality levels of the .
Table 8.
Quality levels of the .
| Level | Risk |
|---|
| Low |
| Moderate |
| Considerable |
| Very High |
Table 9.
ML models established [
32].
Table 9.
ML models established [
32].
| Model | | Hyper-Parameters | |
|---|
| gamboost | mstop = 112 | pruene = no | --- |
| cubist | committees = 44 | neighbors = 0 | --- |
| nnet | size = 5 | decay = 0.0007243555 | --- |
| rf | mtry = 2 | --- | --- |
| rlm | intercept = True | psi = psi.bisquare | --- |
| svmPoly | degree = 2 | scale = 0.05776932 | C = 731.8544 |
Table 10.
Descriptive statistics of indicators analyzed.
Table 10.
Descriptive statistics of indicators analyzed.
| Indicators | Mean,
n = 775 | Min | 1st Q | Median | 3rd Q | Max | p |
|---|
| FCL | 402.5 (765) | 1.1 | 1.1 | 1.1 | 120.0 | 1928.6 | <0.001 |
| EC | 1128.1 (794) | 103.0 | 525.5 | 932.0 | 1467.5 | 3086.2 | <0.001 |
| TDS | 875.0 (577) | 120.0 | 443.0 | 753.0 | 1005.0 | 2300.0 | <0.001 |
| FLU | 0.781 (0.71) | 0.200 | 0.295 | 0.530 | 0.944 | 2.833 | <0.001 |
| HRD | 374.3 (252) | 10.0 | 186.5 | 354.0 | 451.6 | 1016.2 | <0.001 |
| ALK | 237.2 (86) | 50.8 | 177.6 | 244.4 | 286.3 | 442.7 | <0.001 |
| NO3− | 5.5 (5.3) | 0.02 | 1.37 | 4.59 | 6.60 | 19.50 | <0.001 |
| As | 0.024 (0.022) | 0.010 | 0.010 | 0.010 | 0.028 | 0.085 | <0.001 |
| Cd | 0.003 (0) | 0.003 | 0.003 | 0.003 | 0.003 | 0.003 | ns |
| Cr | 0.007 (0.003) | 0.005 | 0.005 | 0.005 | 0.007 | 0.016 | <0.001 |
| Hg | 0.0005 (0) | 0.0005 | 0.0005 | 0.0005 | 0.0005 | 0.0005 | ns |
| Pb | 0.005 (0) | 0.005 | 0.005 | 0.005 | 0.005 | 0.005 | ns |
| Mn | 0.046 (0.10) | 0.002 | 0.002 | 0.002 | 0.035 | 0.349 | <0.001 |
| Fe | 0.189 (0.28) | 0.025 | 0.025 | 0.036 | 0.169 | 0.773 | <0.001 |
Table 11.
Descriptive statistics of quality indexes analyzed.
Table 11.
Descriptive statistics of quality indexes analyzed.
| Indicators | Mean,
n = 775 | Min | 1st Q | Median | 3rd Q | Max | p |
|---|
| 75.87 (26) | 32.24 | 54.58 | 70.73 | 93.59 | 149.38 | <0.001 |
| 27.67 (50) | 0.16 | 1.30 | 2.20 | 9.88 | 126.58 | <0.001 |
| 89.39 (38) | 24.45 | 62.01 | 81.76 | 115.35 | 192.13 | <0.001 |
| 5.15 (2.55) | 2.78 | 2.89 | 4.25 | 6.74 | 11.30 | <0.001 |
| 1.04 (0.83) | 0.41 | 0.41 | 0.87 | 1.18 | 3.62 | <0.001 |
| 61.17 (22) | 46.13 | 46.37 | 50.38 | 66.06 | 121.28 | <0.001 |