A Thermal Regime and a Water Circulation in a Very Deep Lake: Lake Tazawa, Japan
Abstract
1. Introduction
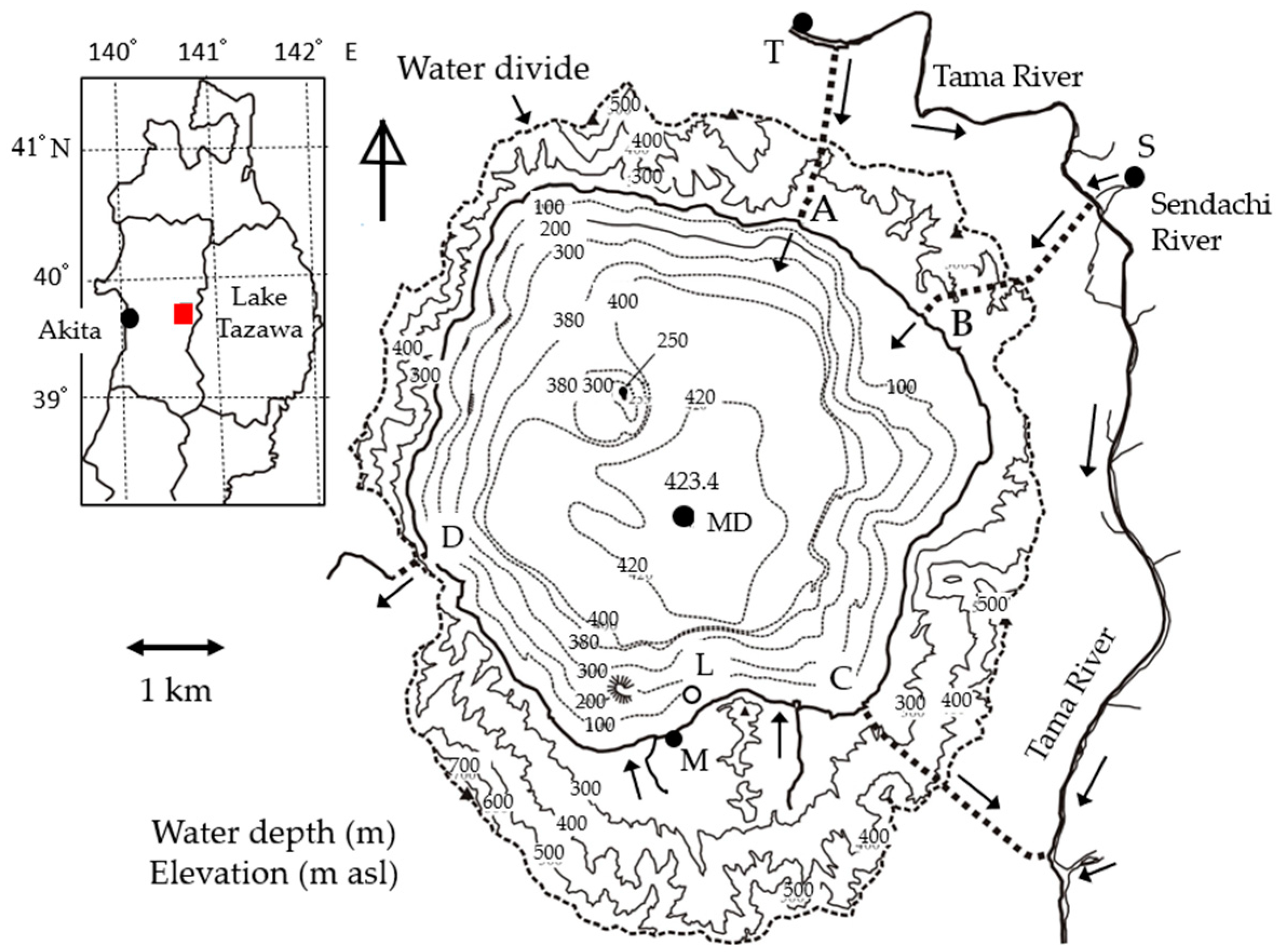
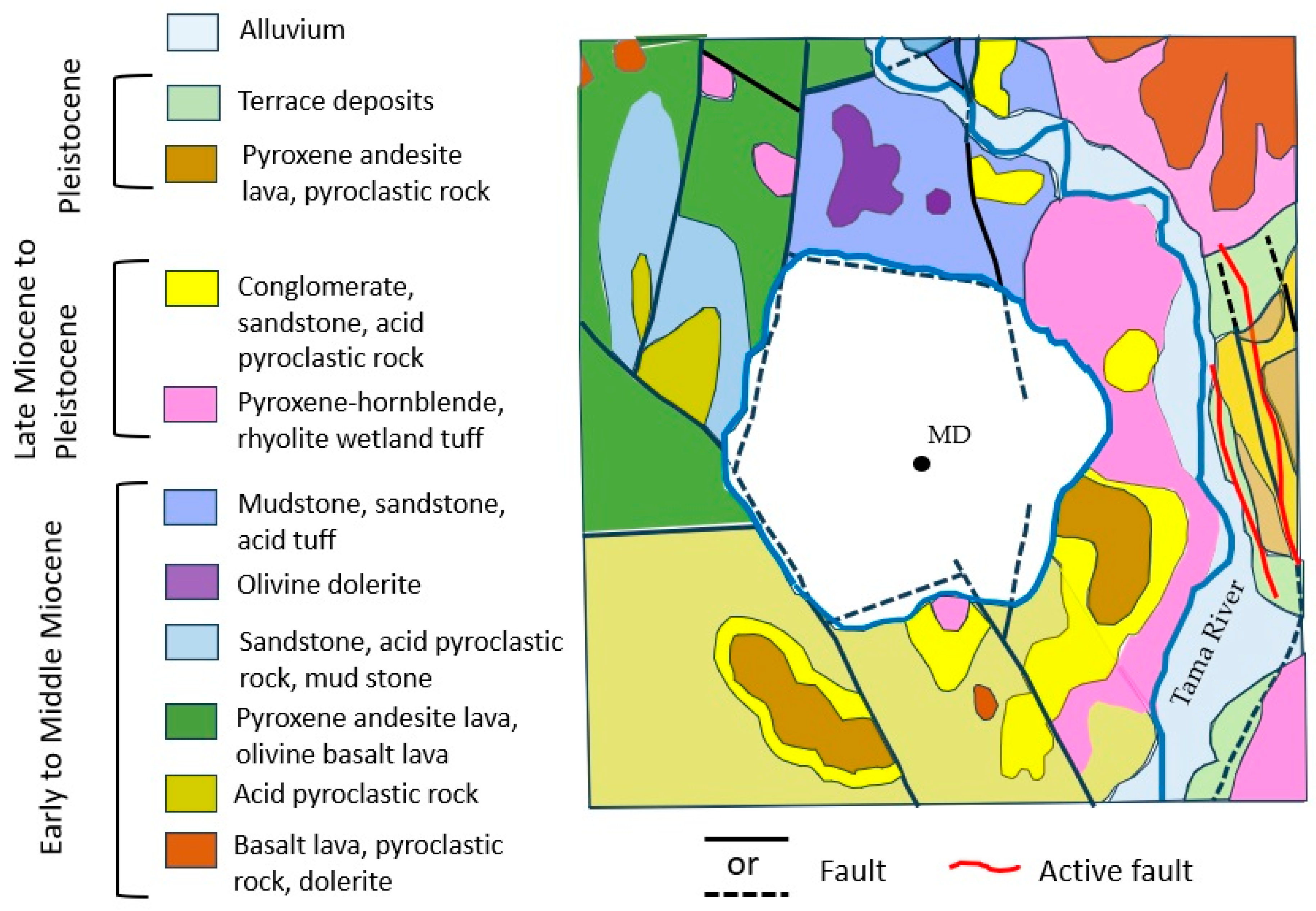
2. Study Area
3. Methods
3.1. Heat Budget of an Open Lake
3.2. Field Observations
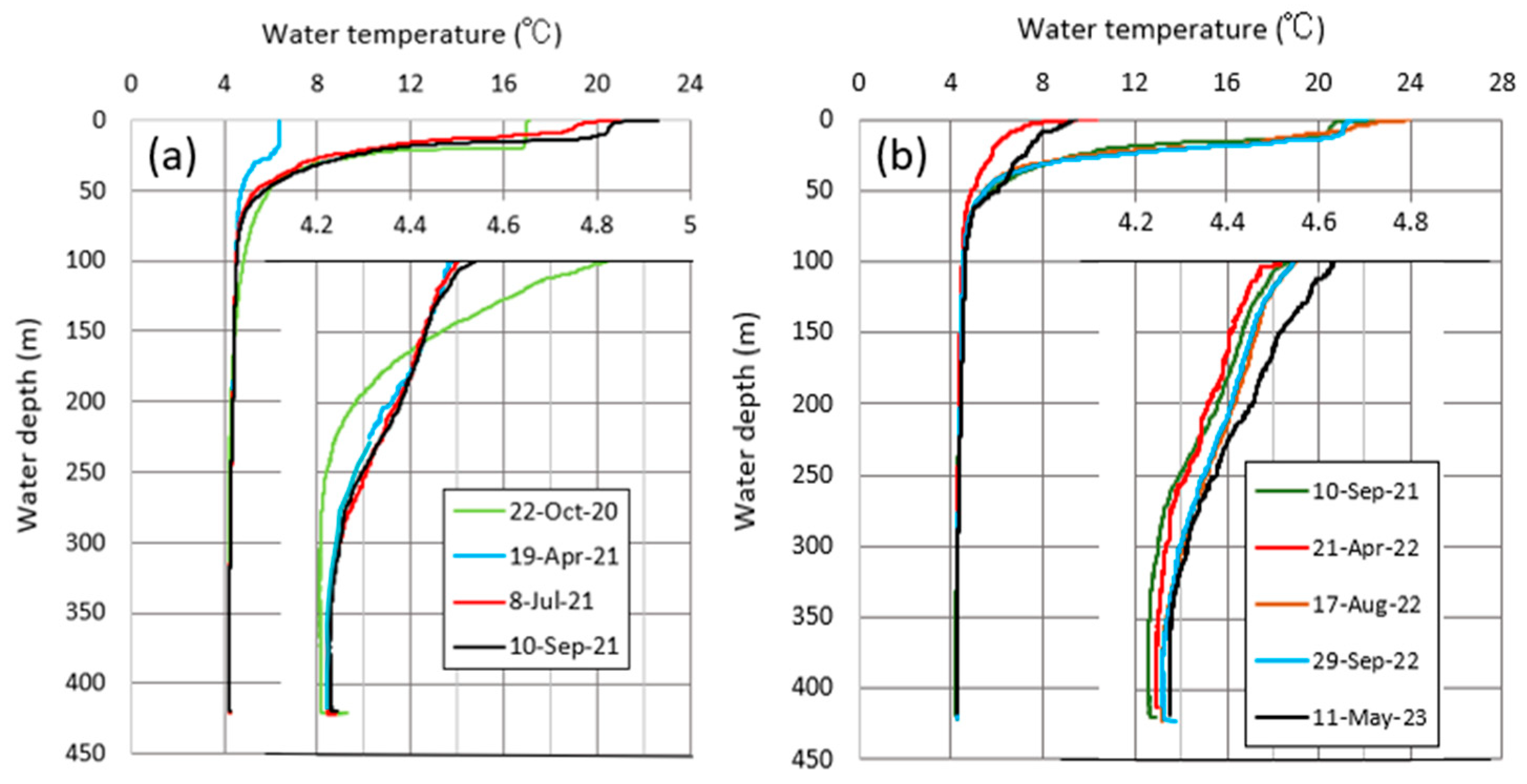
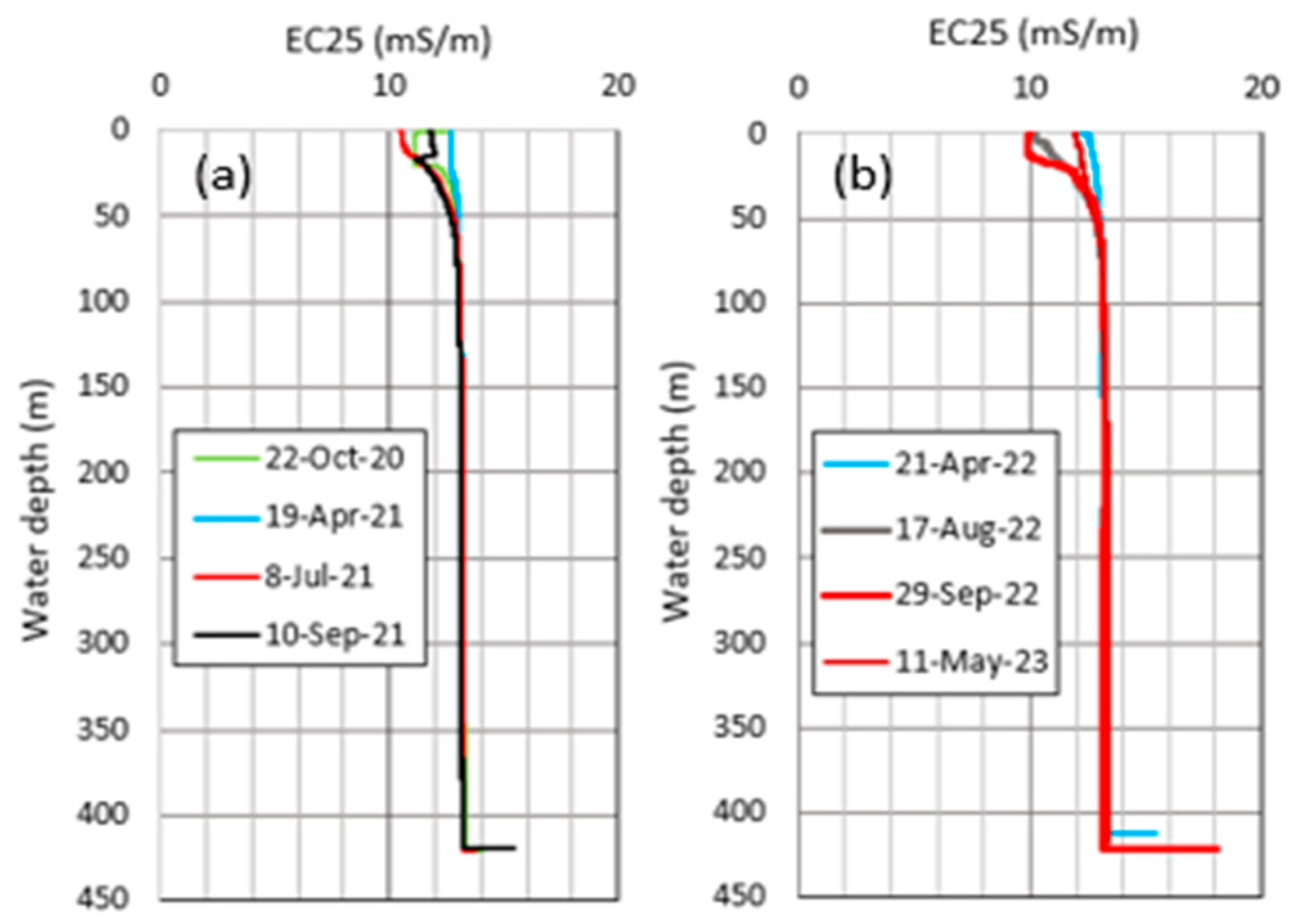
3.3. Data Analysis
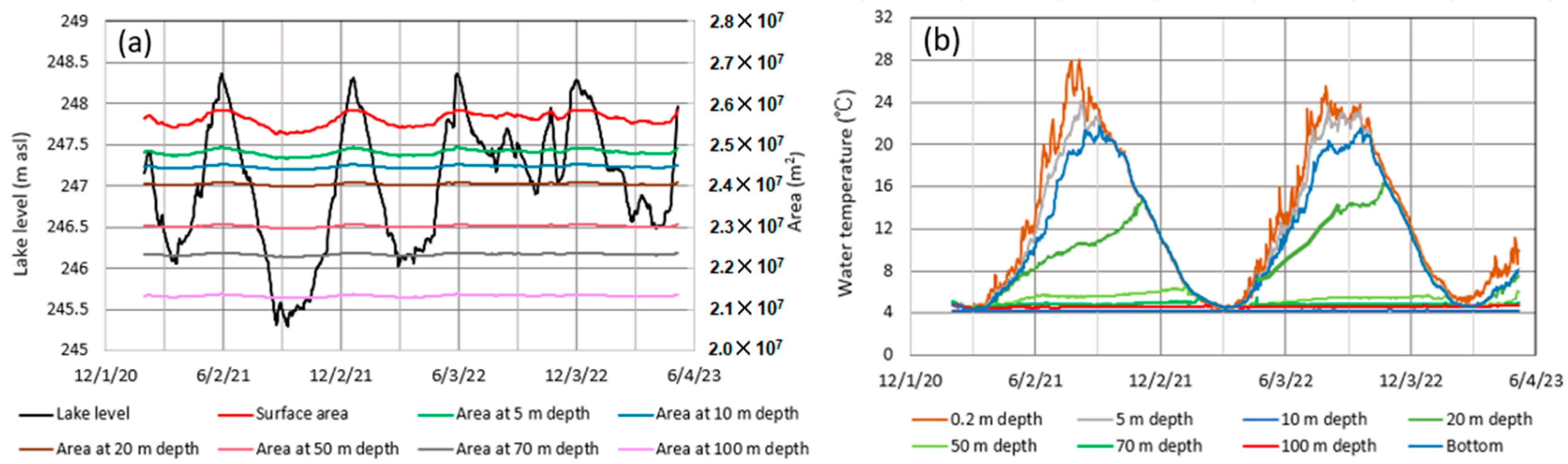
4. Results
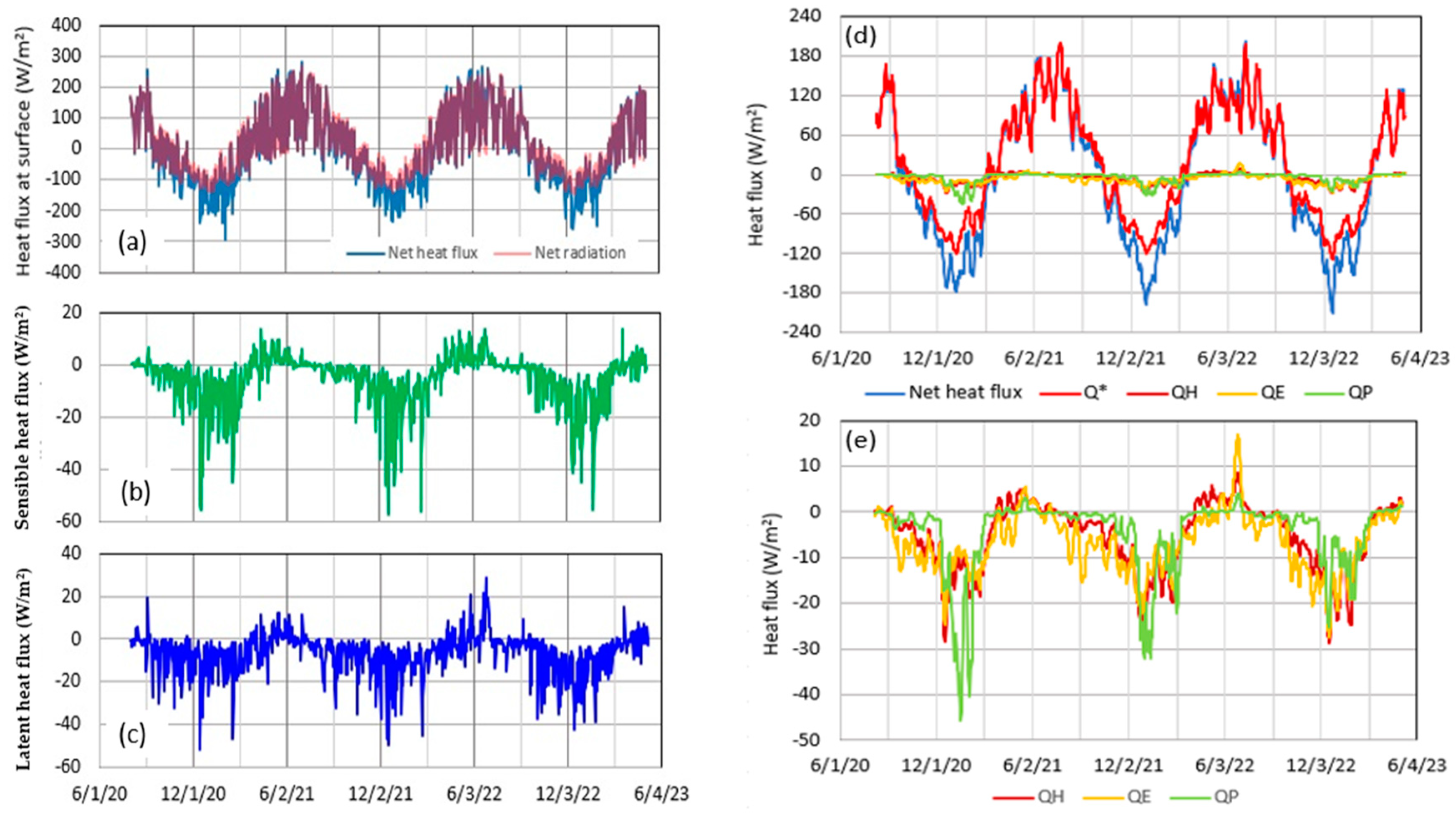
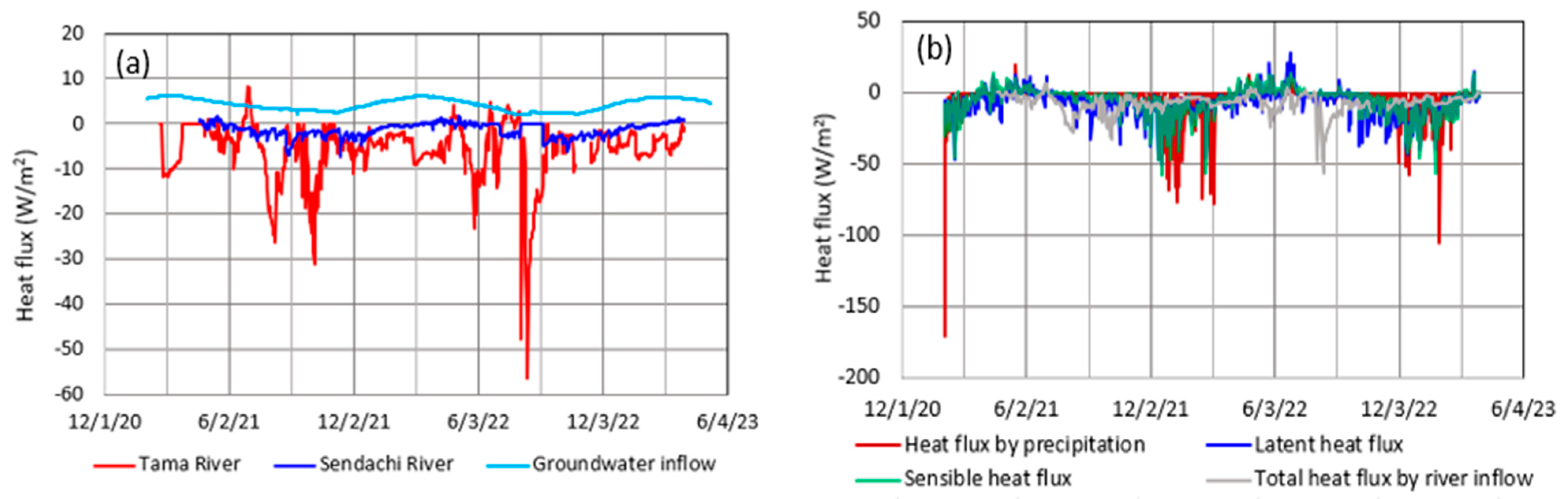
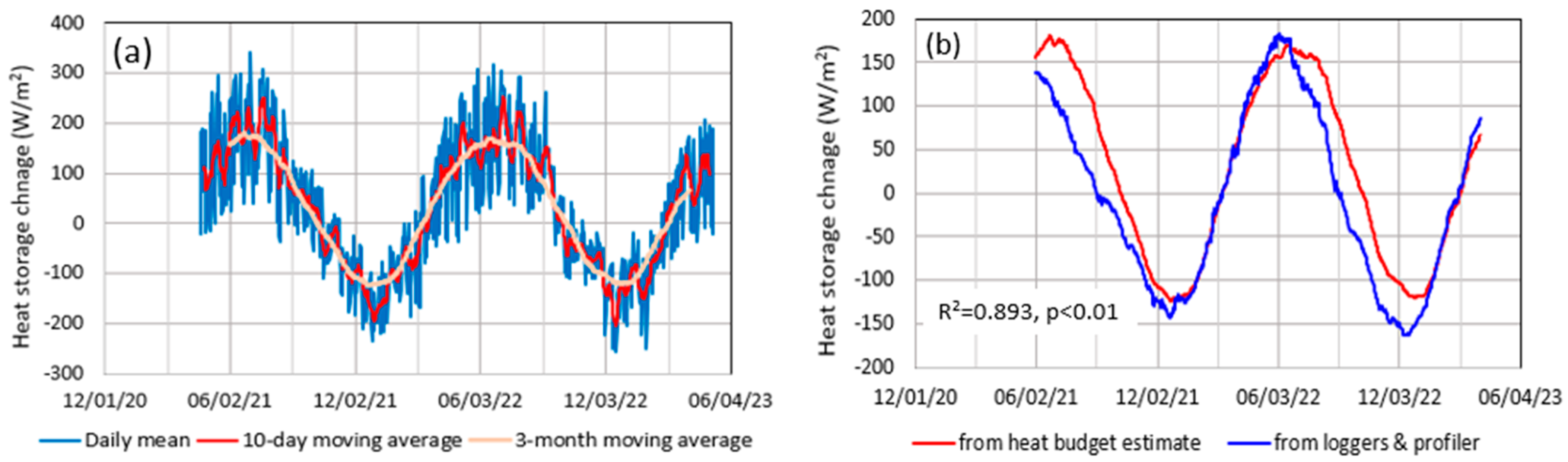
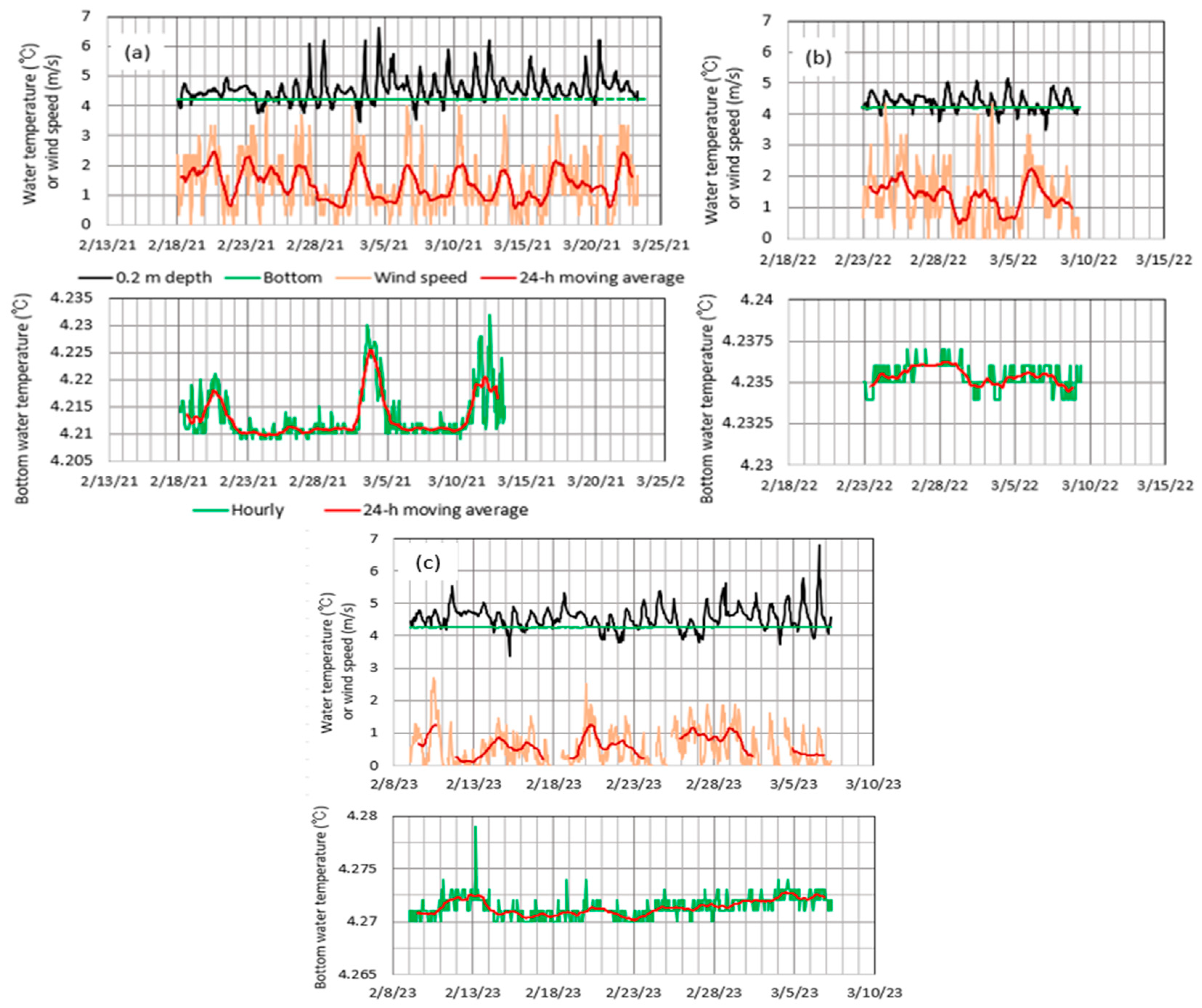
4.1. Heat Budget at Lake Surface
4.2. Heat Flux by River and Groundwater
4.3. Geothermal Heat Flux
5. Discussion
5.1. Comparison of Heat Storage Change
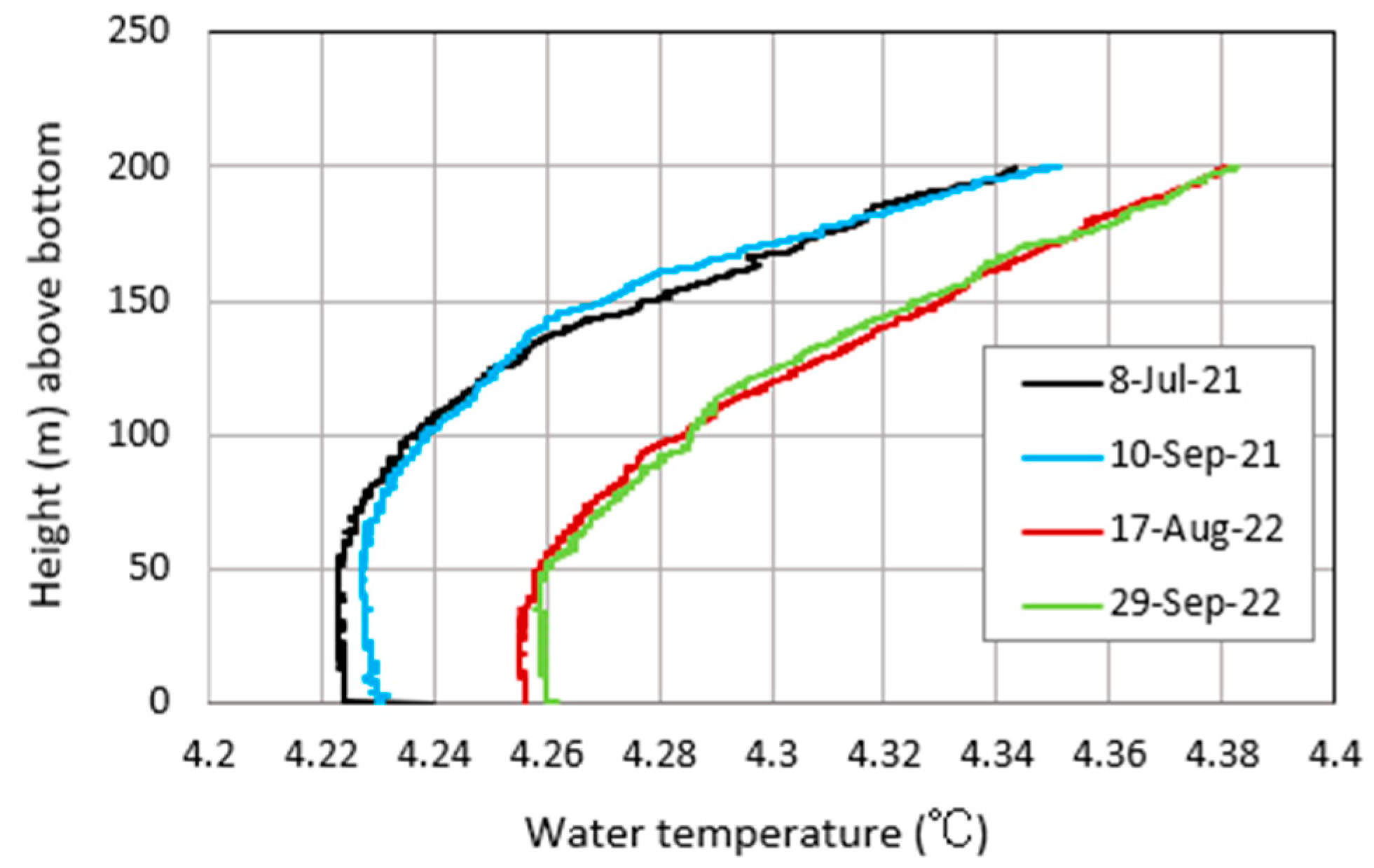
5.2. Lower Limit of Vertical Water Circulation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Senboku City (Ed.) Kunimasu; Akita Sakigake Simpo Co., Ltd.: Akita, Japan, 2017; 32p. [Google Scholar]
- Chikita, K.A.; Amita, K.; Oyagi, H.; Okada, J. Effects of a Volcanic-Fluid Cycle System on Water Chemistry of a Deep Caldera Lake: Lake Tazawa, Akita Prefecture, Japan. Water 2022, 14, 3186. [Google Scholar] [CrossRef]
- Endoh, S.; Yamashita, S.; Kawakami, M.; Okumura, Y. Recent Warming of Lake Biwa Water. Jpn. J. Limnol. 1999, 60, 223–228. Available online: https://www.jstage.jst.go.jp/article/rikusui1931/60/2/60_2_223/_pdf/-char/ja (accessed on 26 December 2023). [CrossRef]
- Woolway, R.I.; Merchant, C.J. Worldwide Alteration of Lake Mixing Regimes in Response to Climate Change. Nat. Geosci. 2019, 12, 271–276. [Google Scholar] [CrossRef]
- Jane, S.F.; Hansen, G.J.A.; Kraemer, B.M.; Leavitt, P.R.; Mincer, J.L.; North, R.L.; Pilla, R.M.; Stetler, J.T.; Williamson, C.E.; Woolway, R.I.; et al. Widespread Deoxygenation of Temperate Lakes. Nature 2021, 594, 66–70. [Google Scholar] [CrossRef] [PubMed]
- Nakada, S.; Imai, A.; Shimotori, K.; Yamada, K.; Yamamoto, H.; Okamoto, T. What interrupted monomictic mixing in Lake Biwa? Heat Budget Analysis Using a Circulation Model. Hydrol. Sci. J. 2023, 68, 2298–2316. [Google Scholar] [CrossRef]
- Momii, K.; Ito, Y. Heat budget estimates for Lake Ikeda, Japan. J. Hydrol. 2008, 361, 362–370. [Google Scholar] [CrossRef]
- Chikita, K.A.; Oyagi, H.; Makino, S.; Kanna, N.; Tone, K.; Sakamoto, H.; Hata, S.; Ando, T.; Shirai, Y. Relations between freezing and climate change in a mountainous lake. J. Jpn. Soc. Phys. Hydrol. 2020, 2, 3–13. [Google Scholar] [CrossRef]
- Katamura, A.; Hayashi, T.; Ishiyama, D.; Oygawa, Y.; Ishiyama, Y. A study of water circulation mechanism based on data of water quality and wind in Lake Tazawa. In Proceedings of the Joint Conference of Japan Society of Hydrology and Water Resources & Japan Association of Hydrological Sciences, Online, 15 September 2021. OP-6-04. [Google Scholar] [CrossRef]
- Farmer, D.M.; Carmack, E. Wind Mixing and Restratification in a Lake near the Temperature of Maximum Density. J. Phys. Oceanogr. 1982, 11, 1516–1533. [Google Scholar] [CrossRef]
- Kelly, C.A.; Rudd, J.W.M.; Furutani, A.; Schindler, D.W. Effects of lake acidification on rates of organic matter decomposition in sediments. Limnol. Oceanogr. 1984, 29, 687–694. [Google Scholar] [CrossRef]
- Liu, S.; He, G.; Fang, H.; Xu, S.; Bai, E. Effects of dissolved oxygen on the decomposers and decomposition of plant litter in lake ecosystem. J. Clean. Prod. 2022, 372, 133837. [Google Scholar] [CrossRef]
- Hayashi, T.; Ishiyama, D.; Ogawa, Y.; Pham Minh, Q. Secular Change of Water Temperature in Hypolimnion of Lake Tazawa. In Proceedings of the JpGU 2018 Conference, Chiba, Japan, 20–24 May 2018; Available online: https://confit.atlas.jp/guide/event-img/jpgu2018/AHW22 (accessed on 28 December 2023).
- Boehrer, B.; Fukuyama, R.; Chikita, K.A. Geothermal Heat Flux into Deep Caldera Lakes Shikotsu, Kuttara, Tazawa and Towada. Limnology 2013, 14, 129–134. [Google Scholar] [CrossRef]
- Tanaka, A. Lake Studies as a Hobby; Shueisha, Co., Ltd.: Tokyo, Japan, 1922. [Google Scholar]
- Kano, K.; Ohguchi, T.; Hayashi, S.; Yanai, K.; Ishizuka, O.; Miyagi, I.; Ishiyama, D. Tazawako caldera, NE Japan and its eruption products. J. Geol. Soc. Jpn. 2020, 126, 233–249. [Google Scholar] [CrossRef]
- Meng, L.; Fu, X.; Wang, Y.; Zhang, X.; Lu, Y.; Jiang, Y.; Yang, H. Internal structure and sealing properties of the volcanic fault zones in Xujianweizi Fault Depression, Songliao Basin, China. Petrol. Explor. Dev. 2014, 41, 165–174. [Google Scholar] [CrossRef]
- Geological Survey of Japan, AIST. Seamless Digital Geological Map of Japan V2 1:200,000, Legend 400 edition, 2023. Available online: https://gbank.gsj.jp/seamless/ (accessed on 17 January 2024).
- Kondo, J. Meteorology in Aquatic Environments; Asakura Publishing Ltd.: Tokyo, Japan, 1994; 350p. [Google Scholar]
- Knobauch, H. Overview of Density Flows and Turbidity Currents; PAP-0816; Water Resources Research Laboratory. 1999; 27p. Available online: https://usbr.gov/tsc/techreferences/hydraulics_lab/pubs/PAP/PAP-0816.pdf (accessed on 30 December 2023).
- Chikita, K.A.; Ochiai, Y.; Oyagi, H.; Sakata, Y. Geothermal linkage between a hydrothermal pond and a deep lake: Kuttara Volcano, Japan. Hydrology 2019, 6, 4. [Google Scholar] [CrossRef]
- Kobayashi, M. Interaction between Lake Water and Groundwater. J. Groundw. Hydrol. 2001, 43, 101–112. [Google Scholar] [CrossRef]
- Arai, T. Hydrology for Regional Analysis; Kokon Shoin Publishers: Tokyo, Japan, 2004; 309p. [Google Scholar]
- Echizen, M.; Sugawara, A.; Takahashi, H.; Kanda, H. The bottom topography off the northern shore of Lake Tazawa. In Proceedings of the Geotechnical Forum 2005, Sendai, Japan, 8–9 September 2005; No. 33. Japan Geotechnical Consultants Association (Zenchiren): Tokyo, Japan, 2005. [Google Scholar]
- Jackett, D.R.; McDougall, T.J.; Freistel, R.; Wright, D.G.; Griffies, S.M. Algorithms for Density, Potential Temperature, Conservative Temperature, and the Freezing Temperature of Seawater. J. Atmos. Ocean. Technol. 2006, 23, 1709–1728. [Google Scholar] [CrossRef]







| A0 | Lake surface area | m2 |
| Az | Surface area at a depth of z | m2 |
| B | Psychrometer constant | hPa/K |
| CE | Dimensionless bulk transfer coefficient for latent heat | - |
| CH | Dimensionless bulk transfer coefficient for sensible heat | - |
| cp | Isobaric specific heat | J/kg/K |
| cpi | Specific heat of ice | J/kg/K |
| cpw | Specific heat of water | J/kg/K |
| ea | Water vapor pressure | hPa |
| ew | Saturated water vapor pressure | hPa |
| G | Heat storage | J |
| Gin | Groundwater inflow | m3/s |
| Gout | Groundwater outflow | m3/s |
| H | Water depth at the deepest point | m |
| HG | Heat flux by groundwater | W/m2 |
| HR | Heat flux by river | W/m2 |
| HS | Geothermal heat flux | W/m2 |
| K↓ | Downward shortwave radiation | W/m2 |
| L | Latent heat of fusion | J/kg |
| L↓ | Downward longwave radiation | W/m2 |
| L↑ | Upward longwave radiation | W/m2 |
| Pr | Rainfall | m/s |
| Pi | Snowfall | m/s |
| p | Air pressure | hPa |
| Q* | Net radiative heat flux | W/m2 |
| QE | Latent heat flux | W/m2 |
| QH | Sensible heat flux | W/m2 |
| QP | Heat flux by precipitation | W/m2 |
| qa | Specific humidity of air | - |
| qs | Saturated specific humidity | - |
| Rin | River inflow | m3/s |
| Rout | River outflow | m3/s |
| T0 | Water temperature of surface layer | °C |
| Tmelt | Ice melting temperature | °C |
| Ta | Air temperature | °C |
| TGin | Temperature of inflowing groundwater | °C |
| TGout | Temperature of outflowing groundwater | °C |
| TL | Representative temperature of lake | °C |
| Ts | Surface water temperature | °C |
| TRin | Water temperature of inflowing river | °C |
| TRout | Water temperature of outflowing river | °C |
| Tw | Wet bulb temperature | °C |
| Tz | Water temperature at a depth of z | °C |
| t | time | s |
| u | Wind speed | m/s |
| V | Lake volume | m3 |
| α | Albedo | - |
| λ | Latent heat of evaporation | J/kg |
| Air density | kg/m3 | |
| Ice density | kg/m3 | |
| Water density | kg/m3 |
| Snowfall Period | Days | Total (mm) | QP (W/m2) | Q* (W/m2) | QH (W/m2) | QE (W/m2) |
|---|---|---|---|---|---|---|
| 13 December 2020–26 February 2021 | 76 | 600.8 | −21.5 (16.1%) | −82.4 (62.0%) | −15.8 (11.9%) | −13.3 (10.0%) |
| Snowfall | 52 | 412.3 | −30.9 (19.2%) | −94.9 (58.9%) | −19.3 (12.0%) | −15.9 (9.9%) |
| Rainfall | 8 | 188.5 | −3.8 (3.9%) | −83.8 (84.1%) | −5.1 (5.1%) | −6.9 (6.9%) |
| No precipitation | 16 | - | - | −41.1 (70.0%) | −8.8 (16.5%) | −7.9 (13.5%) |
| Rainfall Period | Days | Total (mm) | QP (W/m2) | Q* (W/m2) | QH (W/m2) | QE (W/m2) |
| 27 February 2021–1 December 2021 | 278 | 2041.2 | −0.6 | 58.6 | −1.7 | −4.9 |
| Rainfall | 140 | 2041.2 | −1.2 | 18.0 | −2.0 | −5.2 |
| No precipitation | 138 | - | - | 104.6 | −0.7 | −4.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chikita, K.A.; Oyagi, H.; Amita, K. A Thermal Regime and a Water Circulation in a Very Deep Lake: Lake Tazawa, Japan. Hydrology 2024, 11, 40. https://doi.org/10.3390/hydrology11030040
Chikita KA, Oyagi H, Amita K. A Thermal Regime and a Water Circulation in a Very Deep Lake: Lake Tazawa, Japan. Hydrology. 2024; 11(3):40. https://doi.org/10.3390/hydrology11030040
Chicago/Turabian StyleChikita, Kazuhisa A., Hideo Oyagi, and Kazuhiro Amita. 2024. "A Thermal Regime and a Water Circulation in a Very Deep Lake: Lake Tazawa, Japan" Hydrology 11, no. 3: 40. https://doi.org/10.3390/hydrology11030040
APA StyleChikita, K. A., Oyagi, H., & Amita, K. (2024). A Thermal Regime and a Water Circulation in a Very Deep Lake: Lake Tazawa, Japan. Hydrology, 11(3), 40. https://doi.org/10.3390/hydrology11030040








