Abstract
This study employs a temporal fusion transformer (TFT) for predicting overflow from sewer manholes during heavy rainfall events. The TFT utilised is capable of forecasting overflow hydrographs at the manhole level and was tested on a sewer network with 975 manholes. As part of the investigations, the TFT was compared to other deep learning architectures to evaluate its predictive performance. In addition to precipitation measurements and forecasts, the issue of how the additional consideration of measurements in the sewer network as model inputs impacts forecast accuracy was investigated. A varying number of sensors and different measurement signals were compared. The results indicate high performance for the TFT compared to other model architectures like a long short-term memory (LSTM) network or a dual-stage attention-based recurrent neural network (DA-RNN). Additionally, results suggest that considering a single measuring point at the outlet of the sewer network instead of an entire measuring network yields better forecasts. One possible explanation is the high correlation between measurements, which increases model and training complexity without adding much value.
1. Introduction
Heavy rainfall events lead to vast amounts of run-off, particularly in highly sealed urban areas, resulting in overloaded sewer networks. According to the sixth report of the Intergovernmental Panel on Climate Change (IPCC) [1], the number and intensity of such events has increased in recent years and is highly likely to increase further due to ongoing global warming. Past events such as the one in July 2021 in Western Europe [2] or the one in September 2023 in Greece [3] have demonstrated the extent to which such events can be particularly destructive. In Germany, the drainage system is designed for flooding frequencies of up to 10 years [4]. However, it cannot transport the water volumes of such extreme events out of the catchment without causing damage. This highlights the importance of having accurate information on the extent of flooding induced by heavy rainfall, enabling proactive and targeted action.
Hydrodynamic (HD) models have become the state of the art for simulating the run-off behaviour of pluvial flash floods in urban areas. Usually, the flow behaviour in the sewer network is calculated with a 1D model and the flood extent on the surface with a 2D model. Coupled sewer network and surface modelling in a hydrodynamic 1D–2D simulation model has been proven remarkably accurate [5]. Unfortunately, the high level of detail leads to long calculation times of several hours or even days. In parallel to this, using the currently available prediction models, convective heavy rainfall events triggering pluvial flash floods can only be predicted with adequate accuracy with lead times of up to two hours [6,7,8]. Due to these facts, hydrodynamic calculation models are currently unsuitable for real-time applications and thus limited to historical event simulation.
Various approaches have been explored in recent years to reduce the simulation time for estimating flooding and enable forecasts. In addition to reducing the level of detail [9] or simplifying the calculation approaches considered [10,11,12], the use of machine learning (ML) methods [13], especially neural networks [14], has been investigated in particular. In contrast to hydrodynamic calculation models, machine learning methods do not require the physical laws to be described. Instead, they learn the physical relationships between inputs and target variables using predefined examples during a training process.
The performance of machine learning methods has been demonstrated in various areas of application in the field of flood simulation. Multiple studies have illustrated the efficiency of neural networks for estimating flooded areas [15,16,17,18,19]. In addition, various studies have been carried out in modelling urban drainage networks [20], including several on the prediction of overflows. In this context, on the one hand, a distinction is made between approaches generating forecasts for individual central points of the sewer system, such as main structures or outlets [21,22,23,24]. On the other hand, other methods focus on generating predictions down to the manhole level [25,26,27,28,29]. In [30], an integrated consideration of overflow and flooding area predictions was also performed. In addition to precipitation information, the developed model also considers a forecast of overflow from manholes as an additional load to predict the flooded areas for the upcoming time steps.
In this study, a deep learning model was trained to predict the upcoming overflow behaviour at the manhole level based on measurements and forecasts of precipitation, as well as measurements in the pipes of the sewer network. Various deep learning models were compared with one another. In addition, sensitivity analyses were carried out on the influence of the resolution of the measurement network used and the measurement signal taken into account. For this purpose, an artificial sensor network is used with simulated hydrographs retrieved from various locations of the sewer network. On the one hand, the investigations aim to provide the overflow hydrographs required as input data in real time for the flooding area prediction model developed by Burrichter et al. [30]. On the other hand, the quantity and quality of measurements in the sewer network, used as model input, are examined. Based on the results, recommendations for the construction of a sensor network can be derived. The main contributions of this study can be summarised as follows.
- Evaluation of a deep learning-based model capable of forecasting overflow hydrographs at the manhole level. In contrast to other studies, the temporal fusion transformer [31] as a transformer-based network architecture is used. Transformers have proven to be very efficient in processing sequences, and in the case of the temporal fusion transformer, especially in the field of time series analysis and forecasting.
- The influence of a spatially high-resolution sensor network as an additional input variable on the accuracy of the prediction results is evaluated. This approach is compared to a model considering only one sensor at the outlet of the sewer network and a model without measurements in the sewer network.
- The influence of the selected measurement signal on the prediction quality is tested. Signals considered for which the performance of the trained models is evaluated are discharge, water level, filling degree and filling level classes.
2. Methodology
2.1. Model Setup
The model structure shown in Figure 1 was used in this work to predict overflow from sewer manholes. The machine learning model aimed to learn the relationship between the overflow hydrographs at the manholes in the catchment area, as the target variable, and the explanatory variables of precipitation information, predicted precipitation information and measurements in the pipes of the sewer system. The precipitation information included the precipitation intensity, the total accumulated precipitation and the elapsed time since the event’s start. As in similar studies [25,27,28,32], the overflow hydrographs and the in-channel measurements were generated using an HD model. This approach was adopted due to insufficient measurement data for the learning problem described. Accordingly, the model functions as a surrogate to generate the results of an HD model of nearly equivalent quality and in just a few seconds, so it is viable to be implemented in real-time warning systems.

Figure 1.
Model setup with all considered inputs (left) and the predicted overflow hydrographs of sewer manholes (right).
The developed model utilises multivariate time series and exclusively relies on exogenous variables to describe target variables. After training, the model predicts the target variables for a selected prediction horizon H using the recent D time steps of the explanatory features. Only the predicted precipitation information is considered for the forecast horizon H while being part of the inputs. Since the prediction horizon is set to H > 1, multiple time steps are predicted. Ben Taieb et al. [33] describe various strategies for this application in their work. The multi-input, multi-output (MIMO) strategy described there is also used within this study. Using this strategy, prediction is made in multiple stages instead of several single-stage predictions for each time step, as is usual with recursive or direct prediction strategies. Accordingly, a prediction for the upcoming H values (Si,t+1,… Si,t+H) is made for all manholes Si at each time t (see Figure 1). Although this restricts flexibility, as the model has the same structure for each time step, it also offers advantages. On the one hand, the stochastic dependencies between the individual time steps are retained compared to the direct strategy. On the other hand, the prediction errors are not accumulated, as in the recursive strategy [33]. The model setup is treated as a supervised learning problem, as inputs and corresponding target variables are clearly defined. Furthermore, the model predicts target variables as continuous values, making it a regression problem.
2.2. Temporal Fusion Transformer
A temporal fusion transformer (TFT) is a model architecture presented by Lim et al. [31], which is based on the transformer architecture developed by Vaswani et al. [34]. A special feature of transformers is the use of attention mechanisms. The core idea of attention mechanisms is focusing on the most relevant features of the input data. This is achieved by assigning weights to each input within an input sequence depending on its relevance to the target sequence. Common mechanisms are, for example, the variants presented in Bahdanau et al. [35] or Luong et al. [36], as well as the multi-head attention [34] used in the transformer architecture.
TFTs are characterised by their flexibility concerning the input data to be taken into account, which means that they can consider known inputs from past and future time steps as well as static variables. This makes TFTs suitable for a wide range of problems. The overall architecture and individual components of a TFT are shown in Figure 2. In contrast to the transformer architecture developed by Vaswani et al. [34], the basis is an encoder–decoder structure that uses recurrent long short-term memory (LSTM) layers instead of multi-layer perceptron (MLP) layers. Combining the LSTM cell-based encoder–decoder structure with the multi-head attention used in the original transformer enables TFTs to learn both long-term and short-term temporal dependencies. Another component of the TFT architecture are gated residual network (GRN) blocks, which can be found at various points in the overall architecture. These blocks allow unused components to be skipped, which enables the network to adapt its depth and complexity to different tasks and datasets. In addition, the TFT contains variable selection networks (VSN) blocks that accept network inputs and identify the most important input variables while ignoring less relevant inputs. For this purpose, weightings are calculated depending on the influence of the input characteristics on the target variable, making the model interpretable to a certain degree.
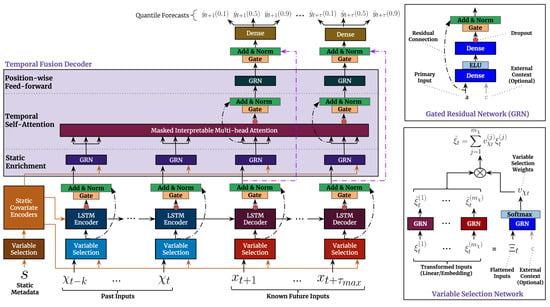
Figure 2.
Representation of the temporal fusion transformer architecture (left) and detailed view of the gated residual network blocks and the variable selection network blocks (right) [31].
The TFT model introduced by Lim et al. [31] is trained with the quantile loss function described in Wen et al. [37]. As a result, the prediction is made based on intervals that specify the range of probable target values for a prediction time step. The intervals are established by specifying the quantiles to be used during training and help to account for model uncertainties during the forecasting process.
3. Case Study
3.1. Study Area and Monitoring Network
The study area is located in the south of the city of Gelsenkirchen and covers an area of 3.1 km². The area is mainly urban and is drained by a combined sewer system. In the north-west of the area, there is a pumping station to which the area drains. This station then transports the collected waste water to a collector and then to a waste-water treatment plant.
A coupled hydrodynamic 1D–2D simulation model was created in MIKE+ software (release 2021, update 1) [38] to calculate the overflow characteristics. The municipal drainage company of Gelsenkirchen provided the sewer network model, comprising 975 manholes and 982 sewers in the investigated area. A grid-based computational mesh with 2 m × 2 m resolution was created for the study area to model the run-off behaviour on the terrain surface. The sewer network model and the surface model were coupled bidirectionally via the manholes so that flows of water from the ground surface into the sewer system and vice versa were recognised. Run-off from roof areas, public traffic areas and paved private areas with increased pollution is assigned to the sewer network model. For the other ground surfaces, run-off is generated directly on the cells of the surface model. This approach has proven to be the most accurate during model calibration.
As part of the KIWaSuS research project [39], in which the presented study was realised, a low-cost sensor network for measurements in the drainage system was planned. The aim was to provide an additional data source for the prediction model. In order to analyse the added value of a monitoring network compared to a single measurement at the area outlet or no measurement at all, an artificial monitoring network of 20 sensors was assumed in this study (see Figure 3). When selecting the locations, it was ensured that they covered the area as representatively as possible and that waste water from multiple pipes flowed to these points. At the shown sensor locations, the simulation results were retained for subsequent use as additional model input during the training process.
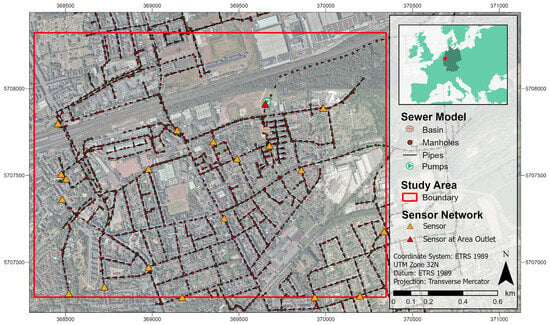
Figure 3.
Illustration of the study area’s sewer network and the artificial sensor network.
3.2. Data Generation and Preprocessing
The data used in this study were obtained following the procedures outlined in Burrichter et al. [30]. As model input, 258 heavy rainfall events were utilised, 105 of which were design rainfall events and 153 natural rainfall events. The design rainfall events were used to sufficiently consider extreme events with long return periods, while the natural rainfall events aimed to represent real event characteristics accurately. The distribution of events based on their return periods is illustrated in Figure 4. For every rainfall event considered, overflow hydrographs were calculated by the hydrodynamic 1D–2D simulation model of the study area. In addition, flow and waste-water level measurements were extracted from the HD model at sewer pipes where a sensor was located, in order to be used in the following training procedure. For the simulation of each flooding event, precipitation was assumed to be spatially uniform, and a period of time of 120 min was considered after the end of the corresponding rainfall event. This was done in order to account for processes after the end of the precipitation event, such as recession in the flooding situation, which should also be forecast accurately.
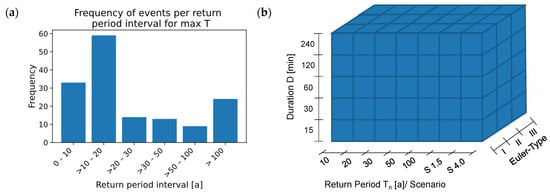
Figure 4.
Distribution of events in the dataset. (a) The maximum return time T distribution for all 153 natural rainfall events. (b) A schematic representation of the design rainfall events, with the selected durations, model rainfall types, and return periods/scenarios. For scenarios S 1.5 and S 4.0, the number indicates the increase factor by which the values of the 100-year design rains were multiplied [30].
Due to the different input feature value ranges, the generated dataset was first standardised. This step was done in Python using the StandardScaler function from the scikit-learn package [40], which subtracts the mean value from the value to be standardised and divides the result by the standard deviation. The mean value and the standard deviation were estimated on the training dataset and then used to standardise the training, validation, and test datasets. A sliding-window approach was utilised to generate the necessary pairs P for training, which consist of inputs and corresponding target variables. A pair is generated for each time step t of an event. For this purpose, the input windows for the last D time steps are set to the interval [t−D+1,…, t], while target variable windows for the following H time steps comprise the interval [t+1,…, tH]. For events consisting of n time steps, the first training pair was formed at time t = D and the last training pair at time tn-H. With a fixed step size of 1, this led to m = n – (D + H) training examples. The moving-window approach used to generate the training pairs is shown in Figure 5 and was applied to all events in the dataset.
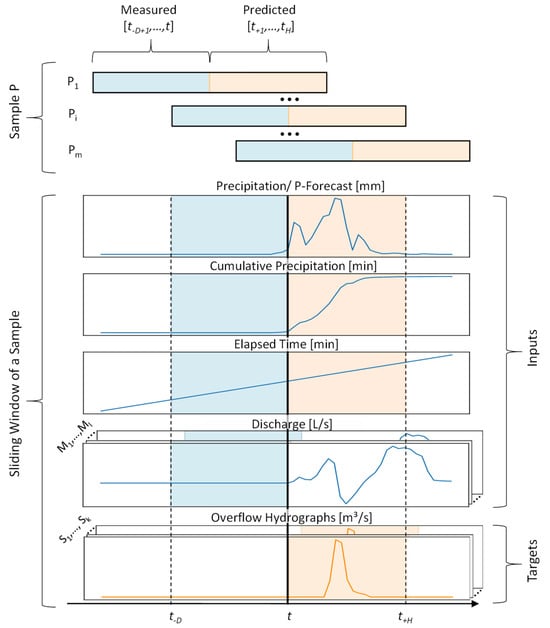
Figure 5.
Conversion of the data into a supervised learning problem.
In the present analysis, a window size of one hour was used for both the past time steps D and the prediction horizon H when generating the training pairs. With the temporal resolution of five minutes considered, this equates to 12 time steps in each case. Although the model can handle longer prediction horizons, investigations have shown that available precipitation forecasts are then often subject to greater uncertainties [41]. Even if one hour is not enough time to implement all necessary response actions, the forecast can be used to warn the population via apps, control digital warning signs at the entry of flooded underpasses, or adjust routes of rescue forces to avoid crossing through flooded areas. The subsequent splitting of the dataset into training, validation, and test datasets was carried out event-wise. Out of the 258 events, samples of 26 events were retained for testing, all from the station closest to the study area. The data pairs of the remaining events were used for training (90%, 209 events) and validation (10%, 23 events).
3.3. Experiments
3.3.1. Comparison with Different Deep Learning Models
Different deep learning models were used as benchmarks to assess the performance of the TFT. These included (i) a convolutional neural network (CNN), (ii) a long short-term memory (LSTM) network, (iii) a sequence-to-sequence (Seq2Seq) model and (iv) a dual-stage attention-based recurrent neural network (DA-RNN). Additionally, (v) a naïve approach was used as a benchmark, which assumed the absence of manhole overflow for each forecast time step. This approach was used to examine whether the prediction models considered can create any benefit at all. The individual architectures are briefly described below, with relevant sources referenced for detailed information. The investigations aimed to determine whether the highly complex TFT architecture outperforms other common deep learning models as well as the naïve forecast. The TFT was implemented in PyTorch Forecasting [42], while the other models were implemented in PyTorch [43]. Other machine learning methods, such as the random forest algorithm or linear regression, were also tested using scikit-learn [40]. However, the computation times of the latter were extremely high due to the lack of GPU support and the large number of time series considered, even if parallel computing on multiple CPU cores were used. Therefore, these methods were not further considered in this study.
- CNN: Convolutional neural networks are a network architecture developed significantly through the work of Le Cun et al. [44], which has proven to be highly effective in image recognition. In addition to processing 2D data such as images, CNNs can also process 1D datasets such as time series. CNNs focus on recognising relevant structures in input data, and are therefore able to localise short-term dependencies and local patterns. In the present use case, the patterns extracted from the input time series are then used to generate the overflow forecast for the upcoming time steps with a fully connected feed-forward layer.
- LSTM Network: Models using the LSTM cells developed by Hochreiter and Schmidhuber [45] are widely used in the field of time series analysis. They are a type of recurrent neural network (RNN), but have additional modifications that make it possible to learn long-term dependencies in sequences, which makes them well-suited for the prediction of time series. Like the CNN model, the LSTM model used here has a fully connected feed-forward layer as an output layer to generate a multi-step prediction.
- Seq2Seq: The Seq2Seq model presented by Sutskever et al. [46] represents a network architecture for processing sequential data that also includes recurrent layers. In contrast to the LSTM model described before, the recurrent layers are arranged in an encoder–decoder structure. The encoder processes the inputs and generates a context vector, while the decoder produces an output sequence based on this vector. Furthermore, Seq2Seq models can provide predictions for several time steps without requiring additional feed-forward layers. LSTM cells are also used as recurrent layers in the Seq2Seq model used in this work.
- DA-RNN: A DA-RNN comprises a Seq2Seq model supplemented with a two-stage attention mechanism [47]. These attention mechanisms are placed before and after the encoder, and similarly to the TFT, are used to consider all time steps of the input sequences and to weight them depending on their influence on the prediction result.
The most important hyperparameters used to build and train the model architectures are listed in Table 1. Model parameters were determined after preliminary investigations or default parameters of the above-mentioned original literature were adopted. For the generation of the training dataset, the batch size was set to 16. In addition, the number of epochs for the training was set to 100 for all models. If there were no improvement in the validation error for 20 epochs, the training was interrupted to avoid overfitting.

Table 1.
Summary of the hyperparameters considered for the individual model setups.
3.3.2. Analyses with Measurements in the Sewer Network
In addition to different deep learning models, the influence of the measurements considered in the sewer network was analysed. For this purpose, the spatial resolution and the signal used in the measurement network were varied. Concerning the spatial resolution, the measurement network shown in Figure 3 consisting of 20 sensors was initially considered as (i) a variant. This variant was compared to (ii) another variant that only considers measurements at the area outlet and with (iii) a variant that does not include any measurements in the sewer network. These three variants were compared to determine how the number of measuring locations impacts the forecast quality. At this point, it should be noted that with the chosen approach, the water level and flow rate at all measuring points are calculated based on a precipitation load using a clearly defined calculation method implemented in the hydrodynamic modelling software (Mike+ 2021, update 1) used. Therefore, the calculated “measured values” correlate strongly, and it was necessary to examine whether additional sensors generate added value or negatively impact the results.
Compared to expensive high-precision measuring devices that can measure flow with high accuracy, low-cost sensors usually rely on other less precise measurement quantities. In the case of the KIWaSuS project, a sensor that converts acoustic measurement signals into filling classes is being developed [49]. This means that a robust and cost-effective measurement method is used, but at the same time, it only allows for lower measurement precision. To test the extent to which the lower measurement precision affects the prediction capacity, (i) discharge and (ii) water level measurements, as well as measurements of (iii) filling degree, were compared with the approach of (iv) filling classes. Discharge and water level measurements were taken from the HD model directly at the sensor locations for the simulated events. The filling degree was calculated from the water level and indicates the filling percentage at the sensor locations. Based on the filling degree, the filling classes were determined by Equation (1), as follows:
3.4. Performance Evaluation
The predicted (ML model) and simulated (HD model) overflow hydrographs are compared to evaluate the overflow prediction. This calculation is performed for the selected forecast horizon of 60 min (12 time steps) for each forecast starting point in the test dataset. When choosing the metrics for evaluating the quality of the model, the focus was placed on the subsequent application, the integration of the overflow prediction as input to the flood area prediction model developed by Burrichter et al. [30]. For this reason, it is essential that the overflow volume is as accurate as possible and that the peak overlaps in terms of magnitude and time step of occurrence, in order to represent the resulting flood areas at the ground surface correctly.
The volume error (VE), the peak error (PE) and the peak time error (PTE) are used as performance criteria. In contrast to the usual practice in water management (e.g., DWA-M 165 [50]), the calculation of the volume error and the peak error are not based on relative errors, but on absolute errors. This is intended to emphasise the error of large overflow volumes, which significantly impact the resulting flooding situation.
The absolute volume error is calculated by comparing the deviation of the accumulated overflow volume between two time series:
Here, n denotes the number of time steps compared and yi represents the respective values of the individual time steps determined with the neural network NN or the hydrodynamic model HD.
The peak error compares the maximum value of two overflow hydrographs, but provides no information regarding the temporal overlapping. For this purpose, the time error of the maximum value was also considered. Both criteria can be calculated using the following equations:
where ypeak and yt,peak indicate the peak value and the time of peak occurrence in the overflow hydrographs calculated with the neural network or the hydrodynamic model.
4. Results
4.1. Evaluation of the Analyses Performed
In the present study, models were created for all the possible combinations of network architectures, number of sensors, and measurement signals listed in Section 3.3 and their performance was compared. The performance metrics were determined for all samples of the 26 test events at all manholes. Table 2 summarises the mean value of every metric for all models. Only the forecast results for samples and manholes where the overflow volume for the forecast horizon is >500 litres in either the HD or ML model are included in the calculation. The aim is to include only relevant overflow events in the assessment. In the case of the TFT, the metrics were calculated using the error for the 0.5 quantile, which corresponds to the mean absolute error. It should be noted that the naïve approach provides the same result in all variants, as no overflow is ever predicted. In addition, the results for the variants without measuring stations do not vary among the measuring signals considered, as no measurements were considered as input. Based on the table, the following conclusions can be drawn with regard to the individual analyses.
- Comparison of model architectures: The comparison of the different model architectures shows that the naïve approach, as well as the CNN and LSTM, deliver significantly worse forecasts than the other model architectures. In some cases, CNN and LSTM even show worse results than the naïve approach. Even if the TFT does not perform best across all the considered variants, a TFT model achieves the best overall result for each metric. However, the results for the Seq2Seq model and the TFT are usually close to each other.
- Comparison of the number of sensors: A larger number of sensors does not have a positive influence on the results, as the variants with 20 sensors tended to achieve poorer results. The variants with one sensor and no sensor, on the other hand, are close to each other in most cases. The best overall results for all three metrics were achieved for a variant with one sensor.
- Comparison of measurement signals: No clear tendency towards one variable can be recognised for the measurement signals considered. In the variants with one station, only the results for the water level stand out negatively for the two best model architectures—Seq2Seq and TFT. The lowest volume error and the lowest peak time error were achieved when measuring the filling degree. The lowest peak error was obtained by the approach with five filling classes.

Table 2.
Evaluation result for all models and variants (the best result for each variant and metric is highlighted in bold, and the best overall result for each metric is additionally underlined).
Table 2.
Evaluation result for all models and variants (the best result for each variant and metric is highlighted in bold, and the best overall result for each metric is additionally underlined).
| Model | 20 Stations | 1 Station | No Station | ||||||
|---|---|---|---|---|---|---|---|---|---|
| VE [L] | PE [L/s] | PTE [min] | VE [L] | PE [L/s] | PTE [min] | VE [L] | PE [L/s] | PTE [min] | |
| Discharge | |||||||||
| Naïve Zero | 138.65 | 199.30 | 27.50 | 138.65 | 199.30 | 27.50 | 138.65 | 199.30 | 27.50 |
| CNN | 235.58 | 148.54 | 20.32 | 228.65 | 169.03 | 25.51 | 208.87 | 152.20 | 20.70 |
| LSTM | 147.61 | 179.65 | 10.55 | 174.80 | 246.92 | 7.84 | 169.46 | 181.34 | 7.84 |
| Seq2Seq | 90.73 | 85.41 | 7.13 | 49.07 | 83.81 | 5.96 | 50.51 | 74.04 | 6.12 |
| DA-RNN | 133.41 | 154.09 | 5.08 | 85.79 | 99.92 | 6.11 | 96.08 | 112.13 | 8.01 |
| TFT | 92.84 | 136.83 | 15.82 | 44.25 | 79.77 | 2.53 | 61.13 | 91.45 | 4.04 |
| Water depth | |||||||||
| Naïve Zero | 138.65 | 199.30 | 27.50 | 138.65 | 199.30 | 27.50 | 138.65 | 199.30 | 27.50 |
| CNN | 200.96 | 137.53 | 22.10 | 259.23 | 154.80 | 22.07 | 208.87 | 152.20 | 20.70 |
| LSTM | 157.30 | 170.15 | 8.20 | 137.15 | 178.62 | 9.29 | 169.46 | 181.34 | 7.84 |
| Seq2Seq | 77.10 | 76.65 | 5.18 | 89.24 | 96.58 | 4.03 | 50.51 | 74.04 | 6.12 |
| DA-RNN | 101.18 | 117.02 | 4.52 | 62.94 | 84.53 | 7.34 | 96.08 | 112.13 | 8.01 |
| TFT | 62.05 | 101.91 | 2.12 | 57.76 | 101.35 | 2.64 | 61.13 | 91.45 | 4.04 |
| Filling degree | |||||||||
| Naïve Zero | 138.65 | 199.30 | 27.50 | 138.65 | 199.30 | 27.50 | 138.65 | 199.30 | 27.50 |
| CNN | 225.52 | 160.67 | 19.54 | 270.09 | 168.48 | 26.15 | 208.87 | 152.20 | 20.70 |
| LSTM | 147.70 | 168.95 | 10.29 | 157.77 | 184.91 | 7.36 | 169.46 | 181.34 | 7.84 |
| Seq2Seq | 97.99 | 98.01 | 9.56 | 43.39 | 90.01 | 2.16 | 50.51 | 74.04 | 6.12 |
| DA-RNN | 80.77 | 100.03 | 4.58 | 108.75 | 103.39 | 8.65 | 96.08 | 112.13 | 8.01 |
| TFT | 43.19 | 78.49 | 3.10 | 36.93 | 77.42 | 2.07 | 61.13 | 91.45 | 4.04 |
| Filling class (5 classes) | |||||||||
| Naïve Zero | 138.65 | 199.30 | 27.50 | 138.65 | 199.30 | 27.50 | 138.65 | 199.30 | 27.50 |
| CNN | 271.46 | 171.68 | 19.61 | 300.05 | 178.35 | 25.37 | 208.87 | 152.20 | 20.70 |
| LSTM | 151.27 | 170.61 | 10.43 | 160.64 | 176.63 | 6.67 | 169.46 | 181.34 | 7.84 |
| Seq2Seq | 78.38 | 91.00 | 10.31 | 59.15 | 78.35 | 4.08 | 50.51 | 74.04 | 6.12 |
| DA-RNN | 102.93 | 126.97 | 7.80 | 65.84 | 93.26 | 5.05 | 96.08 | 112.13 | 8.01 |
| TFT | 86.68 | 125.77 | 4.90 | 44.25 | 73.72 | 2.71 | 61.13 | 91.45 | 4.04 |
Since the selected measurement signal has only a minor effect on the prediction quality, only models with filling classes as input were considered for further analyses. This is because this measurand is the least precise of those tested, so it is more likely to be captured with low-cost sensors. In addition, the variant with one station was considered in the subsequent sections, as the best overall result was obtained with this variant. The model performance of the three best models—Seq2Seq, DA-RNN, and TFT—for the variant with filling classes at one measuring station was analysed in more detail. For this purpose, the violin plot shown in Figure 6 was created for the individual metrics and models. The plot relies on the same metric values used for calculating the mean values in Table 2. Based on the violin plot, the scattering and density of the results are visualised. This clearly shows the better performance of the TFT, which has the least scatter for all metrics and where the highest density of the metrics is close to the optimum in each case. Unlike the Seq2Seq and DA-RNN models, large outliers occur only in the peak time error for the TFT. These appear in the case of long, uniform overflow events, which somewhat weaken their relevance in the overall result analysis. The TFT slightly underestimates the volume and peak value compared to the other models. However, as only forecasts of extreme events with more than 500 litres of overflow volume were taken into account, these deviations are tolerable. Since the results for other measurement signals are similar, no additional visualisation is provided.
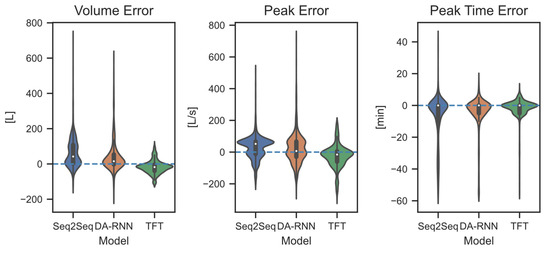
Figure 6.
Violin plot of the metrics for the best three models of the variant with one measuring station and filling classes as measurement signal.
In the next step, the influence of each individual input signal on the forecast results of the TFT was analysed. In particular, the aim was to investigate why the variant with 20 measuring stations led to poorer results in the analyses performed. Due to the VSN blocks described in Section 2.2, it was possible to determine the influence of the individual input features on the result generation for the TFT. Figure 7 shows the importance of the different input features for the encoder and the decoder on the forecast generation. The variants with 1 and 20 measuring stations are illustrated, considering the filling classes as measuring signals. At this point, it should be noted that the encoder receives features of the past time steps and the decoder features of the upcoming time steps as input. As expected, both models show the high relevance of the precipitation forecast, which is used as input for the decoder. In the case of the encoder, it can be seen that while most of the features influence the forecast results in the variant with 1 station, only a few features are relevant in the approach with 20 stations. One reason for this could be the high correlation between the individual filling class measurements with one another, but also with the fallen precipitation. As a result, the added value of the many measurements is low and leads to unnecessary complexity of the model. Since the training dataset used comprises fewer than 10,000 pairs, it can be categorised as relatively small for training deep learning models. Due to the combination of both above-mentioned facts, the capacity of the model to learn the essential features and their underlying patterns is compromised.
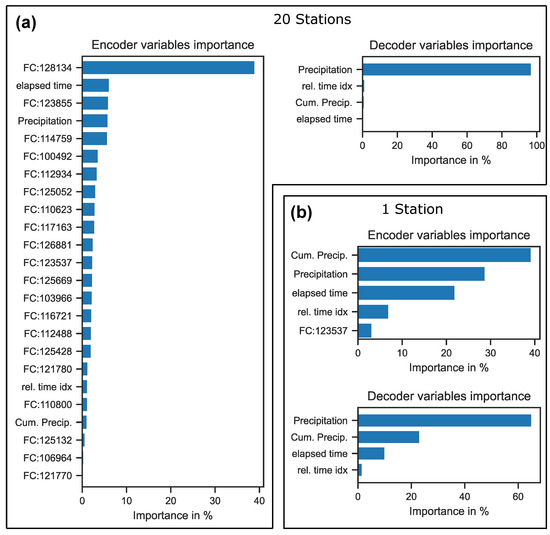
Figure 7.
Feature importance of the encoder and decoder inputs for (a) the variant with 20 stations and (b) the variant with 1 station. The features with FC at the beginning indicate measurements of the filling classes with the respective station ID.
4.2. Forecast for a Historical Heavy Rainfall Event
The TFT model for the variant with one station and filling classes as measurement signal was tested for the final evaluation using two historical heavy rainfall events. The events occurred on 3 July 2009 and 3 July 2010 in the study area and had maximum return periods Tmax of >200 and >1000 years, respectively. It should be noted that the values of the return periods were determined by extrapolation based on applicable extreme precipitation statistics for this study area. Figure 8 shows precipitation forecasts and the predicted overflow hydrographs at six manholes in the catchment area. The following conclusions can be drawn from the figure.
- In some cases, the 0.5 quantile matches the simulated target value very well, but there are also significant deviations in other cases. In addition, the uncertainty range between the 0.02 and 0.98 quantiles increases with larger deviations.
- Longer overflow events can be predicted with high accuracy, while short peaks can result in extreme deviations of >100% at the maximum value and of the resulting overflow volume. This is particularly illustrated in the forecast hydrographs for the event of 3 July 2009. While the longer overflow period at nodes 68079092 and 68079045 is forecast with a high degree of accuracy, the hydrograph for the short peak at node 69079015 deviates significantly.
- In this figure, there is no recognisable tendency of the model to consistently under- or overestimate overflow hydrographs at the manholes shown. This finding can also be confirmed after analyses of other manholes in the catchment area, which are not shown here.
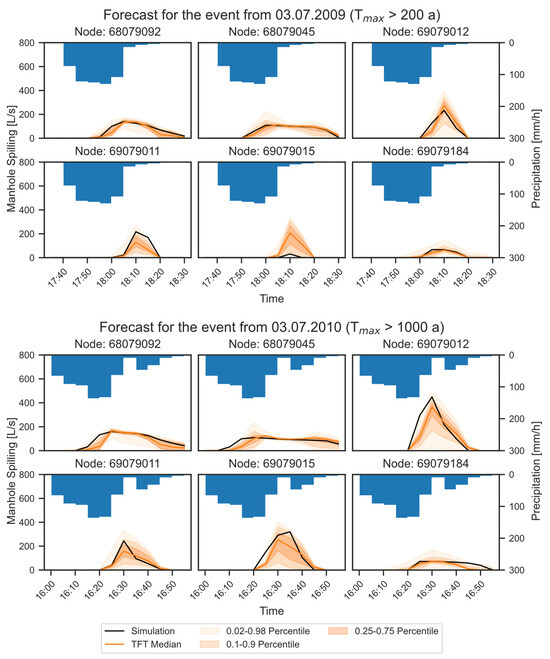
Figure 8.
Forecast results at six manholes for the historic events on 3 July 2009 and 3 July 2010 in Gelsenkirchen.
5. Discussion
The results show the good performance of the TFT compared to the benchmark models. In particular, the scatter of the results is significantly lower, and there are no extreme overestimations compared to the benchmark models. The forecasts of the final model show good agreement with the simulation results in some cases. However, considerable deviations still occur in some cases, particularly during short flooding events. One reason for this is that the prediction of extreme values occurring over short periods is generally a challenging task. The same problem has been identified in similar studies [27,29]. As a possible solution, Palmitessa et al. [29] did not estimate the overflow directly. Instead, they used a network architecture that first calculates the inflows and outflows of a node, with which the overflow is then calculated using a mass balance included as an additional layer. In addition, it should be noted that in the present work, the models used perfect precipitation measurements and forecasts, as well as simulated filling measurements in the drainage system as input. In operational use, these data are subject to uncertainties, which have an additional effect on the prediction results. Accordingly, further investigations with real measurements and forecasts are required to evaluate the impact of these uncertainties on the forecast results. In addition, the overflow prediction should serve as an input for the model developed by Burrichter et al. [30] to predict flooded areas. Thus, a coupled evaluation should also be conducted to determine whether the developed overflow model provides added value.
The reason for the development of the overflow forecasting model described was its integration into an early warning system. Due to the problem that the uncertainties in precipitation forecasts for heavy rainfall events increase substantially after just one or two hours [41,51], the forecast horizon was set to one hour. Short calculation times are an essential requirement for the overflow prediction model to make the best use of this forecast horizon. All models considered in the investigations met this requirement and delivered forecast results within a few seconds. This means that all models, including the TFT, are suitable for real-time operation in inference mode. Nevertheless, at this point, it should be noted that transformer models such as the presented TFT generally have high computational requirements. Although this does not restrict its application for the task proposed, the training on a GPU (NVIDIA RTX 2080 Ti) for 100 epochs lasted 18 h for the TFT compared to a training duration of a few minutes for the other models. Returning to the point regarding suitability for real-time operation and especially when expanding the TFT model to larger areas, it is possible, therefore, that more computing power and consequently higher costs are required to enable low-delay forecast generation.
The poor performance of the models with a measurement network of 20 stations was somewhat unexpected. One assumption is that the high spatial sensor density does not provide any added value in this application due to the high correlation between the measurements. However, it should be noted that this could only be proven in the evaluation with perfect precipitation measurements and forecasts and with no restrictions in the sewer network, for example, due to clogged inlets. As in the real world, such conditions are unlikely, it is therefore expected that considering many sensors and the associated swarm intelligence can result in advantages. Another way to generate added value through the measurement network is to integrate the measurements to correct the model results, as described by Zhu et al. [28]. Processing the sensor measurements as a spatially structured graph sequence instead of an unordered time series may offer further optimisation potential. For example, in the field of traffic forecasting, the combination of transformers with graph neural networks has proven to be very effective [52,53].
A major limitation of the presented approach is the missing generalisability. Due to the absence of system information about the sewer network, the trained model cannot be transferred to other areas. This also means that as soon as changes are made to the network, a new training dataset has to be generated and the model has to be retrained. These changes can be structural changes to the system, the allocation of new areas to the sewer network, or a change in the settings on the controls of central structures. To a certain extent, the resulting uncertainties can be tolerated, but at a certain point, new training is unavoidable. To solve this problem, one approach could be using physically guided [29] or physically informed [54] neural networks.
In addition to the selected ML method, the quality of the results largely depends on the data available for the model training. On the one hand, the quality depends on the hydrodynamic model’s accuracy, which provides target variables for the training process. On the other hand, in operational usage, the input variables should be as accurate as possible. Various approaches for refining existing measurement networks, such as the integration of low-cost precipitation sensors [55], can be helpful in this context. While overflows at central structures of the drainage system are sometimes monitored, it is currently not economically feasible to measure overflows down to manhole level. Accordingly, no suitable measurement data are available as a target variable for model training. Nevertheless, the chosen approach of training machine learning methods using hydrodynamic calculation results offers the possibility of providing a capable real-time prediction model. Additional measurements at manholes that are particularly prone to flooding would therefore be highly desirable to improve the quality of the prediction model beyond that of the HD model by using transfer learning techniques. In addition, measurements of overflow from sewer manholes would be helpful to validate the results of the prediction model.
6. Conclusions
In the present study, an overflow prediction model was developed that forecasts the overflow at 975 manholes in the study area considered. As input, the model uses the measured and forecast precipitation as well as measurements in the sewer network. It was shown that the best results could be achieved with a temporal fusion transformer model. The final model generates forecasts within seconds and is suitable for implementation in early warning systems. A measuring network of 20 sensors in the sewer considered as an additional input variable did not prove to be useful for the application described. In contrast, better results could be achieved by considering only one measuring station at the outlet of the sewer network. With the different measurement signals taken into account, it was shown that the chosen signal only slightly impacts the results. Accordingly, measurement signals with lower quality, such as the filling classes, can also be used.
However, various limitations of the model were also identified during the investigations, and research questions remain unanswered. The following can therefore be emphasised as essential future research needs.
- The optimisation of the final model with regard to the forecast of overflow hydrographs with short peaks. On the one hand, this can be achieved by considering further input features or a larger training dataset. On the other hand, testing with other network architectures, such as graph neural networks or different types of transformer models, could be helpful. In addition, further optimisation to improve the accuracy of the final model could be attempted with the implementation of systematic hyperparameter tuning.
- Investigations on the coupled assessment of real measurement networks and the forecast models for precipitation, overflow and flooded areas. The first step is to evaluate the performance of the coupled forecasting system itself. In addition, it is also necessary to test alternatives for ensuring that the uncertainties of the individual components in the forecasting process are adequately taken into account and visualised.
- Establishing the model’s scalability for broad application at urban-area level is also necessary. One possibility for this could be the use of physically informed or physically guided neural networks, which, if set up appropriately, allow transferability to other areas.
Author Contributions
Conceptualisation, B.B., J.K.d.S. and M.Q.; methodology, B.B. and J.K.d.S.; software, B.B.; formal analysis, B.B.; investigation, B.B.; writing—original draft preparation, B.B.; writing—review and editing, J.K.d.S., A.N. and M.Q.; visualisation, B.B.; supervision, J.K.d.S., A.N. and M.Q.; project administration, M.Q.; funding acquisition, M.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This work is part of the research project “KIWaSuS—KI-basiertes Warnsystem vor Starkregen und urbanen Sturzfluten” (AI-based warning system for heavy rain and urban flash floods) funded by the Federal Ministry of Education and Research (BMBF), Germany (grant 13N15556).
Data Availability Statement
Restrictions apply to the availability of the data used. Data from various institutions were used for the research, and the authors committed to not passing them on to third parties.
Acknowledgments
The authors thank Emschergenossenschaft and Abwassergesellschaft Gelsenkirchen mbH for providing the precipitation data and the hydrodynamic sewer model.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Seneviratne, S.I.; Zhang, X.; Adnan, M.; Badi, W.; Dereczynski, C.; Di Luca, A.; Ghosh, S.; Iskandar, I.; Kossin, J.; Lewis, S.; et al. Weather and Climate Extreme Events in a Changing Climate. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; pp. 1513–1766. [Google Scholar]
- Tradowsky, J.S.; Philip, S.Y.; Kreienkamp, F.; Kew, S.F.; Lorenz, P.; Arrighi, J.; Bettmann, T.; Caluwaerts, S.; Chan, S.C.; de Cruz, L.; et al. Attribution of the heavy rainfall events leading to severe flooding in Western Europe during July 2021. Clim. Change 2023, 176, 90. [Google Scholar] [CrossRef]
- Zachariah, M.; Kotroni, V.; Kostas, L.; Barnes, C.; Kimutai, J.; Kew, S.; Pinto, I.; Yang, W.; Vahlberg, M.; Singh, R.; et al. Interplay of Climate Change—Exacerbated Rainfall, Exposure and Vulnerability Led to Widespread Impacts in the Mediterranean Region; World Weather Attribution, Grantham Institute for Climate Change: London, UK, 2023. [Google Scholar]
- DIN EN 752:2017; Entwässerungssysteme außerhalb von Gebäuden—Kanalmanagement. Deutsches Institut für Normung e.V.: Berlin, Germany; Beuth Verlag GmbH: Berlin, Germany, 2017.
- Henonin, J.; Russo, B.; Mark, O.; Gourbesville, P. Real-time urban flood forecasting and modelling—A state of the art. J. Hydroinf. 2013, 15, 717–736. [Google Scholar] [CrossRef]
- Faure, D.; Schmitt, P.; Auchet, P. Limits of radar rainfall forecasting for sewage system management: Results and application in Nancy. In Proceedings of the 8th International Conference on Urban Storm Drainage, Sydney, Australia, 30 August 1999. [Google Scholar]
- Quirmbach, M. Nutzung von Wetterradardaten für Niederschlags-und Abflussvorhersagen in Urbanen Einzugsgebieten. Ph.D. Thesis, Lehrstuhl für Hydrologie, Wasserwirtschaft und Umwelttechnik, Ruhr-Universität Bochum, Bochum, Germany, 2003. [Google Scholar]
- Jasper-Tönnies, A.; Hellmers, S.; Einfalt, T.; Strehz, A.; Fröhle, P. Ensembles of radar nowcasts and COSMO-DE-EPS for urban flood management. Water Sci. Technol. 2018, 2017, 27–35. [Google Scholar] [CrossRef] [PubMed]
- René, J.-R.; Djordjević, S.; Butler, D.; Mark, O.; Henonin, J.; Eisum, N.; Madsen, H. A real-time pluvial flood forecasting system for Castries, St. Lucia. J. Flood Risk Manag. 2015, 11, 269–283. [Google Scholar] [CrossRef]
- Bates, P.D.; Horritt, M.S.; Fewtrell, T.J. A simple inertial formulation of the shallow water equations for efficient two-dimensional flood inundation modelling. J. Hydrol. 2010, 387, 33–45. [Google Scholar] [CrossRef]
- Austin, R.J.; Chen, A.S.; Savić, D.A.; Djordjević, S. Quick and accurate Cellular Automata sewer simulator. J. Hydroinf. 2014, 16, 1359–1374. [Google Scholar] [CrossRef]
- Jamali, B.; Löwe, R.; Bach, P.M.; Urich, C.; Arnbjerg-Nielsen, K.; Deletic, A. A rapid urban flood inundation and damage assessment model. J. Hydrol. 2018, 564, 1085–1098. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K. Flood Prediction Using Machine Learning Models: Literature Review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Bentivoglio, R.; Isufi, E.; Jonkman, S.N.; Taormina, R. Deep Learning Methods for Flood Mapping: A Review of Existing Applications and Future Research Directions. Hydrol. Earth Syst. Sci. 2022, 26, 4345–4378. [Google Scholar] [CrossRef]
- Berkhahn, S.; Fuchs, L.; Neuweiler, I. An ensemble neural network model for real-time prediction of urban floods. J. Hydrol. 2019, 575, 743–754. [Google Scholar] [CrossRef]
- Guo, Z.; Leitão, J.P.; Simões, N.E.; Moosavi, V. Data-driven flood emulation: Speeding up urban flood predictions by deep convolutional neural networks. J. Flood Risk Manag. 2020, 14, e12684. [Google Scholar] [CrossRef]
- Löwe, R.; Böhm, J.; Jensen, D.G.; Leandro, J.; Rasmussen, S.H. U-FLOOD—Topographic deep learning for predicting urban pluvial flood water depth. J. Hydrol. 2021, 603, 126898. [Google Scholar] [CrossRef]
- Hofmann, J.; Schüttrumpf, H. floodGAN: Using Deep Adversarial Learning to Predict Pluvial Flooding in Real Time. Water 2021, 13, 2255. [Google Scholar] [CrossRef]
- do Lago, C.A.; Giacomoni, M.H.; Bentivoglio, R.; Taormina, R.; Gomes, M.N.; Mendiondo, E.M. Generalizing rapid flood predictions to unseen urban catchments with conditional generative adversarial networks. J. Hydrol. 2023, 618, 129276. [Google Scholar] [CrossRef]
- Garzón, A.; Kapelan, Z.; Langeveld, J.; Taormina, R. Machine Learning-Based Surrogate Modeling for Urban Water Networks: Review and Future Research Directions. Water Resour. Res. 2022, 58, e2021WR031808. [Google Scholar] [CrossRef]
- Chang, F.-J.; Chen, P.-A.; Lu, Y.-R.; Huang, E.; Chang, K.-Y. Real-time multi-step-ahead water level forecasting by recurrent neural networks for urban flood control. J. Hydrol. 2014, 517, 836–846. [Google Scholar] [CrossRef]
- Zhang, D.; Lindholm, G.; Ratnaweera, H. Use long short-term memory to enhance Internet of Things for combined sewer overflow monitoring. J. Hydrol. 2018, 556, 409–418. [Google Scholar] [CrossRef]
- She, L.; You, X. A Dynamic Flow Forecast Model for Urban Drainage Using the Coupled Artificial Neural Network. Water Resour. Manag. 2019, 33, 3143–3153. [Google Scholar] [CrossRef]
- Piadeh, F.; Behzadian, K.; Chen, A.S.; Kapelan, Z.; Rizzuto, J.P.; Campos, L.C. Enhancing Urban Flood Forecasting in Drainage Systems Using Dynamic Ensemble-based Data Mining. Water Res. 2023, 247, 120791. [Google Scholar] [CrossRef]
- Duncan, A.; Chen, A.S.; Kedwell, E.C.; Djordjević, S.; Savić, D.A. RAPIDS: Early Warning System for Urban Flooding and Water Quality Hazards. In Machine Learning in Water Systems: Part of AISB Annual Convention; University of Exeter: Exeter, UK, 2013. [Google Scholar]
- Abou Rjeily, Y.; Abbas, O.; Sadek, M.; Shahrour, I.; Hage Chehade, F. Flood forecasting within urban drainage systems using NARX neural network. Water Sci. Technol. 2017, 76, 2401–2412. [Google Scholar] [CrossRef] [PubMed]
- Kilsdonk, R.A.H.; Bomers, A.; Wijnberg, K.M. Predicting Urban Flooding Due to Extreme Precipitation Using a Long Short-Term Memory Neural Network. Hydrology 2022, 9, 105. [Google Scholar] [CrossRef]
- Zhu, W.; Tao, T.; Yan, H.; Yan, J.; Wang, J.; Li, S.; Xin, K. An optimized long short-term memory (LSTM)-based approach applied to early warning and forecasting of ponding in the urban drainage system. Hydrol. Earth Syst. Sci. 2023, 27, 2035–2050. [Google Scholar] [CrossRef]
- Palmitessa, R.; Grum, M.; Engsig-Karup, A.P.; Löwe, R. Accelerating hydrodynamic simulations of urban drainage systems with physics-guided machine learning. Water Res. 2022, 223, 118972. [Google Scholar] [CrossRef] [PubMed]
- Burrichter, B.; Hofmann, J.; Da Koltermann Silva, J.; Niemann, A.; Quirmbach, M. A Spatiotemporal Deep Learning Approach for Urban Pluvial Flood Forecasting with Multi-Source Data. Water 2023, 15, 1760. [Google Scholar] [CrossRef]
- Lim, B.; Arik, S.O.; Loeff, N.; Pfister, T. Temporal Fusion Transformers for Interpretable Multi-Horizon Time Series Forecasting. 2019. Available online: https://arxiv.org/pdf/1912.09363.pdf (accessed on 17 March 2024).
- Schmid, F.; Leandro, J. An ensemble data-driven approach for incorporating uncertainty in the forecasting of stormwater sewer surcharge. Urban Water J. 2023, 20, 1140–1156. [Google Scholar] [CrossRef]
- Ben Taieb, S.; Bontempi, G.; Atiya, A.F.; Sorjamaa, A. A review and comparison of strategies for multi-step ahead time series forecasting based on the NN5 forecasting competition. Expert Syst. Appl. 2012, 39, 7067–7083. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. 2017. Available online: https://arxiv.org/pdf/1706.03762.pdf (accessed on 17 March 2024).
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate. 2014. Available online: https://arxiv.org/pdf/1409.0473.pdf (accessed on 17 March 2024).
- Luong, M.-T.; Pham, H.; Manning, C.D. Effective Approaches to Attention-Based Neural Machine Translation. 2015. Available online: https://arxiv.org/pdf/1508.04025.pdf (accessed on 17 March 2024).
- Wen, R.; Torkkola, K.; Narayanaswamy, B.; Madeka, D. A Multi-Horizon Quantile Recurrent Forecaster. 2017. Available online: https://arxiv.org/pdf/1711.11053.pdf (accessed on 17 March 2024).
- DHI. MIKE+: Release 2021 Update 1; DHI: Hørsholm, Denmark, 2021; Available online: www.mikepoweredbydhi.com (accessed on 18 November 2022).
- KIWaSuS—KI-Basiertes Warnsystem vor Starkregen und Urbanen Sturzfluten. Available online: https://kiwasus.de/ (accessed on 30 November 2023).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Koltermann da Silva, J.; Burrichter, B.; Quirmbach, M. Application of Artificial Intelligence in Rainfall Nowcasting and Flash Floods Forecast in an Urban Catchment: First Results from Research Project KIWaSuS in Germany; Novatech: Lyon, France, 2023. [Google Scholar]
- Breitner, J. PyTorch Forecasting Documentation—Pytorch-Forecasting Documentation. Available online: https://pytorch-forecasting.readthedocs.io/en/stable/# (accessed on 30 November 2023).
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. 2019. Available online: https://arxiv.org/pdf/1912.01703.pdf (accessed on 17 March 2024).
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to Sequence Learning with Neural Networks. 2014. Available online: http://arxiv.org/pdf/1409.3215.pdf (accessed on 17 March 2024).
- Qin, Y.; Song, D.; Chen, H.; Cheng, W.; Jiang, G.; Cottrell, G. A Dual-Stage Attention-Based Recurrent Neural Network for Time Series Prediction. 2017. Available online: https://arxiv.org/pdf/1704.02971.pdf (accessed on 17 March 2024).
- Wright, L. Ranger—A Synergistic Optimizer; GitHub: San Francisco, CA, USA, 2019. [Google Scholar]
- Frentrup, S.; Schultheis, H.; Quirmbach, M.; Burrichter, B.; Koltermann da Silva, J.; Clemens, C.; Niemann, A.; Kunze, J.E.; Dillhardt, M.; Jörissen, D. Intelligentes Management von Datenströmen und KI-Anwendungen in KIWaSuS. KA Korresp. Abwasser Abfall 2022, 69, 264–270. [Google Scholar] [CrossRef]
- DWA. Niederschlag-Abfluss-und Schmutzfrachtmodelle in der Siedlungsentwässerung—Teil 1: Anforderungen: Merkblatt DWA-M 165-1; Deutsche Vereinigung für Wasserwirtschaft, Abwasser und Abfall (DWA): Hennef, Germany, 2021; ISBN 978-3-96862-092-3. [Google Scholar]
- Sun, J.; Xue, M.; Wilson, J.W.; Zawadzki, I.; Ballard, S.P.; Onvlee-Hooimeyer, J.; Joe, P.; Barker, D.M.; Li, P.-W.; Golding, B.; et al. Use of NWP for Nowcasting Convective Precipitation: Recent Progress and Challenges. Bull. Am. Meteorol. Soc. 2014, 95, 409–426. [Google Scholar] [CrossRef]
- Yu, C.; Ma, X.; Ren, J.; Zhao, H.; Yi, S. Spatio-Temporal Graph Transformer Networks for Pedestrian Trajectory Prediction. 2020. Available online: https://arxiv.org/pdf/2005.08514.pdf (accessed on 17 March 2024).
- Xu, M.; Dai, W.; Liu, C.; Gao, X.; Lin, W.; Qi, G.-J.; Xiong, H. Spatial-Temporal Transformer Networks for Traffic Flow Forecasting. 2020. Available online: https://arxiv.org/pdf/2001.02908.pdf (accessed on 17 March 2024).
- Mahesh, R.B.; Leandro, J.; Lin, Q. Physics Informed Neural Network for Spatial-Temporal Flood Forecasting. In Climate Change and Water Security, 1st ed.; Kolathayar, S., Ed.; Springer: Singapore, 2022; pp. 77–91. ISBN 978-981-16-5500-5. [Google Scholar]
- Clemens, C.; Jobst, A.; Radschun, M.; Himmel, J.; Kanoun, O.; Quirmbach, M. Development of an Inductive Rain Gauge. Sensors 2022, 22, 5486. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).