Short-Term Drought Forecast across Two Different Climates Using Machine Learning Models
Abstract
1. Introduction
2. Materials and Methods
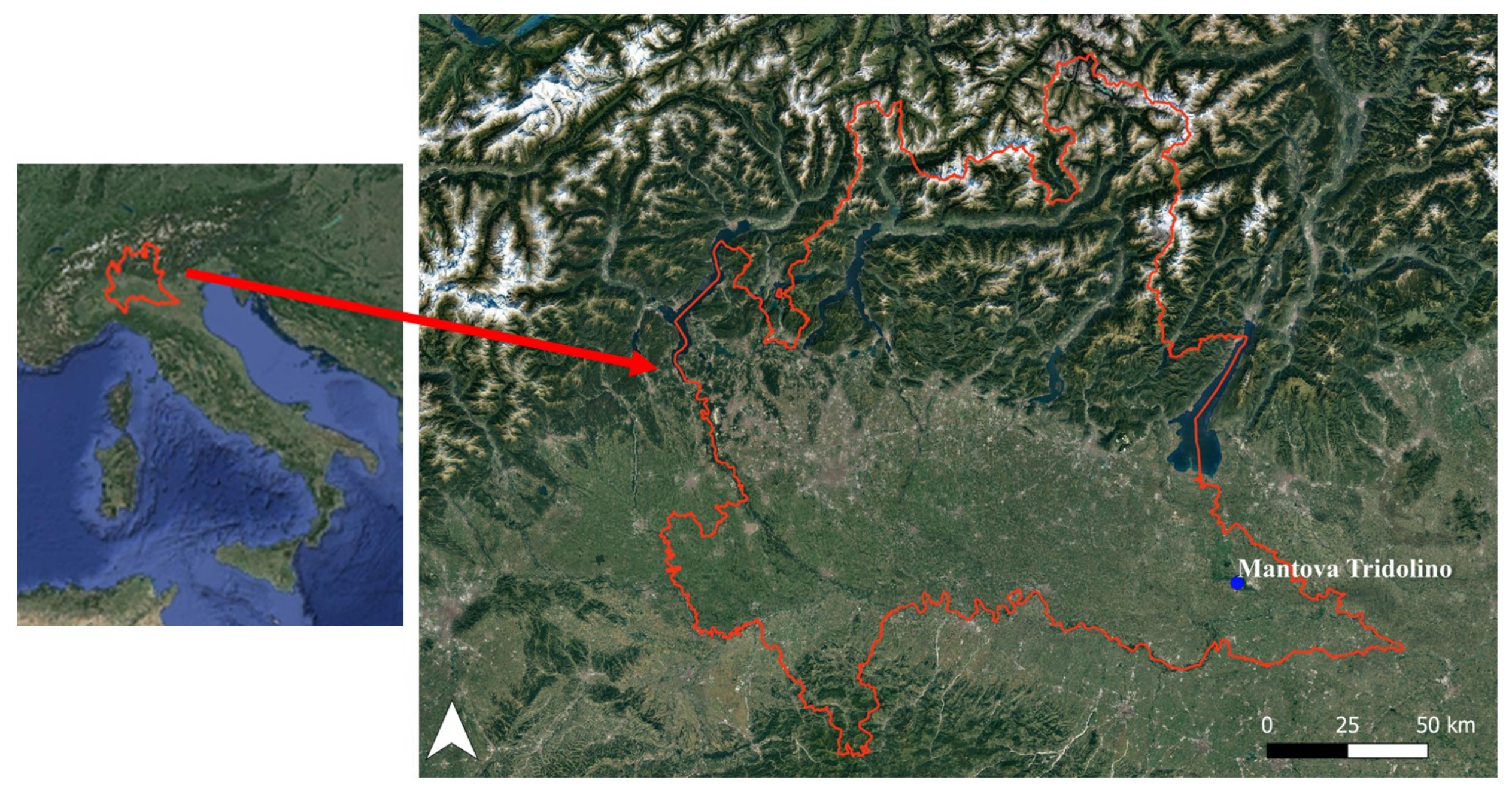
2.1. Study Areas
2.2. Standardized Precipitation Index
2.3. Machine Learning Models
2.3.1. Artificial Neural Networks
2.3.2. eXtreme Gradient Boosting Regressor
2.3.3. K Nearest Neighbors
2.3.4. Multiple Linear Regression
2.4. Feature Importance Analysis
2.5. Performance Criteria
2.6. Confidence Percentages Analysis
3. Results and Discussion
3.1. Results of Comparing Different Models in Terms of Metrics
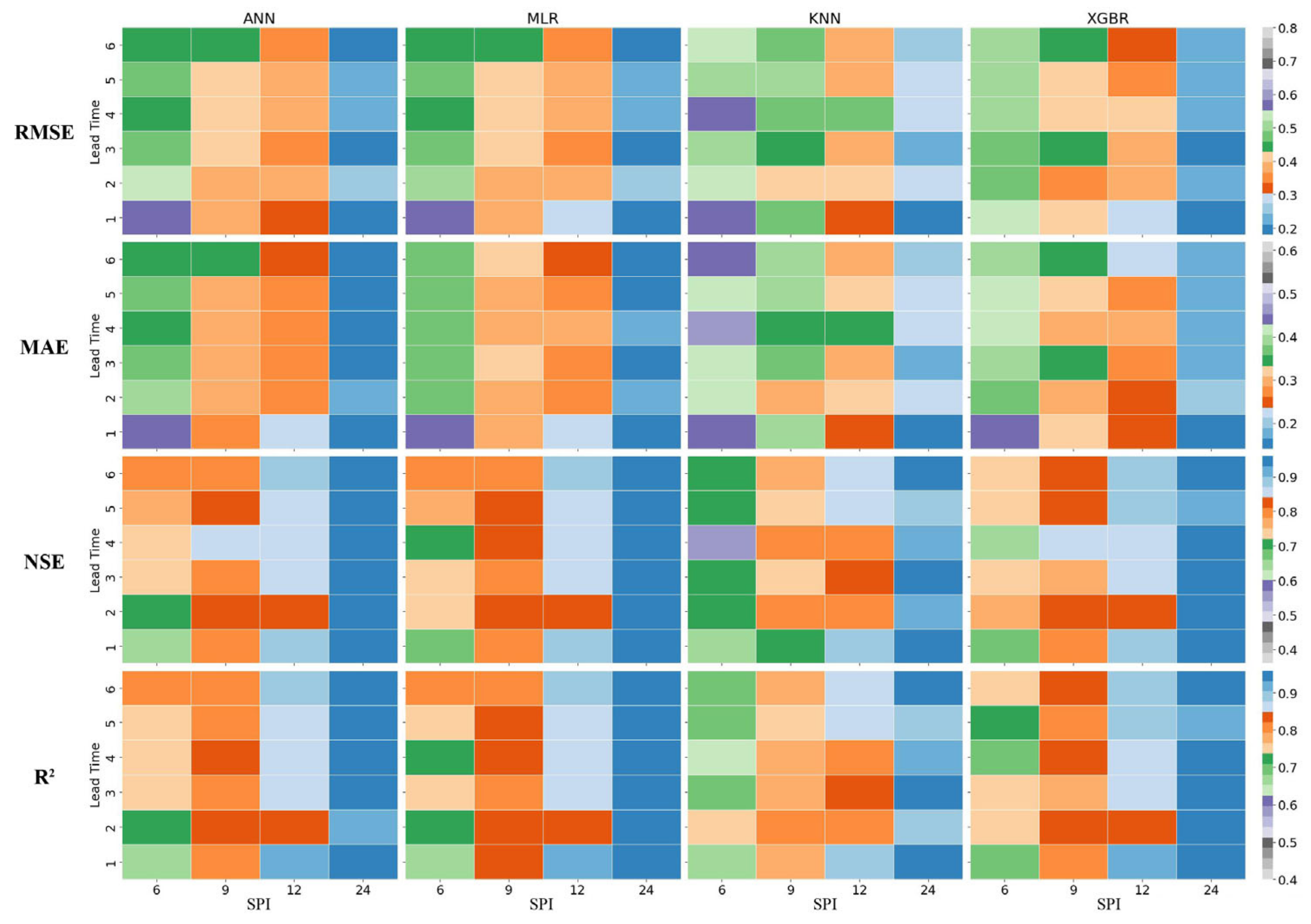
3.1.1. SPI Results for Shiraz Station
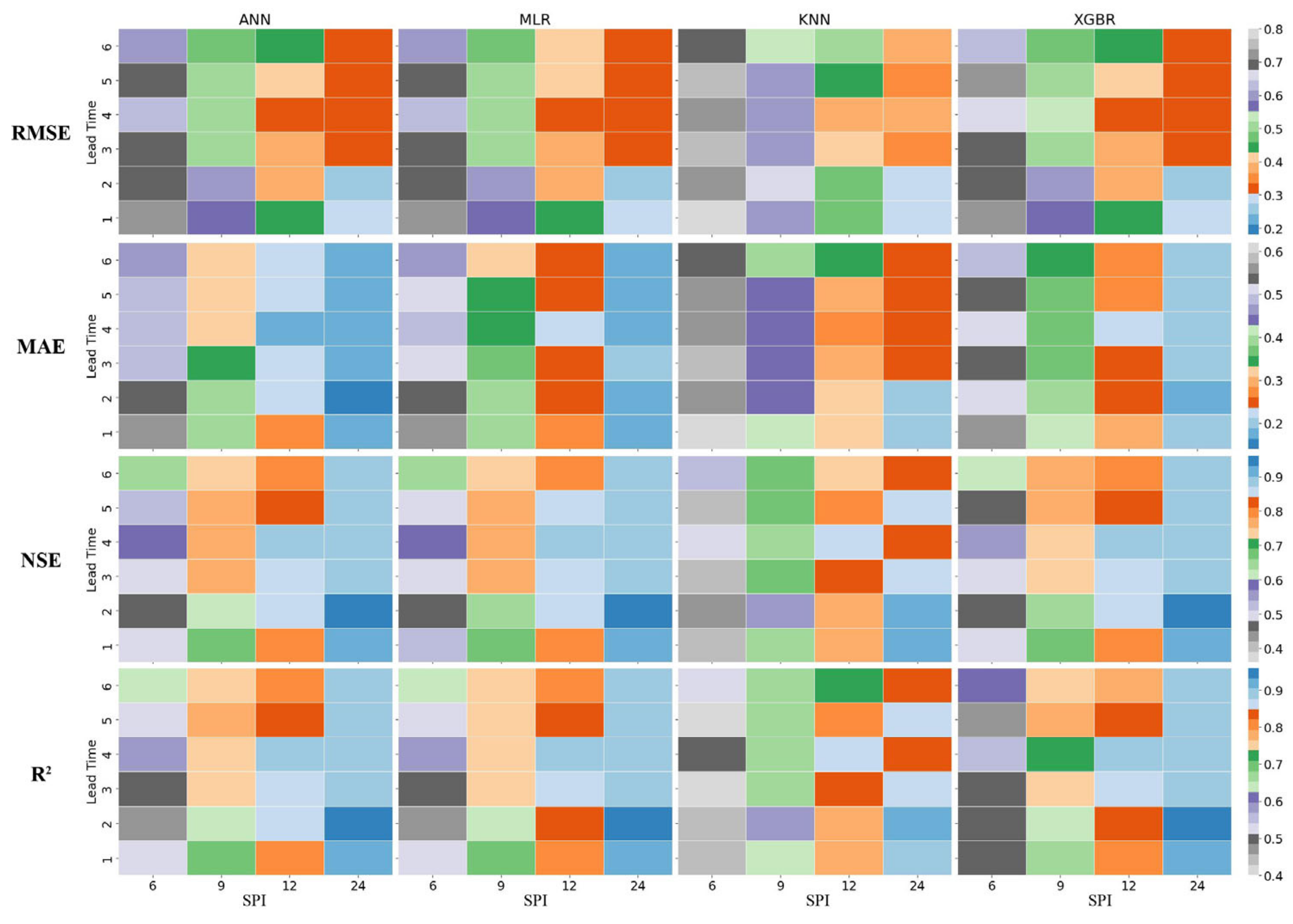
3.1.2. SPI Results for Tridolino Station
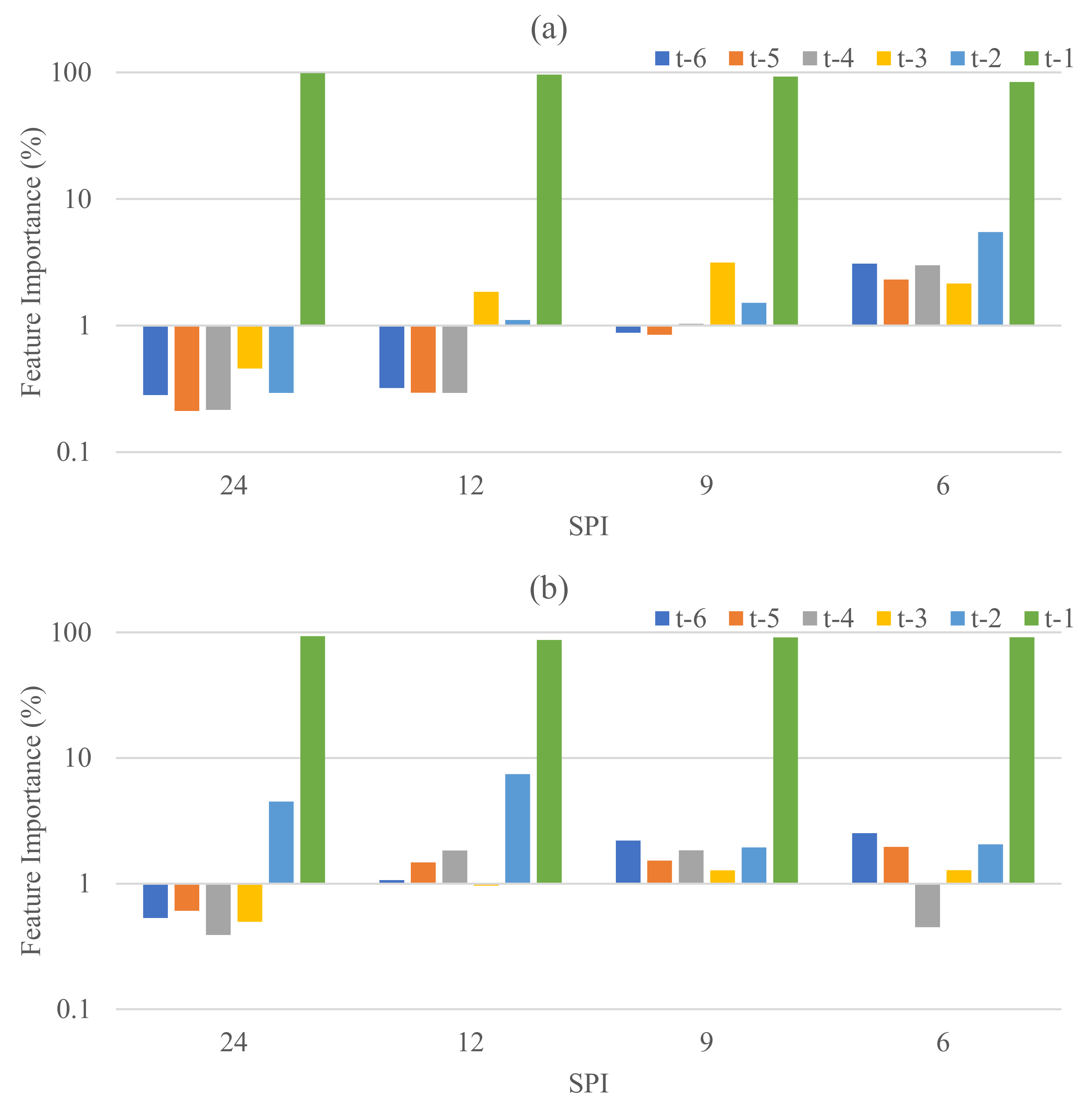
3.2. Results of the Feature Importance Analysis
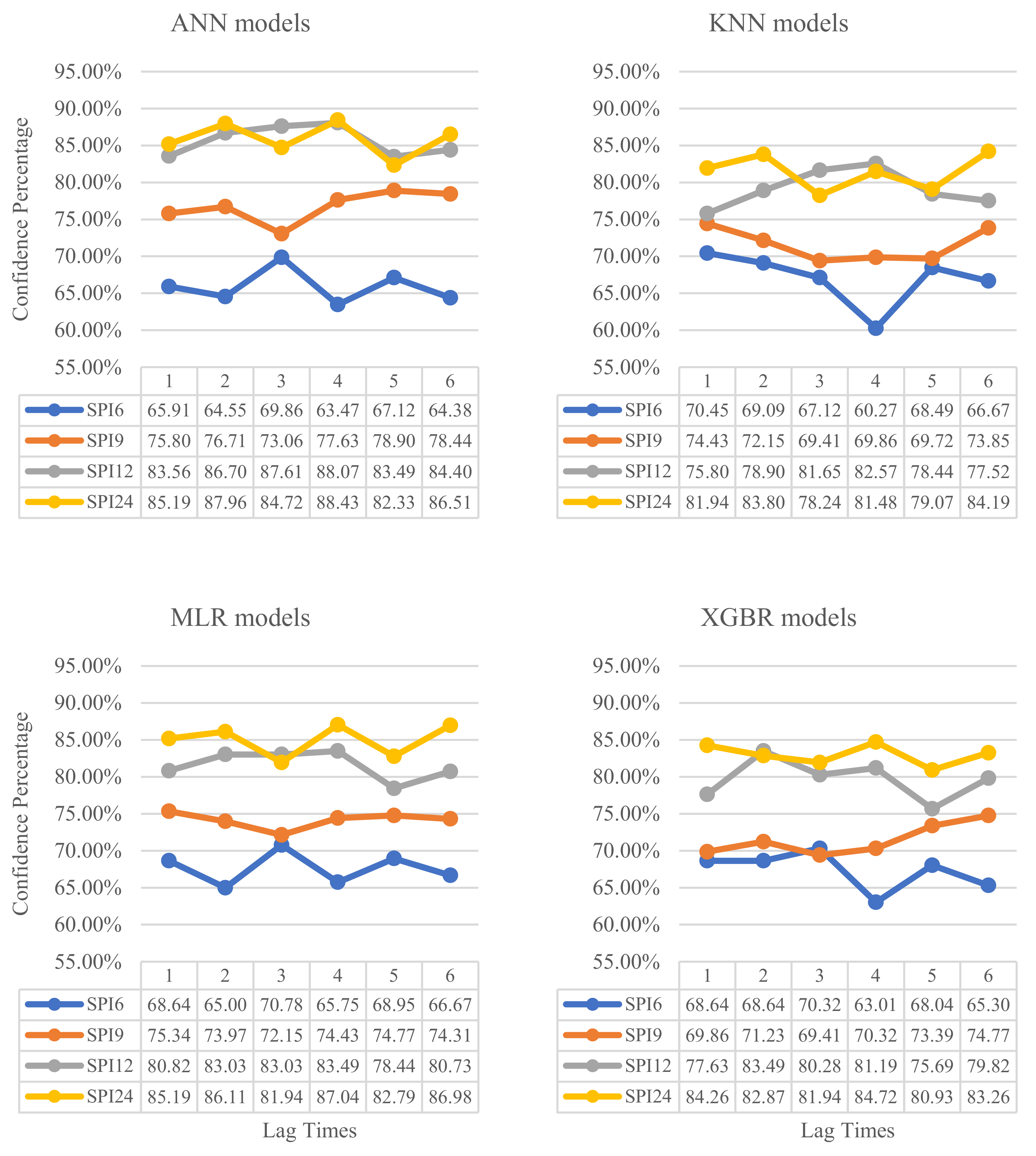
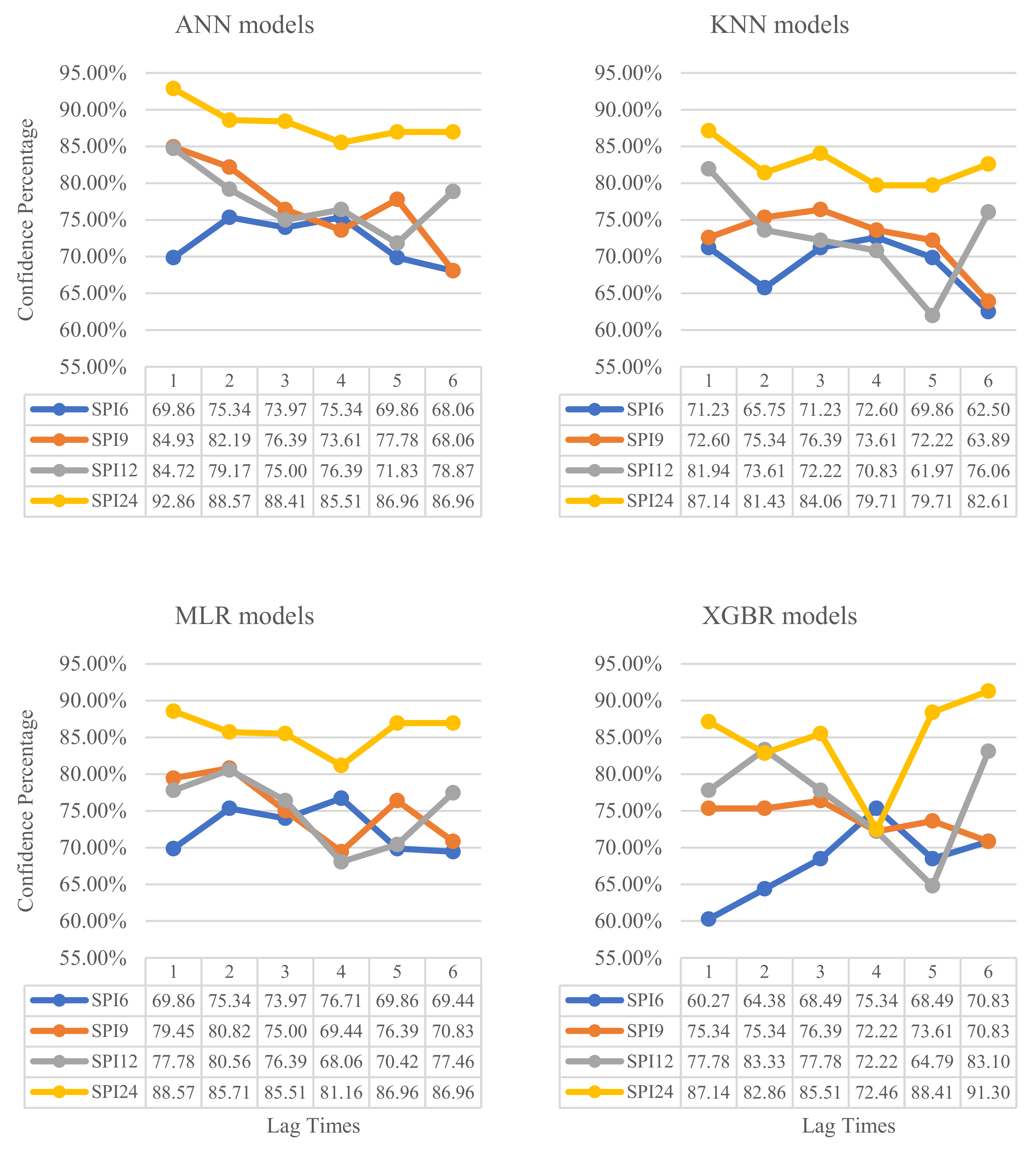
3.3. Results of Confidence Percentages for Machine Learning Models
3.4. Comparison between Two Different Stations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cheng, M.; McCarl, B.; Fei, C. Climate change and livestock production: A literature review. Atmosphere 2022, 13, 140. [Google Scholar] [CrossRef]
- Bouaziz, M.; Medhioub, E.; Csaplovisc, E. A machine learning model for drought tracking and forecasting using remote precipitation data and a standardized precipitation index from arid regions. J. Arid Environ. 2021, 189, 104478. [Google Scholar] [CrossRef]
- Shokoohi, A.; Morovati, R. Basinwide comparison of RDI and SPI within an IWRM framework. Water Resour. Manag. 2015, 29, 2011–2026. [Google Scholar] [CrossRef]
- Hosseini-Moghari, S.M.; Araghinejad, S. Monthly and seasonal drought forecasting using statistical neural networks. Environ. Earth Sci. 2015, 74, 397–412. [Google Scholar] [CrossRef]
- Docheshmeh Gorgij, A.; Alizamir, M.; Kisi, O.; Elshafie, A. Drought modelling by standard precipitation index (SPI) in a semi-arid climate using deep learning method: Long short-term memory. Neural Comput. Appl. 2022, 34, 2425–2442. [Google Scholar] [CrossRef]
- Lotfirad, M.; Esmaeili-Gisavandani, H.; Adib, A. Drought monitoring and prediction using SPI, SPEI, and random forest model in various climates of Iran. J. Water Clim. Change 2022, 13, 383–406. [Google Scholar] [CrossRef]
- Piri, J.; Abdolahipour, M.; Keshtegar, B. Advanced machine learning model for prediction of drought indices using hybrid SVR-RSM. Water Resour. Manag. 2023, 37, 683–712. [Google Scholar] [CrossRef]
- Shakeri, R.; Amini, H.; Fakheri, F.; Ketabchi, H. Assessment of drought conditions and prediction by machine learning algorithms using Standardized Precipitation Index and Standardized Water-Level Index (case study: Yazd province, Iran). Environ. Sci. Pollut. Res. 2023, 30, 101744–101760. [Google Scholar] [CrossRef]
- Elbeltagi, A.; Kumar, M.; Kushwaha, N.; Pande, C.B.; Ditthakit, P.; Vishwakarma, D.K.; Subeesh, A. Drought indicator analysis and forecasting using data driven models: Case study in Jaisalmer, India. Stoch. Environ. Res. Risk Assess. 2023, 37, 113–131. [Google Scholar] [CrossRef]
- Elbeltagi, A.; Pande, C.B.; Kumar, M.; Tolche, A.D.; Singh, S.K.; Kumar, A.; Vishwakarma, D.K. Prediction of meteorological drought and standardized precipitation index based on the random forest (RF), random tree (RT), and Gaussian process regression (GPR) models. Environ. Sci. Pollut. Res. 2023, 30, 43183–43202. [Google Scholar] [CrossRef]
- Coşkun, Ö.; Citakoglu, H. Prediction of the standardized precipitation index based on the long short-term memory and empirical mode decomposition-extreme learning machine models: The Case of Sakarya, Türkiye. Phys. Chem. Earth Parts A/B/C 2023, 131, 103418. [Google Scholar] [CrossRef]
- Adnan, R.M.; Dai, H.-L.; Kuriqi, A.; Kisi, O.; Zounemat-Kermani, M. Improving drought modeling based on new heuristic machine learning methods. Ain Shams Eng. J. 2023, 14, 102168. [Google Scholar] [CrossRef]
- Saha, S.; Kundu, B.; Paul, G.C.; Pradhan, B. Proposing an ensemble machine learning based drought vulnerability index using M5P, dagging, random sub-space and rotation forest models. Stoch. Environ. Res. Risk Assess. 2023, 37, 2513–2540. [Google Scholar] [CrossRef]
- Niazkar, M.; Piraei, R.; Eryılmaz Türkkan, G.; Hırca, T.; Gangi, F.; Afzali, S.H. Drought analysis using innovative trend analysis and machine learning models for Eastern Black Sea Basin. Theor. Appl. Climatol. 2024, 155, 1605–1624. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J. Standard precipitation index drought forecasting using neural networks, wavelet neural networks, and support vector regression. Appl. Comput. Intell. Soft Comput. 2012, 2012, 794061. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J.; Khalil, B.; Ozga-Zielinski, B. Long-term SPI drought forecasting in the Awash River Basin in Ethiopia using wavelet neural network and wavelet support vector regression models. J. Hydrol. 2014, 508, 418–429. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J.; Khalil, B.; Quilty, J. Coupling machine learning methods with wavelet transforms and the bootstrap and boosting ensemble approaches for drought prediction. Atmos. Res. 2016, 172, 37–47. [Google Scholar] [CrossRef]
- Maca, P.; Pech, P. Forecasting SPEI and SPI drought indices using the integrated artificial neural networks. Comput. Intell. Neurosci. 2016, 2016, 3868519. [Google Scholar] [CrossRef]
- El Ibrahimi, A.; Baali, A. Application of Several Artificial Intelligence Models for Forecasting Meteorological Drought Using the Standardized Precipitation Index in the Saïss Plain (Northern Morocco). Int. J. Intell. Eng. Syst. 2018, 11, 267–275. [Google Scholar] [CrossRef]
- Khan, M.M.H.; Muhammad, N.S.; El-Shafie, A. Wavelet based hybrid ANN-ARIMA models for meteorological drought forecasting. J. Hydrol. 2020, 590, 125380. [Google Scholar] [CrossRef]
- Adikari, K.E.; Shrestha, S.; Ratnayake, D.T.; Budhathoki, A.; Mohanasundaram, S.; Dailey, M.N. Evaluation of artificial intelligence models for flood and drought forecasting in arid and tropical regions. Environ. Model. Softw. 2021, 144, 105136. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Rai, P.; Kuriqi, A. Prediction of multi-scalar standardized precipitation index by using artificial intelligence and regression models. Climate 2021, 9, 28. [Google Scholar] [CrossRef]
- Taylan, E.D.; Terzi, Ö.; Baykal, T. Hybrid wavelet–artificial intelligence models in meteorological drought estimation. J. Earth Syst. Sci. 2021, 130, 38. [Google Scholar] [CrossRef]
- Pande, C.B.; Costache, R.; Sammen, S.S.; Noor, R.; Elbeltagi, A. Combination of data-driven models and best subset regression for predicting the standardized precipitation index (SPI) at the Upper Godavari Basin in India. Theor. Appl. Climatol. 2023, 152, 535–558. [Google Scholar] [CrossRef]
- Ham, Y.-S.; Sonu, K.-B.; Paek, U.-S.; Om, K.-C.; Jong, S.-I.; Jo, K.-R. Comparison of LSTM network, neural network and support vector regression coupled with wavelet decomposition for drought forecasting in the western area of the DPRK. Nat. Hazards 2023, 116, 2619–2643. [Google Scholar] [CrossRef]
- Hukkeri, G.S.; Naganna, S.R.; Pruthviraja, D.; Bhat, N.; Goudar, R. Drought forecasting: Application of ensemble and advanced machine learning approaches. IEEE Access 2023, 11, 141375–141393. [Google Scholar] [CrossRef]
- Lalika, C.; Mujahid, A.U.H.; James, M.; Lalika, M.C. Machine learning algorithms for the prediction of drought conditions in the Wami River sub-catchment, Tanzania. J. Hydrol. Reg. Stud. 2024, 53, 101794. [Google Scholar] [CrossRef]
- Mohammed, S.; Arshad, S.; Alsilibe, F.; Moazzam, M.F.U.; Bashir, B.; Prodhan, F.A.; Alsalman, A.; Vad, A.; Ratonyi, T.; Harsányi, E. Utilizing machine learning and CMIP6 projections for short-term agricultural drought monitoring in central Europe (1900–2100). J. Hydrol. 2024, 633, 130968. [Google Scholar] [CrossRef]
- European Commission. Standardized Precipitation Index (SPI), Copernicus European Drought Observatory (EDO), EDO Indicator Factsheet—Standardized Precipitation Index (SPI); European Commission: Brussels, Belgium, 2022. [Google Scholar]
- Guttman, N.B. Accepting the standardized precipitation index: A calculation algorithm 1. JAWRA J. Am. Water Resour. Assoc. 1999, 35, 311–322. [Google Scholar] [CrossRef]
- Piraei, R.; Afzali, S.H.; Niazkar, M. Assessment of XGBoost to Estimate Total Sediment Loads in Rivers. Water Resour. Manag. 2023, 37, 5289–5306. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Chollet, F. Keras: The Python Deep Learning Library; Astrophysics Source Code Library: Houghton, MI, USA, 2018; p. ascl: 1806.022. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Dikshit, A.; Pradhan, B.; Santosh, M. Artificial neural networks in drought prediction in the 21st century—A scientometric analysis. Appl. Soft Comput. 2022, 114, 108080. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, Z.-Y.; Xu, L.-J.; Ou, C.-Q. Meteorological drought forecasting based on a statistical model with machine learning techniques in Shaanxi province, China. Sci. Total Environ. 2019, 665, 338–346. [Google Scholar] [CrossRef] [PubMed]
- Niazkar, M.; Menapace, A.; Brentan, B.; Piraei, R.; Jimenez, D.; Dhawan, P.; Righetti, M. Applications of XGBoost in water resources engineering: A systematic literature review (Dec 2018–May 2023). Environ. Model. Softw. 2024, 174, 105971. [Google Scholar] [CrossRef]
- Ali, S.; Khorrami, B.; Jehanzaib, M.; Tariq, A.; Ajmal, M.; Arshad, A.; Shafeeque, M.; Dilawar, A.; Basit, I.; Zhang, L.; et al. Spatial Downscaling of GRACE Data Based on XGBoost Model for Improved Understanding of Hydrological Droughts in the Indus Basin Irrigation System (IBIS). Remote Sens. 2023, 15, 873. [Google Scholar] [CrossRef]
- Altunkaynak, A.; Jalilzadnezamabad, A. Extended lead time accurate forecasting of palmer drought severity index using hybrid wavelet-fuzzy and machine learning techniques. J. Hydrol. 2021, 601, 126619. [Google Scholar] [CrossRef]
- Raja, A.; Gopikrishnan, T. Drought prediction and validation for desert region using machine learning methods. Int. J. Adv. Comput. Sci. Appl. 2022, 13. [Google Scholar] [CrossRef]
- Fadaei-Kermani, E.; Barani, G.; Ghaeini-Hessaroeyeh, M. Drought monitoring and prediction using K-nearest neighbor algorithm. J. AI Data Min. 2017, 5, 319–325. [Google Scholar]
- Niazkar, M.; Piraei, R.; Zakwan, M. Application of Machine Learning Models for Short-term Drought Analysis Based on Streamflow Drought Index. Water Resour. Manag. 2024, 1–18. [Google Scholar] [CrossRef]
| Study | Year | Stations | SPI Months | ML Models Used for Comparison | Best Resulting Model |
|---|---|---|---|---|---|
| Belayneh and Adamowski [15] | 2012 | 3 | 3, 12 | ANN, SVR, and WN | WN |
| Belayneh et al. [16] | 2014 | 12 | 12, 24 | ARIMA, ANN, SVR, WA-ANN, and WA-SVR | WA-ANN |
| Hosseini-Moghari and Araghinejad [4] | 2015 | 1 | 3, 6, 9, 12, 24 | RMSMLP, DMSMLP, RMSRBF, DMSRBF, RMSGRNN, and DMSGRNN | RMSRBF and RMSGRNN, for smaller time scales, DMSRBF and DMSGRNN for larger ones. |
| Belayneh et al. [17] | 2016 | 3 | 3, 12, 24 | BANN, BSVR, WA-ANN, WA-SVR, BS-ANN, BS-SVR, WBS-ANN, and WBS-SVR | WBS-ANN and WBS-SVR |
| Maca and Pech [18] | 2016 | 2 | 1 | sANN and hANN | hANN |
| El Ibrahimi and Baali [19] | 2018 | 2 | 3, 12 | ANFIS, ANN, and SVR | ANFIS |
| Khan et al. [20] | 2020 | 3 | 1 | WN, ARIMA, ANN, and W-2A | W-2A |
| Adikari et al. [21] | 2021 | 13 | 1 | CNN, LSTM, and WANFIS | WANFIS |
| Malik et al. [22] | 2021 | 7 | 1, 3, 6, 9, 12, 24 | ANN, CANFIS, and MLR | CANFIS and MLR |
| Docheshmeh Gorgij et al. [5] | 2021 | 4 | 3, 6, 9, 12 | LSTM, MARS, ET, and VAR | LSTM |
| Taylan et al. [23] | 2021 | 3 | 3, 6, 9, 12 | ANFIS, SVM, ANN, WA-ANFIS, WA-ANN, and WA-SVR | WA-ANFIS for 12-month SPI and WA-SVR for other SPIs |
| Lotfirad et al. [6] | 2022 | 6 | 1, 3, 6, 9, 12, 24, 48 | RF | RF |
| Piri et al. [7] | 2022 | 11 | 1 | ANN, SVR, SVR-PSO, and SVR-RSM | SVR-RSM |
| Shakeri et al. [8] | 2023 | 1 | 3, 6, 12, 24 | MLR, KNN, GB, DT, XGBR, RF, and ANN | ANN |
| Pande et al. [24] | 2023 | 3 | 3, 6, 12 | AR, RSS, M5P, and BT | M5P and BT |
| Elbeltagi et al. [9] | 2023 | 1 | 3, 6, 12 | RSS, RSS-M5P, RSS-RF, and RSS-RT | RSS-M5P |
| Elbeltagi et al. [10] | 2023 | 2 | 6, 12 | RF, RT, and GPR-PUK kernel | RF |
| Ham et al. [25] | 2023 | 6 | 6, 12 | WLSTMN, WA-ANN, and WA-SVR | WLSTMN |
| Coşkun and Citakoglu [11] | 2023 | 1 | 1, 3, 6 | LSTM, EMD, and ELM | LSTM |
| Adnan et al. [12] | 2023 | 3 | 3, 6, 9, 12 | OP-ELM, DENFIS, and MARS | DENFIS |
| Saha et al. [13] | 2023 | 1 | 3, 6, 12, 24 | M5P, M5P-Dagging, M5P-RSS, and M5P-RTF | M5P-RFT |
| Niazkar et al. [14] | 2023 | 8 | 6, 9, 12, 24 | ANN, MLR, KNN, XGBR | ANN, MLR, and XGBR |
| Hukkeri et al. [26] | 2023 | 12 | 6 | ANN, MARS, GB, CBR | MARS and GB |
| Lalika et al. [27] | 2024 | 5 | 6, 9 | LSTM, MARS, SVR, ELM, M5P | LSTM |
| Mohammed et al. [28] | 2024 | 3 | 3 | BT, RF, DT, M5P | RF |
| Statistical Property | Shiraz Station | Tridolino Station | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| P (mm) | SPI | P (mm) | SPI | |||||||
| 6 | 9 | 12 | 24 | 6 | 9 | 12 | 24 | |||
| Minimum | 0 | −2.51 | −2.51 | −2.51 | −2.50 | 0 | −2.10 | −2.10 | −2.10 | −2.08 |
| Average | 26.81 | 0.02 | 0.001 | 0.001 | 4 × 10−4 | 40.07 | −4 × 10−16 | −7 × 10−16 | −9 × 10−16 | −2 × 10−16 |
| Maximum | 330 | 2.51 | 2.51 | 2.51 | 2.50 | 159.36 | 2.10 | 2.10 | 2.10 | 2.08 |
| Skewness | 2.40 | 0.06 | −0.001 | 0.001 | −5 × 10−4 | 1.00 | 3 × 10−16 | 1 × 10−16 | 1 × 10−15 | 3 × 10−16 |
| Standard deviation | 43.76 | 0.97 | 0.99 | 0.99 | 0.99 | 29.51 | 0.97 | 0.97 | 0.97 | 0.97 |
| Model | Hyperparameter | Description | Range |
|---|---|---|---|
| ANN | activation | The activation function introduces nonlinearity to models. | ‘tanh’, ‘relu’, ‘sigmoid’, and ‘linear’ |
| optimizer | Optimizer algorithm determines optimal weights for the model. | ‘sgd’, ‘rmsprop’, ‘adadelta’, and ‘adam’ | |
| loss | The loss function measures the model performance. | ‘mae’, ‘mse’, or other defined metrics in ‘keras’ library | |
| KNN | p | Power parameter for the Minkowski metric. | float |
| n_neighbors | Number of neighbors. | positive integer | |
| weights | Weight function is used in prediction. | ‘uniform’, ‘distance’, callable or none | |
| algorithm | Algorithm is used to compute the nearest neighbors. | ‘auto’, ‘ball_tree’, ‘kd_tree’, and ‘brute’ | |
| XGBR | n_estimators | Number of trees. | positive integer |
| max_depth | Maximum depth allowed for each tree. | positive integer or none | |
| learning_rate | Step size shrinkage is used to prevent overfitting (eta). | [0, 1] | |
| reg_alpha | L1 weight regularization term. | [0, ∞] | |
| reg_lambda | L2 weight regularization term. | [0, ∞] | |
| min_split_loss | Minimum loss reduction required to make a further partition on a leaf node of the tree (gamma). | [0, ∞] | |
| min_child_weight | Minimum summation of the instance weight needed in a child node. | [0, ∞] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piraei, R.; Niazkar, M.; Gangi, F.; Eryılmaz Türkkan, G.; Afzali, S.H. Short-Term Drought Forecast across Two Different Climates Using Machine Learning Models. Hydrology 2024, 11, 163. https://doi.org/10.3390/hydrology11100163
Piraei R, Niazkar M, Gangi F, Eryılmaz Türkkan G, Afzali SH. Short-Term Drought Forecast across Two Different Climates Using Machine Learning Models. Hydrology. 2024; 11(10):163. https://doi.org/10.3390/hydrology11100163
Chicago/Turabian StylePiraei, Reza, Majid Niazkar, Fabiola Gangi, Gökçen Eryılmaz Türkkan, and Seied Hosein Afzali. 2024. "Short-Term Drought Forecast across Two Different Climates Using Machine Learning Models" Hydrology 11, no. 10: 163. https://doi.org/10.3390/hydrology11100163
APA StylePiraei, R., Niazkar, M., Gangi, F., Eryılmaz Türkkan, G., & Afzali, S. H. (2024). Short-Term Drought Forecast across Two Different Climates Using Machine Learning Models. Hydrology, 11(10), 163. https://doi.org/10.3390/hydrology11100163










