Assessing the Impact of Rainfall Inputs on Short-Term Flood Simulation with Cell2Flood: A Case Study of the Waryong Reservoir Basin
Abstract
1. Introduction
2. Materials and Methods
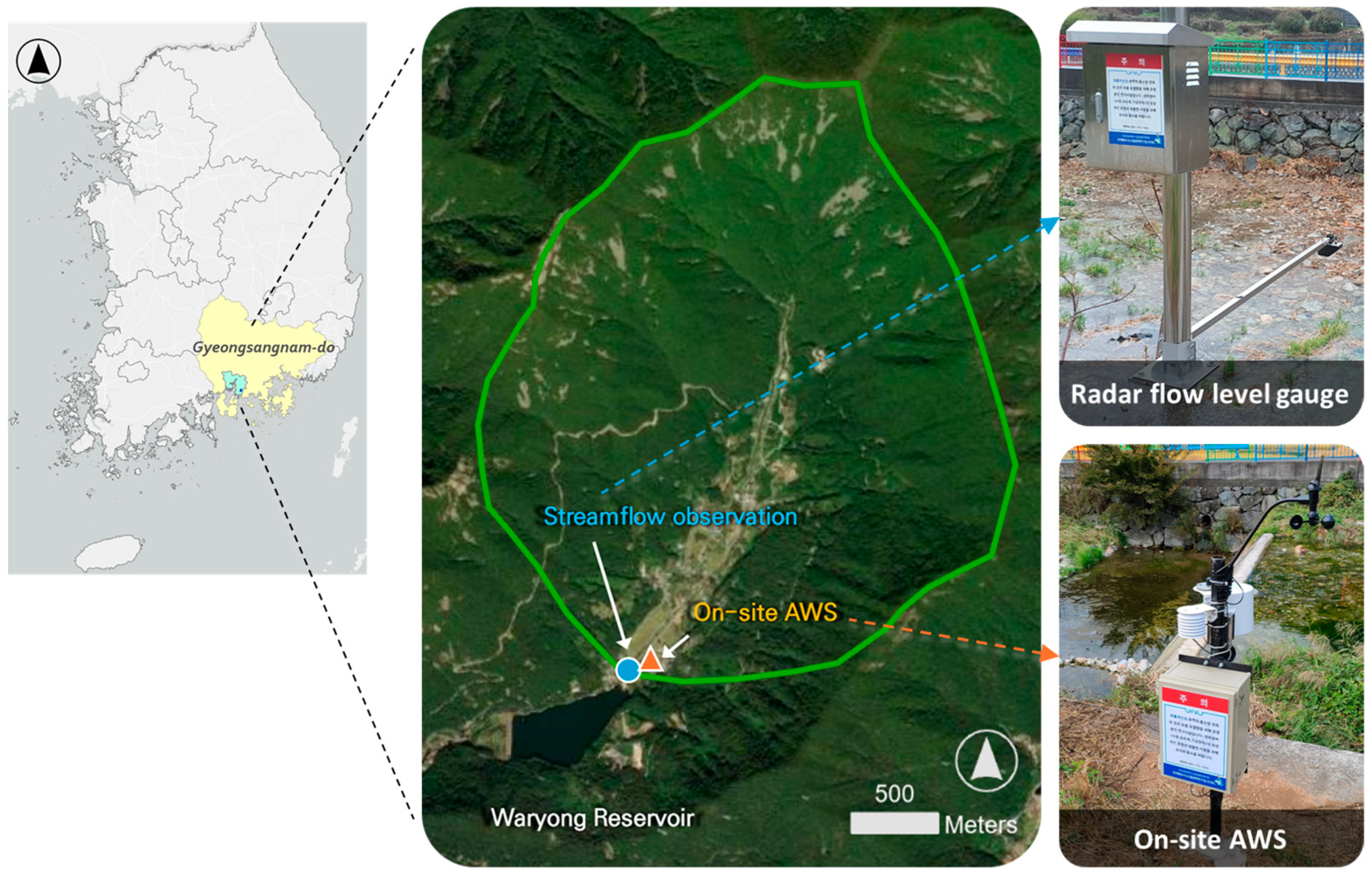
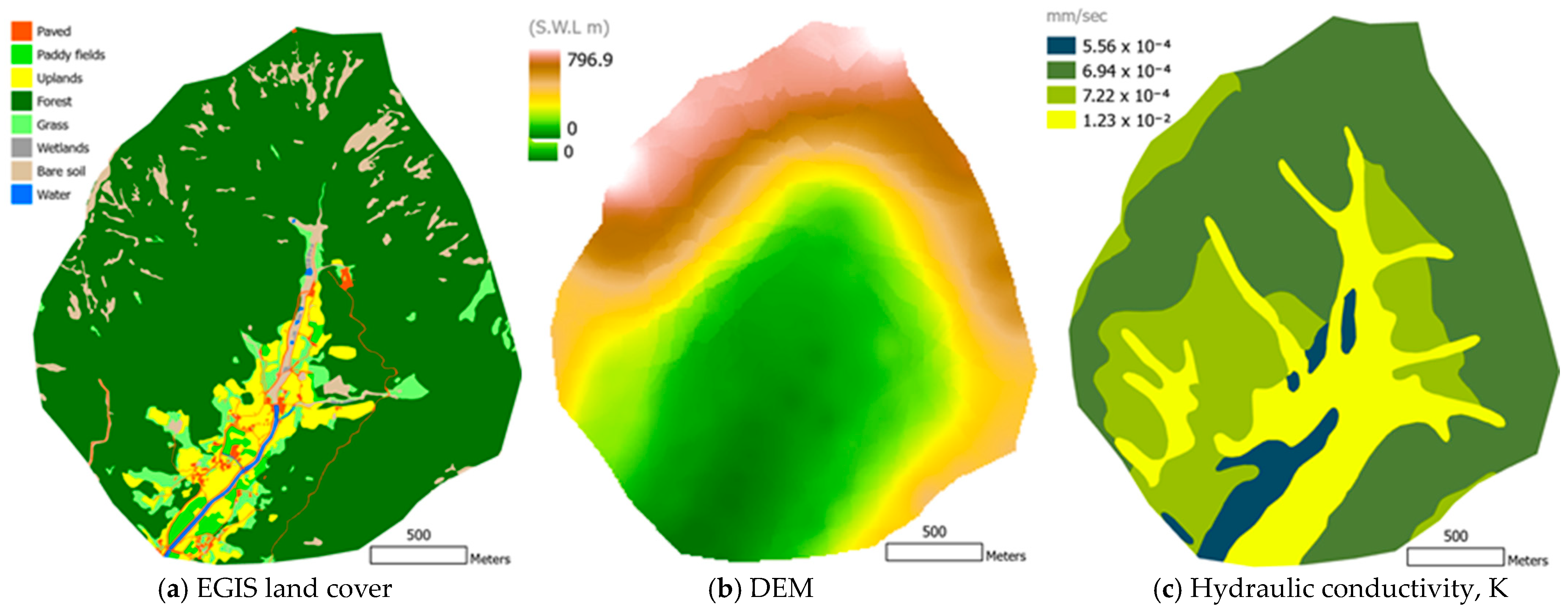
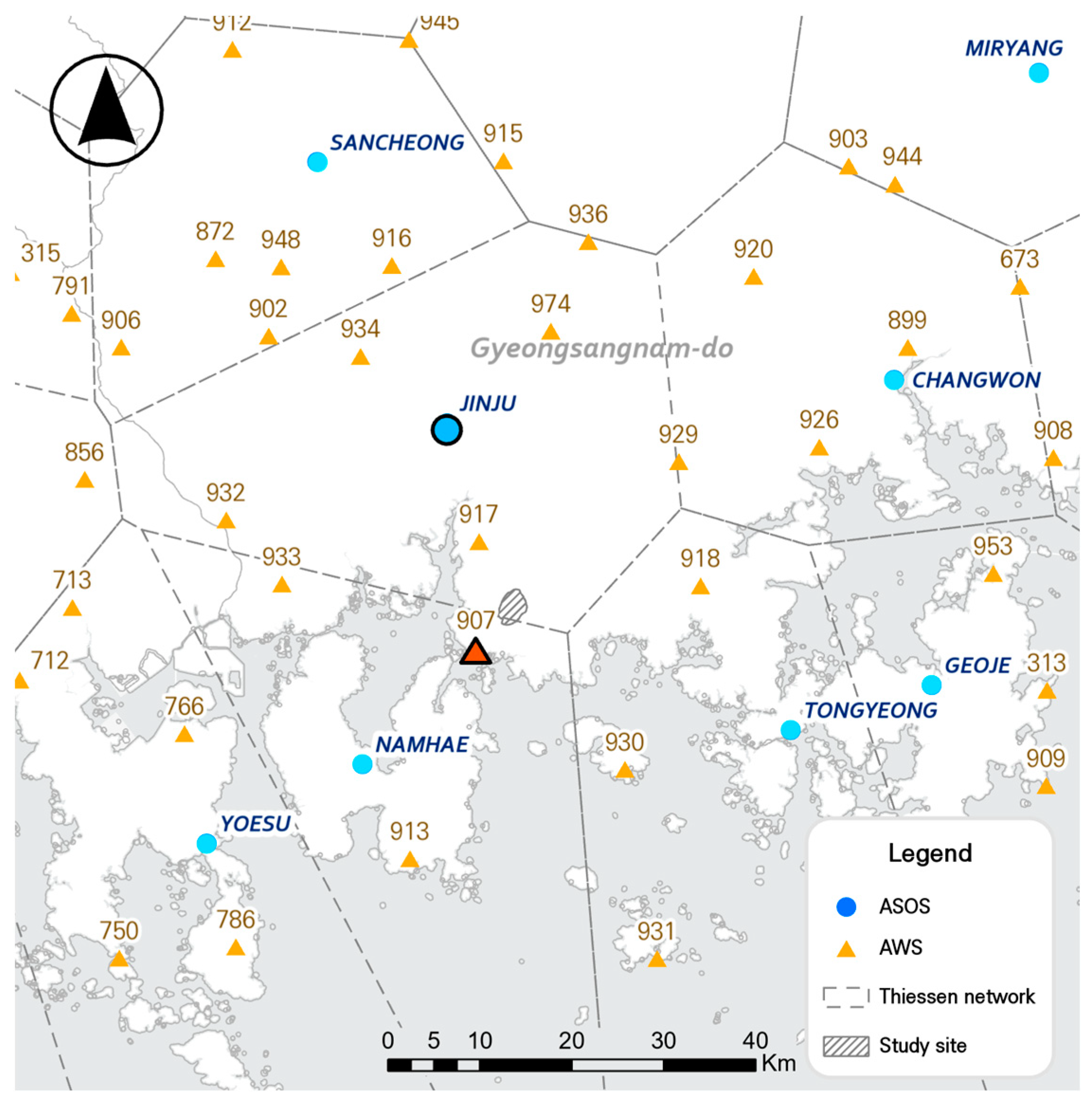
2.1. Study Site
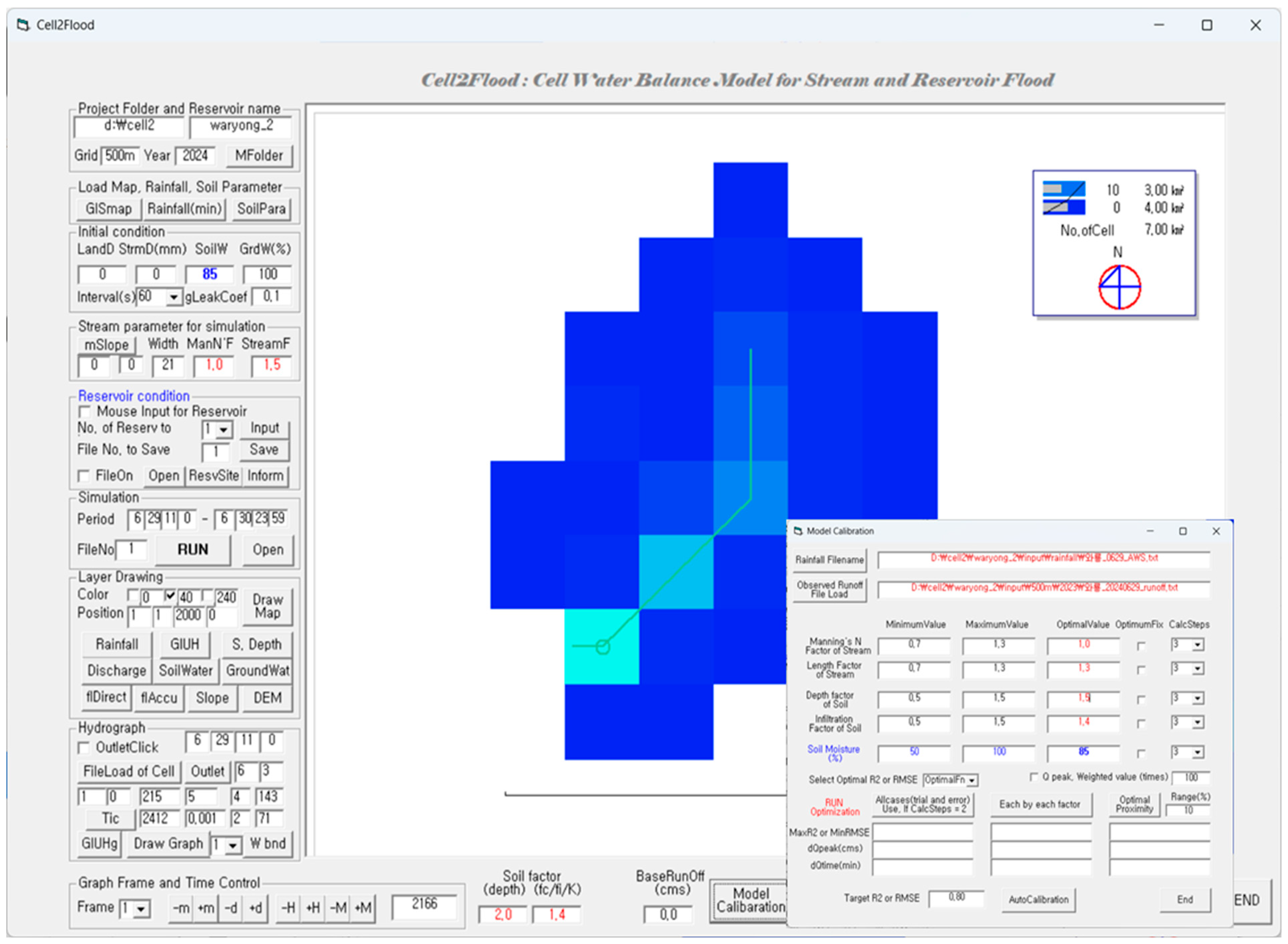
2.2. Short-Term Hydrological Model: Cell2Flood
2.3. Preparation of Rainfall Inputs
2.4. Evaluation Metrics for Correlation and Performance
3. Results and Discussion
3.1. Comparison of Rainfall Inputs
3.1.1. Accumulated Rainfall
3.1.2. Temporal Distribution of Rainfall
3.1.3. Rainfall Intensity
3.1.4. Spatial Distribution of Rainfall
3.1.5. Statistical Difference among Rainfall Inputs
3.2. Runoff Simulation with On-Site Calibrated Parameters
3.2.1. On-Site Parameter Calibration of Cell2Flood
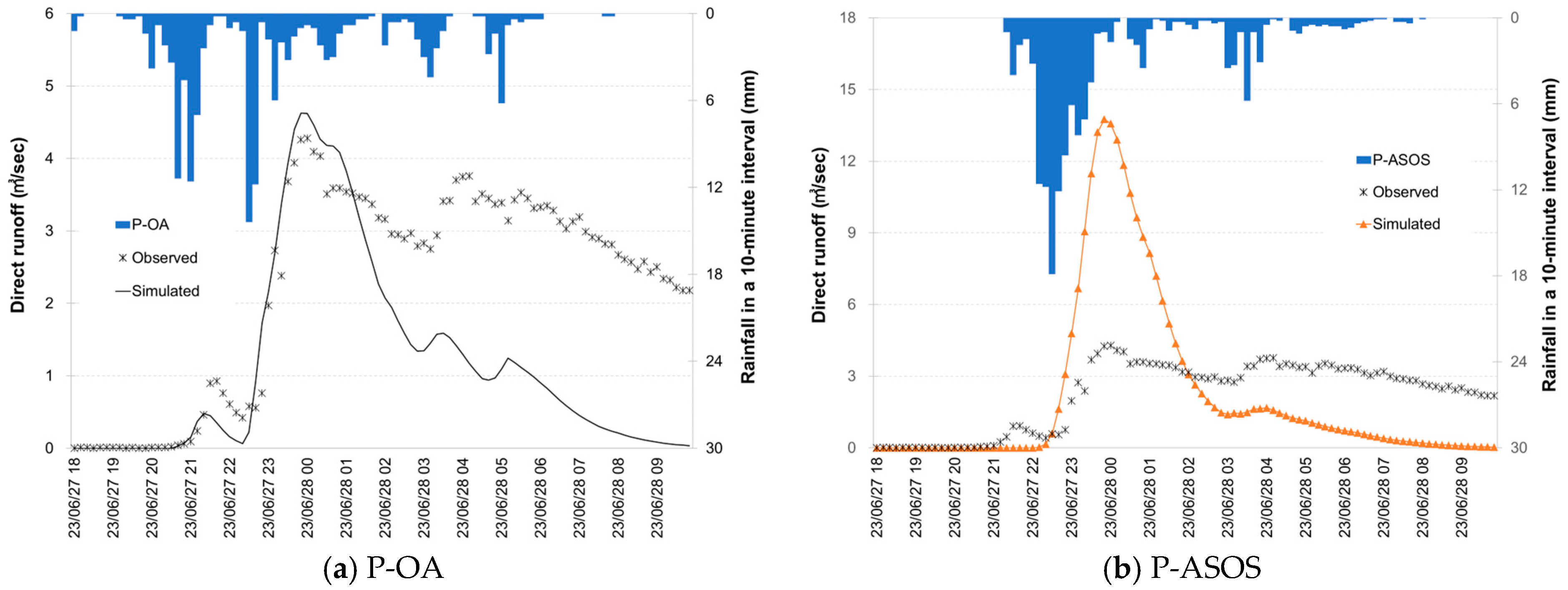
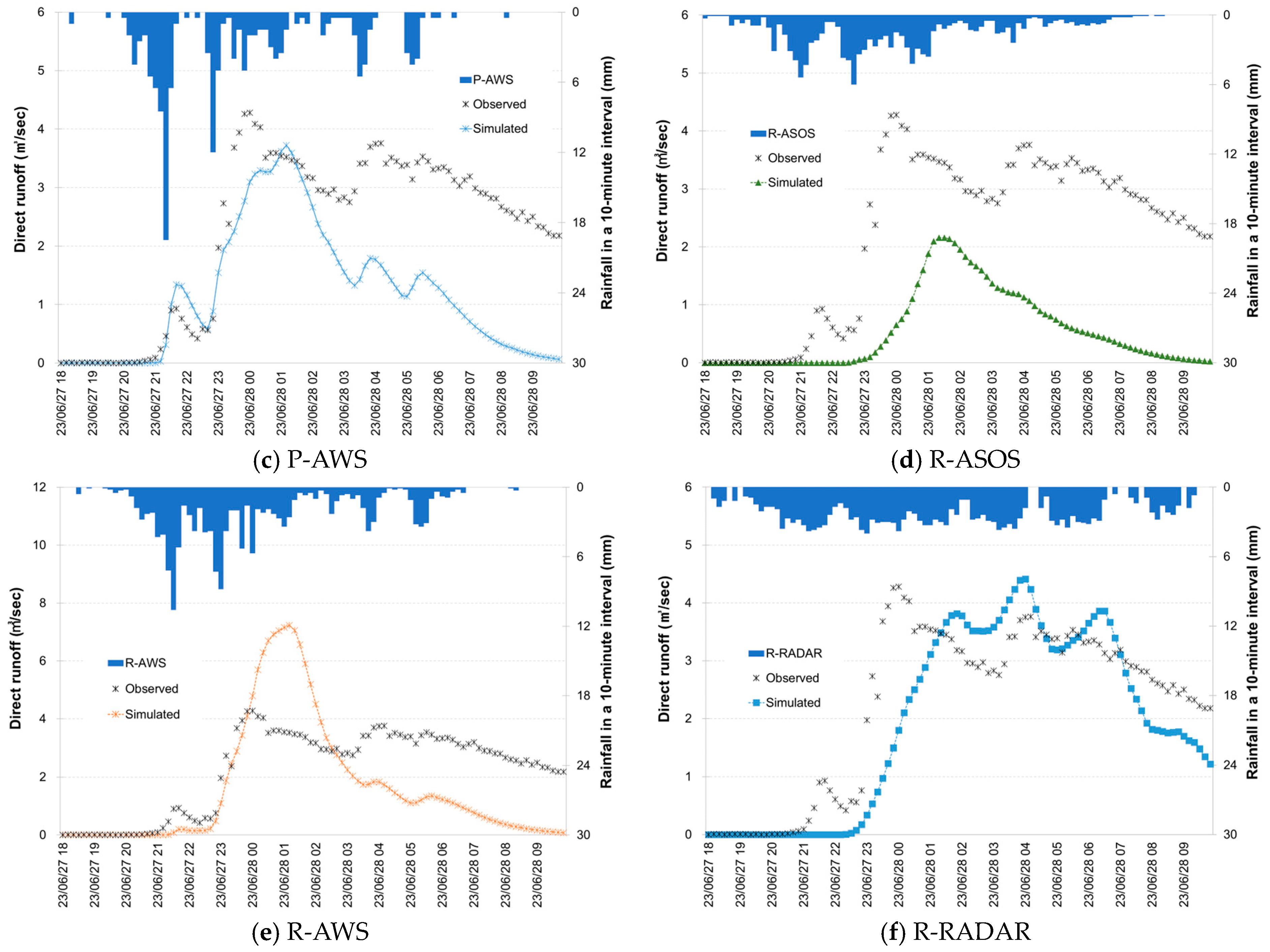
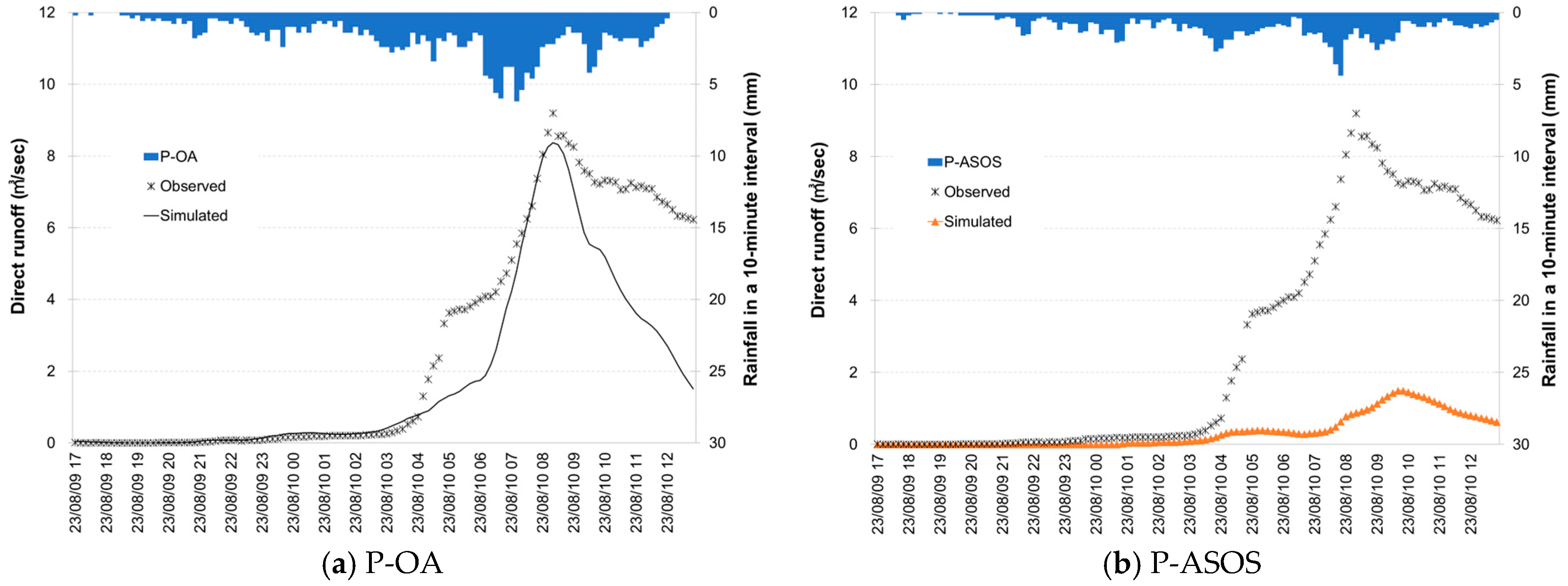
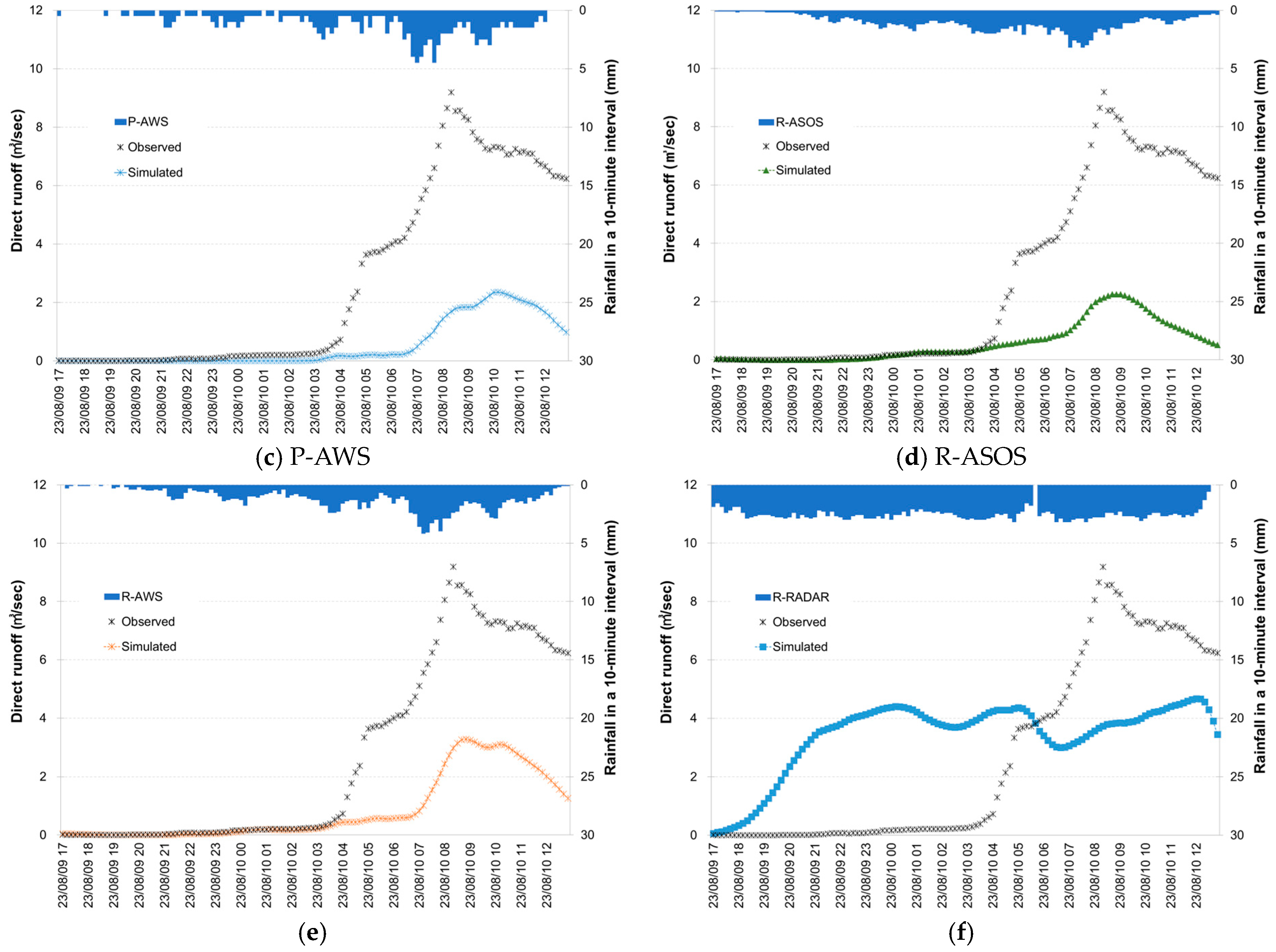
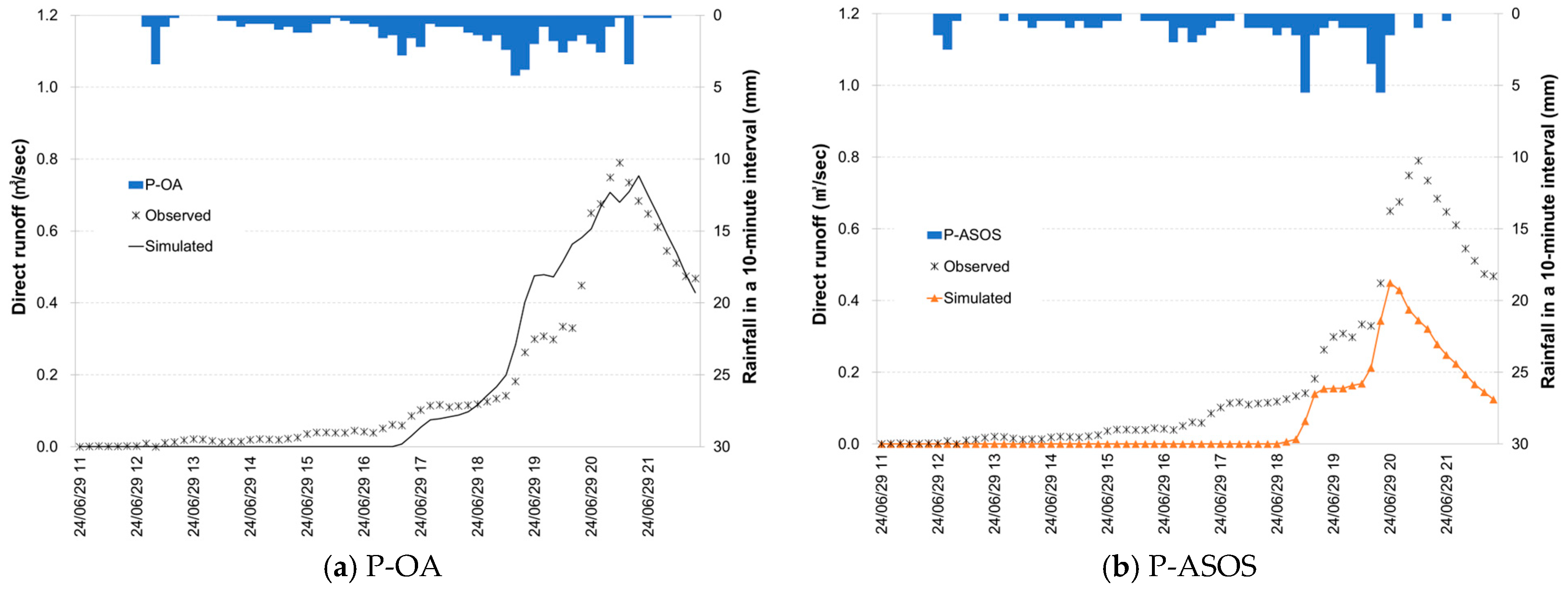
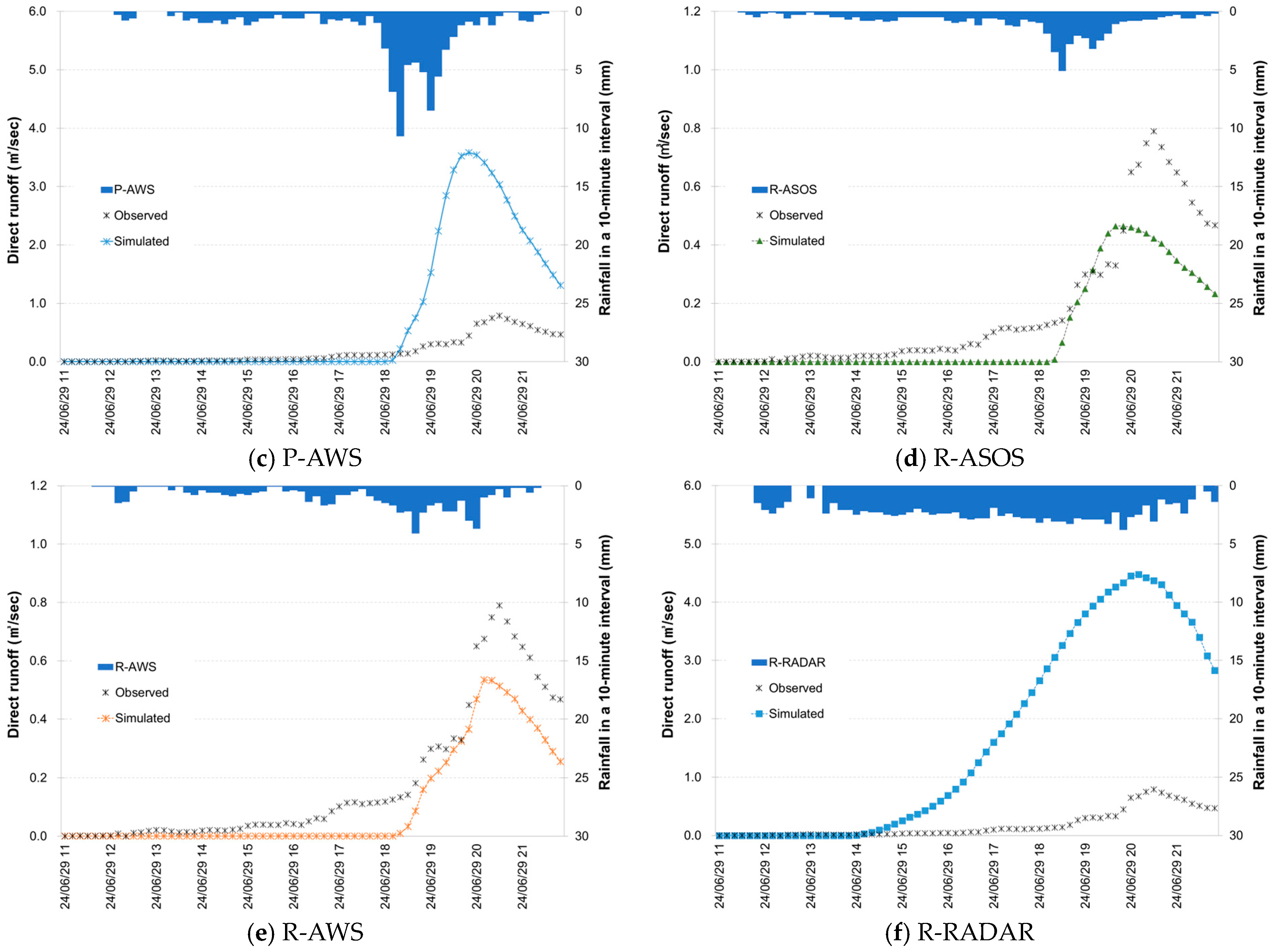
3.2.2. Temporal Variations in Runoff by Rainfall Inputs
3.2.3. Peak Flow by Rainfall Inputs
3.2.4. Evaluation of the Runoff Simulations
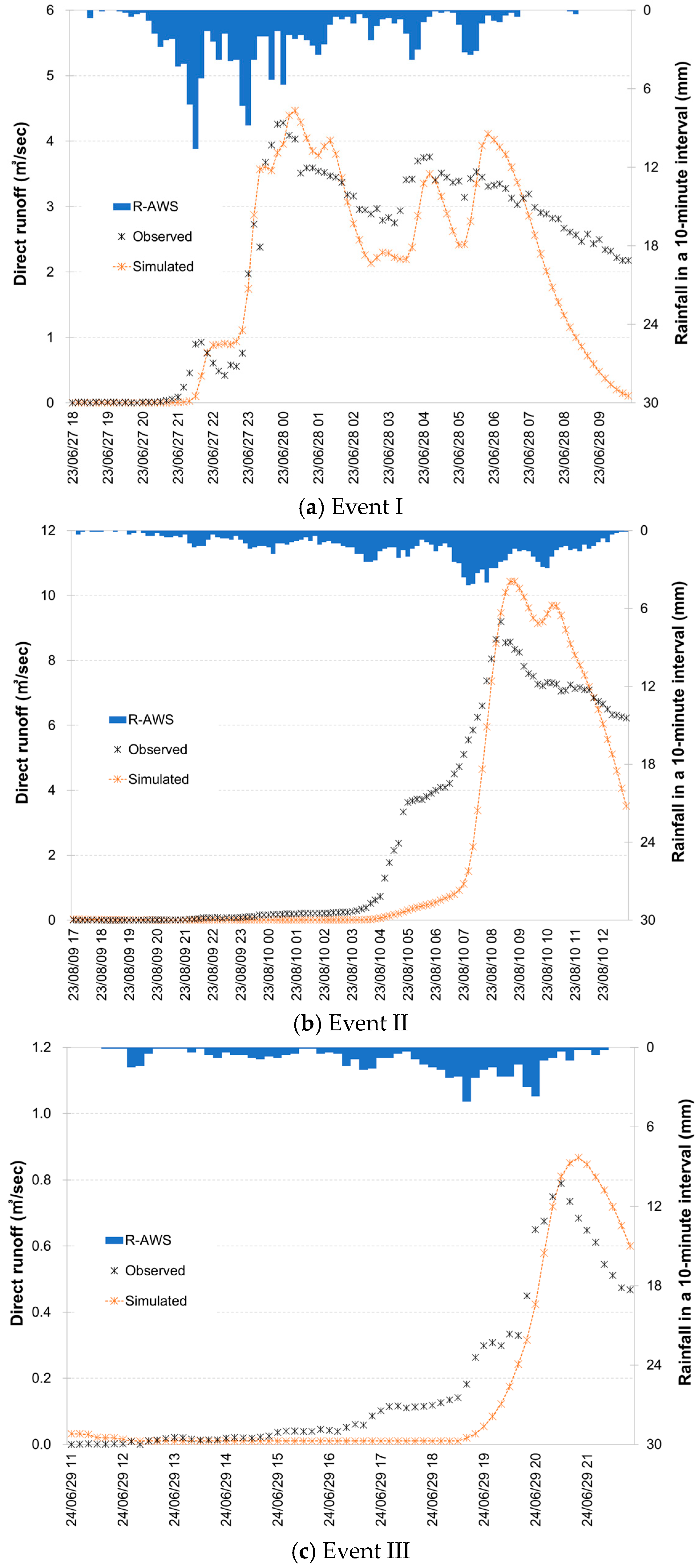
3.3. Runoff Simulation with Input-Specific Calibrated Parameters
3.3.1. Parameter Calibration for Each Rainfall Input
3.3.2. Evaluation of Runoff Simulations with Input-Specific Calibrated Parameters
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, C.; Liu, C.; Yao, Y.; Wu, Q.; Ma, B.; Jian, S. Evaluation of the impact of rainfall inputs on urban rainfall models: A systematic review. Water 2020, 12, 2484. [Google Scholar] [CrossRef]
- Hyun, J.H.; Park, H.; Chung, G. Effects of the difference between ASOS and AWS data on runoff characteristics. J. Korean Soc. Hazard Mitig. 2019, 19, 443–449. [Google Scholar] [CrossRef]
- Byaruhanga, N.; Kibirige, D.; Gokool, S.; Mkhonta, G. Evolution of flood prediction and forecasting models for flood early warning systems: A scoping review. Water 2024, 16, 1763. [Google Scholar] [CrossRef]
- Vaes, G.; Willems, R.; Berlamont, J. Rainfall input requirements for hydrological calculations. Urban Water 2001, 3, 107–112. [Google Scholar] [CrossRef]
- Palanisamy, B.A. Evaluation of SWAT Model—Subdaily Runoff Prediction in Texas Watersheds. Master’s Thesis, Texas A&M University, College Station, TX, USA, May 2006. [Google Scholar]
- Tramblay, Y.; Bouvier, C.; Ayral, P.A.; Marchandise, A. Impact of rainfall spatial distribution on rainfall-runoff modelling efficiency and initial soil moisture conditions estimation. Nat. Hazards Earth Syst. Sci. 2011, 11, 157–170. [Google Scholar] [CrossRef]
- Shakti, P.C.; Nakatani, T.; Misumi, R. The role of the spatial distribution of radar rainfall on hydrological modeling for an urbanized river basin in Japan. Water 2019, 11, 1703. [Google Scholar] [CrossRef]
- Lee, M.; Lee, C.; Yoo, Y.; Kwak, J.; Kim, H.S. Evaluation of hydrological applicability for rainfall estimation algorithms of dual-polarization radar. J. Korea Water Resour. Assoc. 2021, 54, 27–38. [Google Scholar]
- Ahn, S.R.; Jang, C.H.; Kim, S.H.; Han, M.S.; Kim, J.H.; Kim, S.J. Discussion for the effectiveness of radar data through distributed storm runoff modeling. J. Korean Soc. Agric. Eng. 2013, 55, 19–30. [Google Scholar]
- Ahn, S.R.; Jung, C.G.; Kim, S.J. A study on the effectiveness of radar rainfall by comparing with flood inundation record map using KIMSTORM (Grid-based KIneMatic Wave STOrm Runoff Model). J. Korea Water Resour. Assoc. 2015, 48, 925–936. [Google Scholar] [CrossRef][Green Version]
- Vieux, B.E.; Park, J.H.; Kang, B. Distributed hydrologic prediction: Sensitivity to accuracy of initial soil moisture conditions and radar rainfall input. J. Hydrol. Eng. 2009, 14, 671–689. [Google Scholar] [CrossRef]
- Jang, D.W.; Kim, D.K.; Kim, Y.S.; Choi, W.I. Application of SWAT model considering spatial distribution of rainfall. J. Wetl. Res. 2018, 20, 94–103. [Google Scholar]
- Kim, J.H.; Song, Y.H.; Chung, E.S. Uncertainty of future runoff projection according to SSP scenarios and hydrologic model parameters. J. Korea Water Resour. Assoc. 2023, 56, 35–43. [Google Scholar]
- Piadeh, F.; Behzadian, K.; Alani, A.M. A critical review of real-time modelling of flood forecasting in urban drainage systems. J. Hydrol. 2022, 607, 127476. [Google Scholar] [CrossRef]
- Shin, H.J.; Lee, C.; Kim, G.; Kong, J.Y. Sensitivity analysis of precipitation and reservoir storage under climate change for agricultural reservoirs in South Korea. Water 2019, 11, 2578. [Google Scholar]
- Ahmed, S.I.; Rudra, R.; Goel, P.; Khan, A.; Gharabaghi, B.; Sharma, R. A comparative evaluation of using rain gauge and NEXRAD radar-estimated rainfall data for simulating streamflow. Hydrology 2022, 9, 133. [Google Scholar] [CrossRef]
- Thorndahl, S.; Einfalt, T.; Willems, P.; Nielsen, J.E.; ten Veldhuis, M.C.; Arnbjerg-Nielsen, K.; Rasmussen, M.R.; Molnar, P. Weather radar rainfall data in urban hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 1359–1380. [Google Scholar] [CrossRef]
- Thorndahl, S.; Nielsen, J.E.; Rasmussen, M.R. Estimation of storm-centred areal reduction factors from radar rainfall for design in urban hydrology. Water 2019, 11, 1120. [Google Scholar] [CrossRef]
- Kim, D.; An, H.; Jang, M.; Kim, S. Development for a distributed hydrological model considering hydrological change. Korean J. Agri. Sci. 2017, 45, 521–532. [Google Scholar] [CrossRef]
- Kim, D. Development of Spatiotemporal Real-Time Runoff and Flood Prediction System for Agricultural Reservoirs; Korea Institute of Planning and Evaluation for Technology in Food, Agriculture, and Forestry: Jeollanam-do, Republic of Korea, 2022; pp. 47–61. [Google Scholar]
- Rural Agricultural Water Resource Information System (RAWRIS). Available online: https://rawris.ekr.or.kr (accessed on 25 September 2024).
- Korean Soil Information System (KSIS). Available online: https://soil.rda.go.kr (accessed on 25 September 2024).
- Chung, H.W.; Kim, S.J.; Choi, J.Y.; Kim, D.S. GIS application model for temporal and spatial simulation of surface runoff from a small watershed. J. GIS Assoc. Korea 1995, 3, 135–146. [Google Scholar]
- Beven, K. Rainfall-Runoff Modelling: The Primer, 2nd ed.; Wiley-Blackwell: Oxford, UK, 2012; pp. 40–44. [Google Scholar]
- Dwarakish, G.S.; Ganasri, B.P.; De Stefano, L. Impact of land use change on hydrological systems: A review of current modeling approaches. Cogent Geosci. 2015, 1, 1115691. [Google Scholar] [CrossRef]
- Qin, F.; Zhu, Y.; Ao, T.; Chen, T. The development trend and research frontiers of distributed hydrological models—Visual bibliometric analysis based on Citespace. Water 2021, 13, 174. [Google Scholar] [CrossRef]
- Sun, W.; Wang, Y.; Wang, G.; Cui, X.; Yu, J.; Zuo, D.; Xu, Z. Physically based distributed hydrological model calibration based on a short period of streamflow data: Case studies in four Chinese basins. Hydrol. Earth Syst. Sci. 2017, 21, 251–265. [Google Scholar] [CrossRef]
- Environmental Geographic Information Service (EGIS). Available online: https://egis.me.go.kr (accessed on 25 September 2024).
- Jung, I.K.; Lee, M.S.; Park, J.Y.; Kim, S.J. A modified grid-based KIneMatic Wave STOrm Runoff Model (ModKIMSTORM) (I): Theory and model. KSCE J. Civ. Eng. 2008, 28, 697–707. [Google Scholar]
- Zhang, M.; de Leon, C.; Migliaccio, K. Evaluation and comparison of interpolated gauge rainfall data and gridded rainfall data in Florida, USA. Hydrolog. Sci. J. 2018, 63, 561–582. [Google Scholar] [CrossRef]
- Jung, S.; Oh, S.; Lee, D.; Le, X.H.; Lee, G. Application of convolutional autoencoder for spatiotemporal bias-correction of radar precipitation. J. Korea Water Resour. 2021, 54, 453–462. [Google Scholar]
- Keum, H.; Kim, H.; Jo, T. Estimation of flood discharge in complex basins and assessment of downstream conveyance in development areas. J. Korean Soc. Hazard Mitig. 2021, 21, 187–195. [Google Scholar] [CrossRef]
- Habaïeb, H.; Troch, P.A.; De Troch, F.P. A coupled rainfall-runoff and runoff-routing model for adaptive real-time flood forecasting. Water Resour. Manag. 1991, 5, 47–61. [Google Scholar] [CrossRef]
- Kwon, S.; Jung, S.H.; Lee, G.W. Inter-comparison of radar rainfall rate using constant altitude plan position indicator and hybrid surface rainfall maps. J. Hydrol. 2015, 531, 234–247. [Google Scholar] [CrossRef]
- Lee, J.K. Analysis of uncertainty in quantitative radar rainfall estimation. In Proceedings of the Autumn Meeting of Korea Meteorological Society, Jeju, Republic of Korea, 12–14 October 2015; pp. 274–275. [Google Scholar]
- Oh, K.; Lee, S.C.; Ahn, W.S.; Choi, B.G.; Kang, T.H. Application of RAIDOM for rainfall-runoff simulation. In Proceedings of the Korea Water Resources Association Conference, Gyeongju, Republic of Korea, 22–23 May 2008; pp. 684–688. [Google Scholar]
- Yoon, S.S.; Choi, S.M.; Lee, B.J.; Choi, Y.J. Urban flood and inundation analysis using high-density ground rainfall observation networks and radar rainfall data. In Proceedings of the Autumn Meeting of Korea Meteorological Society, Jeju, Republic of Korea, 12–14 October 2015; pp. 380–381. [Google Scholar]
- Lyu, G.; Park, H.M.; Jung, S.H.; Oh, Y.; Lee, G.W. Accuracy evaluation of composite hybrid surface rainfall (HSR) using KMA weather radar network. J. Korean Earth Sci. Soc. 2017, 38, 496–510. [Google Scholar] [CrossRef]
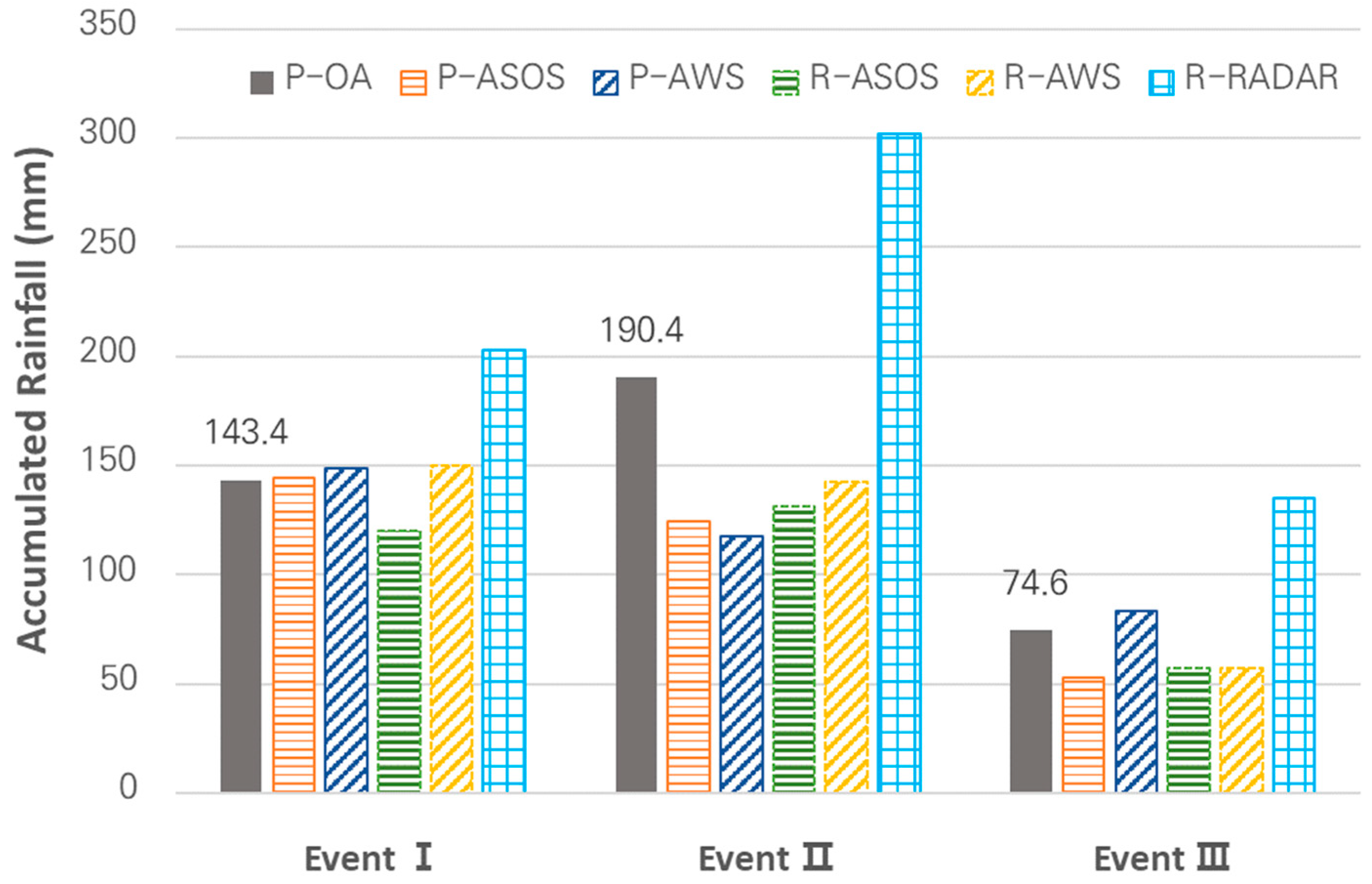
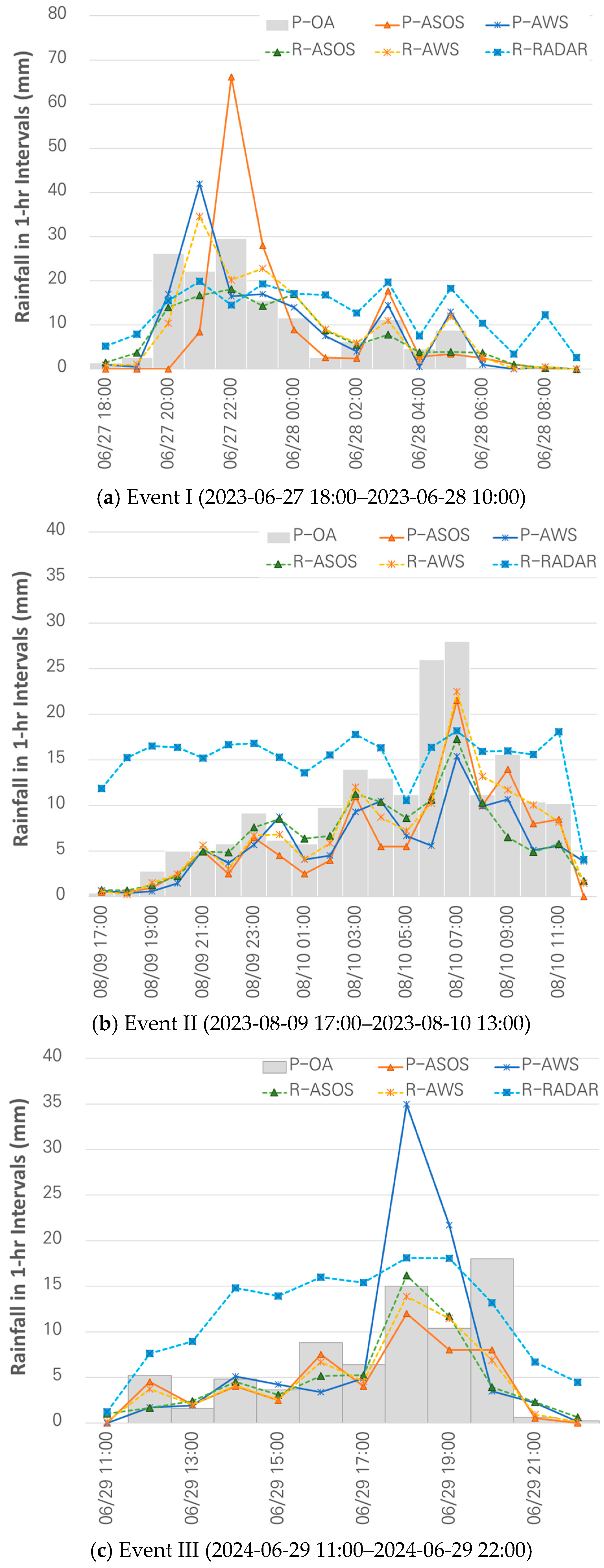
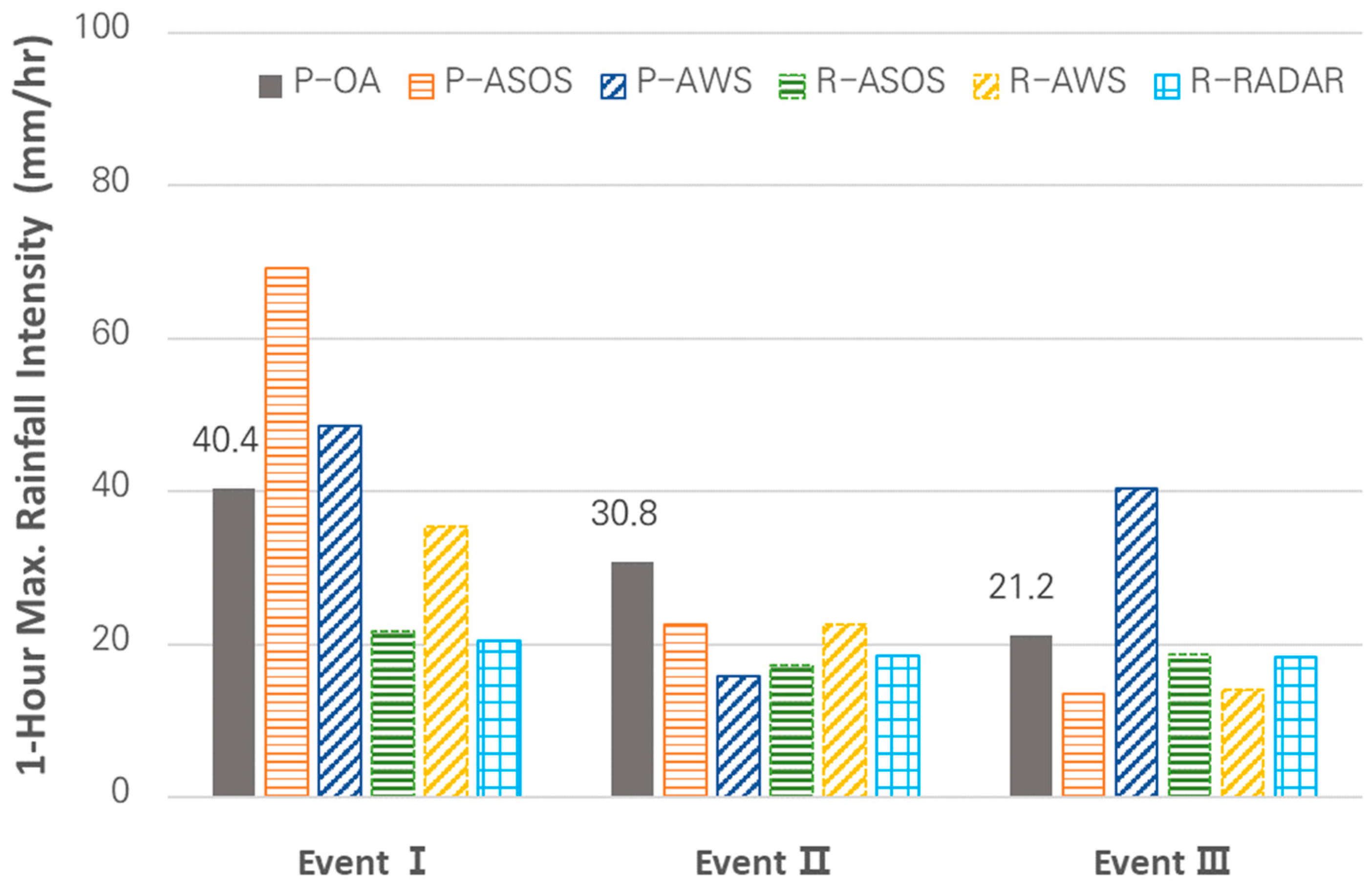





| Events | Starting Time | Ending Time | Duration (h) | Accumulated Rainfall (mm) | Average Rainfall Intensity (mm/h) |
|---|---|---|---|---|---|
| I | 2023.06.27. 18:00 | 2023.06.28. 10:00 | 16:00 | 143.4 | 10.2 |
| II | 2023.08.09. 17:00 | 2023.08.10. 13:00 | 20:00 | 190.4 | 11.3 |
| III | 2024.06.29. 11:00 | 2024.06.29. 22:00 | 11:00 | 74.6 | 6.2 |
| Events | Errors | P-ASOS (1) | P-AWS (2) | R-ASOS (3) | R-AWS (4) | R-RADAR (5) |
|---|---|---|---|---|---|---|
| I | RMSE (mm) | 3.00 | 3.33 | 2.05 | 2.88 | 2.60 |
| NSE | −0.24 | −0.53 | 0.42 | -0.14 | 0.06 | |
| Pearson’s r | 0.47 | 0.27 | 0.68 | 0.29 | 0.35 | |
| R-square | 0.22 | 0.07 | 0.46 | 0.09 | 0.12 | |
| P-bias (%) | −0.49 | −3.91 | 16.20 | −4.55 | −41.63 | |
| MAE (mm) | 1.52 | 1.63 | 1.12 | 1.62 | 1.83 | |
| NPE | 0.24 | 0.35 | −0.60 | −0.22 | −0.72 | |
| PTE (min) | 0.00 | 70.00 | −10.00 | 60.00 | −30.00 | |
| II | RMSE (mm) | 1.04 | 1.31 | 1.06 | 0.96 | 1.56 |
| NSE | 0.42 | 0.07 | 0.40 | 0.50 | −0.31 | |
| Pearson’s r | 0.75 | 0.50 | 0.75 | 0.76 | 0.36 | |
| R-square | 0.57 | 0.25 | 0.56 | 0.58 | 0.13 | |
| P-bias (%) | 34.61 | 38.08 | 30.89 | 25.11 | −58.61 | |
| MAE (mm) | 1.08 | 1.72 | 1.12 | 0.93 | 2.43 | |
| NPE | −0.27 | −0.29 | −0.47 | −0.31 | −0.48 | |
| PTE (min) | −40.00 | 10.00 | 10.00 | 0.00 | 40.00 | |
| III | RMSE (mm) | 0.96 | 2.19 | 1.54 | 1.07 | 1.74 |
| NSE | 0.63 | −0.91 | 0.05 | 0.54 | −0.20 | |
| Pearson’s r | 0.84 | 0.29 | 0.34 | 0.78 | 0.41 | |
| R-square | 0.70 | 0.09 | 0.12 | 0.61 | 0.17 | |
| P-bias (%) | 28.95 | −12.06 | 23.16 | 23.44 | −80.82 | |
| MAE (mm) | 0.91 | 4.80 | 2.39 | 1.15 | 3.02 | |
| NPE | −0.50 | −0.03 | −0.55 | −0.62 | −0.65 | |
| PTE (min) | 20.00 | 10.00 | 10.00 | 0.00 | −70.00 |
| Parameters | Description | Value |
|---|---|---|
| nratio | Ratio factor for streamflow adjustment based on Manning’s roughness coefficient, which primarily governs surface discharge by accounting for surface roughness and flow resistance | 25.0 |
| Aratio | Ratio factor for classifying the stream area in a cell, affecting channel flow and travel time on the surface layer | 26.0 |
| Dratio | Ratio factor for the effective soil depth of each cell, affecting soil saturation in the interflow layer | 0.4 |
| Kratio | Ratio factor for the steady infiltration rate of each cell, affecting soil moisture on the interflow layer | 3.0 |
| GWleak | Groundwater leakage rate accounting for surface flow losses | 0.1 |
| Parameters | Unit | Description | Events | ||
|---|---|---|---|---|---|
| I | II | III | |||
| SWini | % | Initial soil moisture | 45.0 | 100.0 | 81.0 |
| GWini | % | Initial groundwater level based on the surface elevation | 95.0 | 95.0 | 95.0 |
| Items | Observation | P-OA | P-ASOS | P-AWS | R-ASOS | R-AWS | R-Radar |
|---|---|---|---|---|---|---|---|
| Event I (2023-06-27 18:00~06-28 10:00) | |||||||
| Peak discharge (m3/s) | 4.28 | 4.62 | 13.75 | 3.73 | 2.16 | 7.23 | 4.41 |
| Time-to-peak | 06-27 23:50 | 06-27 23:58 | 06-27 23:55 | 06-28 01:10 | 06-28 01:22 | 06-28 01:13 | 06-28 05:00 |
| Event II (2023-08-09 17:00~08-10 13:00) | |||||||
| Peak discharge (m3/s) | 9.19 | 8.37 | 1.5 | 2.36 | 2.25 | 3.28 | 4.67 |
| Time-to-peak | 08-10 08:20 | 08-10 08:26 | 08-10 09:49 | 08-10 10:12 | 08-10 08:42 | 08-10 08:50 | 08-10 12:04 |
| Event III (2024-06-29 11:00~06-29 22:00) | |||||||
| Peak discharge (m3/s) | 0.79 | 0.75 | 0.45 | 3.58 | 0.47 | 0.54 | 4.48 |
| Time-to-peak | 06-29 20:30 | 06-29 20:50 | 06-29 20:04 | 06-29 19:50 | 06-29 19:40 | 06-29 20:10 | 06-29 20:10 |
| Events | Errors | P-OA | P-ASOS | P-AWS | R-ASOS | R-AWS | R-RADAR |
|---|---|---|---|---|---|---|---|
| I | RMSE (m3/s) | 1.60 | 3.12 | 1.47 | 2.02 | 1.75 | 0.86 |
| NSE | −0.26 | −3.81 | −0.06 | −1.01 | −0.51 | 0.63 | |
| R-square | 0.41 | 0.27 | 0.49 | 0.41 | 0.39 | 0.73 | |
| P-bias (%) | 48.47 | 1.96 | 47.26 | 75.26 | 27.83 | 13.16 | |
| MAE (m3/s) | 1.22 | 2.17 | 1.12 | 1.68 | 1.36 | 0.60 | |
| NPE | 0.08 | 2.21 | −0.13 | −0.50 | 0.69 | 0.03 | |
| PTE (min) | 2.00 | 25.00 | −70.00 | −82.00 | −73.00 | −300.00 | |
| II | RMSE (m3/s) | 1.63 | 3.64 | 3.28 | 3.31 | 2.85 | 3.06 |
| NSE | 0.75 | 0.85 | 0.87 | 0.89 | 0.90 | 0.81 | |
| R-square | 0.84 | 0.91 | 0.84 | 0.94 | 0.86 | 0.04 | |
| P-bias (%) | 32.46 | 89.82 | 87.42 | 73.52 | 72.93 | −98.78 | |
| MAE (m3/s) | 0.94 | 1.45 | 1.42 | 1.22 | 1.19 | 2.71 | |
| NPE | −0.09 | −0.89 | −0.80 | −0.76 | −0.64 | −0.52 | |
| PTE (min) | −6.00 | −89.00 | −112.00 | −22.00 | −30.00 | −224.00 | |
| III | RMSE (m3/s) | 0.07 | 0.17 | 1.14 | 0.13 | 0.11 | 2.13 |
| NSE | 0.92 | 0.50 | −22.55 | 0.69 | 0.80 | −81.24 | |
| R-square | 0.94 | 0.88 | 0.80 | 0.84 | 0.96 | 0.75 | |
| P-bias (%) | −3.09 | 59.52 | −304.14 | 41.43 | 41.64 | −825.36 | |
| MAE (m3/s) | 0.04 | 0.11 | 0.61 | 0.09 | 0.08 | 1.51 | |
| NPE | −0.05 | −0.43 | 3.54 | −0.41 | −0.32 | 4.66 | |
| PTE (min) | −20.00 | 26.00 | 40.00 | 50.00 | 20.00 | 20.00 |
| Parameters | P-ASOS | P-AWS | R-ASOS | R-AWS | R-RADAR |
|---|---|---|---|---|---|
| nratio | 1.0 | 6.0 | 0.5 | 5.0 | 1.0 |
| Aratio | 1.0 | 1.0 | 1.0 | 5.0 | 10.0 |
| Dratio | 1.9 | 0.5 | 3.2 | 2.5 | 2.5 |
| Kratio | 3.5 | 4.4 | 1.5 | 1.2 | 3.5 |
| GWleak | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Events | Errors | P-ASOS | P-AWS | R-ASOS | R-AWS | R-RADAR |
|---|---|---|---|---|---|---|
| I | RMSE (m3/s) | 0.70 | 1.99 | 1.58 | 0.81 | 0.75 |
| NSE | 0.76 | −0.97 | −0.24 | 0.68 | 0.73 | |
| R-square | 0.85 | 0.15 | 0.43 | 0.77 | 0.74 | |
| P-bias (%) | 14.74 | 47.03 | 50.78 | 15.09 | −7.62 | |
| MAE (m3/s) | 0.50 | 1.57 | 1.20 | 0.57 | 0.66 | |
| NPE | 0.04 | 0.12 | −0.01 | 0.04 | 0.00 | |
| PTE (min) | 17.00 | −17.00 | −73.00 | −19.00 | −99.00 | |
| II | RMSE (m3/s) | 0.91 | 1.37 | 1.08 | 1.60 | 1.66 |
| NSE | 0.92 | 0.82 | 0.88 | 0.75 | 0.73 | |
| R-square | 0.92 | 0.89 | 0.90 | 0.82 | 0.87 | |
| P-bias (%) | −1.42 | 5.69 | 15.85 | 16.95 | −29.03 | |
| MAE (m3/s) | 0.60 | 0.88 | 0.63 | 1.00 | 1.08 | |
| NPE | 0.03 | 0.13 | 0.00 | 0.14 | 0.10 | |
| PTE (min) | −79.00 | −9.00 | 11.00 | −29.00 | −219.00 | |
| III | RMSE (m3/s) | 0.09 | 0.18 | 0.10 | 0.11 | 0.07 |
| NSE | 0.86 | 0.39 | 0.80 | 0.79 | 0.91 | |
| R-square | 0.92 | 0.59 | 0.90 | 0.87 | 0.95 | |
| P-bias (%) | 19.89 | 41.31 | −0.17 | 14.83 | 9.68 | |
| MAE (m3/s) | 0.06 | 0.12 | 0.06 | 0.08 | 0.05 | |
| NPE | 0.03 | 0.10 | 0.11 | 0.10 | −0.09 | |
| PTE (min) | −5.00 | −31.00 | 37.00 | −19.00 | 8.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Kim, D.-S.; Nam, W.-H.; Jang, M.-W. Assessing the Impact of Rainfall Inputs on Short-Term Flood Simulation with Cell2Flood: A Case Study of the Waryong Reservoir Basin. Hydrology 2024, 11, 162. https://doi.org/10.3390/hydrology11100162
Kim H, Kim D-S, Nam W-H, Jang M-W. Assessing the Impact of Rainfall Inputs on Short-Term Flood Simulation with Cell2Flood: A Case Study of the Waryong Reservoir Basin. Hydrology. 2024; 11(10):162. https://doi.org/10.3390/hydrology11100162
Chicago/Turabian StyleKim, Hyunjun, Dae-Sik Kim, Won-Ho Nam, and Min-Won Jang. 2024. "Assessing the Impact of Rainfall Inputs on Short-Term Flood Simulation with Cell2Flood: A Case Study of the Waryong Reservoir Basin" Hydrology 11, no. 10: 162. https://doi.org/10.3390/hydrology11100162
APA StyleKim, H., Kim, D.-S., Nam, W.-H., & Jang, M.-W. (2024). Assessing the Impact of Rainfall Inputs on Short-Term Flood Simulation with Cell2Flood: A Case Study of the Waryong Reservoir Basin. Hydrology, 11(10), 162. https://doi.org/10.3390/hydrology11100162







