Performance Evaluation of Gradient Descent Optimizers in Estuarine Turbidity Estimation with Multilayer Perceptron and Sentinel-2 Imagery
Abstract
1. Introduction
2. Materials and Methods
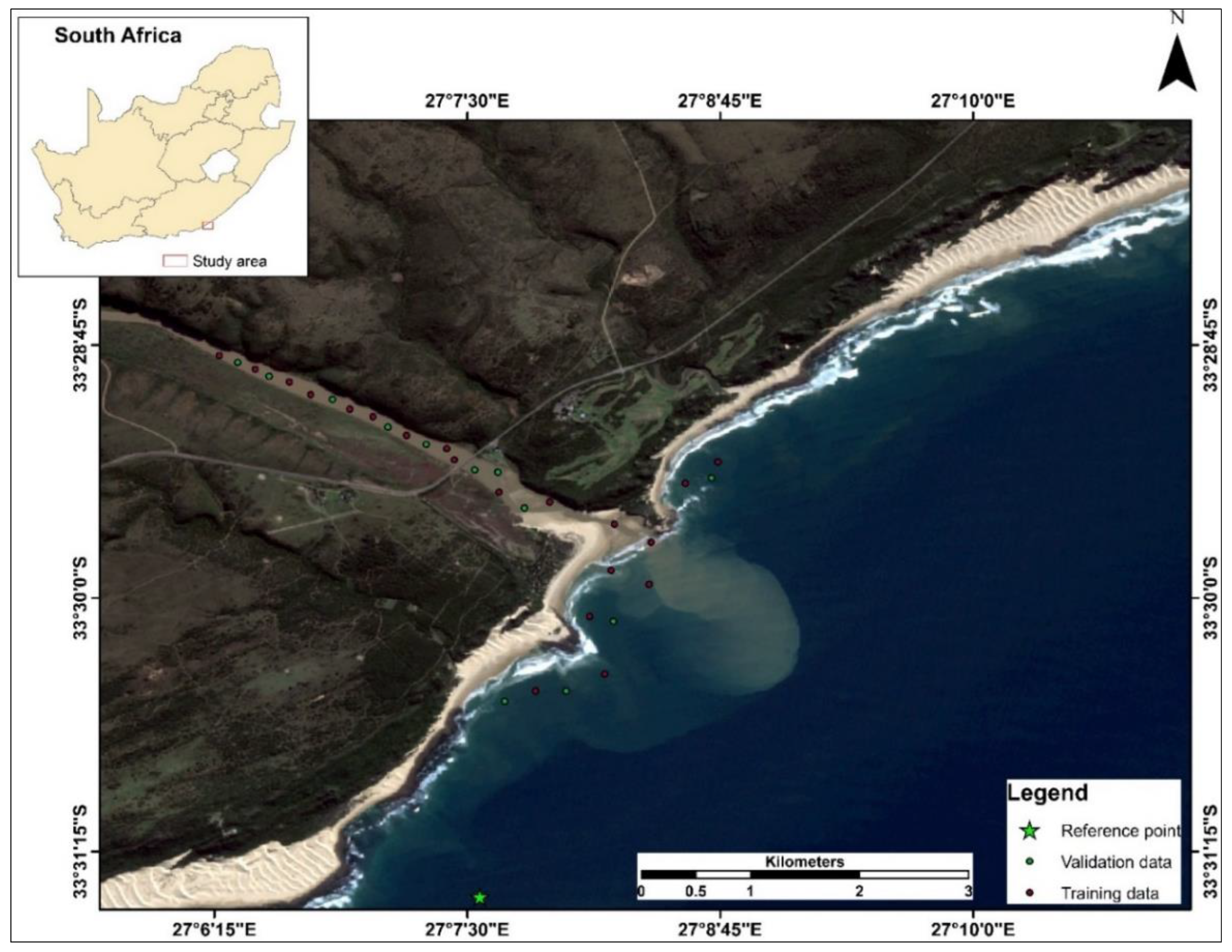
2.1. Study Area
2.2. Methods
2.3. Data Acquisition
2.3.1. Satellite Data
2.3.2. Field Data Collection
2.4. Pre-Processing of Sentinel-2 Imagery
2.5. Estuarine Water Body Demarcation
2.6. Analyzing Spatial Variability in Water Radiance Values across Selected Spectral Bands
2.7. Spatial Pattern Analysis of Turbidity
2.8. Binarization of IDW Image and Thresholding of Turbidity Level
2.9. Model Training
2.9.1. Linear Regression
2.9.2. Training MLP with Sigmoid Activation Function and SGD
2.9.3. Training MLP with Sigmoid Activation Function and MGD
2.10. Evaluation of the Model Performance
3. Results
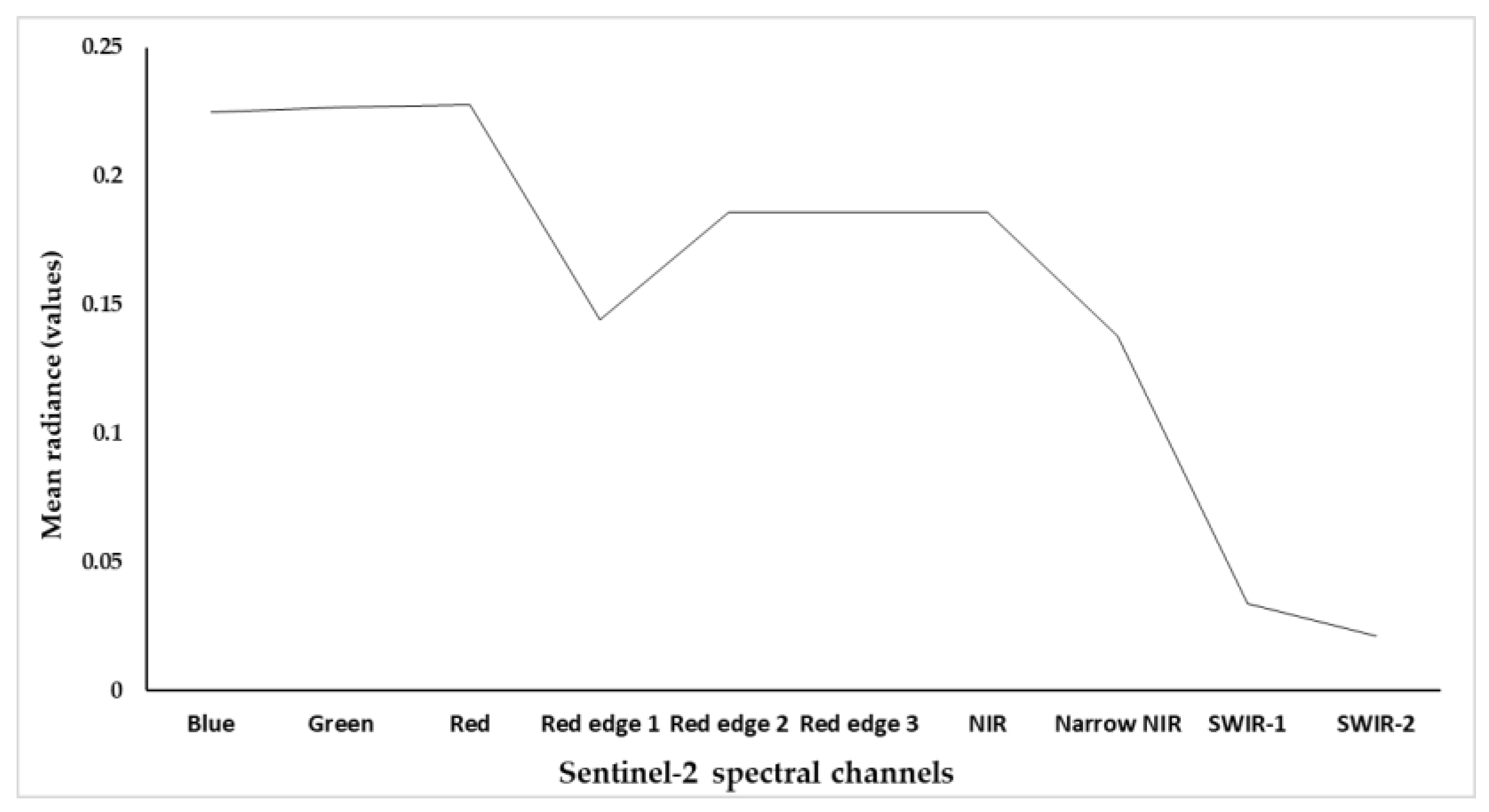
3.1. Spectral Radiance Patterns of Estuarine Turbid Waters
3.2. Mean Radiance Values of Various Sentinel-2 Spectral Channels
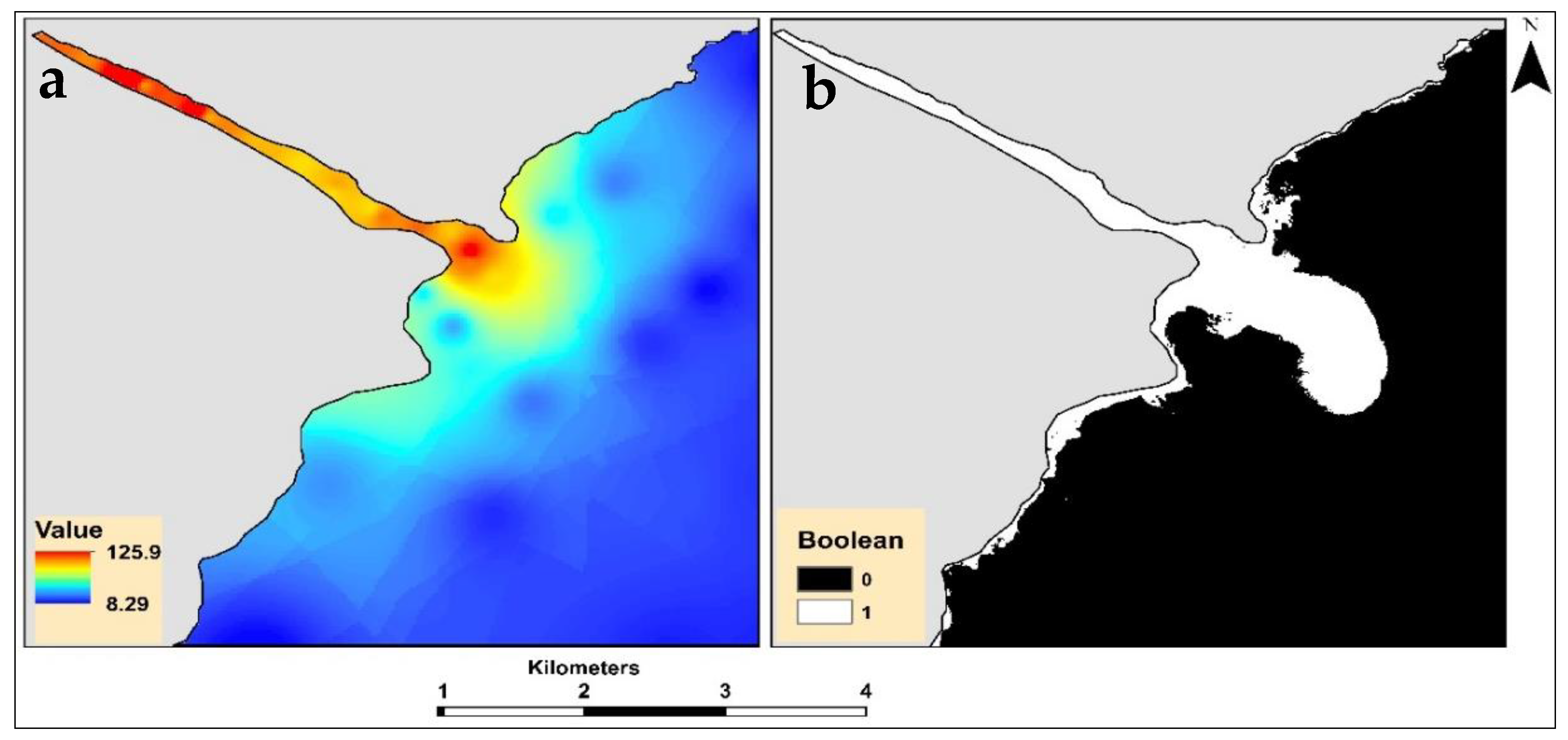
3.3. Spatial Patterns of Turbidity across the Surveyed Sites
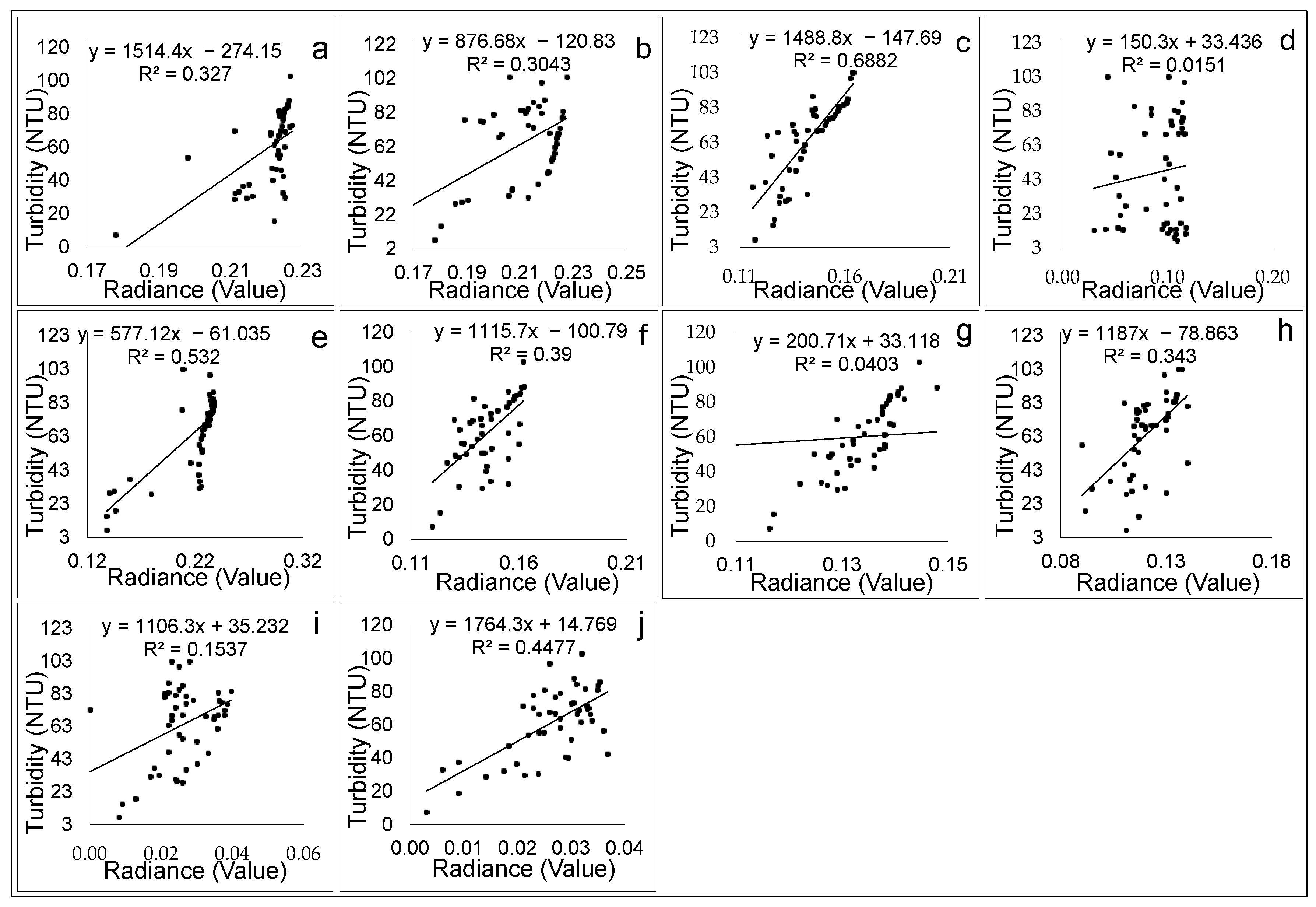
3.4. Relationship Establishment between Sentinel-2 Spectral Radiance Values and Turbidity Concentration
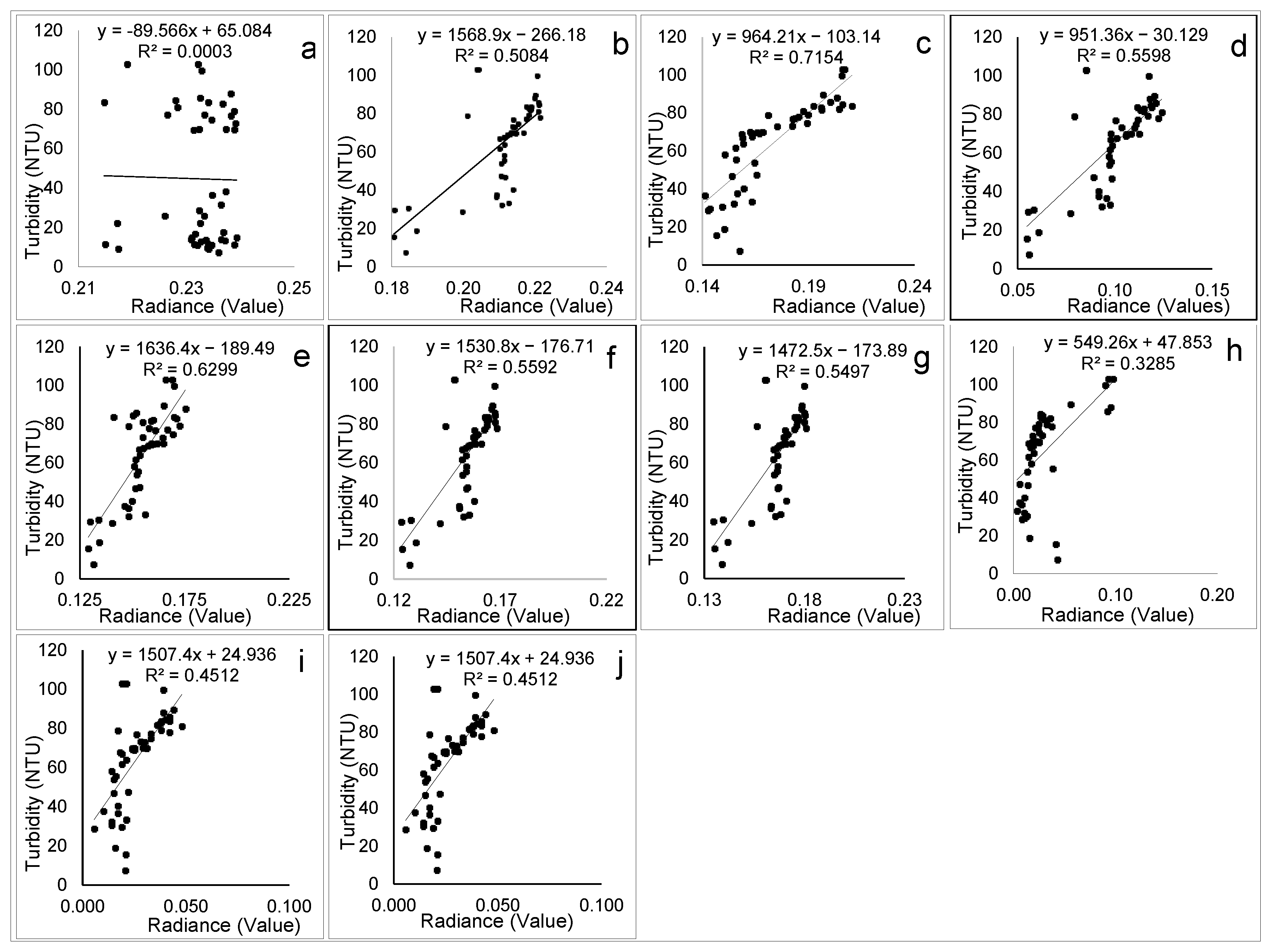
3.4.1. Linear Regression Model on Uncalibrated Spectral Bands
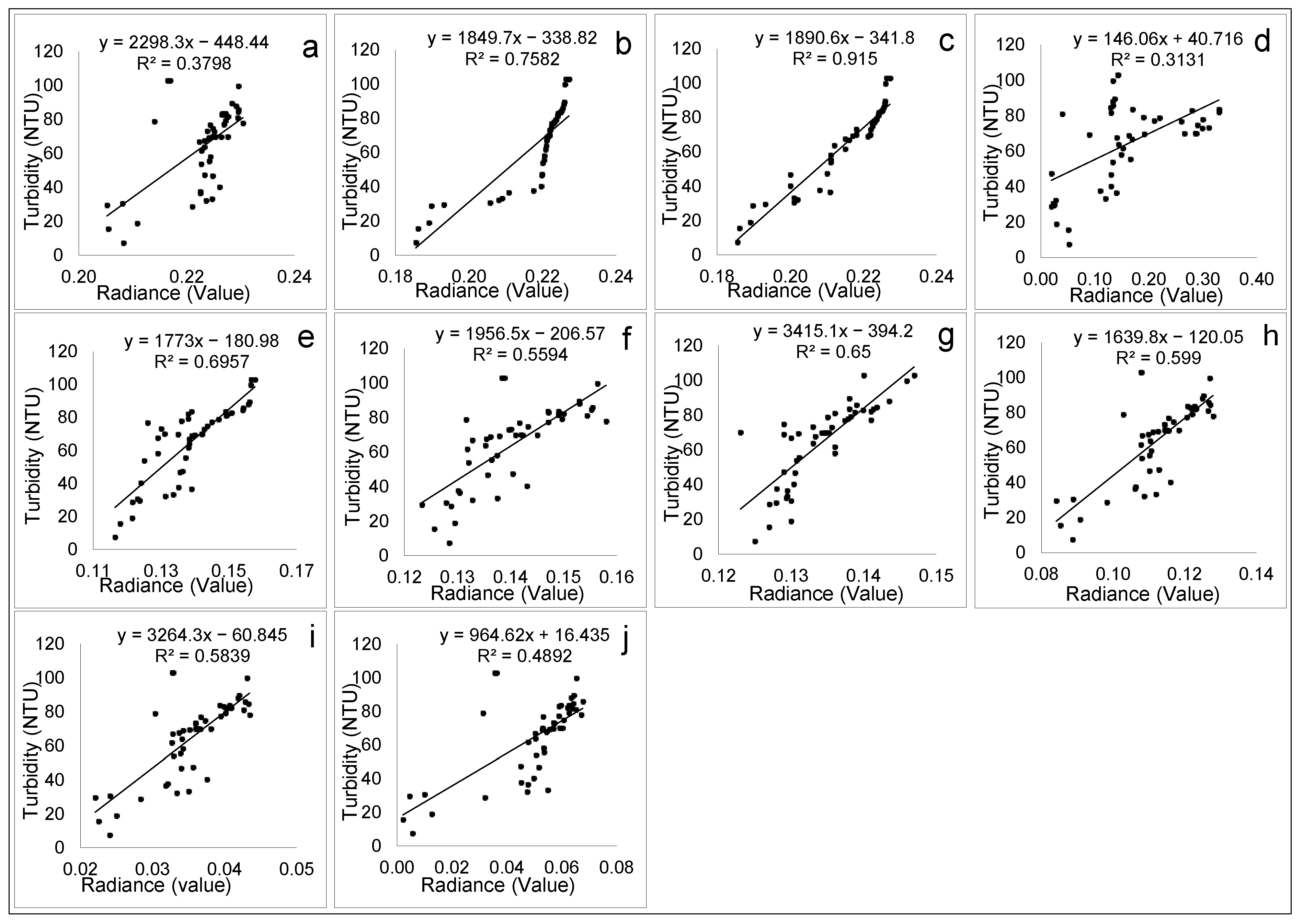
3.4.2. MLP Trained with Sigmoid Calibration Function
Demarcation of Training Sites
Linear Regression Model on Spectral Bands Calibrated with Stochastic Gradient Descent
Linear Regression Model on Spectral Bands Calibrated with Momentum Gradient Descent
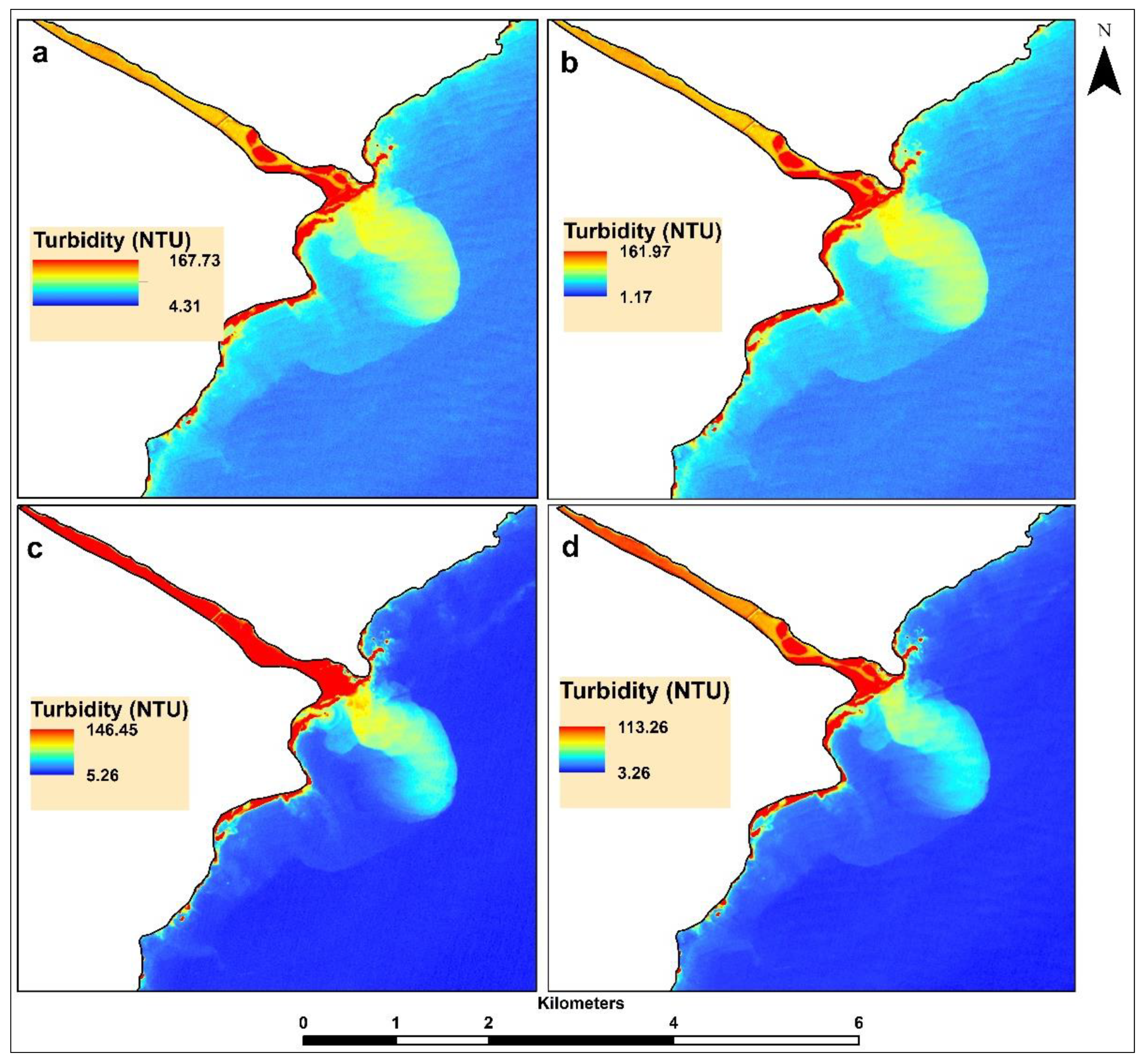
3.4.3. Spatial Modeling of Turbidity Concentration
3.4.4. Performance Evaluation of the Models Deployed
R-Squared Results
3.5. REM Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Miglino, D.; Jomaa, S.; Rode, M.; Isgro, F.; Manfreda, S. Monitoring Water Turbidity Using Remote Sensing Techniques. Environ. Sci. Proc. 2022, 21, 63. [Google Scholar] [CrossRef]
- Tananaev, N.I.; Debolskiy, M.V. Turbidity Observations in Sediment Flux Studies: Examples from Russian Rivers in Cold Environments. Geomorphology 2014, 218, 63–71. [Google Scholar] [CrossRef]
- Golubkov, M.S.; Golubkov, S.M. Secchi Disk Depth or Turbidity, Which Is Better for Assessing Environmental Quality in Eutrophic Waters? A Case Study in a Shallow Hypereutrophic Reservoir. Water 2024, 16, 18. [Google Scholar] [CrossRef]
- Jacobsen, L.; Berg, S.; Baktoft, H.; Nilsson, P.A.; Skov, C. The effect of turbidity and prey fish density on consumption rates of piscivorous Eurasian perch Perca fluviatilis. J. Limnol. 2014, 73, 187–190. [Google Scholar] [CrossRef]
- Caballero, I.; Stumpf, R.P.; Meredith, A. Preliminary Assessment of Turbidity and Chlorophyll Impact on Bathymetry Derived from Sentinel-2A and Sentinel-3A Satellites in South Florida. Remote Sens. 2019, 11, 645. [Google Scholar] [CrossRef]
- Atangana, M.S.B.; Ngoupayou, R.N.; Deliege, J.F. Hydrogeochemistry and Mercury Contamination of Surface Water in the Lom Gold Basin (East Cameroon): Water Quality Index, Multivariate Statistical Analysis and Spatial Interpolation. Water 2023, 15, 2502. [Google Scholar] [CrossRef]
- Saqib, N.; Rai, P.K.; Kanga, S.; Kumar, D.; Đurin, B.; Singh, S.K. Assessment of Ground Water Quality of Lucknow City under GIS Framework Using Water Quality Index (WQI). Water 2023, 15, 3048. [Google Scholar] [CrossRef]
- Feng, C.; Wang, H.; Lu, N.; Chen, T.; He, H.; Lu, Y.; Tu, X.M. Log-Transformation and Its Implications for Data Analysis. Shanghai Arch. Psychiatry 2014, 26, 105–109. [Google Scholar]
- Fermont, V.A.; Benson, T. Estimating Yield of Food Crops Grown by Smallholder Farmers: A Review in the Uganda Context Evolution of Farming Systems in Africa View Project; International Food Policy Research Institute: Washington, DC, USA, 2011. [Google Scholar]
- Lopez-Betancur, D.; Moreno, I.; Guerrero-Mendez, C.; Saucedo-Anaya, T.; González, F.; Bautista-Capetillo, C.; González-Trinidad, J. Convolutional Neural Network for Measurement of Suspended Solids and Turbidity. Appl. Sci. 2022, 12, 6079. [Google Scholar] [CrossRef]
- Garg, V.; Senthil-Kumar, A.; Aggarwal, S.P.; Kumar, V.; Dhote, P.R.; Thakur, P.K.; Nikam, B.R.; Sambare, R.S.; Siddiqui, A.; Muduli, P.R.; et al. Spectral similarity approach for mapping turbidity of an inland waterbody. J. Hydrol. 2017, 550, 527–537. [Google Scholar] [CrossRef]
- Li, S.; Kutser, T.; Song, K.; Liu, G.; Li, Y. Lake Turbidity Mapping Using an OWTs-bp Based Framework and Sentinel-2 Imagery. Remote Sens. 2023, 15, 2489. [Google Scholar] [CrossRef]
- Molner, J.V.; Soria, J.M.; Pérez-González, R.; Sòria-Perpinyà, X. Estimating Water Transparency Using Sentinel-2 Images in a Shallow Hypertrophic Lagoon (The Albufera of Valencia, Spain). Water 2023, 15, 3669. [Google Scholar] [CrossRef]
- Hossain, A.K.M.A.; Mathias, C.; Blanton, R. Remote Sensing of Turbidity in the Tennessee River Using Landsat 8 Satellite. Remote Sens. 2021, 13, 3785. [Google Scholar] [CrossRef]
- Bygate, M.; Ahmed, M. Monitoring Water Quality Indicators over Matagorda Bay, Texas, Using Landsat-8. Remote Sens. 2024, 16, 1120. [Google Scholar] [CrossRef]
- Sakuno, Y.; Matsunaga, T.; Kozu, T.; Katsumi, T. Preliminary Study of the Monitoring for Turbid Coastal Waters Using a New Satellite Sensor, “ASTER”. In Proceedings of the Twelfth International Offshore and Polar Engineering Conference, Kitakyushu, Japan, 26–31 May 2002; Available online: https://onepetro.org/ISOPEIOPEC/proceedings-abstract/ISOPE02/All-ISOPE02/ISOPE-I-02-185/8839 (accessed on 13 July 2024).
- Cartwright, P.J.; Fearns, P.R.; Branson, P.; Cuttler, M.V.; O’Leary, M.; Browne, N.K.; Lowe, R.J. Identifying Metocean Drivers of Turbidity Using 18 Years of MODIS Satellite Data: Implications for Marine Ecosystems under Climate Change. Remote Sens. 2021, 13, 3616. [Google Scholar] [CrossRef]
- Wang, G.; Lu, J.; Choi, K.S.; Zhang, G. A Transfer-Based Additive LS-SVM Classifier for Handling Missing Data. IEEE Trans. Cybern. 2020, 50, 739–752. [Google Scholar] [CrossRef]
- Twardowski, M.; Tonizzo, A. Ocean Color Analytical Model Explicitly Dependent on the Volume Scattering Function. Appl. Sci. 2018, 8, 2684. [Google Scholar] [CrossRef]
- Amani, M.; Mehravar, S.; Asiyabi, R.M.; Moghimi, A.; Ghorbanian, A.; Ahmadi, S.A.; Ebrahimy, H.; Moghaddam, S.H.A.; Naboureh, A.; Ranjgar, B.; et al. Ocean Remote Sensing Techniques and Applications: A Review (Part II). Water 2022, 14, 3401. [Google Scholar] [CrossRef]
- Wu, J.; Wang, Z. A Hybrid Model for Water Quality Prediction Based on an Artificial Neural Network, Wavelet Transform, and Long Short-Term Memory. Water 2022, 14, 610. [Google Scholar] [CrossRef]
- Pisanti, A.; Magri, S.; Ferrando, I.; Federici, B. Sea Water Turbidity Analysis from Sentinel-2 Images: Atmospheric Correction and Bands Correlation. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Florence, Italy, 22–28 August 2022; Volume XLVIII-4/W1-2022. Available online: https://isprs-archives.copernicus.org/articles/XLVIII-4-W1-2022/371/2022/isprs-archives-XLVIII-4-W1-2022-371-2022.pdf (accessed on 13 July 2024).
- Chen, R.; Rubanova, Y.; Bettencourt, J.; Duvenaud, D. Neural ordinary differential equations. In Advances in Neural Information Processing Systems; Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; The MIT Press: Cambridge, MA, USA, 2018; Volume 31, pp. 6571–6583. [Google Scholar]
- Haber, E.; Ruthotto, L. Stable architectures for deep neural networks. Inverse Probl. 2017, 34, 014004. [Google Scholar] [CrossRef]
- Hafeez, S.; Wong, M.S.; Ho, H.C.; Nazeer, M.; Nichol, J.; Abbas, S.; Tang, D.; Lee, K.H.; Pun, L. Comparison of Machine Learning Algorithms for Retrieval of Water Quality Indicators in Case-II Waters: A Case Study of Hong Kong. Remote Sens. 2019, 11, 617. [Google Scholar] [CrossRef]
- Kwon, Y.S.; Baek, S.H.; Lim, Y.K.; Pyo, J.C.; Ligaray, M.; Park, Y.; Cho, K.H. Monitoring Coastal Chlorophyll-a Concentrations in Coastal Areas Using Machine Learning Models. Water 2018, 10, 1020. [Google Scholar] [CrossRef]
- Phyo, P.; Jeenanunta, C. Advanced ML-Based Ensemble and Deep Learning Models for Short-Term Load Forecasting: Comparative Analysis Using Feature Engineering. Appl. Sci. 2022, 12, 4882. [Google Scholar] [CrossRef]
- Rashedi, K.A.; Mohd, T.I.; Al Wadi, S.; Serroukh, A.; Alshammari, T.S.; Jaber, J.J. Multi-Layer Perceptron-Based Classification with Application to Outlier Detection in Saudi Arabia Stock Returns. J. Risk Financ. Manag. 2024, 17, 69. [Google Scholar] [CrossRef]
- Jiang, W.; He, G.; Long, T.; Ni, Y.; Liu, H.; Peng, Y.; Lv, K.; Wang, G. Multilayer Perceptron Neural Network for Surface Water Extraction in Landsat 8 OLI Satellite Images. Remote Sens. 2018, 10, 755. [Google Scholar] [CrossRef]
- Rustam, F.; Ishaq, A.; Kokab, S.T.; de la Torre Diez, I.; Mazón, J.L.V.; Rodríguez, C.L.; Ashraf, I. An Artificial Neural Network Model for Water Quality and Water Consumption Prediction. Water 2022, 14, 3359. [Google Scholar] [CrossRef]
- Kim, N.H.; Kim, D.H.; Park, S.H. Prediction of the Turbidity Distribution Characteristics in a Semi-Enclosed Estuary Based on Machine Learning. Water 2024, 16, 61. [Google Scholar] [CrossRef]
- Hadsell, R.; Rao, D.; Rusu, A.A.; Pascanu, R. Embracing Change: Continual Learning in Deep Neural Networks. Trends Cogn. Sci. 2020, 24, 1028–1040. [Google Scholar] [CrossRef]
- Rojas, M.G.; Olivera, A.C.; Vidal, P.J. Optimising Multilayer Perceptron weights and biases through a Cellular Genetic Algorithm for medical data classification. Array 2022, 14, 100173. [Google Scholar] [CrossRef]
- Lee, H. Tuning the Weights: The Impact of Initial Matrix Configurations on Successor Features’ Learning Efficacy. Electronics 2023, 12, 4212. [Google Scholar] [CrossRef]
- Masood, S.; Doja, M.N.; Chandra, P. Analysis of weight initialization methods for gradient descent with momentum. In Proceedings of the 2015 International Conference on Soft Computing Techniques and Implementations (ICSCTI), Faridabad, India, 8–10 October 2015; pp. 131–136. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Let a biogeography-based optimizer train your multi-layer perceptron. Inf. Sci. 2014, 269, 188–209. [Google Scholar] [CrossRef]
- Lu, Y.; Huo, Y.; Yang, Z.; Niu, Y.; Zhao, M.; Bosiakov, S.; Li, L. Influence of the parameters of the convolutional neural network model in predicting the effective compressive modulus of porous structure. Front. Bioeng Biotechnol. 2022, 10, 985688. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Jing, X.; Du, W.; Chen, G. Learning dynamics of gradient descent optimization in deep neural networks. Sci. China Inf. Sci. 2021, 64, 150102. [Google Scholar] [CrossRef]
- Van Speybroeck, V. Challenges in modelling dynamic processes in realistic nanostructured materials at operating conditions. Philos. Trans. R. Soc. A 2023, 381, 2250. [Google Scholar] [CrossRef] [PubMed]
- Wilson, R.; Mercier, P.H.J.; Navarra, A. Integrated Artificial Neural Network and Discrete Event Simulation Framework for Regional Development of Refractory Gold Systems. Mining 2022, 2, 123–154. [Google Scholar] [CrossRef]
- Fekri-Ershad, S.; Alsaffar, M.F. Developing a Tuned Three-Layer Perceptron Fed with Trained Deep Convolutional Neural Networks for Cervical Cancer Diagnosis. Diagnostics 2023, 13, 686. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, Y. Multi-layer Perceptron Trainability Explained via Variability. arXiv 2021, arXiv:2105.08911. [Google Scholar] [CrossRef]
- Chen, B.; Wang, H.; Ba, C. Differentiable Self-Adaptive Learning Rate. arXiv 2022. [Google Scholar] [CrossRef]
- Phyo, P.P.; Jeenanunta, C.; Hashimoto, K. Electricity load forecasting in Thailand using deep learning models. Int. J. Electr. Electron. Eng. Telecommun. 2019, 8, 221–225. [Google Scholar] [CrossRef]
- Yang, Y.; Mo, L.; Hu, Y.; Long, F. The Improved Stochastic Fractional Order Gradient Descent Algorithm. Fractal Fract. 2023, 7, 631. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, Y.; Zhou, H.; Hu, H. Plant Diseases Identification through a Discount Momentum Optimizer in Deep Learning. Appl. Sci. 2021, 11, 9468. [Google Scholar] [CrossRef]
- Van Laarhoven, T.L. Regularization versus Batch and Weight Normalization. arXiv 2017, arXiv:1706.05350. [Google Scholar]
- Ward, R.; Wu, X.; Bottou, L. AdaGrad stepsizes: Sharp convergence over nonconvex landscapes. J. Mach. Learn. Res. 2020, 21, 9047–9076. [Google Scholar]
- Bengio, Y.; Léonard, N.; Courville, A. Estimating or Propagating Gradients through Stochastic Neurons for Conditional Computation. arXiv 2013, arXiv:1308.3432. [Google Scholar]
- Pan, H.; Ye, Z.; He, Q.; Yan, C.; Yuan, J.; Lai, X.; Su, J.; Li, R. Discrete Missing Data Imputation Using Multilayer Perceptron and Momentum Gradient Descent. Sensors 2022, 22, 5645. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Son, S.; Bae, J.; Park, S.; Seo, J.; Seo, D.; Lee, Y.; Kim, J. Single-Temporal Sentinel-2 for Analyzing Burned Area Detection Methods: A Study of 14 Cases in Republic of Korea Considering Land Cover. Remote Sens. 2024, 16, 884. [Google Scholar] [CrossRef]
- Ndou, N. Geostatistical inference of Sentinel-2 Spectral Reflectance Patterns to Water Quality Indicators in the Setumo Dam, South Africa. Remote Sens. Appl. Soc. Environ. 2023, 30, 100945. [Google Scholar] [CrossRef]
- Singh, R.; Saritha, V.; Pande, C.B. Monitoring of wetland turbidity using multi-temporal Landsat-8 and Landsat-9 satellite imagery in the Bisalpur wetland, Rajasthan, India. Environ. Res. 2024, 241, 117638. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, J.; Tian, L.; Feng, L.; Li, J.; Xing, Q. Remotely sensed water turbidity dynamics and its potential driving factors in Wuhan, an urbanizing city of China. J. Hydrol. 2021, 593, 125893. [Google Scholar] [CrossRef]
- Ma, Y.; Song, K.; Wen, Z.; Liu, G.; Shang, Y.; Lyu, L.; Du, J.; Yang, Q.; Li, S.; Tao, H.; et al. Remote Sensing of Turbidity for Lakes in Northeast China Using Sentinel-2 Images with Machine Learning Algorithms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 9132–9146. Available online: https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=9529058 (accessed on 17 July 2024). [CrossRef]
- Katlane, R.; Nechad, B.; Ruddick, K.; Zargouni, F. Optical remote sensing of turbidity and total suspended matter in the Gulf of Gabes. Arab. J. Geosci. 2013, 6, 1527–1535. [Google Scholar] [CrossRef]
- Quillon, S.; Douillet, P.; Petrenko, A.; Neveux, J.; Dupouy, C.; Froidefond, J.; Andréfouët, S.; Muñoz-Caravaca, A. Optical Algorithms at Satellite Wavelengths for Total Suspended Matter in Tropical Coastal Waters. Sensors 2008, 8, 4165–4185. [Google Scholar] [CrossRef] [PubMed]
- Hafeez, S.; Wong, M.S.; Abbas, S.; Asim, M. Evaluating Landsat-8 and Sentinel-2 Data Consistency for High Spatiotemporal Inland and Coastal Water Quality Monitoring. Remote Sens. 2022, 14, 3155. [Google Scholar] [CrossRef]
- Nas, B.; Ekercin, S.; Karabork, H.; Berktay, A.; Mulla, D.J. An Application of Landsat-5TM Image Data for Water Quality Mapping in Lake Beysehir, Turkey. Water Air Soil Pollut. 2010, 212, 183–197. [Google Scholar] [CrossRef]
- Joshi, I.D.; D’Sa, E.J.; Osburn, C.L.; Bianchi, T.S. Turbidity in Apalachicola Bay, Florida from Landsat 5 TM and field data: Seasonal patterns and response to extreme events. Remote Sens. 2017, 9, 4. [Google Scholar] [CrossRef]
- Chowdhury, M.; Vilas, C.; van Bergeijk, S.; Navarro, G.; Laiz, I.; Caballero, I. Monitoring turbidity in a highly variable estuary using Sentinel 2-A/B for ecosystem management applications. Front. Mar. Sci. 2023, 10, 1186441. [Google Scholar] [CrossRef]
- Abirhire, O.; Davies, J.M.; Hudson, J. Understanding the factors associated with long-term reconstructed turbidity in Lake Diefenbaker from Landsat imagery. Sci. Total Environ. 2020, 724, 138222. [Google Scholar] [CrossRef]
- Surisetty, V.V.A.K.; Sahay, A.; Ramakrishnan, R.; Samal, R.B.; Rajawat, A.S. Improved turbidity estimates in complex inland waters using combined NIR–SWIR atmospheric correction approach for Landsat 8 OLI data. Int. J. Remote Sens. 2018, 39, 7463–7482. [Google Scholar] [CrossRef]
- Phiri, D.; Simwanda, M.; Salekin, S.; Nyirenda, V.R.; Murayama, Y.; Ranagalage, M. Sentinel-2 Data for Land Cover/Use Mapping: A Review. Remote Sens. 2020, 12, 2291. [Google Scholar] [CrossRef]
- Wei, Z.; Wei, L.; Yang, H.; Wang, Z.; Xiao, Z.; Li, Z.; Yang, Y.; Xu, G. Water Quality Grade Identification for Lakes in Middle Reaches of Yangtze River Using Landsat-8 Data with Deep Neural Networks (DNN) Model. Remote Sens. 2022, 14, 6238. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalized difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Pare’, G.; Cook, N.R.; Ridker, P.M.; Chasman, D.I. On the Use of Variance per Genotype as a Tool to Identify Quantitative Trait Interaction Effects: A Report from the Women’s Genome Health Study. PLoS Genet. 2010, 6, e1000981. [Google Scholar] [CrossRef]
- Emmert-Streib, F.; Dehmer, M. Understanding Statistical Hypothesis Testing: The Logic of Statistical Inference. Mach. Learn. Knowl. Extr. 2019, 1, 945–961. [Google Scholar] [CrossRef]
- Chin, R.J.; Lai, S.H.; Loh, W.S.; Ling, L.; Soo, E.Z.X. Assessment of Inverse Distance Weighting and Local Polynomial Interpolation for Annual Rainfall: A Case Study in Peninsular Malaysia. Eng. Proc. 2023, 38, 61. [Google Scholar] [CrossRef]
- Lu, G.Y.; Wong, D.W. An adaptive inverse-distance weighting spatial interpolation technique. Comput. Geosci. 2008, 34, 1044–1055. [Google Scholar] [CrossRef]
- Kopsachilis, V.; Siciliani, L.; Polignano, M.; Kolokoussis, P.; Vaitis, M.; de Gemmis, M.; Topouzelis, K. Semantically Aware Retrieval of Oceanographic Phenomena Annotated on Satellite Images. Information 2021, 12, 321. [Google Scholar] [CrossRef]
- Fierro, E.N.; Faúndez, C.A.; Muñoz, A.S.; Cerda, P.I. Application of a Single Multilayer Perceptron Model to Predict the Solubility of CO2 in Different Ionic Liquids for Gas Removal Processes. Processes 2022, 10, 1686. [Google Scholar] [CrossRef]
- Shimodaira, H. Multi-Layer Neural Networks. In Informatics Learning; Informatics Forum: Edinburgh, UK, 2020; Available online: https://www.inf.ed.ac.uk/teaching/courses/inf2b/learnnotes/inf2b-learn12-notes-nup.pdf (accessed on 30 April 2024).
- Platt, J. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. Adv. Large Margin Classif. 1999, 10, 61–74. [Google Scholar]
- Kaddoura, S. Evaluation of Machine Learning Algorithm on Drinking Water Quality for Better Sustainability. Sustainability 2022, 14, 11478. [Google Scholar] [CrossRef]
- Yan, Q.; Yang, C.; Wan, Z. A Comparative Regression Analysis between Principal Component and Partial Least Squares Methods for Flight Load Calculation. Appl. Sci. 2023, 13, 8428. [Google Scholar] [CrossRef]
- Ndou, N.; Thamaga, K.H.; Mndela, Y.; Nyamugama, A. Radiometric Compensation for Occluded Crops Imaged Using High-Spatial-Resolution Unmanned Aerial Vehicle System. Agriculture 2023, 13, 1598. [Google Scholar] [CrossRef]
- Kuhn, C.; de Mantos Valerio, A.; Ward, N.; Loken, L.; Sawakuchi, H.O.; Kampel, M.; Richey, J.; Stadler, P.; Crawford, J.; Striegel, R.; et al. Performance of Landsat-8 and Sentinel-2 surface reflectance products for river remote sensing retrievals of chlorophyll-a and turbidity. Remote Sens. Environ. 2019, 224, 104–118. [Google Scholar] [CrossRef]
- Zhan, Y.; Delegido, J.; Erena, M.; Soria, J.M.; Ruiz-Verdú, A.; Urrego, P.; Sòria-Perpinyà, X.; Vicente, E.; Moreno, J. Mar Menor lagoon (SE Spain) chlorophyll-a and turbidity estimation with Sentinel-2. Limnetica 2022, 41, 305–323. [Google Scholar] [CrossRef]
- Cui, M.; Sun, Y.; Huang, C.; Li, M. Water Turbidity Retrieval Based on UAV Hyperspectral Remote Sensing. Water 2022, 14, 128. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, L.; Sun, X.; Gao, Y.; Lan, Z.; Wang, Y.; Zhai, H.; Li, J.; Wang, W.; Chen, M.; et al. A New Method for Calculating Water Quality Parameters by Integrating Space–Ground Hyperspectral Data and Spectral-In Situ Assay Data. Remote Sens. 2022, 14, 3652. [Google Scholar] [CrossRef]
- Hassan, N.; Woo, C.S. Machine Learning Application in Water Quality Using Satellite Data. IOP Conf. Ser. Earth Environ. Sci. 2021, 842, 012018. Available online: https://iopscience.iop.org/article/10.1088/1755-1315/842/1/012018/pdf (accessed on 17 July 2024). [CrossRef]
- Souza, A.P.; Oliveira, B.A.; Andrade, M.L.; Starling, M.C.V.M.; Pereira, A.H.; Maillard, P.; Nogueira, K.; dos Santos, J.A.; Amorim, C.C. Integrating remote sensing and machine learning to detect turbidity anomalies in hydroelectric reservoirs. Sci. Total Environ. 2023, 902, 165964. [Google Scholar] [CrossRef]
- Liu, H.; Hub, S.; Zhou, Q.; Li, Q.; Wu, G. Revisiting effectiveness of turbidity index for the switching scheme of NIRSWIR combined ocean color atmospheric correction algorithm. Int. J. Appl. Earth Obs. Geoinf. 2019, 76, 1–9. [Google Scholar] [CrossRef]
- Zeng, J.; Matsunaga, T.; Saigusa, N.; Shirai, T.; Nakaoka, S.; Tan, Z.H. Technical note: Evaluation of three machine learning models for surface ocean CO2 mapping. Ocean Sci. 2017, 13, 303–313. [Google Scholar] [CrossRef]
- Dubey, S.R.; Singh, S.K.; Chaudhuri, B.B. Activation functions in deep learning: A comprehensive survey and benchmark. Neurocomputing 2022, 503, 92–108. [Google Scholar] [CrossRef]
- Yan, P.; Lin, K.; Wang, Y.; Zheng, Y.; Gao, X.; Tu, X.; Bai, C. Spatial Interpolation of Red Bed Soil Moisture in Nanxiong Basin, South China. J. Contam. Hydrol. 2021, 242, 103860. [Google Scholar] [CrossRef] [PubMed]
- Wan, S.; Yeh, M.; Ma, H.; Chou, T. The Robust Study of Deep Learning Recursive Neural Network for Predicting Turbidity of Water. Water 2022, 14, 761. [Google Scholar] [CrossRef]
- Marin, I.; Skelin, A.K.; Grujic, T. Empirical Evaluation of the Effect of Optimization and Regularization Techniques on the Generalization Performance of Deep Convolutional Neural Network. Appl. Sci. 2020, 10, 7817. [Google Scholar] [CrossRef]
- Patel, V.; Zhang, S.; Tian, B. Global Convergence and Stability of Stochastic Gradient Descent. In Proceedings of the 36th Conference on Neural Information Processing Systems (NeurIPS 2022), New Orleans, LA, USA, 28 November–9 December 2022; Available online: https://proceedings.neurips.cc/paper_files/paper/2022/file/ea05e4fc0299c27648c9985266abad47-Paper-Conference.pdf (accessed on 17 July 2024).
- Jelassi, S.; Li, Y. Towards understanding how momentum improves generalization in deep learning. In Proceedings of the 39th International Conference on Machine Learning, PMLR, Baltimore, MD, USA, 17–23 July 2022; Volume 162. [Google Scholar]
- Yan, C.; Yuan, J.; Ye, Z.; Yang, Z. A Discrete Missing Data Imputation Method Based on Improved Multi-Layer Perceptron. In Proceedings of the 2021 11th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS), Krakow, Poland, 22–25 September 2021; pp. 480–484. [Google Scholar]
- Defazio, A. Understanding the role of momentum in nonconvex optimization: Practical insights from a Lyapunov analysis. arXiv 2020, arXiv:2010.00406. [Google Scholar]
- Sutskever, I.; Martens, J.; Dahl, G.; Hinton, G. On the importance of initialization and momentum in deep learning. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 1139–1147. [Google Scholar]
- Lu, S.; He, M.; He, S.; He, S.; Pan, Y.; Yin, W.; Li, P. An Improved Cloud Masking Method for GOCI Data over Turbid Coastal Waters. Remote Sens. 2021, 13, 2722. [Google Scholar] [CrossRef]
- Chen, Z.; Hu, C.; Muller-Karger, F. Monitoring turbidity in Tampa Bay using MODIS/Aqua250-m imagery. Remote Sens. Environ. 2006, 109, 207–220. [Google Scholar] [CrossRef]
- Xu, P.; Du, P.; Shen, Q.; Xu, Z.B. Research on Remote Sensing Inversion Mode of Suspended Matter Density and Turbidity based on GF-1 WFV Image Data in Hunhe River. J. Shenyang Norm. Univ. 2017, 35, 180–184. [Google Scholar]
- Potes, M.; Costa, M.J.; Salgado, R. Satellite remote sensing of water turbidity in Alqueva reservoir and implications on lake modelling. Hydrol. Earth Syst. Sci. 2011, 8, 11357–11385. [Google Scholar] [CrossRef]
- Choubey, V.K. Correlation of turbidity with Indian remote sensing satellite-1A data. Hydrol. Sci. J. 1992, 37, 129–140. [Google Scholar] [CrossRef]



| Spectral Band | Wavelength Center (nm) | Spatial Resolution (m) |
|---|---|---|
| Blue | 490 | 10 |
| Green | 560 | 10 |
| Red | 665 | 10 |
| Red edge 1 | 705 | 20 |
| Red edge 2 | 740 | 20 |
| Red edge 3 | 783 | 20 |
| Near-infrared | 842 | 10 |
| Red edge 4 | 865 | 20 |
| Shortwave infrared 1 | 1610 | 20 |
| Shortwave infrared 2 | 2190 | 20 |
| MLP with Sigmoid Activation Function and SGD for Predicting Turbidity from Sentinel-2 Spectral Data | |||||
|---|---|---|---|---|---|
| Blue | Green | Red | NIR | ||
| Input specifications | Independent variables | Radiance values of all bands | Radiance values of all bands | Radiance values of all bands | Radiance values of all bands |
| Dependent variable | Radiance values of blue wavelength | Radiance values of green wavelength | Radiance values of red wavelength | Radiance values of NIR wavelength | |
| Max. training sample used | 300 | 300 | 300 | 300 | |
| Max. testing sample used | 300 | 300 | 300 | 300 | |
| Network topology | No. of input layer nodes | 4 | 4 | 4 | 4 |
| No. of output layer nodes | 1 | 1 | 1 | 1 | |
| No. of hidden layers | 2 | 2 | 2 | 2 | |
| Layer 1 nodes | 5 | 5 | 5 | 5 | |
| Training parameters | Training type | Automatic | Automatic | Automatic | Automatic |
| Learning rate type | Dynamic | Dynamic | Dynamic | Dynamic | |
| Learning rate start | 0.01 | 0.01 | 0.01 | 0.01 | |
| Learning rate end | 0.001 | 0.001 | 0.001 | 0.001 | |
| Momentum factor | 0.9 | 0.9 | 0.9 | 0.9 | |
| Sigmoid constant | 1.0 | 1.0 | 1.0 | 1.0 | |
| Stopping criteria | Iteration | 10,000 | 10,000 | 10,000 | 10,000 |
| Actual training pixels | 490 | 497 | 474 | 483 | |
| Actual testing pixels | 491 | 497 | 475 | 483 | |
| Learning rate | 0.001 | 0.001 | 0.001 | 0.001 | |
| RMS | 0.01 | 0.01 | 0.01 | 0.01 | |
| Training RMS | 0.0322 | 0.034 | 0.035 | 0.019 | |
| Testing RMS | 0.0344 | 0.037 | 0.033 | 0.02 | |
| R Sqr. | 0.942 | 0.987 | 0.992 | 0.979 | |
| N | DF | Min | Max | μ | σ | SE Mean | Coeff. Var | p-Value | |
|---|---|---|---|---|---|---|---|---|---|
| Blue | 300 | 299 | 0.212 | 0.264 | 0.225 | 0.006 | 0.001 | 0.03 | <0.001 |
| Green | 300 | 299 | 0.202 | 0.283 | 0.227 | 0.009 | 0.001 | 0.04 | |
| Red | 300 | 299 | 0.169 | 0.323 | 0.228 | 0.016 | 0.001 | 0.07 | |
| Red edge | 300 | 299 | 0.079 | 0.221 | 0.144 | 0.02 | 0.001 | 0.14 | |
| Red edge | 300 | 299 | 0.134 | 0.314 | 0.186 | 0.026 | 0.002 | 0.14 | |
| Red edge | 300 | 299 | 0.132 | 0.315 | 0.186 | 0.028 | 0.002 | 0.15 | |
| NIR | 300 | 299 | 0.132 | 0.315 | 0.186 | 0.028 | 0.002 | 0.15 | |
| Narrow NIR | 300 | 299 | 0.095 | 0.305 | 0.138 | 0.032 | 0.002 | 0.24 | |
| SWIR-1 | 300 | 299 | 0.013 | 0.244 | 0.034 | 0.032 | 0.002 | 0.94 | |
| SWIR-2 | 300 | 299 | 0.016 | 0.09 | 0.021 | 0.008 | 0.001 | 0.41 |
| Statistical Results | Turbidity |
|---|---|
| Count | 40 |
| μ | 43.31 |
| σ | 32.34 |
| SE Mean | 8.84 |
| t-test | 5.12 |
| p-Value (2-sided) | <0.001 |
| UC (2-sided, 95%) | 63.67 |
| LC (2-sided, 95%) | 26.89 |
| REM Results | |||
|---|---|---|---|
| Model | REM | ||
| LR on uncalibrated red band | 60.42 | 85.21 | −41.03 |
| MLP on red band calibrated with sigmoid and SGD | 60.42 | 88.48 | −46.44 |
| MLP on green band calibrated with sigmoid and MGD | 60.42 | 72.69 | −20.31 |
| MLP on red band calibrated with sigmoid and MGD | 60.42 | 66.06 | −9.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ndou, N.; Nontongana, N. Performance Evaluation of Gradient Descent Optimizers in Estuarine Turbidity Estimation with Multilayer Perceptron and Sentinel-2 Imagery. Hydrology 2024, 11, 164. https://doi.org/10.3390/hydrology11100164
Ndou N, Nontongana N. Performance Evaluation of Gradient Descent Optimizers in Estuarine Turbidity Estimation with Multilayer Perceptron and Sentinel-2 Imagery. Hydrology. 2024; 11(10):164. https://doi.org/10.3390/hydrology11100164
Chicago/Turabian StyleNdou, Naledzani, and Nolonwabo Nontongana. 2024. "Performance Evaluation of Gradient Descent Optimizers in Estuarine Turbidity Estimation with Multilayer Perceptron and Sentinel-2 Imagery" Hydrology 11, no. 10: 164. https://doi.org/10.3390/hydrology11100164
APA StyleNdou, N., & Nontongana, N. (2024). Performance Evaluation of Gradient Descent Optimizers in Estuarine Turbidity Estimation with Multilayer Perceptron and Sentinel-2 Imagery. Hydrology, 11(10), 164. https://doi.org/10.3390/hydrology11100164






