Effects of Pore Connectivity on the Sorption of Fluids in Nanoporous Material: Ethane and CO2 Sorption in Silicalite
Abstract
:1. Introduction
2. Materials and Methods
3. Results
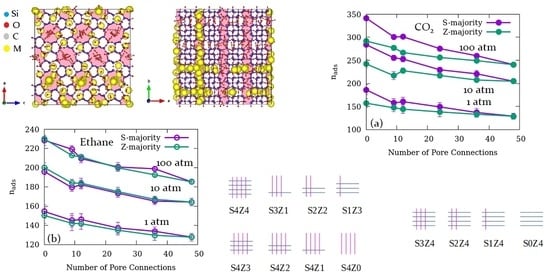
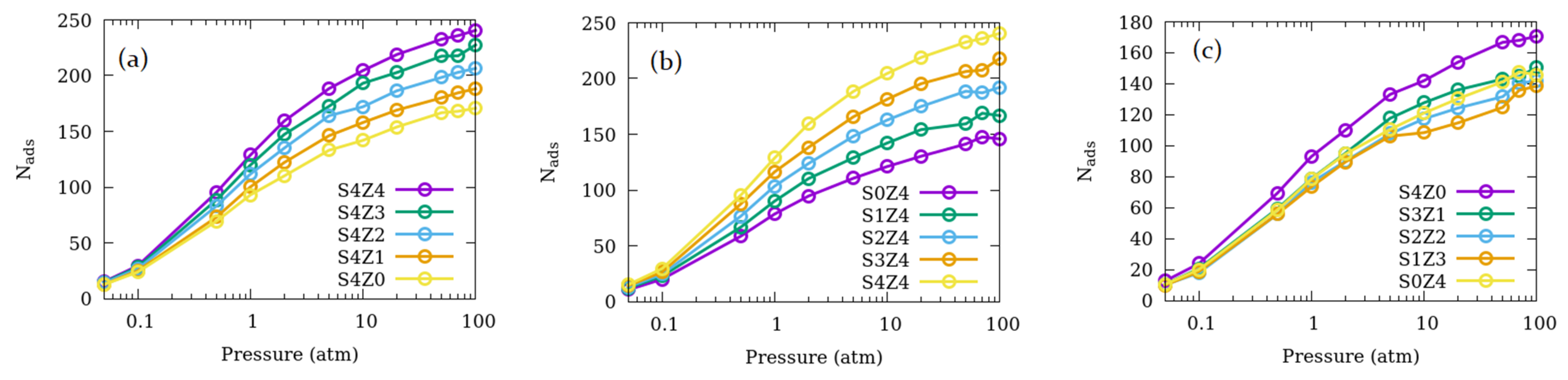
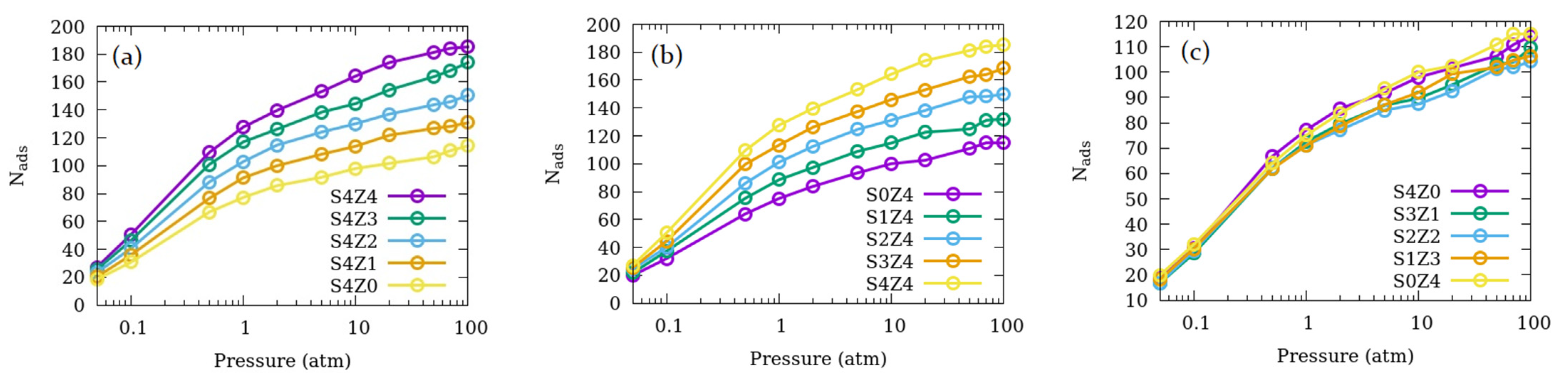
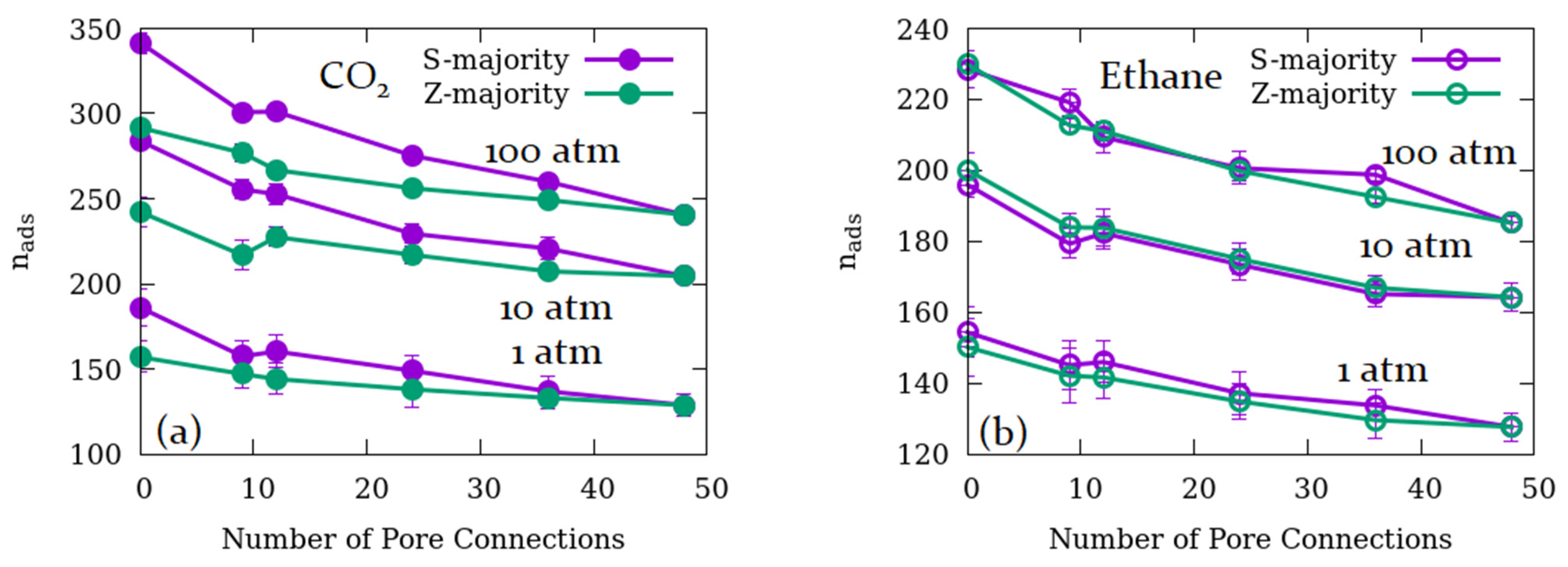
3.1. Effects of the Relative Number of Open Channels Available for Adsorption and Pore Connections
3.2. Fluid-Fluid and Fluid-Substrate Interactions in S2Z2
3.3. Effect of Pore Connectivity on the Orientational Distribution of Fluid Molecules in the Straight Channels
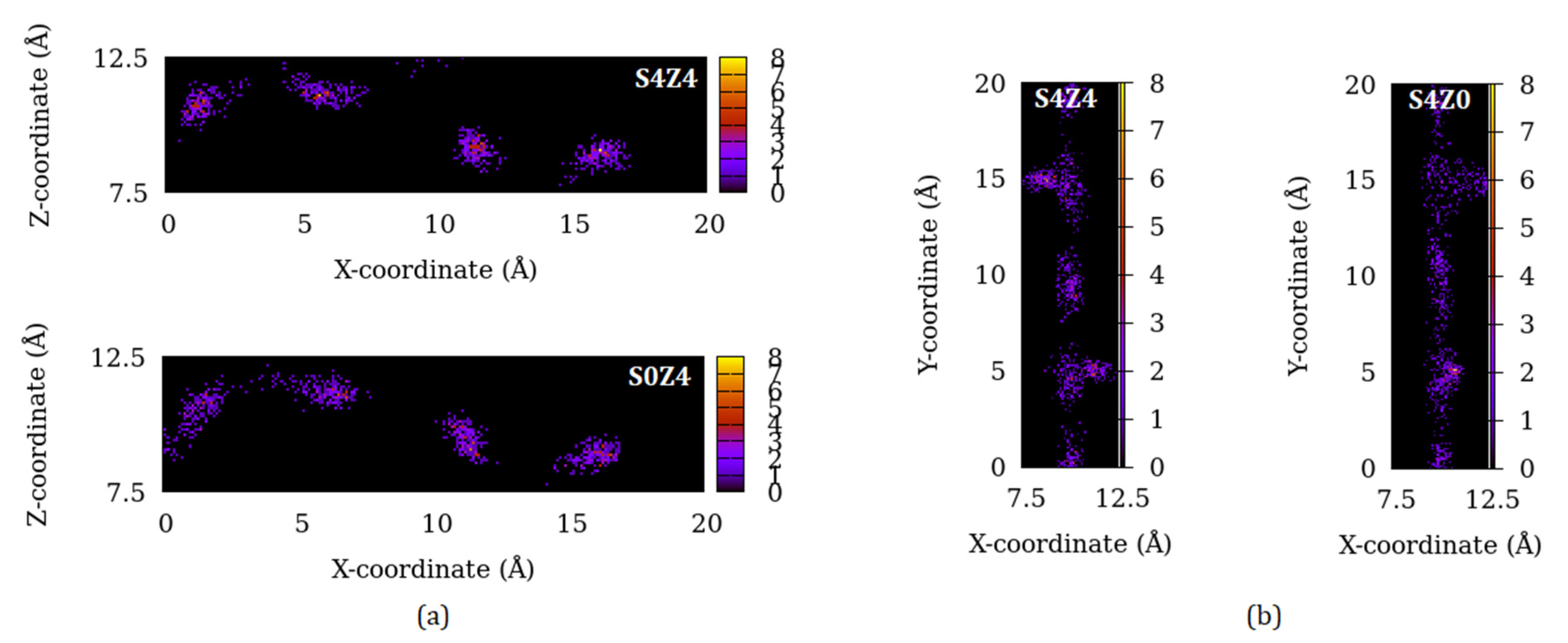
3.4. Effect of Pore Connectivity on the Distribution of Fluid Molecules in the Channels
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Králik, M. Adsorption, chemisorption, and catalysis. Chem. Pap. 2014, 68, 1625–1638. [Google Scholar] [CrossRef]
- Modak, A.; Jana, S. Advances in porous adsorbents for CO2 capture and storage. In Carbon Dioxide Chemistry, Capture and Oil Recovery; Books on Demand: Norderstedt, Germany, 2018; pp. 165–183. [Google Scholar]
- Klewiah, I.; Berawala, D.S.; Walker, H.C.A.; Andersen, P.Ø.; Nadeau, P.H. Review of experimental sorption studies of CO2 and CH4 in shales. J. Nat. Gas Sci. Eng. 2020, 73, 103045. [Google Scholar] [CrossRef]
- Smit, B.; Maesen, T.L.M. Molecular simulations of zeolites: Adsorption, diffusion, and shape selectivity. Chem. Rev. 2008, 108, 4125–4184. [Google Scholar] [CrossRef] [PubMed]
- Gautam, S.S.; Ok, S.; Cole, D.R. Structure and dynamics of confined C-O-H fluids relevant to the subsurface: Application of magnetic resonance, neutron scattering, and molecular dynamics simulations. Front. Earth Sci. 2017, 5, 43. [Google Scholar] [CrossRef] [Green Version]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Gautam, S.; Cole, D.R. Effects of inter-crystalline space on the adsorption of ethane and CO2 in silicalite: Implications for enhanced adsorption. Phys. Chem. Chem. Phys. 2020, 22, 13951–13957. [Google Scholar] [CrossRef]
- Gautam, S.; Cole, D. CO2 Adsorption in Metal-Organic Framework Mg-MOF-74: Effects of Inter-Crystalline Space. Nanomaterials 2020, 10, 2274. [Google Scholar] [CrossRef]
- Zhen, S.; Seff, K. Structures of organic sorption complexes of zeolites. Microporous Mesoporous Mater. 2000, 39, 1–18. [Google Scholar] [CrossRef]
- García-Pérez, E.; Parra, J.B.; Ania, C.; García-Sánchez, A.; Van Baten, J.M.; Krishna, R.; Dubbeldam, D.; Calero, S. A computational study of CO2, N2, and CH4 adsorption in zeolites. Adsorption 2007, 13, 469–476. [Google Scholar] [CrossRef] [Green Version]
- Razavian, M.; Fatemi, S.; Masoudi-Nejad, M. A comparative study of CO2 and CH4 adsorption on silicalite-1 fabricated by sonication and conventional method. Adsorpt. Sci. Technol. 2014, 32, 73–87. [Google Scholar] [CrossRef] [Green Version]
- Gautam, S.; Liu, T.; Patankar, S.; Tomasko, D.; Cole, D. Location dependent orientational structure and dynamics of ethane in ZSM5. Chem. Phys. Lett. 2016, 648, 130–136. [Google Scholar] [CrossRef] [Green Version]
- Dhiman, I.; Bhowmik, D.; Shrestha, U.R.; Cole, D.; Gautam, S. Effect of molecular shape on rotation under severe confinement. Chem. Eng. Sci. 2018, 180, 33–41. [Google Scholar] [CrossRef]
- Dhiman, I.; Shrestha, U.; Bhowmik, D.; Cole, D.; Gautam, S. Influence of molecular shape on self-diffusion under severe confinement: A molecular dynamics study. Chem. Phys. 2019, 516, 92–102. [Google Scholar] [CrossRef] [Green Version]
- Kummali, M.; Cole, D.; Gautam, S. Effect of Pore Connectivity on the Behavior of Fluids Confined in Sub-Nanometer Pores: Ethane and CO2 Confined in ZSM-22. Membranes 2021, 11, 113. [Google Scholar] [CrossRef]
- Sakai, M.; Sasaki, Y.; Kaneko, T.; Matsukata, M. Contribution of Pore-Connectivity to Permeation Performance of Silicalite-1 Membrane; Part I, Pore Volume and Effective Pore Size. Membranes 2021, 11, 382. [Google Scholar] [CrossRef]
- Sakai, M.; Sasaki, Y.; Kaneko, T.; Matsukata, M. Contribution of Pore-Connectivity to Permeation Performance of Silicalite-1 Membrane; Part II, Diffusivity of C6 Hydrocarbon in Micropore. Membranes 2021, 11, 399. [Google Scholar] [CrossRef]
- Chandra, D.; Vishal, V.; Bahadur, J.; Sen, D. A novel approach to identify accessible and inaccessible pores in gas shales using combined low-pressure sorption and SAXS/SANS analysis. Int. J. Coal Geol. 2020, 228, 103556. [Google Scholar] [CrossRef]
- Van Koningsveld, H.; Van Bekkum, H.; Jansen, J.C. On the location and disorder of the tetrapropylammonium (TPA) ion in zeolite ZSM-5 with improved framework accuracy. Acta Crystallogr. Sect. B Struct. Sci. 1987, 43, 127–132. [Google Scholar] [CrossRef] [Green Version]
- Martin, M.G.; Siepmann, J.I. Transferable potentials for phase equilibria. 1. United-atom description of n-alkanes. J. Phys. Chem. B 1998, 102, 2569–2577. [Google Scholar] [CrossRef]
- Cygan, R.T.; Liang, J.-J.; Kalinichev, A. Molecular models of hydroxide, oxyhydroxide, and clay phases and the development of a general force field. J. Phys. Chem. B 2004, 108, 1255–1266. [Google Scholar] [CrossRef]
- Purton, J.A.; Crabtree, J.C.; Parker, S.C. DL_MONTE: A general purpose program for parallel Monte Carlo simulation. Mol. Simul. 2013, 39, 1240–1252. [Google Scholar] [CrossRef]
- Potoff, J.J.; Siepmann, J.I. Vapor-liquid equilibria of mixtures containing alkanes, carbon dioxide, and nitrogen. AIChE J. 2001, 47, 1676–1682. [Google Scholar] [CrossRef]
- Gautam, S.; Liu, T.; Cole, D. Sorption, Structure and Dynamics of CO2 and Ethane in Silicalite at High Pressure: A Combined Monte Carlo and Molecular Dynamics Simulation Study. Molecules 2019, 24, 99. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Sequaris, J.-M.; Klumpp, E. Effects of natural organic matter on the microporous sorption sites of black carbon in a Yangtze River sediment. Environ. Sci. Pollut. Res. 2013, 20, 6992–6998. [Google Scholar] [CrossRef] [PubMed]
- Xue, Y.; Markmann, J.; Duan, H.; Weissmüller, J.; Huber, P. Switchable imbibition in nanoporous gold. Nat. Commun. 2014, 5, 4237. [Google Scholar] [CrossRef] [Green Version]
- Koya, A.N.; Zhu, X.; Ohannesian, N.; Yanik, A.A.; Alabastri, A.; Zaccaria, R.P.; Krahne, R.; Shih, W.-C.; Garoli, D. Nanoporous Metals: From Plasmonic Properties to Applications in Enhanced Spectroscopy and Photocatalysis. ACS Nano 2021, 15, 6038–6060. [Google Scholar] [CrossRef] [PubMed]
- Momma, K.; Fujio, I. VESTA: A three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 2008, 41, 653–658. [Google Scholar] [CrossRef]
- Williams, T.; Kelley, C.; Lang, R.; Kotz, D.; Campbell, J. Gnuplot 4.6: An Interactive Plotting Program. 2014. Available online: http://gnuplot.info (accessed on 2 June 2021).

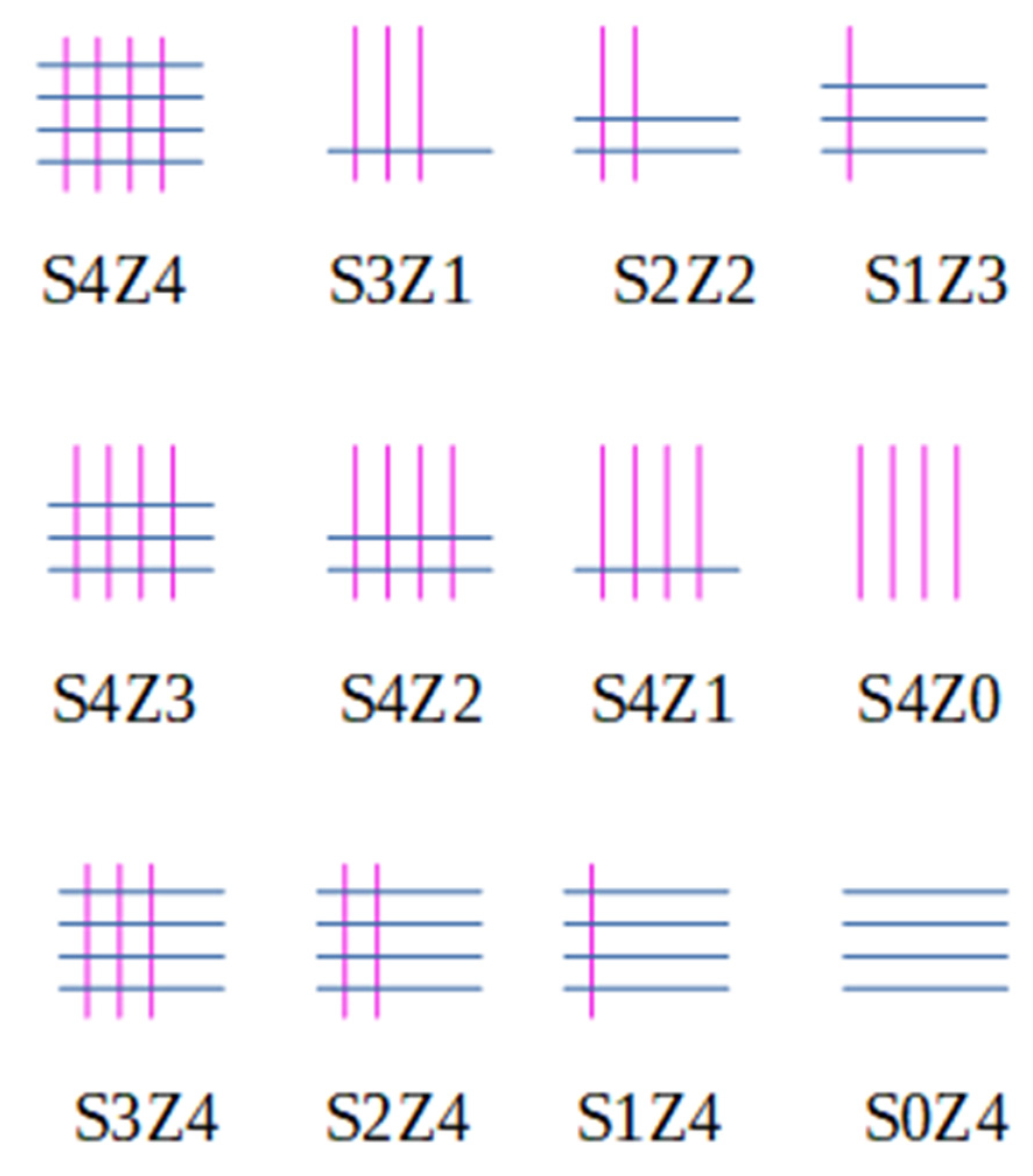




| System name | Open Straight Channels (% of Total) | Open Sinusoidal Channels (% of Total) | Number of Pore Connections | Fraction of Total Pore Volume Available |
|---|---|---|---|---|
| S4Z4 | 100 | 100 | 48 | 1.0 |
| S4Z3 | 100 | 75 | 36 | 0.875 |
| S4Z2 | 100 | 50 | 24 | 0.75 |
| S4Z1 | 100 | 25 | 12 | 0.625 |
| S4Z0 | 100 | 0 | 0 | 0.50 |
| S3Z1 | 75 | 25 | 9 | 0.50 |
| S2Z2 | 50 | 50 | 12 | 0.50 |
| S1Z3 | 25 | 75 | 9 | 0.50 |
| S0Z4 | 0 | 100 | 0 | 0.50 |
| S1Z4 | 25 | 100 | 12 | 0.625 |
| S2Z4 | 50 | 100 | 24 | 0.75 |
| S3Z4 | 75 | 100 | 36 | 0.875 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gautam, S.; Cole, D.R. Effects of Pore Connectivity on the Sorption of Fluids in Nanoporous Material: Ethane and CO2 Sorption in Silicalite. ChemEngineering 2021, 5, 55. https://doi.org/10.3390/chemengineering5030055
Gautam S, Cole DR. Effects of Pore Connectivity on the Sorption of Fluids in Nanoporous Material: Ethane and CO2 Sorption in Silicalite. ChemEngineering. 2021; 5(3):55. https://doi.org/10.3390/chemengineering5030055
Chicago/Turabian StyleGautam, Siddharth, and David R. Cole. 2021. "Effects of Pore Connectivity on the Sorption of Fluids in Nanoporous Material: Ethane and CO2 Sorption in Silicalite" ChemEngineering 5, no. 3: 55. https://doi.org/10.3390/chemengineering5030055
APA StyleGautam, S., & Cole, D. R. (2021). Effects of Pore Connectivity on the Sorption of Fluids in Nanoporous Material: Ethane and CO2 Sorption in Silicalite. ChemEngineering, 5(3), 55. https://doi.org/10.3390/chemengineering5030055