Optimizing the Control System of Clinker Cooling: Process Modeling and Controller Tuning
Abstract
:1. Introduction
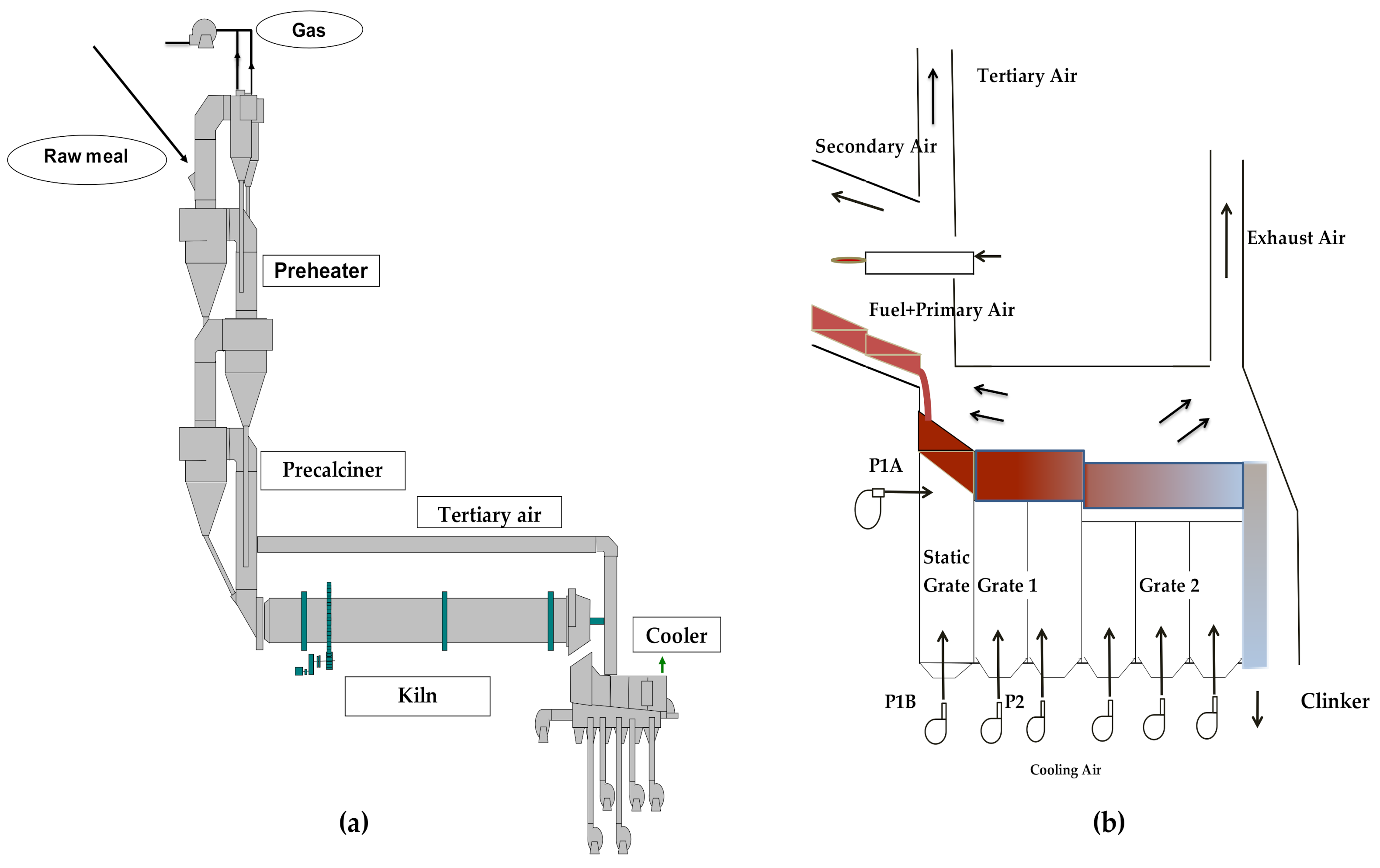
2. Hardware Setup and Software Operation
- Data extraction from PI and storing to SQL;
- Data extraction from SQL and determination of the best models;
- PID design;
- Simulation of the process to find the optimal PID gains.
3. Process Model
- The flow rate and granulometry of clinker dropping from the kiln to the cooler;
- The flow rate, the number, and the quality of conventional and alternative fuels;
- The possible existence of rings inside the kiln;
- The pressures and probable clogging inside the preheater.
4. Model Identification and Controller Design
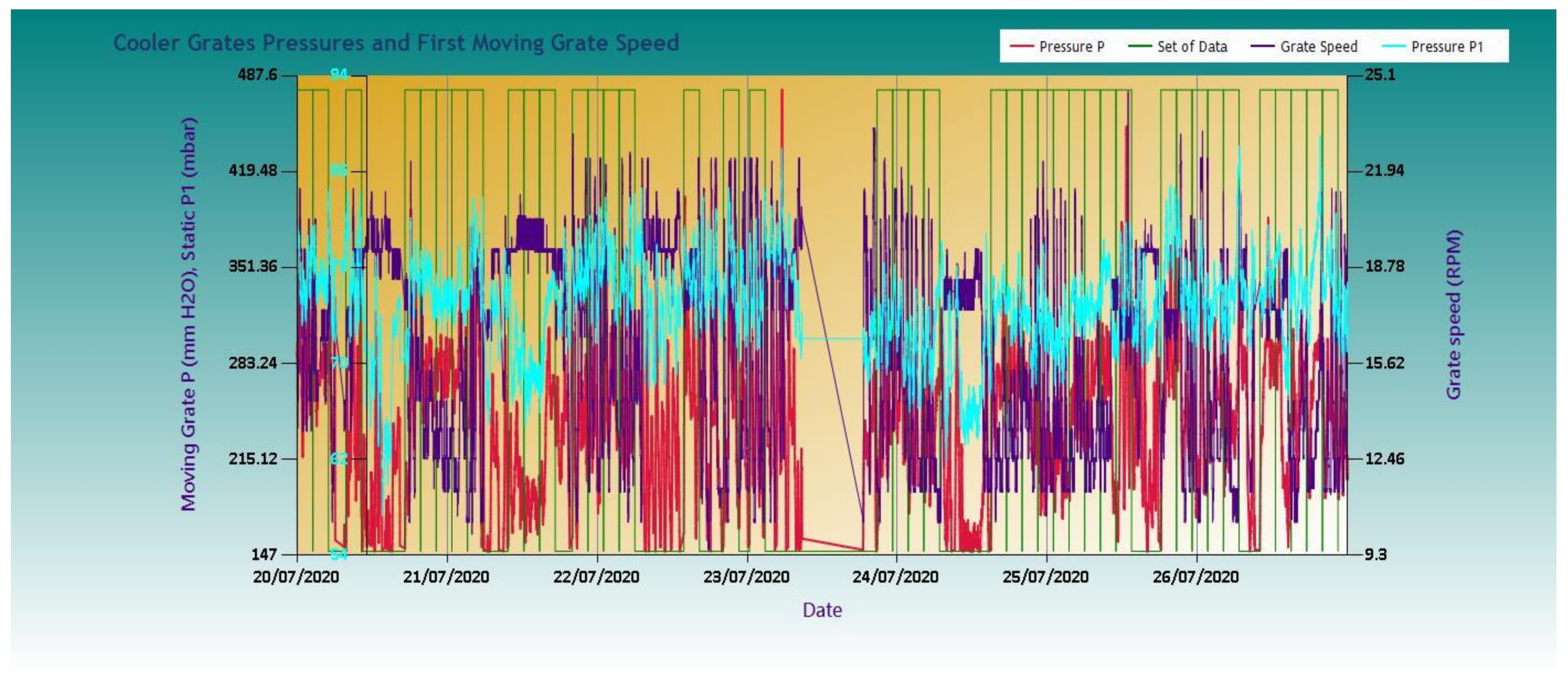
4.1. Determining the Best Models
- As far as the model regression coefficient is concerned, RMod, for 4 ≤ Ng ≤ 7 and 4 ≤ Np ≤ 9, more than 77% of the data sets present a RMod ≥ 0.7.
- The regression coefficient, RP, between P, P1, and S is higher than 0.8 for more than 67% of the data sets if Ng ≥ 4.
- As to the corresponding regression coefficient between P1 and S, there exist enough combinations of (Np, Ng) pairs where more than 42% of the total sets have a RP1 ≥ 0.7.
- RP1 is generally less than RP due to the load disturbances coming from the kiln side.
- The modeling verifies the measurable impact of the speed of the moving grate on the pressure of the static grate.
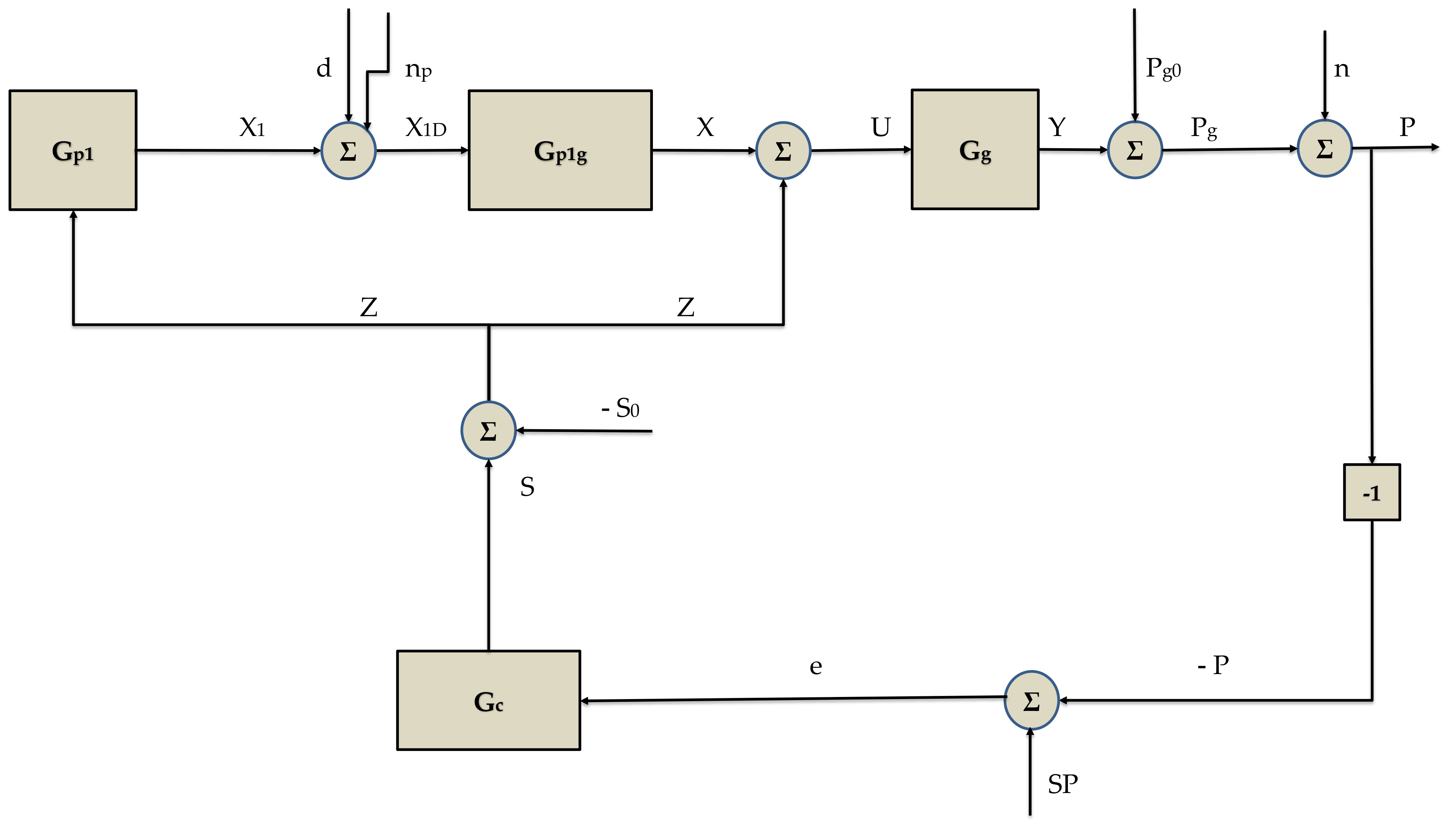
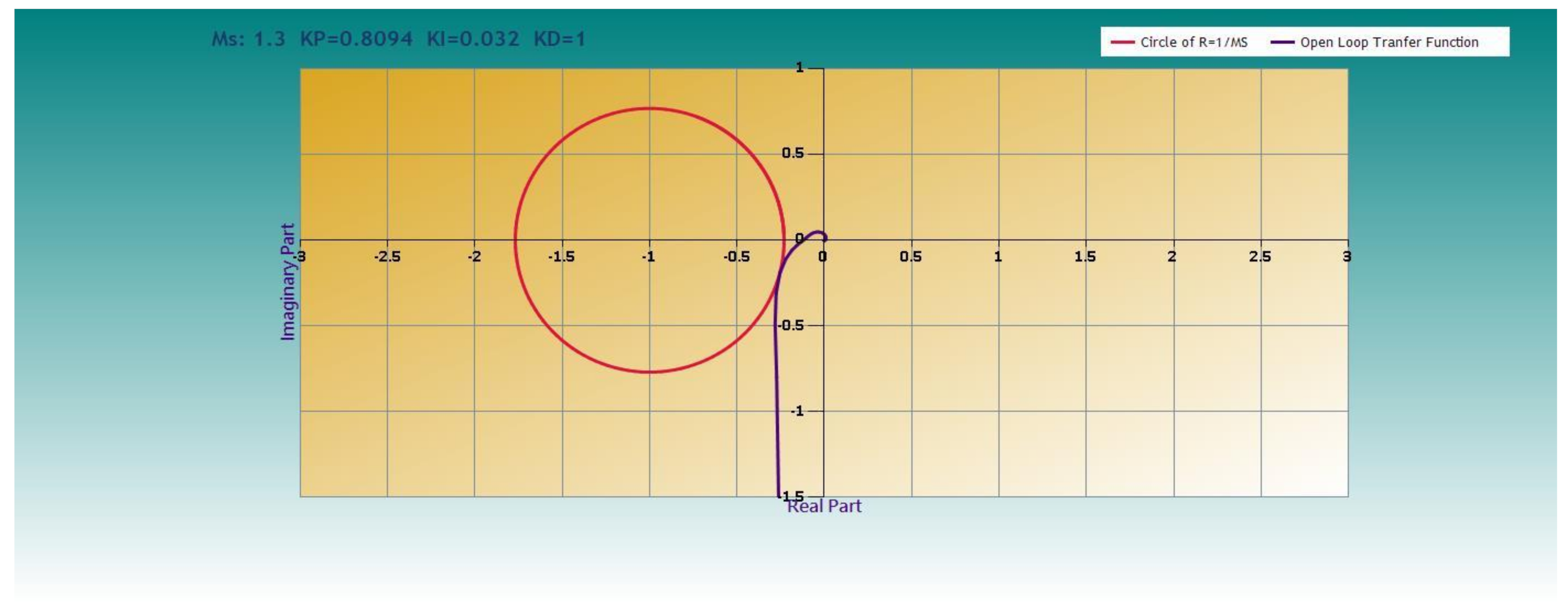
4.2. PID Controller Design
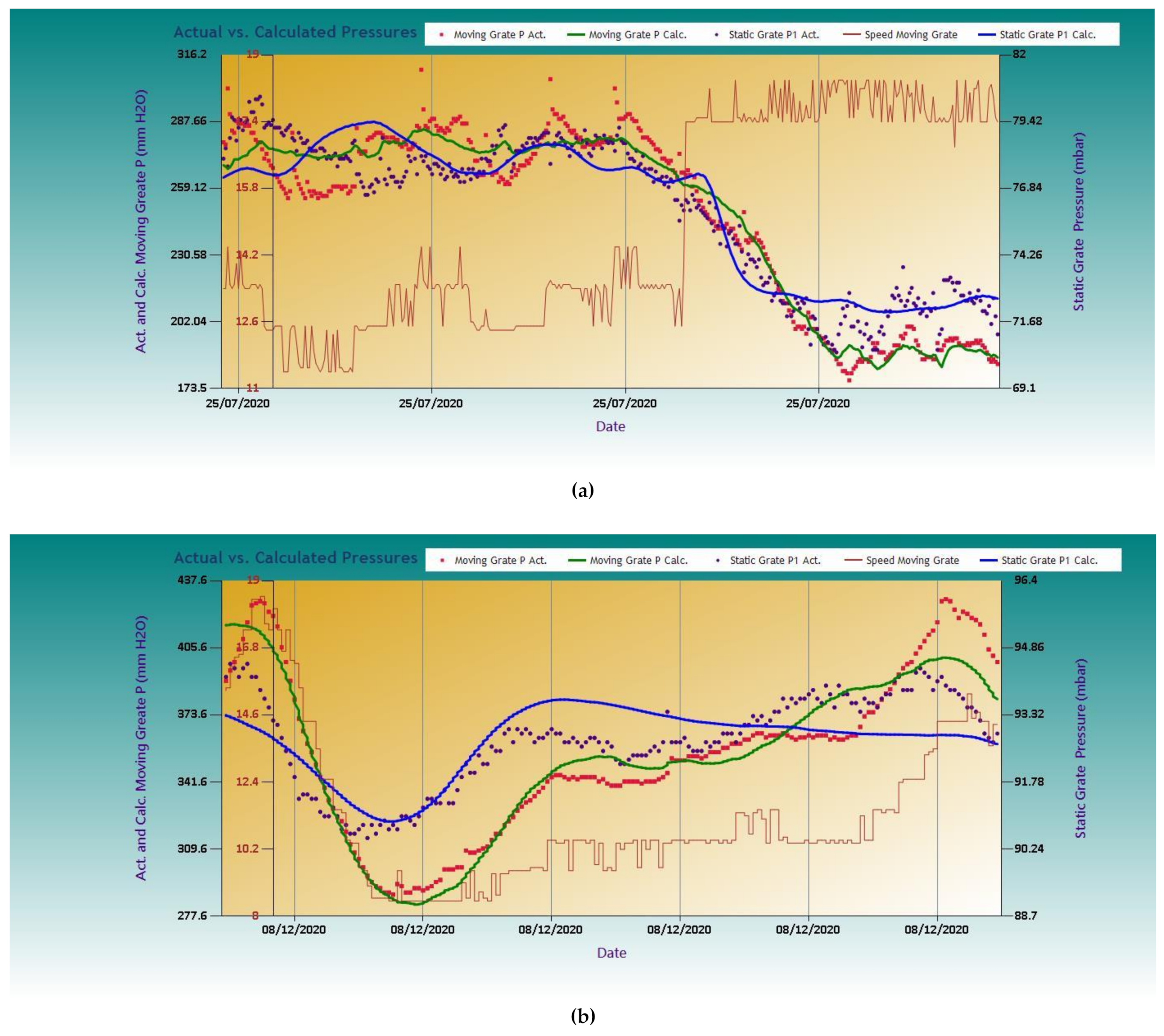
4.3. Autoregressive Model
5. PID Optimization by Simulation
- (i)
- The setpoint of pressure, Pa, of moving grate, SPa;
- (ii)
- The current minimum value of speed, Scmin;
- (iii)
- The values of dynamic and steady-state parameters of the transfer functions (1), (3) and (4);
- (iv)
- Percent disturbance margin for each of the nine dynamic and steady-state parameters;
- (v)
- The values of coefficients, A1P and A2P, and of standard error, StdErrP, of Equation (11);
- (vi)
- The values of coefficients, A1P1 and A2P1, and of standard error, StdErrP1, of Equation (12);
- (vii)
- The values of residual errors, sResP1 and sResP, according to Equations (17) and (18);
- (viii)
- The sampling and actuator period, Ts;
- (ix)
- The total time of simulation, Toper;
- (x)
- The minimum and maximum number of sampling periods during which the load disturbance is present;
- (xi)
- The total number of simulations per software module execution, NI.
5.1. Short Description of the Simulator
5.2. Initial Simulations
- Ms = 1.1, kP = 0.289, kI = 0.011, kD = 0.0;
- Ms = 1.3, kP = 0.78, kI = 0.031, kD = 0.5;
- Ms = 1.65, kP = 1.348, kI = 0.056, kD = 0.0.
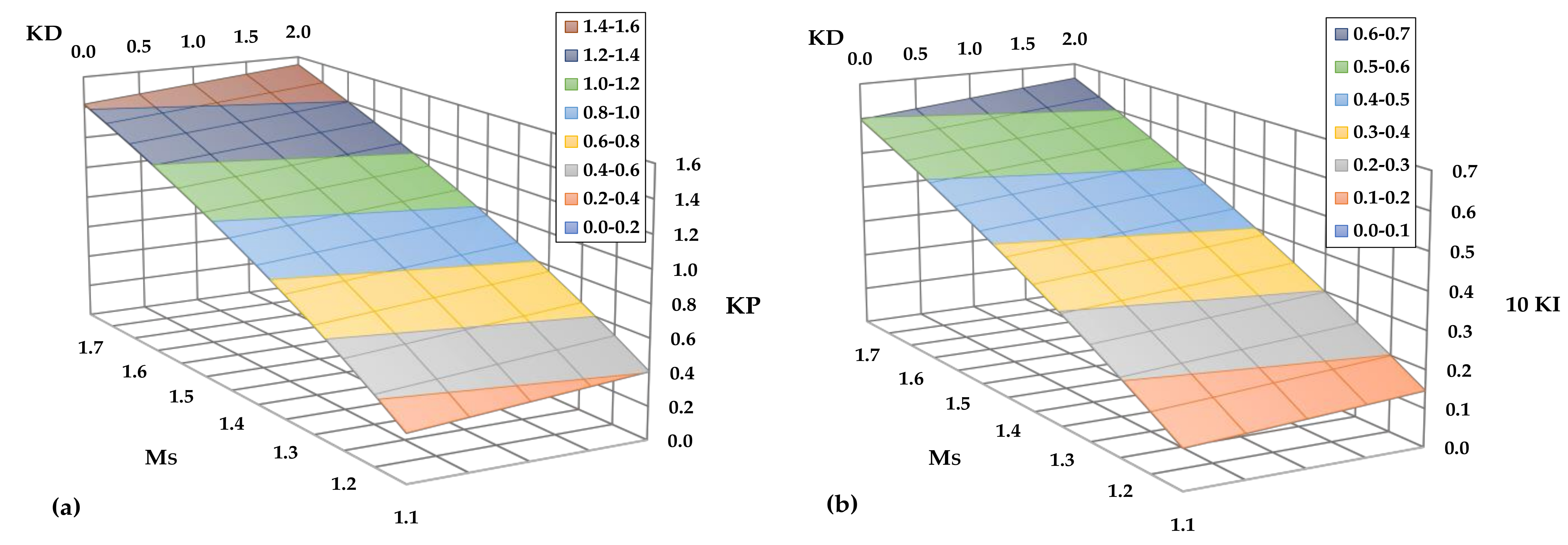
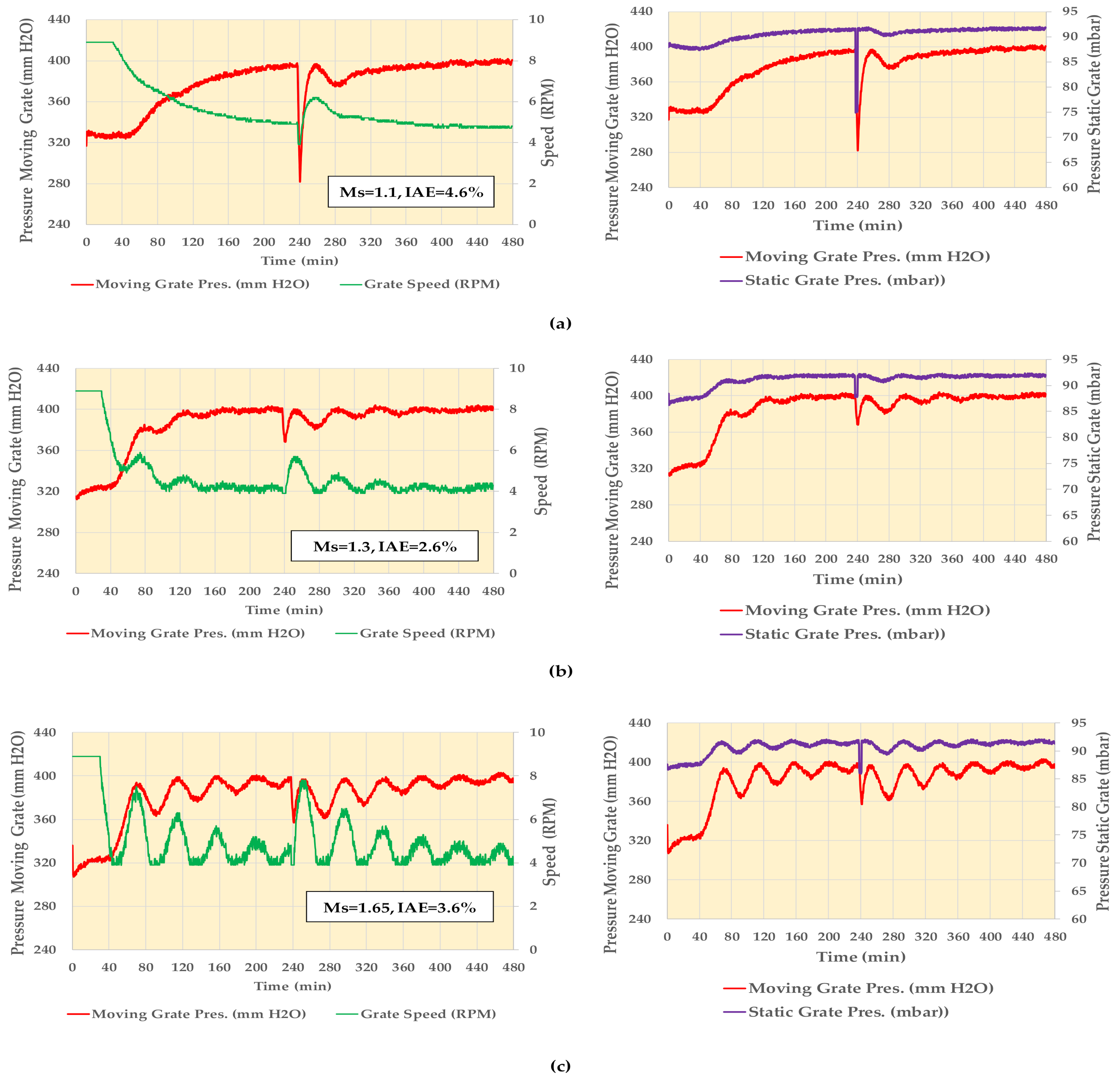
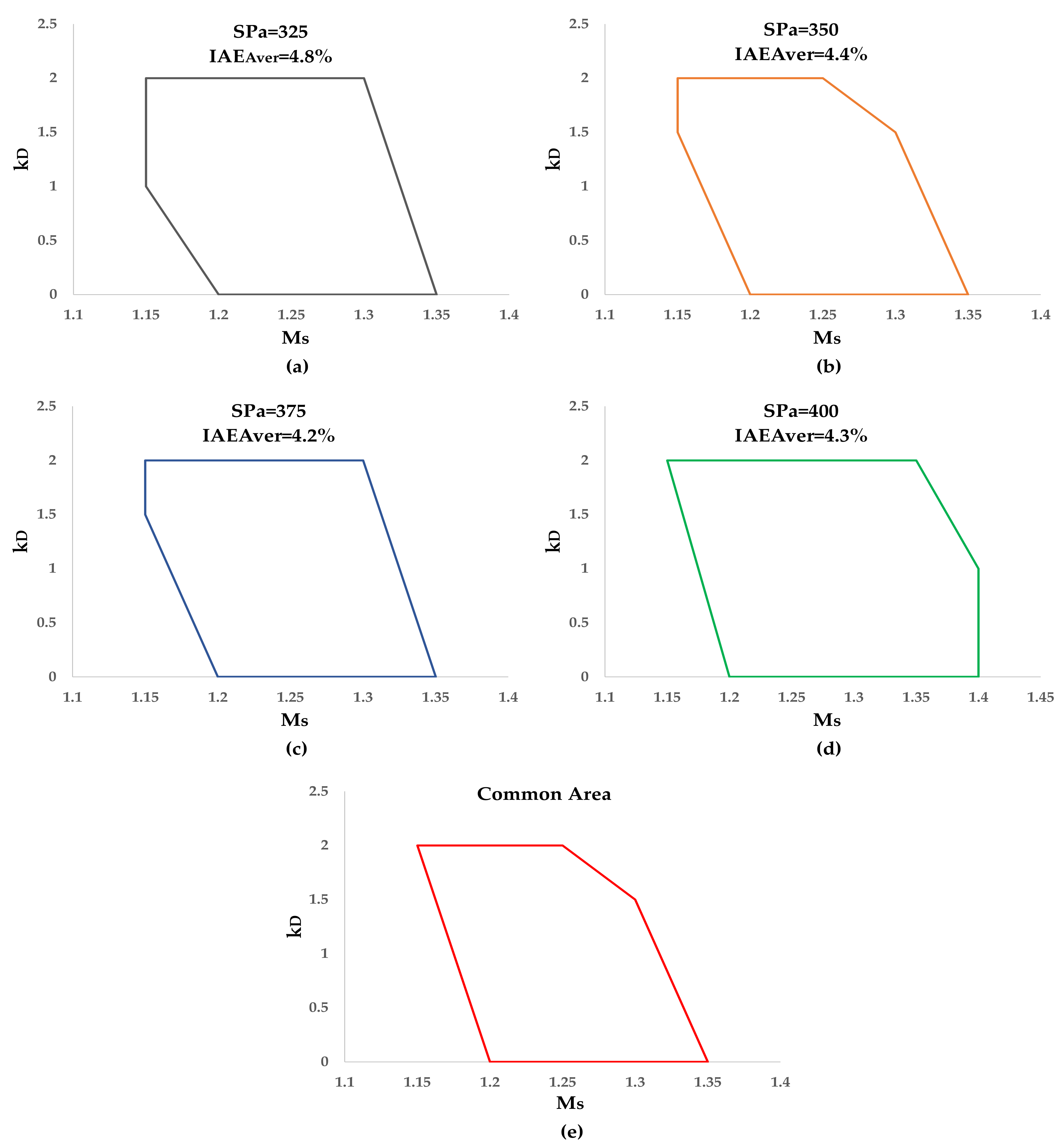
5.3. Full Simulation and PID Optimization
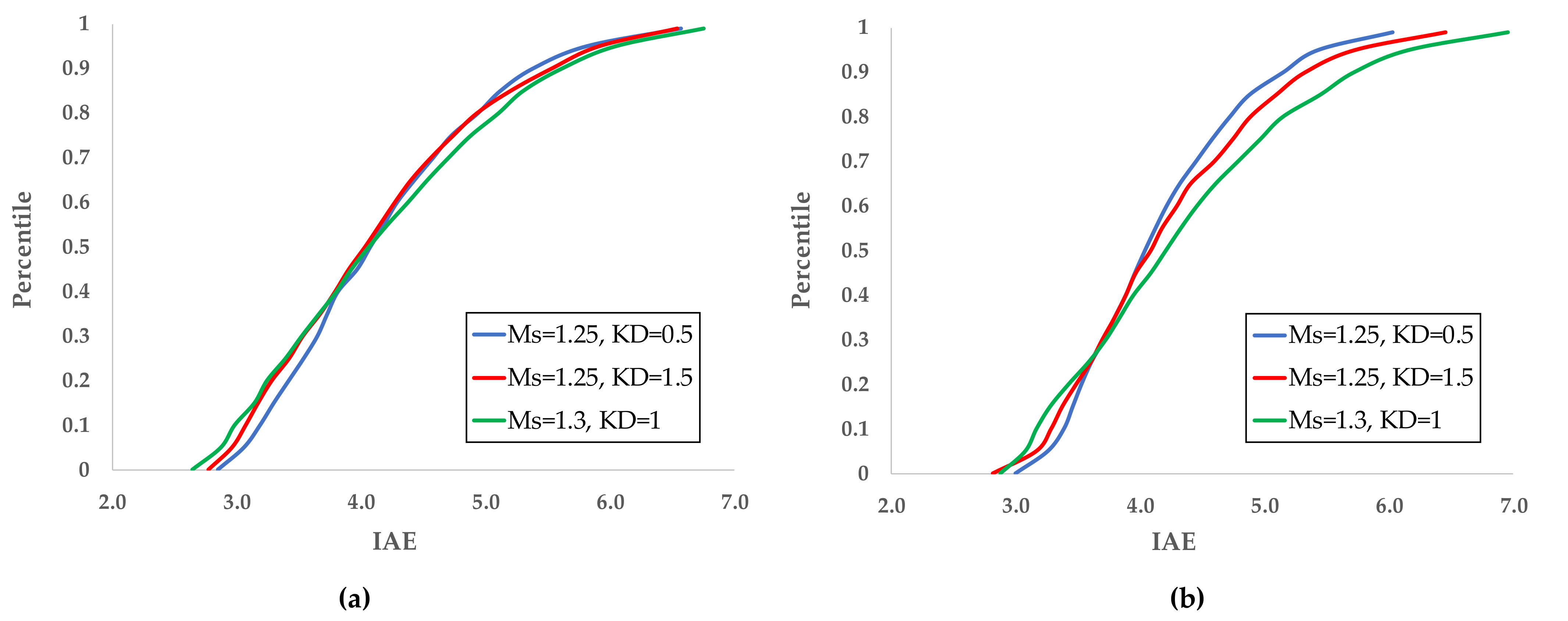
- (a)
- The PID set providing the minimum IAEAver,Min was found;
- (b)
- The sets with IAEAver ≤ 1.1·IAEAver,Min were determined;
- (c)
- This area constitutes the optimum region of the PID coefficients.
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A1P, A2P | Coefficients of the autoregressive Equation (11) |
| A1P1, A2P1 | Coefficients of the autoregressive Equation (12) |
| d | Pressure load disturbance on the fixed grate, % |
| D0 | Maximum height of the disturbance, d, % |
| e | Control error between SP and P, % |
| ErrP | Error between P and PCalc |
| ErrP1 | Error between P1 and P1,Calc |
| IAE | Integral of absolute error, % |
| k0 | Number of independent variables in Equation (8) |
| kD | Derivative gain of the PID controller, min |
| kI | Integral gain of the PID controller, min−1 |
| kP | Proportional gain of the PID controller |
| kvp | Gain of the transfer function Gp1 |
| kvpg | Gain of the transfer function Gp1g |
| kvg | Gain of the transfer function Gg |
| Gc | Transfer function of the PID controller |
| Gg | Transfer function between moving grate speed and pressure of moving grate |
| GL | Open-loop transfer function |
| Gp1 | Transfer function between moving grate speed and pressure of static grate |
| Gp1g | Transfer function between pressures of static and moving grate |
| M | Count of data in the defined period |
| Ms | Maximum sensitivity |
| NI | Number of simulations |
| Np | Exponent of the function Gp1 |
| np | Pressure noise on the fixed grate, % |
| Ng | Exponent of the function Gg |
| ng | Pressure noise on the moving grate, % |
| P | Pressure of moving grate after the addition of the noise, n, % |
| Pa | Pressure of moving grate, mm H2O |
| PaMax | Maximum pressure of moving grate, mm H2O |
| P1a | Pressure of static grate, mbar |
| P1aMax | Maximum pressure of static grate, mm H2O |
| PCalc | Calculated pressure of moving grate, % |
| Pg | Pressure of moving grate, % |
| P1 | Pressure of static grate, % |
| P1,Calc | Calculated pressure of static grate, % |
| P10 | Steady-state pressure of static grate, % |
| Pg | Pressure of moving grate, % |
| Pg0 | Steady-state pressure of moving grate, % |
| RMod | Model regression coefficient for pressures P and P1 |
| RP | Regression coefficient between pressures P and PCalc |
| RP1 | Regression coefficient between pressures P1 and P1,Calc |
| S(iω) | Sensitivity function |
| S | Moving grate speed, % |
| Sa | Moving grate speed, RPM |
| SaMax | Maximum speed, Sa, RPM |
| SaMin | Minimum speed, Sa, RPM |
| SMax | Maximum speed, S, % |
| SMin | Minimum speed, S, % |
| S0 | Steady-state speed of moving grate, % |
| SLow | Low limit of grate speed, % |
| sP | Standard deviation of the population of pressures, P, % |
| SP | Set-point of pressure in moving grate, % |
| SPa | Set-point of pressure in moving grate, RPM |
| sP1 | Standard deviation of the population of pressures, P1, % |
| sRes | Residual error between actual and calculated pressures, % |
| sResP | Residual error between pressures P and PCalc, % |
| sResP1 | Residual error between pressures P1 and P1,Calc, % |
| StdErrP | Standard error of the Equation (11), % |
| StdErrP1 | Standard error of the Equation (12), % |
| t0 | Integration time in Equation (24), min |
| tD | Duration of the disturbance, d, min |
| Tp | Time constant of the transfer function Gp1, min |
| Tpg | Time constant of the transfer function Gp1g, min |
| Ts | Sampling and actuation period, s |
| Tg | Time constant of the transfer function Gg, min |
| U | Sum of the signals X and Z, % |
| Χ | Output pressure from the transfer function Gp1g, % |
| X1 | Difference between P1 and P10, % |
| Y | Difference between Pg and Pg0, % |
| X1D | Sum of the signals X1, d, and np, % |
| Z | Difference between S and S0, % |
References
- Miglay, H.G. The formation and phase composition of portland cement clinker. In The Chemistry of Cements, 2nd ed.; Taylor, H.F.W., Ed.; Academic Press Inc.: New York, NY, USA, 1972; Volume 1, pp. 103–106. [Google Scholar]
- Astrom, K.J.; Hagglund, T. Advanced PID Control; Instrumentation, Systems and Automatic Society: Raleigh, NC, USA, 2006; pp. 1, 25, 33, 206–221. [Google Scholar]
- Astrom, K.J. Model Uncertainty and Robust Control, Lecture Notes on Iterative Identification and Control Design, Lund University. 2000. Available online: https://www.researchgate.net/publication/228602986_Model_Uncertainty_and_Robust_Control/ (accessed on 1 July 2021).
- Tsamatsoulis, D. Simplified Modeling of Clinker Cooling Based on Long Term Industrial Data. In Proceedings of the Recent Researches in System Science, 15th WSEAS International Conference on Systems, Corfu Island, Greece, 14–16 July 2011; WSEAS Press: Stevens Point, WI, USA, 2011; pp. 143–147. Available online: http://www.wseas.us/e-library/conferences/2011/Corfu/SYSTEMS/SYSTEMS-21.pdf (accessed on 1 July 2021).
- Srividhya, G.; Guruprasath, M.; Jayalalitha, S. Maintenance of under Grate Pressure in Grate Coolers Used in Cement Kilns by IMC Based PID Controller. Int. J. Adv. Res. Electr. Electron. Instrum. Eng. 2015, 4, 1692–1699. Available online: http://www.ijareeie.com/upload/2015/march/63_MAINTENANCE_new.pdf (accessed on 1 July 2021).
- Yu, H.; Sun, Y.; Huang, B.; Zheng, Z. Research on Modelling of Grate Cooler Based on Typical Operating Conditions. In Proceedings of the 2nd International Conference on Intelligent Manufacturing and Materials—Volume 1, Guangzhou, China, 15–16 June 2018; Sup, K., Ed.; pp. 556–561. Available online: https://www.scitepress.org/Papers/2018/75356/75356.pdf/ (accessed on 11 June 2021).
- Wang, X.; Wu, S.; Shen, T.; Fan, Y. The Grey Predictive Control on Grate Cooler System. In Proceedings of the 2007 Chinese Control Conference, Zhangjiajie, China, 26–31 July 2007; pp. 218–221. Available online: https://ieeexplore.ieee.org/document/4347202 (accessed on 1 July 2021).
- Jun, Z.M.; Qingjin, M.; Hongliang, Y. The Application of Dynamic Matrix Control in the Grate Cooler. In Proceedings of the 2017 IEEE 2nd Advanced Information Technology, Electronic and Automation Control Conference, Chongqing, China, 25–26 March 2017; pp. 2630–2633. Available online: https://ieeexplore.ieee.org/document/8054501 (accessed on 1 July 2021).
- Wang, Z.; Yuan, M. A Self-Tuning Fuzzy PID Control Method of Grate Cooler Pressure Based on Kalman Filter. In Proceedings of the 2012 International Conference on Computer Science and Information Processing, Xi’an,China, 24–26 August 2012; Available online: http://www.greenid.ir/wpimages/13GREENID%20A%20Self-tuning%20Fuzzy%20PID%20Control%20Method.pdf/ (accessed on 12 June 2021).
- Zhang, X.; Lu, J. Fuzzy Control of Heat Recovery Systems of Cement Clinker Cooler. J. Theor. Appl. Inf. Technol. 2012, 4, 182–190. Available online: http://www.jatit.org/volumes/Vol42No2/5Vol42No2.pdf (accessed on 1 July 2021).
- Karikov, E.B.; Rubanov, V.G.; Korneevich, K.V. Construction of a Dynamic Neural Network Model as a Stage of Grate Cooler Automation. World Appl. Sci. J. 2013, 25, 227–232. Available online: https://www.idosi.org/wasj/wasj25(2)13/9.pdf (accessed on 1 July 2021).
- Elman, J.L. Finding Structure in Time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Seraj, M.; Shooredeli, M.A. Data-Driven Predictor and Soft-Sensor Models of a Cement Grate Cooler Based on Neural Network and Effective Dynamics. In Proceedings of the 2017 Iranian Conference on Electrical Engineering, Tehran, Iran, 2–4 May 2017; pp. 726–731. Available online: https://ieeexplore.ieee.org/document/7985134 (accessed on 1 July 2021).
- Geng, Y.; Wang, X.; Jiang, P. Prediction of the Cement Grate Cooler Pressure in the Cooling Process Based on a Multi-Model Fusion Neural Network. IEEE Access 2020, 8, 115028–115040. Available online: https://ieeexplore.ieee.org/document/9118923 (accessed on 1 July 2021). [CrossRef]
- Wang, S.; Yu, H.; Lu, S.; Wang, X.; Liu, H. Application of Least Square Support Vector Machine with Adaptive Particle Swarm Parameter Optimization in Grate Pressure Optimization Setting of Grate Cooler. In Proceedings of the 2020 35th Youth Academic Annual Conference of Chinese Association of Automation, Zhanjiang, China, 16–18 October 2020; pp. 632–637. Available online: https://ieeexplore.ieee.org/document/9337619 (accessed on 1 July 2021).
- Astrom, K.J.; Panagopoulos, H.; Hagglund, T. Design of PI Controllers Based on Non-Convex Optimization. Automatica 1998, 34, 585–601. [Google Scholar] [CrossRef]
- Tsamatsoulis, D. Effective Optimization of the Control System for the Cement Raw Meal Mixing Process: I. PID Tuning Based on Loop Shaping. WSEAS Trans. Syst. Control 2011, 6, 239–253. Available online: http://www.wseas.us/e-library/transactions/control/2011/52-480.pdf (accessed on 13 June 2021).
- Tsamatsoulis, D. Effective Optimization of the Control System for the Cement Raw Meal Mixing Process: II. Optimizing Robust PID Controllers Using Real Process Simulators. WSEAS Trans. Syst. Control 2011, 6, 276–288. Available online: http://wseas.us/e-library/transactions/control/2011/52-697.pdf (accessed on 13 June 2021).
- Tsamatsoulis, D. Modelling and simulation of raw material blending process in cement raw mix milling installations. Can. J. Chem. Eng. 2014, 92, 1882–1894. [Google Scholar] [CrossRef]
- Tsamatsoulis, D. Dynamic Behavior of Closed Grinding Systems and Effective PID Parameterization. WSEAS Trans. Syst. Control 2009, 4, 581–602. Available online: http://www.wseas.us/e-library/transactions/control/2009/29-816.pdf (accessed on 13 June 2021).
- Tsamatsoulis, D. Optimizing the control system of cement milling: Process modeling and controller tuning based on loop shaping procedures and process simulations. Braz. J. Chem. Eng. 2014, 31, 155–170. [Google Scholar] [CrossRef]
- Tsamatsoulis, D.; Zlatev, G. PID Parameterization of Cement Kiln Precalciner Based on Simplified Modeling. Available online: https://www.naun.org/main/NAUN/neural/2016/a142016-083.pdf (accessed on 14 June 2021).
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. SIAM J. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Zolotas, A.C.; Halikias, G.D. Optimal Design of PID Controllers Using the QFT Method. IEE Proc. Control Theory Appl. 1999, 146, 585–590. Available online: https://digital-library.theiet.org/content/journals/10.1049/ip-cta_19990746 (accessed on 1 July 2021). [CrossRef] [Green Version]
- Yaniv, O.; Nagurka, M. Automatic Loop Shaping of Structured Controllers Satisfying QFT Performance. J. Dyn. Syst. Meas. Control 2005, 127, 472–477. Available online: https://www.researchgate.net/publication/229003095_Automatic_Loop_Shaping_of_Structured_Controllers_Satisfying_QFT_Performance (accessed on 1 July 2021). [CrossRef] [Green Version]
- Astrom, K.J.; Hagglund, T. Revisiting the Ziegler–Nichols step response method for PID control. J. Process. Control 2004, 14, 635–650. [Google Scholar] [CrossRef]


| Characteristic | Value |
|---|---|
| Cooler length, m | 20 |
| Cooler width, m | 2.4 |
| Number of static grates | 1 |
| Number of moving grates | 2 |
| Max. speed of the first moving grate, RPM | 25 |
| Max. measured pressure of the first moving grate, mm H2O | 800 |
| Kiln production, tons of clinker per day | 1600 |
| Ng | Np | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 2 | 61.0 | 68.5 | 70.3 | 70.1 | 70.5 | 70.9 | 71.1 | 70.5 | 70.4 |
| 3 | 66.1 | 73.4 | 75.1 | 75.6 | 75.4 | 75.8 | 75.7 | 75.7 | 75.3 |
| 4 | 67.1 | 75.4 | 76.7 | 77.3 | 77.3 | 77.3 | 76.9 | 77.0 | 77.1 |
| 5 | 68.4 | 75.8 | 77.6 | 78.4 | 78.1 | 78.3 | 78.0 | 78.3 | 78.2 |
| 6 | 68.0 | 76.2 | 76.7 | 77.3 | 78.2 | 78.3 | 77.9 | 78.0 | 78.2 |
| 7 | 67.3 | 76.2 | 76.3 | 77.9 | 76.4 | 77.4 | 77.2 | 77.2 | 77.7 |
| 8 | 67.1 | 74.8 | 76.0 | 77.4 | 76.7 | 75.8 | 75.7 | 76.0 | 76.2 |
| 9 | 66.1 | 74.7 | 76.3 | 76.7 | 76.7 | 76.3 | 76.0 | 75.1 | 76.5 |
| Ng | Np | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 2 | 13.2 | 37.0 | 45.0 | 45.5 | 45.9 | 46.8 | 46.2 | 45.7 | 45.2 |
| 3 | 11.5 | 34.1 | 42.4 | 42.9 | 43.1 | 44.2 | 43.9 | 43.2 | 42.9 |
| 4 | 11.3 | 33.4 | 41.4 | 42.6 | 41.8 | 43.2 | 42.9 | 42.0 | 42.1 |
| 5 | 11.1 | 33.3 | 40.5 | 41.5 | 42.2 | 42.9 | 42.7 | 42.0 | 41.5 |
| 6 | 11.2 | 33.6 | 41.3 | 42.5 | 42.2 | 42.3 | 42.5 | 41.5 | 41.1 |
| 7 | 11.4 | 33.7 | 41.0 | 41.4 | 43.7 | 42.4 | 41.6 | 41.2 | 41.4 |
| 8 | 10.7 | 33.2 | 40.2 | 40.3 | 41.6 | 42.1 | 41.2 | 41.4 | 40.1 |
| 9 | 10.7 | 32.7 | 40.2 | 41.1 | 40.7 | 42.5 | 41.2 | 40.4 | 39.8 |
| Ng | Np | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 2 | 59.7 | 59.2 | 59.1 | 58.8 | 59.3 | 59.6 | 59.7 | 59.4 | 59.4 |
| 3 | 65.8 | 65.2 | 65.3 | 65.5 | 64.7 | 65.2 | 65.5 | 65.4 | 65.5 |
| 4 | 67.6 | 67.6 | 67.1 | 67.6 | 67.5 | 67.5 | 67.7 | 67.5 | 68.2 |
| 5 | 68.8 | 68.6 | 69.1 | 69.2 | 69.1 | 69.3 | 69.2 | 69.2 | 69.4 |
| 6 | 68.7 | 69.4 | 68.6 | 68.5 | 68.7 | 69.8 | 69.2 | 69.3 | 69.5 |
| 7 | 68.7 | 69.9 | 69.0 | 70.0 | 67.7 | 69.4 | 69.2 | 69.3 | 69.5 |
| 8 | 68.9 | 68.8 | 68.5 | 69.4 | 69.0 | 68.2 | 68.6 | 69.1 | 69.0 |
| 9 | 68.2 | 69.0 | 69.2 | 68.5 | 68.9 | 68.8 | 68.5 | 67.8 | 69.0 |
| Ng | Np | |||
|---|---|---|---|---|
| 4 | 5 | 6 | 7 | |
| 4 | X | X | X | |
| 5 | X | X | X | |
| 6 | X | X | X | X |
| 7 | X | X | ||
| 8 | X | |||
| 9 | X | |||
| (Np, Ng) | Statistic | kvp | Tp | P10 | kvpg | Tpg | kvg | Tg | Pg0 | S0 | sRes | RMod |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| min | % | min | min | % | % | |||||||
| (6, 6) | Mean | 0.69 | 4.45 | 81.9 | 0.63 | 4.85 | 0.36 | 5.18 | 35.1 | 39.9 | 2.03 | 0.84 |
| Std. dev. | 1.49 | 3.16 | 7.7 | 0.36 | 3.06 | 0.68 | 2.11 | 7.0 | 5.9 | |||
| (4, 4) | Mean | 0.45 | 6.07 | 82.0 | 0.65 | 5.21 | 0.31 | 5.70 | 35.4 | 39.9 | 2.06 | 0.84 |
| Std. dev. | 0.90 | 3.12 | 7.6 | 0.37 | 3.15 | 0.69 | 1.82 | 7.1 | 5.6 |
| (Np, Ng) | Statistic | A1P1 | A2P1 | A1P1 + A2P1 | StdErrP1 | R | A1P | A2P | A1P + A2P | StdErrP | R | sResP1 | sResP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| % | % | % | % | % | % | % | % | % | % | ||||
| (6, 6) | Mean | 0.78 | 0.18 | 0.96 | 0.37 | 0.96 | 1.15 | −0.17 | 0.98 | 0.32 | 0.98 | 1.72 | 2.22 |
| Std. dev. | 0.14 | 0.13 | 0.06 | 0.28 | 0.27 | 0.02 | |||||||
| (4, 4) | Mean | 0.78 | 0.19 | 0.97 | 0.36 | 0.96 | 1.15 | −0.17 | 0.98 | 0.32 | 0.98 | 1.73 | 2.25 |
| Std. dev. | 0.14 | 0.13 | 0.06 | 0.28 | 0.28 | 0.02 |
| Pa | Pg0 | S0 | P10 |
|---|---|---|---|
| mm H2O | % | % | % |
| 250 | 31.2 | 45.3 | 78.1 |
| 275 | 34.4 | 40.9 | 81.3 |
| 300 | 37.5 | 36.5 | 84.5 |
| 325 | 40.4 | 32.1 | 87.6 |
| No | Setting | Value |
|---|---|---|
| 1 | Moving grate pressure set-point, SPa, mm H2O | 325 to 400 with step 25 |
| 2 | Minimum grate speed, SLow, % | 25 |
| 3 | Ng | 4 |
| 4 | kvg | 0.12 |
| 5 | Tg, min | 7 |
| 6 | Pg0, % | From Table 8 |
| 7 | S0, % | From Table 8 |
| 8 | Margin of disturbance of kvg, % | 10 |
| 9 | Margin of disturbance of Tg, % | 10 |
| 10 | Margin of disturbance of Pg0, % | 10 |
| 11 | Margin of disturbance of S0, % | 10 |
| 12 | kvpg | 0.59 |
| 13 | Tpg, min | 4.3 |
| 14 | Margin of disturbance of kvpg, % | 10 |
| 15 | Margin of disturbance of Tpg, % | 10 |
| 16 | Np | 4 |
| 17 | kvp | 0.26 |
| 18 | Tp, min | 5.2 |
| 19 | P10, % | From Table 8 |
| 20 | Margin of disturbance of kvp, % | 10 |
| 21 | Margin of disturbance of Tp, % | 10 |
| 22 | Margin of disturbance of P10, MP10, % | 20 |
| 23 | sResP, % | 2.25 |
| 24 | A1P | 1.15 |
| 25 | A2P | −0.17 |
| 26 | StdErrP | 0.32 |
| 27 | sResP1, % | 1.73 |
| 28 | A1P1 | 0.78 |
| 29 | A2P1 | 0.19 |
| 30 | StdErrP1 | 0.36 |
| 31 | Number of simulations for each PID set, NI | 200 |
| 32 | Sampling and actuation period, Ts, s | 20 |
| 33 | Min. points of load disturbance, Nmin − Nmin·Ts/60 = Tdist,min, min | 6 |
| 34 | Max. points of load disturbance, Nmax − Nmax·Ts/60 = Tdist,max, min | 15 |
| 35 | Total simulation time, min | 360 |
| Ms | kP | kI | kD |
|---|---|---|---|
| 1.25 | 0.676 | 0.026 | 0.5 |
| 1.25 | 0.734 | 0.029 | 1.5 |
| 1.30 | 0.809 | 0.032 | 1.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsamatsoulis, D. Optimizing the Control System of Clinker Cooling: Process Modeling and Controller Tuning. ChemEngineering 2021, 5, 50. https://doi.org/10.3390/chemengineering5030050
Tsamatsoulis D. Optimizing the Control System of Clinker Cooling: Process Modeling and Controller Tuning. ChemEngineering. 2021; 5(3):50. https://doi.org/10.3390/chemengineering5030050
Chicago/Turabian StyleTsamatsoulis, Dimitris. 2021. "Optimizing the Control System of Clinker Cooling: Process Modeling and Controller Tuning" ChemEngineering 5, no. 3: 50. https://doi.org/10.3390/chemengineering5030050
APA StyleTsamatsoulis, D. (2021). Optimizing the Control System of Clinker Cooling: Process Modeling and Controller Tuning. ChemEngineering, 5(3), 50. https://doi.org/10.3390/chemengineering5030050





