Abstract
In this paper, we present a methodological study of modelling red blood cells (RBCs) in shear-induced flows based on the discrete multiphysics (DMP) approach. The DMP is an alternative approach from traditional multiphysics based on meshless particle-based methods. The proposed technique has been successful in modelling multiphysics and multi-phase problems with large interfacial deformations such as those in biological systems. In this study, we present the proposed method and introduce an accurate geometrical representation of the RBC. The results were validated against available data in the literature. We further illustrate that the proposed method is capable of modelling the rupture of the RBC membrane with minimum computational difficulty.
1. Introduction
The human red blood cell (RBC; erythrocyte) is a homogeneous biconcave disk-like microparticle that is surrounded by a fluidic incompressible lipid bilayer membrane that is underpinned by a thin elastic cytoskeleton [1]. The membrane and its underlying cytoskeleton have been naturally selected to be sufficiently flexible to allow passage of the RBC through capillaries of 4 m diameter in all tissues; this is approximately half of the cell’s main diameter. The main physiological function of the RBC is the transfer of oxygen from the lungs to all tissues and the return of to the lungs where it is exhaled. The RBC actively metabolises glucose that provides free energy from its bond cleavage to phosphorylate ADP to make ATP, the ‘energy currency’ of the cell. In the RBC, an ionic disequilibrium exists across the membrane with a much higher concentration outside in the blood plasma, while inside the concentration of is relatively high. The steady-state of these concentrations is maintained by the membrane protein Na, K-ATPase that catalyses the hydrolysis of one molecule of ATP for three ion ejected and two taken up. The detailed kinetics of RBC metabolism and ATP turnover are encapsulated in a comprehensive computer model [2,3,4].
Other functions of the RBC are mooted to involve the transfer of ATP and ADP agents inward and outward in the cell to release various molecules in blood flow through cell deformation in shear-induced strain fields [5]. These purines are proposed by some to be key effectors of arteriolar smooth muscle tone and hence affect peripheral resistance to blood flow and thence blood pressure. The dynamics and deformation of the RBC in shear flows are crucial in numerous biomedical applications including the detection of diseases associated with tissue perfusion, the experimental separation of healthy cells from infected parasitised ones, and studying human metabolism in vivo, and using nuclear magnetic resonance spectroscopy (MRS) [6]. The cell might also undergo membrane rupture (haemolysis) under conditions of extreme deformation. To have a deep understanding of these cellular responses, the dynamics of the RBC require investigation.
Furthermore, mechanobiology is concerned with the relationship between cell shape and energy consumption. Experimental methods to study this interrelationship are few, but NMR spectroscopy of RBCs distorted in stretched or compressed hydrogels is one recent example in this field. Specifically, stretching human RBCs by a factor of two enhances their rate of glucose consumption by approximately the same factor [7]. Therefore, being able to model the extent of altered membrane geometry will be key to understanding the role of mechanical or flow induced shape changes of RBCs (and other cells) in whole body energy metabolism.
There are some notable examples of numerical modelling for investigating the complex fluid dynamics of the RBC in shear-induced flows. RBCs in this context have been modelled by many methods including the lattice Boltzmann method (LBM ) [8,9,10] and the finite element (FE) method [11,12,13] in which the fluid–solid interface is captured by the immersed boundary method (IBM). Particle-based methods such as the smoothed particle hydrodynamics (SPH) [14,15,16], discrete particle dynamics (DPD) [17], and moving-particle semi-implicit (MPS) [18] methods have also been used for modelling RBC shape in shear induced fluid flow.
The Lagrangian feature of particle-based methods is one of its advantages by which fluid–solid interfaces such as the RBC membrane can be explicitly captured. In all these methods, it is challenging to represent the RBC shape accurately. It is this that undergoes large deformations while leading to no structural damage. The RBC displays in-plane area incompressibility as observed in experimental studies [19,20].
In general, there are two main approaches to representing the RBC membrane, namely shell-based, and spring-based models. In the shell-based model [21], the membrane is represented by a zero-thickness quasi-two-dimensional structure. This view provides a continuum representation of the membrane that can be coupled with several constitutive laws including the neo-Hookean [22,23,24] and Skalak [13,25,26] laws for evaluating in-plane tension and transverse shear. A detailed comparison and investigation of the effect of the requisite constitutive laws has been conducted by Lac et al. [27] for spherical capsules under shear-induced deformations. On the other hand, spring-based models e.g., the lattice-spring model (LSM) and mass-spring model (MSM) represent the membrane through a (structured) geometrical network of points and particles that are inter-connected by means of virtual springs. In the latter approach, the mechanical response of the membrane depends on the geometry of the structured network (i.e., triangular, tetrahedral, etc.) and it is specified through mathematical correlations that relate the spring constant of the connecting bonds with the overall elastic properties of the membrane. For specifying the in-plane area incompressibility of the membrane in mathematical correlations, we can use linear models that employ Hookean spring characteristics [28], or nonlinear correlations that include virtual dampers [29], or angular springs [30,31]. In addition to these two main approaches (LSM and MSM), other models have also been used for capturing the deformation of the RBC membrane; these include an area-difference-elasticity-theory [32,33]; linear finite element (LFE) method [34], and high fidelity simulations of RBCs [35,36].
As mentioned above, the modelling of RBC behaviour under conditions of flow might also include the sporadic occurrence of haemolysis (membrane rupture) under specific conditions. Taking into account that haemolysis might occur in extreme conditions, a comprehensive model should be able to accommodate all these possible scenarios. On the other hand, and to the best of our knowledge, all models thus far in the literature are not fully comprehensive in this regard. Therefore, this motivated our use of hybrid multiphysics numerical modelling, which is fully capable of capturing all possible scenarios of the RBCs under a shear field.
Therefore, we present a methodological study of modelling RBCs in shear-induced flows based on using what we call the discrete multiphysics (DMP) approach [37,38,39]. DMP is an alternative approach from traditional multiphysics by combining particle-based methods, e.g., the SPH for solving fluid flow and the MSM for capturing the elastic deformation of flexible solid materials, and it has been particularly successful in modelling biological systems [40,41,42]. The SPH method is a Lagrangian particle-based technique, which was developed for astrophysical studies [43,44]. The method was later extended for modelling fluid flow [45,46]. In SPH modelling the fluid domain is discretised into Lagrangian computational particles that possess fluid properties viz. density, viscosity, and internal energy, while interacting with their neighbouring particles in a way that is described mathematically by a kernel function [47]. The Lagrangian nature of the SPH method makes it suitable for simulating systems that undergo large deformations, such as occur in free surface flows [46,48], droplet and bubble dynamics [49,50,51], and fluid–solid interactions [52,53]. Within the DMP framework, the MSM was used to generate the RBC membrane through a linear mathematical correlation. In order to accommodate haemolysis in our model, we extended the DMP by setting a limited strain threshold beyond which the virtual bonds, that connect the membrane particles are dispelled, thus representing membrane rupture.
2. Methodology
2.1. General Equations
An incompressible Newtonian fluid in laminar flow is governed by:
where is the velocity vector, while , , and p are the fluid properties density, kinematic viscosity, and pressure, respectively. is the material time derivative where t denotes time, and denotes denotes the volumetric body force.
We note once again that the present numerical approach was based on the DMP model [38], which combines the SPH method for modelling fluid flow, and the MSM for representing the elastic properties of membrane particles. It is relevant to outline these approaches along with how their coupling has been achieved mathematically.
2.2. The SPH Method
The governing equations of motion i.e., Equations (1) and (2) are solved by the SPH method over computational particles using a kernel function, . The kernel function, which can be concisely represented by , relates particle i with its neighbouring particle j [46,54], based on their distance , and the smoothing length, h as the horizon limit for the interactions with neighbouring particles. Figure 1 represents the interactions between two-dimensional SPH particles based on their relative proximity, through a smoothing kernel function. Among several kernel functions in the literature, the Lucy kernel function [44] was used in this study:
where and h) for three-dimensional simulations.
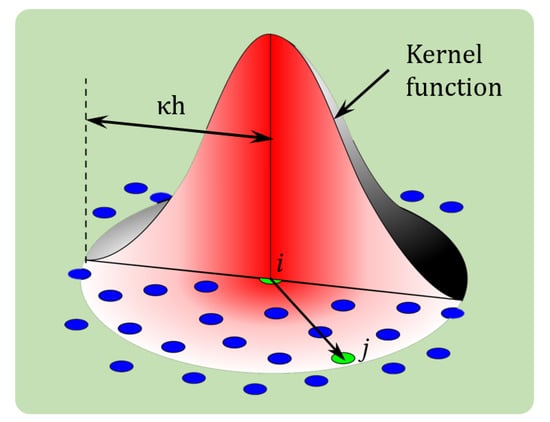
Figure 1.
Schematic of the SPH method representing the interaction between particles through the kernel function.
In the SPH method, any field variable f can be approximated using the summation over discrete particles as:
where and denote the mass and the number of computational neighboring particles for particle i. The SPH method discretizes the continuity and momentum equations, Equations (1) and (2) into the following form as:
In Equation (6), the first term is the pressure gradient and the second is the dissipation term that conforms to a laminar viscosity model [55]. To evaluate the pressure term in the SPH method, one may solve a Poisson equation to obtain an incompressible solution [50,56,57] or might consider a weakly compressible SPH (WCSPH) approach [48,58,59], in which the pressure is obtained by an equation of state (EOS) using density variations. We used this approach by using the so-called Tait EOS [47,48]:
where, is the reference speed of sound. In order to keep density variations below 1%, it is recommended that the speed of sound should be set at least one order of magnitude larger than the maximum velocity in the domain [45]. is the reference density (1000 ), and is empirically set to be 7 in this power law equation [45,46].
2.3. The MSM
As mentioned, the MSM [60], which is sometimes referred to as coarse grained molecular dynamics (CGMD) [38], was employed to implement elasticity of the RBC membrane. In the MSM [61], a network of harmonic bonds connects computational particles, allowing them to deform and stretch according to the Newtonian equations of motion using linear spring bonds. Figure 2 shows the structure of the MSM for a quasi-two-dimensional RBC membrane. To account for Hookean elasticity, harmonic bonds are used as follows:
where and are the coefficient and the equilibrium distance of Hookean springs, respectively. In this methodological approach, our emphasis is on the discretization and implementation of the model, so we adopted the linear Hookean model for the sake of simplicity and lower computational costs, while other nonlinear models can be easily replaced without further difficulties. Another advantage of the MSM is inherited in the modelling of membrane rupture, for which we nullified the springs once their length exceed the ultimate threshold set equal to 1.05 of their initial value.
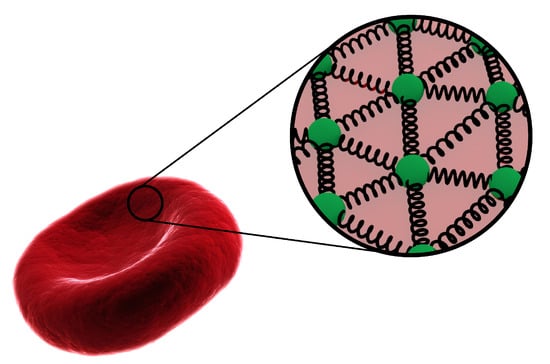
Figure 2.
Schematic of the MSM representing the network of interconnected particles via spring network.
2.4. Coupling of SPH and MSM
To model the physical properties at the fluid–solid interface, we considered three types of boundary conditions to be taken into consideration [62], i.e., the no-penetration, the no-slip, and continuity of stresses at the interface. In continuum mechanics these conditions are often represented, respectively, as:
and
where represents the unit normal vector. and denote the solid displacement and fluid velocity, respectively, while the solid and fluid stresses are represented by and . Within the DMP framework, we considered ghost SPH particles, which are assigned to MSM particles at the fluid–solid interface. To satisfy all three boundary conditions, these particles have dual identity; they interact with the SPH fluid particles for solving fluid properties but they interact with other MSM particles as membrane particles.
2.5. Numerical Algorithm
The velocity verlet (VV) algorithm was used to integrate over time by using a first-order Euler approach with a variable time step, specified by the following stability condition, . Here, represents the dynamic viscosity equal to and provided satisfactory results [38]. Considering that and superscripts denote variables at the intermediate and nth time step, the particle velocities were calculated using the VV algorithm as:
Then, particle densities were calculated according to:
In the above equation, is the rate of density variations according to Equation (5), in which the density should be updated based on the velocity difference between the particles . However, using causes numerical instabilities arising from the lag of the velocity in the VV algorithm. So, we use an extrapolated velocity in the calculation of the rate of density variations, which can be represented as:
where . Once particle velocities are updated, computational particles are moved to their new positions using:
Then, , and were calculated at the time step using Equations (5) and (6), respectively. Finally, the velocity and density were calculated at the time step, respectively, as:
and,
We have extensively used the above-mentioned numerical algorithm in our previous studies [28,63,64] where we can refer interested readers to for more detailed discussions.
3. Problem Set-Up
The literature contains several models of the geometry of the RBC, including the frequently cited one by Evans et al. [25]. In this study, we used a model which we consider represents the dimples of the biconcave disc more accurately. The model consists of a set of three parametric equations that involve Jacobi elliptic functions [65] as:
and
where, , , and are the Jacobi elliptic functions. The coefficient A was defined by using three geometrical distances obtained from experimental electron microscope measurements.
This was used to define other intermediate parameters. Also, and,
The key specific lengths of the RBC are the cell diameter at the plane splitting the biconcave into two cup-shaped halves m, the thickness of the cell at the thickest position (like the width of the tyre on a car wheel) m, and the thickness at the centre of the dimple, m. Considering these parameters, the surface area and volume of the RBC are found to be equal to fL and m respectively [65]. Figure 3 shows the shape of the RBC in a two dimensional projection of the three-dimensional body.
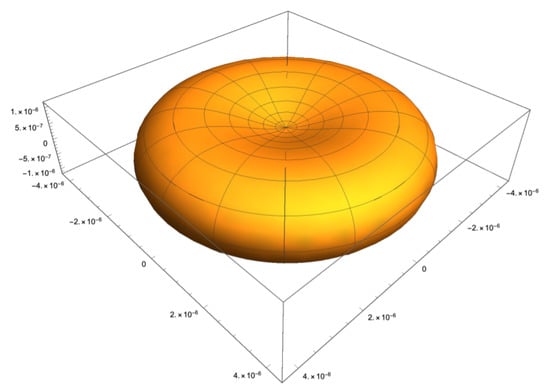
Figure 3.
A representative illustration of an RBC.
In the present analysis the RBC was represented by a hybrid model, as described in Section 2 by which the SPH was used for modelling the fluid flow, and the RBC membrane was simulated by the MSM. In order to apply the surface area incompressibility of the membrane (conservation of area), the spring constants were taken to be sufficiently large so that a change in the net surface area was minimized. The spring constant could not be taken to be very large since large spring constants resulted in numerical instabilities. Here, the spring constant was set to . The shear modulus of the RBC was tuned by adjusting the angular spring constant. It has been seen that the angular constant of led to convincing simulated behaviours in shear fields.
Figure 4 represents the 3D simulation domain with height, width, and depth of H, W, and D, respectively. The top and bottom walls abide the no-slip boundary conditions, while periodic boundary conditions were implemented on the rest of boundaries. To maintain a constant shear rate , the top and bottom boundaries were given with velocity U and , respectively. The RBC was placed at the centre, equidistant from all domain boundaries. A uniformly-spaced Cartesian grid was used to populate the domain with fluid particles. All in all, there were four different types of particles in this model: (1) particles of the top boundary (white); (2) particles of the bottom boundary (red); (3) the RBC particles (blue); (4) the fluid particles (green), as illustrated in Figure 4. In total, the simulation domain contained more than one million computational particles comprising all four particle types. It should be noted that a particle-resolution study was carried out for four different particle resolutions in a shear flow [28] in our previous study, and it was observed that the results and hydrodynamics did not improve significantly beyond the resolution that is equivalent to the one we used in this study. The test-case was simulated on the UK’s national super computing facilities (ARCHER with 2.7 GHz, 12-core Intel Xeon E5-2697). The computational cost was 23 h of wall-time on approximately 1500 CPU cores (MPI) for each test-case.
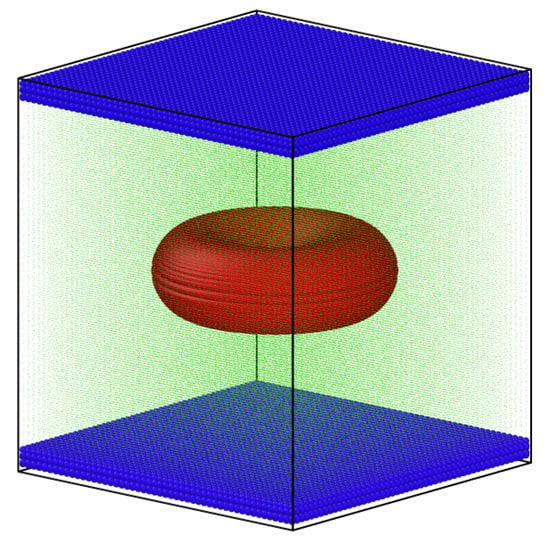
Figure 4.
Computational domain for cell under shear rate; the RBC is illustrated by red particles, the top and bottom boundaries are blue, and the fluid particles are green (different particle size, particularly for green and red particles, is a post-processing trick for better illustration and has no further modelling or physical interpretations).
The domain undergoes shear in the x-direction by moving the top and bottom boundary particles in opposite directions. Subsequently, the shear imposed RBC deformation are described and analysed in the next section.
4. Results
In this section, we show that the presented model was capable of capturing the dynamics of the RBC with superior features, relative to other models reported in the literature. Thus, we show how the current model could predict membrane rupture that was induced by extreme flow conditions.
In order to characterise the deformation of the RBC, a quantitative measure was introduced. Specifically, this was the deformation index, , where and were the length of the RBC in the plane passing through its origin in the direction of the main axis, and its transverse direction, respectively. Figure 5 represents the variation of the deformation index for three capillary numbers with respect to dimensionless simulation time and compares them with the numerical data in the literature [13]. It was shown that the present model produced accurate results with respect to the models in the literature and it captured the frequency of deformation with the sinusoidal variations of flow rate. Any discrepancy in the results was due to the different geometries used to model a RBC; these produced a larger amplitude in the sinusoidal variation of the deformation index [13].
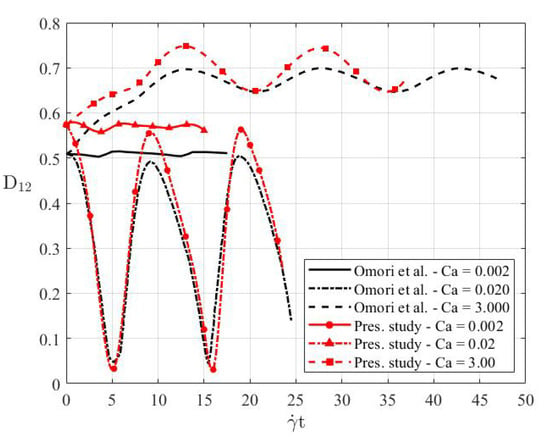
Figure 5.
Validation of the present RBC model with those of Omori et al. [13].
Considering the variations of the deformation index shown in Figure 6, it was interesting to note that the RBC underwent a tumbling motion, and it rotated around its centre of mass when the shear rates were symmetrical. This is the reason why there was a sinusoidal trend in the deformation index. At small capillary numbers, the RBC did not deform very much, and accordingly the deformation index exhibited minimal variation over time. The variation of the deformation index was restricted between for the smallest capillary number. At moderate capillary numbers i.e., , the deformation index indicated sinusoidal behaviour of large amplitude. This was interpreted to be due to the resistance of the RBC against the applied shear. When the applied shear met the RBC when it was oriented such that its main diameter was along the flow direction, the RBC geometry was similar to its undisturbed shape. This was the point in time when the deformation index was at its peak value. On the other hand, when the main diameter of the RBC was transverse to the flow direction, the deformation index decreased considerably. For large capillary numbers, the shear rate was sufficiently high to stretch the RBC along the direction of shear. The variation of the deformation index with such high capillary numbers was also due to the re-orientation of the RBC during its tumbling motion.
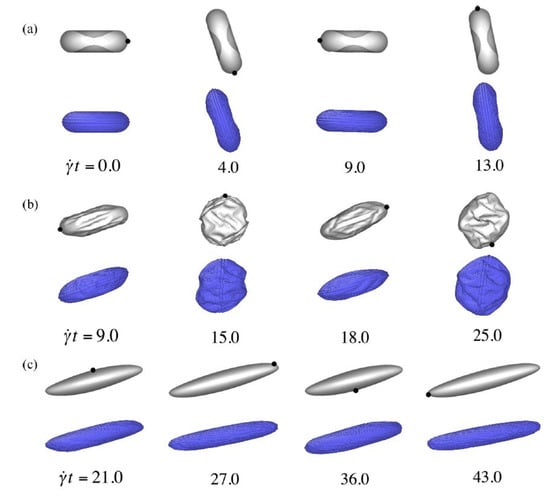
Figure 6.
Validation of the present RBC model with those of Omori et al. [13] for three test-cases (a) Ca = 0.002, (b) Ca = 0.02, and (c) Ca = 3.0 at different dimensionless times.
Figure 6 represents the RBC shape at different simulation times for three capillary numbers corresponding to Figure 6. Our numerical model was further compared with data in the literature [13] and it showed that the shape of the RBC was accurately captured. The shape of the RBC remained almost undisturbed during its tumbling motion. For moderate values of capillary number, the RBC was similar in shape to its undisturbed form whereby its major diameter was along the direction of the applied shear. For large capillary numbers, the RBC was stretched along it direction of shear.
In many applications, once RBCs are exposed to high shear rates, the membranes of unhealthy cells might rupture. To simulate this biomedical eventuality is difficult but our method is one that can model the responses under shear of healthy cells and unhealthy or parasite-infected ones. On the other hand, current numerical techniques generally have systemic problems for modelling the membrane rupture of RBCs under shear fields. In summary, we present in Figure 7 membrane rupture of a RBC under flow-induced shear. It was clear that rupture could occur at relatively low shear rates in contrast to when the RBC was exposed to extreme shear such as those in Figure 5.
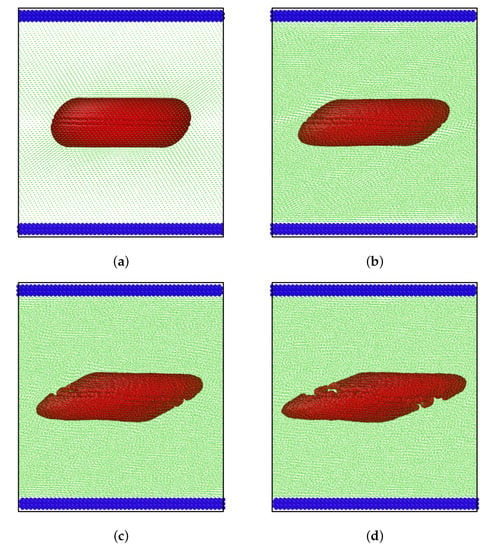
Figure 7.
Rupture of the membrane under shear (Ca = 2.0) at different dimensionless times (a) = 0, (b) = 2, (c) = 4, and (d) = 6.
The modelling is a numerical depiction of RBCs under shear and serves to illustrate its capabilities for applications to particles of other geometries and elastic properties. In other words, in order to simulate realistic membrane rupture, careful experimental analysis and membrane characterisation were required to determine the threshold strain that must be in the numerical model. These characterisations lie in the realm of cellular biophysics of RBCs (and other cell types) that will be developed as we refine the current numerical modelling to help interpret experimental data.
5. Conclusions
In this study, we employed a novel numerical technique using the DMP model for simulating the deformation of RBCs in shear-induced flows. This methodological study describes a simple but accurate and flexible numerical technique for simulating a myriad of problems involving RBCs in in vivo and in vitro applications. In this study, we discussed the methodology in details from the mathematical, numerical, and technical perspectives, describing the governing equations, numerical algorithm, and implementation techniques.
The model has a Lagrangian particle-based nature and utilised a complex mathematical formulation derived from the Jacobi elliptic functions, which provided an accurate representation of the RBC geometry. Then, the proposed mathematical formulation was linked to the MSM, which modelled the RBC through a complex network of interconnected particles on its interface. The proposed model is employed for modelling RBC deformation under shear at various capillary numbers. It was observed that RBCs represented a sinusoidal behaviour in their deformation index factor which is accurately comparable with available data in the literature.
We have further extended the model to simulate the rupture of the RBC’s membrane under extremely large shear rates, which could be used in many biological and pharmaceutical applications. The membrane rupture was implemented via breaking the spring bonds between particles of which their deformation exceeded a certain strain threshold. Another advantage of the proposed method is that it can be easily extended to other complex physics, and applied to other real-world problems.
Author Contributions
Conceptualization, P.K. and A.A.; methodology, A.R., P.K. and A.A.; software, A.R. and A.A.; validation, A.R.; formal analysis, A.R.; investigation, A.R.; resources, M.B. and A.A.; writing—original draft preparation, A.R.; writing—review and editing, P.K. and A.A.; visualization, A.R.; supervision, A.A.; project administration, A.A.; funding acquisition, M.B. and A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the UK Engineering and Physical Sciences Research Council (EPSRC) under Grant No. EP/N033698/1. Philip Kuchel acknowledges an Australian Research Council Discovery Project Grant, DP190100510. Amin Rahmat acknowledges a financial support from the Birmingham International Engagement Fund (BIEF).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
CGMD: coarse grained molecular dynamics; DMP: discrete multi-physics; DPD: discrete particle dynamics; EOS: equation of state; FE: finite element; IBM: immersed boundary method; ISPH: incompressible smoothed particle hydrodynamics; LBM: lattice Boltzmann method; LFE: linear finite element; LSM: lattice spring model; MSM: mass spring model; MPS: moving-particle semi-implicit; SPH: smoothed particle hydrodynamics; VV: velocity verlet; WCSPH: weakly compressible smoothed particle hydrodynamics.
References
- Mohandas, N.; Evans, E. Mechanical properties of the red cell membrane in relation to molecular structure and genetic defects. Annu. Rev. Biophys. Biomol. Struct. 1994, 23, 787–818. [Google Scholar] [CrossRef] [PubMed]
- Mulquiney, P.J.; Bubb, W.A.; Kuchel, P.W. Model of 2, 3-bisphosphoglycerate metabolism in the human erythrocyte based on detailed enzyme kinetic Equations (1): In vivo kinetic characterization of 2, 3-bisphosphoglycerate synthase/phosphatase using 13C and 31P NMR. Biochem. J. 1999, 342, 567–580. [Google Scholar] [CrossRef]
- Mulquiney, P.J.; Kuchel, P.W. Model of 2, 3-bisphosphoglycerate metabolism in the human erythrocyte based on detailed enzyme kinetic equations: Equations and parameter refinement. Biochem. J. 1999, 342, 581–596. [Google Scholar] [CrossRef] [PubMed]
- Mulquiney, P.J.; Kuchel, P.W. Model of 2, 3-bisphosphoglycerate metabolism in the human erythrocyte based on detailed enzyme kinetic equations: Computer simulation and metabolic control analysis. Biochem. J. 1999, 342, 597–604. [Google Scholar] [CrossRef]
- Wan, J.; Ristenpart, W.D.; Stone, H.A. Dynamics of shear-induced ATP release from red blood cells. Proc. Natl. Acad. Sci. USA 2008, 105, 16432–16437. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shishmarev, D.; Kuchel, P.W.; Pagès, G.; Wright, A.J.; Hesketh, R.L.; Kreis, F.; Brindle, K.M. Glyoxalase activity in human erythrocytes and mouse lymphoma, liver and brain probed with hyperpolarized 13 C-methylglyoxal. Commun. Biol. 2018, 1, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Kuchel, P.W.; Shishmarev, D. Accelerating metabolism and transmembrane cation flux by distorting red blood cells. Sci. Adv. 2017, 3, eaao1016. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dupin, M.; Halliday, I.; Care, C.; Munn, L. Lattice Boltzmann modelling of blood cell dynamics. Int. J. Comput. Fluid Dyn. 2008, 22, 481–492. [Google Scholar] [CrossRef]
- Shi, X.; Lin, G.; Zou, J.; Fedosov, D.A. A lattice Boltzmann fictitious domain method for modeling red blood cell deformation and multiple-cell hydrodynamic interactions in flow. Int. J. Numer. Methods Fluids 2013, 72, 895–911. [Google Scholar] [CrossRef]
- Zhang, J. Lattice Boltzmann method for microfluidics: Models and applications. Microfluid. Nanofluid. 2011, 10, 1–28. [Google Scholar] [CrossRef]
- Chen, M.; Boyle, F.J. Investigation of membrane mechanics using spring networks: Application to red-blood-cell modelling. Mater. Sci. Eng. C 2014, 43, 506–516. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eggleton, C.D.; Popel, A.S. Large deformation of red blood cell ghosts in a simple shear flow. Phys. Fluids 1998, 10, 1834–1845. [Google Scholar] [CrossRef] [PubMed]
- Omori, T.; Ishikawa, T.; Barthès-Biesel, D.; Salsac, A.V.; Imai, Y.; Yamaguchi, T. Tension of red blood cell membrane in simple shear flow. Phys. Rev. E 2012, 86, 056321. [Google Scholar] [CrossRef] [Green Version]
- Hosseini, S.M.; Feng, J.J. A particle-based model for the transport of erythrocytes in capillaries. Chem. Eng. Sci. 2009, 64, 4488–4497. [Google Scholar] [CrossRef]
- Freund, J.B. Numerical simulation of flowing blood cells. Annu. Rev. Fluid Mech. 2014, 46, 67–95. [Google Scholar] [CrossRef] [Green Version]
- Wu, T.; Feng, J.J. Simulation of malaria-infected red blood cells in microfluidic channels: Passage and blockage. Biomicrofluidics 2013, 7, 044115. [Google Scholar] [CrossRef] [Green Version]
- Boryczko, K.; Dzwinel, W.; Yuen, D.A. Dynamical clustering of red blood cells in capillary vessels. J. Mol. Model. 2003, 9, 16–33. [Google Scholar] [CrossRef] [PubMed]
- Tsubota, K.; Wada, S.; Yamaguchi, T. Particle method for computer simulation of red blood cell motion in blood flow. Comput. Methods Programs Biomed. 2006, 83, 139–146. [Google Scholar] [CrossRef]
- Hochmuth, R.; Mohandas, N. Uniaxial loading of the red-cell membrane. J. Biomech. 1972, 5, 501–509. [Google Scholar] [CrossRef]
- Hochmuth, R.; Wiles, H.; Evans, E.; McCown, J. Extensional flow of erythrocyte membrane from cell body to elastic tether. II. Experiment. Biophys. J. 1982, 39, 83–89. [Google Scholar] [CrossRef] [Green Version]
- Pozrikidis, C. Effect of membrane bending stiffness on the deformation of capsules in simple shear flow. J. Fluid Mech. 2001, 440, 269–291. [Google Scholar] [CrossRef]
- Zhang, J.; Johnson, P.C.; Popel, A.S. An immersed boundary lattice Boltzmann approach to simulate deformable liquid capsules and its application to microscopic blood flows. Phys. Biol. 2007, 4, 285. [Google Scholar] [CrossRef] [PubMed]
- Bagchi, P. Mesoscale simulation of blood flow in small vessels. Biophys. J. 2007, 92, 1858–1877. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barthes-Biesel, D.; Diaz, A.; Dhenin, E. Effect of constitutive laws for two-dimensional membranes on flow-induced capsule deformation. J. Fluid Mech. 2002, 460, 211–222. [Google Scholar] [CrossRef]
- Evans, E.A.; Skalak, R. Mechanics and Thermodynamics of Biomembranes; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar]
- Sui, Y.; Chew, Y.; Roy, P.; Cheng, Y.; Low, H. Dynamic motion of red blood cells in simple shear flow. Phys. Fluids 2008, 20, 112106. [Google Scholar] [CrossRef]
- Lac, E.; Barthes-Biesel, D.; Pelekasis, N.; Tsamopoulos, J. Spherical capsules in three-dimensional unbounded Stokes flows: Effect of the membrane constitutive law and onset of buckling. J. Fluid Mech. 2004, 516, 303–334. [Google Scholar] [CrossRef] [Green Version]
- Rahmat, A.; Barigou, M.; Alexiadis, A. Deformation and rupture of compound cells under shear: A discrete multiphysics study. Phys. Fluids 2019, 31, 051903. [Google Scholar] [CrossRef]
- Secomb, T.W.; Styp-Rekowska, B.; Pries, A.R. Two-dimensional simulation of red blood cell deformation and lateral migration in microvessels. Ann. Biomed. Eng. 2007, 35, 755–765. [Google Scholar] [CrossRef]
- Fedosov, D.A.; Caswell, B.; Karniadakis, G.E. A multiscale red blood cell model with accurate mechanics, rheology, and dynamics. Biophys. J. 2010, 98, 2215–2225. [Google Scholar] [CrossRef] [Green Version]
- Fedosov, D.A.; Peltomäki, M.; Gompper, G. Deformation and dynamics of red blood cells in flow through cylindrical microchannels. Soft Matter 2014, 10, 4258–4267. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ziherl, P.; Svetina, S. Nonaxisymmetric phospholipid vesicles: Rackets, boomerangs, and starfish. EPL Europhys. Lett. 2005, 70, 690. [Google Scholar] [CrossRef]
- Svetina, S.; Ziherl, P. Morphology of small aggregates of red blood cells. Bioelectrochemistry 2008, 73, 84–91. [Google Scholar] [CrossRef] [PubMed]
- MacMeccan, R.M.; Clausen, J.; Neitzel, G.; Aidun, C. Simulating deformable particle suspensions using a coupled lattice-Boltzmann and finite-element method. J. Fluid Mech. 2009, 618, 13. [Google Scholar] [CrossRef]
- Janoschek, F.; Toschi, F.; Harting, J. Simplified particulate model for coarse-grained hemodynamics simulations. Phys. Rev. E 2010, 82, 056710. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Melchionna, S. A Model for Red Blood Cells in Simulations of Large-scale Blood Flows. Macromol. Theory Simul. 2011, 20, 548–561. [Google Scholar] [CrossRef] [Green Version]
- Alexiadis, A. A smoothed particle hydrodynamics and coarse-grained molecular dynamics hybrid technique for modelling elastic particles and breakable capsules under various flow conditions. Int. J. Numer. Methods Eng. 2014, 100, 713–719. [Google Scholar] [CrossRef]
- Alexiadis, A. The discrete multi-hybrid system for the simulation of solid-liquid flows. PLoS ONE 2015, 10, e0124678. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alexiadis, A. A new framework for modelling the dynamics and the breakage of capsules, vesicles and cells in fluid flow. In Proceedings of the Iutam Symposium on Dynamics of Capsules, Vesicles and Cells in Flow, Rio de Janeiro, Brazil, 8–12 September 2015; Barthes Biesel, D., Blyth, M.G., Salsac, A.V., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 80–88. [Google Scholar]
- Ariane, M.; Vigolo, D.; Brill, A.; Nash, F.; Barigou, M.; Alexiadis, A. Using Discrete Multi-Physics for studying the dynamics of emboli in flexible venous valves. Comput. Fluids 2018, 166, 57–63. [Google Scholar] [CrossRef]
- Mohammed, A.M.; Ariane, M.; Alexiadis, A. Using Discrete Multiphysics Modelling to Assess the Effect of Calcification on Hemodynamic and Mechanical Deformation of Aortic Valve. ChemEngineering 2020, 4, 48. [Google Scholar] [CrossRef]
- Schütt, M.; Stamatopoulos, K.; Simmons, M.; Batchelor, H.; Alexiadis, A. Modelling and simulation of the hydrodynamics and mixing profiles in the human proximal colon using Discrete Multiphysics. Comput. Biol. Med. 2020, 121, 103819. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed Particle Hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Monaghan, J.J. Simulating free surface flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Kocharyan, A. SPH simulation of multi-phase flow. Comput. Phys. Commun. 1995, 87, 225–235. [Google Scholar] [CrossRef]
- Monaghan, J.; Kos, A. Solitary waves on a Cretan beach. J. Waterw. Port. Coast. Ocean Eng. 1999, 125, 145–155. [Google Scholar] [CrossRef]
- Ozbulut, M.; Tofighi, N.; Goren, O.; Yildiz, M. Investigation of Wave Characteristics in Oscillatory Motion of Partially Filled Rectangular Tanks. J. Fluids Eng. 2018, 140, 041204. [Google Scholar] [CrossRef]
- Rahmat, A.; Tofighi, N.; Yildiz, M. Numerical simulation of the electrohydrodynamic effects on bubble rising using the SPH method. Int. J. Heat Fluid Flow 2016, 62, 313–323. [Google Scholar] [CrossRef]
- Rahmat, A.; Tofighi, N.; Shadloo, M.; Yildiz, M. Numerical simulation of wall bounded and electrically excited Rayleigh-Taylor Instability using incompressible Smoothed Particle Hydrodynamics. Colloids Surf. A Physicochem. Eng. Asp. 2014, 460, 60–70. [Google Scholar] [CrossRef]
- Shadloo, M.; Rahmat, A.; Yildiz, M. A Smoothed Particle Hydrodynamics study on the electrohydrodynamic deformation of a droplet suspended in a neutrally buoyant Newtonian fluid. Comput. Mech. 2013, 52, 693–707. [Google Scholar] [CrossRef]
- Rahmat, A.; Barigou, M.; Alexiadis, A. Numerical simulation of dissolution of solid particles in fluid flow using the SPH method. Int. J. Numer. Methods Heat Fluid Flow 2019. [Google Scholar] [CrossRef]
- Rahmat, A.; Nasiri, H.; Goodarzi, M.; Heidaryan, E. Numerical investigation of anguilliform locomotion by the SPH method. Int. J. Numer. Methods Heat Fluid Flow 2019. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Lattanzio, J.C. A refined particle method for astrophysical problems. Astron. Astrophys. 1985, 149, 135–143. [Google Scholar]
- Morris, J.P.; Fox, P.J.; Zhu, Y. Modeling low Reynolds number incompressible flows using SPH. J. Comput. Phys. 1997, 136, 214–226. [Google Scholar] [CrossRef]
- Tofighi, N.; Ozbulut, M.; Rahmat, A.; Feng, J.; Yildiz, M. An incompressible Smoothed Particle Hydrodynamics method for the motion of rigid bodies in fluids. J. Comput. Phys. 2015, 297, 207–220. [Google Scholar] [CrossRef]
- Morris, J.P. Simulating surface tension with Smoothed Particle Hydrodynamics. Int. J. Numer. Methods Fluids 2000, 33, 333–353. [Google Scholar] [CrossRef]
- Fatehi, R.; Rahmat, A.; Tofighi, N.; Yildiz, M.; Shadloo, M. Density-Based Smoothed Particle Hydrodynamics Methods for Incompressible Flows. Comput. Fluids 2019, 185, 22–33. [Google Scholar] [CrossRef]
- Hopp-Hirschler, M.; Shadloo, M.S.; Nieken, U. A Smoothed Particle Hydrodynamics approach for thermo-capillary flows. Comput. Fluids 2018, 176, 1–19. [Google Scholar] [CrossRef]
- Kilimnik, A.; Mao, W.; Alexeev, A. Inertial migration of deformable capsules in channel flow. Phys. Fluids 2011, 23, 123302. [Google Scholar] [CrossRef]
- Lloyd, B.; Székely, G.; Harders, M. Identification of spring parameters for deformable object simulation. IEEE Trans. Vis. Comput. Graph. 2007, 13. [Google Scholar] [CrossRef]
- Esmon, C.T. Basic mechanisms and pathogenesis of venous thrombosis. Blood Rev. 2009, 23, 225–229. [Google Scholar] [CrossRef] [Green Version]
- Rahmat, A.; Meng, J.; Emerson, D.; Wu, C.Y.; Barigou, M.; Alexiadis, A. A practical approach for extracting mechanical properties of microcapsules using a hybrid numerical model. Microfluid. Nanofluid. 2021, 25, 1–17. [Google Scholar] [CrossRef]
- Rahmat, A.; Weston, D.; Madden, D.; Usher, S.; Barigou, M.; Alexiadis, A. Modeling the agglomeration of settling particles in a dewatering process. Phys. Fluids 2020, 32, 123314. [Google Scholar] [CrossRef]
- Kuchel, P.W.; Fackerell, E.D. Parametric-equation representation of biconcave erythrocytes. Bull. Math. Biol. 1999, 61, 209–220. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).