Abstract
The droplet deformation in dispersing units of high-pressure homogenizers (HPH) is examined experimentally and numerically. Due to the small size of common homogenizer nozzles, the visual analysis of the transient droplet generation is usually not possible. Therefore, a scaled setup was used. The droplet deformation was determined quantitatively by using a shadow imaging technique. It is shown that the influence of transient stresses on the droplets caused by laminar extensional flow upstream the orifice is highly relevant for the droplet breakup behind the nozzle. Classical approaches based on an equilibrium assumption on the other side are not adequate to explain the observed droplet distributions. Based on the experimental results, a relationship from the literature with numerical simulations adopting different models are used to determine the transient droplet deformation during transition through orifices. It is shown that numerical and experimental results are in fairly good agreement at limited settings. It can be concluded that a scaled apparatus is well suited to estimate the transient droplet formation up to the outlet of the orifice.
1. Introduction
The break-up of tiny droplets due to the action of a flow field and instabilities has been widely studied, as this process is very important in many industrial sectors. The beginnings of the investigations go back to the investigations of Taylor in 1934 [1]. Among the many investigations carried out, a distinction can be made between studies dealing with the integral process of emulsification, where, for example, correlations between the energy input and the resulting drop size are obtained, or studies focusing on the individual processes of single drop break-up under different conditions. The integral correlation approaches are important for the industrial design of HPH, as this empirical approach leads to the desired droplet distribution, even without knowing the mechanisms responsible for the break-up in all its details. Due to the complexity of the drop break-up mechanism, technical designs are usually carried out empirically using integral correlation approaches [2].
The phenomenological investigations of the droplet breakup can be divided into different fields of application, but also depending on the flow regime. When classifying the investigations according to different flow regimes, most investigations fall into the group of investigations on laminar flows where the stresses are in dynamic equilibrium with the deformation of the drop. The aim of these investigations is to determine the stress limits of the different forms of break-up in dependency on the material properties [3]. In general, it is assumed that a drop can be stressed up to a critical capillary number [4]. Much more complex are investigations in the turbulent regime, which is usually present in economically relevant homogenization plants. Under these conditions, it is much more difficult to determine critical stress limits, since drops can be attacked super critically without significant droplet deformation if the time periods are too short to cause drop break-up. Furthermore individual processes may overlap so that clear relationships between cause and effect are difficult to establish.
To resolve the droplet break-up under realistic conditions measurements using imaging techniques [5,6,7] are well suited. These investigations have greatly contributed to the current understanding of drop break-up as individual processes can be clearly identified and understood. However, it is usually difficult to apply imaging techniques in realistic homogenization processes, because the experimental conditions, e.g., very high pressure and small apparatus dimensions, hardly allow this, as the imaging of small objects is diffraction limited. In order to make investigations nevertheless possible, plants need to be scaled up so that a geometric imaging of the processes becomes possible. Innings and Trägardh [8], for example, carried out investigations in a two-dimensional flat valve model that had two optical accesses. Within the gap of the valve, an elongation of the drops could be observed. Additionally, the break-up of very coarse droplets in a turbulent flow could be shown. These measurements allowed the breakup area to be located behind the constriction. Kolb et al. [5] carried out investigations in a scaled orifice unit. Due to the high optical accessibility, the drop could be detected before, in and after the orifice by means of a high-speed camera. The images show an elongation of the drop in the orifice to a cylindrical filament, which is split into many secondary drops behind the orifice. Kelemen et al. [9] performed extensive experimental work with appropriate optical access to the breakup process of primary droplets in homogenizer orifices. Depending on the conditions as, e.g., viscosity ratio of the phases, Weber- and Reynolds-numbers of the main flow, different behavior of the transient deformation has been observed. In practically any case, primary droplets are elongated to a greater or lower extent and deformed to threads at sufficient loads. For low viscosity ratios and low Reynolds numbers, threads were observed falling apart far downstream by the Rayleigh mechanism. Further observations revealed a mostly turbulent wake-zone behind the orifice also influencing the subsequent breakup process. Areas close to the center (laminar core region of the free jet) only undergo turbulent dispersion after some running length while areas closer to the border of the free jet (turbulent shear-layer) emerging from the orifice show stochastic deformations earlier in the turbulent shear layer. Comparable observations were reported in Budde et al. [10]. These investigations were carried out in a large scaled orifice unit in order to better observe the phenomena of drop break-up. They also described for the first time a set of six independent, dimensionless ratios that must be considered when scaling or comparing drop break-up descriptions.
T Reynolds number () is calculated with the diameter of the orifice (), the pressure loss across the orifice () and the density () and viscosity () of the continuous phase (index c). The pressure ratio describes the ratio of the external forces, which are characterized by the pressure drop across the orifice plate with the orifice diameter, and the internal forces, which are influenced by the interfacial tension (). The viscosity ratio () and density ratio () are calculated from the viscosity and density of the disperse (index d) and continuous phase. The drop size ratio () relates the primary droplet size of an initially spherical droplet to the orifice diameter. The channel size ratio () compares the diameter of the outlet channel () behind the orifice with low ambient pressure and also the region were droplet break up takes place to the orifice diameter.
Besides integral measurements and correlations to drop break-up as well as optical measurement methods to improve the understanding of the individual processes, numerical simulations have been also carried out [11,12] and showed that the duration of deforming shear forces is significant and that the deforming energy is temporally stored as surface energy. Thanks to ever more powerful computer capacities, more and more flow phenomena, both stationary and transient, can be simulated numerically with increasing accuracy. The simulation of multi-phase processes is also becoming increasingly accurate, although the underlying models must be validated in part through experimentation.
Inspired by previous investigations, a scaled experimental setup was designed, fabricated and qualified to examine systematically with high spatial and temporal resolution the effect of transient drop elongation in concentric orifices on the droplet beak-up. The comparability of the experimental setup between the original scale with micro-scale orifice dimensions and the enlarged experimental setup, in which optical measurements are much easier, can be found in Preiss et al. [13].
Due to the geometric scaling, the orifice diameter and the channel dimensions before and after the orifice were enlarged. In addition, the primary droplet diameter was adapted. In order to keep the dimensionless numbers from Equations (1)–(6) constant, the material parameters (density, viscosity and interfacial tension) were adjusted by selecting very specific material formulations.
Furthermore numerical models were used to describe the observed phenomena. Even though the basic behavior of droplets passing through orifices has been observed in the past with large scaled devices, several questions are still to be solved. Many observations have been performed with pre-emulsions containing droplets of different size. The attribution of the results, i.e., the secondary drop sizes to different size classes of primary droplets however is difficult. Therefore, first issues deal with the size of primary droplets and their response to the load when exposed to extensional flow in front of the orifice and to turbulence behind the orifice. Even though there were hints about the effect of local transition trajectories through the device on the breakup process, systematic observations are still outstanding.
2. Materials and Methods
2.1. Experimental Setup
The experimental investigations on drop elongation during homogenization were performed with orifice plates. The orifice has a circular cross-section and is scaled with a scale factor of 50 with reference to a typical HPH. A detailed description of the test facility can be found in Mutsch and Kähler [14]. The orifice plate has a diameter of 10 mm. In order to make the results comparable to classical HPH, not only the geometry was scaled, but also the choice of liquids and the operating parameters were adjusted. A detailed description of the scaling can be found in Preiss et al. [13]. As a result of the scaling, the operating pressure decreases to a fraction of the original operating pressure. This makes it possible to build the measuring section out of glass or acrylic glass, so that optical measurements are possible without simplification or modification of the flow chamber. In addition, the flow velocity decreases due to the reduced operating pressure, so that time-resolved measurements can be carried out with high-speed cameras. Figure 1 shows the measuring section. The dimensions of the orifice plate shown in Figure 2 correspond to the orifice diameter of 10 mm.
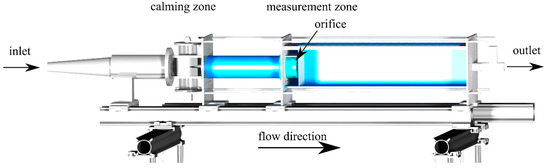
Figure 1.
Schematic of the homogenization setup in the scaled experiments.
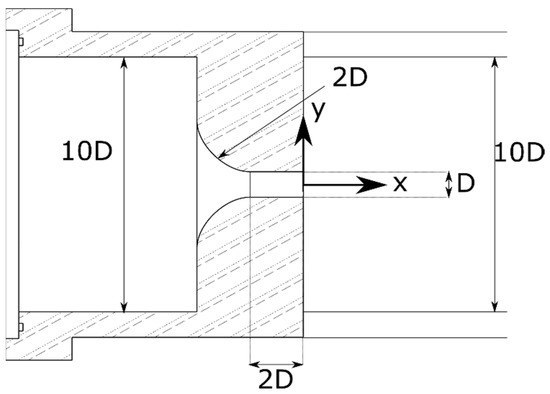
Figure 2.
Sketch of the orifice plate with scales in respect to the orifice diameter D and marking of the origin for the further representations.
The investigations of drop deformation when passing through the orifice plate are carried out with single drops. The primary drops are generated in an external production facility during operation of the system. They are sheared off from a small capillary tube by a continuous phase flow. By changing the velocity of the continuous phase that tears the droplets off the capillary, the droplet size of the primary droplets can be adjusted. The design of the drop production unit allows this to be done without affecting the main process in the experimental plant. The dispersed phase droplets produced are passed through another capillary with a small continuous phase flow rate to the front of the orifice. The capillary outlet can be positioned freely in axial and radial position. This is important, as deformation of the droplet depends on the specific streamline of the base flow, but also the intensity of the turbulence is position dependent. The introduction of the drops is designed in such a way that the flow to the orifice plate is disturbed as little as possible. The droplet size of the droplets under investigation is determined based on the recorded images in the laminar inflow area of the orifice plate, in which the droplets are undeformed and spherical, before they are subjected to stress.
Since the flow in the test facility is driven by a continuously controllable centrifugal pump, the velocity in the orifice plate, respectively, the pressure drop over the orifice plate can be controlled. The theoretical orifice velocity () is calculated from the pressure loss across the orifice.
Figure 3 shows the test setup with two high-speed cameras of the type Photron Fastcam SA-Z. The cameras were aligned side by side to raise the field of view without reducing the spatial resolution. To determine the elongation in the test setup shown, basically only one camera is needed, which is focused on the area of the orifice plate, i.e., the inlet area and the constriction. The 2nd camera is used to determine the length of the stretched drop filament directly behind the orifice plate, because depending on the test conditions the drops are stretched so much that the drop front has already left the orifice plate while the rear part is still in the orifice plate and is stretched even further. The evaluation of the finally stretched drop filament behind the orifice can be used to estimate the final elongation. Table 1 summarizes the image acquisition properties.

Figure 3.
Visualization of the experimental setup to measure the droplet deformation inside the orifice and right behind the orifice with two high-speed cameras; camera 1 (Cam 1) focused on the orifice, and camera 2 (Cam 2) focused on the space behind the orifice.

Table 1.
Image acquisition properties for the two cameras.
Due to the shape of the orifice, i.e., the curved inner edge, optical distortions occur, but they can be corrected by calibration. The step-shaped diameter reduction of 10 orifice diameters to the beginning of the rounded inlet with an initial diameter of 5 orifice diameters causes an inaccessible area due to total reflections in the range of to orifice diameters before the orifice outlet. Figure 4 shows a picture of the orifice. The non-visible area is clearly recognizable. This problem occurred during drop visualization as well as during velocity field measurements for which the same camera setup was used.

Figure 4.
Image of the orifice inlet.
The experiments were carried out with 3 oils of different viscosities as the disperse phase. The continuous phase always consisted of the same solution so that 3 viscosity ratios (λ = 0.3, λ = 3.0 and λ = 10.8) could be investigated. The other material values are approximately the same for the three oils used, so that the greatest difference is caused by the viscosity. In addition to the investigation of the influence of the viscosity ratio, the Reynolds number was also varied over 3 test series between , and . The droplet size ratio, i.e., the ratio of the primary droplet size to the orifice diameter, is in between 0.191 < < 0.202 for the comparison of the experimental and numerical investigations.
A Wilhelmy plate (DCAT11, dataphysics, Filderstadt, Germany) was used to measure the interfacial tension. It was determined to 17 mN/m for the low viscosity oil, to 20 mN/m for the medium viscosity oil and to 18 mN/m for the high viscosity oil after a measuring time of 2 h at a temperature of 20 °C. The density of the continues phase was determined with the density determination set DIS 11 (DCAT11, dataphysics, Filderstadt, Germany) to 1146 kg/m3 at 20 °C. A dynamic viscosity of the continues phase of 32.5 mPa∙s was measured with a rotational rheometer (Anton Paar Physica MCR 301, Graz, Austria) at a temperature of 20 °C.

Table 2.
Process parameters.

Table 3.
Properties of the three different viscosity ratio systems.
2.2. Droplet Visualization
The visualization of the drops was achieved by the shadow imaging method, whereby several very bright, homogeneous LED panels (TH2 Series, Vision Light Tech, Uden, The Netherlands) were mounted behind the measuring section. The frame rate during the measurements was set to 40 kHz. The image scale was approx. 21.5 px/mm for camera 1 and approx. 13.7 px/mm for camera 2.
The recorded images were processed using MATLAB 2019b (Mathworks, Nantucket, MA, USA). First, the images were binarized, and based off these binarized images, the length of the droplet filaments were measured. Figure 5 shows the comparison of the raw grayscale image and the final binarized image of a droplet entering the orifice.
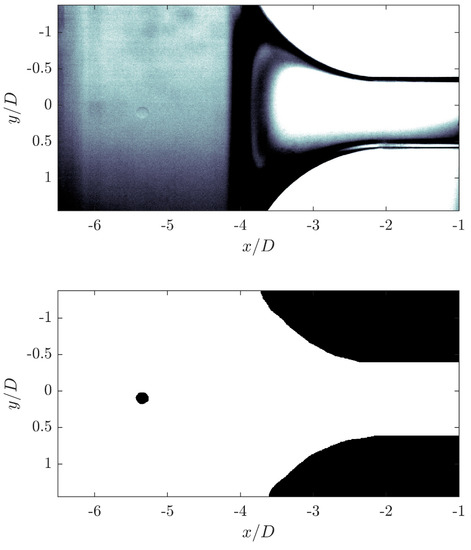
Figure 5.
Comparison of the original image and the binarized image of a droplet flowing into the orifice.
2.3. Flowfield Characterization
The velocity fields in the homogenization unit are determined by means of planar (2D2C) particle image velocimetry (PIV), which is able to resolve two velocity components within the light sheet plane aligned with the symmetry axis of the flow [15]. Two Photron Fastcam SA-Z cameras (Photron, Tokyo, Japan), which are also used for drop visualization, are used to record the velocity fields. An Innolas Blizz laser (InnoLas Photonics GmbH, Kraillingen, Germany) is used for illumination. The laser light sheet is aligned vertically into the channel from below and is oriented along the main flow direction into the channel. Glass hollow spheres [110P8, Lavision GmbH] (LaVision GmbH, Göttingen, Germany) with an average particle size of 16 µm and a density adjusted for water at 20 °C are used to sample the flow velocity. The calculation of the vector fields from the particle images was done using the commercial software Davis 8 (LaVision, Göttingen, Germany) and a standard evaluation method [15].
2.4. Numerical Modelling
The transient deformation process of droplets during transition through orifices has been described numerically by Walzel [16] based on concepts from Cox [17] applied for low capillary numbers, i.e., . For larger capillary numbers as within the high extension rate range the model of Kalb et al. [18] was used neglecting the capillary effect. The latter however applies to the 2D-case, and deviations to the proximate existing 3D-extensional case must therefore be expected according to Elmendorp [19]. Thus far, only limited validation exists.
The numerical calculation following the movement of the droplets in time steps was first based on creeping flow of the continuous phase around the droplets and spherical drop shapes. Streamlines at the center of the channel of the orifice were chosen, and minor deviations less than 5% of the extension rate were found for streamlines close to the wall at the given Reynolds numbers . The instant flow force on the droplet can be obtained from CFD of the main flow along streamlines following the trajectory of the droplets. With calculations based on the new experimental data, validation is now possible. It also clearly showed the necessity for further refinement. First, increased flow forces on spherical drops for higher Reynolds numbers were compiled with the model of Schiller and Naumann [20], but were still too low. Further adaptation was achieved considering the flow force on prolate cylindrical droplets also for intermediate drop Reynolds numbers. The flow force has been modified according to Richter and Nikrityuk [21] with a correction factor. It also comprises the case of elliptically deformed droplets in laminar flow [22]. The extension rate was corrected with a factor , which is calculated with the Reynolds number and the deformation ratio (), i.e., the ratio of the deformed drop length () compared to the primary drop diameter. Figure 6 shows an example of the course for different deformation ratios.
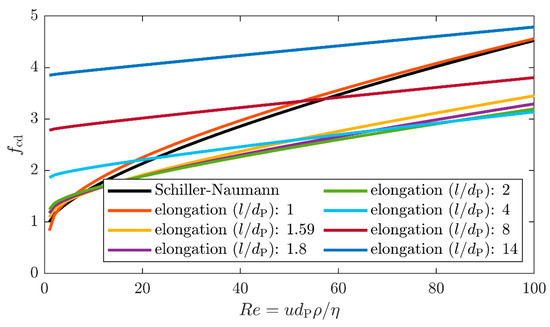
Figure 6.
Visualization of the correction factor as a function of the deformation ratio.
This leads to a modified, i.e., increased Capillary number, based on the dimensionless elongation ratio (), the primary droplet diameter and the continuous phase viscosity ratio and the interfacial tension.
The correction factor relates the resistance of the spheroid to that of a fixed sphere with diameter with the same volume within a uniform creeping flow field. This may also lead to differences as in the case here only the downstream part of the spheroid beyond its great circle applies. The drop Reynolds number is obtained from Equation (10).
For the given cases drop Reynolds numbers up to were traced.
The increased flow force within the range of was considered in the Kalb model as described by Walzel [16].
The viscosity ratio constant was matched here in simplified manner with and . Again calculations were executed for the trajectory in the center of the orifice as also primary drops were released at this position upstream the orifice in the experiment outlined above. The primary droplet size () was set to 2 mm or a drop size ratio of 0.2, respectively. This size corresponds to the experimental conditions. For the numerical flow simulations, a slightly modified orifice shape was used. In comparison to the experimental orifice plate, the cylindrical part of the orifice plate was omitted. However, this is not a problem, as only trajectories up to the smallest cross-section are considered in the numerical study.
3. Results
Due to the very good optical accessibility and the high spatial resolution, the single phase flow fields in the orifice plate can be investigated in detail by means of PIV. The time-averaged velocity field in the flow direction is shown in Figure 7 for the Reynolds number . The mean velocity field is normalized with the theoretical orifice velocity. Displayed is only every 30th vector for clarity.
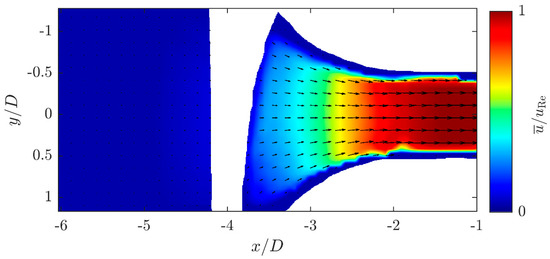
Figure 7.
Velocity field of the continuous phase inside the orifice at the Reynolds number , normalized by the theoretical orifice velocity measured by 2D2C PIV.
The velocity fields for the three Reynolds numbers investigated match quite well in the normalized representation. Figure 8 shows the exemplary velocity profiles on the axis of symmetry of the orifice plate for the three Reynolds number cases investigated. The area not visible ( to ) due to total reflection is replaced by interpolated values.
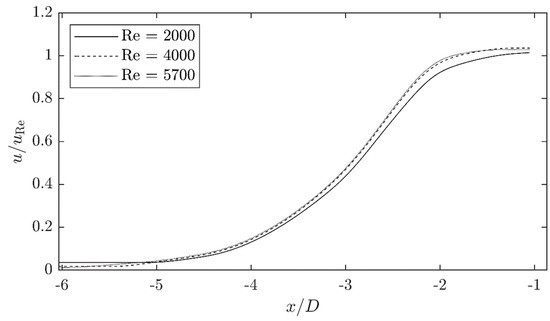
Figure 8.
Velocity profiles on the axis of symmetry of the orifice based on the flow field characterizations at three different Reynolds numbers normalized by theoretical orifice velocity.
The similarity of the velocity fields is confirmed by the very similar patterns. Only the velocity profile of the lowest Reynolds number differs slightly, but within the experimental limits. This shows that in the investigated Reynolds number range () and the investigated region, i.e., the inlet of the orifice, there is no dependence on the flow regime.
From the velocity profiles the dimensionless elongation rate can be calculated according to Equation (12).
Figure 9 shows the curves for the different Reynolds numbers. At the peak, elongation rates of approx. 0.65 are achieved for all three Reynolds numbers in the inlet area shortly before the cylindrical area (). Directly before the cylindrical area, the elongation rate drops sharply towards almost zero. The deviations in the range of can be explained by measurement uncertainties, since the velocity fields were recorded in such a way that the area of high velocities could be captured well, while the areas of low velocities, which are generally rather irrelevant, are captured less accurately due to the smaller particle image displacement [15]. The comparison of the stress profiles is very well possible through the standardization, but it should be noted that the absolute stresses increase with the Reynolds number.
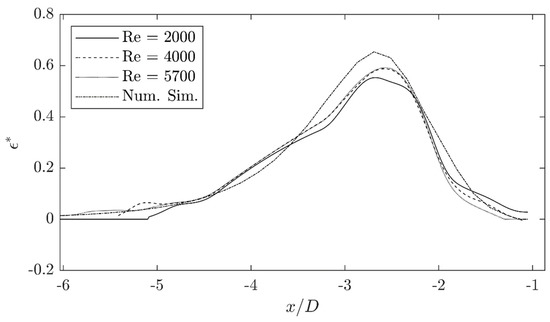
Figure 9.
Dimensionless elongational rate profiles on the axis of symmetry of the orifice for three Reynolds numbers.
Besides the dimensionless elongation rates of the experimental test series, Figure 9 shows the dimensionless elongation rate profile of the numerical simulation results. Since the numerical, non-dimensionalized elongation rate curves are the same for all Reynolds numbers, only one curve is displayed. The agreement between the experimental and numerical results is quite good for this test case, as expected.
The experimental measurements on drop elongation with a fixed elongation rate profile of the main flow that there is a clear influence of the viscosity ratio on the elongation of the drops when passing through the orifice plate.
Figure 10 shows three series of binarized drop images for the three viscosity ratios at a Reynolds number of and a drop injection near the axis of symmetry.
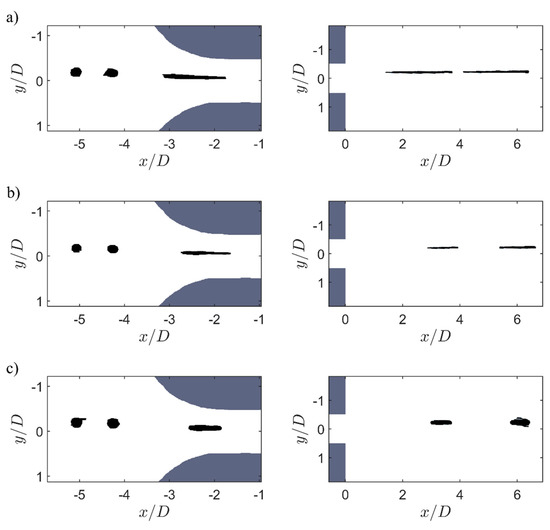
Figure 10.
Timeseries of droplet deformations at different viscosity ratios at a Reynolds-number of : (a) low viscous oil , (b) medium viscous oil and (c) high viscous oil .
It becomes clear that the elongation is greatest behind the orifice plate in case of low viscosity ratios and decreases with increasing viscosity ratio. The process of droplet elongation begins shortly before the orifice plate narrows (range to ), starting at a non-dimensional length of . In this range, the initial round drops are slightly stretched to form ellipsoids. This elongation also depends on the viscosity ratio and is particularly pronounced in the case of low-viscosity ratio. The greatest elongation occurs in the orifice contraction in the range from to . In the cylindrical area of the orifice from on, no significant elongation occurs, as no convective acceleration of the flow exist, but also no relaxation towards the round droplet state is visible in this flow region. The stretched droplet filaments only relax slightly behind the orifice plate, but this relaxation process is much slower in the spatial dimension than the stretching, so that the filaments just behind the orifice plate have almost the maximum length as in the orifice. The described course of the drop elongation fits very well with the elongation course determined by the velocity profiles. The deformation rate of the drops is highest in the area of the highest elongation rates and also fits well with the described elongation rates in the other areas.
Figure 11 shows the influence of the increase of the Reynolds number on the droplet elongation of the high viscosity ratio system. The investigation of the influence of the Reynolds number, i.e., the load, must be carried out with the high viscosity ratio system, since with the lower viscosity ratio systems, the drops are so strongly deformed, i.e., stretched, that they can no longer be measured in their full length.
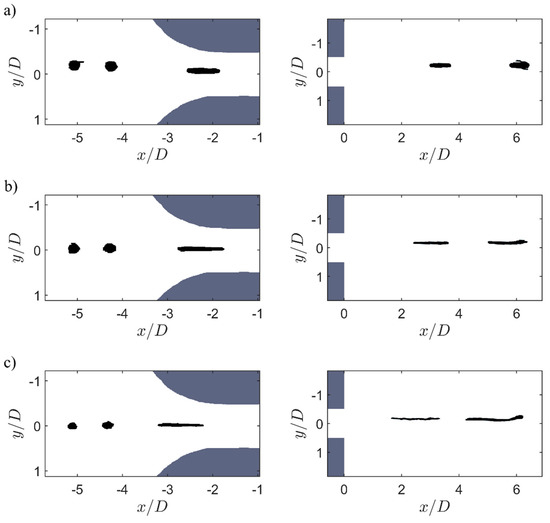
Figure 11.
Temporal evolution of droplet deformations at different Reynolds numbers for the high viscous (viscosity ratio ): (a) , (b) and (c) .
The comparison of the images of the three Reynolds numbers again makes it clear that the drop is stretched more and more with increasing stress intensity (a) to (c). This is particularly evident when comparing the images behind the orifice. While the drop deformed at a Reynolds number of has an aspect ratio of approx. 2–3, the drop stressed at a Reynolds number of is already stretched to twice this length. This effect is even more pronounced for the most stressed drop (). This drop appears smaller than the others in the inlet area, but the actual size was similar to the other cases.
The drop size or the length of the deformed drop filaments can be determined quantitatively from the recorded drop images by using digital image analysis techniques. However, the binarized drop images are not suitable for determining the drop filament diameters, because the relative measurement uncertainties become too large a small scales are measured. Therefore, the filament diameter is determined from the drop volume instead. This can be determined without significant error from the diameter of the undeformed primary drops. Using the time-resolved measurements, the elongation of the drops can be determined reliably by means of this approach.
Figure 12 shows the measured drop elongation along the x-position for the three viscosity ratios at the Reynolds number . Figure 13 illustrates the influence of the Reynolds number on the elongation for the high viscosity oil (λ = 10.8).
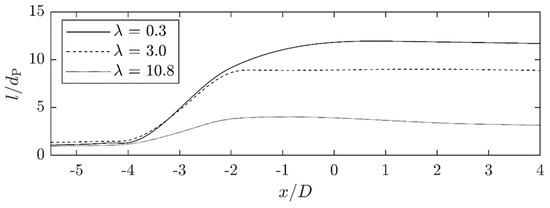
Figure 12.
Comparison of the aspect ratio of three drops with different viscosity ratios while traveling through the orifice at a Reynolds number of .
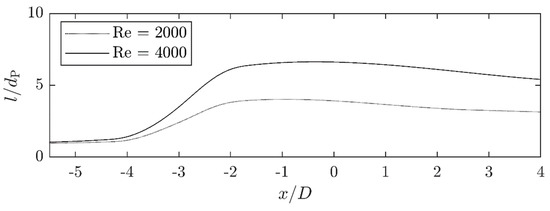
Figure 13.
Comparison of the aspect ratio of two drops with the viscosity ratio of stressed at different Reynolds numbers.
The curves show the elongation ratio recorded by the two individual cameras, whereby the elongation ratio is shown over the observed position of the center of the droplet. This point may already be located in zones of higher or lower elongation rates, while the drop front or end is located in other zones and thus exposed to different elongation rates. This effect becomes greater the longer the drop filament is stretched. Therefore, in the illustrations shown, the drop is stretched even further in the range of to . The drop length is normalized with the diameter of the undeformed round primary drop (). In cases were the drop length is very large and close to the end of the field of view of camera 1, the correct length at one position could not be measured instantaneously and had to be interpolated. In case of high viscosity ratio drops, a slight relaxation can be recognized.
In general, the statistical courses of along x-axis in Figure 11 and Figure 12 confirm the individual visual observations on drop elongation displayed in Figure 9 and Figure 10.
In Figure 14, Figure 15, Figure 16 and Figure 17, the individual experimental length curves for the three different viscosity ratios and for the highest viscosity ratio for the two Reynolds numbers are compared with the numerical results. Due to the model, two curves are shown for elongation ratios of , one according to the model of Cox and one according to the model of Kalb et al. [17,18].
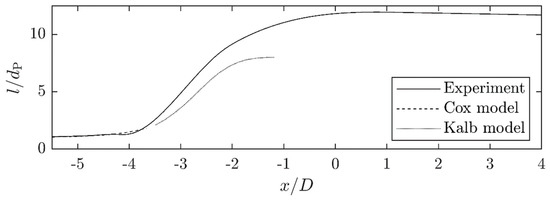
Figure 14.
Comparison of the drop aspect ratio development when passing through the orifice between the experimental measurement and the numerical simulation according to the Cox or Kalb model for a low viscosity drop (/) at a Reynolds number of .
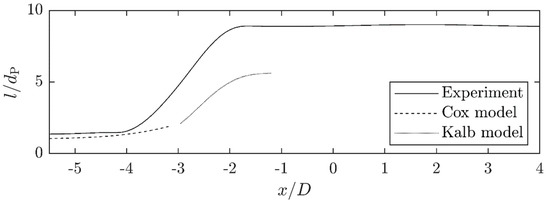
Figure 15.
Comparison of the drop aspect ratio development when passing through the orifice between the experimental measurement and the numerical simulation according to the Cox or Kalb model for a medium viscosity drop (/) at a Reynolds number of .
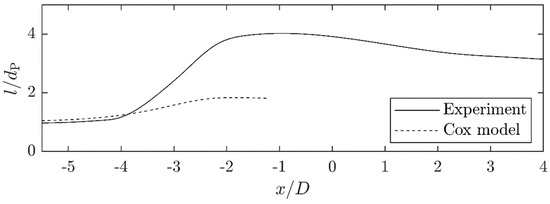
Figure 16.
Comparison of the drop aspect ratio development when passing through the orifice between the experimental measurement and the numerical simulation according to the Cox for a high viscosity drop (/) at a Reynolds number of .
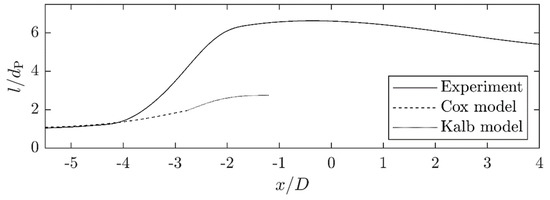
Figure 17.
Comparison of the drop aspect ratio development when passing through the orifice between the experimental measurement and the numerical simulation according to the Cox or Kalb model for a high viscosity drop () at a Reynolds number of .
For the low viscosity case (λ = 0.3) at the low Reynolds number (), the numerical calculation according to Kalb of the maximum length deformation underestimates the length compared to the experimental results by about 33%. The Kalb model is used for deformation ratios of and higher in the calculations according to the Cox model, which initially reproduces the deformation process very well. For deformation ratios , the Cox model is no longer valid, so the curve only represents the theoretical values. These values decrease from a distance of .
At the medium viscosity ratio (λ = 3.0) and the low Reynolds number (), the final drop length of the numerical simulation according to the Kalb model and the experimental measurement deviate again and the numerical simulation underestimates the final filament length compared to the experiment by approx. 38%. Additionally, the temporal or spatial course of both methods deviates strongly.
In the case of the two highly viscous (λ = 10.8) drop deformation curves at Reynolds numbers of and , the numerical calculations deviate strongly from the experimentally determined length curves. However, the trend of the final deformation length, that for the higher Reynolds number a greater droplet length can be achieved, is well reproduced.
Table 4 summarizes the results of the experimental measurements and the numerical simulations with respect to the final drop length or filament length for the different cases.

Table 4.
Summary of the experimental and numerical results concerning drop elongation and its deviation for the different cases.
From the data, the dimensionless rate of elongation of the drop () can also be calculated.
This is shown for the three different viscosity ratios in Figure 18 at the low Reynolds number () and both the experimental data and the numerical simulations. It is again clear that the elongation rate is distributed very differently in time and space between the experiments and the numerical simulations. The experimental measurements show a greater elongation rate of the drops than the numerical simulations. The shape of the elongation rate curves is similar, but in the experimental measurements the elongation process starts slightly later and increases stronger. This can be caused by the distortions due to the optical access.
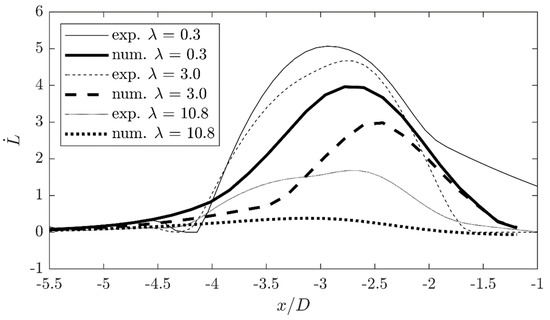
Figure 18.
Comparison of the elongation rate for the different viscosity ratios at a Reynolds number of based on the experimental measurements and the numerical simulations.
In order to verify the experimental results with regard to the evaluation of the raw images, investigations were carried out with smaller primary drops, so that the drop elongation takes place completely in the field of view of camera 1. The elongation curve of this series of measurements is shown in Figure 19. The course of the curves for all examined primary drop sizes is similar and matches the course of the originally examined drop size (black curve). This shows that the deviations of the experimental results from the numerical simulations do not result from the image evaluation algorithm or the problems that arise when the drop moves out of the field of view.
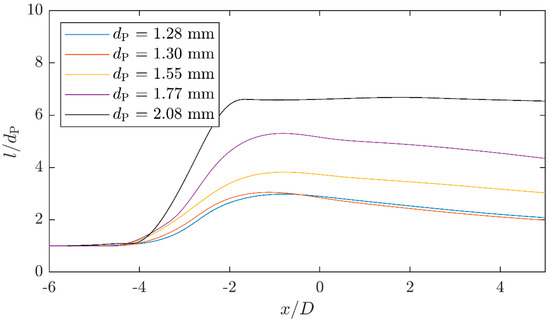
Figure 19.
Dimensionless elongation curves for different initial drop diameters () at and .
4. Discussion
The investigations show that the elongation of the primary droplets at constant Reynolds number in the laminar inlet area increases with decreasing viscosity ratio starting from a very low elongation at the highest viscosity ratio investigated. Likewise, the elongation of drops with constant viscosity ratio to the continuous phase increases with increasing Reynolds number. These investigations fit well with previous investigations on the influence of viscosity ratio on elongation in orifice plates [9]. However, what is new is the knowledge about the temporal and spatial course of the elongation of the drops in the inlet area. In these investigations, there are deviations in the temporal/spatial course between the experimental investigations and the numerical simulations based on the Cox [17] and Kalb et al. [18] models, indicating the lack of understanding. The numerical models underestimate the integral elongation as well as the local elongation rate.
In the experimental test, several factors can lead to the desired operating parameters not being set correctly. The continuous phase is circulated by a centrifugal pump in the test plant. Since the centrifugal pump has a frequency converter, a control software and a PID controller can be used to set any flow velocity in the system or in the orifice plate, and thus the Reynolds number. Due to the low operating pressures resulting from scaling even at comparatively high Reynolds numbers, a centrifugal pump is suitable as a drive. This is naturally low-pulsation, so that hardly any fluctuations are caused by the drive itself. Nevertheless, fluctuations in the range of 1 mbar can occur over time, which can lead to an error of the Reynolds number of up to 7 points.
To control the flow velocity and thus the Reynolds number in the test facility, the pressure loss through the orifice plate is measured. Due to the position of the measuring ports, the pressure loss across the orifice plate may be overestimated, since not only the loss across the constriction is measured, but also across a short section of the measurement section before and after the orifice plate. Due to the low fluid velocities and the high cannel diameters in these sections the error can be neglected. The error caused by the accuracy of the pressure sensor causes an error of the Reynolds number of about 9 points. The orifice plate was manufactured as a lathe work of acrylic glass. To make the orifice plate optically accessible, the surfaces were polished. The accuracy of the production in relation to the diameter cannot be checked more exactly. However, a deviation from the nominal diameter of the orifice bore by 1/10 mm causes a deviation of the Reynolds number by 20 points. In the worst case, the errors that may occur in this way are in the range of approx. 1% of the nominal value of the Reynolds number. Overall, the measurements of the velocity fields show that the error is very small, since the velocities and the derived elongation rate profiles fit the numerical values very well (see Figure 9). The primary drop size, which varied during the experimental investigations, should be a minor factor with regard to the deviations between the experimental and numerical investigations, since, for example, in the two experiments with the highest viscosity ratio () and the two Reynolds numbers and , the experimental primary drop size was mm and mm, respectively. The numerical calculations carried out with a primary drop size of mm led in both cases to an underestimation of the drop expansion, although the primary drop size in the experiment deviated at times downwards and at times upwards.
In addition to the errors in the flow field measurement described above, errors in the evaluation of the camera recordings can still occur. The drop dimensions are automatically derived from the camera images. A detection algorithm is used to mask the drops on the camera image. This can possibly determine the edges of the drops incorrectly by about four pixels, which can lead to an error in the range of ±0.2 mm due to the resolution of the images of 21.5 px/mm. Motion blur caused by the fast movement speed of the drops and the exposure time was minimized by very short exposure times. With the set exposure time of both cameras and the maximum speed of approx. 16.1 m/s at the highest Reynolds number of , the maximum motion blur is 0.06 mm or less than two pixels in camera 1 or one pixel in camera 2.
Overall, the differences between the numerical calculation of the drop elongation and the experimentally determined drop elongation can only in a small portion be explained by inaccuracies in the experimental procedure or the automatic image evaluation.
In addition to the differences that can be caused by the experimental procedure or the automatic image evaluation, deviations can also be caused by numerical modeling. On the one hand, the modelling parameters such as the orifice shape and the simulated viscosity ratios deviate slightly from the experimental test conditions. For example, no cylindrical orifice plate extension was simulated in the simulations or the deviation in viscosity ratio or primary drop size. On the other hand, due to the partly very strong elongated droplet filaments, it is difficult to allocate them experimentally to one location and thus to a certain flow profile or stress condition. This can partly explain the deviations in the temporal and spatial course of the expansion process. The greatest deviations between the experimental results on drop expansion and the numerical simulations are found when comparing the elongation for large viscosity ratios. As the experimental uncertainties and the possible mismatch between the experimental and numerical geometry of the model does not explain the observed differences, it is likely that the numerical model used for the calculation of the drop elongation is not adapted to these high viscosity cases. In addition, the Kalb model is designed for plane elongational flows and not for three-dimensional elongational flows.
5. Conclusions
The experimental investigations on drop elongation in concentric orifices with rounded inlet edge could show that the viscosity ratio and the Reynolds number have a significant influence on the elongation ratio. The droplets are stretched into straight linear filaments with the length depending on the viscosity ratio and the Reynolds number for droplets with the same primary droplet diameter. Higher viscosity ratios lead to a reduction in drop elongation compared to lower viscosity ratios. An increase in the Reynolds number leads to longer drop filaments or higher elongation ratios. The scaling is linear in both cases according to our investigation. A larger primary droplet diameter results in an increased filament length. With regard to the spatial and temporal expansion characteristics, the measured drop expansions fit very well with the measured flow velocity characteristics. However, it has to be taken into account that the drop has a spatial extent and is thus increasingly stressed differently with increasing elongation, since it extends over a wide range.
The numerical simulations according to the model of Cox and the model of Kalb et al. generally reflect the trend of the resulting drop elongation. Especially at low viscosity ratios and the lower Reynolds numbers, the numerical and experimental results fit quite well. At higher viscosity ratios, there are significant systematic deviations when compared quantitatively, but the trend of the increasing elongation with raising Reynolds number is correctly represented. When comparing the spatial or temporal elongation curves between the numerical simulations and the experimental curves, clear deviations can be seen, with the simulation underestimating the drop deformation. Even though quantitative description of the drop extension at different process conditions was not yet possible with the models applied, numerical studies show good agreement with observed tendencies. The preceding deformation of primary droplets when entering into the turbulent region of the jet behind the orifice must affect further deformation and breakup. This issue is investigated in [23].
Author Contributions
Conceptualization, P.W., C.J.K. and B.M.; software, B.M. and P.W.; formal analysis, B.M. and P.W.; investigation, B.M., and P.W.; writing—original draft preparation, B.M. and P.W.; writing—review and editing, P.W. and C.J.K.; visualization, B.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the German Research Foundation (DFG), grant number KA 1808/19.
Data Availability Statement
Data available on request.
Acknowledgments
The authors thank the German Research Foundation (DFG) for the financial support of the project “Investigations on the measurement of the relevant flow conditions for the deformation and break-up of droplets during high-pressure homogenization with orifices and on the scalability of the methods” (grant number KA 1808/19). Special thanks to the project partners F. J. Preiss and H. P. Karbstein for their practical help and advice.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Taylor, G.I. The formation of emulsions in definable fields of flow. Proc. R. Soc. Lond. A 1934, 146, 501–523. [Google Scholar] [CrossRef] [Green Version]
- Bisten, A.; Schuchmann, H.P. Optical Measuring Methods for the Investigation of High-Pressure Homogenisation. Processes 2016, 4, 41. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X. Drop breakup in dilute Newtonian emulsions in simple shear flow: New drop breakup mechanisms. J. Rheol. 2007, 51, 367–392. [Google Scholar] [CrossRef]
- Walstra, P. Principles of emulsion formation. Chem. Eng. Sci. 1993, 48, 333–349. [Google Scholar] [CrossRef]
- Kolb, G.; Wagner, G.; Ulrich, J. Untersuchungen zum Aufbruch von Einzeltropfen in Dispergiereinheiten zur Emulsionsherstellung. Chem. Ing. Tech. 2001, 73, 80–83. [Google Scholar] [CrossRef]
- Galinat, S.; Masbernat, O.; Guiraud, P.; Dalmazzone, C.; Noı¨k, C. Drop break-up in turbulent pipe flow downstream of a restriction. Chem. Eng. Sci. 2005, 60, 6511–6528. [Google Scholar] [CrossRef]
- Galinat, S.; Garrido Torres, L.; Masbernat, O.; Guiraud, P.; Risso, F.; Dalmazzone, C.; Noik, C. Breakup of a drop in a liquid–liquid pipe flow through an orifice. AIChE J. 2007, 53, 56–68. [Google Scholar] [CrossRef]
- Innings, F.; Trägårdh, C. Visualization of the Drop Deformation and Break-Up Process in a High Pressure Homogenizer. Chem. Eng. Technol. 2005, 28, 882–891. [Google Scholar] [CrossRef]
- Kelemen, K.; Gepperth, S.; Koch, R.; Bauer, H.-J.; Schuchmann, H.P. On the visualization of droplet deformation and breakup during high-pressure homogenization. Microfl. Nanofl. 2015, 19, 1139–1158. [Google Scholar] [CrossRef]
- Budde, C.; Schaffner, D.; Walzel, P. Modellversuche zum Tropfenzerfall an Blenden in Flüssig/Flüssig/Dispersionen. Chem. Ing. Tech. 2002, 74, 101–104. [Google Scholar] [CrossRef]
- Cristini, V.; Blawzdziewicz, J.; Loewenberg, M.; Collins, L.R. Breakup in stochastic Stokes flows: Sub-Kolmogorov drops in isotropic turbulence. J. Fluid Mech. 2003, 492, 231–250. [Google Scholar] [CrossRef] [Green Version]
- Komrakova, A.E. Single drop breakup in turbulent flow. Can. J. Chem. Eng. 2019, 97, 2727–2739. [Google Scholar] [CrossRef]
- Preiss, F.J.; Mutsch, B.; Kähler, C.J.; Karbstein, H.P. Scaling of Droplet Breakup in High-Pressure Homogenizer Orifices. Part I: Comparison of Velocity Profiles in Scaled Coaxial Orifices. ChemEngineering 2021, 5, 7. [Google Scholar] [CrossRef]
- Mutsch, B.; Kähler, C.J. Charakterisierung eines Versuchsstands zur Messung der relevanten Strömungsbedingungen für die Deformation und den Aufbruch von Tropfen beim Hochdruckhomogenisieren mit Blenden. Fachtag. Exp. Strömungsmechanik 2017, 25. Available online: https://docplayer.org/181915229-Charakterisierung-eines-versuchsstands-zur-messung-der-relevanten-stroemungsbedingungen-fuer-die-deformation-und-den-aufbruch.html (accessed on 22 June 2021).
- Raffel, M.; Willert, C.E.; Scarano, F.; Kähler, C.J.; Wereley, S.T.; Kompenhans, J. Particle Image Velocimetry: A Practical Guide, 3rd ed.; Springer: Cham, Switzerland, 2018; ISBN 978-3-319-68852-7. [Google Scholar]
- Walzel, P.E. High-Pressure Homogenization: Simplified Drop Deformation Estimate during Transition through Orifices. Chem. Eng. Technol. 2017, 40, 405–411. [Google Scholar] [CrossRef]
- Cox, R.G. The deformation of a drop in a general time-dependent fluid flow. J. Fluid Mech. 1969, 37, 601–623. [Google Scholar] [CrossRef]
- Kalb, B.; Cox, R.G.; St. John Manley, R. Hydrodynamically induced formation of cellulose fibers. J. Colloid Interface Sci. 1981, 82, 286–297. [Google Scholar] [CrossRef]
- Elmendorp, J.J. A Study on Polymer Blending Microrheology. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1986. [Google Scholar]
- Schiller, L.; Naumann, A. Fundamental calculations in gravitational processing. Z. Ver. Dtsch. Ing. 1933, 77, 318–320. [Google Scholar]
- Richter, A.; Nikrityuk, P.A. Drag forces and heat transfer coefficients for spherical, cuboidal and ellipsoidal particles in cross flow at sub-critical Reynolds numbers. Int. J. Heat Mass Transf. 2012, 55, 1343–1354. [Google Scholar] [CrossRef]
- Loth, E. Lift of a Spherical Particle Subject to Vorticity and/or Spin. AIAA J. 2008, 46, 801–809. [Google Scholar] [CrossRef]
- Mutsch, B.; Preiss, F.J.; Dagenbach, T.; Karbstein, H.P.; Kähler, C.J. Scaling of Droplet Breakup in High-Pressure Homogenizer Orifices. Part II: Visualization of the Turbulent Droplet Breakup. ChemEngineering 2021, 5, 31. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).