Scaling of Droplet Breakup in High-Pressure Homogenizer Orifices. Part II: Visualization of the Turbulent Droplet Breakup

Abstract

Emulsion formation is of great interest in the chemical and food industry and droplet breakup is the key process. Droplet breakup in a quiet or laminar flow is well understood, however, actual in-dustrial processes are always in the turbulent flow regime, leading to more complex droplet breakup phenomena. Since high resolution optical measurements on microscopic scales are extremely dif-ficult to perform, many aspects of the turbulent droplet breakup are physically unclear. To over-come this problem, scaled experimental setups (with scaling factors of 5 and 50) are used in con-junction with an original scale setup for reference. In addition to the geometric scaling, other non-dimensional numbers such as the Reynolds number, the viscosity ratio and the density ratio were kept constant. The scaling allows observation of the phenomena on macroscopic scales, whereby the objective is to show that the scaling approach makes it possible to directly transfer the findings from the macro- to the micro-/original scale. In this paper, which follows Part I where the flow fields were compared and found to be similar, it is shown by breakup visualizations that the turbulent droplet breakup process is similar on all scales. This makes it possible to transfer the results of detailed parameter variations investigated on the macro scale to the micro scale. The evaluation and analysis of the results imply that the droplet breakup is triggered and strongly influenced by the intensity and scales of the turbulent flow motion.

1. Introduction

Emulsions are mixtures of at least two phases that are not miscible in each other, such as oil in water or vice versa and play an important role in many areas of daily life, particularly in the cosmetics, food or pharmaceutical industries [1]. Besides the production of finished products (especially in the pharmaceutical and food industry), the chemical industry also uses emulsions in intermediate products, which makes them economically very relevant [2].

Depending on the field of application, different properties are required of an emulsion, so that there is a broad production spectrum. An essential property of the emulsion is the droplet size or the droplet size distribution. Amongst other factors, it determines the shelf life of the product defined by the creaming time, i.e., the time until separation occurs due to the possibly different densities of the product phases [3,4]. An important process for the production of low- to medium-viscosity emulsions with small droplet size is high-pressure homogenization. In this process, a pre-emulsion, which is a coarse mixture of the continuous and the disperse phases, is passed through a disruption unit with a small channel cross-section under high pressure. The high pressure forces the mixture through the small channels at large velocities [5]. This causes the disperse phase to be broken up into fine droplets within the continuous phase. Although this process is widely used, its details are not fully understood [6]. However, a better understanding is desired to enhance the product quality (narrow or wide droplet size distribution) and the product yield (lower number of droplets with undesired sizes).

Beginning with the first investigations by Taylor [7] up to, for example, the classification into different breakup regions according to Zhao [8], the breakup of droplets in laminar flow profiles was investigated in great detail and described by theories. The economically much more relevant break-up of droplets due to turbulent flow conditions in rotor stators [9,10] or high-pressure homogenizers [11] is however much more complex. Most of the investigations on turbulent droplet break-up were initially aimed at determining correlations between the process parameters and the resulting droplet size distributions or maximal droplet size. This includes in particular the Kolmogorov-Hinze theory [12,13] and further developments of it [14,15], but also other correlations [4,16]. Only with a significant improvement of optical measurement techniques and the continuously more powerful computer hardware it is possible to investigate the droplet break-up under turbulent conditions in detail experimentally or by numerical simulations.

To gain a better understanding of the droplet break-up, research has been focused on the flow processes in homogenization units to explain the resulting droplet size distribution. The flow fields in high-pressure homogenization plants with flat valves [17,18] or with orifices [18,19,20] were measured, for example, by means of particle image velocimetry (PIV). The flow profiles in flat valves [21,22] or orifices [23] were also investigated via numerical simulations. Based on this knowledge about the flow processes in the turbulent region of the high-pressure homogenizers, the theories of droplet break-up developed from the laminar flow region or the Kolmogorov-Hinze theory can be modified, e.g., population balances [24].

In addition to these single-phase flow investigations, there is also a large number of studies dealing with the multi-phase process of the droplet break-up itself or the actual process in high-pressure homogenizers. Swartz [25] investigated the drolet break-up in turbulent pipe flows, while similar investigations were carried out by Hesketh [26] for both droplets and gas bubbles in turbulent flow tubes. Kolb [27] visualized the droplet break-up in a scaled test facility with an orifice as a homogenizing unit. Due to the large scaling factor, both the primary and the secondary droplets could be visualized. Galinat et al. [28] investigated the droplet break-up and the break-up location in a test facility with an orifice. The droplet break-up took place in the area of the shear layer [29]. Innings et al. [30] studied droplet break-up in a 2D model of a flat valve and were able to visualize the break-up location as well as different break-up mechanisms [31]. In particular, the comprehensive and detailed visualization research of Kelemen et al. [32] allowed for classification of the individual theoretical and experimental droplet break-up phenomena.

The droplet break-up itself was also investigated numerically. Cristini et al. [33] investigated the break-up of droplets which are smaller than the Kolmogorov length of turbulence and are therefore only stressed by laminar shear flows and showed that, in addition to the elongation, the elongation duration is decisive. Komrakova [34] investigated droplet deformation and break-up of droplets exposed to isotropic turbulence and showed that the energy stored as surface energy until breakup can be different. Maniero et al. [35] simulated the break-up of droplets in a system-specific high-pressure homogenizer with orifice and generated experimental results very similar to those obtained from the numerical model.

The homogenization process is performed economically in appropriately designed apparatus on a very small scale (with channel dimensions in the range of approximately 100 µm) and at very high operating pressures [36]. Due to the sometimes extremely high pressures, the plants are usually constructed out of stainless steel parts and therefore normally have no visual access. Individual model systems have been developed for various investigations in such a way that at least a low level of optical accessibility is available. This means that there is a camera access and [19], if necessary, a further access for the illumination of the measuring volume in the homogenization unit [30]. Detailed investigations of the temporal and spatial processes are nevertheless difficult to perform, since the flow velocities can be in the range of several hundred m/s due to the high pressure differences and the small channel dimensions with limited accessibility [37,38].

A size scaling of the fragmentation unit during homogenization, performed to simplify the study of the processes, bears the danger that the process under investigation is not comparable with the process on the original scale, so that the transferability of the knowledge gained on an enlarged scale is not legitimate [39]. In this paper, the results on droplet break-up of three different homogenization units are presented: one is a concentric orifice on the original scale (M1), while the other two orifices are scaled with the scale factor 5 (M5) and 50 (M50). In order to make the results transferable, scaling rules were established similar to those of Budde et al. [40].

A more detailed description of the scaling considerations and a comparison of the flow profiles in the three homogenization units of different scales is given by Preiss et al. [41]. The objective of this study is to show that it is possible to transfer results from one scale to another when there is a well-developed scaling concept. By means of investigation of different scales, the knowledge about droplet break-up during homogenization can be extended, since in large scale facilities experiments can be carried out more easily. Break-up events are compared for different Reynolds numbers and droplet trajectories.

2. Materials and Methods

2.1. Setup

The three orifices studied are geometrically quite similar. In order to enable the transferability of the measurements, not only was the geometric similarity taken into account in the design of the experiments shown, but the fluid mechanical similarity was also achieved by retaining the Reynolds number, which is calculated with the orifice diameter $D$ the pressure drop acros the orifice $\mathsf{\Delta }p$ and the continuous phase density ${\rho }_{\mathrm{c}}$ and viscosity ${\eta }_{\mathrm{c}}$.

$$Re=\frac{D\sqrt{2\mathsf{\Delta }p{\rho }_{\mathrm{c}}}}{{\eta }_{\mathrm{c} }}$$

(1)

In addition, the material systems were selected in such a way that all relevant dimensionless numbers ($We$, $Re$, $\lambda ={\eta }_{\mathrm{d}}/{\eta }_{\mathrm{c}}$, $\kappa ={\rho }_{\mathrm{d}}/{\rho }_{\mathrm{c}}$; ${\eta }_{\mathrm{d}}$ denotes the disperse phase viscosity, ${\rho }_{\mathrm{d}}$ denotes the disperse phase density) are kept constant. Aside from certain limitations [41], the transferability of the velocity fields and the material properties of the three different homogenization units have already been shown.

Figure 1 shows the cross-section of the original scale orifice from the M5 meso scale (Figure 1b) and M50 macro scale orifice (Figure 1a). In the macro scale, the incoming fluid flows through a round channel, from left to right. The orifice is a concentric round hole. The flow behind the orifice is directed through a square channel. The dimensions of the orifices are summarized in

Table 1. Comparison of the different lengths of the orifice in the different scales.

Scaling Factor	1	5	50
D	0.2 mm	1 mm	10 mm
L	0.4 mm	2 mm	20 mm
${\mathrm{D}}_{\mathrm{i}}$	2 mm	10 mm	100 mm
${\mathrm{D}}_{\mathrm{o}}$	2 mm	10 mm	100 mm
$\alpha$	60	60	-
R	-	-	20 mm

. Similar to the M5 orifice, the original orifice consists of a square inflow channel, a concentrically mounted cylindrical orifice and a square low-pressure channel. In the meso scale, the pre-emulsion, which is produced in a side stream with a droplet generator [42], is reinjected in front of the orifice with a 1/8” stainless steel capillary with an inner diameter of 2 mm (TECHLAB GmbH, Braunschweig, Germany). The capillary was either on the center axis or close to the wall. Due to the small dimensions of the original scale orifice, no positioning of the pre-emulsion was possible in this scale.

As shown in previous investigations [43] where the original scale (M1) design was also tested in the M50 setup, the differences in the inlet area of the orifice do not cause major differences in the flow behind the orifice as long as cavitation can be avoided. The advantage of scaling by a scaling factor of 50 is that, in this test facility, the entire measurement section can be made of glass or acrylic glass and is therefore optically well accessible. Manufacturing is also easier and more accurate. Due to the simplified test setup, 3D measurements for droplet break-up are possible. In addition, the flow velocities in the orifice are reduced by increasing the characteristic lengths. This allows a time-resolved investigation of the processes during deformation and break-up of single droplets with a very high spatial resolution.

Table 2. Comparison of the advantages (+) and disadvantages (−) of the different tests and scales.

Scaling Factor	1	5	50
Validity	original	model	model
Spatial resolution	O	+	+
Temporal resolution	−	−	+
Optical access	−	−	+
Tomographic measurements	−	−	+
Easy manufacturing	−	O	+
Max. disperse phase fraction [%]	0.0125	0.006	0.000125
PSD analysis	+	O	−
Cavitation control	+	+	−
Influence on the droplet trajectory	−	+	+
Pre-emulsion droplet size distribution	wide	tight	tight

compares the advantages and disadvantages of the experiments in the different scales.

Figure 2 shows the test plant (M50) scaled with the scale factor 50. The already described test section (a) in the upper area is arranged horizontally and is passed through from left to right. The fluid is continuously circulated by a pump (b) (Grundfos, Bjerringbro, Denmark). Due to the scaling, the desired pressure in front of the orifice is low enough that a naturally pulsation-free centrifugal pump can be used. The centrifugal pump used is equipped with a frequency converter, so that the pump performance and therefore the pressure can be smoothly adjusted. The pressure loss across the orifice is used to control the flowrate or the set Reynolds number. A partial flow of the system is cooled in a constantly operated heat exchanger (c) so that the test temperature can be kept at 20 °C. This is important for keeping the desired material values, especially the viscosities, constant. Without the cooling with a heat exchanger the through the pump applied energy would lead to a heating of the facility. The droplet break-up tests are performed with single droplets. These droplets are produced in an external plant, which is shown in the upper part of Figure 2d. In this apparatus, disperse phase droplets are sheared off from a capillary by the continuous phase flow around it. A similar approach is used by Preiss et al. [42]. The continuous phase used for this purpose is removed from the main circuit as a bypass. The size of the primary droplets can be adjusted by throttling the volume flow of the continuous phase in the bypass or by moving the capillary further down in the conical channel. The primary droplets produced are fed through a fluid-mechanically optimized inlet, to avoid a turbulent inflow to the orifice, into a capillary just before the homogenization unit. The position of the capillary can be adjusted so that different trajectories for the droplet can be set. Since the pressure droplet is low even for the higher Reynolds number investigated, cavitation does not occur and back pressure is not needed. A detailed description and characterization of the system can be found in Mutsch and Kähler [44,45].

The experimental setup of the original scale plant is shown in Figure 3. The continuous phase is pressed from a pressure vessel (b) through the setup. A nitrogen gas cylinder (a) is used to pressurize the pressure vessel. The pressure drop of the optically accessible orifice (e) is recorded continuously. The mass flow is determined by the continuous read-out of a scale. To prevent cavitation at the outlet of the orifice, a back pressure is applied with a needle valve [46]. The Thoma number, the ratio of the pressure behind the orifice ($p_{\mathrm{o}}$) and the pressure before the orifice ($p_{\mathrm{i}}$), was set to 0.3, where:

$$Th=\frac{p_{\mathrm{o}}}{p_{\mathrm{i}}}$$

(2)

During the experiments, the applied pressure on the pressure vessel is altered to achieve the desired mass flow of the continuous phase. If the system is at steady state, the valve downstream of the pressure vessel is closed and the coarse emulsion is filled from the beaker (c) in the pipe coil (d) to avoid creaming of the emulsion. Subsequently, the valve is opened again and the colored droplets are visualized in the optically accessible orifice. A sample of the emerging fine emulsion is collected by closing the valve of the pressure vessel again and discharging the sample from the hose (f) into a beaker (g) using the three-way valve.

Figure 4 shows the flow diagram of the experimental setup which is scaled with a scaling factor of 5. Similar to the setup operated at original scale, the continuous phase is pumped through the setup from a pressure vessel (a). The volume flow, the temperature and the pressure drop of the orifice are recorded during an experiment. The droplets are produced in a side stream in a droplet generator (d). The droplet generator consists of pressure stable co-flowing micro fluidic setup. The colored disperse phase is pumped via a displacement pump (c) (TECHLAB Minipumpe, TECHLAB GmbH, Braunschweig, Germany) through a fused silica capillary with an outer diameter of 150 µm (Chromatographie Handel Müller GmbH, Fridolfing, Germany). Droplets with a diameter of about 200 µm are produced and reinjected in front of orifice (e) either on the centerline or close to the wall with a 1/8” steel capillary with an inner diameter of 2 mm (TECHLAB GmbH, Braunschweig, Germany). The droplet generator is described in detail in Preiss et al. [42]. The back pressure is set with a needle valve (h). The Thoma number in this scale was also set to 0.3. The samples from the emerging fine emulsion are collected similarly to the original scale, from a hose between the orifice and the needle valve.

2.2. Materials and Experimental Conditions

Due to the scaling of the test facilities, the material values were adjusted for each differently-scaled experiment.

Table 3. Summary of the relevant material parameters in the similarity tests for droplet break-up in the different scales.

Parameter	M1	M5	M50
Reynolds number	2000/5700	2000/5700	2000/5700
Continuous phase viscosity/mPas	4.25	9.42	32.5
Continuous phase density/kg/m3	1145.3	1148.6	1146
Viscosity variant			medium	low	high
Disperse phase density/kg/m3	928	920 *	960 *	930	970
Viscosity ratio/-	3.5	3.1	3.0	0.3	10.8
Density ratio/-	0.81	0.80	0.84	0.81	0.84
Interfacial tension/mN/m	4.31	3.99	20	17	18
Drop size ratio/-	0.16	0.186	0.2

* according to the supplier’s datasheet.

shows the material values and the dimensionless ratios. The continuous phase of the originally scaled orifice (M1) consisted of 65.5 wt % demineralized water, 34 wt % sucrose, and 0.5 wt % polysorbate 20 (Tween 20^®, Carl Roth, Karlsruhe, Germany) as emulsifier. The disperse phase was a mixture of the oils Miglyol 810^® (IOI Oleo GmbH, Witten, Germany) and Miglyol 840^® (IOI Oleo GmbH) in weight ratio of 41:59. To the oil mixture 0.012 wt. % of the fluorescence color Nile red (9-(diethyl-amino)benzo[a]phenoxazin-5(5H)-one, Sigma-Aldrich Chemie GmbH, Taufkirchen, Germany) was added.

The continuous phase of the orifice scaled fivefold (M5) consisted of 58.528 wt % glycerol, 40.672 wt % demineralized water, and 0.5 wt % polysorbate 20 (Tween 20^®, Carl Roth). Moreover, 0.2 wt % potassium sorbate and 0.1 wt % citric acid were added as preservatives. The disperse phase comprised of the oil Miglyol 812^® (IOI Oleo GmbH) with 0.012 wt % Nile red (9-(diethyl-amino)benzo[a]phenoxazin-5(5H)-one, Sigma-Aldrich).

The continuous phase of the fiftyfold orifice (M50) consisted of 61.5 wt % demineralized water, 27.5 wt % sucrose and 10.5 wt % PVP K30 (polyvinylpyrrolidone, BTC Europe GmbH, Monheim am Rhein, Germany). Furthermore, potassium sorbate (0.26 wt %) (Wittig Umweltchemie GmbH, Grafschaft-Ringen, Germany) and citric acid (0.24 wt %) (Schwarzmann GmbH, Laaber, Germany) were again used as preservatives. The disperse phase consisted of either WACKER^® AK 10 (Wacker Chemie AG, Stuttgart, Germany), WACKER^® AK 100 (Wacker Chemie AG) or WACKER^® AK 350 (Wacker Chemie AG).

Newtonian flow behavior was determined for each disperse and continuous phase of the three scales with a rotational rheometer (Anton Paar Physica MCR 301, Graz, Austria) at a temperature of 20 °C in the shear rate range of 0.1–100 s⁻¹. As the disperse phase fraction was below 1 wt % for all experiments, it is expected that Newtonian flow behavior is also present at higher shear rates during the process [47,48]. The densities of the phases were determined if not otherwise specified by the density determination set DIS 11 (DCAT11, dataphysics, Filderstadt, Germany). A Wilhelmy plate (DCAT11, dataphysics) was used to measure the interfacial tension at temperature of 20 °C. It is expected that the equilibrium interfacial tension is reached after a measurement time of 2 h.

In order to ensure that the flow conditions are also comparable, the Reynolds number was adjusted during the tests. The Reynolds numbers were set to Re = 2000 or Re = 5700 for all investigations in all scales. The primary droplet size was also adjusted, whereby a pre-emulsion with a Sauter mean diameter of approximately 32 µm was used for the test plant in original size. The coarse emulsion with a disperse phase fraction of 5 wt % was produced with an Ultra-Turrax^® (IKA^®-Werke GmbH & Co. KG, Staufen, Germany) dispersing machine at 3400 rpm and a time of 10 min. Subsequently, the emulsion was diluted with the continuous phase to a disperse phase fraction of 0.0125 wt %. The test plant scaled with the factor 5 used in the inline droplet generator. The emerging droplets had a diameter in the range of 190–220 µm. In the test plant on the macro scale, the primary droplets were generated during operation of the plant. The primary droplet size was set to approx. 1.9–2.1 mm. In order to investigate the influence of the viscosity ratio on the droplet break-up, tests were carried out on the M50 scale with three oils of different viscosity. The continuous phase properties were kept constant. The parameters for the 3 different oils are summarized in Table 3. The medium viscosity oil corresponds to the strictly scaled system.

2.3. Droplet Visualization

2.3.1. Macro Scale (M50)

The examination of the droplet break-up process necessitates visualization of the drop. For this purpose, the shadow image method with high-speed cameras is used in the test plant scaled with a factor of 50. Due to the optical accessibility of the measuring section, the investigation is possible in front of, inside and behind the orifice. In addition, the processes can be examined from several directions. Thus, both the droplet position in space and the droplet size can be determined accurately without any assumptions. Since the oil droplet causes only a very weak shadow when using the normal shadow image method, a new visualization method was developed, with which the refraction of light at the interface could be used to visualize the drop. In Mutsch and Kähler [45], a more detailed description and illustration of the method can be found.

In order to be able to observe the entire droplet break-up process, four high-speed cameras are used side by side, so that a field of view (FOV) with a sufficiently large aspect ratio can be achieved. This is mainly due to the fact that the convective movement of the droplet in the main flow direction is much faster than across the main flow direction and the velocities in the scaled test facility are also still too fast for the cameras to be moved with the same velocity. Figure 5 shows the measurement setup.

The cameras used were the Photron Fastcam SA-Z (Photron, Tokyo, Japan) which can record up to 20 kHz in full-frame mode, with a sensor size of 1048 × 1048 px pixels and a pixel size of 20 × 20 µm. The images were recorded with a frame rate of 40 kHz or 72 kHz, and consequently the active sensor size had to be reduced to 512 ×1024 px or 304 × 896 px, respectively.

Since the droplets or droplet filaments are very thin behind the orifice despite the high resolution, a fifth camera is used to determine the droplet volume. This camera observes the droplets as they enter the orifice with a particularly high spatial resolution. Since the droplets are round in front of the orifice, the droplet volume can be easily determined. From the droplet volume and the length of the droplet filament the filament thickness or the diameter of the filament, which is assumed to be a cylinder in the first approximation, is determined if necessary. The filament length can be determined with low uncertainty from the images behind the orifice, where there is a straight elongated filament. Due to the lower speed at this measurement location the recording frequency could be reduced. At this position, a Phantom V12.1 (Vision Reaserch, Wayne, NJ, USA) camera with a recording frequency of 2 kHz at full sensor size of 1200 × 800 px was used. With this camera, the active pixel size is 20 × 20 µm.

2.3.2. Micro and Meso Scale (M1 and M5)

In the two experimental plants M1 and M5, the fluorescent dye Nile red (9-(diethyl-amino)benzo[a]phenoxazin-5(5H)-one, Sigma-Aldrich) is added to the oil droplets to visualize the drop. This allows the droplet to be recorded by illumination at the proper wavelength of the dye. A Nd:YAG laser (Dual-Power 30–15 of Dantec Dynamics, Skovlunde, Denmark), operated at 30 mJ/pulse and at a wavelength of 532 nm, is used to illuminate the flow. The laser pulse has a duration of a few nanoseconds, which allowed sharp pictures of the deformed droplets even at high velocity. A high-speed double frame CCD camera (FlowSense 4M Camera Kit, Dantec Dynamics) with a 12-bit resolution and 2048 × 2048 px is used to take recordings at a frame rate of 7.4 Hz. Due to the small channel dimensions, the camera is mounted to a microscope (Dantec HiPerformance Microscope, Dantec Dynamics). An objective lens with a magnification of 5 is used for the original scale setup, while an objective lens with a magnification of 1.75 is used for the setup scaled fivefold. With this setup, a spatial resolution of 1.5 µm/px (M1) and 6 µm/px (M5) is achieved. The droplet breakup is visualized in several overlapping sections which are superimposed in the post processing step. 2000 recordings are taken in every section. Subsequently, an average image is subtracted from every picture in Dynamic Studio 6.10 (Dantec Dynamics). Small objects smaller than than 20 px are removed for noise reduction in the post processing step in MATLAB 2019b (MathWorks, Nantucket, MA, USA). Furthermore, circular and out of focus droplets, located in the back flow areas (see Kelemen et al. [19]), are also removed from the images. Since the speed in these experimental facilities is much too fast compared to the spatial dimensions to generate time-resolved data even with high-speed cameras low-speed cameras are used for droplet deformation imaging.

2.4. Measurement of the Resulting Droplet Size Distribution

The resulting droplet size distributions of the collected samples of the original scale were determined by a laser diffraction particle analyser (HORIBA LA-940, Retsch Technology, Haan, Germany) in a stirred measurement cell. The automated dynamic image analysis system Sysmex FPIA3000 (Malvern Panalytical GmbH, Kassel, Germany) was used to determine the resulting droplet size distribution of the system scaled fivefold. The droplet size distribution was calculated based on 1200 evaluated droplets of every sample. Each process parameter combination was addressed three times. The software OriginPro 2019 (OriginLab Corp., Northampton, MA, USA) was used for the statistical analysis, calculation of averages and standard deviations.

3. Results

The experiments on the M50 scale are best suited to understand the transient processes during droplet break-up in high-pressure homogenizers, due to the possibility of time-resolved measurements, which are hardly possible with the smaller experimental plants. However, even with this experimental setup, where measurements were made with a maximum recording frequency of up to 72 kHz, it is not possible to analyze all processes in detail since they occur extremely fast and take place in relatively small spaces; increasing the Reynolds number only exacerbates this issue. At low Reynolds numbers, however, the problem is that the droplets are deformed over a relatively large space or a long running length and finally break up into very fine droplets. In order to record these processes which extend over a large spatial scale, four cameras with overlapping fields of view were used. The investigations of droplet break-up were carried out with single droplets, so that drop-drop interactions can be excluded before the break-up takes place. Furthermore, coalescence is prevented by adjusting a sufficiently low droplet concentration.

In order to relate the observations made during the measurement of droplet break-up to the flow conditions, single-phase flow measurements were first carried out on each experimental scale to be investigated. The comparison of these single-phase measurements to the experimental scale is investigated by Preiss et al. [41].

3.1. Break-Up Visualization

The determination of the 3D droplet trajectory in the trailing area of the free jet with the location of the droplet break-up point on the area of the shear layer has already been carried out in Mutsch and Kähler [45]. In the following section, the entire droplet break-up is shown in high temporal and spatial resolution.

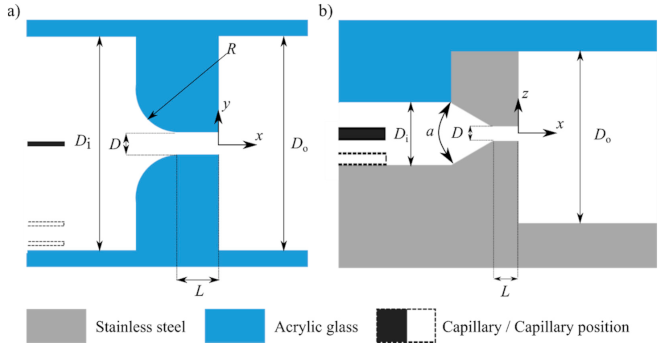
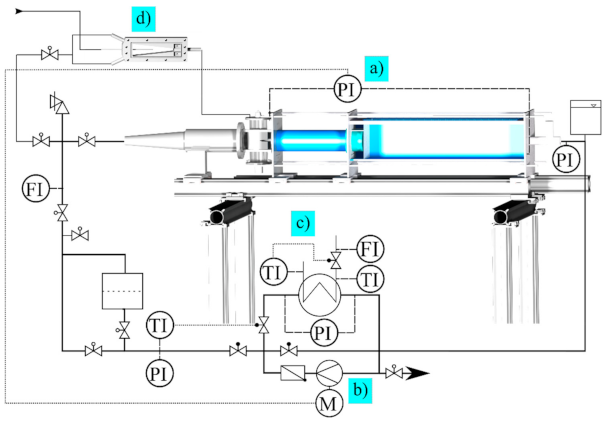
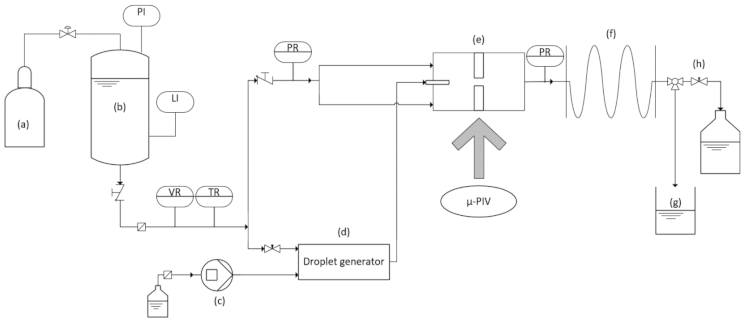
3.1.1. Time Resolved Investigation at the Macro Scale

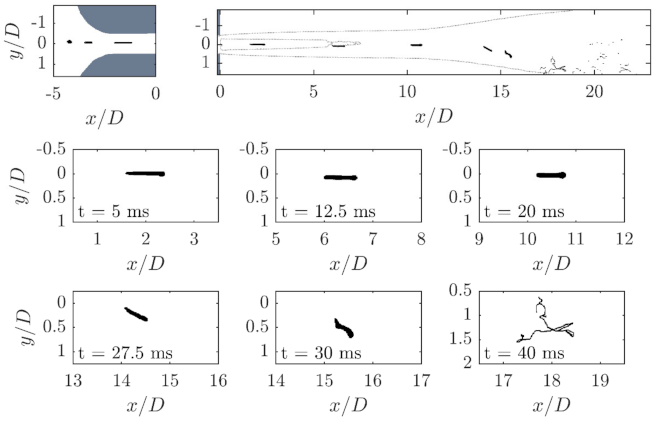
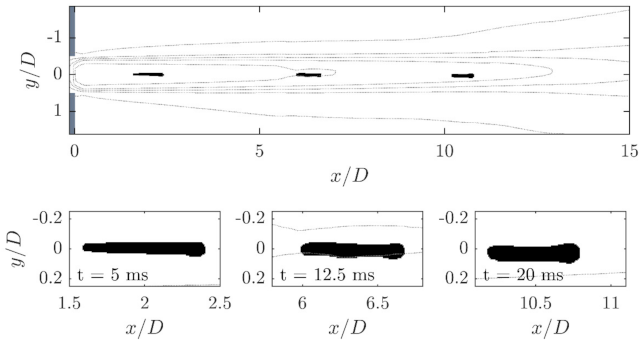
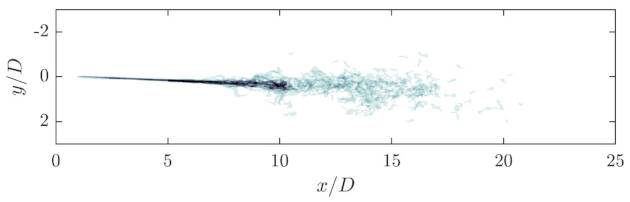
Figure 6 shows a time series of droplet image recordings before, inside and behind the orifice. These images correspond to a strictly scaled material system with a viscosity ratio $\lambda =3$ and $Re=2000$. The coordinate origin is in all representations the axis of symmetry of the orifice bore at the height of the orifice outlet. It is clear that the droplet is strongly deformed when passing through the orifice, but does not disintegrate. The aspect ratio ($l/d_{\mathrm{P}}$) of the elongated drop, which is the filament length divided by the diameter of the undeformed drop, is approximately 4.5. The deformation is caused by the shear and elongation flows in the inlet area, just upstream of and at the beginning of the constriction of the orifice. The droplet breaks up after the orifice, as it transitions from the laminar core area of the jet to the turbulent area of the free jet boundary layer. This happens in the $x/D$range between 10 and $14$.

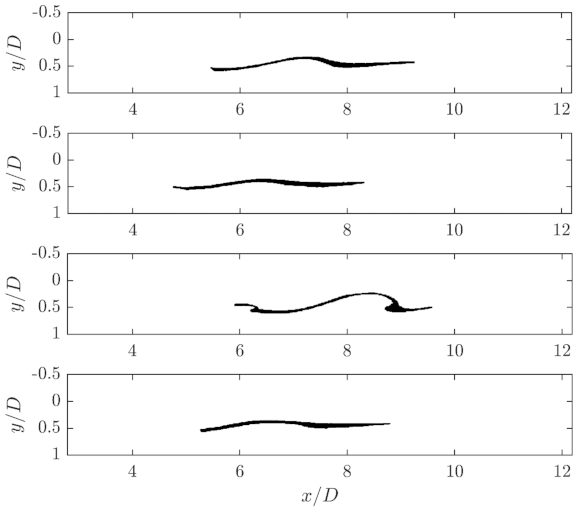
Until the droplet reaches this area, it travels relatively undisturbed within the core flow. Due to the absence of external stresses, the droplet can partially relax because the internal or restoring forces dominate. To visualize this process, three images of the same droplet at different times are shown in Figure 7. The decrease in length can be clearly seen in these enlarged views.

.

When the stable jet breaks down, the droplet follows the free jet, whereby the previously straight path is deflected. Due to the steadily increasing turbulence of the flow, the stretched droplet is deformed three-dimensionally. During this process, the filament is significantly stretched. The stretching of the filament due to the turbulent action is achieved by many simultaneously occurring drop-vortex interactions, which is why the filament is highly stretched within a very short time. This process is mainly dominated by turbulence and is highly three-dimensional and chaotic. The filament diameters can become very small, making an exact detection with the camera setup impossible.

Nevertheless, it is possible to observe single spherical secondary droplets in the wake of the free jet, which are caused by pinching of the filament. In the area of low velocity and turbulence downstream of the orifice, the stresses are no longer strong enough to stretch or break the stretched filament further, so that the fragments relax into round secondary droplets.

The localization of the droplet break-up on the area of the turbulent shear layer can be carried out by superimposing flow fields determined by PIV and the droplet position and has already been shown in Mutsch and Kähler [44]. Furthermore, this is shown by the temporally resolved turbulent droplet movement.

The droplet breakup occurs because the vortices deform and stretch the drop. The first vortices with which the droplet interacts are relatively large, since they are relatively undisturbed Kelvin-Helmholtz vortices, and therefore lead to a viscous 3D deformation and twisting of the droplet filaments. This drop-vortex interaction can also cause the droplet to stretch. As the process continues, the vortices become smaller in accordance with the vortex cascade, whereas the droplet or droplet filament becomes longer. Due to this increasing spatial extension compared to the eddies, the droplet interacts with several eddies simultaneously, which leads to a turbulent 3D twisting and stretching of the filament. Since the vortices stress the filament spatially differently, the elongation and the associated reduction in cross-section of the filament are not uniform. At a certain point, the filament breaks up into fine secondary droplets. However, this break-up does not take place simultaneously over the entire droplet filament, but occurs locally, depending on the stress ratio.

3.1.2. Comparison of the Droplet Trajectory

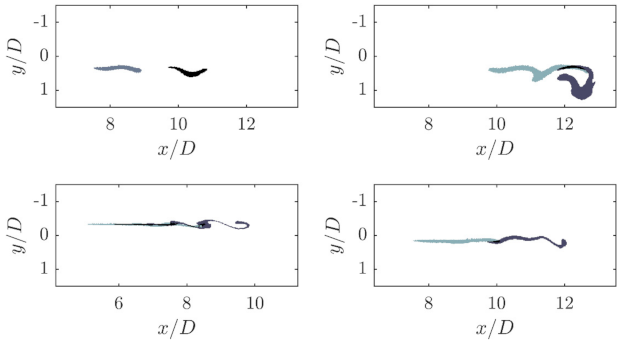
The droplet shown in Figure 6 flows through the orifice almost on the axis of symmetry. In the test plant used, the droplet feed point can be shifted relative to the orifice or the axis of symmetry, so that it is possible to investigate the influence of the droplet trajectory on droplet break-up. The droplet trajectory is characterized by the dimensionless radius of the droplet injection point:

$${\mathrm{r}}^{*}=\frac{r}{D/2 }$$

(3)

These investigations on the influence of the droplet trajectory show that the droplet feeding position or, in production plants, the statistical droplet distribution over the inflow cross-section has an important influence on the resulting droplet break-up. Figure 8 and Figure 9 show the evolution of droplets that have passed through the orifice on different trajectories compared to the path shown in Figure 6.

Droplets passing through the orifice close to the axis of symmetry (see Figure 6) are mainly pre-stretched by the elongational flow in the inlet area of the orifice. Due to the smooth flow along the axis of symmetry inside the orifice and in the core region of the free jet, this droplet has the longest time to relax, since the free jet core is statistically longest along the axis of symmetry. The droplet break-up therefore occurs comparatively far downstream. Droplets flowing further outside through the orifice reach the shear layer faster due to slight fluctuations in velocity and therefore break-up earlier.

.

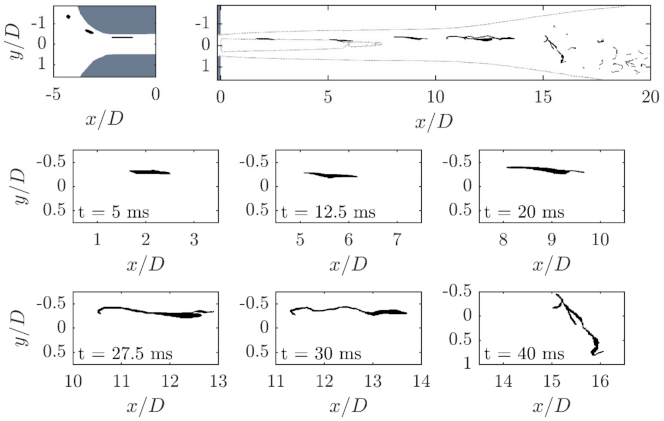
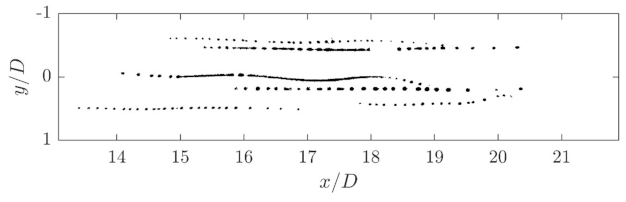
The droplet shown in Figure 8 is injected on a trajectory close to the edge of the channel (${\mathrm{r}}^{*}=0.8$) and is highly affected by the shear layer. The initially symmetrical droplet passes through the orifice in the area of the boundary layer. As a result, half of the droplet facing the axis of symmetry of the orifice is exposed to a higher flow velocity than the side facing away from the axis of symmetry of the orifice. As a result of this shear field, the droplet is deformed. In the time series shown in Figure 8, the inner trailing edge of the initially approximately cylindrical droplet filament appears to be shifted forward relative to the center of the drop. The outer trailing edge of the droplet stops according to the slow ambient flow, thus stretching the filament. As a result of this process, the filament length increases to a multiple of the cylindrical filament length created by the elongational flow in the inlet area of the orifice. From a running length of $x/D \approx 9$, the first vortices collide with the filament which is stretched further and further by the shear, so that a deformation perpendicular to the flow direction also occurs. This might be the effect of the Kelvin-Helmholtz vortex rings building up, whereby a slight wave movement of the filament is initially visible. As the turbulence of the free jet increases, the relatively ordered deformation of the droplet by the shear flow is replaced by a turbulence-induced deformation process. This causes a three-dimensional deformation process as described above in connection with the break-up of the droplet moving on the axis of symmetry of the orifice. The filament length increases very rapidly and the filament is simultaneously twisted three-dimensionally until it finally disintegrates.

Droplets that pass the orifice very close to the wall (${\mathrm{r}}^{*}=0.9$), like the one shown in Figure 9, experience a very high shear and elongation flow already at the entry, which is why the droplets are elongated to very high aspect ratios. Within the cylindrical part of the orifice, they continue to experience high shear flow, which is why the droplets can hardly relax. When leaving the orifice, the droplets quasi-immediately reach the developing shear layer and are influenced by it. The Kelvin-Helmholtz instabilities caused by the extreme velocity gradient at the edge of the free jet represent the starting point for all other vortices contained downstream in the free jet. Droplets, which already penetrate the shear layer early on, follow these first Kelvin-Helmholtz vortices very clearly. In some cases, several vortices can be visualized simultaneously, as well as the growth of these vortices by twisting of the filament.

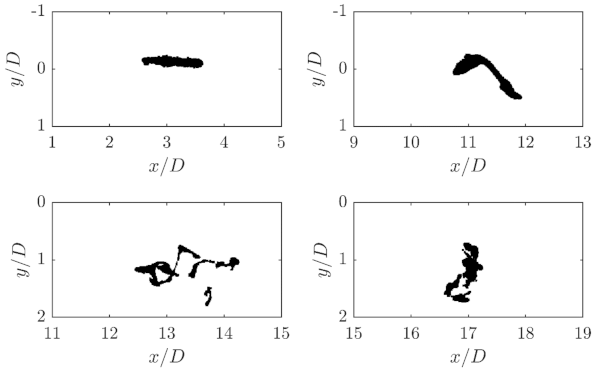
To illustrate this process, Figure 10 depicts four snapshots of a time series of the Kelvin-Helmholtz vortex–droplet interaction. It appears that the droplet filament is periodically deformed. When the filament reaches the center of the vortex, it becomes twisted into a very tight loop, resulting in a local compression or thickening of the filament. This shape is caused by the vortex accelerating the filament front outwards from the free jet. As the vortices move with the free jet in the direction of flow, this filament structure migrates downstream. In the area between two such Kelvin-Helmholtz vortex rings, the filament is stretched more strongly by the interaction with the vortices. This stretching is so strong that the filament periodically migrating in the range of $x/D=5$ to $8$ can no longer be clearly resolved.

Due to the extreme elongation which is already achieved within the orifice for droplets on these trajectories, the droplets disintegrate very quickly at small running lengths behind the orifice. With these trajectories, it is particularly clear that the droplet front disintegrates, while the rear part of the droplet filament is still unaffected and partly still within the orifice.

When comparing the time series in Figure 6, Figure 8 and Figure 9, it becomes clear that droplet break-up is dependent on the trajectory of the orifice. The closer the droplets are to the edge as they travel through the orifice, i.e., at the shear layer of the free jet flow, the easier the droplet break-up occurs. Based on this observation, it can again be confirmed that droplet break-up during high-pressure homogenization does not occur spontaneously or simultaneously for the entire droplet as a result of the Plateau-Rayleigh instability.

The extent of droplet deformation in the inlet area not only depends on the droplet viscosity or viscosity ratio and the initial droplet diameter, but also on the Reynolds number or flow conditions. In addition, the droplet trajectory plays a decisive role on the deformation when entering the orifice. The shear rates are very high particularly at the edge area of the orifice, causing the initially round primary droplet to be stretched to a long filament when passing through the cylindrical part of the orifice. A break-up of the droplet in this area of the orifice could not be observed in any measurement despite locally very high stresses.

Within the cylindrical constriction and in the core area of the free jet behind the orifice, there is, apart from the boundary layer close to the wall, a largely laminar flow without significant temporal and spatial fluctuations. Due to the absence of external stresses, a slight relaxation of the droplet filament occurs in this area. Only in the area behind the orifice, when the droplet enters the turbulent shear layer of the collapsing laminar free jet core, is the droplet subjected to a second stress period. The turbulent vortices cause a chaotic droplet deformation compared to the inlet into the orifice. In addition, the intensity of the deformation is significantly greater in most cases. The turbulent vortices lead to a further stretching of the in most of the time elongated droplet filament. Depending on the elongation, the filament is captured by several eddies at the same time from the onset, since the extent of the droplet is already so great that the droplet develops into several structures simultaneously. In the case of relaxed droplets, the interaction with the first high-intensity, large eddies cause renewed stretching. In the course of the droplet through the shear layer, in which the droplet or filament interacts with vortices again and again and is stretched further, the filament twists three-dimensionally until, at a certain point, the droplet breaks up into fine secondary droplets. At this range, the sequence of drop-vortex-interactions is so fast that no relaxation occurs. The observed break-up does not necessarily take place in the entire filament at the same time, but takes place depending on local elongation or superimposed external stress. After the primary droplet has broken up into smaller secondary droplets, no further disintegration of the resulting droplets can be observed, but the secondary droplets are transported downstream only by the superimposed convection. With increasing distance from the orifice, the intensity of the turbulent eddies decreases, so that no further break-up step takes place downstream. This is also unlikely due to the higher energy required for breaking up smaller droplet diameters, so that a single-stage break-up process can be assumed at the investigated process conditions.

3.1.3. Influence of the Reynolds Number

The influence of the Reynolds number of the flow on the droplet deformation can be shown in Figure 11. As already shown in the comparison of the flow fields [41], the turbulent free jet zone shifts towards the orifice, since the free jet becomes unstable more quickly due to the higher velocity gradients and therefore the laminar core area decays earlier. The relative velocity fluctuations are similarly large as in the case of $Re=2000$, but the reference value is significantly larger, so that the absolute velocity fluctuations are also significantly larger for $Re=5700$. The disintegration of the droplets therefore takes place much earlier along the x-axis ($x/D=5$) and also faster, i.e., over a shorter distance after the beginning of the turbulent area.

In addition to the accelerated break-up behavior due to the higher Reynolds number, the elongation of the droplets changes due to the elongation flow in the inlet area of the orifice.

Figure 12 shows a comparison of two droplets after passing through the orifice at $Re=2000$ and $Re=5700$ on the meso scale. Relaxation of the droplets can be neglected. It is clear that an increase in Reynolds number leads to an increase in the elongation of the droplet to a longer filament. A more detailed study of the elongation of the droplets as they pass through the orifice can be found in Mutsch et al. [49].

3.1.4. Scale Comparison

The phenomena detected at the macro scale can also be observed on non time-resolved images at the two smaller experimental facilities, M1 and M5. Since PIV cameras, that can record double image, are used for droplet visualization at these scales, individual droplets can sometimes be observed over two time steps, so that not only individual snapshots but also droplet movements and deformations can be detected.

Therefore, in the following section, the phenomena are first presented in their original scale as evidence of the processes shown above.

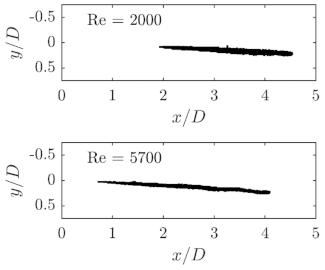
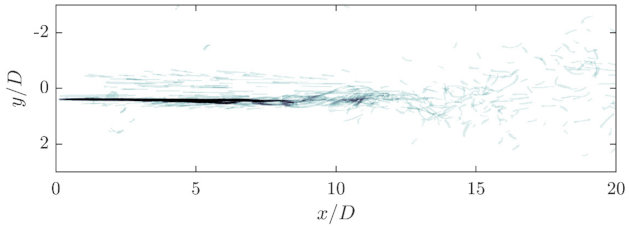
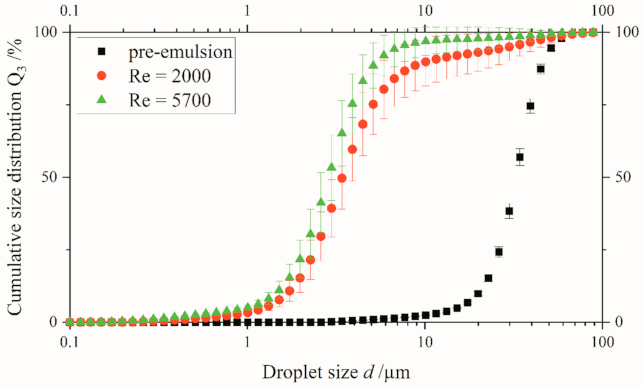
Figure 13 depicts a superposition of several droplet images from the original system downstream of the orifice exit. The grey intensities are intended to show the overlapping of several droplets and help to better follow the individual filaments. The Reynolds number of the flow from the droplet images shown is $Re=2000$, while the viscosity ratio equals $\lambda =3.5$. The deformation of the droplets is clearly visible and fits well with the droplet filaments observed on the macro scale, which are deformed by several vortices.

Due to the shown superposition of the individual droplet images, it appears that the droplet break-up occurs closer to the orifice than on the macro scale. This conclusion is supported by the fact that only larger or clearly recognized and deformed droplets are shown as droplets; this is necessary due to the lower spatial resolution. The comparison of the flow fields (Preiss et al. [41]) shows, however, that the flow fields are spatially similar, so that a coincident droplet break-up location can be assumed.

On the original scale as well, the Kelvin-Helmholtz vortices play an important role in the breakup of the droplets. This is due to the fact that droplets break-up directly within this vortex structure, but also because the further vortex cascade has its origin here.

The deformation of droplets due to the interaction with the Kelvin-Helmholtz vortices that have not yet detached is shown in Figure 14. The central figure again shows a superposition of several droplets deformed by the Kelvin-Helmholtz vortices, whereas in the other figures below, individual droplets are shown in pairs for the sake of a better overview.

It becomes very clear that the elongated filaments leaving the orifice at the edge are deformed by the vortex structure. In addition, the growth of the vortex structures becomes visible with increasing length. At first, the filaments only oscillate slightly, which can be seen in a slight wave motion of the otherwise straight droplets. With longer drop-vortex interaction, the filaments increasingly follow the vortex structure and are sometimes even twisted into loops. This process is accompanied by a slight further stretching of the filaments in addition to the deformation. Since the images can only be taken from one viewing direction and the free jet diameter exceeds the depth of field of the images, only droplets that are deformed in the xy-plane are shown, but it seems plausible, especially through the investigations in the macro scale, that these processes occur similarly in the entire free jet mantle area.

Figure 15 shows double images of droplets taken at different times to show several deformation phenomena already seen at the macro scale to prove the similarity between the different scales. In this illustration, the images of the two time steps are superimposed so that the individual droplets of the different time steps can be seen as well as the evolution of the deformation process. The second droplet is displayed darker. These images clearly show the movement of the droplets and the twisting of the droplets. Again, due to the optical restrictions in this setup, it can only be assumed that the filaments are twisted three-dimensionally, which is considered very reasonable.

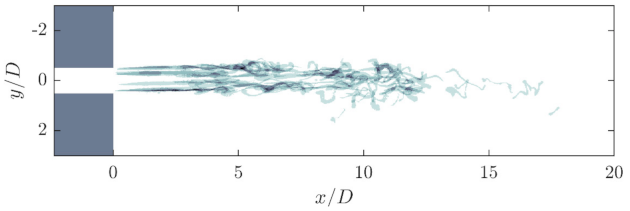
In the experimental system scaled with a scale factor of 5, two trajectories, namely at the axis of symmetry of the orifice (${\mathrm{r}}^{*}=0$) and at a position further to the edge (${\mathrm{r}}^{*}=0.75$), can be investigated in the investigations on droplet break-up. The primary droplet size was set to about 200 µm. Figure 16 shows a superposition of about 700 individual droplets entering the orifice on the axis of symmetry in the area of the free jet behind the orifice.

Only deformed droplets are shown. It is clear that most of the droplets exit the orifice on a narrowly defined path. On this scale also, a stable free jet core is initially seen, in which the droplets are hardly stressed three-dimensionally. However, the figure also shows that the droplet path is slightly inclined and is also true for the exiting jet (not shown here). This may be due to the fact that the orifice bore is not exactly parallel to the channel due to manufacturing or alignment inaccuracies. In the range of $x/D \approx 10$, the droplet swarm begins to expand and leave the uniform trajectory because the droplets follow the turbulent decaying free jet, whereby they are also deformed. Due to the fact that not all droplets pass through the orifice on the same trajectory, or because already broken-up droplets are returned to the free jet by the recirculation flow, the break-up of the droplet trajectory in the range of $x/D \approx 10$ can be somewhat overestimated.

Figure 17 shows individual droplets from different stages in the free jet. At first, the elongated droplet can be seen in the core area of the free jet. In the further course, large scale deformations of the droplet are visible at a run length of $x/D \approx 11$. Since the deformations in the turbulent area of the free jet are very fast, the droplet shown in the next step is already deformed to a much greater extent by small-scale vortices. The droplet shown in the last figure is so strongly deformed that no clear structure can be seen. This image may be affected by the fact that fine structures, such as filaments, are either not resolved or are not recognized as droplet filaments during the digital evaluation. It is also possible that several fragments are superimposed and thus create the impression of a very large droplet fragment. Furthermore, when comparing the displayed individual images, it must be noted that the temporal course of a droplet is not shown, rather four individual droplets at different points in time and space are displayed. The droplets may differ slightly in their initial size and trajectory.

The influence the droplet trajectory has on the droplet breakup can be seen by comparing Figure 16 and Figure 18. Figure 18 shows the summed-up images of droplets exiting the orifice closer to the edge of the orifice.

It can again clearly be seen that most of the droplets pass the orifice on the same path. Beside this main trajectory, however, some single droplets are also visible, which do not run on this trajectory, but are distributed over the entire free jet cross-section and pass the orifice. These droplets can be already broken-up droplets that are drawn inwards into the free jet from the surrounding area. With the droplets moving on the desired trajectory, it is clearly visible that the droplet shape or the initially straight path is twisted at $x/D \approx 8$ and the free jet breaks up. In the range of $x/D \approx 10$, a clear wave motion of the trajectory can be seen, which is caused by an increasing Kelvin-Helmholtz vortex, which at this running length of the free jet is apparently large enough to deflect the droplets along their trajectory. Figure 19 shows four droplets that are deformed by these Kelvin-Helmholtz vortices. Downstream, the droplets break-up into smaller filaments that follow the turbulent flow in the free jet layer.

In the case of $Re=5700$ (see Figure 20), the trajectories of the droplets in the beginning are also clearly recognizable. However, especially in the case of the droplet injection on the axis of symmetry, a clear shift of the point of break-up of the droplets towards the orifice can be seen. This observation fits very well with the observations of the flow fields [41]. In the case of the droplets that are not dosed on the axis of symmetry of the orifice but rather at the edge of the orifice (see Figure 21), the free jet or the point of break-up does not appear to be shifted forward at first, but this may be due to the visualization or superposition of the droplets. A closer look reveals that the droplets deviate from the uniform path already at a run length of $x/D \approx 5$. In addition, the droplet break-up seems to have already been completed at a run length of $x/D \approx 18$, as filaments are no longer visualized.

In the investigations on the droplet break-up of eccentrically dosed droplets at $Re=2000$, a different break-up mechanism than what is observed on the macro scale can be seen for certain droplets. These droplets do not break up according to the turbulent decay pattern described above, but rather to the Plateau-Rayleigh instability. To illustrate this principle, a compilation of individual droplet break-up images is shown in Figure 22. This break-up mechanism can only be observed under these operating conditions and only for measurements from a distance of $x/D \approx 13$ onward. Consequently, it can be stated that this break-up mechanism takes more time compared to the turbulent break-up mechanism and a critical stretching is required.

It can be clearly seen that the droplets that are stretched into long filaments break-up into a series of droplets of almost the same size. Therefore, when a very narrow size distribution is desired, this instability mechanism should be used to generate the droplets. The disintegration begins at the ends and continues towards the middle over the entire length of the filament. The droplets are distributed over the entire free jet and are not particularly strongly deformed three-dimensionally. Therefore, it does not appear to be the primary droplets on the set droplet trajectory, but rather droplets drawn into the free jet from outside. These can be partially unbroken droplet fragments or larger droplets in the backflow area due to coalescence of smaller droplets.

3.1.5. Influence of Viscosity Ratio

In order to further investigate the influence of the droplet viscosity or the viscosity ratio between the disperse and continuous phases, additional experiments were carried out with oil droplets of various viscosities. Here, the elongation of the droplet in the inlet area of the orifice can be identified as the main difference.

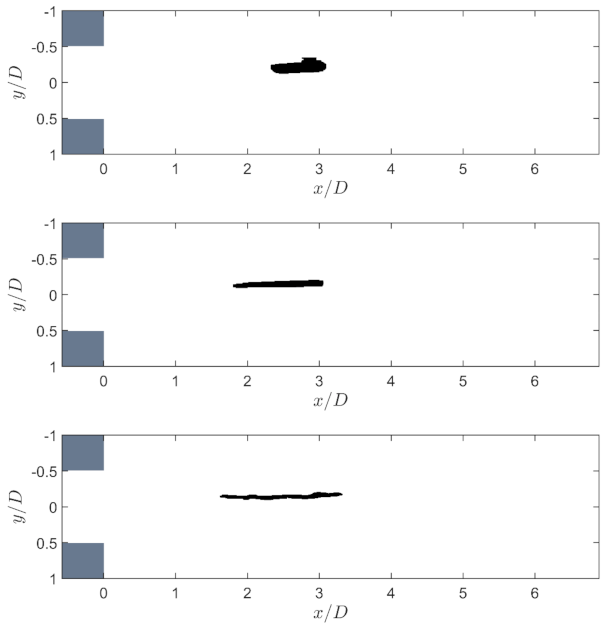
Figure 23 shows three droplets shortly after passing through the orifice close to the axis of symmetry of the orifice at $Re=2000$. The viscosity ratios in these experiments are $\lambda =0.3$, $\lambda =3.0$ and $\lambda =10.8$. It is clear that the low viscosity droplet was stretched the most. The droplets with higher viscosity ratios are significantly less stretched. The primary reason for the noticeable droplet elongation is the superposition of the shear and elongational flow in the inlet area of the orifice. Although $Re=2000$ is comparatively low, the elongation of the low viscosity droplet is already very high. The $\lambda =3.0$ droplet is stretched to a thin filament, but it remains only about half as long as the low viscosity drop. The $\lambda =10.8$ droplet is also stretched, but the elongation is rather small. The aspect ratios based on the length of the filament and the primary droplet diameter are approximately 8, 6 and 3.5, in order of increasing viscosity ratios.

A more detailed investigation of the elongation behavior of the droplets as they pass through the orifice and a comparison to numerical models can be found in Mutsch et al. [49].

As the droplets shown are still in the core area of the free jet, they have hardly undergone any further deformation up to this point. Only when the droplet filaments enter the turbulent flow area of the free jet do the droplets undergo further deformation and elongation, as shown above. The influence of viscosity is shown by the fact that the low viscosity droplet is elongated into a long filament due to the laminar flow into the orifice and the associated stresses, whereas the droplets of higher viscosity are significantly less elongated. Due to this large linear elongation, the droplet already extends over a wide range at the beginning of the drop-vortex interaction, so that several vortices act simultaneously on the droplet already at the beginning of its entry into the turbulent shear layer. In addition, the droplet diameter is comparatively small due to the pre-expansion. Furthermore, these first vortices have a very high intensity and contribute to a very strong deformation and elongation of the drop. The highly viscous drop, on the other hand, is hardly spatially stretched due to the laminar flow in the inlet of the orifice. Therefore, the first vortices mainly interact with the droplet individually and their high intensity initially contributes to stretching and elongating the rather round or elliptical drop. In order to illustrate the different break-up processes at different viscosity ratios, Figure 24 and Figure 25 portray two time series of the droplet break-up process behind the orifice of both a low and a high viscosity drop, respectively.

The figures show that the highly viscous droplet in the core area of the free jet initially relaxes almost completely. The low viscosity droplet could also relax in this low-stress area, but the time span is too short-and the restoring force is too small-to reverse the very high elongation, so that complete relaxation of the filament does not occur. When the turbulent shear layer is reached, the relaxation ends and both droplets are deformed again as the external forces predominate. As described above, the low viscosity droplet disintegrates very quickly due to the stress of several vortices, whereby it is first stretched to form a long, thin and twisted filament. The diameter of the three-dimensionally stretched filament is too small to be visualized clearly with this measurement technique or setup.

The highly viscous droplet initially meanders with the fluid, since the first, individual eddies are not sufficient to deform the droplet by shear. Only when several eddies meet is the droplet stretched. Similarly, the droplet is, in this case, twisted into a three-dimensional filament, but this filament is neither as long nor as thin as in the $\lambda =0.3$ drop. Finally, the $\lambda =10.8 \mathrm{droplet}$can also be broken up at $Re=2000$, but the droplet size achieved appears to be much larger than in the case of low viscous droplets.

3.2. Droplet Size Distribution

Due to the low disperse phase concentration, it is not possible to determine the droplet size distributions by laser diffraction on this scale (M50). In both the original and the M5 scales, it is possible to determine droplet size distributions due to the test procedure with a pre-emulsion or a series of monodisperse primary droplets, because higher disperse phase fractions can be reached. Figure 26 illustrates the droplet size distribution of the pre-emulsion as well as the secondary droplet size distribution of two processed emulsions at $Re=2000$ and $Re=5700$.

The pre-emulsion has an average droplet diameter of $d_{50,3}=32 \mu \mathrm{m}$. Due to homogenization, the mean droplet size is strongly reduced for both investigated Reynolds numbers. The mean droplet diameter at $Re=2000$ is approximately $d_{50,3}=3.7 \mu \mathrm{m}$, while it is rather $d_{50,3}=3.4 \mu \mathrm{m}$ at $Re=5700$. Despite almost tripling, no significant difference can be determined. Although the average droplet size is relatively constant, there is a difference in the droplet size distribution, which is evident in the upper droplet size range. The emulsion loaded with lower stresses showcased, in certain measurements, a slightly bimodal droplet size distribution with an appreciable proportion of coarse droplets, but due to the high standard deviations, no significant differences could be determined for the $d_{90,3}$ droplet size.

These differences in the droplet size distribution may be due to the fact that the turbulent vortex structures are generally intense enough at both Reynolds numbers to stretch the droplets and to break them up when sufficiently stretched. Since the time-resolved measurements have shown that only a one-step break-up process from the primary droplet to the fine secondary droplet swarm takes place, the break-up with respect to the fine particles seems to proceed similarly at both loads. However, coarser droplets persist at the lower stress level, which can be seen in the upper part of the distribution. This may be due to the inhomogeneity of the turbulent structures. The coarse droplets are formed from sections of the droplet filaments that have not been subjected to very high stress, while the opposite is true for fine droplets. Under comparatively favorable conditions, even at the lower Reynolds number, very fine filaments and finally droplets seem to be produced by the vortex structures, but the probability of these intensive spots seems to decrease, so that more coarse filament segments remain, which eventually disintegrate if stretched for long enough. The large deviations between the measurements can also be a result of pressure fluctuations if the flow was not yet in a steady state after opening the valve of the pressure vessel.

On the meso scale, the disperse phase content was too low to use the laser diffraction method to analyze the droplet size distribution, but an automated image analysis system was used to analyze the droplet size distribution. The resulting droplet size distribution at $Re=2000$ depending on the droplet trajectory which was processed on the M5 scale is depicted in Figure 27. The pre-emulsion has a droplet size of ~208 µm. The droplets enter the orifice either on the center axis or close to the wall.

The monodisperse emulsion is broken into droplets within the range of $0.6 \mu \mathrm{m}<d<20 \mu \mathrm{m}$ for both trajectories. A mono modal droplet size distribution is found for both trajectories. Droplets which travel on a trajectory close to the wall result in significantly smaller secondary droplets compared to droplets which travel on the center axis of the orifice. An average droplet size of $d_{50,0}=2.29 \mu \mathrm{m}$ is determined for droplets on the trajectory close to the wall, while the secondary droplet size is rather $d_{50,0}=2.74 \mu \mathrm{m}$ on the center axis trajectory.

4. Discussion

The results displayed in this article prove that it is possible to upscale the local events in high-pressure dispersing units, both from the point of view of flow characteristics and the response of droplets to them in terms of deformation and break-up. This enables, in particular, investigating specific effects mechanistically and to select the appropriate scale for each case. In contrast to Hakansson [39], great importance was assigned to a strictly geometric scaling and to an exact scaling of the other parameters.

The results shown here and in Preiss et al. [41] depict that droplet break-up in a restricted free-jet as found after high-pressure orifices is largely controlled by turbulence and droplet vortex interaction. The vortices are created by the Kelvin-Helmholtz instability, the roll up of the very steep velocity gradient between the free jet and the resting ambient fluid. As a result of instabilities, the vortex rings around the free jet detach asynchronously, causing the free jet to change into a turbulent flow field and meander spatially as the run length increases after the core region. The disintegrating vortices overlap, lose intensity and size until the energy is completely dissipated. Droplets entering this area are deformed and stretched by the vertical motion. The viscosity ratio, the Reynolds number which influences the absolute turbulence intensity and, due to the inhomogeneity of the turbulence, the trajectory of the droplets all play a significant role. In addition, the trajectory of the droplet plays an important role since the droplets in the inlet area of the orifice are stressed and stretched differently depending on the trajectory.

The significant influence of the droplet trajectory on the droplet break-up can be shown by the time-resolved experiments in the macro scale and also by the series of experiments with droplet size analysis in the scale M5.

The macro scale measurements show that the droplets on the different trajectories are stretched to different extents as they pass through the orifice and thus have different initial states due to the laminar flow stresses. Downstream of the orifice, the droplets reach the shear layer at different times due to their trajectory and the shape of the free jet. This is accompanied by different stress processes in the area behind the orifice, especially in the turbulent shear layer. The peripheral droplets are stretched in the orifice inlet much more than the droplets flowing centrally through the orifice and are therefore significantly longer. Behind the orifice, these droplets reach the shear layer much earlier. Moreover, the shear layer is not yet completely turbulent at this early stage, but rather the droplet filaments follow the Kelvin-Helmholtz vortices. In this process, the droplets are elongated and stretched very much and disintegrate very shortly behind the orifice. The droplet passing centrally through the orifice is less stretched due to the laminar elongation flow at the orifice inlet. Behind the orifice, after a short phase without external stress in the core area of the orifice in which the droplet may relax slightly, this droplet reaches the shear layer, in which it is stretched by the vortices and finally disintegrates.

Similar to the variation of the trajectory of the drop, the variation in viscosity ratio appears to have a comparable effect. Compared to high viscosity droplets, low viscosity droplets are already elongated by the inlet elongational flow of the orifice as seen in Kelemen et al. [32], so that the first high-intensity vortices do not interact with a round droplet or short droplet filament and lead to elongation, but with droplets that are already extended over a wide space. They interact directly with several high-intensity vortices at the same time and are thus broken up faster.

The secondary droplets are formed by the breaking of the droplet filaments when they are supercritically stretched by the turbulent structures for a sufficiently long period of time. The fact that even highly viscous droplets with a viscosity ratio greater than $\lambda =4$ can be disintegrated in turbulent flows is a sign that, in addition to the high shear forces, strong three-dimensional elongation flows due to the interaction of several vortices with the droplet also play a decisive role. The observations show that the disintegration of the stretched filament only takes place in the region of lower turbulence intensities can be explained by the experiments of Stone et al. [50], in which the disintegration only took place after the external flow field was switched off, or by the fact that the elongation must exist for a sufficiently long period of time before individual areas of the filament are pinched off so that the droplet disintegrates. This needed time or elongation is not reached during the first interaction with strong vortices but after several interactions, even though the later ones are less intense, causing the elongation rate of the droplet to decrease, but remain positive.

Given the elongation of the primary droplets in the laminar elongation flow and especially in the transition area from the laminar free jet core to the turbulent shear layer, the droplets are axially stretched by intensive and large eddies. Therefore, the investigated droplets or droplet filaments are always larger compared to the subsequent vortices. Furthermore, despite the existing difference in density, the droplets follow the flow closely and therefore experience a continuous load curve without abrupt load changes. As a result, the filament is constantly deformed and stretched. However, what becomes clear is that the droplets interact with different sized vortex structures as they pass through the shear layer until they disintegrate. This can lead to local small-scale deformations that overlay the integral twisting of the filament. This can also be observed in the investigations of Innings et al. [31]. Nevertheless, no droplets were observed where turbulent velocity fluctuations lead to a tearing of secondary droplets from a primary droplet.

These observations of the break-up process from the time-resolved macro scale can be found again in the micro and meso scale images. In addition to the break-up mechanism, the droplet break-up location can also be determined more precisely on the basis of the investigations and lies within the turbulent shear layer. This corroborates previous investigations, such as Innings et al. [30] and Galinat et al. [28,29], where the droplet break-up is also located in the area of the turbulent shear layer.

The Plateau-Rayleigh instability mechanism observed on the meso scale with some secondary droplets drawn into the free jet from the outside, in which the droplets break-up into a large number of fine droplets of almost identical size, is further evidence that droplet break-up requires an extremely long, stretched droplet filament. This break-up mechanism can also be seen in the figures of Kelemen et al. [32], where the Reynolds number was significantly lower in these investigations ($Re=285$) and the viscosity ratio was slightly lower ($\lambda =2$). This lower viscosity ratio may be the reason why the aspect ratio in the investigations of Kelemen et al. [32] may be significantly higher than in the present investigations.

The fact that this break-up mechanism could only be observed at this size scale can be explained by the fact that on the macro scale, the disperse phase concentration is significantly lower. Therefore, hardly any secondary droplets are present in the recirculation area. Since the primary droplets experience a different stress profile at all tested injection positions, this disintegration process was not investigated. On the micro-scale, the resolution may not be sufficient to observe this decay process of the secondary droplets, or the relatively rare break-up on the meso scale is not recorded statistically.

During the investigations in the original scale, the disperse phase fraction was set large enough to carry out a conventional droplet size analysis by laser diffraction. The measurements showed that, in the investigated Reynolds number range, the Reynolds number has an almost negligible effect on the resulting droplet size distribution. The droplet size distribution may be due to the fact that, individual droplets or droplet fragments are not completely broken up, but leave the highly turbulent area of the free jet without being subjected to strong stress, and therefore without having been stretched particularly strongly. The corresponding areas of the droplet filament may be nodes or narrow folding points [51] of the twisted filament which have been less stressed by drop-vortex interaction. Since the mean droplet size is nearly the same for the Reynolds numbers investigated, the higher turbulence intensity seems to have only a minor influence on the size of the actually more stressed droplet filament areas. The finest particles can be satellite droplets, which can occur during break-up due to Plateau-Rayleigh instabilities or end pinching [50,51]. On the meso scale, the measurements showed that the primary droplets with an average droplet size of about 208 µm were broken up into secondary droplets in the size range of 0.6–20 µm. This size range was found for both trajectories (central axis or close to the edge). Nevertheless, the size distribution was different. Droplets on the trajectory close to the edge of the orifice resulted in smaller droplets compared to droplets on the central trajectory. This indicates that the higher deformation of the primary droplets, caused by the high shear close to the edge of the orifice and the high turbulence in the shear layer, results in smaller secondary droplets. The smaller resulting droplet size distribution of the droplets which travel on a trajectory close to the wall can be caused by the stronger deformation when leaving the orifice, as previously shown, prior to droplet break-up in the turbulent shear layer. The thinner deformed droplets are stretched further by vortices and subsequently broken up. The break-up of secondary droplets entrained again into the jet from the recirculation region and broken up following the Plateau-Rayleigh mechanism does not result in a multi modal size distribution. This may be due to the fact that this break-up process has only been observed very rarely and therefore has no particular influence on the droplet size distribution. It is hypothesized that the influence of the droplet trajectory on the resulting droplet size distribution is increasing with decreasing distance to the wall which will be investigated in future research.

5. Conclusions

The investigations on droplet break-up at three different experimental scales show that the approach of scaling droplet break-up in high-pressure orifices can be used to investigate droplet break-up in high-pressure homogenizers on a mechanistic level. While local flow conditions could be well investigated at all scales, specific effects in droplet disruption require exact up-scaling of both geometric and operating conditions. With respect to droplet break-up, the processes with high spatial and temporal resolution were investigated in the system scaled with a scale factor of 50. It was found that droplet break-up is mainly caused by the turbulence prevailing in the decaying free jet behind the orifice. The influence of viscosity ratio, droplet trajectory and Reynolds number on droplet break-up was investigated. As the droplets pass through two stress periods, first when entering the orifice and subsequently in the free jet behind the orifice, it is not possible to separate the individual parameters and their influence on the break-up. That being said, an integral consideration has been made in this manuscript.

After having investigated the viscosity ratio, it is clear that a lower viscosity ratio leads to a longer elongation of the droplet filament due to the inlet flow. This stretched droplet filament breaks up very easily in the turbulent area of the decaying free jet. Due to the turbulent vortices, the filament is stretched very long and twisted three-dimensionally until it finally breaks up into secondary droplets. As the viscosity ratio increases, the pre-stretching of the droplets in the orifice inlet decreases and the droplets are essentially only stretched in the turbulent shear layer. Due to the short residence time in the high-intensity region required for the entire elongation, the final droplet size seems to be larger than at low viscosity ratios. Since the investigations on viscosity ratios were only carried out on a macro scale, a droplet size analysis could not be performed in contrast to the investigations on droplet trajectory and Reynolds number.

The trajectory of the droplet through the orifice and then through the free jet also has a clear influence on droplet break-up. For droplets passing through the orifice in the boundary layer or the edge region, the break-up process is determined to a large extent by the intense vortices of the Kelvin-Helmholtz shear layer. For the remaining droplets passing through the orifice, the disintegration takes place further downstream in the turbulent shear layer.

Droplets with a trajectory close to the wall resulted in smaller droplets compared to droplets on the center axis. But the trajectory had no influence on the width of the droplet size distribution and did not cause a multi modal droplet size distribution.

The effects of the Reynolds number on droplet break-up were also investigated. It was shown that at higher Reynolds numbers, droplet break-up occurs earlier behind the orifice and is faster. However, the effects on droplet size distribution, which were only investigated on the micro scale, are very small in relation to the mean droplet diameter.

Drop break-up due to Plateau-Rayleigh instabilities were observed on the meso scale for some single droplets entrained from the backflow. Due to the experimental conditions in the macro scale, this process could not be observed with temporal resolution. Since this mechanism is not visible in the original scaled investigations either, it seems to be a very rare event which, under the given conditions (especially at higher Reynolds number), does not seem to have a significant effect on the droplet size distribution.