Abstract
Properties of emulsions such as stability, viscosity or color can be influenced by the droplet size distribution. High-pressure homogenization (HPH) is the method of choice for emulsions with a low to medium viscosity with a target mean droplet diameter of less than 1 µm. During HPH, the droplets of the emulsion are exposed to shear and extensional stresses, which cause them to break up. Ongoing work is focused on better understanding the mechanisms of droplet breakup and relevant parameters. Since the gap dimensions of the disruption unit (e.g., flat valve or orifice) are small (usually below 500 µm) and the droplet breakup also takes place on small spatial and time scales, the resolution limit of current measuring systems is reached. In addition, the high velocities impede time resolved measurements. Therefore, a five-fold and fifty-fold magnified optically accessible coaxial orifice were used in this study while maintaining the dimensionless numbers characteristic for the droplet breakup (Reynolds and Weber number, viscosity and density ratio). Three matching material systems are presented. In order to verify their similarity, the local velocity profiles of the emerging free jet were measured using both a microparticle image velocimetry (µ-PIV) and a particle image velocimetry (PIV) system. Furthermore, the influence of the outlet geometry on the velocity profiles is investigated. Similar relationships were found on all investigated scales. The areas with the highest velocity fluctuations were identified where droplets are exposed to the highest turbulent forces. The Reynolds number had no influence on the normalized velocity fluctuation field. The confinement of the jet started to influence the velocity field if the outlet channel diameter is smaller than 10 times the diameter of the orifice. In conclusion, the scaling approach offers advantages to study very fast processes on very small spatial scales in detail. The presented scaling approach also offers chances in the optimization of the geometry of the disruption unit. However, the results also show challenges of each size scale, which can come from the respective production, measurement technology or experimental design. Depending on the problem to be investigated, we recommend conducting experimental studies at different scales.
1. Introduction
Emulsions have a wide field of application and can frequently be found, among others, in the chemical, pharmaceutical and food industry. Their properties, such as stability, viscosity or color, can be influenced by the droplet size distribution (DSD) which is set during the production process. Emulsions with a low to medium viscosity of 1–200 mPa∙s are mostly produced with the high-pressure homogenization (HPH) process [1], during which droplet diameters of less than 1 µm can be achieved. A high-pressure homogenizer consists of a high-pressure pump and a subsequent disruption unit. During the process, a pre-emulsion that still has large droplets is pumped through the disruption unit at a pressure of several hundred bar. In the disruption unit, the emulsion’s flow is strongly accelerated by a reduction of the cross-section where the droplets are exposed to shear and elongational strain stresses [2], which then deform the droplets to either ellipsoids or thin threads [3], depending on the process conditions before leaving the disruption unit as a limited free jet at the outlet. The deformed droplets are exposed to turbulent viscous and turbulent inertia forces [4,5] in the turbulent free jet, where finally the droplet breakup takes place [3,6].
Bisten et al. [2] and Kelemen et al. [7] already investigated the flow pattern in modified orifice-type HPH disruption units. They located the areas with the highest strains in the inlet region and the highest velocity fluctuations at the outlet. Comparable investigations in scaled high pressure homogenizer flat valves were made by Håkansson et al. [8] and Innings et al. [9].
The breakup of the droplets has already been investigated in detail under stationary laminar conditions [10,11,12,13]. However, these findings cannot be transferred 1:1 to the complex flow field in a high-pressure homogenizer. The stresses on the droplets are continuously changing during their passage through the disruption unit and thus no stationary conditions are achieved.
The influence of the process parameters and geometry on the resulting stress history as well as the influence of this stress history on the droplet breakup itself are the focus of current research [14,15,16,17,18].
Kelemen et al. [3] and Bisten et al. [2] have visualized the droplet deformation and breakup in modified optically accessible orifices. Innings et al. [6] have performed comparable investigations in an optically accessible high-pressure homogenizer flat valve.
Since the dimensions of the disruption unit is in the micrometer scale and the droplet breakup takes place in the nanometer scale at short time scales, the resolution limit of current measuring systems is reached. Furthermore, high pressures and high velocities restrict the inside view of the process. Therefore, scaling of the process is a promising approach to get a better understanding of the droplet breakup mechanism in high-pressure homogenizers (HPH). First investigations on the scalability of breakup processes were made by Walzel [19]. As there is no widely accepted approach on which dimensionless numbers have to be kept constant when scaling the droplet break in an HPH, a number of approaches were used in the past. Kolb et al. [20] only maintained the geometrical similarity and the Reynolds number in the smallest gap of the orifice. Budde et al. [21] further included the viscosity ratio, the density ratio and the Weber number. Innings et al. [5] additionally included turbulent quantities, for example, the Kolmogorov length, in their scaling approach. Although the three investigations used different viscosity ratios and Reynolds numbers, they all showed similar droplet behavior downstream from the constriction. The deformed droplets were further deformed into complex basketlike shapes when entering the turbulent mixing area of the free jet and subsequently broke up in many small droplets [5]. However, the scaled system of Kolb et al. [20] resulted in a relaxation of the deformed droplet before leaving the constriction. In contrast to that, the scaled system of Budde et al. [21] resulted in significant higher deformation of the droplets when leaving the orifice compared to the other investigations. The differences of the droplet deformation might be caused by differences in the geometry of the disruption unit and in the process parameters used, for example, the viscosity ratio. Håkansson [22] has already shown that variations in droplet breakup in differently scaled high-pressure homogenizers are presumable if the similarity of the process parameters is not obtained. Therefore, complete physical and geometrical similarity of the homogenization system should be achieved.
Using a similarity approach, this investigation concentrated on scaling factors for droplet breakup mechanisms of oil-in-water emulsions in high pressure orifices. By using this similarity approach, the dimensionless numbers characteristic for the droplet breakup (Reynolds number Re, Weber number We, density ratio κ, viscosity ratio λ) were maintained in order to preserve all processes involved in the droplet breakup. Two scaling factors were chosen, namely 5 and 50. The original scale orifice (scaling factor of 1) had dimensions that correspond to typical laboratory high-pressure homogenizers. The scaling approach used by Budde et al. [21] was used here to determine the geometry dimensions and the material properties while maintaining all relevant quantities.
Flow patterns and the transient droplet breakup were visualized in detail. Flow patterns were characterized in more detail and compared on a nondimensional basis, following the hypothesis that droplets should move in equal flow fields in all scales to guarantee equal conditions for droplet breakup.
2. Materials and Methods
2.1. Droplet Breakup Scaling Theory
When investigating the droplet breakup, a droplet with a viscosity , a density , an interfacial tension and a diameter is considered. The droplet flows with a velocity through a disruption unit with a diameter of the smallest cross-section in a surrounding fluid with a viscosity and a density . To simplify the investigation, the Buckingham π theorem [23] is used to reduce the variables to dimensionless numbers that describe physical relations of the droplet breakup. The seven influencing variables can be written in the following equation:
As the rank of the dimensional matrix is three (length, time, weight), four dimensionless numbers can be formed. These are the Reynolds number Re, the Weber number We, the density ratio κ and the viscosity ratio λ.
These dimensionless numbers have to be kept constant when scaling the droplet breakup to achieve physical similarity of the original scale (index O) and the scaled system (index M).
Furthermore, the ratios of the geometry dimensions need to be kept constant.
Here, is the width of the inlet channel and is the width of the outlet channel, respectively. A scaling factor is introduced to describe the ratio of the droplet diameters of the original and the scaled system. Analogically, the scaling factors for the density, for the interfacial tension and for the viscosity are introduced. The density and the interfacial tension should be kept constant when scaling the droplet breakup to reduce the degrees of freedom of the system of equations, which results in .
When using Equations (6) and (8), the scaling factor can be written as:
With Equation (9) the desired viscosity of the scaled system can easily be calculated according to the scaling factor of the system. The resulting Sauter mean diameter ratio should remain constant with the scaling approach used. Budde et al. [21] has shown with a similar approach that the dwell time is extended with a scaling factor of . As cavitation and the diffusion of the emulsifier, for example, cannot be scaled, cavitation was always suppressed by applying a backpressure [24]. As the usage of an emulsifier is sometimes necessary to ensure droplet stability during the experiments, some deviations on the transient surface properties may appear.
2.2. Materials
An overview of the ingredients and the properties of the dispersed and continuous phases of the three scales can be found in Table 1.

Table 1.
Material specification of all three scales.
2.2.1. Original Scale System
The continuous phase for velocity measurements of the original scale system consisted of five components in total: 65.7 wt % demineralized water with 34 wt % sucrose form the basis. To this, 0.2 wt % potassium sorbate (VWR International GmbH, Darmstadt, Germany) and 0.1 wt % citric acid (Carl Roth GmbH + Co. KG, Karlsruhe, Germany) were added to inhibit the growth of molds during storing between experiments; 0.00125 wt % Nile red coated polystyrene particles with a diameter of 1.97 µm (microparticles GmbH, Berlin, Germany) were added to the continuous phase to visualize the streamlines. These particles have a comparable density to the continuous phase and are small enough to follow the streamlines of the flow while not influencing it. This composition was found suitable to achieve an adequate particle concentration in the interrogation areas of the particle image velocimetry (PIV) algorithm [2] that was applied.
For later droplet visualization experiments within the original scale system , the continuous phase consisted of 65.5 wt % demineralized water and 34 wt % sucrose, and 0.5 wt % polysorbate 20 (Tween 20®, Carl Roth, Karlsruhe, Germany) that prevents coalescence of droplets. For this mixture, Newtonian flow behavior was determined with a rotational rheometer (Anton Paar Physica MCR 301, Graz, Austria) at a temperature of 20 °C in the shear rate range of 0.1–100 s−1. A dynamic viscosity of 0.00425 Pa∙s was measured. As the disperse phase fraction was below 1 wt % for all experiments, it was expected that Newtonian flow behavior was also present at higher shear rates during the process [25,26]. The density of the continuous phase was determined with the density determination set DIS 11 (DCAT11, dataphysics, Filderstadt, Germany) to be 1145.3 kg/m3 at 20 °C.
A mixture of middle-chain two triglycerides was used as disperse phase. The oils Miglyol 810® (IOI Oleo GmbH, Witten, Germany) and Miglyol 840® (IOI Oleo GmbH, Witten, Germany) were mixed in ratio of 41:59. Added to these was 0.012 wt % of the fluorescence color Nile red (9-(diethyl-amino)benzo[a]phenoxazin-5(5H)-one, Sigma-Aldrich Chemie GmbH, St. Louis, MO, USA), which was dissolved in the oil mixture and stirred overnight. Any undissolved Nile red crystals were removed by filtering the next day. Subsequently, the dynamic viscosity of the disperse phase was measured with a rotational rheometer (Anton Paar Physica MCR 301, Graz, Austria) at a temperature of 20 °C to 0.0149 Pa∙s with Newtonian flow behavior. A Wilhelmy plate (DCAT11, dataphysics, Filderstadt, Germany) was used to measure the interfacial tension between the continuous (for droplet visualization) and the disperse phase. For interfacial tension, a value of 4.316 mN/m was determined after a measuring time of 2 h at a temperature of 20 °C, while a density of 928.33 kg/m3 was measured for the disperse phase with the density determination set DIS 11 (DCAT11, dataphysics, Filderstadt, Germany) at 20 °C.
2.2.2. Five-Fold Scaled System
The continuous phase for velocity measurements of the 5-fold scaled system consisted of 58.823 wt % glycerol (purity 99.5%, SuboLab GmbH, Pfinztal-Söllingen, Germany) and 40.877 wt % demineralized water, to which 0.2 wt % potassium sorbate (VWR International GmbH, Darmstadt, Germany) and 0.1 wt % citric acid (Carl Roth GmbH + Co. KG, Karlsruhe, Germany) were added as preservatives. Supplementary, 0.00255 wt % Nile red coated polystyrene particles with a diameter of 12 µm (microparticles GmbH, Berlin, Germany) were added. For this composition, Newtonian flow behavior was determined. A dynamic viscosity of 0.00942 Pa∙s was measured with a rotational rheometer (Anton Paar Physica MCR 301, Graz, Austria) at a temperature of 20 °C.
For later droplet visualization experiments in the 5-fold scaled system, the continuous phase consisted of consisted of 58.528 wt % glycerol, 40.672 wt % demineralized water, 0.2 wt % potassium sorbate, 0.1 wt % citric acid and 0.5 wt % polysorbate 20 (Tween 20®, Carl Roth, Karlsruhe, Germany). The density was determined with the density determination set DIS 11 (DCAT11, dataphysics, Filderstadt, Germany) to 1148.55 kg/m3 at 20 °C.
A middle-chain triglyceride Miglyol 812® (IOI Oleo GmbH, Witten, Germany) with 0.012 wt % Nile red (9-(diethyl-amino)benzo[a]phenoxazin-5(5H)-one, Sigma-Aldrich Chemie GmbH, St. Louis, MO, USA) was used as the disperse phase of the 5-fold scaled system. The Nile red was dissolved using the same procedure as in the original scale system. The dynamic viscosity of the disperse phase was 0.02947 Pa∙s with Newtonian flow behavior, which again was measured with a rotational rheometer (Anton Paar Physica MCR 301, Graz, Austria) at a temperature of 20 °C. Parallel to the originally scaled system, a Wilhelmy plate (DCAT11, dataphysics, Filderstadt, Germany) was used to measure the interfacial tension between the continuous (for droplet visualization) and the disperse phase, which was determined to 3.986 mN/m after a measuring time of 2 h at a temperature of 20 °C. The density of the disperse phase was 920 kg/m3 according to the supplier’s datasheet.
2.2.3. 50-Fold Scaled System
The continuous phase for velocity measurements of the 50-fold scaled system consisted of 61.5 wt % demineralized water, 27.5 wt % sucrose, 10.5 wt % PVP K30 (Polyvinylpyrrolidone) (BTC Europe GmbH, Monheim am Rhein, Germany), 0.26 wt % potassium sorbate (Wittig Umweltchemie GmbH, Grafschaft-Ringen, Germany) and 0.24 wt % citric acid (Schwarzmann GmbH, Laaber, Germany).
Newtonian flow behavior of this formulation was identified. A dynamic viscosity of 0.0314 Pa∙s was measured with a rotational rheometer (Anton Paar Physica MCR 301, Graz, Austria) at a temperature of 20 °C, and a density of 1145.4 kg/m3 at 20 °C was determined with the density determination set DIS 11 (DCAT11, dataphysics, Filderstadt, Germany).
The silicone oil WACKER® AK 100 (Wacker Chemie AG, Stuttgart, Germany) was used as disperse phase, which had a density of 960 kg/m3 according to the supplier’s datasheet. Its dynamic viscosity was again measured with a rotational rheometer (Anton Paar Physica MCR 301, Graz, Austria) at a temperature of 20 °C to 0.1066 Pa∙s.
2.3. Experimental Setup
The experimental setup of the original scale system with an optically accessible orifice is presented in Figure 1. A nitrogen pressurized gas cylinder (a) was used to pump the continuous phase into the pressure vessel (b) through the pipe system. Due to the pressurized gas cylinder, no pressure fluctuations were expected, which allowed velocity measurement under constant conditions. A filter unit behind the pressure vessel’s exit was used to avoid blocking of the orifice by dirt particles. The pressure loss of the orifice was measured with two digital pressure sensors (Wika S-20 (0–160 bar), Klingenberg, Germany). Their current signal was converted into a voltage signal, which was then recorded with a USB-6210 device (National Instruments Germany GmbH, München, Germany) and Labview 2019 (National Instruments, Austin, TX, USA). The needle valve (d) was used to adjust the backpressure to the desired Thoma number , under which conditions no cavitation was visible on the images that were recorded with the high-speed camera of the microparticle image velocimetry (µ-PIV) measurement system. For the duration of a complete experiment, the mass flow was determined by continuous reading off the scale with Labview while the Reynolds number in the smallest cross-section of the orifice was kept constant.
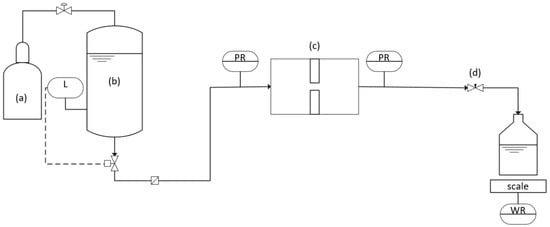
Figure 1.
Experimental setup of the original scale system () with pressurized gas cylinder (a), pressure vessel (b), optically accessible orifice (c) and needle valve (d). The level of the pressure vessel (L) is measured constantly to avoid a complete emptying. The values of the pressure sensors (PR) and the scale (WR) are recorded during the experiment.
The experimental setup of the 5-fold scaled system with an optically accessible orifice is presented in Figure 2. As in the original scale setup, the pressure vessel (b) was pressurized with a nitrogen pressurized gas cylinder (a). The continuous phase was filtered before passing the volume flow (VSI 0,2/16 EPO 12V-32W15/4, VSE Volumentechnik GmbH, Neuenrade, Germany) and temperature sensor. The volume flow and the current temperature of the continuous phase were recorded with a USB-6210 device (National Instruments Germany GmbH, München, Germany) and Labview 2019 (National Instruments, Austin, TX, USA). The inlet pressure of the orifice and the backpressure at the outlet channel were measured with two digital pressure sensors (Wika S-20 (0–160 bar), Klingenberg, Germany) and again recorded with the USB-6210 device and Labview. The continuous phase was additionally pumped through a bypass towards the droplet generator (d), which was not in use when velocity measurements were performed. After flowing through the droplet generator, the fluid was reinjected in front of the orifice with a stainless-steel capillary. The needle valve (f) was used to achieve the desired backpressure for the Thoma number .
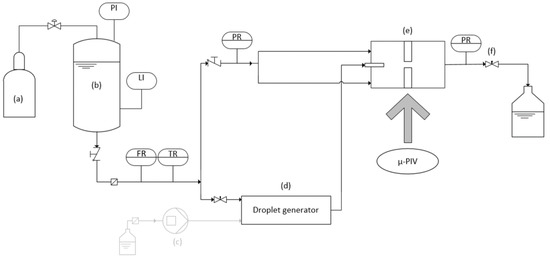
Figure 2.
Experimental setup of the 5-fold scaled system () with pressurized gas cylinder (a), pressure vessel (b), droplet generator (d), optically accessible orifice (e) and needle valve (f). The positive displacement pump (c) was not used when performing velocity measurements. The values of the pressure sensors (PR), scale volume flow sensor (FR) and temperature sensor (TR) were recorded during the experiment. The pressure in the vessel (PI) and the level in the vessel (LI) are indicated at the test rig. The µ-PIV system was used to measure the velocity profile in the optically accessible orifice.
The experimental setup of the 50-fold scaled system with an optically accessible orifice is presented in Figure 3. The continuous phase is circulated by a centrifugal pump (Grundfos, Bjerringbro, Denmark). The centrifugal pump can be controlled continuously by a frequency converter, so that the inlet pressure and thus the flow velocity in the plant can be adjusted. The measuring section is made of glass or acrylic glass so that there is extensive optical access. The inlet channel upstream of the orifice has a circular cross-section while the outlet channel downstream of the orifice has a square cross-section. The low-pressure side of the orifice plate is atmospherically vented so that there is no back pressure. The pressure sensors for measuring the pressure drop of the orifice are placed at the inlet of the inlet channel and at the end of the outlet channel, respectively. The distance between the measurement positions is about 1 m. The outlet channel dimension can be altered by placing smaller square channels in the outlet channel that are sealed to the outlet wall of the orifice. The dissipated energy of the pump, which would result in a heating of the fluid in the test site, is removed with a heat exchanger to ensure constant process conditions.
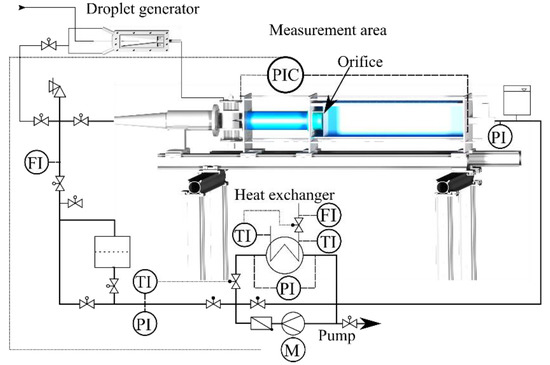
Figure 3.
Experimental setup of the 50-fold scaled system () with the optically accessible inlet, outlet channel and orifice. The continuous phase is circulated by a centrifugal pump. The droplet generator was not used and disconnected during velocity measurements. The temperature (TI), the volume flow (FI) and the pressure (PI) are indicated at several places in the test rig. The motor of the pump (M) is controlled according to the pressure signal of the orifice pressure drop sensor (PIC).
Figure 4 shows the geometry of both the original and 5-fold scaled orifice (a), and the 50-fold scaled orifice (b). The square inlet channel has a constant width of 2 mm ) and 10 mm ). In contrast, the inlet channel of the 50-fold scaled orifice has a circular cross-section with a diameter of 100 mm 0). The conical inlets of the original and 5-fold scaled orifices each have an angle of 60°, while the inlet of the 50-fold scaled orifice was designed with a radius of 20 mm. This was done since the orifice with round edges resulted in better optical accessibility, as shown in Figure 4d. The round edges did not cause a different velocity profile at the outlet compared to a conical inlet [27]. The smallest cross sections, being circular, have a diameter of , and , respectively. The length–diameter ratio for the smallest cross-section was kept constant for all scales. The square outlet channel of the original scale orifice has widths of 2, 3 and 4 mm, while the 5-fold scaled one has a diameter of 10 mm. The 50-fold scaled orifice again shows a square outlet channel with widths of 50, 100, 150 and 200 mm. The exit of each of the orifices is always in the center of the outlet channel. Therefore, the inlet channel of the original scale orifice needs to be lower than the surface by a distance . This distance is compensated by the acrylic glass cover plate to maintain the square cross-section of the inlet channel.
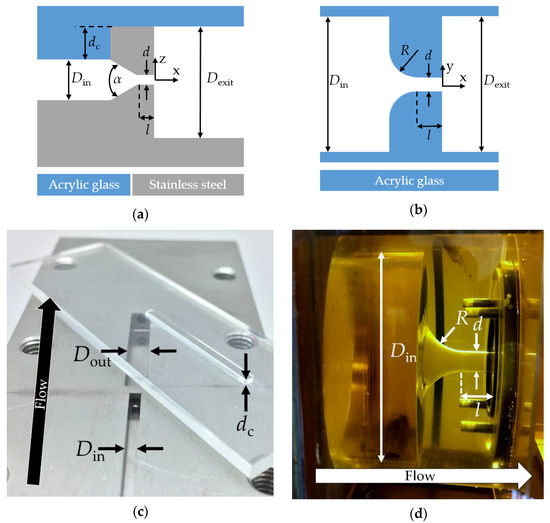
Figure 4.
Geometry of the original and the 5-fold scaled orifice: (a) geometry of the 50-fold scaled orifice and (b) image of the original scale orifice with demounted acrylic glass cover plate (flow from bottom to top). The protrude bar on the acrylic glass plate is fitted in the inlet channel (c); image of the 50-fold scaled orifice (flow from left to right) (d). The related dimensions can be found in Table 2.
The original scale and the 5-fold scaled orifice are made of stainless steel, the inlet channel and the orifice with the outlet channel being produced separately. Steel construction makes it impossible to make either the conical inlet or the smallest cross-section optically accessible. Both parts are screwed together and sealed with glue (Loctite 3472, Henkel AG & Co. KGaA, Düsseldorf, Germany). After a polishing step, the orifice is then sealed with an acrylic glass plate that has a protrude bar with a height , as depicted in Figure 4c, which, depending on the outlet geometry, fits in the inlet channel and creates a quadratic inlet channel. An overview of all dimensions can be found in Table 2.

Table 2.
Dimensions of all orifice scales.
2.4. µ-PIV Measurements
A microparticle image velocimetry measurement system (µ-PIV) was used to determine the velocity field in the scales and . A CCD camera (FlowSense 4M Camera Kit, Dantec Dynamics, Skovlunde, Denmark) with 12-bit resolution and 2048 × 2048 pixels was mounted to an inverse microscope (Dantec HiPerformance Microscope, Skovlunde, Denmark) and used to take double pictures. The laser beam of a double-pulsed neodymium-doped yttrium aluminum garnet (ND:YAG) laser (Dual-Power 30-15 of Dantec Dynamics, Skovlunde, Denmark), which was operated at 30 mJ/pulse at a wavelength of 532 nm, was conducted to the microscope with a light guide. The laser and the camera were then synchronized. For the original scale orifice ), a camera adapter with a 0.5× magnification combined with an objective lens (C PLAN, Leica Microsystems Wetzlar GmbH, Wetzlar, Germany) with a 10× magnification and a numerical aperture of NA = 0.22 was used. The same camera adapter with a 0.5× magnification was combined with an objective lens (HC Plan Fluotar 2.5×/0.07, Leica Microsystems Wetzlar GmbH, Wetzlar, Germany) with a 2.5× magnification to record the experiment using the 5-fold scaled orifice ). This resulted in a 5× magnification for the original scale and in a 1.75× magnification for the 5-fold scaled system. The visual field of the original scale setup has an area of about 3 × 3 mm2, which corresponds to a spatial resolution of 1.5 µm/px. Compared to the 5-fold scaled setup, the visual field of the original scale setup has an area of about 12 × 12 mm2, which corresponds to a spatial resolution of 6 µm/px. A minimum of 2000 double pictures was taken in each measurement run for statistical convergence.
The pictures were processed in commercial software Dynamic Studio 6.10 (Dantec Dynamics, Skovlunde, Denmark), an average picture calculated and subsequently subtracted from the images to increase the signal to noise ratio. Afterwards, an adaptive particle image velocity (PIV) algorithm was used to calculate the velocity vector map for the original scale orifice. The grid size distance was set to 8 pixel and the interrogation area was set in the range of 128 × 128 pixel to 16 × 16 pixel to achieve a minimum of 5 particles within. The interrogation area of the second frame of the double picture was moved according to the velocity gradient. A vector was assumed to be valid if the signal to noise ratio during the cross-correlation was larger than 7. In a next step, the velocity vector maps were combined to an average velocity vector map whereby only valid velocity vectors were used for the calculation. Outlier vectors were detected in a 3 × 3 neighborhood and substituted by the neighborhood median vector. Between 350 and 450 valid vectors were found on every grid point.
The velocity vector map of the 5-fold scaled orifice was calculated with a self-developed particle tracking algorithm in MATLAB 2019b (Mathworks, Nantucket, MA, USA), based on the nearest neighbor principle, as described by Ohmi and Li [28]. The found vectors were binned in 10 × 10 pixel areas with a grid size of 10 pixel. This resulted in a vector spacing of about 60 µm. Within the bins, vectors that were outside one standard deviation were treated as outliers and subsequently removed from the calculation. In the next step, the average velocity and the standard deviation were recalculated on every grid point. Between 50 and 100 valid vectors were found on every grid point.
The correct level of the z-plane was determined by measuring the velocity map at the outlet of the orifice at several levels with a distance of . The one layer where the highest velocity and the thinnest turbulent shear layer were present was set as the measuring z-plane for future measurements. This procedure was repeated for every orifice geometry while all measurements were performed in the x–y plane. The orifice was moved relative to the objective lenses with a SCAN IM 120 × 100−2 mm (Märzhäuser Wetzlar GmbH & Co. KG, Wetzlar, Germany) to measure the velocity map farther downstream from the orifice exit. The orifice itself was moved a distance of between two measurement runs to ensure a sufficient overlay of the measurement area. The velocity maps of the sections were interpolated on a new grid and, wherever overlapping, averaged with MATLAB 2019b (Mathworks, Nantucket, MA, USA).
2.5. PIV Measurements
Particle image velocity (PIV) measurements were carried out for the measurements of the velocity fields in scale 50. Six sCMOS cameras (pco.edge 5.5, PCOAG, Kehlheim, Germany) with a 16-bit resolution and 2160 × 2560 pixel (pixel size: 6.5 µm × 6.5 µm) were used for visualization synchronously in double image mode, so that a field of view with a large aspect ratio could be recorded (34 mm × 6.9 mm). The optical magnification is about 4.7. The cameras were equipped with Makro planar lenses with a focal length of 100 mm (Carl-Zeiss, Oberkochen, Germany)
Hollow glass spheres with an average particle size of 16 µm were used as seeding particles. The density of the glass spheres was adjusted to water. The illumination of the measurement was performed by an Evergreen 200 Nd:YAG double pulse laser (Quantel, Lannion, France) with a pulse energy of up to 200 mJ and focused through lenses on a light sheet of about 1 mm thickness. Two thousand double images were recorded, with a recording frequency of 7 Hz.
The evaluation of the double images was performed with the commercial software Davis 8.4 (LaVision, Göttingen, Germany) with an iterative evaluation algorithm. The final interrogation window size was 16 × 16 pixel with 50% overlap. The vector resolution was about 4.1 px/mm. The postprocessing and stitching of the individual camera field of views was done with MATLAB 2019b (Mathworks, Nantucket, MA, USA).
3. Results
3.1. Matching of Orifice Dimensions and Material System
Two material systems and the dimensions of the related orifices were adapted to achieve the required scaling factors. The material systems had to allow µ-PIV and PIV measurements as well as droplet visualization. Transparent fluids were necessary to monitor the movement of the seeding particles and the deformation of the droplets. Both the disperse and continuous phase need to have Newtonian flow behavior. Furthermore, the fluorescence color Nile red had to be soluble in the disperse phase while being insoluble in the continuous phase of the 5-fold scaled system.
These specifications resulted in a water–glycerin system for the 5-fold scaled system. The dimensions and the parameters achieved for the material system are presented in Table 3. As can be seen, an actual scaling factor of five was reached for all dimensions of the orifice. Furthermore, a scaling factor of 2.22 could be achieved for the viscosity of the continuous phase. The scaling factor for the viscosity of the disperse phase is 1.978, whereas the interfacial tension of the scaled system with a measured value of 3.986 mN/m resulted in a scaling factor of 0.9247.

Table 3.
Resulting scaling factors, material properties and dimensions of the system.
The scaling factors achieved for all dimensions (d, D, l) allow complete geometric similarity. Furthermore, the physical similarity of the viscosity, density and interfacial tension was achieved with minor deviations of the scaling factors.
For the 50-fold scaled system , a water–sucrose system was found to be suitable. The resulting dimensions and material parameters are presented in Table 4. As with the 5-fold scaled system , the target scaling factor was reached for all dimensions of the orifice. The scaling factor reached for the viscosity of the disperse phase is 7.154. Furthermore, a scaling factor of 1.00 for the density of the continuous phase and a scaling factor of 1.03 for the density of the disperse phase were achieved accordingly. Scaling the viscosity of the continuous phase resulted in a value of 7.39. The water–sucrose system with AK100 oil resulted in an interfacial tension of 20.074 mN/m, entailing an interfacial tension scaled by a factor of 4.6571.

Table 4.
Resulting scaling factors, material properties and dimensions of the system.
With these values for the dimensions of the orifice (d, D, l), complete geometric similarity could be reached while difficulties arose when attempting to scale the interfacial tension properly. The use of an emulsifier to lower the interfacial tension in this system results in an accumulation of the disperse phase, preventing any measurement. The higher interfacial tension compared to the target value results in a smaller We number, which may influence the droplet breakup in the 50-fold scaled orifice. Any results from this scaled experimental setup therefore need to be interpreted with caution. It is presumed, though, that the diffusion time of the emulsion to the newly created surface during droplet deformation is much higher than the breakup process itself [29,30]. Hence, the influence of the higher interfacial tension on the droplet may be moderate.
Table 5 shows the resulting dimensionless numbers of all three scales based on a Reynolds number Re = 2000 in the gap of the disruption unit. When looking at the density ratio and the viscosity ratio , it can be noticed that the 5-fold and 50-fold scaled systems result in only slightly diverging dimensionless numbers. Closer inspection of the table, however, shows that the abovementioned failed scaling of the interfacial tension of the 50-fold scaled system results in only 23% of the target Weber number of the original scale system. Compared to that, the 5-fold scaled system results in a Weber number that is very close to the target value. As discussed before, the results from the 50-fold experimental setup therefore need to be interpreted with caution.

Table 5.
Resulting dimensionless numbers of the droplet breakup for all three scales based on a Reynolds number Re = 2000 in the disruption unit and droplets with a diameter of 40, 200 and 2000 µm, respectively.
3.2. Comparison of the Flow Pattern in the Orifices
At the exit of the orifice, the fluid flows with a uniform velocity in the almost quiescent surrounding fluid. A free jet is formed that consists of a potential core and an enclosing boundary layer. The potential core represents the area where the velocity remains constant. The enclosing boundary layer, which is also called shear or mixing layer, grows with increasing distance from the orifice. Vortices are formed at the edges of the core region, which results in velocity fluctuations. Simultaneously, the diameter of the potential core is decreasing until it completely vanishes [31,32].
It is hypothesized that the normalized velocity on the center axis of all three scales is equal if the Reynolds number Re is kept constant. Furthermore, it is hypothesized that all three scales result in a comparable velocity fluctuation field.
3.2.1. Comparison of the Normalized Velocity and the Normalized Velocity Fluctuations
Figure 5 presents an overview of the normalized velocity field at (a), normalized velocity fluctuation at (b), normalized velocity field at (c) and normalized velocity fluctuation at (d), for all three orifice scales. All velocity fields were normalized with the theoretical velocity according to Bernoulli’s principle [33]:
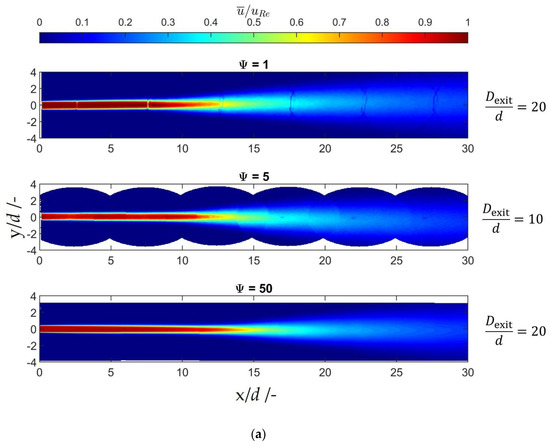
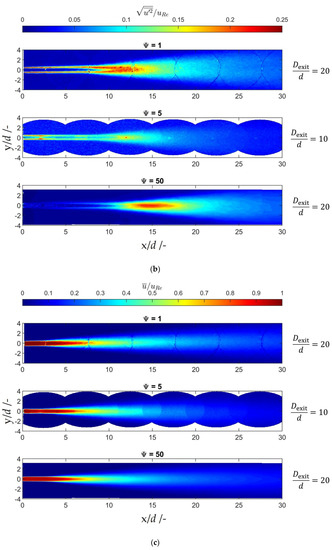
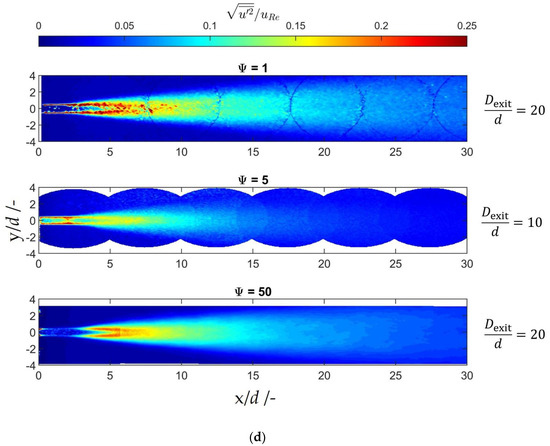
Figure 5.
(a) Normalized velocity fields of all three scales at Re = 2000; (b) normalized velocity fluctuation of all three scales at Re = 2000; (c) normalized velocity fields of all three scales at Re = 5700; (d) normalized velocity fluctuation of all three scales at Re = 5700. Due to the limited working distance of the microscope, it was not possible to conduct measurements within the 5-fold scaled system for any diameter ratios larger than 10.
The measurements show similar velocity fields for the three scales, although the 5-fold scaled system uses a deviating outlet channel diameter ratio instead of . The influence of the outlet channel diameter ratio is discussed in Section 3.2.3. The region with a constant normalized velocity of about 1 represents the potential core, see Figure 5a,c. A shear layer surrounds the potential core where the velocity is decreased by the ambient fluid. This region with lower velocities grows with increasing distance from the orifice exit, which results in a smaller diameter of the potential core. The energy of the jet is dissipated in the emerging turbulent eddies in the shear layer. Furthermore, the outer diameter of the jets increases downstream from the orifice by entrainment of the ambient fluid.
The normalized velocity fluctuations in Figure 5b,d show the location of the turbulent shear layer. Eddies in the shear layer result in increased velocity fluctuations. Both the original and the 50-fold scaled orifice show similar peak values of the normalized velocity fluctuation at both Reynolds numbers. The original scale orifice results in high velocity fluctuation values in the area where the shear layer thickness stays constant, while the 5-fold scaled orifice also shows higher velocity fluctuations and a thicker shear layer in the region . It can be noticed that higher velocity fluctuations are present in the area of the potential core in the 5-fold scaled orifice compared to the other two scales.
The areas with the highest normalized velocity fluctuations at Re = 5700 are located at about at all scales. Comparing the results with the normalized velocity fluctuations at , it stands out that the maximum velocity fluctuations are located farther downstream. Furthermore, the maximum velocity fluctuations of the original scale orifice are located slightly closer to the orifice outlet compared to the 50-fold scaled orifice . Moreover, it is surprising that the velocity fluctuations at the end of the potential core in the 5-fold scaled orifice are lower and reach only values of about 0.15 compared to values of about 0.2 in the other two scales.
The higher velocity fluctuations in the shear layer in the original and 5-fold scaled orifice may be caused by the change in the measurement system. The µ-PIV measurements were performed at lower seeding particle density compared to the PIV measurements in the 50-fold scaled orifice to keep the background noise low, which is caused by out of focus seeding particles. Therefore, less valid vectors could be calculated. Besides, slow particles of the ambient can thus distort the velocity in the shear layer if the interrogation window of the adaptive PIV algorithm is partially in the shear layer and partially in the ambient fluid. Furthermore, remaining burr at the orifice outlet edge can cause stronger and earlier velocity fluctuations in the shear layer of the original scale and 5-fold scaled orifice.
In general, the normalized velocity fields of all three scales are similar, apart from some small deviations of the potential core length that can be caused by the production inaccuracies in the small scales. Furthermore, it can be concluded that the absolute values of the velocity fluctuations are increasing while the normalized velocity fluctuations remain constant when increasing the Re number.
3.2.2. Comparison of the Normalized Velocity on the Center Axis
In the following, the normalized velocity on the center axis at the exit of the orifice is determined at the three different scales for two different Re numbers. Furthermore, the restrictions of this scaling approach are highlighted. The following section illustrates the comparability of the flow pattern of the 50-fold scaled orifice with the original scale.
The normalized velocity remains constant for both scales in the region of at a Reynolds number Re = 5700 in Figure 6a. This area represents the potential core of the free jet where the flow develops [32]. The absolute values of the normalized velocity differ slightly in the different scales, showing a value of 1.01 in the original scale , while it is at 0.95 in the 50-fold scaled orifice . Figure 6a also reveals a steep decrease of the normalized velocity in the region . The absolute value of the slope at which the normalized velocity declines decreases with increasing distance from the orifice outlet . Comparing the results farther downstream , it can be observed that the slope is similar for both scales. The normalized velocity decreases to a value of about 0.14 at a normalized distance of in both orifices. The original scale orifice shows higher normalized velocities than the scaled orifice within the whole investigated region.
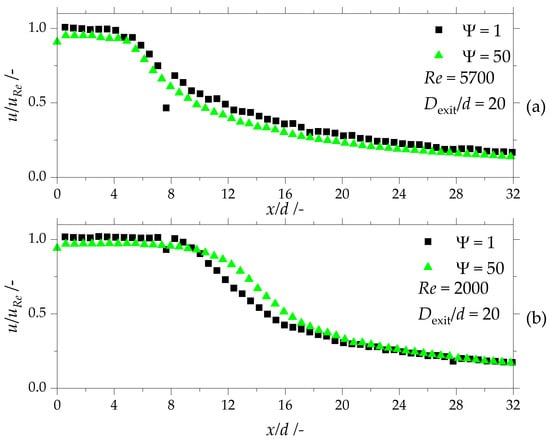
Figure 6.
(a) Normalized velocity on the center axis at a Reynolds number Re = 5700 at the outlet of an orifice and of a 50-fold scaled orifice with an outlet channel diameter ratio of . (b) Normalized velocity on the center axis at a Reynolds number Re = 2000 at the outlet of an orifice and of a 50-fold scaled orifice with an outlet channel diameter ratio of .
Figure 6b shows the experimental data on the normalized velocity on the center axis of the 50-fold scaled and the original scaled orifice in the area at Re = 2000. The normalized velocity remains constant in the region for both scales, which indicates the potential core of the free jet [32]. The original scale orifice reaches a value of about 1.02 in this region while the scaled orifice reaches a value of about 0.95. In the region of , the normalized velocity within the scaled orifice differs from the original scale as the velocity decreases faster in the original scale orifice. However, the measurements show equally normalized velocities for both orifice scales in the region of .
The higher velocity in the original scale orifice at both Re numbers might either be caused by a slightly smaller diameter d of the orifice due to production inaccuracy or could be a result of a measurement error of the pressure sensors. These sensors have a higher measurement error at very low and very high pressures, potentially leading to errors, especially for the low pressure at the outlet. The lower value of the normalized velocity of 0.95 at the outlet of the 50-fold scaled orifice might be a result of the pressure sensor arrangement as the pressure loss was measured from the inlet of the inlet channel to the outlet of the outlet channel. This could result in higher pressure losses compared to the pressure loss just over the orifice. The length of the potential core of fully turbulent free jet should be about 5 long [32]. In contrast to the literature, a potential core length of was found at Re = 5700. This might indicate that the jet is evenly confined in the wide outlet channel geometry. As the length of the potential core at Re = 2000 is double the length stated by Rajaratnam [32], it can be assumed that the jet in the outlet is not fully turbulent and rather in the transitional flow regime.
Overall, these results indicate that scaling was successful for the 50-fold scaled orifice. The development of the normalized velocity in the center axis is comparable for both scales apart from the possible errors caused by the pressure sensors in both scales. Moreover, the results show that minimal production inaccuracies in the original scale can result in large deviations in the velocity profile.
Figure 7a compares the normalized velocity on the center axis of the 5-fold scaled orifice with the velocity profile of the original and the 50-fold scaled orifice at Re number of 5700. The normalized velocity of the 5-fold scaled orifice is about 0.95, with some fluctuations in the region , which represents the potential core of the emerging jet. The original scale orifice shows a normalized velocity of about 1.00 at the exit of the orifice. Unexpectedly, the velocity starts to decrease immediately downstream from the exit of the orifice, which indicates that there is no potential core. The original scale orifice shows significantly lower normalized velocities compared to the two scaled orifices in the whole investigated area. This large deviation might be affected by a slightly tilted drilling hole in the original orifice. The unsteady steps in the velocity development are an indication for this explanation. Followed by the potential core, the velocity in the 5-fold scaled orifice declines parallel to the 50-fold scaled orifice. The normalized velocity in the 5-fold and 50-fold scaled orifice are equal at a normalized distance larger than . The normalized velocity decreases to a value of about 0.14 at a normalized distance of in both scaled orifices, whereas the original scale orifice leads to a decrease of the normalized velocity to a value of about 0.06 at a normalized distance of .
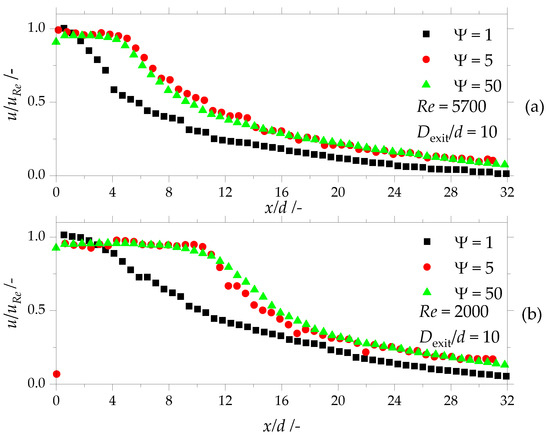
Figure 7.
(a) Normalized velocity on the center axis at a Reynolds number Re = 5700 at the outlet of an orifice , of a 5-fold scaled orifice and of a 50-fold scaled orifice with an outlet channel diameter ratio of ; (b) normalized velocity on the center axis at a Reynolds number Re = 2000 at the outlet of an orifice , of a 5-fold scaled orifice and of a 50-fold scaled orifice with an outlet channel diameter ratio of .
The normalized velocity on the center axis of the 5-fold scaled orifice is compared with the velocity profile of the original and the 50-fold scaled orifice at Re number of 2000 in Figure 7b. The two scaled orifices result in constant normalized velocity of about 0.95 in the region . The original scale orifice again shows a short region with a constant normalized velocity for . Farther downstream, the normalized velocity decreases in the original scale orifice. The scaled orifice shows similar velocity decay downstream the potential core.
The rising and decreasing normalized velocity in the potential core of the 5-fold scaled orifice can by caused by the optical distortion of the images. Due to the still small dimension of the orifice, it was not possible to perform an image dewarping.
Taken together, these results suggest that normalized velocity profiles of the 5-fold and the 50-fold scaled orifice are almost equal and should result in comparable droplet breakup positions. The original scale is prone to production inaccuracies (tilted drilling hole, diameter deviations, remaining burr) and the 5-fold scaled orifice shows some deviations due to optical distortion. Besides, the 5-fold scaled system shows more fluctuations that are caused by the lower number of valid vectors of the PTV measurements, due to the low seeding density compared to PIV measurements of the 50-fold scaled system.
3.2.3. Influence of Confinement on the Normalized Velocity on the Center Axis
The following section illustrates the influence of the confinement on the flow pattern downstream the original and in the 50-fold scaled orifice depending on the Reynolds number.
Figure 8 compares the normalized velocity on the center axis of the original scale orifice in the area at a Reynolds number Re = 2000 (a) and Re = 5700 (b). The normalized velocity stays constant in a region of at a Reynolds number Re = 2000. On the other hand, the velocity stays constant only in a region of at a Reynolds number Re = 5700. At a Reynolds number Re = 5700, the orifices with the outlet channel diameter ratio of and show the same decrease of the normalized velocity for a normalized distance from the outlet of . Both geometries result in a normalized velocity of 0.15 at a normalized distance from the outlet of . Similarly, the orifices with the outlet channel diameter ratio of and show the same decrease of the normalized velocity for a normalized distance from the outlet of at a Reynolds number Re = 2000. In the section, the orifice with the outlet channel diameter ratio of results in higher normalized velocity values than the orifice with the outlet channel diameter ratio of .
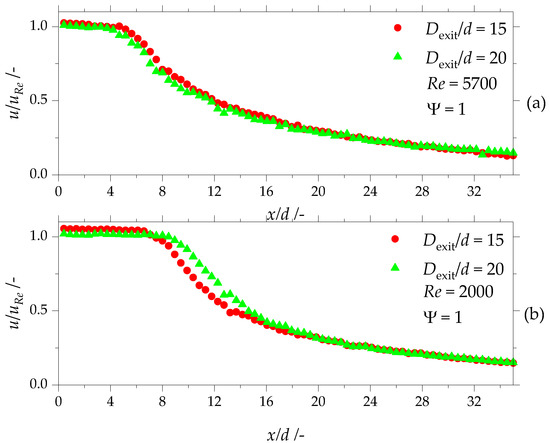
Figure 8.
(a) Normalized velocity on the center axis of the original scale orifice with altered outlet channel diameter ratio at a Reynolds number Re = 5700; (b) normalized velocity on the center axis of the original scale orifice with altered outlet channel diameter ratio at a Reynolds number Re = 2000.
In conclusion, the measurements reveal that the confinement of the free jet in the original scale orifice is not pronounced if the outlet diameter ratio is larger than .
In Figure 9, the normalized velocity on the center axis of the 50-fold scaled orifice in the area at a Reynolds number Re = 2000 (b) and Re = 5700 (a) is presented. The normalized velocity stays constant in the region of at a Reynolds number Re = 2000, independently of the outlet geometry. Similarly, at a Reynolds number Re = 5700, the normalized velocity stays constant in the region of , again independently of the outlet geometry. The decline of the normalized velocity downstream the constant velocity region is stronger at the Reynolds number Re = 5700 compared to the measurements with a Reynolds number Re = 2000. In the section, the orifice with the outlet channel diameter ratio of results in higher normalized velocity values than the other outlet geometries at a Reynolds number Re = 2000. The orifice with an outlet channel diameter ratio of shows smaller values of the normalized velocity at at a Reynolds number Re = 2000 compared to orifices with a wider outlet channel ratio. Likewise, the orifice with an outlet channel diameter ratio of shows smaller values of the normalized velocity at at a Reynolds number Re = 5700. Furthermore, the decline of the normalized velocity is more pronounced at the higher Reynolds number. As Figure 9 shows, there is a significant difference of the normalized velocity between the orifice with an outlet channel diameter ratio of and the orifices with an outlet channel diameter ratio of . At a Reynolds number Re = 2000, the normalized velocity decreases stronger at a normalized distance compared to the wider outlet geometries. At a Reynolds number Re = 5700, the normalized velocity decrease starts to diverge from the other outlet geometries at a normalized distance of . This decrease of the normalized velocity stagnates at a Reynolds number Re = 5700 in the orifices with an outlet channel diameter ratio of and reaches a constant value of 0.024.
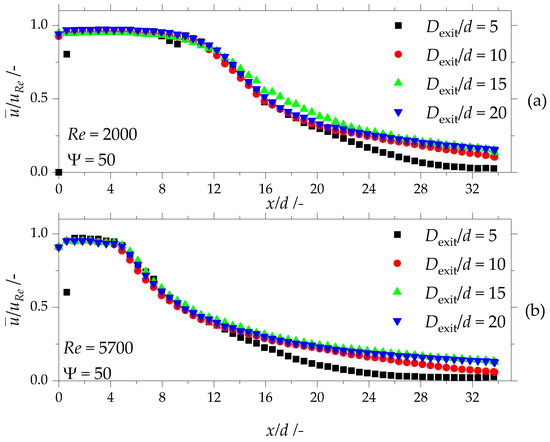
Figure 9.
(a) Normalized velocity on the center axis of a 50-fold scaled orifice with altered outlet channel diameter ratio at a Reynolds number Re = 2000; (b) normalized velocity on the center axis of a 50-fold scaled orifice with altered outlet channel diameter ratio at a Reynolds number Re = 5700.
The most striking result to emerge from the data is that the influence of the confinement in the 50-fold scaled orifice starts at an outlet diameter ratio of as well and therefore shows similar behavior to that in the original scale orifice. Furthermore, the results show that the influence of the confinement on the free jet is more pronounced at higher Reynolds numbers as the velocity development in the orifice with an outlet diameter ration of differs more strongly from the wider outlet geometries at a Reynolds number Re = 5700, as is the case at Re = 2000.
Concluding Section 3.2.3, the 50-fold and the original scale both showed no influence of the confinement on the normalized velocity on the center axis if . Besides, further comparison of the original scale with the 50-fold scales orifice at smaller outlet channel diameter was not possible as the original scale is vulnerable to production inaccuracies that prevented usable measurements. Even slight geometry deviations have a large impact on the velocity profile in the original scale. In addition, the 5-fold scale orifice did not allow any change of the outlet channel geometry due to the limited working distance of the microscope. Therefore, it is recommended to use the 50-fold scaled orifice for further investigation on the influence of the confinement on the velocity profile.
4. Discussion
It was hypothesized that the droplet breakup in high-pressure homogenizer orifices can be scaled with the theory of similarity. Essential for this assumption is the similarity of all droplet-relevant dimensionless numbers (Re, We, κ, λ). The current investigation showed that it is possible to reach complete geometrical similarity. The approach may be somewhat limited by the material system. Limitations of the measurement systems of the 50-fold scaled orifice prevented an accordingly scaled interfacial tension; thus, physical similarity could not be fully reached. This mismatch may cause differences when investigating the droplet deformation and breakup in detail at the 50-fold scale. Since it is assumed that the diffusion of the emulsifier in the original scale process is much slower than the breakup process [6,29,30], the influence of the emulsifier on the breakup is, however, expected to be moderate, which would still allow the comparison of the droplet breakup in all three scales.
Comparing the normalized velocity on the center axis of scaled orifices with an original scale orifice showed that the development of the normalized velocity is similar on all three scales. Caution should still be exercised when working at the original scale. Here, higher values for the normalized velocity were measured compared to the upscaled setups. The higher values could be attributed to production inaccuracies or measurement errors of the pressure sensor of the original scale. Moreover, the placement of the pressure sensor farther downstream and upstream from the 50-fold scaled orifice can cause higher measurement values of the pressure drop over the orifice, which would cause lower normalized velocities. Attention should therefore be paid to identical experimental setups over the scales, even in such details as in the mounting of the sensors.
The original scale is also more prone to production inaccuracies compared to the scaled systems as even small deviations of the geometry can cause large deviations in the velocity profile. The patterns of the normalized velocity fluctuations show that there are some differences between the original and the 50-fold scaled orifices, which can be caused by the less accurate measurements of the fluctuation with the µ-PIV system.
The original scale and the 5-fold scaled orifice resulted in large deviations of the velocity fluctuation field compared to the original and the 50-fold scaled orifice. The limited seeding density in the original and the 5-fold scaled system, in the general high velocities, the high velocity gradients of the free jet and the ambient fluid, and the production inaccuracies impeded especially the velocity fluctuation measurements. Therefore, it can be concluded that a higher scale-up factor in combination with PIV measurements is advantageous and reasonable for investigating the turbulent free jet downstream from an HPH orifice.
Due to production inaccuracies in the original scale and due to the limited working distance of the microscope of the 5-fold scaled system, the influence of the confinement on the velocity profile of the free jet was investigated in detail in the 50-fold scaled system. The confinement of the free jet in the outlet channel starts to influence the velocity decrease if the outlet channel diameter ratio is equal or smaller than . It results in a stronger velocity decrease in the area where the highest normalized velocity fluctuations are located. The influence of the confinement was more pronounced at higher Reynolds numbers. A stronger confinement may result in a better droplet stabilization as the droplet contact time should be reduced by the stronger turbulence that causes the velocity decrease.
5. Conclusions
In total, it can be concluded that the scaling approach used in this study was successful in terms of showing relevant scaling strategies. It also revealed limitations of working on the different scales.
For example, a small inaccuracy in the production process—which can hardly be avoided on very small scales ()—has an effect especially at the beginning of the free jet area. Here, velocity fluctuations in the peripheral areas of the free jet were not in agreement with data from the different scales. This could affect later evaluations of the stress history acting on the droplets in this area.
The middle scale approach () resulted in problems when measuring the velocity fluctuations due to a limited seeding particle density. In addition, the velocity measurements were influenced by the optical distortion, which could not be corrected due to the still small dimensions. The measurements in the original and 5-fold scaled orifice did not allow time-resolved measurements, due to the still high velocities (up to ), which are necessary for investigating the forces acting on the droplets in the turbulent eddies in the shear layer of the free jet.
When working on very large scales (), on the other hand, one has to struggle with problems caused by the resulting very large volumes that have to be handled. Not only does the experimental setup become large, details such as temperature control become more complex. The continuous phase must also be circulated, as the continuous phase is a mixture of chemicals and cannot be discarded after one loop. This leads on the one hand to microbiological problems. On the other hand, for later work with droplets, a droplet separator must be provided, which removes even the smallest daughter droplets, which would otherwise disturb the signal/noise ratio of the PIV measuring system. In general, however, the 50-fold scaled approach is the most promising scale for precise measurement of the velocity and the velocity fluctuations due to the highest number of valid velocity vectors that can be calculated.
The results of this study can be used to determine the turbulent stress history of droplets following a defined trajectory. It is also possible to link the location of droplet breakup with the turbulent forces acting on the droplet at this location. In this way, it will be possible in the future to study droplet breakup in detail under transient, rapidly changing conditions. In addition, the scaling approach presented allows for a more targeted development of optimized disruption units, e.g., by working on details of the inlet flow. Investigations into droplet breakup mechanisms on larger scales will also simplify or enable analyzing, for example, the influence of emulsifiers or droplet-internal flow.
Future studies will therefore focus on the visualization of the droplet breakup at the different scales (Ψ = 1, 5 and 50).
Author Contributions
Conceptualization, H.P.K., C.J.K., F.J.P. and B.M.; software, F.J.P. and B.M.; formal analysis, F.J.P. and B.M.; investigation, F.J.P. and B.M.; writing—original draft preparation, F.J.P. and B.M.; writing—review and editing, H.P.K. and C.J.K.; visualization, F.J.P. and B.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the German Research Foundation (DFG), grant number 265685259.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available on request due to restrictions eg privacy or ethical.
Acknowledgments
The authors thank Dennis Scherhaufer and Heinz Lambach of the Institute for Micro Process Engineering (Micro Apparatus Engineering—FAB) for manufacturing of the original scale orifice. We also thank Jürgen Kraft, Markus Fischer and Annette Berndt for design of the test site and assistance during the experiments. We thank Ralf Dorsner (wbk Institute of Production Science) and Wolfgang Schäfer (Institute for Applied Materials—Materials Science and Engineering) for polishing the orifices. The authors thank Dieter Waltz and Peter Fischer of the Institute of Physical Chemistry for manufacturing the 5-fold scale orifice. The authors also thank Thomas Fuchs (Institute of Fluid Mechanics and Aerodynamics, Faculty of Aerospace Engineering, Universität der Bundeswehr München) for providing the PTV algorithm. Furthermore, the authors thank the IOI Oleo GmbH for providing the oil. The authors also thank Peter Walzel for fruitful discussions on the concept of this study. We acknowledge support by the KIT-Publication Fund of the Karlsruhe Institute of Technology.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Håkansson, A. Emulsion Formation by Homogenization: Current Understanding and Future Perspectives. Annu. Rev. Food Sci. Technol. 2019, 10, 239–258. [Google Scholar] [CrossRef] [PubMed]
- Bisten, A.; Rudolf, D.; Karbstein, H.P. Comparison of flow patterns and droplet deformations of modified sharp-edged and conical orifices during high-pressure homogenisation using µPIV. Microfluid. Nanofluid. 2018, 22, 607. [Google Scholar] [CrossRef]
- Kelemen, K.; Gepperth, S.; Koch, R.; Bauer, H.-J.; Schuchmann, H.P. On the visualization of droplet deformation and breakup during high-pressure homogenization. Microfluid. Nanofluid. 2015, 19, 1139–1158. [Google Scholar] [CrossRef]
- Walstra, P.; Smulders, I. Making Emulsions and Foams: An Overview. In Food Colloids: Proteins, Lipids and Polysaccharides; Dickinson, E., Bergenståhl, B., Eds.; Woodhead Publishing: Cambridge, England, 1997; pp. 367–381. ISBN 978-1-85573-783-9. [Google Scholar]
- Innings, F.; Fuchs, L.; Trägårdh, C. Theoretical and experimental analyses of drop deformation and break-up in a scale model of a high-pressure homogenizer. J. Food Eng. 2011, 103, 21–28. [Google Scholar] [CrossRef]
- Innings, F.; Trägårdh, C. Visualization of the Drop Deformation and Break-Up Process in a High Pressure Homogenizer. Chem. Eng. Technol. 2005, 28, 882–891. [Google Scholar] [CrossRef]
- Kelemen, K.; Crowther, F.E.; Cierpka, C.; Hecht, L.L.; Kähler, C.J.; Schuchmann, H.P. Investigations on the characterization of laminar and transitional flow conditions after high pressure homogenization orifices. Microfluid. Nanofluid. 2015, 18, 599–612. [Google Scholar] [CrossRef]
- Håkansson, A.; Fuchs, L.; Innings, F.; Revstedt, J.; Trägårdh, C.; Bergenståhl, B. High resolution experimental measurement of turbulent flow field in a high pressure homogenizer model and its implications on turbulent drop fragmentation. Chem. Eng. Sci. 2011, 66, 1790–1801. [Google Scholar] [CrossRef]
- Innings, F.; Trägårdh, C. Analysis of the flow field in a high-pressure homogenizer. Exp. Therm. Fluid Sci. 2007, 32, 345–354. [Google Scholar] [CrossRef]
- Taylor, G.I. The formation of emulsions in definable fields of flow. Proc. R. Soc. A 1934, 146, 501–523. [Google Scholar]
- Rumscheidt, F.D.; Mason, S.G. Particle Motion in Sheared Suspensions: XII. Deformation and Burst of Fluid Drops in Shear and Hyperbolic Flow. J. Colloid Sci. 1961, 16, 238–261. [Google Scholar] [CrossRef]
- Rallison, J.M. The deformation of small viscous drops and bubbles in shear flows. Annu. Rev. Fluid Mech. 1984, 16, 45–66. [Google Scholar] [CrossRef]
- Acrivos, A. The Breakup of Small Drops and Bubbles in Shear Flows. Ann. N. Y. Acad. Sci. 1983, 404, 1–11. [Google Scholar] [CrossRef]
- Hövekamp, T.B. Experimental and Numerical Investigation of Porous Media Flow with Regard to the Emulsion Process; ETH Zurich: Zürich, Switzerland, 2002. [Google Scholar]
- Egholm, R.D.; Fischer, P.; Feigl, K.; Windhab, E.J.; Kipka, R.; Szabo, P. Experimental and numerical analysis of droplet deformation in a complex flow generated by a rotor–stator device. Chem. Eng. Sci. 2008, 63, 3526–3536. [Google Scholar] [CrossRef]
- Feigl, K.; Baniabedalruhman, A.; Tanner, F.X.; Windhab, E.J. Numerical simulations of the breakup of emulsion droplets inside a spraying nozzle. Phys. Fluids 2016, 28, 123103. [Google Scholar] [CrossRef]
- Kaufmann, S. Experimentelle und Numerische Untersuchungen von Tropfendispergiervorgängen in Komplexen Laminaren Strömungsfeldern; ETH Zurich: Zürich, Switzerland, 2002. [Google Scholar]
- Megias-Alguacil, D.; Windhab, E.J. Experimental Study of Drop Deformation and Breakup in a Model Multitoothed Rotor-Stator. J. Fluids Eng. 2006, 128, 1289–1294. [Google Scholar] [CrossRef]
- Walzel, P. Advanteges and Limits in large Scale Modeling of Atomizers. In Proceedings of the 2nd International Conference on Liquid Atomization and Spray Systems, ICLASS-’82, Madison, WI, USA, 20–24 June 1982; Crosby, E.J., Ed.; Department of chemical engineering—University of Wisconsin: Madison, WI, USA, 1982; pp. 187–194. [Google Scholar]
- Kolb, G.; Wagner, G.; Ulrich, J. Untersuchungen zum Aufbruch von Einzeltropfen in Dispergiereinheiten zur Emulsionsherstellung. Chem. Ing. Tech. 2001, 73, 80–83. [Google Scholar] [CrossRef]
- Budde, C.; Schaffner, D.; Walzel, P. Drop Breakup in Liquid-Liquid Dispersions at an Orifice Plate Observed in a Large-Scale Model. Chem. Eng. Technol. 2002, 25, 1164–1167. [Google Scholar] [CrossRef]
- Håkansson, A. Scale-down failed—Dissimilarities between high-pressure homogenizers of different scales due to failed mechanistic matching. J. Food Eng. 2017, 195, 31–39. [Google Scholar] [CrossRef]
- Bertrand, J. Sur l’homogeneite dans les formules de physique. Cahiers de Rech. de l’Academie de Sci. 1878, 86, 916–920. [Google Scholar]
- Schlender, M.; Minke, K.; Spiegel, B.; Schuchmann, H.P. High-pressure double stage homogenization processes: Influences of plant setup on oil droplet size. Chem. Eng. Sci. 2015, 131, 162–171. [Google Scholar] [CrossRef]
- Barnes, H.A. Shear-Thickening (“Dilatancy”) in Suspensions of Nonaggregating Solid Particles Dispersed in Newtonian Liquids. J. Rheol. 1989, 33, 329–366. [Google Scholar] [CrossRef]
- Mardles, E.W.J. Viscosity of Suspensions and the Einstein Equation. Nature 1940, 145, 970. [Google Scholar] [CrossRef]
- Mutsch, B.; Kähler, C.J. Charakterisierung eines Versuchsstands zur Messung der relevanten Strömungsbedingungen für die Deformation und den Aufbruch von Tropfen beim Hochdruckhomogenisieren mit Blenden: Characterization of a setup for investigations on fluid dynamics leading to droplet deformation and breakup in high-pressure-homogenizers. In Experimentelle Strömungsmechanik: 25. Fachtagung, 5–7. September 2017, Karlsruhe; Ruck, B., Gromke, C., Leder, A., Dopheide, D., Eds.; Deutsche Gesellschaft für Laser-Anemometrie: Karlsruhe, Germany, 2017; pp. 44-1–44-8. ISBN 978-3-9816764-3-3. [Google Scholar]
- Ohmi, K.; Li, H.-Y. Particle-tracking velocimetry with new algorithms. J. Fluids Eng. 2000, 11, 603–616. [Google Scholar] [CrossRef]
- Windhab, E.J.; Dressler, M.; Feigl, K.; Fischer, P.; Megias-Alguacil, D. Emulsion processing—from single-drop deformation to design of complex processes and products. Chem. Eng. Sci. 2005, 60, 2101–2113. [Google Scholar] [CrossRef]
- Walzel, P.E. High-Pressure Homogenization: Simplified Drop Deformation Estimate during Transition through Orifices. Chem. Eng. Technol. 2017, 40, 405–411. [Google Scholar] [CrossRef]
- Abramovič, G.N. The Theory of Turbulent jets; M.I.T. Press: Cambridge, MA, USA, 1963. [Google Scholar]
- Rajaratnam, N. Turbulent Jets; Elsevier: Amsterdam, The Netherlands, 1976; ISBN 0444413723. [Google Scholar]
- Clancy, L.J. Aerodynamics; Wiley: New York, NY, USA; Pitman: London, UK, 1978; ISBN 9780470158371. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).