Is Mixtures’ Additivity Supported by Empirical Data? A Case Study of Developmental Toxicity of PFOS and 6:2 FTS in Wildtype Zebrafish Embryos
Abstract
:1. Introduction
2. Materials and Methods
2.1. Test Material Sources
2.2. Dose Regimens
2.3. Quality Assurance/Quality Control (QA/QC)
2.4. Zebrafish Husbandry
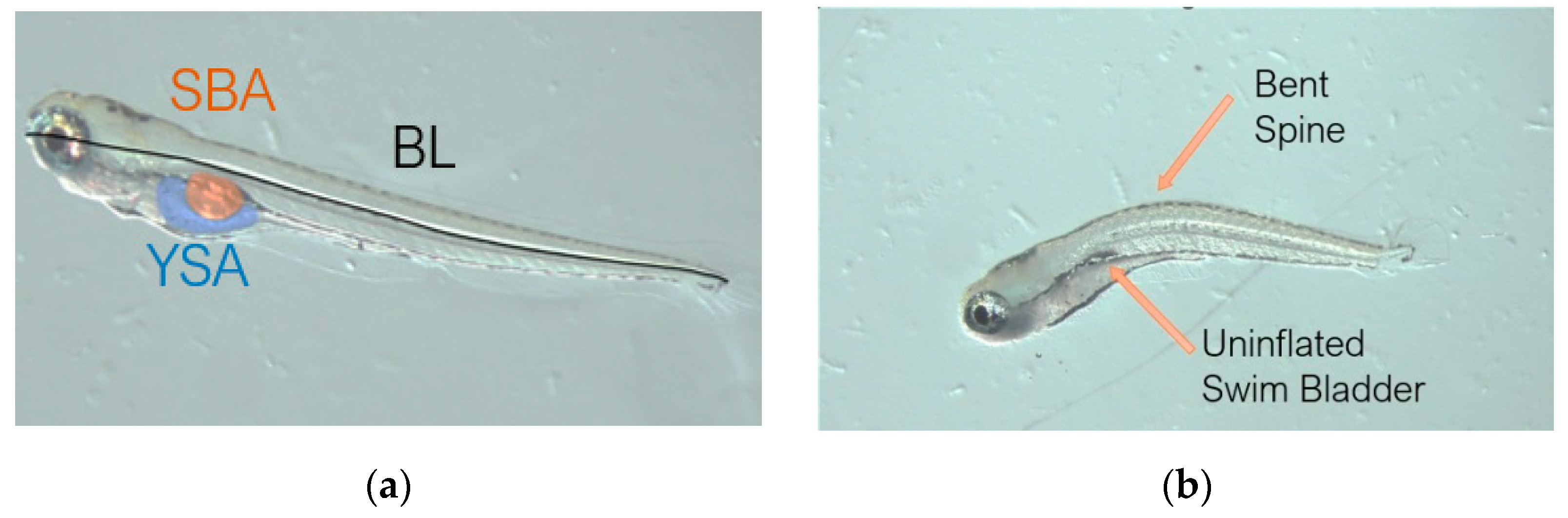
2.5. Microscopy and Image Analysis
2.6. Statistical Analysis
3. Results and Discussion
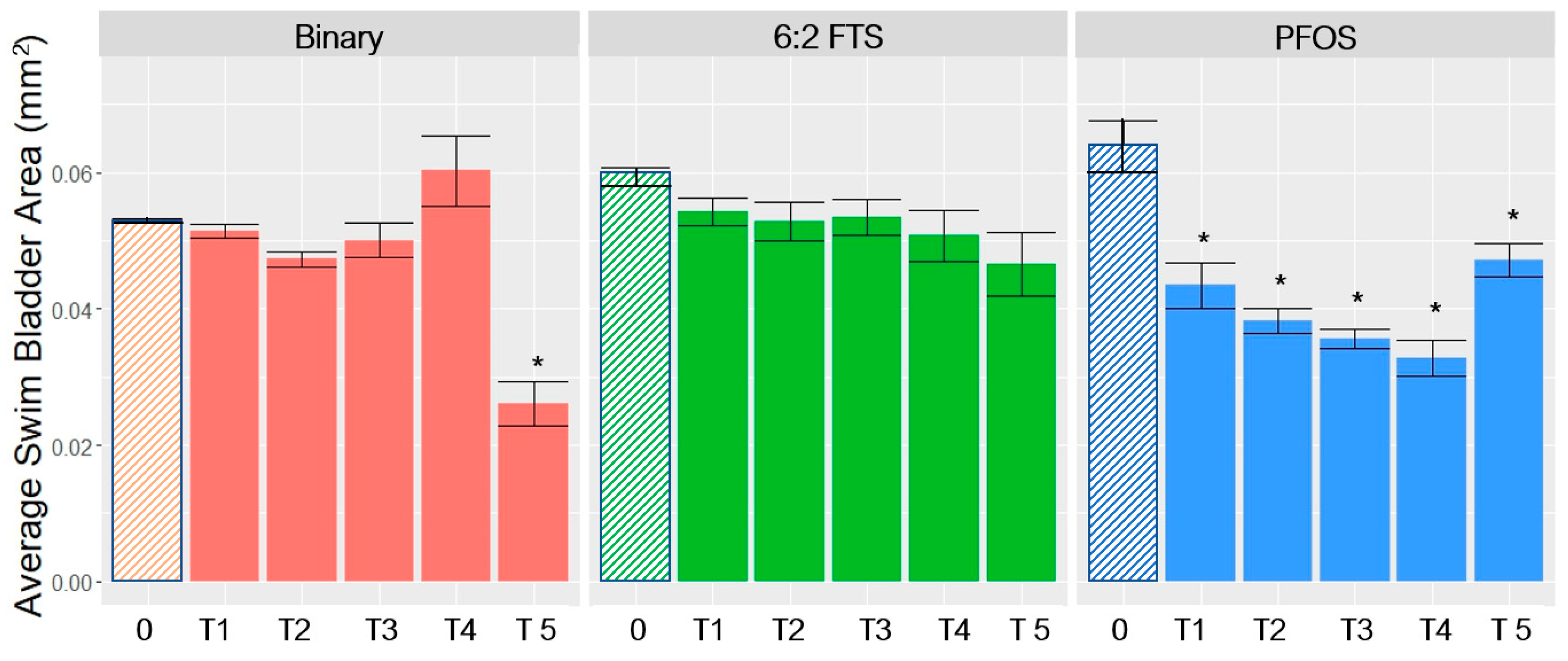
3.1. Ratios of NOAELs and LOAELs
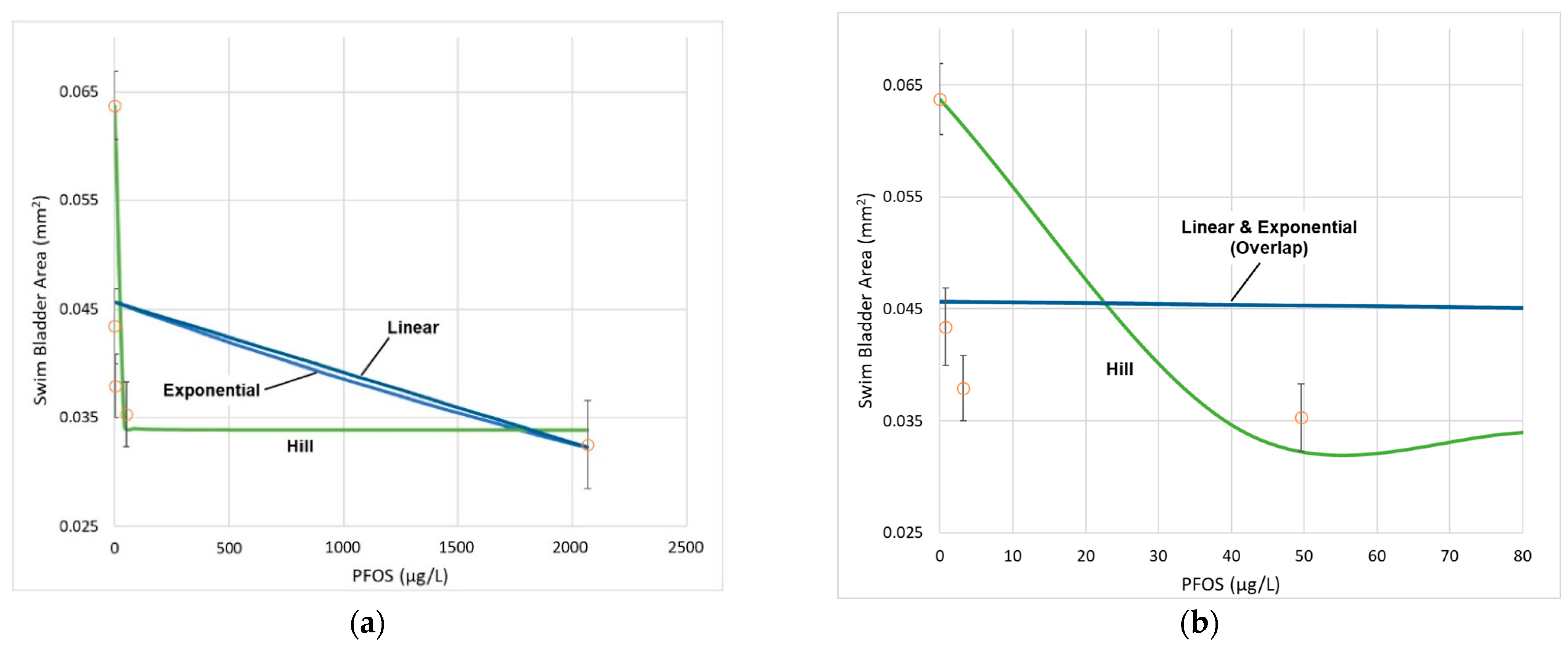
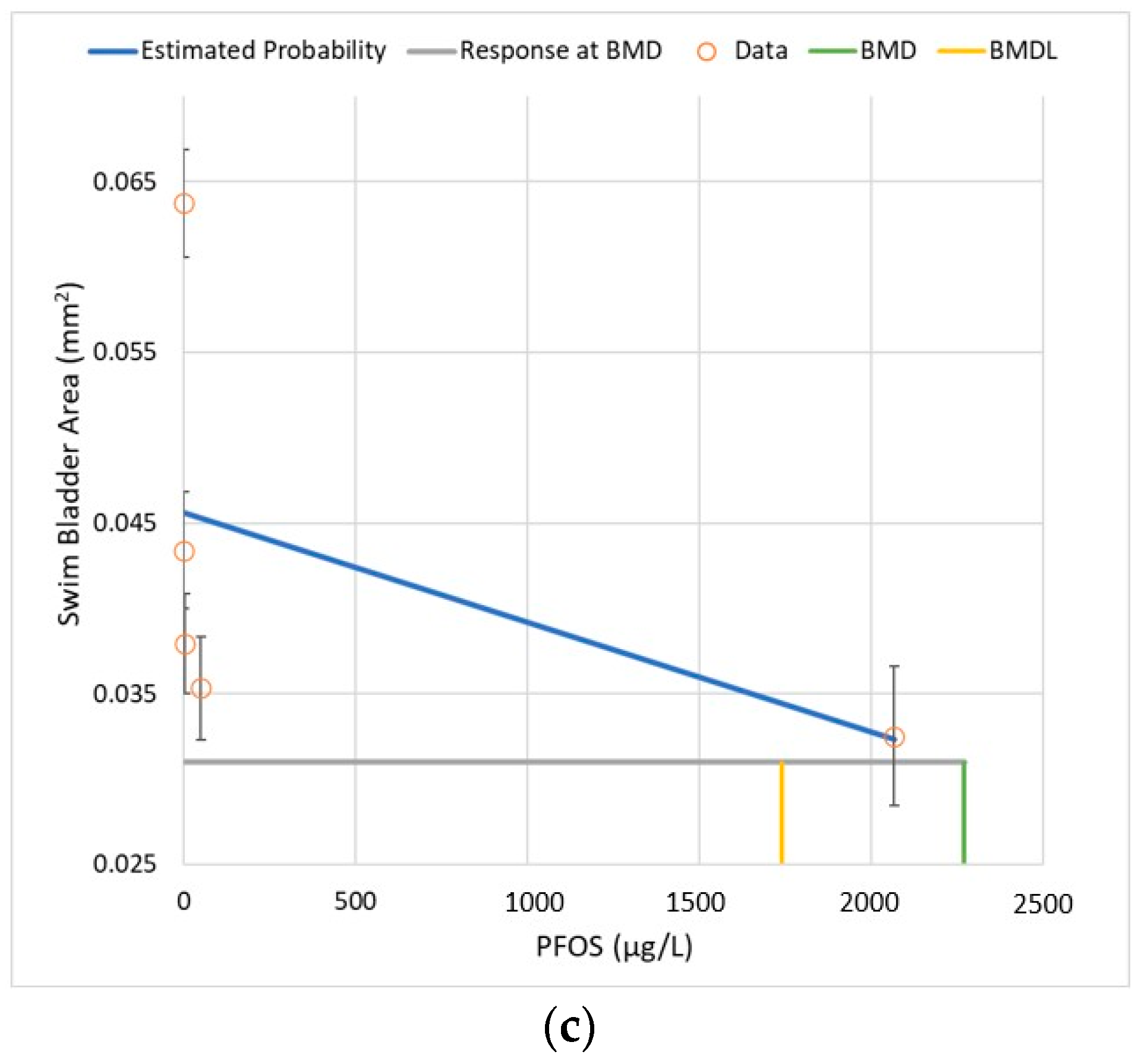
3.2. Dose–Response Analysis—Ratio of BMDLs
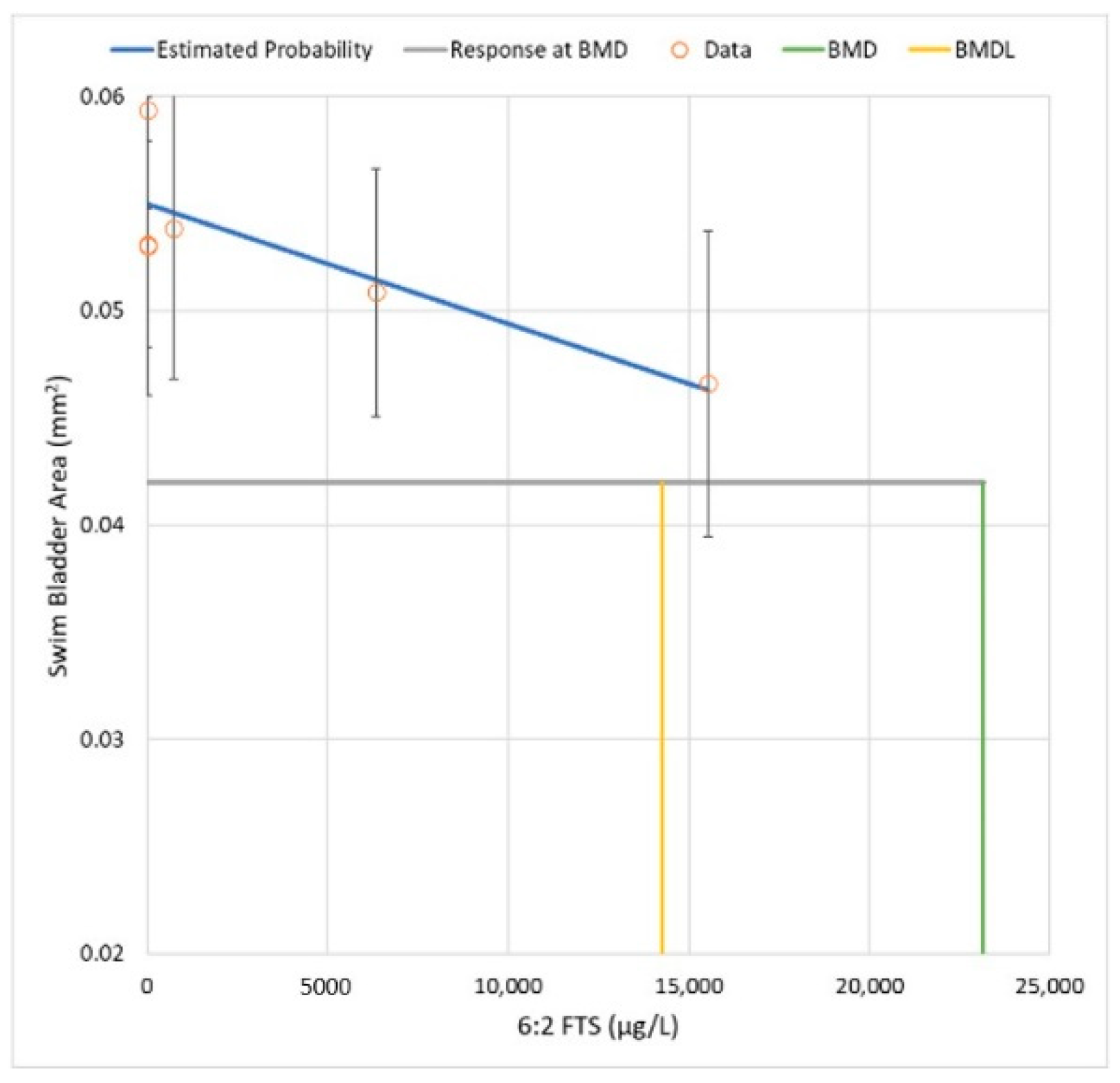
3.3. Dose–Response Analysis—Full Dose–Response with Individual Chemical Experiments
- Ri = response at the ith dose (e.g., SBA in units mm2);
- Di = dose (μg/L);
- a = intercept (mm2);
- b = slope (mm2 per μg/L).
- Ri = response (mm2) at the ith dose;
- R0 = control group response (mm2) at D = 0 μg/L.
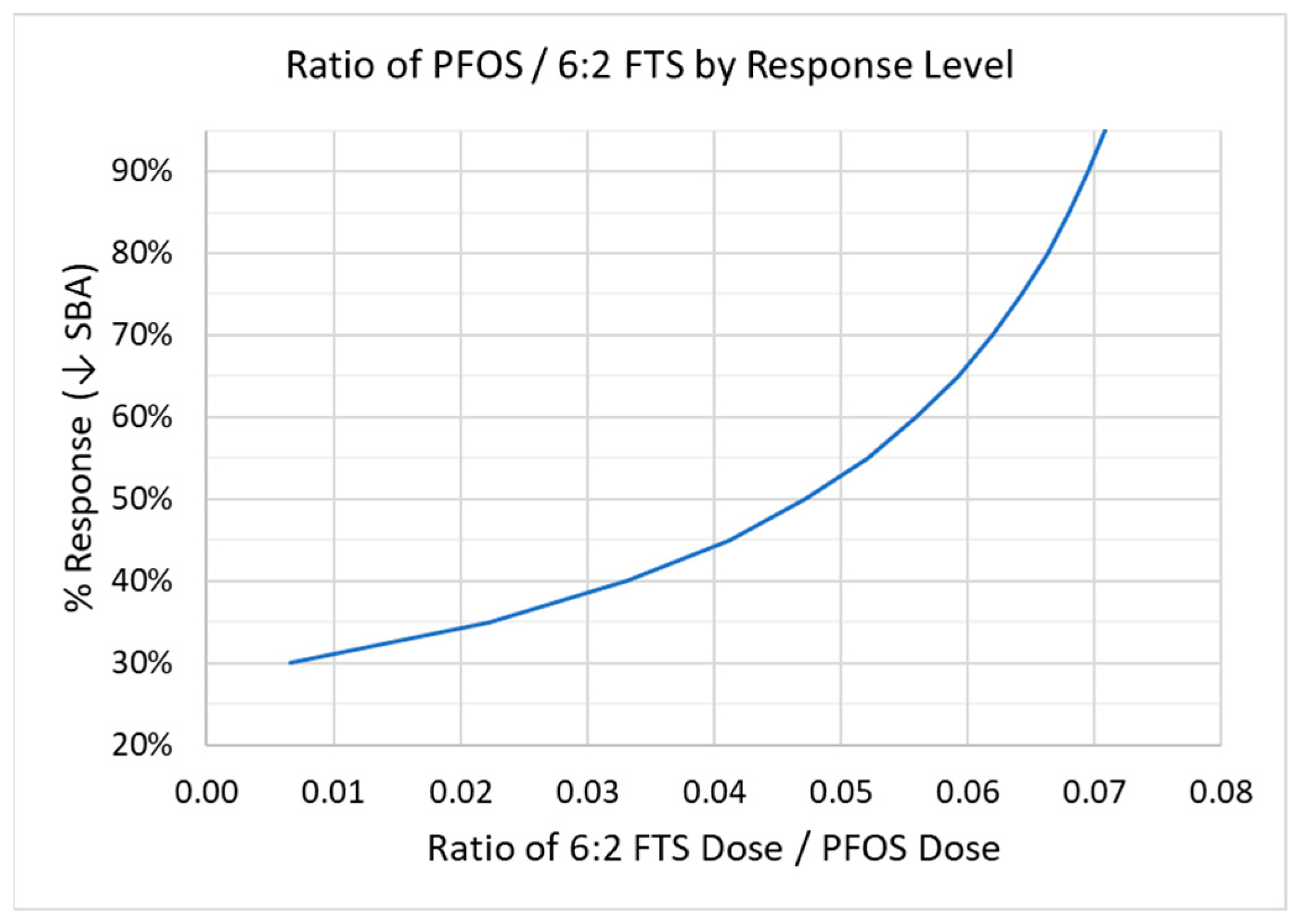
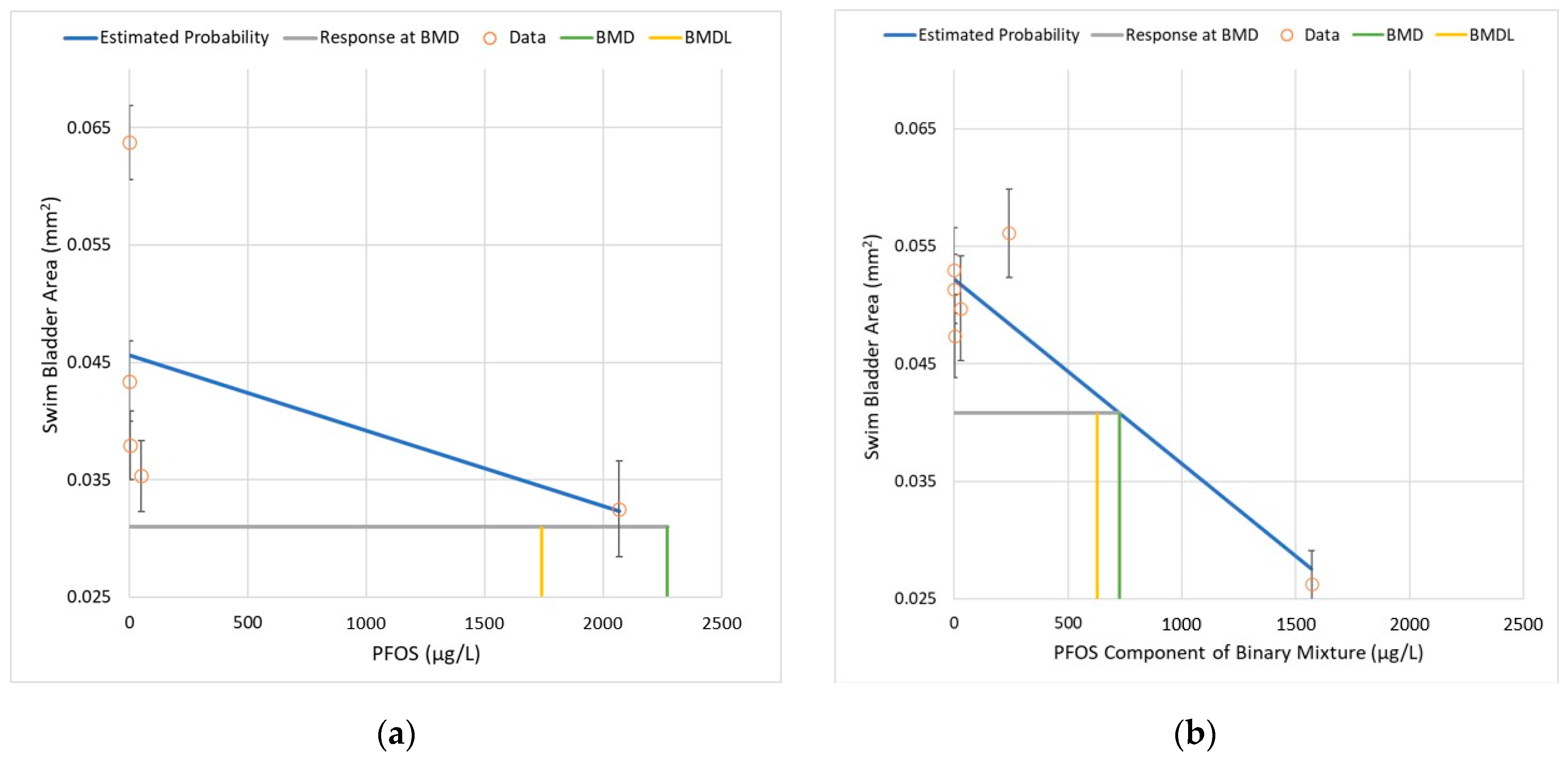
3.4. Dose–Response Analysis—Full Dose–Response with Binary Mixtures
- Across a full % response range, calculate the corresponding PFOS dose from the individual component study (see Table 5).
- Fit a D–R model to the PFOS component of the binary mixtures experiment and use the D–R model to predict the PFOS dose at each % response level (Figure 6a).
- Subtract the dose from #2 (mixtures experiment) from the dose from #1 (individual component experiment); the PFOS balance remaining is presumably attributable to additional toxicity from 6:2 FTS.
- Fit a D–R model to the 6:2 FTS component of the binary mixtures experiment and use the D–R model to predict the 6:2 FTS dose at each % response level (Figure 6b).
- Calculate the relative potency as the ratio of the PFOS balance remaining (#3) by the predicted 6:2 FTS (#4).
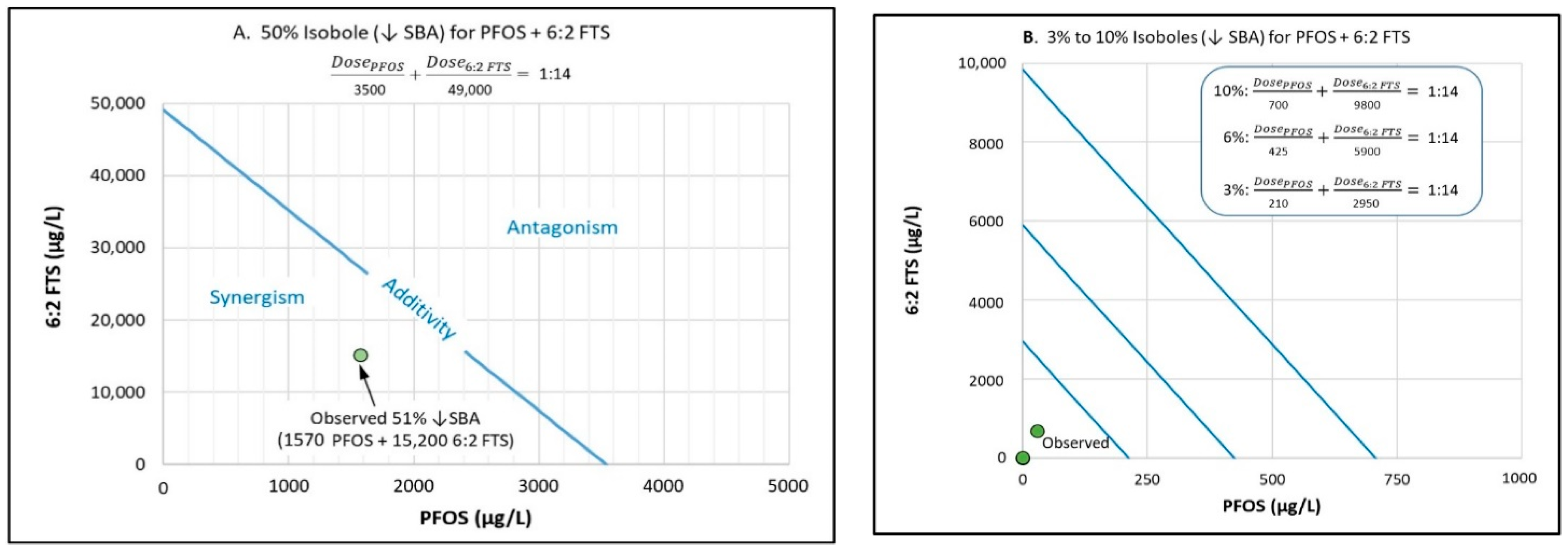
3.5. Response Additivity
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- European Food Safety Authority Scientific Committee; More, S.J.; Bampidis, V.; Benford, D.; Bennekou, S.H.; Bragard, C.; Halldorsson, T.I.; Hernandez-Jerez, A.F.; Koutsoumanis, K.; Naegeli, H.; et al. Guidance on harmonized methodologies for human health, animal health and ecological risk assessment of combined exposure to multiple chemicals. EFSA J. 2019, 17, 77. [Google Scholar]
- Rotter, S.; Beronius, A.; Boobis, A.R.; Hanberg, A.; van Klaveren, J.; Luijten, M.; Machera, K.; Nikolopoulou, D.; van der Voet, H.; Zilliacus, J.; et al. Overview on legislation and scientific approaches for risk assessment of combined exposure to multiple chemicals: The potential EuroMix contribution. Crit. Rev. Toxicol. 2018, 48, 796–814. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- U.S. Environmental Protection Agency (USEPA). Supplementary Guidance for Conducting Health Risk Assessment of Chemical Mixtures Risk Assessment Forum; U.S. EPA: Washington DC, USA, 2000.
- World Health Organization (WHO). Chemical Mixtures in Source Water and Drinking-Water; World Health Organization: Geneva, Switzerland, 2017.
- Goodrum, P.E.; Anderson, J.K.; Luz, A.L.; Ansell, G.K. Application of a framework for grouping and mixtures toxicity assessment of PFAS: A closer examination of dose-additivity approaches. Toxical. Sci. 2021, 179, 262–278. [Google Scholar] [CrossRef]
- U.S. EPA. Draft Aquatic Life Ambient Water Quality Criteria for Perfluorooctane Sulfonic Acid (PFOS). Office of Water, EPA-842-D-22-002, April 2022. Available online: https://www.epa.gov/wqc/aquatic-life-criteria-perfluorooctane-sulfonate-pfos (accessed on 1 May 2022).
- U.S. EPA. Draft Aquatic Life Ambient Water Quality Criteria for Perfluorooctanoic Acid (PFOA). Office of Water, EPA-842-D-22-001, April 2022. Available online: https://www.epa.gov/wqc/aquatic-life-criteria-perfluorooctanoic-acid-pfoa (accessed on 1 July 2022).
- Winata, C.L.; Korzh, S.; Kondrychyn, I.; Zheng, W.; Korzh, V.; Gong, Z. Development of zebrafish swimbladder: The re-quirement of Hedgehog signaling in specification and organization of the three tissue layers. Dev. Biol. 2009, 331, 222–236. [Google Scholar] [CrossRef]
- Huang, H.; Huang, C.; Wang, L.; Ye, X.; Bai, C.; Simonich, M.T.; Tanguay, R.L.; Dong, Q. Toxicity, uptake kinetics and behavior assessment in zebrafish embryos following exposure to perfluorooctanesulphonic acid (PFOS). Aquat. Toxicol. 2010, 98, 139–147. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martínez, R.; Navarro-Martín, L.; Luccarelli, C.; Codina, A.E.; Raldúa, D.; Barata, C.; Tauler, R.; Piña, B. Unravelling the mechanisms of PFOS toxicity by combining morphological and transcriptomic analyses in zebrafish embryos. Sci. Total Environ. 2019, 674, 462–471. [Google Scholar] [CrossRef]
- Annunziato, K.; Doherty, J.; Lee, J.; Clark, J.M.; Liang, W.; Clark, C.W.; Nguyen, M.; Roy, M.A.; Timme-Laragy, A.R. Chemical characterization of legacy aqueous film-forming foam sample and developmental toxicity in zebrafish (Danio rerio). Environ. Health Perspect. 2020, 128, 097006. [Google Scholar] [CrossRef] [PubMed]
- Ding, G.; Zhang, J.; Chen, Y.; Wang, L.; Wang, M.; Xiong, D.; Sun, Y. Combined effects of PFOS and PFOA on zebrafish (Danio rerio). Arch. Environ. Contam. Toxicol. 2013, 64, 668–675. [Google Scholar] [CrossRef]
- Hagenaars, A.; Stinckens, E.; Vergauwen, L.; Bervoets, L.; Knapen, D. PFOS affects posterior swim bladder chamber inflation and swimming performance of zebrafish larvae. Aquat. Toxicol. 2014, 157, 225–235. [Google Scholar] [CrossRef]
- Zheng, X.; Liu, H.; Shi, W.; Wei, S.; Giesy, J.P.; Yu, H. Effects of perfluorinated compounds on development of zebrafish embryos. Environ. Sci. Pollut. Res. 2012, 19, 2498–2505. [Google Scholar] [CrossRef]
- Suski, J.G.; Salice, C.J.; Chanov, M.K.; Ayers, J.; Rewerts, J.; Field, J. Sensitivity and accumulation of perfluorooctanesulfonate and perfluorohexanesulfonic acid in fathead minnows (Pimephales promelas) exposed over critical life stages of reproduction and development. Environ. Toxicol. Chem. 2021, 40, 811–819. [Google Scholar] [CrossRef] [PubMed]
- Jantzen, C.E.; Annunziato, K.A.; Bugel, S.M.; Cooper, K.R. PFOS, PFNA, and PFOA sub-lethal exposure to embryonic zebrafish have different toxicity profiles in terms of morphometrics, behavior, and gene expression. Aquat. Toxicol. 2016, 175, 160–170. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sant, K.E.; Jacobs, H.M.; Borofski, K.A.; Moss, J.B.; Timme-Laragy, A.R. Embryonic exposures to perfluorooctanesulfonic acid (PFOS) disrupt pancreatic organogenesis in the zebrafish, Danio rerio. Environ. Pollut. 2017, 220, 807–817. [Google Scholar] [CrossRef] [Green Version]
- Kherzi, A.; Fraser, T.W.K.; Nourizadeh-Lillabadi, R.; Kamstra, J.H.; Berg, V.; Zimmer, K.E.; Ropstad, E. A mixture of persistent organic pollutants and perfluorooctanesulfonic acid induces similar behavioural responses, but different gene expression profiles in zebrafish larvae. Int. J. Mol. Sci. 2017, 18, 291. [Google Scholar] [CrossRef] [Green Version]
- Maes, J.; Verlooy, L.; Buenafe, O.E.; de Witte, P.A.M.; Esguerra, C.V.; Crawford, A.D. Evaluation of 14 organic solvents and carriers for screening applications in zebrafish embryos and larvae. PLoS ONE 2012, 7, e43850. [Google Scholar] [CrossRef] [PubMed]
- Emerce, E.; Çetin, Ö. Genotoxicity assessment of perfluoroalkyl substances on human sperm. Toxicol. Ind. Health 2018, 34, 884–890. [Google Scholar] [CrossRef]
- Zebrafish International Resource Center. E2 Embryo Media with Methylene Blue. May 2013. Available online: https://wahoo.cns.umass.edu/sites/default/files/2019-01/E2_solution.pdf (accessed on 1 May 2022).
- Norström, K.; Viktor, T.; Palm Cousins, A.; Rahmberg, M. Risks and Effects of the Dispersion of PFAS on Aquatic, Terrestrial and Human Populations in the Vicinity of International Airports. 2015. Available online: https://repath.ivl.se/download/18.343dc99d14e8bb0f58b557e/1443615397431/B2232_RE-PATH%20FINAL_20150923.pdf (accessed on 1 May 2022).
- Kimmel, C.B.; Ballard, W.W.; Kimmel, S.R.; Ullmann, B.; Schilling, T.F. Stages of Embryonic Development of the Zebrafish. Dev. Dyn. 1995, 203, 253–310. [Google Scholar] [CrossRef]
- Shi, X.; Du, Y.; Lam, P.K.S.; Wu, R.S.S.; Zhou, B. Developmental Toxicity and Alteration of Gene Expression in Zebrafish Embryos Exposed to PFOS. Toxicol. Appl. Pharmacol. 2008, 230, 23–32. [Google Scholar] [CrossRef]
- Parichy, D.M.; Elizondo, M.R.; Mills, M.G.; Gordon, T.N.; Engeszer, R.E. Normal table of postembryonic zebrafish development: Staging by externally visible anatomy of the living fish. Dev. Dyn. Off. Publ. Am. Assoc. Anat. 2009, 238, 2975–3015. [Google Scholar] [CrossRef] [Green Version]
- R Development Core Team. R: A Language and Environment for Statistical Computing, Version 4.2.0; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 1 May 2022).
- Wickham, H.; François, R.; Henry, L.; Müller, K. dplyr: A Grammar of Data Manipulation. R Package Version 1.0.8. 2022. Available online: https://CRAN.R-project.org/package=dplyr (accessed on 1 May 2022).
- Lenth, R. emmeans: Estimated Marginal Means, aka Least-Squares Means. R Package Version 1.7.3. 2022. Available online: https://CRAN.R-project.org/package=emmeans (accessed on 1 May 2022).
- Crump, K.S. Calculation of benchmark doses from continuous data. Risk Anal. 1995, 15, 79–89. [Google Scholar] [CrossRef]
- Haber, L.T.; Dourson, M.L.; Allen, B.C.; Hertzberg, R.C.; Parker, A.; Vincent, M.J.; Maier, A.; Boobis, A.R. Benchmark dose (BMD) modeling: Current practice, issues, and challenges. Crit. Rev. Toxicol. 2018, 48, 387–415. [Google Scholar] [CrossRef] [PubMed]
- United States Environmental Protection Agency (EPA). Benchmark Dose Software Version 3.2. User Guide. EPA/600/R-20/216. August 2020. Available online: https://www.epa.gov/bmds (accessed on 1 March 2022).
- World Health Organization (WHO). Environmental Health Criteria 240. Principles and Methods for the Risk Assessment of Chemicals in Food, Chapter 5: Dose-Response Assessment and Derivation of Health-Based Guidance Values. Joint Food and Agriculture Organization of the United Nations (FAO)/WHO Expert Committee on Food Additives (JECFA). Second Edition, 2020. Available online: https://inchem.org/documents/ehc/ehc/ehc240_chapter5.pdf (accessed on 1 March 2022).
- Flynn, R.W.; Hoover, G.; Iacchetta, M.; Guffey, S.; de Perre, C.; Huerta, B.; Li, W.; Hoverman, J.; Lee, L.; Sepúlveda, M.S. Comparative Toxicity of Aquatic Per- and Polyfluoroalkyl Substance Exposure in Three Species of Amphibians. Environ. Toxicol. Chem. 2022, 41, 1407–1415. [Google Scholar] [CrossRef] [PubMed]
- Rericha, Y.; Cao, D.; Truong, L.; Simonich, M.T.; Field, J.A.; and Tanguay, R.L. Sulfonamide functional head on short-chain perfluorinated substance drives developmental toxicity. iScience 2022, 25, 103789. [Google Scholar] [CrossRef] [PubMed]
- Hoover, G.M. Effects of Per/Polyfluoroalkyl Substance Exposure on Larval Amphibians. Ph.D. Thesis, Department of Forestry and Natural Resources, Purdue University, West Lafayette, IN, USA, 2018. [Google Scholar]
- Flynn, W.; Hoover, G.; Iacchetta, M.; Guffey, S.; Li, W.; Hoverman, J.T.; Lee, L.S.; Sepulveda, M.S. Comparative Toxicity of Aquatic Per- and Polyfluoroalkyl Substance Exposure in Three Species of Amphibians. Purdue Univ. Res. Repos. 2022. [Google Scholar] [CrossRef]
- Hoke, R.A.; Ferrell, B.D.; Ryan, T.; Sloman, T.L.; Green, J.W.; Nabb, D.L.; Mingoia, R.; Buck, R.C.; Korzeniowski, S.H. Aquatic hazard, bioaccumulation and screening risk assessment for 6: 2 fluorotelomer sulfonate. Chemosphere 2015, 128, 258–265. [Google Scholar] [CrossRef]
- Palmer, S.J.; Van Hoven, R.L.; Krueger, H.O. Perfluorooctanesulfonate, Potassium Salt (PFOS): A 96-hr Static Acute Toxicity Test with the Rainbow Trout (Oncorhynchus mykiss); Report No. 454A-145. EPA Docket AR226-1030a044; Wildlife International Ltd.: Easton, MD, USA, 2002. [Google Scholar]
- Beach, S.A.; Newsted, J.L.; Coady, K.; Giesy, J.P. Ecotoxicological evaluation of perfluorooctanesulfonate (PFOS). Rev. Environ. Contam. Toxicol. 2006, 186, 133–174. [Google Scholar]
- Vogs, C.; Johanson, G.; Näslund, M.; Wulff, S.; Sjödin, M.; Hellstrandh, M.; Lindberg, J.; Wincent, E. Toxicokinetics of perfluorinated alkyl acids influences their toxic potency in the zebrafish embryo (Danio rerio). ES&T 2019, 53, 3898–3907. [Google Scholar] [CrossRef] [Green Version]


| Treatment Group | Single Chemical Experiments 1 | Binary Mixture 1 | ||
|---|---|---|---|---|
| PFOS (μg/L) 2 | 6:2 FTS (μg/L) 3 | PFOS (μg/L) 4 | 6:2 FTS (μg/L) 5 | |
| Control | 0 | 1.9 (0) | 0 | 0 (0) |
| T1 | 0.76 (0.1) | 1.2 (1) | 0.075 (0.1) | 1.3 (1) |
| T2 | 3.2 (2) | 23 (20) | 0.63 (2) | 21 (20) |
| T3 | 50 (60) | 731 (600) | 29 (60) | 683 (600) |
| T4 | 2066 (600) | 6331 (6000) | 241 (600) | 5825 (6000) |
| T5 | 7475 (1980) | 15,530 (19,800) | 1570 (1980) | 15,229 (19,800) |
| Group Comparison 1 | PFOS 2 | Binary Mixture 2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MR | HR | BL | SBA | YSA | MR | HR | BL | SBA | YSA | |
| T0 vs. T1 | L * | L * | ||||||||
| T0 vs. T2 | ||||||||||
| T0 vs. T3 | N | |||||||||
| T0 vs. T4 | L | N | N | |||||||
| T0 vs. T5 | N * | N * | N * | N * | L | L | N * | |||
| POD | Effect Endpoint | PFOS (μg/L) 1 | 6:2 FTS (μg/L) 2 | PFOS/ 6:2 FTS 3 | 6:2 FTS/ PFOS 4 |
|---|---|---|---|---|---|
| NOAEL | BL | 50 | >15,530 | <3.2 × 10−3 | >310 |
| SBA | <0.76 | >15,530 | <4.9 × 10−5 | >20,400 | |
| YSA | <0.76 | >15,530 | <4.9 × 10−5 | >20,400 | |
| LOAEL | BL | 2066 | >15,530 | <1.3 × 10−1 | >7.5 |
| SBA | <0.76 | >15,530 | <4.9 × 10−5 | >20,400 | |
| YSA | <0.76 | >15,530 | <4.9 × 10−5 | >20,400 |
| Dose–Response Model | BMD (μg/L) | BMDL (μg/L) | AIC | Scaled Residual at Dose Group Near BMR |
|---|---|---|---|---|
| Linear | 2268 | 1739 | −1155.8 | 0.097 |
| Power 1 | 2268 | 1732 | −1155.8 | 0.097 |
| Polynomial 1 | 2268 | 1744 | −1155.8 | 0.097 |
| Exponential 2 | 2287 | 1642 | −1156.0 | 0.136 |
| Hill | 0.2 3 | 0.1 3 | −1277.5 | 0.023 |
| % Response | PFOS (μg/L) 1 | 6:2 FTS (μg/L) 2 | PFOS/ 6:2 FTS | 6:2 FTS/ PFOS |
|---|---|---|---|---|
| 20% | -- 3 | 13,362 | -- 3 | -- 3 |
| 30% | 158 | 23,973 | 0.007 | 151 |
| 40% | 1147 | 34,583 | 0.033 | 30.1 |
| 50% | 2136 | 45,193 | 0.047 | 21.2 |
| 60% | 3125 | 55,804 | 0.056 | 17.9 |
| 70% | 4113 | 66,414 | 0.062 | 16.1 |
| 80% | 5102 | 77,025 | 0.066 | 15.1 |
| 90% | 6091 | 87,635 | 0.070 | 14.4 |
| % Response | PFOS Only (μg/L) | PFOS in Mixture (μg/L) 1 | PFOS Balance (μg/L) | 6:2 FTS in Mixture (μg/L) 2 | PFOS/ 6:2 FTS | 6:2 FTS/ PFOS |
|---|---|---|---|---|---|---|
| 20% | -- 3 | 627 | -- 3 | 7287 | -- 3 | -- 3 |
| 30% | 158 | 965 | -- 4 | 11,091 | -- 4 | -- 4 |
| 40% | 1147 | 1303 | -- 4 | 14,895 | -- 4 | -- 4 |
| 50% | 2136 | 1641 | 495 | 18,699 | 0.026 | 37.8 |
| 60% | 3125 | 1979 | 1146 | 22,503 | 0.051 | 19.6 |
| 70% | 4113 | 2317 | 1796 | 26,307 | 0.068 | 14.6 |
| 80% | 5102 | 2656 | 2446 | 30,111 | 0.081 | 12.3 |
| 90% | 6091 | 2994 | 3097 | 33,915 | 0.091 | 11.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fey, M.E.; Goodrum, P.E.; Razavi, N.R.; Whipps, C.M.; Fernando, S.; Anderson, J.K. Is Mixtures’ Additivity Supported by Empirical Data? A Case Study of Developmental Toxicity of PFOS and 6:2 FTS in Wildtype Zebrafish Embryos. Toxics 2022, 10, 418. https://doi.org/10.3390/toxics10080418
Fey ME, Goodrum PE, Razavi NR, Whipps CM, Fernando S, Anderson JK. Is Mixtures’ Additivity Supported by Empirical Data? A Case Study of Developmental Toxicity of PFOS and 6:2 FTS in Wildtype Zebrafish Embryos. Toxics. 2022; 10(8):418. https://doi.org/10.3390/toxics10080418
Chicago/Turabian StyleFey, Megan E., Philip E. Goodrum, N. Roxanna Razavi, Christopher M. Whipps, Sujan Fernando, and Janet K. Anderson. 2022. "Is Mixtures’ Additivity Supported by Empirical Data? A Case Study of Developmental Toxicity of PFOS and 6:2 FTS in Wildtype Zebrafish Embryos" Toxics 10, no. 8: 418. https://doi.org/10.3390/toxics10080418
APA StyleFey, M. E., Goodrum, P. E., Razavi, N. R., Whipps, C. M., Fernando, S., & Anderson, J. K. (2022). Is Mixtures’ Additivity Supported by Empirical Data? A Case Study of Developmental Toxicity of PFOS and 6:2 FTS in Wildtype Zebrafish Embryos. Toxics, 10(8), 418. https://doi.org/10.3390/toxics10080418






