2.1. Burial of Objects
To analyze the mobilization of objects on the seabed, the state of their burial must be known. This is basic information. Burial of objects is caused by various effects. Numerous research works deal with the subsequent burial depths due to self-burial, especially for cylindrical objects [
2,
4,
5]. Self-burial is caused by the flow structure around the object.
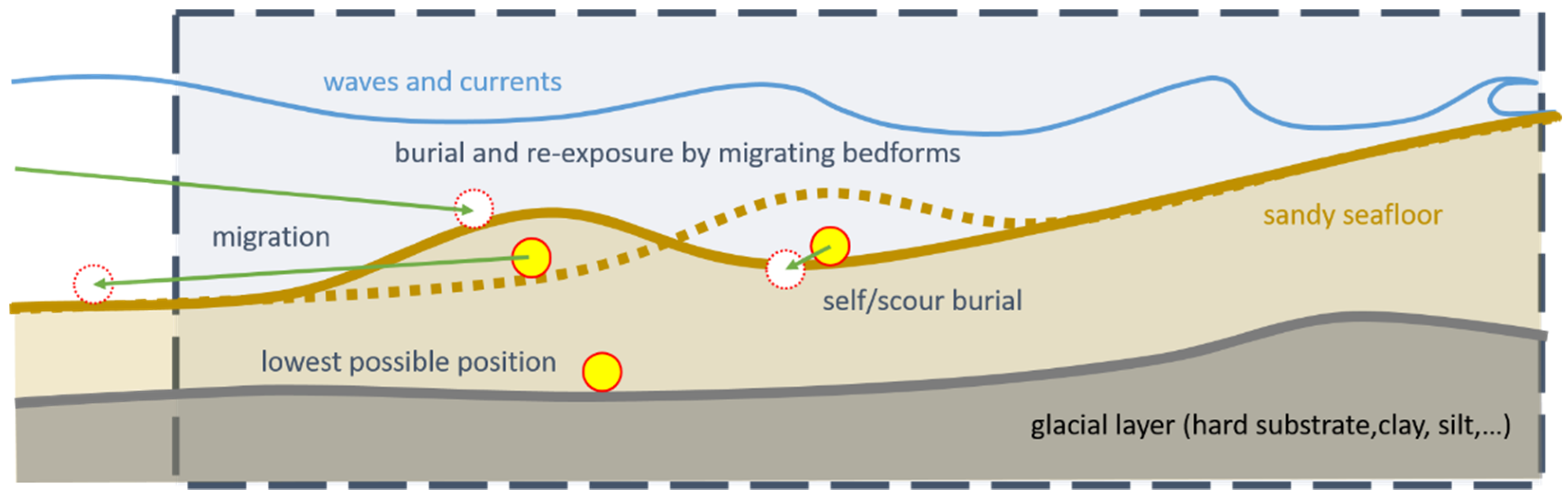
The process of self-burial due to currents shown in
Figure 2 was published in [
6,
7]. As shown in [
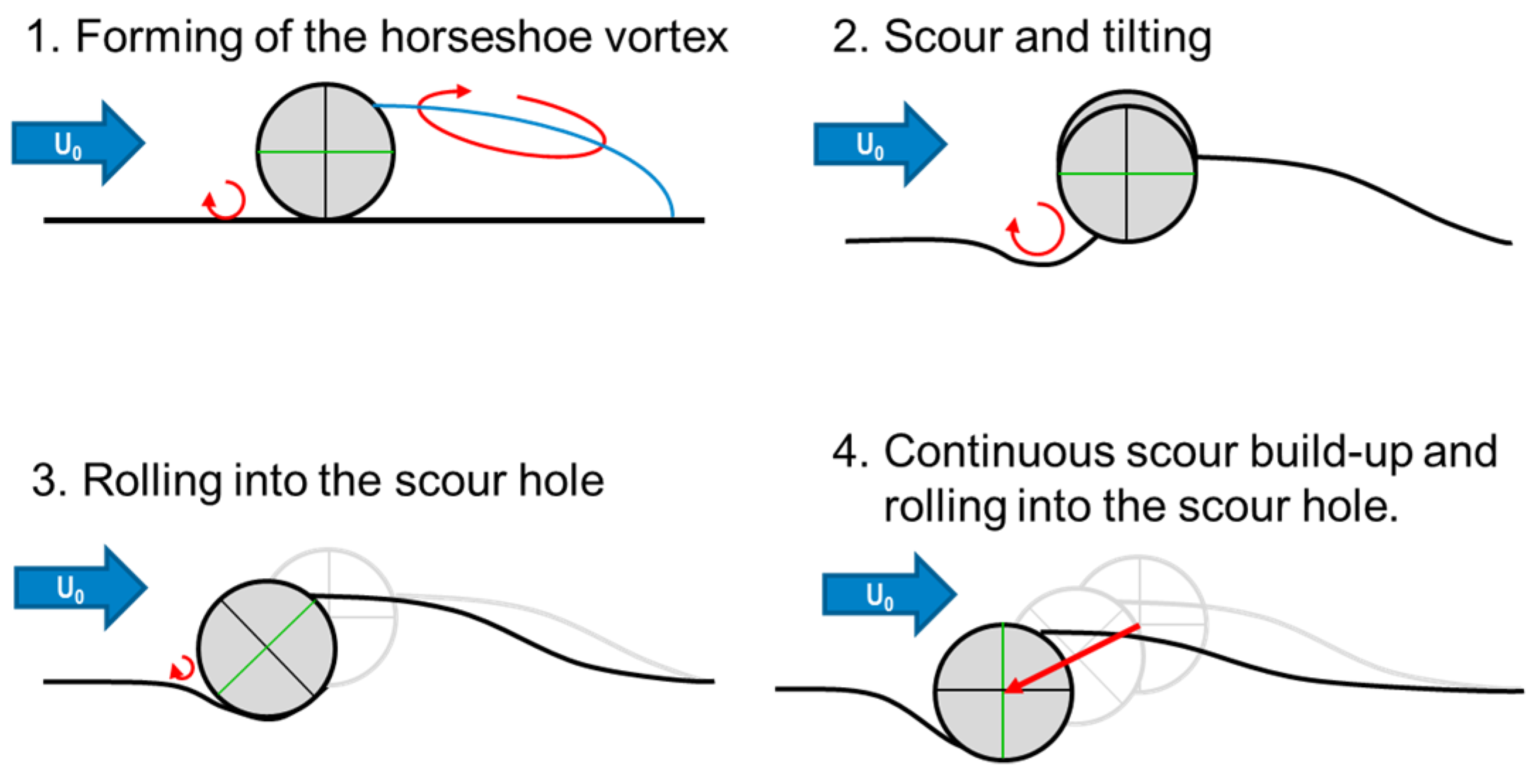
8], the preferred orientation of a cylindrical object on the seafloor is perpendicular to the incident current, caused by the Munk moment described in [
9]. Due to the presence of the object, the bottom boundary layer in front of the object forms a vortex—the horseshoe vortex. This vortex leads to a very thin bottom boundary layer, which results in a high load on the sediment particles eroding in this area. The resulting trough becomes larger and larger until the object begins to move into it. An arcuate vortex in the wake forms the recirculation area, which acts as a sorting sediment trap. The formed region of accumulation prevents the object from rolling downstream. The upstream and downward displacement of the object occurs until the object is buried by about 115% of its diameter, as published in [
4]. Thus, the horizontal displacement is limited to about one diameter of the object. Compared to the goal of this study, to determine if an object can be mobilized to travel over longer distances, this is a small displacement. At this point, it is important to note that the displacement caused by self-burial must be distinguished from object mobilization, which can enable migration over greater distances.
Another process of object burial is caused by far-field effects that occur independently of the object in place. These effects are general seafloor changes and large-scale ripples (mega-ripples) that can be observed in highly morphodynamic regions such as the North Sea or estuaries. In these effects, the object is not mobilized, but sediment is deposited on the object. These effects can also lead to re-exposure of the objects and must therefore be taken into account when analyzing the mobilization of objects.
The effects described above occur on sandy seabeds. In areas with mud, objects can sink into the mud without external forces acting on the object or the sediment. In contrast, objects located on silt or clay are not buried because this sediment is usually not eroded by currents and waves. Similar behavior is observed on rocky substrates and in areas with high seagrass beds. Therefore, these regions must be treated separately.
2.2. Current-Induced Mobilization
Assuming that an object on a sandy seabed is at least partially but not completely buried by self-burial, it is still subject to flow- and wave-induced stresses. In [
3], wind tunnel experiments, experiments in large flow tanks, and numerical simulations were used to determine the critical flow velocity,
, required to mobilize an object from a partially buried position.
This velocity is defined to attack 20 cm above the seabed. The parameters in this equation are the density of the water
and of the object
, the gravitational acceleration
, the dynamic viscosity
, the average diameter of the object
, its length
, and its volume
. The burial depth
describes the fraction of the object diameter that is buried. The parameters
and
are determined by statistics and also published in [
3].
2.3. Wave-Induced Mobilization
Especially in shallow waters, the influence of surface waves on objects on the seafloor cannot be neglected. Compared to the wavelength of the surface wave, it can be assumed that large parts of the North Sea are shallow during a considerable number of days per year. More precisely, the hydrodynamic effects of surface waves must be considered during most of the year for almost the entire German Bight. This changes in the protected areas of the Wadden Sea, where the wave effect can be neglected.
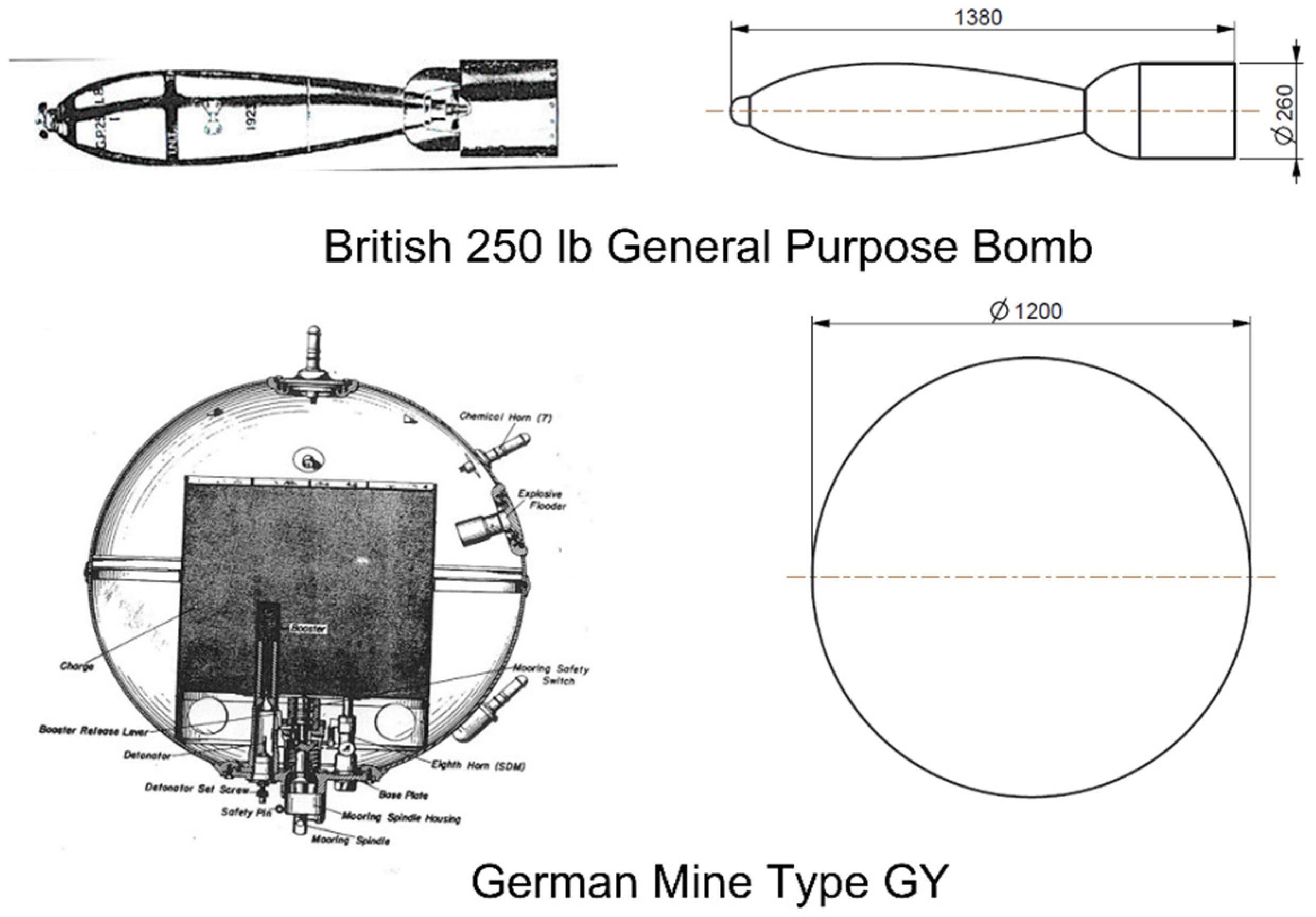
Quantifying the critical surface waves that trigger the mobilization of an object on the seafloor is much more complex than quantifying the critical current velocity because many more unknown variables must be considered. The analysis published in [
10] is applied to typical UXO found in the North Sea. These are, for example, the British 250-pound general purpose bomb and the German mine type GY, as shown in
Figure 3. The German mine type GY is assumed to be completely flooded. The absolute mass of the British 250-pound general purpose bomb is given as
while the flooded absolute mass of the German mine type GY is approximated by
. All dimensions are given in
Table 1.
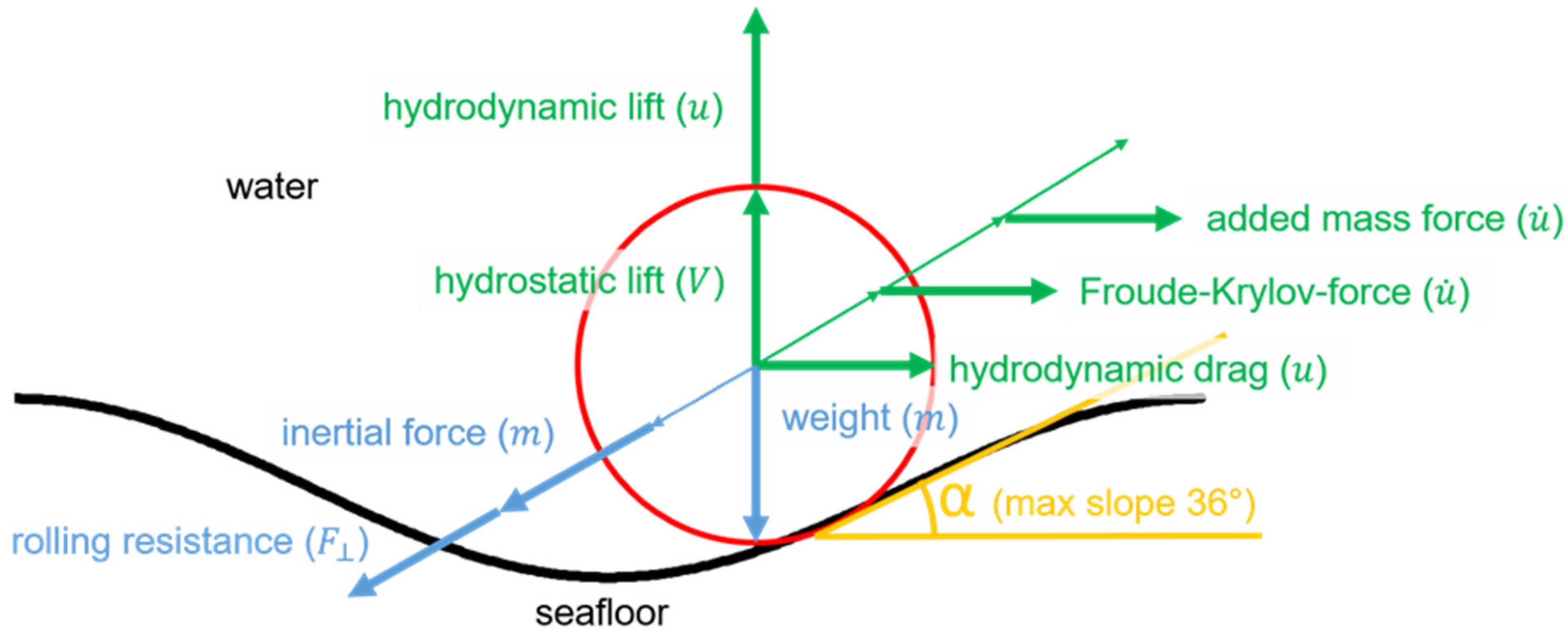
In contrast to flow-dominated scenarios, the scour trough shown in
Figure 2 builds up on both sides of the object, such that the accumulation area in the “wake” shown in [
7] is absent. Under this assumption, the load balancing model with a sinusoidal scour trough published in [
10] and shown in
Figure 4 can be applied.
Using the relationship published in [
11], known as the Morrison equation, the horizontal loads can be balanced as follows:
where
is the mass of the object;
and
are the volume and cross-section of the object, respectively;
and
are the horizontal velocity and acceleration of the water, respectively;
and
are the horizontal velocity and acceleration of the object, respectively;
is the density of the water;
is the coefficient of added mass, and
is the drag coefficient. On the left side, the inertia is determined taking into account the rotation. Since the mass distribution of the objects is not completely known, a homogeneous mass distribution is assumed. On the right side of the equation, we find the Froude–Krylov force, the added mass force, and the hydrodynamic drag force. The hydrodynamic lift force is considered for the vertical component. The governing coefficients in this equation are the dimensionless coefficients for drag, lift, and added mass, which are not constant with the Reynolds number and burial depth. For the objects considered here, they are about
and
.
The dimensionless coefficients in Equation (2) were derived from experiments and CFD simulations for the objects in
Figure 3. They depend on several variables such as the Reynolds number and burial depth. The velocity and acceleration of the water at the location of the objects were derived from the wave period, wave height, and water depth using Stokes’ wave theory of 3rd order. By substituting all of the above variables into Equation (2) and the equivalent equation for the vertical loads, the acceleration of the object can be calculated.
2.4. Critical Waves for Mobilization
The wave-induced mobilization of objects can be derived from the equations presented above. In practice, the equation for wave-induced mobilization cannot be solved directly. Therefore, a simulation method must be used. A numerical integration of these equations over time yields a motion simulation that is used to decide whether the object leaves the scour trough and is thus mobilized, or whether it remains within the trough. For this simulation, 10 monochromatic waves were considered and resolved by 360 phase steps each. By testing different water depths (
with 0.1 m discretization), wavelengths, and periods (
with 0.1 s discretization), the critical parameter combinations leading to mobilization of a single object at a single burial depth were determined. The results of this simulation for the British 250-pound general purpose bomb, neglecting the ring tail, are exemplarily shown in
Figure 5.
Each curve in the diagram represents the critical wave height for a given water depth at a burial depth of 50% of the object diameter (). Higher wave heights and longer wavelengths mobilize the object. However, these generalized results can later be related to wave data for a particular site, whereas data from a site (e.g., from weather forecasts or directly measured) are usually available as statistical data that must first be converted to individual waves. As a worst-case scenario, the maximum wave height and peak wave period were used for further analysis.
2.5. Recurrence Interval
The results shown in
Figure 5 can be used for monitoring purposes by comparing them, for example, with short-term weather forecasts or real-time wave monitoring data. However, for planning purposes and to assess the likelihood of recurrent mobilization in a given sea area, the analysis of historical data from a spatial wave model, as performed in this study, can be very useful. Here, the recurrence interval (or recurrence period) method is a common method for statistically predicting the time between special or extreme events from historical observations. Typically, this method is used for severe storm events or similar extreme weather situations that typically occur every 10, 20, 50, or 100 years. For these analyses, the recurrence time
is derived by hand from a time series of
events within
years or days as follows:
However, determining the average recurrence interval of the mobilization of objects on the seafloor is a complex matter. This is primarily because these events tend to occur much more frequently at certain times of the year, such as during the storm season. For example, if an object can be mobilized once per day for two consecutive months during the local storm season, determining the return times using the above approach would yield a return time of about 366/60 = 6.1 days. However, the desired result would be more of a return time of one year, in the sense that it migrates once a year on a consecutive number of days, so that wind farm operators know that checking mobilization once a year is sufficient.
The analysis of these historical data usually requires the evaluation of both temporally and spatially large datasets. In order to be able to automatically evaluate the mobilization return times with the desired result mentioned above, a new automatic algorithm was developed in this research. In the first step, the object mobilization is determined on a daily basis with the binary information “mobilization” or “no mobilization” on a spatial and temporal grid of arbitrary resolution. This is necessary because wave-induced mobilization depends strongly on local conditions such as water depth, which changes rapidly near the coast; local flow systems near river mouths, and similar effects. In addition, seafloor sediments and seafloor mobility must be considered. Therefore, high spatial resolution for the recurrence interval is required for decision making.
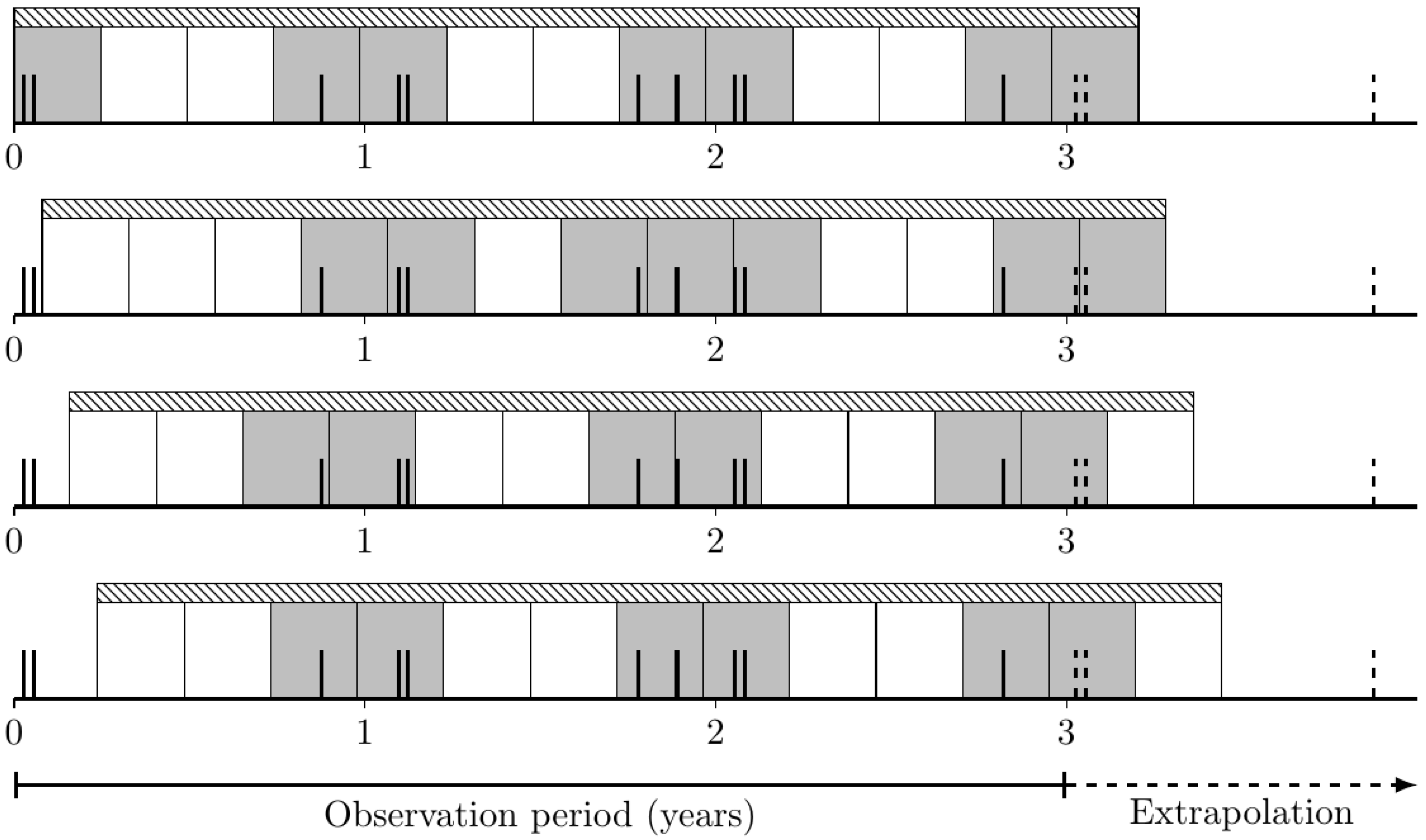
As mentioned earlier, mobilization events accumulate during certain periods of the year. This accumulation is observed because, for example, a single storm event may last several days, resulting in repeated mobilization of an object during that time. If only Equation (3) were used, this would result in multiple counts of an event that is actually a single event. To solve this problem, the entire observation period is divided into a different number of time intervals. This is performed several times with different interval lengths, where the shortest length is one day and the longest is half of the total observation period. The principle is illustrated in
Figure 6. For each interval length, the number of intervals containing an event is counted (see gray intervals in
Figure 6).
It should be noted that the total observation period is usually not an integer multiple of the interval length under investigation. This remainder becomes more significant the longer the interval length is. To include the information in the remainder, the observed data must be extrapolated by the missing information at the end to fill the last interval. For this purpose, the data from the beginning of the observation period are simply appended to the end of the data series.
The recurrence interval is then determined from the proportion of intervals that contain an event. For this purpose, the interval length is determined where every second interval contains an event. The corresponding average recurrence time is then to be determined as twice the interval length, since there is then, on average, an interval that does not contain an event between two intervals that do contain an event. Accordingly, the time from the center of an interval containing an event to the center of the next corresponding interval is just twice the interval length. An example of this procedure is shown in
Figure 6, where the last interval length satisfies this criterion and yields a return time of about half a year. Although it can be argued that a return time of one year might be even more realistic, this approach produces more realistic results than applying Equation (3) but is still conservative.
Finally, several events may occur close to the edge of the intervals containing them, leading to significantly different results if the entire observation frame is shifted by only a small number of days. To minimize the impact of these effects of events at the edge of intervals, the analysis is repeated several times for each interval length by shifting the beginning of the first interval upward by all possible days into the corresponding interval length to be analyzed, as shown in
Figure 7. The number of intervals with events is then averaged for all analyses with the same interval length.
2.6. Obtaining Regional Information through Spatial Planning
For spatial planning, it may be necessary to perform a recurrence interval analysis for the mobilization of a particular object of interest in a region of interest. From Equations (1) and (2), it can be seen that the geometric parameters of the object, water depth, current, and wave information are needed.
The composition of the seafloor (sediment types) was taken from the “Geopotenzial Deutsche Nordsee (gpdn)-project”, described in [
12,
13]. The near-bottom tidal currents were taken from the BSH Operational Circulation Model (BSHcmod). The wave parameters were taken from the German Weather Service (DWD) and its Coastal Wave Model (CWAM) and European Wave Model (EWAM). The data used represent the forecasts for the next 12 h until the next model run in 3-hour increments. A complete list of all input data can be found in
Table 2. The far-field accumulation and erosion data are from the AufMod project, published in [
14]. These data were used to determine the object-specific mobilization characteristics.
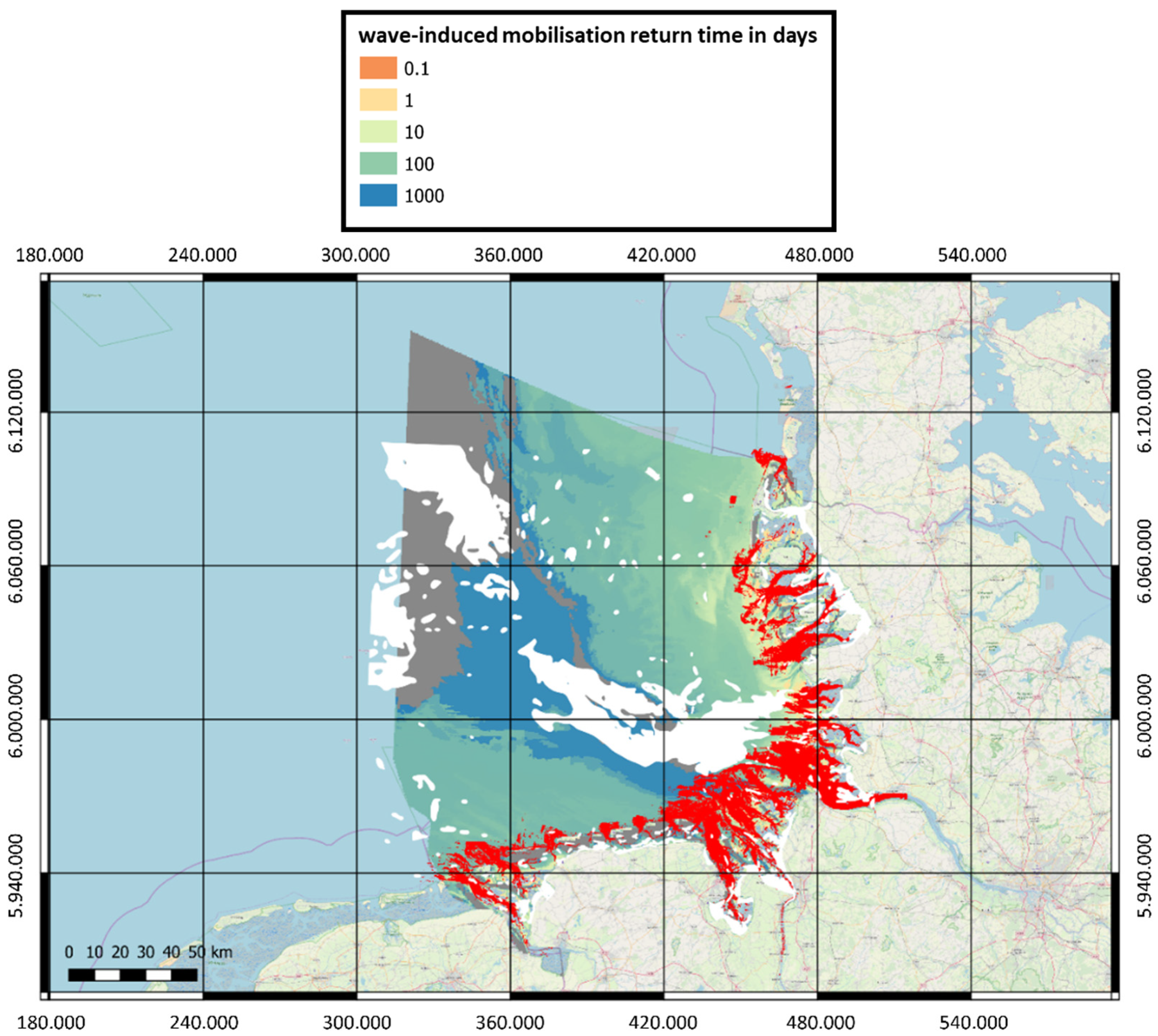
The spatial information, including the maps of the recurrence interval for a given object, is processed in QGIS based on a hierarchical decision tree shown in
Figure 8, which does not necessarily represent a schedule of processing but shows the important decisions. In practice, both wave-induced mobilization analysis and flow-induced mobilization analysis run separately and are used as inputs to the GIS.
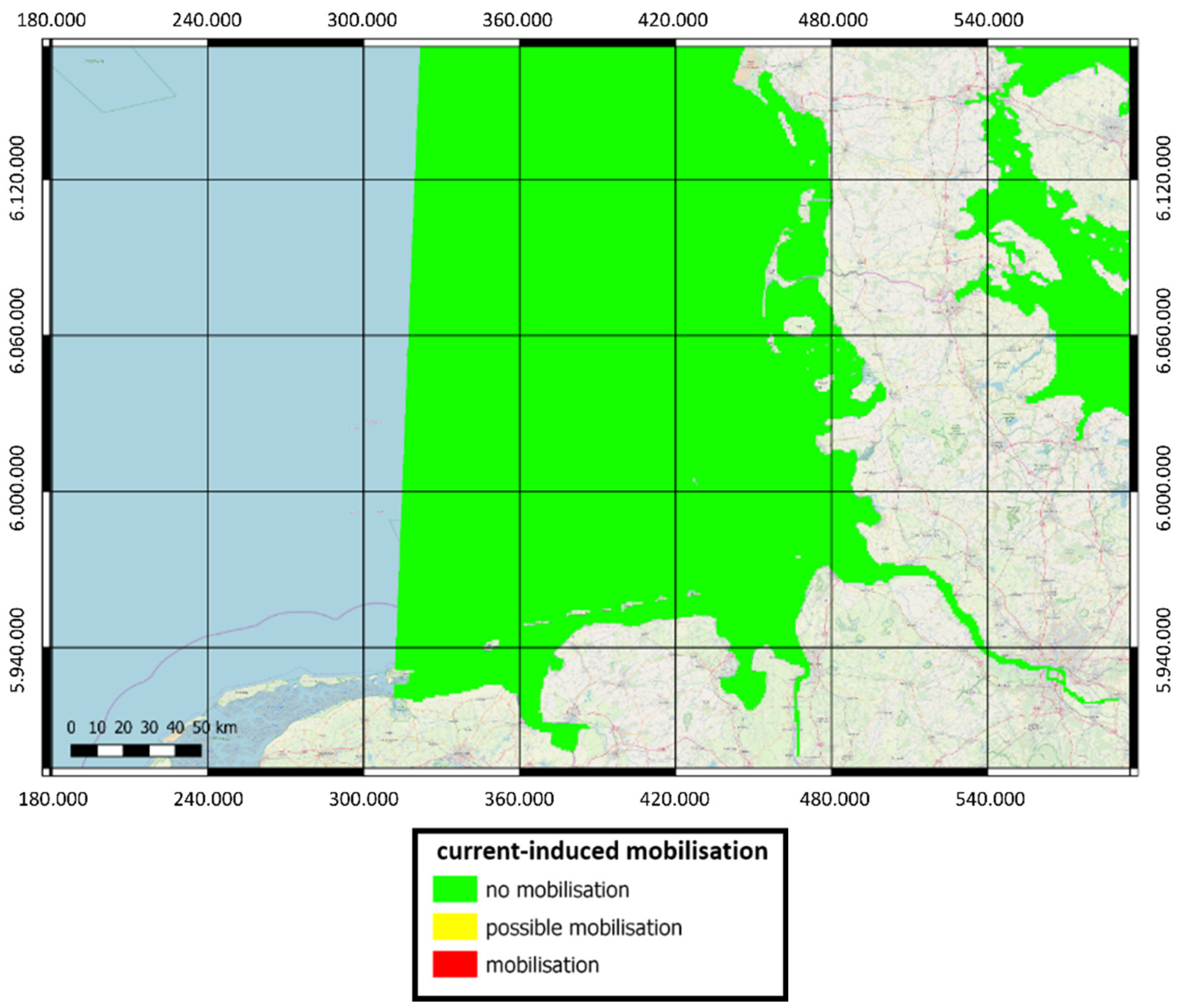
However, the first GIS analysis is based on sediment type. Here, it is assumed that an object located in a muddy area may be immobile for a long time due to the heavy burial and suction effect, while objects on hard substrates such as silt and clay may not even be buried and therefore be very mobile. Since the physical processes in these areas are not considered, these regions are excluded from further analysis (cut away in the GIS).
For some regions, seafloor morphology datasets are available from an extended seafloor analysis. These datasets include regions where mega-ripples and dunes are present. Within these regions, further analysis can be performed depending on the quality of the information. If only the presence of mega-ripples is indicated, it is assumed that objects may be completely buried but may also be uncovered after an unknown time. Therefore, these regions are also excluded from the GIS analysis as long as no further information is available.
Further analysis of seafloor morphology will be performed using information from the AufMod project. From these data, the mean annual change in the seafloor and the annual standard deviation are calculated. A distinction is made between mean annual accumulation of more than half an object diameter, erosion of more than half an object diameter, and change of less than half an object diameter. Depending on which case occurs, complete exposure or the chance of complete burial is assumed. In the case of severe sediment erosion, the object may be fully exposed. Unless the self-burial process is described by a model, it is assumed that the object can be mobilized very easily. A recurrence interval for mobilization cannot be specified for this case. For the alternative cases, another analysis is performed considering the standard deviation of the annual seafloor change. If the mobilization return time is large compared to the annual standard deviation of seafloor change, the standard deviation can be neglected and the object is assumed to be completely buried. Otherwise, its value must be checked, which is done even in the case of low mean accumulation and erosion. If the annual standard deviation is greater than half of the object diameter, the object may be completely exposed from time to time and thus be highly mobile. Regions with this behavior are considered unsafe and therefore excluded from the map of return periods in the GIS. In the case of a low standard deviation, the return time method and mobilization prediction are applicable. These are the remaining regions in the map shown in
Figure 9.