Abstract
By applying first principles density functional theory (DFT) methods, different metal fluorides and their surfaces have been characterized. One of the most investigated metal fluorides is AlF3 in different polymorphs. Its chloride-doped analogon AlClxF3−x (ACF) has recently attracted much attention due to its application in catalysis. After presenting a summary of different first-principle studies on the bulk and surface properties of different main group fluorides, we will revisit the problem of the stability of different -AlF3 surfaces and extend the investigation to chloride-doped counterparts to simulate the surface properties of amorphous ACF. For each material, we have considered ten different surface cuts with their respective terminations. We found that terminations of () and () yield the most stable surfaces for -AlF3 and for the chlorine substituted surfaces. A potential equilibrium shape of the crystal for both -AlF3 and ACF is visualized by a Wulff construction.
1. Introduction
Heterogeneous catalysis is nowadays mainly performed with metal oxides; therefore, a vast amount of publications, both experimentally and computationally, deal with the investigation of metal oxide surfaces as model systems for heterogeneous catalysis (for a recent review, see [1]). However, for increasing the catalytic active sites in the material, realistic catalysts are very often so-called high-surface materials with crystalline particle sizes in the nanometer regime. The concept of nanotechnology was first introduced by R. P.Feynman in 1959, in his famous speech “There’s plenty of room at the bottom” [2], meaning that “the control of materials and their properties in the atomic scale comprised a new frontier of opportunity in science and technology”. About 30 years later, Gleiter et al. launched the systematic study of nanoscopic materials, introducing the terms “nanocrystalline” and “nanocrystal” [3]. Due to their size-dependent physical and chemical properties [4], nanomaterials are spread over a wide range of applications in many areas of human activity, particularly in electronics [5,6,7,8], optics [9,10] and medicine [11,12,13]. For a long period of time, the interest in metal-based compounds was confined to oxides [14,15,16]. Only recently, considerable attention has been devoted to metal fluorides [17,18,19], especially after the development of the sol–gel route to their synthesis [20]. Originally used for the synthesis of nanoscopic AlF3 [21,22,23] and successfully applied to MgF2-based materials [24], fluorolytic sol–gel synthesis has been operated on many other fluorides [25,26], including ZnF2 [27] and the alkaline-earth fluorides CaF2, SrF2 and BaF2 [28,29]. In a sol–gel procedure, a metal precursor reacts with hydrogen fluoride in a suitable organic solvent to form a transparent sol. After a post-treatment, the desired nanomaterial is obtained.
Due to their high surface area and moderate to high Lewis acidity, the sol–gel synthesized aluminum fluoride and magnesium fluoride have revealed outstanding catalytic performance with high activity, as well as high selectivity for a broad range of chemical reactions [20,30,31,32,33,34,35,36,37,38,39], for example the fluorination of 2-chloropyridine to 2-fluoropyridine [40]. They have also shown excellent applicability in antireflective optical coatings [41], where metal fluoride-based thin films of high mechanical resistance were obtained. Moreover, they are used as inorganic components embedded in an organic polymer matrix to form composite materials with new functionalities [42]. Alkaline earth fluorides catalyze the dehydrohalogenation of chlorofluorobutanes, with BaF2 showing an interesting catalytic activity with high selectivity for the dehydrochlorination of 3-chloro-1,1,1,3-tetrafluorobutane [43]. ZnF2 combined with chiral diamine ligands has been found to exhibit a high catalytic activity for the asymmetric allylation of acylhydrazono esters [44].
Motivated by the outlined diversity in applications of the sol–gel prepared metal fluorides and the versatile path to their synthesis, computational work on these materials started with the investigation of the AlF3 surface both in the - and -modification [45,46]. The emphasis was placed on the modeling of the Lewis-acid sites and the catalytic behavior of the fluoride materials. CO-adsorption and the corresponding frequency shift were computationally determined for MgF2 [47] at different levels of accuracy including coupled cluster treatment [48]. We extended the studies to ZnF2 [49,50], which has the same crystal structure, but worse catalytic properties. We could not find any difference in the surface structure and the Lewis acidity of the surface cations [50] compared to MgF2, so the different catalytic activity is not of electronic origin. The bulk and surface properties of alkaline earth fluorides CaF2, SrF2 and BaF2 are widely investigated in experimental, as well as in theoretical studies [51,52,53,54,55,56,57].
In this publication, we want to revisit the problem of the Lewis acidity of the nanoscopic AlF3 and extend the study to chloride-doped AlF3, better known as ACF [58]. It is known to be a very strong Lewis acid similar to SbF5. The use of ACF has further advantages over SbF5, as it is less expensive, less toxic and, as a heterogeneous catalyst, more easy to handle. ACF has applications in various catalytic reactions like addition, elimination, cycloaddition, isomerization and dismutation reactions with organic poly halogen compounds [59]. ACF abstracts the fluoride from the reactant to turn it into a reactive species. To gain more insight into the nature of these types of solids and their Lewis acidity, we focus in this work on the stability of different low-index surfaces of -AlF3 and on the effects of chlorine substitution on these surfaces. -AlF3 crystallizes in the Rc space group [60] and exhibits six aluminum atoms per unit cell with an octahedral coordination of fluorides each (see Figure 1).
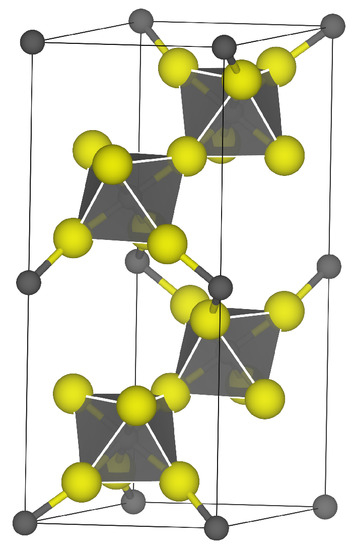
Figure 1.
Representation of the hexagonal unit cell of -AlF3 with experimental lattice constants = 4.931 Å and = 12.466 Å. The grey circles indicate aluminum and the yellow circles fluoride atoms. The octahedral structure formed by the fluorides is highlighted by the grey transparent area. Grey = aluminum, yellow = fluorine.
We restrict ourselves here to electronic structure calculations with density functional methods, but it is known that the nanoscopic structure of a solid is strongly influenced by the temperature and pressure of the surrounding atmosphere, either of which is not included in electronic structure calculations, and therefore, all calculated physical properties are only valid at K and atm (vacuum). However, electronic structure calculations can be combined with thermodynamics to include the effects of temperature and pressure. This combination, referred to as ab initio surface thermodynamics, can be employed to link results from electronic structure calculations to macroscopic properties and predict the stability of different surfaces under realistic conditions. The method was established and applied to metals and metal oxides in contact with an oxygen gas phase [61,62,63]. Later, surface thermodynamics were employed to predict the stability of AlF3 [45], MgF2 surfaces in a mixed HF/H2O environment [64] and the morphology of different alkali earth fluorides under HF pressure [56].
We focus in this study on the T = 0 K properties of the investigated surfaces and will first in the next section explain the methodology and models used and present the results afterwards.
2. Methodology and Models
2.1. Calculation of Surface Energy
The general formula to calculate surface energies is:
where is the surface energy, is the energy of the slab, is the bulk energy per unit cell, n is the number of the bulk unit cells in the slab and A is the area of the surface. The factor of 2 in the denominator arises since the surfaces on both sides of the slab contribute. Therefore, the formula requires slabs to be constructed symmetrically. In addition, unfortunately, Equation (1) can only be applied if n is an integer, i.e., if the slab is stoichiometric. Constructing slabs in this way for AlF3 is not always possible for every termination and surface cut while keeping the terminations the same on both sides of the slabs. An approach towards overcoming this challenge was suggested by Bailey et al. [45] via the chemical potential:
where is the number of ions of element i that have a chemical potential . The chemical potential for aluminum was taken to be the energy per atom obtained from the calculation of a pure aluminum crystal with the fcc structure (lattice constant = 4.037 Å [65]) at the same level of theory as for the AlF3 slabs. The chemical potential of fluorine was then calculated by subtracting the determined chemical potential for each aluminum in the cell from the energy of the bulk of AlF3. Calculating the chemical potential of chlorine requires a different approach. We cannot simply substitute some fluorides in the AlF3 bulk by chlorides and use the previously calculated chemical potentials of Al and F to get the chemical potential of Cl, because the total energy of this substituted bulk is dependent on the relative position and patterns of the chlorides. This can be avoided by calculating the chemical potential of Cl only with respect to the chemical potential of fluorine from HF and HCl.
Our primary approach for studying fluorine substitutions in ACF surfaces is to replace a fluoride on (or closest to) the exposed surface with a chloride ion. The internal coordinates of the resulting slab are then allowed to relax. In this case, there is no need to substitute on both sides of the slab, as the surface energy of the unsubstituted surface can easily be subtracted, where is the surface energy of the one side substituted slab:
2.2. Slab Construction
Two-dimensional surface models (slabs) are directly constructed from preceding bulk calculations. These bulk computations were performed at the experimentally-determined lattice constants [60], while at the same time, atomic positions (internal coordinates) were allowed to relax. When the cell constants were allowed to relax too, they showed only small deviations from the experimental structure with a variation of = −0.49% and = 0.93% compared to the experimental values (a = 4.907 Å, c = 12.582 Å). Such relaxations introduce a rather small volume change of 0.348 Å3 and an energy lowering of about 11 meV per unit cell. For this reason, we fixed the lattice constants to the experimental values in our model to keep it strictly systematic for different slabs.
Symmetric slabs with different surface terminations were obtained by cutting through the respective planes and identifying the different terminations. A handy tool to perform this task is, e.g., Xcrysden [66]. In the presented work, we have calculated the surface energies of all the possible terminations of ten low-index surfaces of -AlF3, which are the (0001), , , , , , , , and surfaces. A vacuum of 20 Å was kept for all slabs and was found to be sufficient for convergence. The number of layers necessary to achieve converged surface energies varied for different surfaces. This is because one layer is typically defined for atoms with the same (or very similar) z-coordinate (vertical position). Thus, atoms with a different z-coordinate are typically partitioned into different layers. As a consequence, whenever a cut through the bulk generates a slab unit cell, where there are many atoms with different z-coordinates, there is also a larger number of layers. For example, in the (0001) surface, the typical distance between the consecutive layers is about 1 Å, whereas it is between 0.1 and 0.2 Å for a surface like (). Thus, the convergence in the surface energy for the former was reached with 20 layers, while the latter required 95 layers. As a consequence, it is not the number of layers, but the actual thickness of the slab that matters. In our cases, a thickness of 15 Å or slightly more leads to surface energies converged within 0.01 J m−2.
2.3. Computational Details
All computations in this work were performed by applying the Vienna Ab Initio Simulation Package (Vasp) [67,68,69,70]. Within the Vasp code, we employed plane wave DFT with the PBE functional [71], together with the projector augmented wave (PAW) potentials [72] and the Γ-centered Monkhorst–Pack grid of size 6 × 6 × 2 [73]. Dispersion corrections were included via the D3-method [74] including BJ damping [75]. In various ionic compounds, PBE yields reasonable results [76,77,78,79]. The van der Waals radius for D3-BJ corrections in the calculations was assigned to be 20 Å. The convergence criteria for the electronic self-consistent field loop was set to 1 × 10−5 eV. The plane waves cut-off criterion was set to 600 eV. In addition, we utilized the tetrahedron method with Blöchl corrections [80]. The force and stress tensors were calculated, and ions were allowed to relax for a fixed cell shape and volume using the conjugate gradient algorithm. The ionic relaxations were stopped when all forces acting on the ions were below 0.01 eV/Å. Vesta [81] was used for visualization, and a Wulff construction [82,83,84] of the crystal shape was performed. The Bader charge analysis was performed with the charge density grid method [85,86,87]. For constructing the FFT mesh, 200 grid points were used along the lattice vectors for the coarse grid and 400 points for the fine one.
2.4. Effect of DFT-D3 Correction
To estimate the impact of the D3-BJ corrections, we have inspected the stable surface terminations also without the D3-BJ corrections. The bulk structure without the D3-BJ correction was slightly larger with = 5.002 Å ( = 1.4%) and = 12.604 Å ( = 1.1%). Based on these bulk parameters, slabs for the surface analysis were created. All relaxed surfaces without DFT-D3 corrections show very similar structural rearrangements compared to the ones with D3 corrections. The surface energy was calculated using the same techniques as mentioned earlier. When calculated without the D3 correction, the surface energies of all the terminations decreased uniformly by about 0.22 J m−2. This means D3 adds a significant contribution to the surface energies and that dispersive interactions play an important role. However, due to the uniform decrease over all surface energies, the shape of the crystal is nearly unaffected by the D3 correction. However, the absolute numbers of the surface energies should be interpreted with care.
3. Results and Discussion
3.1. -AlF3
We calculated the surface energies of all the possible terminations of ten low-index surfaces of -AlF3, namely the (0001), , , , , , , , and surfaces. The entirety of the various computed surface energies considered is summarized in Table 1 together with the formal charges of the terminating layers determined as the sum of the formal charges of the contributing ions (Al: +3, F: −1).

Table 1.
The calculated (PBE-D3 (BJ)) surface energies and the net charge of each of the possible terminations of the various surfaces. The most stable surfaces are highlighted in bold.
The most stable surface was found to be the neutral surface, which was closely followed by the neutral termination of . Both of these surfaces are stoichiometric, i.e., the ratio of the F to Al on the surface was 3:1. The only other stoichiometric termination was that of , which was the fourth most stable surface. It appears that the neutrality of the surface owing to the exact stoichiometry improved the stability drastically. For non-stoichiometric terminations, the surfaces whose net charge was closer to zero were generally more stable than the ones whose charge was considerably higher or lower. Among those, the surfaces with a net positive charge were more stable than the negatively-charged ones. This trend is clearly seen in Figure 2, where all the determined surface energies are plotted against the net charge of the surface. A higher positive charge yields only a small increase in the surface energy, whereas negative charges have a highly destabilizing effect.
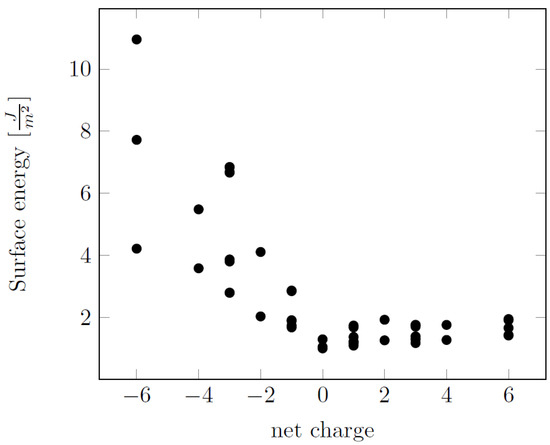
Figure 2.
Calculated (PBE-D3(BJ)) surface energy against the net charge of the surface layer.
With the energies of the most stable terminations of these 10 different low index surfaces, we could depict a reliable Wulff construction to quantify the occurrence of surfaces in a realistic crystal in a vacuum. The equilibrium shape of the -AlF3-crystal according to the Wulff scheme is shown in Figure 3.
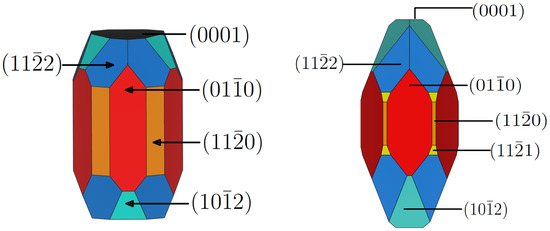
Figure 3.
Equilibrium shape of the AlF3 crystal (left) and AlClxF3−x (ACF) (right) in a vacuum according to the Wulff scheme. For ACF, the most stable chloride substituted -AlF3 surfaces are regarded, namely , , , (0001), and (PBE-D3(BJ)).
The most stable surface, , was also the one with the highest surface exposure as it covered about 35% of the surface area. Surprisingly, it was followed by the fourth most stable surface, , which made up about 28% of the crystal area. The , (0001) and contributed with 16%, 11% and 8%, respectively. Only five out of the ten cuts that were considered actually showed up in the crystal in the vacuum. The surfaces , , , and did not contribute, in spite of having a surface energy smaller than some of the present ones.
Only the (0001) and surfaces of the crystal, which contributed less than 20% of the total surface, exposed aluminum centers, which were assumed to be active reaction sites. The most often occurring surfaces of and did not directly expose an aluminum center on the surfaces. Rearrangement of the fluorides yielded shielded aluminum centers with a coordination number of four.
The structural changes of the most stable terminations for the -AlF3-surfaces, their respective surface energies and the coordination numbers of the aluminum centers closest to the surface are summarized in Table 2. Looking in more detail at the structural properties, the most stable surface of had four-fold coordinated Al centers on the unrelaxed surface. Upon structural optimization, the fluorides rearranged to form a tetrahedron around the Al center, maintaining the coordination number. The length of the top Al–F bond was 1.63 Å, contrary to 1.81 Å in the bulk. This indicates a stronger Al–F bond, due to the under-coordinated aluminum centers on the surface. The initial and the optimized structures are depicted in Figure 4.

Table 2.
Surface energies ( in J m−2) of the pure and chlorine substituted surface, the coordination number (CN) of the aluminum centers at the surface and the reaction energy (kcal mol−1) for that substitution of one chlorine. PBE-D3(BJ).
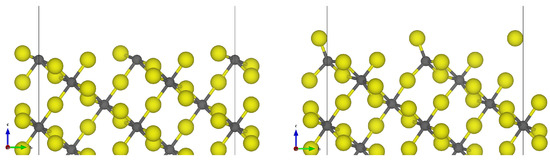
Figure 4.
-AlF3- surface: unrelaxed surface cut of the most stable termination (left) and corresponding structurally-optimized surface (right). Grey = aluminum, yellow = fluorine.
In the case of the surface, all the aluminum centers closest to the surface had a coordination number of five. In the unrelaxed case, aluminum was coordinated by fluorides, forming a pyramidal shape with the exposed aluminum facing upwards. On structural optimization, the coordination number remained five, but the shape was distorted towards a trigonal bipyramidal coordination sphere, as seen in Figure 5. The distance between the terminal fluorides and the aluminum atoms was reduced to 1.657 Å. This shift indicated strengthening of the bond, similar to the case.
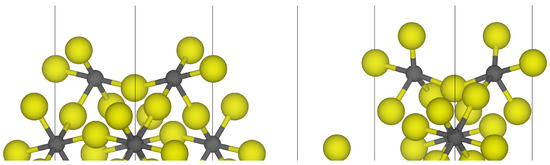
Figure 5.
-AlF3- surface: unrelaxed surface cut of the most stable termination (left) and corresponding structurally-optimized surface (right). Grey = aluminum, yellow = fluorine.
The most stable termination of the surface had three-fold, four-fold and five-fold coordinated aluminum centers when the surface was cut directly from the bulk. However, upon structural relaxation, the three-fold coordinated center shifted to form a four-fold coordinated distorted square planar structure. The four-fold coordinated structure rearranged to a tetrahedron-like structure with the terminal fluoride exhibiting a bond length of 1.63 Å. The five-fold coordinated relaxed into a trigonal bipyramidal coordination sphere, similar to the one seen in the surface. The terminal fluorine of this trigonal bipyramid had a bond length of 1.65 Å. The four-fold and five-fold coordinated aluminum centers of the surface showed rearrangements similar to those seen in the for the four-fold coordinated aluminum centers and the for the five-fold coordinated aluminum centers. Three-fold coordinated aluminum centers occurred on the and (0001) surfaces. In both cases, almost no rearrangements upon structural relaxation could be observed, resulting in structures as shown in Figure 6.
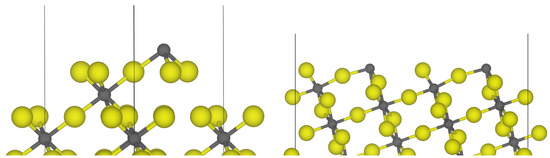
Figure 6.
Optimized structure of the -AlF3-(0001) surface (left) and optimized structure of the -AlF3- surface (right). Grey = aluminum, yellow = fluorine.
The bond distance between the surface Al of the and (0001) surfaces and the closest bridging fluorides to it was about 1.84 Å and 1.85 Å, respectively. This is slightly higher than observed in the bulk.
Bader charge analysis of the bulk and the surfaces elucidated the binding situation even further. In the AlF3 bulk, the charge at the fluorine was −0.855 e, where “e” is the absolute charge of an electron, while the charge on aluminum was 2.565 e. This indicates a strong ionic binding character of the compound. Apart from being a reference for understanding the changes in charge when the surface was formed, these values also help in confirming that the thickness of the slab was sufficient. The charge analysis of the (0001) surface shows that the charge of the three-fold coordinated aluminum center on the surface had reduced drastically to 1.41 e. The three fluorides in its coordination sphere, however, showed only a slight decrease in their charge (−0.892 e). The terminal fluorides on slightly increased their charges to about −0.814 e. The charges on the aluminum atoms, closest to the surfaces, decreased slightly to 2.524 e and thus showed no significant changes compared to the bulk. This charge analysis yielded very similar results for all surfaces regarding similar structural motifs.
3.2. Chlorine Substitution of -AlF3
To understand more about the structural and electronic properties of the surface of ACF, we substitute selected fluoride ions on the top and in the bulk with chlorides. The analysis of the corresponding reaction energies of a hypothetical reaction gave more insight into the stability of the systems.
For the bulk reaction energies, one and two substituted chlorines per unit cell—corresponding to = 0.166 and = 0.333, respectively—were considered. For = 0.166, the reaction was endothermic with an energy of 81.77 kcal mol−1. For the doubly-substituted bulk, the energy depended on the relative positions of the substituted chlorides and was about −82 kcal mol−1 per chlorine atom. This negative value is in line with the experimental observation that the dechlorination of AlCl3 towards the AlF3 composition was exothermic [59]. Most probably, the small amount of chlorine in the dechlorination reaction was due to kinetic effects, which are beyond the scope of this work. Regarding the chlorination on the surfaces, the reaction energies for replacing a terminal fluoride were reduced compared to the bulk and varied from 41–48 kcal mol−1 depending on the surface. In general, the reaction energy was lower if the terminal fluorides were replaced compared to the replacement of bridging fluorides, ranging from 52–86 kcal mol−1 depending on the surface (see Table 2).
Especially for the most stable surfaces with terminal fluorides, the reaction was far less endothermic than the one with respect to the bulk. Even for replacing the bridging fluoride, as was the case in the (0001) surface, the reaction energy was still smaller by 25% than the bulk. A Wulff construction [82,83,84] of the crystal of the chlorine substituted surface showed that except for the small amount of the surface occurring, the surfaces that appeared were the same compared to the pure crystal. The relative surfaces energies were however different, and thus, the shape of the Wulff construction changed.
Having first a closer look at the rearrangement for the terminal fluoride replacement, like that of the surface, we see that the coordination sphere around the aluminum center was nearly unchanged (Figure 7) and that the Al–Cl bond length (2.05 Å) was longer than the Al–F bond. A similar trend was seen for the terminal substitution on the and surfaces. In summary, this shows that the substitution of a terminal fluoride did not change the structure significantly and that the surface energies only increased slightly.
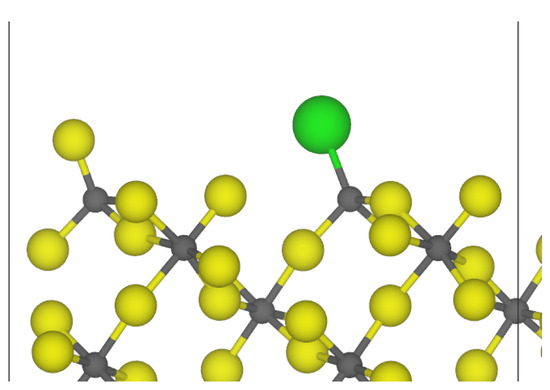
Figure 7.
Relaxed structure of the terminally-substituted ACF- surface(grey = aluminum, yellow = fluorine, green = chlorine).
This is different if the bridging fluorides are substituted. This was accompanied by a considerable change in the atomic structure, as shown in Figure 8 for several surfaces, and also, the substitution energy was very diverse for different surfaces. For example, the bridging substitution of the surface with an energy of 86 kcal mol−1 was bulk-like. After relaxation, the chloride remained a bridging one and thus maintained the coordination number of the aluminum centers. The bond distance of the Al–Cl bond here was 2.20 Å to both aluminum centers. For the substitution on the surface, the reaction energy for the bridging substitution was 55.4 kcal mol−1, quite similar to the terminal one (47.5 kcal mol−1). Here, the bridging fluorides were closer to the surface. After relaxation, the chloride bent upwards, and the Al–Cl bond distances were 2.48 Å and 2.24 Å. This rearrangement, which changed the coordination sphere of the Al center, is seen in Figure 8. A similar rearrangement of the bridging chloride moving upwards was also found for the () and () surfaces (see also Figure 8).
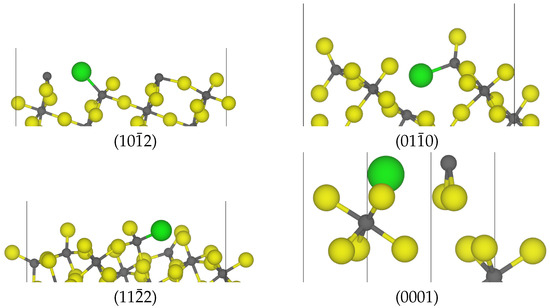
Figure 8.
Optimized structures of the bridging chloride substitution of various ACF surface cuts (grey = aluminum, yellow = fluorine, green = chlorine).
Regarding the (0001)-surface, chloride substitutions yielded structural changes where two-fold coordinated Al-sites occurred on the surface, which can be regarded as very reactive. Although the substituted chloride looked like a terminal one, the distance between Al–Cl was about 2.4 Å, which is significantly larger than the Al–Cl bond length observed for terminal substitutions. In other cases like the surface, the substitution of the bridging fluoride resulted in a similar change.
Bader charge analysis of the substituted surfaces showed that the charge on the chloride was slightly smaller than that of the fluoride it substituted by about 0.05 e. Thus, the chloride substitutions did not change the charge distribution on the surface, but could change the structure significantly. These structural changes could be responsible for the higher catalytic activity of ACF compared to AlF3.
4. Conclusions
DFT-based first principle calculations can help to elucidate the structural and energetic properties of various surfaces occurring in nanoscopic materials. These results are a first step in the understanding of the catalytic properties of nanoscopic materials and the basis of further investigations like the adsorption of probe molecules and the related frequency shifts or surface thermodynamics studies. With the knowledge of the possible surface structures, in a long-term perspective, catalytic reactions can be modeled, and by the search for the transition state, also kinetic properties can be described. For our presented example, -AlF3 and ACF, we could clearly identify the most stable surfaces, which are the () and the () planes. Depending on which fluoride is substituted by chloride at the surface, these surface energies are changed quite significantly for ACF. However, overall the charge distribution is not affected dramatically upon substitution, and changes in reactivity are due to the strong structural changes that leave aluminum sites exposed prominently. Surface energies are generally destabilized upon substitution of fluorine by chloride. The overall shape of the crystals determined via the Wulff construction is only slightly effected by the substitution of a few fluorides at the surface, but the exposed aluminum, in those surfaces, can lead to strong changes in the reactivity.
Author Contributions
R.P. performed the calculation together with C.B. and J.H.B. and Z.K. prepared the results part of the manuscript. All authors contributed to the final version of the manuscript. B.P. supervised the project.
Funding
The project was funded by the Freie Universität Berlin and the German Science Foundation (DFG) through GRK 1582 and SBF 1109.
Acknowledgments
This project was supported by the German Science Foundation (DFG) within the Graduate School 1582—Fluorine as a Key Element and the Collaborative Research Center 1109: Understanding of Metal Oxide/Water Systems at the Molecular Scale: Structural Evolution, Interfaces and Dissolution. Additionally, we thank the North-German Supercomputing Alliance (Norddeutscher Verbund zur Förderung des Hoch-und Höchstleistungsrechnens HLRN) and the Zentraleinrichtung für Datenverarbeitung (ZEDAT) at the Freie Universität Berlin for computational resources.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Védrine, J.C. Heterogeneous Catalysis on Metal Oxides. Catalysts 2017, 7, 341. [Google Scholar] [CrossRef]
- Feynman, R.P. There’s plenty of room at the bottom. J. Microelectromech. Syst. 1992, 1, 60–66. [Google Scholar] [CrossRef]
- Birringer, R.; Gleiter, H.; Klein, H.P.; Marquardt, P. Nanocrystalline materials an approach to a novel solid structure with gas-like disorder? Phys. Lett. A 1984, 102, 365–369. [Google Scholar] [CrossRef]
- Murray, C.B.; Kagan, C.R.; Bawendi, M.G. Synthesis and Characterization of Monodisperse Nanocrystals and Close-Packed Nanocrystal Assemblies. Annl. Rev. Mat. Sci. 2000, 30, 545–610. [Google Scholar] [CrossRef]
- Kosmala, A.; Wright, R.; Zhang, Q.; Kirby, P. Synthesis of silver nano particles and fabrication of aqueous Ag inks for inkjet printing. Mater. Chem. Phys. 2011, 129, 1075–1080. [Google Scholar] [CrossRef]
- Holzinger, M.; Le Goff, A.; Cosnier, S. Nanomaterials for biosensing applications: A review. Front. Chem. 2014, 2, 63. [Google Scholar] [CrossRef] [PubMed]
- Cushing, B.L.; Kolesnichenko, V.L.; O’Connor, C.J. Recent Advances in the Liquid-Phase Syntheses of Inorganic Nanoparticles. Chem. Rev. 2004, 104, 3893–3946. [Google Scholar] [CrossRef] [PubMed]
- Millstone, J.E.; Kavulak, D.F.J.; Woo, C.H.; Holcombe, T.W.; Westling, E.J.; Briseno, A.L.; Toney, M.F.; Fréchet, J.M.J. Synthesis, Properties, and Electronic Applications of Size-Controlled Poly(3-hexylthiophene) Nanoparticles. Langmuir 2010, 26, 13056–13061. [Google Scholar] [CrossRef] [PubMed]
- Khlebtsov, N.G.; Dykman, L.A. Optical properties and biomedical applications of plasmonic nanoparticles. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 1–35. [Google Scholar] [CrossRef]
- Unser, S.; Bruzas, I.; He, J.; Sagle, L. Localized Surface Plasmon Resonance Biosensing: Current Challenges and Approaches. Sensors 2015, 15, 15684–15716. [Google Scholar] [CrossRef] [PubMed]
- Loureiro, A.G.; Azoia, N.C.G.A.; Cavaco-Paulo, A. Albumin-Based Nanodevices as Drug Carriers. Curr. Pharm. Des. 2016, 22, 1371–1390. [Google Scholar] [CrossRef] [PubMed]
- Martis, E.; Badve, R.; Degwekar, M. Nanotechnology based devices and applications in medicine: An overview. Chron. Young Sci. 2012, 3, 68–73. [Google Scholar] [CrossRef]
- Nikalje, A.P. Nanotechnology and its Applications in Medicine. Med. Chem. 2015, 5, 81–89. [Google Scholar] [CrossRef]
- Reddy, M.V.; Subba Rao, G.V.; Chowdari, B.V.R. Metal Oxides and Oxysalts as Anode Materials for Li Ion Batteries. Chem. Rev. 2013, 113, 5364–5457. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Marks, T.J.; Fachetti, A. Metal oxides for optoelectronic applications. Nat. Mat. 2016, 15, 383–396. [Google Scholar] [CrossRef] [PubMed]
- Toh, R.J.; Sofer, Z.; Pumera, M. Transition Metal Oxides for the Oxygen Reduction Reaction: Influence of the Oxidation States of the Metal and its Position on the Periodic Table. Chemphyschem 2015, 16, 3527–3531. [Google Scholar] [CrossRef] [PubMed]
- Yi, J.; Robert, W.; Molt, J.; Blackburn, G.M. Metal Fluorides: Tools for Structural and Computational Analysis of Phosphoryl Transfer Enzymes. Top. Curr. Chem. 2017, 375, 1–31. [Google Scholar] [CrossRef]
- Lee, Y.; Sun, H.; Young, M.J.; George, S.M. Atomic Layer Deposition of Metal Fluorides Using HF–Pyridine as the Fluorine Precursor. Chem. Mat. 2016, 28, 2022–2032. [Google Scholar] [CrossRef]
- Wang, F.; Kim, S.W.; Seo, D.H.; Kang, K.; Wang, L.; Su, D.; Vago, J.J.; Wang, J.; Graetz, J. Ternary metal fluorides as high-energy cathodes with low cycling hysteresis. Nat. Commun. 2015, 6, 6668. [Google Scholar] [CrossRef] [PubMed]
- Rüdiger, S.; Kemnitz, E. The fluorolytic sol–gel route to metal fluorides—A versatile process opening a variety of application fields. Dalton Trans. 2008, 1117–1127. [Google Scholar] [CrossRef] [PubMed]
- Kemnitz, E.; Groß, U.; Rüdiger, S.; Shekar, C.S. Amorphous Metal Fluorides with Extraordinary High Surface Areas. Ang. Chem. Int. Ed. 2003, 42, 4251–4254. [Google Scholar] [CrossRef] [PubMed]
- Rüdiger, S.K.; Groß, U.; Feist, M.; Prescott, H.A.; Shekar, S.C.; Troyanov, S.I.; Kemnitz, E. Non-aqueous synthesis of high surface area aluminum fluoride—A mechanistic investigation. J. Mater. Chem. 2005, 15, 588–597. [Google Scholar] [CrossRef]
- Rüdiger, S.; Groß, U.; Kemnitz, E. Non-aqueous sol–gel synthesis of nano-structured metal fluorides. J. Fluor. Chem. 2007, 128, 353–368. [Google Scholar] [CrossRef]
- Nickkho-Amiry, M.; Eltanany, G.; Wuttke, S.; Rüdiger, S.; Kemnitz, E.; Winfield, J.M. A comparative study of surface acidity in the amorphous, high surface area solids, aluminum fluoride, magnesium fluoride and magnesium fluoride containing iron(III) or aluminum(III) fluorides. J. Fluor. Chem. 2008, 129, 366–375. [Google Scholar] [CrossRef]
- Kemnitz, E. Nanoscale metal fluorides: A new class of heterogeneous catalysts. Catal. Sci. Technol. 2015, 5, 786–806. [Google Scholar] [CrossRef]
- Schacht, J.; Budau, J.H.; Gaston, N.; Paulus, B. Aluminum oxo-fluoride clusters: A first principle investigation of stability, synthetic considerations, and the interaction with water. J. Comp. Chem. 2018, 39, 1208–1214. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Wuttke, S.; Vimont, A.; Daturi, M.; Lavalley, J.C.; Teinz, K.; Kemnitz, E. Novel sol–gel prepared zinc fluoride: Synthesis, characterisation and acid–base sites analysis. J. Mater. Chem. 2012, 22, 14587–14593. [Google Scholar] [CrossRef]
- Rehmer, A.; Scheurell, K.; Kemnitz, E. Formation of nanoscopic CaF2 via a fluorolytic sol–gel process for antireflective coatings. J. Mater. Chem. C 2015, 3, 1716–1723. [Google Scholar] [CrossRef]
- Schmidt, L.; Emmerling, F.; Kirmse, H.; Kemnitz, E. Sol–gel synthesis and characterisation of nanoscopic strontium fluoride. RSC Adv. 2014, 4, 32–38. [Google Scholar] [CrossRef]
- Candu, N.; Wuttke, S.; Kemnitz, E.; Coman, S.; Parvulescu, V. Friedel-Crafts alkylations on nanoscopic inorganic fluorides. Recent Developments in Model Catalysis—Closing the Gap to Technical Applications. Appl. Catal. A Gen. 2011, 391, 169–174. [Google Scholar] [CrossRef]
- Coman, S.; Wuttke, S.; Vimont, A.; Daturi, M.; Kemnitz, E. Catalytic Performance of Nanoscopic, Aluminium Trifluoride-Based Catalysts in the Synthesis of (all-rac)-α-Tocopherol. Adv. Synth. Catal. 2008, 350, 2517–2524. [Google Scholar] [CrossRef]
- Coman, S.; Parvulescu, V.; Wuttke, S.; Kemnitz, E. Synthesis of Vitamin K1 and K1-Chromanol by Friedel–Crafts Alkylation in Heterogeneous Catalysis. Chem. Cat Chem. 2010, 2, 92–97. [Google Scholar] [CrossRef]
- Negoi, A.; Wuttke, S.; Kemnitz, E.; Macovei, D.; Parvulescu, V.I.; Teodorescu, C.M.; Coman, S.M. One-Pot Synthesis of Menthol Catalyzed by a Highly Diastereoselective Au/MgF2 Catalyst. Ang. Chem. Int. Ed. 2010, 49, 8134–8138. [Google Scholar] [CrossRef] [PubMed]
- Coman, S.M.; Patil, P.; Wuttke, S.; Kemnitz, E. Cyclisation of citronellal over heterogeneous inorganic fluorides—Highly chemo- and diastereoselective catalysts for (±)-isopulegol. Chem. Commun. 2009, 460–462. [Google Scholar] [CrossRef] [PubMed]
- Troncea, S.B.; Wuttke, S.; Kemnitz, E.; Coman, S.M.; Parvulescu, V.I. Hydroxylated magnesium fluorides as environmentally friendly catalysts for glycerol acetylation. Appl. Catal. B Environ. 2011, 107, 260–267. [Google Scholar] [CrossRef]
- Kemnitz, E.; Wuttke, S.; Coman, S.M. Tailor-Made MgF2-Based Catalysts by Sol–Gel Synthesis. Eur. J. Inorg. Chem. 2011, 2011, 4773–4794. [Google Scholar] [CrossRef]
- Prescott, H.A.; Li, Z.J.; Kemnitz, E.; Deutsch, J.; Lieske, H. New magnesium oxide fluorides with hydroxy groups as catalysts for Michael additions. J. Mater. Chem. 2005, 15, 4616–4628. [Google Scholar] [CrossRef]
- Wuttke, S.; Coman, S.; Kröhnert, J.; Jentoft, F.; Kemnitz, E. Sol–gel prepared nanoscopic metal fluorides—A new class of tunable acid-base catalysts. Catal. Today 2010, 152, 2–10. [Google Scholar] [CrossRef]
- Wuttke, S.; Coman, S.; Kröhnert, J.; Jentoft, F.; Kemnitz, E. Catalysis by Acids and Bases: New materials and surface studies ABC-6. In Proceedings of the 6th World Congress on Catalysis by Acids and Bases, Genova, Italy, 10–14 May 2009. [Google Scholar]
- Astruc, A.; Cochon, C.; Dessources, S.; Célérier, S.; Brunet, S. High specific surface area metal fluorides as catalysts for the fluorination of 2-chloropyridine by HF. Appl. Catal. A Gen. 2013, 453, 20–27. [Google Scholar] [CrossRef]
- Krüger, H.; Hertwig, A.; Beck, U.; Kemnitz, E. Low temperature sol–gel metal oxide and fluoride layer stacks for optical applications. Thin Solid Films 2010, 518, 6080–6086. [Google Scholar] [CrossRef]
- Noack, J.; Schmidt, L.; Gläsel, H.J.; Bauer, M.; Kemnitz, E. Inorganic-organic nanocomposites based on sol–gel derived magnesium fluoride. Nanoscale 2011, 3, 4774–4779. [Google Scholar] [CrossRef] [PubMed]
- Teinz, K.; Wuttke, S.; Börno, F.; Eicher, J.; Kemnitz, E. Highly selective metal fluoride catalysts for the dehydrohalogenation of 3-chloro-1,1,1,3-tetrafluorobutane. J. Catal. 2011, 282, 175–182. [Google Scholar] [CrossRef]
- Kobayashi, S.; Hamada, T.; Manabe, K. The Catalytic Asymmetric Mannich-Type Reactions in Aqueous Media. J. Am. Chem. Soc. 2002, 124, 5640–5641. [Google Scholar] [CrossRef] [PubMed]
- Bailey, C.L.; Mukhopadhyay, S.; Wander, A.; Searle, B.G.; Harrison, N.M. Structure and Stability of α-AlF3 Surfaces. J. Phys. Chem. C 2009, 113, 4976–4983. [Google Scholar] [CrossRef]
- Bailey, C.L.; Wander, A.; Mukhopadhyay, S.; Searle, B.G.; Harrison, N.M. Characterization of Lewis acid sites on the (100) surface of β-AlF3: Ab initio calculations of NH3 adsorption. J. Phys. Chem. 2008, 128, 224703. [Google Scholar] [CrossRef] [PubMed]
- Huesges, Z.; Müller, C.; Paulus, B.; Hough, C.; Harrison, N.; Kemnitz, E. Characterising MgF2 surfaces with CO adsorption calculations. Surf. Sci. 2013, 609, 73–77. [Google Scholar] [CrossRef]
- Hammerschmidt, L.; Müller, C.; Paulus, B. Electron correlation contribution to the physisorption of CO on MgF2(110). J. Chem. Phys. 2012, 136, 124117. [Google Scholar] [CrossRef] [PubMed]
- Kaawar, Z.; Paulus, B. A computational study of the structure of zinc fluoride surfaces. AIP Conf. Proc. 2015, 1653, 020051. [Google Scholar] [CrossRef]
- Kaawar, Z.; Müller, C.; Paulus, B. Theoretical investigations of the CO adsorption on ZnF2 surfaces. Surf. Sci. 2017, 656, 48–53. [Google Scholar] [CrossRef]
- Barth, J.; Johnson, R.L.; Cardona, M.; Fuchs, D.; Bradshaw, A.M. Dielectric function of CaF2 between 10 and 35 eV. Phys. Rev. B 1990, 41, 3291–3294. [Google Scholar] [CrossRef]
- Camy, P.; Doualan, J.; Renard, S.; Braud, A.; Ménard, V.; Moncorgé, R. Tm3+:CaF2 for 1.9 µm laser operation. Optics Comm. 2004, 236, 395–402. [Google Scholar] [CrossRef]
- Kumar, G.A.; Riman, R.; Chae, S.C.; Jang, Y.N.; Bae, I.K.; Moon, H.S. Synthesis and spectroscopic characterization of CaF2:Er3+ single crystal for highly efficient 1.53 µm amplification. J. App. Phys. 2004, 95, 3243–3249. [Google Scholar] [CrossRef]
- Tsujibayashi, T.; Toyoda, K.; Sakuragi, S.; Kamada, M.; Itoh, M. Spectral profile of the two-photon absorption coefficients in CaF2 and BaF2. App. Phys. Lett. 2002, 80, 2883–2885. [Google Scholar] [CrossRef]
- Giessibl, F.J.; Reichling, M. Investigating atomic details of the CaF2(111) surface with a qPlus sensor. Nanotechnology 2005, 16, S118. [Google Scholar] [CrossRef]
- Kaawar, Z.; Mahn, S.; Kemnitz, E.; Paulus, B. On the Morphology of Group II Metal Fluoride Nanocrystals at Finite Temperature and Partial Pressure of HF. Molecules 2017, 22, 663. [Google Scholar] [CrossRef] [PubMed]
- Kawaar, Z. Theoretical Investigations of Bulk and Surface Properties of Group II and Group XII Metal Fluorides. Ph.D. Thesis, Department of Biology, Chemistry and Pharmacy of Freie Universität Berlin, Berlin, Germany, 2018. [Google Scholar]
- Krahl, T.; Vimont, A.; Eltanany, G.; Daturi, M.; Kemnitz, E. Determination of the Acidity of High Surface AlF3 by IR Spectroscopy of Adsorbed CO Probe Molecules. J. Phys. Chem. C 2007, 111, 18317–18325. [Google Scholar] [CrossRef]
- Kemnitz, E.; Menz, D.H. Fluorinated metal oxides and metal fluorides as heterogeneous catalysts. Prog. Solid State Chem. 1998, 26, 97–153. [Google Scholar] [CrossRef]
- Daniel, P.; Bulou, A.; Rousseau, M.; Nouet, J.; Fourquet, J.L.; Leblanc, M.; Burriel, R. A study of the structural phase transitions in AlF 3: X-ray powder diffraction, differential scanning calorimetry (DSC) and Raman scattering investigations of the lattice dynamics and phonon spectrum. J. Phys. Condens. Matter 1990, 2, 5663. [Google Scholar] [CrossRef]
- Reuter, K.; Scheffler, M. Composition, structure, and stability of RuO2(110) as a function of oxygen pressure. Phys. Rev. B 2001, 65, 035406. [Google Scholar] [CrossRef]
- Geysermans, P.; Finocchi, F.; Goniakowski, J.; Hacquart, R.; Jupille, J. Combination of (100), (110) and (111) facets in MgO crystals shapes from dry to wet environment. Phys. Chem. Chem. Phys. 2009, 11, 2228–2233. [Google Scholar] [CrossRef] [PubMed]
- Stampfl, C.; Kreuzer, H.J.; Payne, S.H.; Pfnür, H.; Scheffler, M. First-Principles Theory of Surface Thermodynamics and Kinetics. Phys. Rev. Lett. 1999, 83, 2993–2996. [Google Scholar] [CrossRef]
- Kanaki, E.; Gohr, S.; Müller, C.; Paulus, B. Theoretical study on the morphology of MgF2 nanocrystals at finite temperature and pressure. Surf. Sci. 2015, 632, 158–163. [Google Scholar] [CrossRef]
- Fortes, A.D.; Wood, I.G.; Vočadlo, L.; Knight, K.S.; Marshall, W.G.; Tucker, M.G.; Fernandez-Alonso, F. Phase behavior and thermoelastic properties of perdeuterated ammonia hydrate and ice polymorphs from 0 to 2GPa. J. App. Crystall. 2009, 42, 846–866. [Google Scholar] [CrossRef]
- Kokalj, A. Computer graphics and graphical user interfaces as tools in simulations of matter at the atomic scale. Comp. Mat. Sci. 2003, 28, 155–168. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comp. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Wirth, J.; Schacht, J.; Saalfrank, P.; Paulus, B. Fluorination of the Hydroxylated α-Al2O3 (0001) and Its Implications for Water Adsorption: A Theoretical Study. J. Phys. Chem. C 2016, 120, 9713–9718. [Google Scholar] [CrossRef]
- Budau, J.H.; Paulus, B.; Steenbergen, K.G. Theoretical investigation of the crystal structure of AlOF. Chem. Phys. 2017, 491, 112–117. [Google Scholar] [CrossRef]
- Li, X.; Paier, J.; Sauer, J.; Mirabella, F.; Zaki, E.; Ivars-Barcelo, F.; Shaikhutdinov, S.; Freund, H.J. Surface Termination of Fe3O4(111) Films Studied by CO Adsorption Revisited. J. Phys. Chem. B 2018, 122, 527–533. [Google Scholar] [CrossRef] [PubMed]
- Vandichel, M.; Biswas, S.; Leus, K.; Paier, J.; Sauer, J.; Verstraelen, T.; Van Der Voort, P.; Waroquier, M.; Van Speybroeck, V. Catalytic Performance of Vanadium MIL-47 and Linker-Substituted Variants in the Oxidation of Cyclohexene: A Combined Theoretical and Experimental Approach. Chem. Plus Chem. 2014, 79, 1183–1197. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. It VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Cryst. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Wulff, G. Zur Frage der Geschwindigkeit des Wachsthums und der Auflösung der Krystallflächen. Z. Kristall. Crystal. Mat. 1901, 34. [Google Scholar] [CrossRef]
- Gibbs, J.W. The Collected Works of J. Willard Gibbs; Longmans, Green: New York, NY, USA, 1928. [Google Scholar]
- Von Laue, M. Der Wulffsche Satz für die Gleidigewichtsform von Kristallen. Z. Kristall. Crystal. Mat. 1943, 105. [Google Scholar] [CrossRef]
- Tang, W.; Sanville, E.; Henkelman, G. A grid-based Bader analysis algorithm without lattice bias. J. Phys. Condens. Matter 2009, 21, 84204–84210. [Google Scholar] [CrossRef] [PubMed]
- Sanville, E.; Kenny, S.D.; Smith, R.; Henkelman, G. Improved grid-based algorithm for Bader charge allocation. J. Comp. Chem. 2007, 28, 899–908. [Google Scholar] [CrossRef] [PubMed]
- Henkelman, G.; Arnaldsson, A.; Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comp. Mat. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).