Mechanical Modelling of Integration and Debonding Process of Ultra-Thin Inorganic Chips

Abstract

The research on ultra-thin inorganic chips is an important field in the development of inorganic flexible electronics. By thinning the inorganic (mainly silicon-based) chip to less than 50 μm, it will gain a certain degree of flexibility. After the ultra-thin chip is integrated into the flexible substrate, it is bent repeatedly during the operation of the system. When the bending angle is excessively large, the chip and substrate will debond, or the chip will break. In this process, whether the chip can be stably adhered to the substrate depends on many factors, and debonding can only be reduced by continuously adjusting the process parameters. From an energy method perspective, this study divides the bending process of flexible silicon-based chips and flexible films into two states: debonding and non-debonding. A debonding mechanical model of flexible chips is established, and the regulatory relationship between the adhesion coefficient between the chip and film, chip geometric size, and material parameters was established. Experiments were also conducted to verify the relevant theoretical results. The theoretical results show that the risk of chip debonding decreases with a reduction in chip thickness, an increase in interface adhesion, and an increase in bending radius. Improving the interface adhesion during the bending process can effectively stabilize the adhesion of flexible chips. This paper provides a theoretical basis for the integration and bending of ultra-thin flexible chips and flexible substrates, promoting the practical assembly and application of ultra-thin chips.

1. Introduction

Since their inception, flexible electronics have attracted countless researchers with their ever-changing electronic device morphology and rich application prospects, and they continue to develop rapidly [1,2]. From the organic devices to the inorganic devices, the research on flexible electronics has progressed from a simple concept to a flourishing field in various fields in the past 20 years. Flexible electronic devices with various forms, functions, and principles have emerged. Energy devices [3], sensors [4], display equipment [5], microsystems [6], skin-like devices [7], and other types of flexible electronic technologies have been widely used in consumer electronics, medical electronics, military fields, and biological monitoring. Compared with traditional electronic devices, flexible electronic devices can withstand external loads, such as bending and stretching, without failure; therefore, they can adapt to surfaces of different shapes [8], especially in terms of integration with the surface of human skin, which has a unique advantage [9].

There are two main research directions for flexible electronic devices: organic flexible electronics based on organic materials [10] and inorganic flexible electronics based on inorganic semiconductor materials. Organic flexible electronic devices have material flexibility and ductility but weak electrical properties, while inorganic electronic devices have good electrical properties but are fragile and easy to damage due to the characteristics of the material. Therefore, since the proposal of inorganic flexible electronic devices, improving their flexibility and ductility has been a hot topic in academic research [11]. Converting hard electronics into flexible electronics through structural and mechanical design is a major research direction in inorganic flexible electronics. The development of flexible electronic technology requires chips to be flexible and conform to the bending of flexible substrates. The chip thickness can be designed to have a certain bending and deformation capability. Unlike traditional chips, flexible chips are required to perform the set functions under large deformations, which is also the key to their application [12,13]. In recent years, the bending performance and flexibility of flexible electronic devices have been continuously improved by structural design and material optimization. Related research includes colloidal QD photodetectors [14], silicon solar cells [15,16], and sensors [17,18]. However, the better the bending performance, the greater the deformation. Currently, the reliability of flexible electronic devices, especially chip bonding reliability, is becoming increasingly demanding.

During the preparation of flexible packaging systems, the peeling of flexible chips and the bonding reliability of flexible substrates are extremely important. After the system is packaged, it often needs to withstand an external bending load, causing a certain amount of bending deformation. If the bonding reliability of the flexible chip and flexible substrate is insufficient, debonding will occur at the bonding interface. Therefore, to verify whether the interface between the chip and flexible substrate is sufficiently reliable after pasting, the system is generally bent at a fixed bending radius tens of millions of times after the chip is bonded to confirm whether the interface has sufficient strength under the bending load.

Some studies have been conducted to analyze the interface problems of flexible chips and substrates, such as the double-layer chip-substrate model [19] and three-layer chip-adhesive-substrate model [20,21,22]. Modeling of the adhesive layer is particularly important for analysis. There are many analytical models for the interface behavior of layered structures as well, which can be mainly divided into two categories. The first type is the model based on fracture mechanics theory [23], which uses characteristic parameters such as the J integral [24], stress intensity factor [25], and energy release rate [26]. The second type is a model based on classical strength theory [27]. Some models describe the generation of singular stress fields at the edge of layered bounded structures and at the interface crack tip [28], and some describe the debonding process based on the theoretical bilinear cohesive zone model [29]. In addition to theoretical models, experimental test methods have also been proposed [30].

However, most existing work focuses on the chip peeling process. The chip peeling process requires the use of concentrated forces, such as ejector pins, or the setting of pressure distribution to peel the chip. When analyzing this external force, the type of external force must be preset in advance. It is difficult to determine a fixed external force in the bending process of a flexible system. Therefore, if a method can be found to analyze the bending state of the chip from the perspective of the state without setting the type of external force, it will be beneficial for simplifying the analysis process. At the same time, methods based on fracture mechanics often require a preset crack path, which also has a certain impact on the analysis.

In this study, a debonding mechanical model of flexible chips was established from an energy standpoint. The bending process of flexible silicon-based chips and flexible films was divided into two states: debonding and non-debonding. The effects of the adhesion coefficient, geometric dimensions, and material parameters on the chip debonding process were studied, the critical thickness of the flexible chip was determined, and experiments were conducted to verify the relevant theoretical results.

2. Results

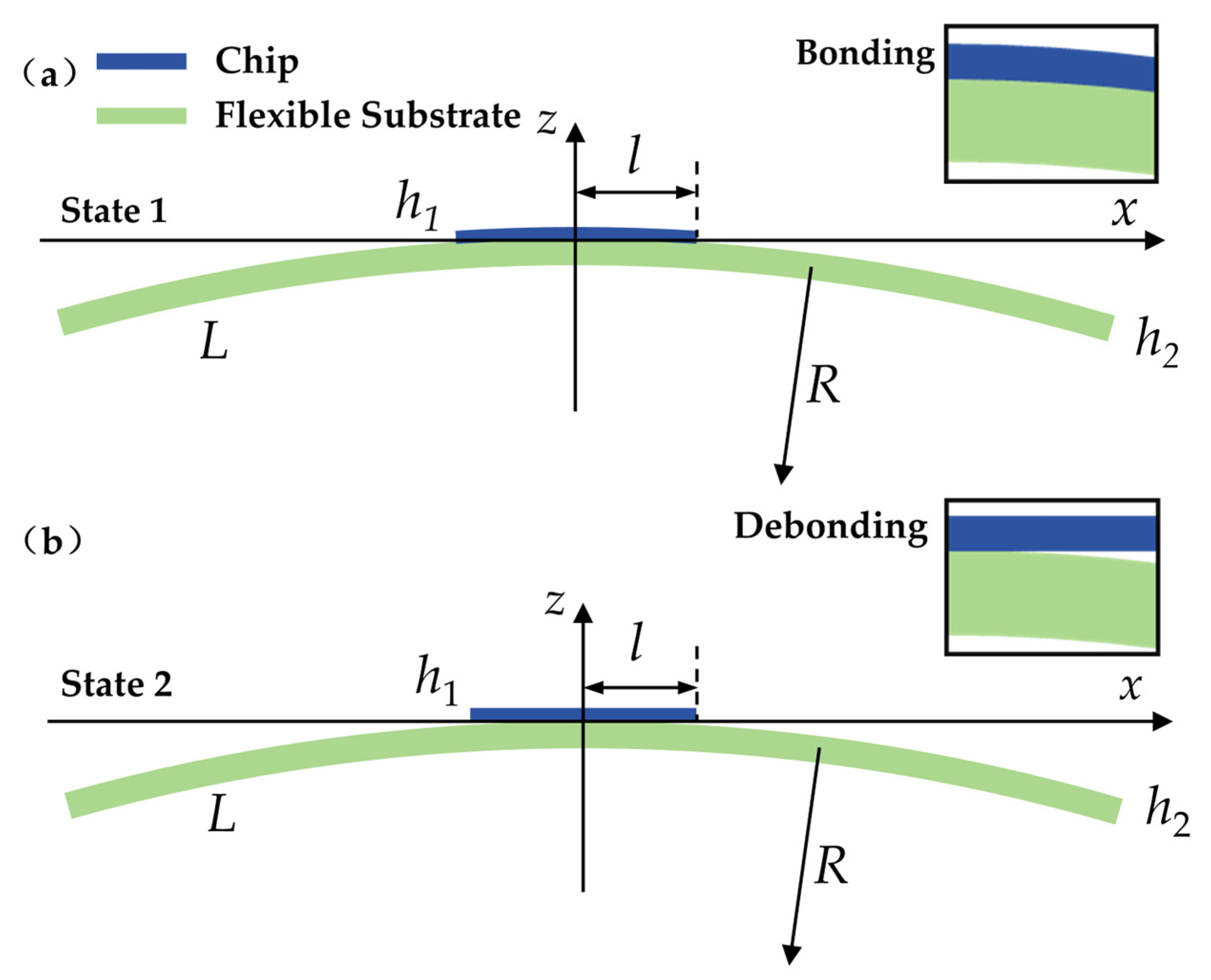
2.1. Modeling

The bonding interface of the chip has a significant impact on the reliability of the flexible system. In order to better control this process, the mechanical behavior of the chip and system when bent is analyzed here. In the bending experiment, the experimental device imposes an additional bending radius $R$ on the entire system. The bent system is shown in Figure 1, where the deformation of the flexible substrate board can be approximated to an arc. In this model, since the interface properties of the chip when it is debonded are explored, the situation when the system is bent downward is considered. When the system is bent upward, the chip has no corresponding debonding trend; therefore, this type of situation is not considered.

In Figure 1, the length of the chip is $2l$, the length of the flexible substrate is $2L$, the thickness of the chip is $h_1$, and the thickness of the flexible substrate is $h_2$. During the bending process of the system, there are two states between the chip and flexible substrate: the first state is that the chip deforms together with the system and flexible substrate, which is defined as state 1 (Figure 1a); the second state is the interface debonding between the chip and flexible substrate. At this time, the chip does not deform, the flexible substrate deforms, and the interface energy of the interface between the chip and flexible substrate is released at the same time, which is defined as state 2 (Figure 1b). Next, using the energy principle, we compared the total energies of the system in States 1 and 2. The system always tends to a state with lower energy, which is used to obtain the standard for determining whether the chip and flexible substrate are in a debonding state.

As shown in the coordinate axis of Figure 1, for flexible substrates, the external load of the general reliability analysis is a bending load with a certain bending radius. Therefore, it is assumed that the deformation of the flexible substrate and the chip are both arcs, and pure bending occurs within the linear elastic range. Generally speaking, the external bending radius $R$ and the thickness of the chip h₁ meet the inequality $R\gg h_1$, so it can be approximately considered that the bending radius of the flexible substrate and the chip is $R$. For pure bending loads, it is easy to obtain the strain energy of the chip:

$$U_{chip}={\displaystyle \frac{\overline{E_1}{h}_1^3}{24}}·{\displaystyle \frac{2l}{R^2}}={\displaystyle \frac{\overline{E_1}{h}_1^{3}l}{12R^2}},$$

(1)

where $\overline{E_1}=E_1/\left(1-{v_1}^2\right)$ is the plane strain elastic modulus, $E_1$ is the elastic modulus of the chip material, and $v_1$ is the Poisson’s ratio of the chip material.

By summing the strain energies of the chip and flexible substrate, the total energy of the chip/flexible substrate system in the two states can be obtained as follows:

$$\begin{array}{cc}{U}_1& \hfill =U_{chip}+U_{sub}\\ & ={\displaystyle \frac{\overline{E_1}{h}_1^{3}l}{12R^2}}+U_{sub}\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill U_2& =U_{inter}+U_{sub}\hfill \\ & =2\gamma l+U_{sub}\hfill \end{array}$$

(3)

where $\gamma$ is the interface energy per unit length between the chip and the flexible substrate.

By subtracting Equation (2) from Equation (3), the total energy difference between the two states is

$$\Delta U=U_2-U_1=2\gamma l-{\displaystyle \frac{\overline{E_1}{h}_1^{3}l}{12R^2}}$$

(4)

In addition, when the bending radius of the system is much larger than the chip size, the small deflection theory can be applied, and the deflection expression of the chip is as follows:

$$w=-R+\sqrt{R^2-x^2}.$$

(5)

The second derivative of (5) is

$${\displaystyle \frac{d^{2}w}{d{x}^2}}=-{\displaystyle \frac{R^2}{{(R^2-x^2)}^{\frac{3}{2}}}}$$

(6)

Thus, the strain energy of the chip when it is deformed can be calculated as follows:

$$\begin{array}{cc}\hfill U_{chip}^{\prime }& ={\displaystyle \frac{\overline{E_1}{h}_1^3}{12}}{{\displaystyle {\int }_{-l}^l\frac{1}{2}\left(\frac{d^{2}w}{d{x}^2}\right)}}^{2}dx\hfill \\ & ={\displaystyle \frac{\overline{E_1}{h}_1^3}{12}}{{\displaystyle {\int }_{-l}^l\frac{1}{2}\left(-\frac{R^2}{{(R^2-x^2)}^{\frac{3}{2}}}\right)}}^{2}dx\hfill \\ & ={\displaystyle \frac{\overline{E_1}{h}_1^3}{12}}{\displaystyle \frac{\frac{5R^{3}l-3R{l}^3}{{(R^2-l^2)}^2}+3arctanh\left(\frac{l}{R}\right)}{8R}}\hfill \end{array}$$

(7)

The parameters are made dimensionless as follows:

$${\displaystyle \frac{l}{R}}={\lambda }_1$$

(8)

Then, (7) can be simplified as

$$U_{chip}^{\prime }={\displaystyle \frac{\overline{E_1}{h}_1^3}{96R}}\left[{\displaystyle \frac{5{\lambda }_1-3{{\lambda }_1}^3}{{(1-{{\lambda }_1}^2)}^2}}+3arctanh\left({\lambda }_1\right)\right]$$

(9)

The strain energy of the substrate can also be calculated as follows: Here we consider $\Delta U$: when $\Delta U<0$, $U_2<U_1$, the chip/flexible substrate system tends to state 2, and the chip and the flexible substrate are debonded; when $\Delta U>0$, $U_2>U_1$, the chip/flexible $U_2<U_1$ system tends to state 1, and the chip and the flexible substrate are deformed together. Observing (4), it can be seen that when the chip length $2l$ remains unchanged, the chip thickness $h_1$, the interface energy per unit length $\gamma$, and the bending radius $R$ will affect the value of the energy difference, thereby affecting whether the system interface debonds.

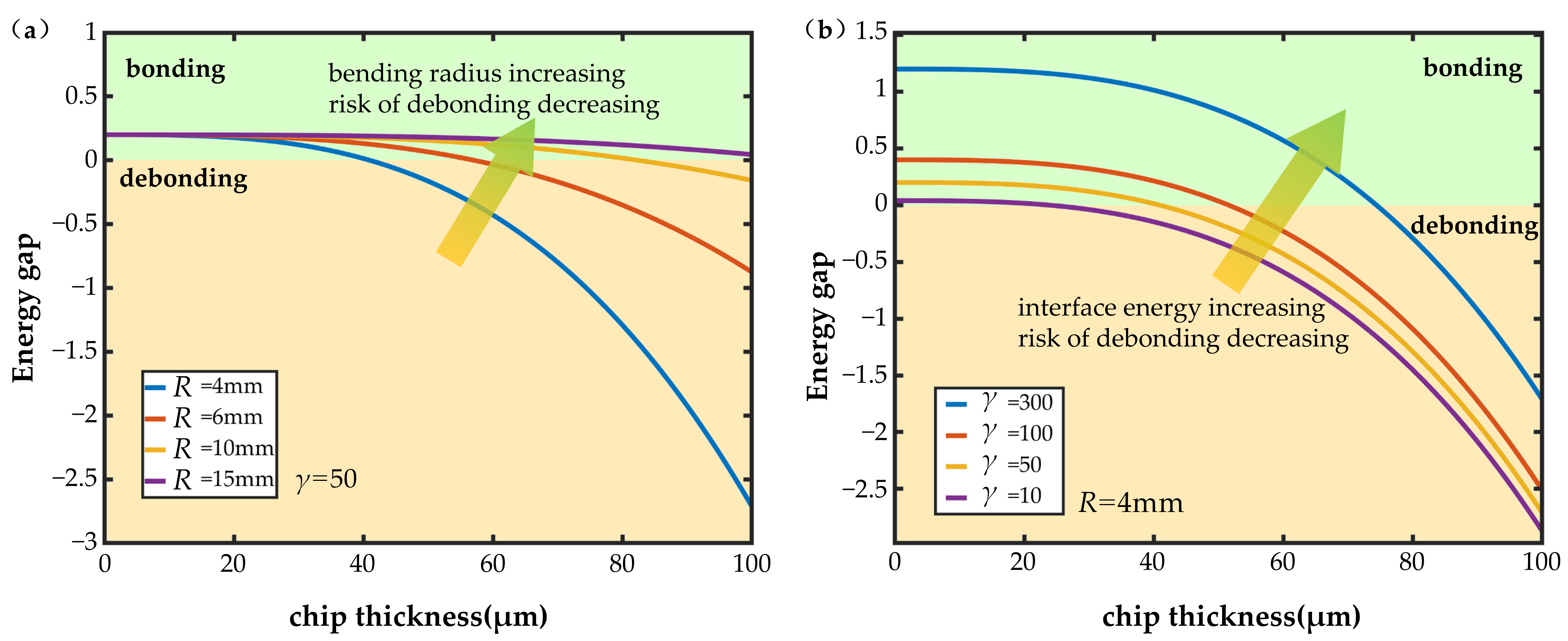
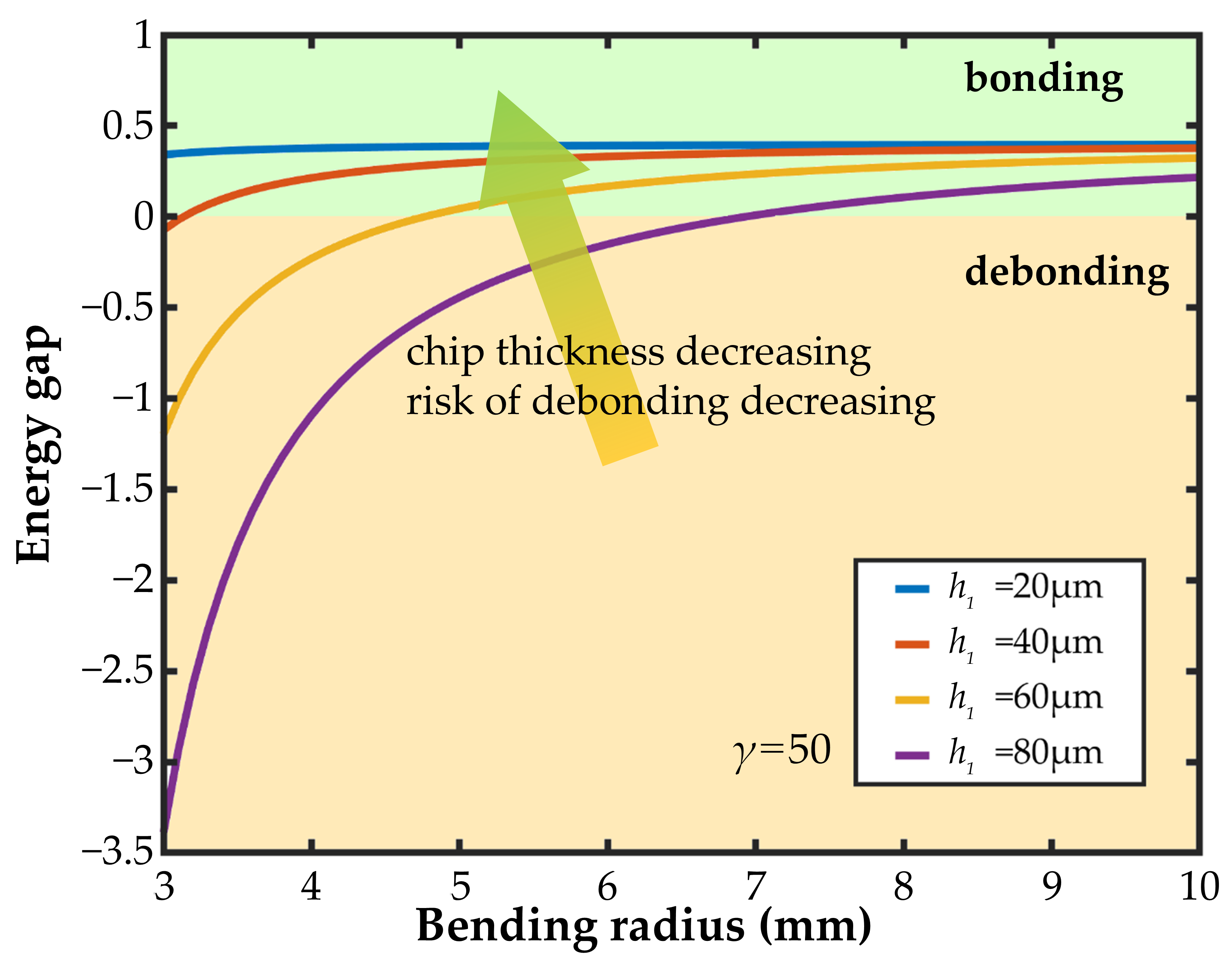
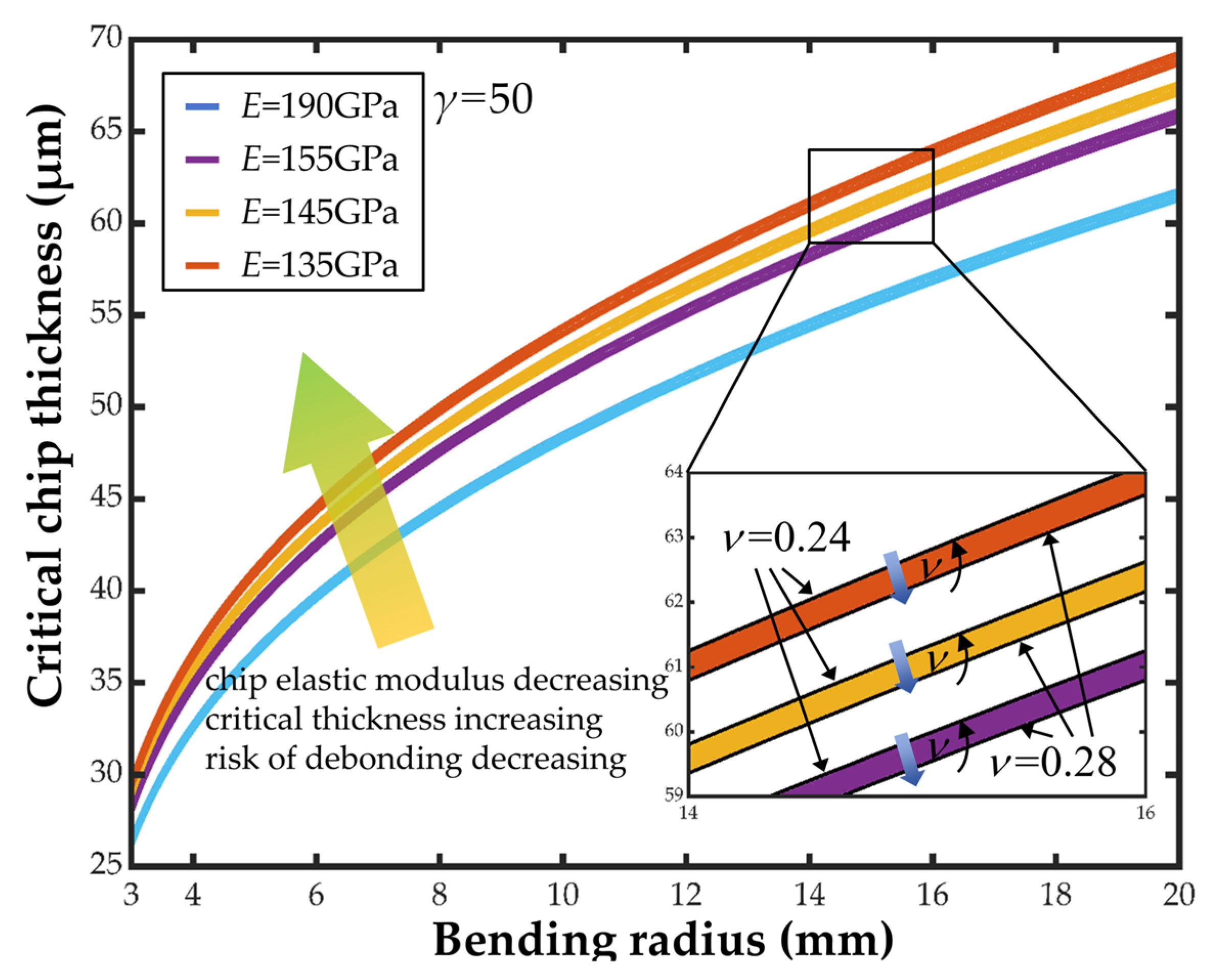
2.2. Effect of Various Parameters

First, the relationship between chip thickness $h_1$ and energy difference when the interface energy per unit length $\gamma$ and bending radius $R$ change is studied. The ultra-thin chip studied in this paper is mainly based on a semiconductor material, silicon. Since the thickness of the chip functional layer is much smaller than the thickness of silicon, it is believed that the mechanical properties of the chip are approximately the mechanical properties of silicon, elastic modulus $E_1=190\mathrm{GPa}$ and Poisson’s ratio ${\nu }_1=0.28$. The chip length is taken as $2l=4\mathrm{mm}$, and the relationship between the energy difference and the chip thickness is calculated, as shown in

Table 1. Material parameters used for calculations in this paper.

$E_1$	${\nu }_1$	$2l$
190 GPa	0.28	4 mm

. The results are presented in Figure 2. As shown in the figure, as the chip thickness increases, the energy difference gradually decreases, which means that the thicker the chip, the easier it is for the chip/flexible substrate system to debond, which is one of the reasons for achieving full flexibility in flexible electronics. The thicker the chip, the easier it is to detach from the flexible substrate when the system as a whole is subjected to a bending moment, and the more likely it is that the system will fail. By contrast, the thinner the chip, the easier it is to adhere to the flexible substrate. At the same time, since the absolute value of the slope of the curve increases, it can be considered that regardless of the size of the interface energy per unit length and the bending radius, as long as the system is bent, there must be a chip thickness that is sufficiently large to cause the chip and the flexible substrate to debond. Therefore, chip thickness significantly influences the interface reliability of the chip/flexible substrate system in a bent state.

As can be seen from Figure 2a, when the interface energy per unit length $\gamma$ remains unchanged, that is, when the viscosity of the interface does not change, the larger the bending radius, the more the system energy tends to state 2, that is, the smaller the absolute value of the slope of the curve, that is, the less likely the system is to debond. Therefore, the smaller the curvature applied to the flexible system, the more likely the chip is to debond, which is consistent with the experimental results. As can be seen from Figure 2b, when the bending radius $R$ does not change, changing the interface energy per unit length, the system energy tends to state 2, that is, the absolute value of the slope of the curve is the same, but the starting point of the curve is different. Increasing the interface energy per unit length $\gamma$ helps the system maintain state 1; that is, it is more difficult for debonding to occur.

Subsequently, the relationship between the bending radius $R$ and the energy difference $\Delta U$ when the chip thickness $h_1$ changes is studied. The results are presented in Figure 3. It can be observed that with an increase in the bending radius, the system energy tends to change from state 2 to state 1; that is, the system is less likely to debond. Under a certain unit length interface energy $\gamma$, for chips of certain thicknesses, as shown in the curve $h_1=20\mathsf{\mu }\mathrm{m}$ in the figure, the bending radius is reduced to 3 mm, and the chip cannot be debonded. Therefore, according to different system application scenarios and requirements, it is very important to adapt ultra-thin flexible chips of different thicknesses for the production of flexible electronics.

3. Discussion

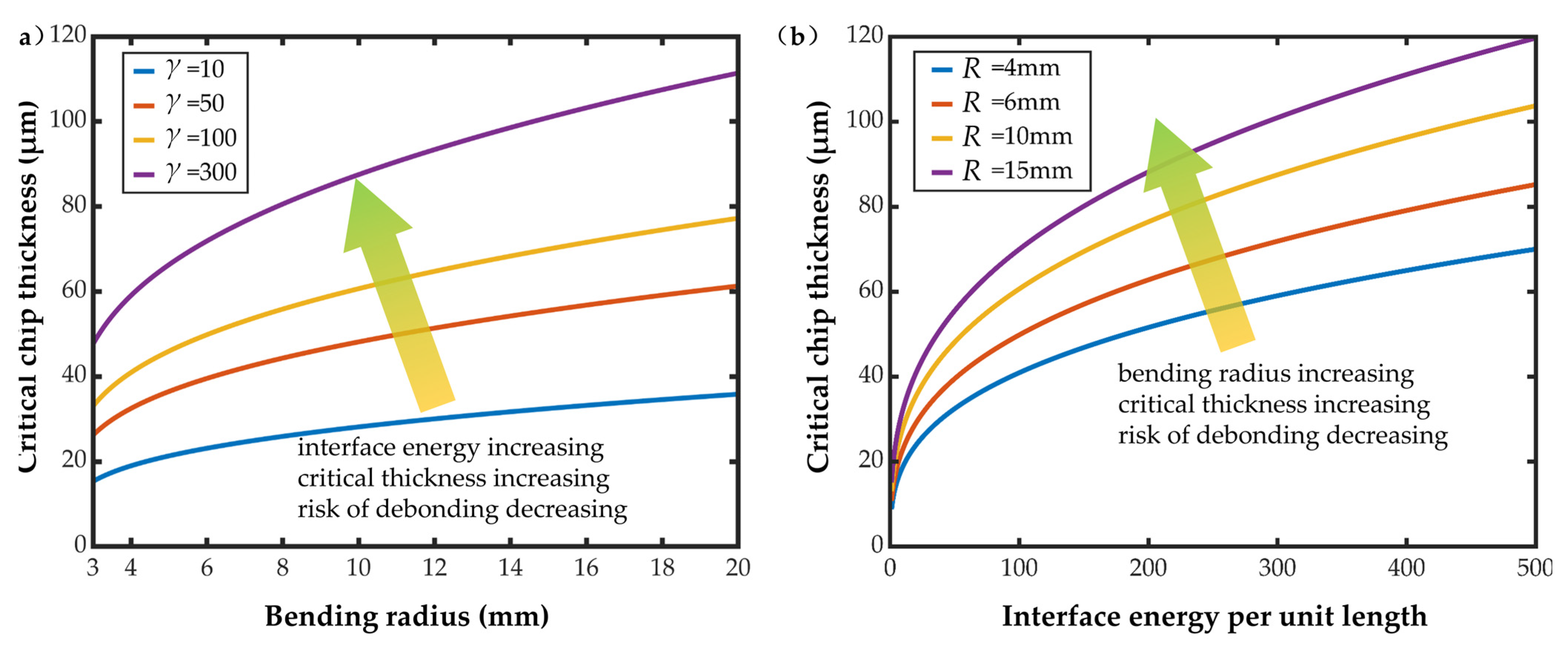
3.1. Critical Thickness

Further research on Figure 2 and Figure 3 shows that there is a certain chip thickness $h_1$ or bending radius $R$ that can put the system in a critical state $\Delta U=0$. Assuming that the chip thickness when $\Delta U=0$ is the critical thickness for the chip not to fall off, then from (4) we can obtain:

$$h_{1\mathrm{cri}}=\sqrt[3]{{\displaystyle \frac{24\gamma R^2}{\overline{E_1}}}}$$

(10)

Continue to take the elastic modulus of the flexible chip $E_1=190\mathrm{GPa}$, Poisson’s ratio ${\nu }_1=0.28$, and the chip length $2l=4\mathrm{mm}$ as the condition, and draw the relationship between the critical chip thickness $h_{1cri}$, the interface energy per unit length $\gamma$, and the bending radius $R$, as shown in Figure 4:

Figure 4a shows the relationship between the critical chip thickness $h_{1cri}$ and the bending radius $R$ under different interface energies per unit length $\gamma$. It can be observed that the critical thickness of the bonded chip increases with the bending radius, but the increasing trend slows down. A larger interface energy per unit length increases the critical thickness. Figure 4b shows the relationship between the critical chip thickness $h_{1cri}$ and the interface energy per unit length $\gamma$ under different bending radii $R$. It can be observed that the critical thickness of the chip that can be bonded increases with an increase in the interface energy per unit length, and the increasing trend also slows down. Therefore, it can be considered that when the interface energy per unit length increases to a certain extent, its influence on the critical thickness of the chip is minimal.

3.2. Effect of Changes in Silicon Material Properties

According to relevant research [31], the material properties of silicon wafers change to a certain extent after the thickness is reduced and doped. According to research [32], the elastic modulus of doped silicon wafers decreases. When boron is doped, the elastic modulus is about 155 GPa; when phosphorus is doped, the elastic modulus is about 145 GPa; and when arsenic is doped, the elastic modulus is about 135 GPa. In addition, according to relevant research [33], the Poisson’s ratio of the silicon film is reduced to about 0.24.

In this study, bulk silicon was used for the calculations. Considering the impact of changes in the silicon wafer material properties on the calculation results, a theoretical estimate of the impact of the critical thickness of silicon wafers when the elastic modulus and Poisson’s ratio change is made here, as shown in Figure 5.

As shown in Figure 5, when the elastic modulus decreases, the critical thickness of the chip continues to decrease, and at the same time, the risk of debonding of the chip-substrate system decreases. Therefore, it can be considered that when the chip thickness decreases and the chip is doped, the risk of chip debonding decreases, and the calculated critical thickness of the chip increases by about 7%~11% compared with that of bulk silicon.

On the other hand, the inset of Figure 5 (inset image) shows the change in the critical thickness of the silicon wafer when the Poisson’s ratio of the silicon chip changes. Regardless of the elastic modulus, when the Poisson’s ratio of the silicon wafer decreases from 0.28 to 0.24, the critical thickness increases slightly by about 0.8%, that is, it will not change. Therefore, the critical thickness of the silicon wafer is not sensitive to changes in its Poisson’s ratio.

3.3. Chip Bending Experiment

The performance of ultra-thin chips in a bent state was tested based on the conclusions obtained in this study. Figure 6 shows an ultrathin chip with a thickness of 20 μm bonded to a glass rod and bent. In the state shown in Figure 6, the radius of the glass rod, that is, the bending radius of the ultra-thin chip, is continuously changed to observe whether the ultra-thin chip is debonded. The bending radius gradually decreases from 40 mm. The experiment shows that when the bending radius of the chip is greater than or equal to 5 mm, the chip can be deformed during bonding. After the bending radius decreases to 3 mm, the chip debonds. In the reliability test of flexible electronic systems, the bending radius of the system is generally set to 8 mm. It can be seen that ultra-thin chips can adapt to the corresponding packaging requirements of flexible integrated systems and have certain advantages.

3.4. Interfacial Adhesion-Regulating Layer

In order to develop the relevant conclusions obtained in this work, we conceived and designed a method to transfer flexible chips by regulating the interface adhesion coefficient. After the chip is thinned, a polyimide (PI) film and DAF Film (Die) (Nitto EM-715L2 (-P)) are attached to the back of the chip. The PI film is a strength support film for the flexible chip, and the DAF film is an interface adhesion-regulating film during the pickup and placement of the flexible chip. During the wafer thinning and dicing process, the DAF film can fix the flexible chip and the blue film used for thinning together. The interface between the DAF film and the flexible chip exhibited strong adhesion. Both the blue film and DAF film were sticky and could support the completion of the dicing and cutting processes. After the dicing process is completed, irradiating the blue film with ultraviolet light can weaken the adhesion between the DAF film and the blue film, thereby regulating the adhesion between the flexible chip and the blue film and completing the peeling process. After the flexible chip is peeled off from the blue film, it is transferred to a flexible circuit board to complete the placement of the flexible chip. During the mounting process, the flexible circuit board was heated to 120 °C, and a pressure greater than 0.1 MPa was applied to the flexible chip for a time greater than 2 s, so that the DAF film completed the adhesion transition and the interface between the flexible chip and the flexible circuit board became a strong adhesion interface, thereby achieving the mounting of the flexible chip, as shown in Figure 6.

Compared with the previous chip peeling process analysis, this work focuses more on the bending state after the chip is integrated with the flexible substrate. The energy method used in this work analyzes the chip debonding state from the perspective of the bending state without the need to pre-assume the specific form of the external force. At the same time, in the process of calculating the energy difference, the strain energy of the substrate is eliminated; therefore, the focus of the analysis can be placed on the chip rather than the substrate. In addition, the energy method analyzes the entire process without the need to preset the crack path, which is relatively simple and clear. Of course, the energy method also has certain problems, that is, the calibration of related parameters is difficult, which is also the focus we hope to solve in future work.

4. Materials and Methods

The analysis method used in this paper is a mechanical analysis method based on the small deflection theory and linear elasticity assumption. That is, the curvature is approximated as the second derivative of the bending deformation, and the load and deformation are considered linearly related.

In general, the pure bending strain of a silicon wafer at a specific bending radius can be expressed as $\epsilon =\frac{h}{2R}$: where ‘a’ $h$ is the thickness of the silicon wafer and $R$ is the bending radius. In this work, the thickness of the silicon-based chip was less than 100 µm, and the minimum bending radius was 3 mm. The maximum strain calculated was 1.67%, which meets the 5% standard of the small deformation theory.

Another assumption involved in this article is the linear elastic assumption, that is, the chip deforms linearly when bent. Silicon is a hard and brittle material, and plastic deformation usually does not occur during the fracture process, but directly from elastic deformation to fracture [34]. Researchers have also conducted bending experiments on silicon-based chips [35]. The results show that the load-displacement curve of the silicon-based chips during the bending fracture process is approximately linear, and there is no obvious plastic area. Therefore, it is reliable to use the linear elastic assumption to analyze the chip-substrate bending process.

The chip used in this paper is the Bluetooth chip AC8976A8 (1.8 mm × 1.7 mm, JieLi Tech, Zhuhai, China).

This paper did not use any relevant database data. This paper did not involve animal or human experiments. GenAI was not used in this paper except for text editing.

5. Conclusions

In summary, this work established a debonding model for ultra-thin inorganic chip integration based on the energy method. The results show that as the chip thickness decreases, the bending radius and interface strength increase, and the risk of chip debonding decreases. Based on the above analysis, the critical thickness of the chip is used as an indicator to provide a criterion for determining whether the chip debonds after integration with the flexible substrate.