Tuning Magneto-Birefringence of Two-Dimensional Vermiculite Dispersions Through Magnetic Ion Exchange

Abstract

Liquid crystals based on dispersions of two-dimensional (2D) materials have recently been developed for light modulation, exhibiting superior performances compared to conventional organic liquid crystals in a variety of prototypical applications, including coloration, solar-blind communications and blue-light fluoresce. Among the diverse family of 2D liquid crystals, vermiculite-based liquid crystals stand out with advantages in low cost, ease of mass production and environmental sustainability, owing to the high natural abundance of the material. Here, we demonstrated magnetic-field tunable optics with 2D vermiculite dispersions prepared through a facile ‘exchange and redispersion’ method. By exploiting the intrinsic ion-exchange capability of clay minerals, we observed a significantly enhanced magneto-birefringence of the vermiculite dispersion upon replacing the native cations with magnetic ions, manifesting in a doubled Cotton–Mouton coefficient, representing the highest value among previous reports. Magnetization measurements reveal that there is a remarkable magnetic anisotropy in Fe ion-exchanged vermiculite samples in contrast to the isotropic magnetism of pristine vermiculite, which accounts for the observed enhancement of magneto-birefringence. Our findings demonstrate that ion exchange can serve as a simple and effective strategy to modulate the physical and chemical properties of 2D materials’ dispersions, thereby opening avenues for broader and more diverse applications.

1. Introduction

Liquid crystals (LCs) based on inorganic materials offer advantages such as low toxicity and potential for mass production, making them attractive alternatives to conventional organic LCs [1,2]. In particular, inorganic LCs derived from 2D materials, including hexagonal boron nitride [1] (h-BN), cobalt titanium oxide [3] (CoTiO_x) and vermiculite (VMT) [4], have recently been developed and shown to exhibit excellent field response, along with promising applications in light modulation. Among the reported 2D LCs, VMT stands out as especially well-suited for mass production due to its high abundance in nature [5,6]. It is the most common phyllosilicates in the van der Waals (vdW) materials family, with over 200 minerals in this category [4,6,7]. The VMT crystal consists of aluminosilicate layers interconnected by weak vdW forces, allowing for easy exfoliation along its basal plane to obtain thin flakes with a high aspect ratio [5,8]. Like other phyllosilicate minerals, VMT carries negative charge as a result of the substitution of Si by Al in the aluminosilicate layers. The negatively charged surface of VMT, with a zeta potential of ~−30 mV in its aqueous dispersion [4], facilitates the formation of stable dispersions with high concentrations of 2D materials, which can be used as LCs [9]. Furthermore, dispersions of VMT have recently been investigated and shown desirable field-tunable optical properties, notably their birefringence [4]. In the presence of an external magnetic or electric field, the VMT flakes orient themselves to align with the external field due to the field responsiveness of individual nanoflakes, and the dispersion develops a finite directional order. While an individual VMT flake exhibits large birefringence owing to its 2D nature, the whole ordered VMT dispersion behaves as a macroscopic birefringent medium with the birefringence tunable by external fields [10]. In particular, the figure of merit used to characterize the responsivity of the birefringent medium to the magnetic field is the so-called Cotton–Mouton coefficient C where a larger C suggests higher responsivity to the magnetic field [10]. Huang et al. investigated the magneto-optical effects in VMT dispersions and reported a Cotton–Mouton coefficient on the order of 1000, which is substantially higher than that observed in conventional organic LCs [4]. This high Cotton–Mouton coefficient is not only attributed to the large shape anisotropy of 2D VMT nanosheets, but also the responsiveness imparted by iron (Fe) impurities naturally present in VMT. Despite the low concentration (~1 at.%), Fe ions possess significant magnetic moments and strongly influence the magnetic behavior of their VMT host [11]. Therefore, the deliberate modulation of magnetic ion contents presents a viable strategy for tuning the magneto-optical properties of VMT dispersions.

Mineral crystals that contain magnetic ions have recently attracted numerous research interests, as they provide a system that are unusually stable among the magnetic 2D crystals [12,13]. Among these, Fe—the most abundant magnetic element in the Earth’s crust—has been identified as a key contributor to the paramagnetic and/or ferromagnetic responses observed in the various minerals [14]. For instance, Fe-rich talc minerals have been explored as ion-rich 2D magnets, exhibiting remarkable stability compared to conventional 2D magnetic materials [15]. However, naturally occurring iron-rich minerals are scarce, highlighting the importance of developing approaches to modulate magnetic-ion quantities in abundant minerals like VMT.

Phyllosilicate minerals, including vermiculite, are composed of the negatively charged aluminosilicate layers balanced with exchangeable cations located both on the surfaces and within the interlayer spaces. These native cations, such as Mg²⁺ and K⁺, can be readily replaced through a facile ion-exchange process by immersing the materials in an appropriate electrolyte solution [16]. Despite its simplicity, ion exchange with magnetic cations has rarely been employed to tailor the magnetic properties of VMT or related phyllosilicate materials for functional applications. This underutilization significantly constrains their potential in field-sensitive applications such as magneto-responsive LCs.

In this work, we demonstrate a strategy that allows the fabrication of dispersions of ion-intercalated 2D crystals. We applied this strategy to fabricate magnetic ion-exchanged dispersions of 2D vermiculites. The successful incorporation of Fe ions in the crystal is confirmed by compositional and structural characterizations using advanced transmission electron microscopy. We further investigate into the magneto-birefringence of the 2D Fe ion-exchanged vermiculite, which exhibits a Cotton–Mouton coefficient that is two-times as that of the pristine samples. Magnetization measurements reveal a remarkable increase in magnetic anisotropy in ion-exchanged samples. Detailed magnetization analysis is conducted to explain the mechanisms behind the observed amplification of the magneto-optical response.

2. Results and Discussions

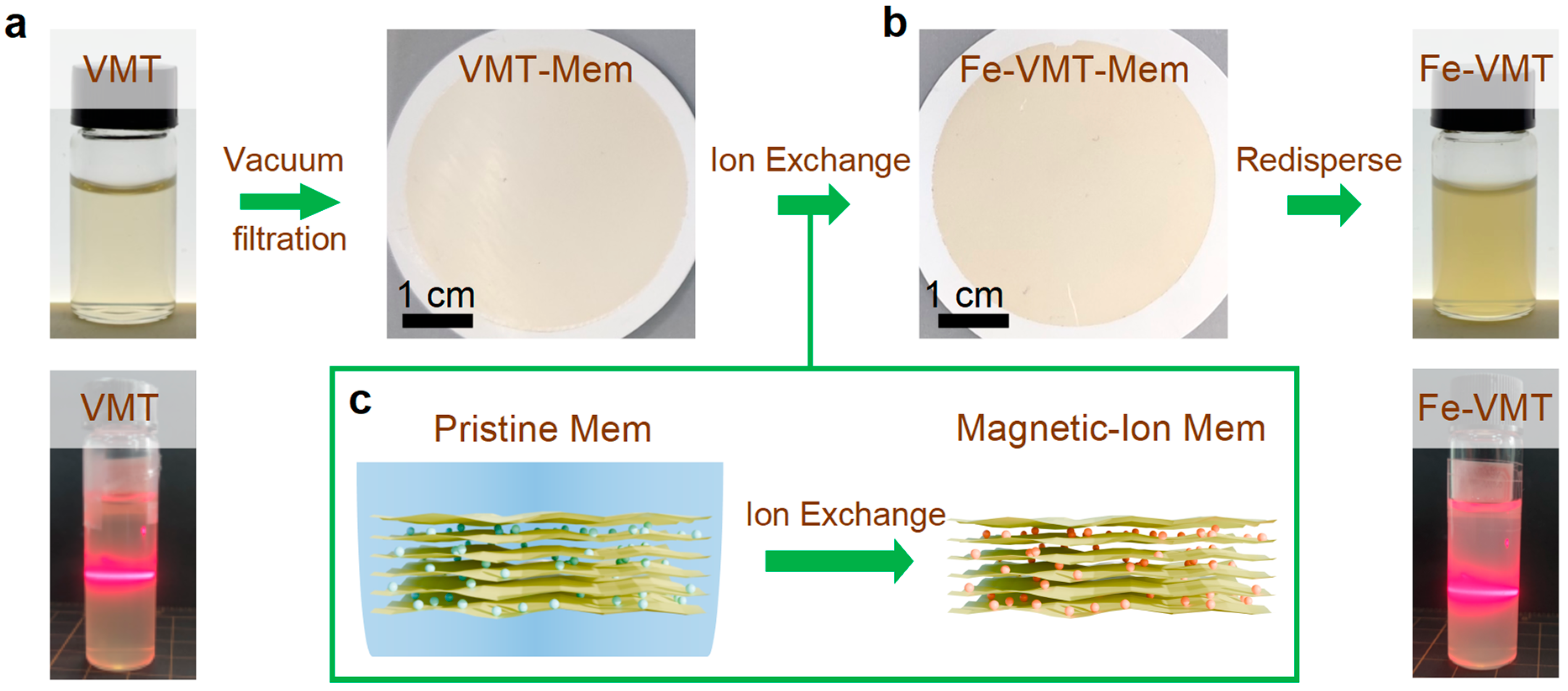
To fabricate the magnetic-ion VMT dispersion, we developed an ‘exchange and redispersing’ procedure, as schematically shown in Figure 1. The process involves three key steps: self-assembly of exfoliated flakes via vacuum filtration, ion exchange to replace native ions with magnetic ions and subsequent redispersing of the ion-exchanged flakes. Stable VMT dispersions were first prepared by a previously reported liquid-exfoliation method based on a two-step Na⁺ and Li⁺ ion exchange approach (see Section 3, Methods) [16]. To enable an efficient ion-exchange, self-assembled membranes were prepared from the pristine dispersion through vacuum filtration (Figure 1b), allowing for the subsequent ion exchange for entire 2D flakes in an assembly. Magnetic-ion exchange was then performed through immersing the membranes in a mild electrolyte solution (e.g., 0.01 M FeCl₃ for 4 h), allowing the Fe ions to diffuse into the interlayer space of VMT laminates and replacing the pristine cations such as Li and Mg ions (Figure 1c). After ion exchange, the membrane was thoroughly rinsed and immersed for an additional 1 h in de-ionized (DI) water to remove loosely bonded surface ions. The ion-exchanged membranes were redispersed in DI water assisted by sonication, yielding a stable Fe-VMT dispersion (Figure 1b; see Section 3, Methods for details). Figure 1a,b displays the photographs of the resulting pristine VMT and Fe-VMT dispersion, respectively, both showing visual transparency. The as-fabricated dispersion shows a strong Tyndall effect, confirming the successful disassembly of the membrane into colloidally stable 2D flakes. Zeta potential measurements indicate that Fe-VMT dispersion (around −37 mV) retains a surface charge comparable to that of the pristine VMT dispersion (around −32 mV), suggesting preserved colloidal stability. The Fe-VMT dispersion remains stable for at least 5 days after letting down under an ambient environment, with no visible sediments. These results demonstrate that the proposed redispersion strategy enables effective incorporation of magnetic ions while maintaining electrostatic stability necessary for high-quality 2D dispersions.

To characterize the morphology and structure of the as-fabricated Fe-VMT flakes, we conducted atomic force microscopy (AFM), scanning electron microscopy (SEM) and transmission electron microscopy (TEM). VMT crystal possesses a layered triclinic structure composed of negatively charged aluminosilicate layers, balanced by interlayer and surface cations, which are substituted by the Fe ions through ion-exchange (Figure 2a). AFM and SEM images reveal that the Fe-VMT 2D flakes adopt a nanosheet morphology with smooth surfaces (Figure 2b–d). Statistical analysis indicates an average thickness of ~3.5 nm and a lateral size of ~1.1 µm, corresponding to an aspect ratio of ~300 (Figure 2c). The phase purity and crystal quality of the Fe-VMT flakes are confirmed by sharp electron diffraction shown in Figure 2e. High-angle annular dark-field scanning TEM (HAADF-STEM) imaging provides an overview of the Fe-VMT flakes (Figure 2f), and energy-dispersive X-ray spectroscopy (EDS) mapping confirms a uniform distribution of elements after ion exchange. Quantitative EDS analysis from the summed spectrum reveals an Fe ion concentration of ~2.0 at.% in Fe-VMT, largely enhanced compared to ~1.0 at.% in the pristine flakes (Figure 2g). We further conducted atomic-resolution imaging of the Fe-VMT flakes, as shown in Figure 2h,i. Since Fe is a comparatively heavier element compared to the other elements such as Mg, Al and Si in vermiculite, the bright atomic columns show the occupation of Fe ions in the crystal. We observed both randomly distributed Fe ions on the surface (Figure 2h) and regularly distributed Fe ions in the interlayer space (Figure 2i). The above results indicate the successful incorporation of Fe ions into the vermiculite structure without compromising crystal quality.

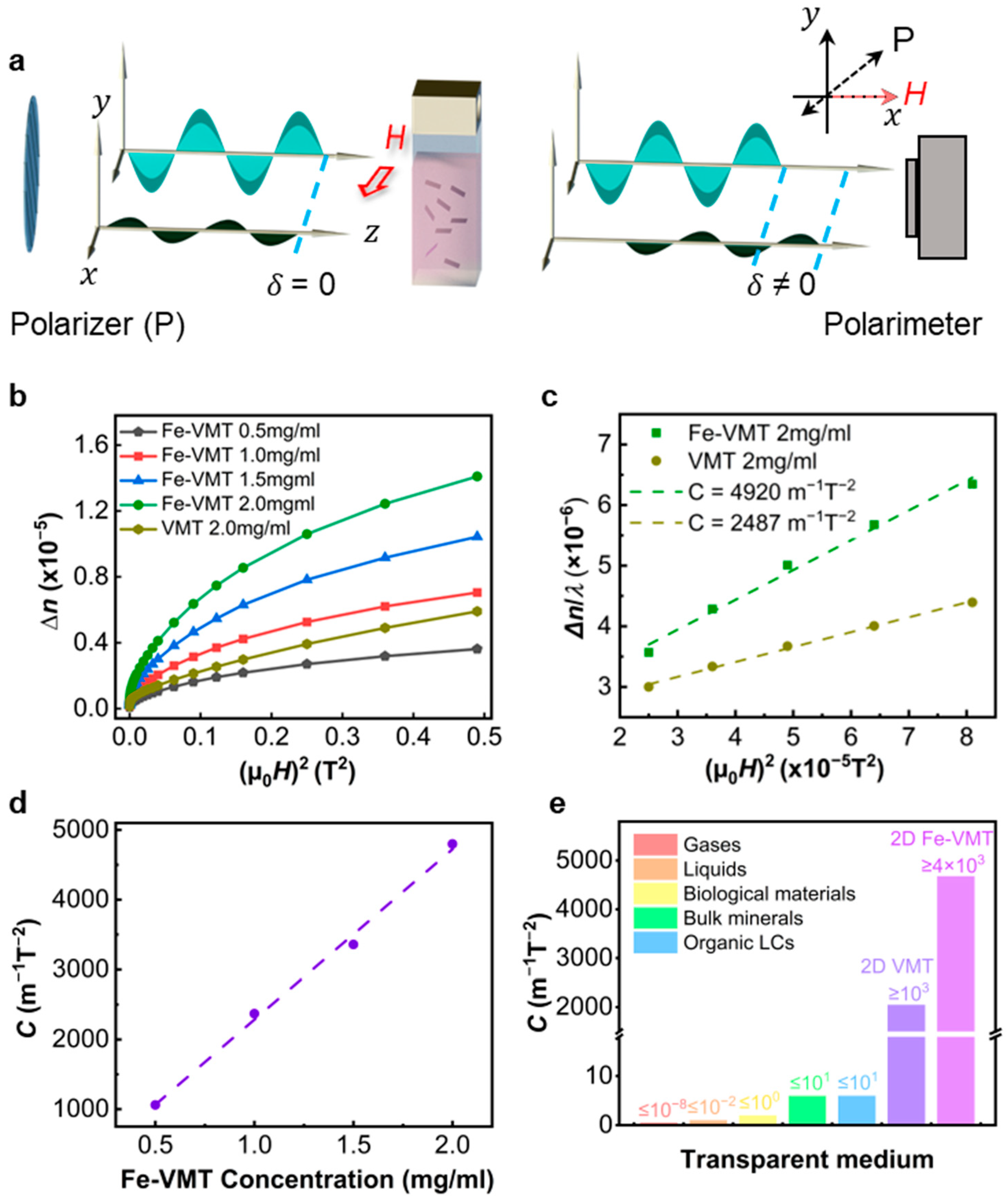
The optical setup for the magneto-birefringence measurement is illustrated in Figure 3a, where the light from a laser transmits through a quartz cuvette containing either vermiculite or Fe-vermiculite LCs [4]. The polarization direction of the light, determined by the polarizer, makes an 45° angle to the magnetic field. The birefringence of the LC is experimentally determined by measuring the phase retardation ($\delta$) of the transmitted light using a polarimeter. The birefringence $\mathsf{\Delta }n$ is calculated as Δn = δλL/2π, where L is the optical path, λ represents the wavelength of the light which is 650 nm used in this work. The magneto-birefringence of both VMT and Fe-VMT LCs is presented in Figure 3b. Both systems show an increased birefringence with increasing magnetic field from zero, approaching a saturation at higher magnetic fields. The mechanism underlying the phenomenon of magneto-birefringence can be explained as follows (Figure 3a). When a polarized light beam passes through the LC, it can be decomposed into two orthogonal, in-phase polarization components (with δ = 0), one of which oscillates along the direction of magnetic field. In the absence of an external magnetic field (μ₀H = 0), the suspended nanoflakes are randomly orientated subject to the Brownian motion, and the LC macroscopically behaves as an isotropic medium. The two polarization components experience identical phase retardation when transverse the LC medium. Subsequently, when the magnetic field is applied, the suspended nanoflakes rotate under the magnetic torque due to finite magnetic anisotropy of the material. The angle between the nanoflake surface and the magnetic field is governed by the balance of magnetization energy and thermal agitation, and it follows a statistical Boltzmann distribution. As a result, the LC transitions to a more ordered state, exhibiting finite birefringence ($\mathsf{\Delta }$n ≠ 0). The two polarization components now experience distinct phase retardation (δ ≠ 0) after transmission. As the magnetic field increases, the system’s magnetization energy grows, leading to an increased ordering in LC medium and, consequently, a greater birefringence (Figure 3b).

To quantitatively compare the magneto-birefringence of the VMT and Fe-VMT samples, we measure the Cotton–Mouton CM coefficient C, a widely used parameter for characterizing the sensitivity of inorganic LC induced birefringence to the magnetic field. The relationship between $\mathsf{\Delta }$n and CM coefficient can be described as $\mathsf{\Delta }n=C\lambda {\left({\mu }_{0}H\right)}^2$ in the small magnetic field regime, which is also observed in our case (Figure 3b,c). Figure 3b shows the as measured $\mathsf{\Delta }$n vs. H curves, which are indeed linear under fields below 10 mT (Figure 3c). C can therefore be extracted from the experimental $\mathsf{\Delta }$n vs. H curves. We further measured CM coefficients of Fe-VMT LCs with various concentrations, which exhibit a linear dependence on concentration, as demonstrated in Figure 3d. This trend is consistent with the general quantitatively statistical model for a 2D LC system i.e., $C={\displaystyle \frac{∆n^p\phi ∆\chi }{15k_{B}T\lambda }}$, where φ denotes the volume fraction, $∆n^p$ denotes the specific birefringence, $∆\chi$ denotes the magnetic anisotropy on susceptibilities, k_B denotes the Boltzmann constant and T is the temperature. Since $∆n^p$, $∆\chi$, k_B and T are constants for a particular material system measured at a specific condition, $C$ is expected be linearly depended on φ. For the Fe-VMT LC with a concentration of 2.0 mg/mL (~0.08 vol.%), as shown in Figure 3c, the CM coefficient was determined to be as high as 4920 m⁻¹T⁻², representing nearly a doubled value compared to the pristine VMT samples (Figure 3c). In fact, our Fe-VMT samples demonstrate a CM coefficient four times higher than the previous reported VMT, despite a comparatively low aspect ratio, and also orders of magnitude higher than the CM coefficients measured from other types of materials (Figure 3e) [4].

To elucidate the observed enhancement of magneto-birefringence in Fe-vermiculite (Fe-VMT) dispersions, magnetization measurements were performed on the membrane samples assembled from the 2D flakes, as shown in Figure 1 (see Section 3, Methods for details). The magnetization was measured using a superconducting quantum interference device (SQUID) magnetometer (MPMS-3, Quantum Design) to ensure high magnetic sensitivity. To mitigate the magnetic background inference from the sample holder and fixation components, measurements were conducted at liquid-helium temperatures. The magnetic anisotropy of the sample was investigated by aligning the membrane either along the in-plane ($\parallel$) or the out-of-plane ($\perp$) relative to the applied magnetic field during the measurements. 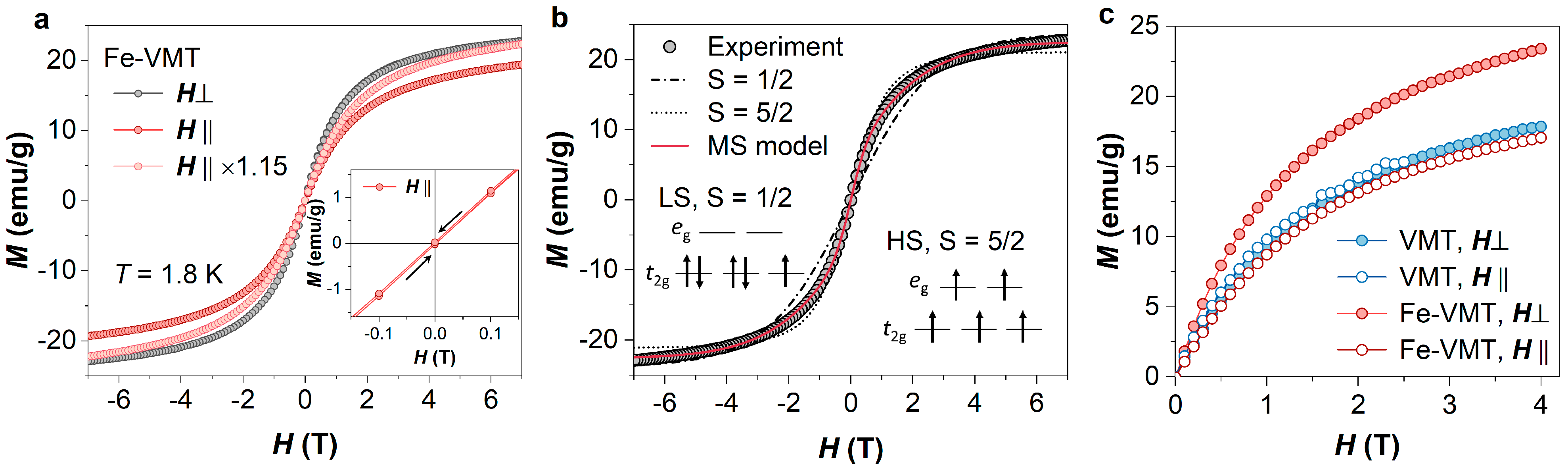Figure 4a illustrates the isothermal magnetization curves of Fe-VMT in both field directions. Despite the low concentration of Fe ions, Fe-VMT sample displays strong magnetism, with the magnetization surpassing 20 emu/g at 7 T. The field dependence of magnetization follows typical paramagnetic behavior in both field directions, exhibiting no magnetic hysteresis, as verified by the fully reversible magnetization at small fields (see inset of Figure 4a). The absence of magnetic hysteresis suggests the lack of ferromagnetic order, as expected for the dilute concentration of Fe ions in the VMT host matrix. Figure 4a also presents a notable magnetic anisotropy in Fe-VMT, with an easy magnetization axis along the out-of-plane direction. To confirm that the observed difference in magnetization between the in-plane and out-of-plane measurements is attributed to magnetic anisotropy, rather than experimental artefacts (such as errors in sample mass), we compare the out-of-plane magnetization curve with the in-plane curve magnified by a factor of 1.15 to align their magnetization values at 7 T. As demonstrated in Figure 4a, the two curves exhibit distinct behaviors, thereby substantiating the magnetic anisotropy in Fe-VMT. In contrast, pristine VMT samples exhibit only negligible magnetic anisotropy (see Figure 4c).

To gain a further insight into the magnetism of Fe-VMT, we performed a theoretical analysis of the magnetization data by fitting with paramagnetic models. The mass magnetization (per gram) of paramagnetic materials can be described as

$$M=n{N}_{\mathrm{m}\mathrm{a}\mathrm{g}}{g}_J{\mu }_{B}J{B}_J\left(x\right)$$

(1)

$$x={\displaystyle \frac{g_J{\mu }_{B}JH}{k_{B}T}}$$

(2)

where $n$ represents the number of spins per magnetic ions, $N_{\mathrm{m}\mathrm{a}\mathrm{g}}$ is the number of magnetic ions, ${\mu }_B$ is the Bohr magneton, $J$ is the total angular momentum number, $H$ is the magnetic field, $g_J$ is the Landé g-factor and $B\left(x\right)$ is the Boullion function, given as

$$B\left(x\right)={\displaystyle \frac{2J+1}{2J}}\coth \left({\displaystyle \frac{2J+1}{2J}}x\right)-{\displaystyle \frac{1}{2J}}\coth \left({\displaystyle \frac{1}{2J}}x\right)$$

(3)

In Fe-VMT, the Fe ions predominantly exist in the Fe³⁺ valence state [18], with five 3d orbital electrons contributing to the magnetism. As shown in the inset of Figure 4c, due to the octahedral structure of VMT host, the d orbitals of Fe³⁺ are energetically split such that the three $t_{2g}$ orbitals lie below the two $e_g$ orbitals. Depending on the crystal field strength and the coordination environment of the magnetic ions, the five 3d electrons can fill the five d orbitals in primarily two configurations: either a low-spin (LS) state ($S=1/2$) with a single unpaired electron in the strong crystal field regime or a high-spin (HS) state ($S=5/2$) with all five 3d electrons unpaired in the case of weak crystal field. Therefore, in applying the paramagnetic model for analysis, we considered both the low-spin ($S=1/2$) and high-spin ($S=5/2$) states. However, as shown in Figure 4b, none of the above models fits the experimental data well. The magnetization of Fe-VMT saturates more rapidly than the low-spin state model but more slowly than the high-spin state model. Even the intermediate state model with $S=3/2$, although less stable and generally not expected in our case, does not yield a proper fit (Figure 4b). Considering there are various occupying sites of Fe within the VMT (Figure 2h,i), Fe ions probably experience varying crystal fields, leading to a mixture of spin states [19]. To account for this, we developed a mixed-spin state (MS) model combining LS and HS states of Fe, such that

$$M=M_{\mathrm{L}\mathrm{S}}+M_{\mathrm{H}\mathrm{S} }$$

(4)

where $M_{\mathrm{L}\mathrm{S}}$ and $M_{\mathrm{H}\mathrm{S} }$ are the magnetization contributions from the respective spin states, as described by the standard paramagnetic model. As shown in Figure 4b, the mixed-spin state model provides an excellent fit to the experimental data of the perpendicular-field ($H^{\perp }$) magnetization. From the fitting, the number of spins in the LS state is found to be $n_{\mathrm{L}\mathrm{S}}^{\perp }\approx 1.52\times {10}^{-3} N_A$ per gram (or mol$\cdot$g⁻¹), while for the HS state, $n_{\mathrm{H}\mathrm{S}}^{\perp }\approx 2.06\times {10}^{-4}{ N}_A$ per gram, where $N_A\cong 6.022\times {10}^{23}$ is the Avogadro constant, and the total spin concentrations is calculated to be $n_{\mathrm{s}\mathrm{p}\mathrm{i}\mathrm{n}}^{\perp }=n_{\mathrm{L}\mathrm{S}}^{\perp }+n_{\mathrm{H}\mathrm{S}}^{\perp }\approx 1.73\times {10}^{-3}$mol$\cdot$g⁻¹. This agrees well with the concentration of Fe ions $n_{\mathrm{F}\mathrm{e}}=1.35\times {10}^{-3}$ mol$\cdot$g⁻¹ determined separately from the compositional (e.g., EDS) and weight measurements for the membrane.

Intriguingly, while the Fe-VMT exhibits a clear enhancement of the magnetic anisotropy compared to the pristine VMT samples, the magnetization of VMT in both field directions closely resembles the in-plane magnetization of Fe-VMT (Figure 4c). This indicates that the incorporation of Fe ions enhances the magnetic anisotropy by majorly enriching the out-of-plane magnetization of the material. These results are in consistency with previous reports that Fe ion strengthens the interlayer binding force in VMT and Fe intercalation can reduce the interlayer spacing [18,20]. In contrast, the intralayer crystalline structure remains largely unchanged. The ion-exchange induced change of interlayer interaction would therefore considerably modify the local binding environment of Fe ions, including the coordination symmetry, pressure and crystal field strength, for which a high-spin state of Fe ions is favored [21,22]. This argument is supported by performing a similar analysis on the parallel-field magnetization with our mixed-spin state model. While the model fitting yields a nearly identical spin concentration of LS state ($n_{\mathrm{L}\mathrm{S}}^{\parallel }\approx 1.54\times {10}^{-3}$ mol$\cdot$g⁻¹) to the perpendicular-field case ($n_{\mathrm{L}\mathrm{S}}^{\perp }\approx 1.52\times {10}^{-3}$mol$\cdot$g⁻¹, the spin concentration of HS state is much less ($n_{\mathrm{L}\mathrm{S}}^{\parallel }\approx 7.02\times {10}^{-5}$mol$\cdot$g⁻¹ vs. $n_{\mathrm{H}\mathrm{S}}^{\perp }\approx 2.06\times {10}^{-4}$), indicating more Fe ions involves in the HS state in response to the perpendicular field after Fe ion exchange and thus an enhanced magnetic anisotropy in Fe-VMT.

We now discuss the enlarged Cotton–Mouton coefficient in dispersions of Fe-VMT and its correlation with the increased magnetic anisotropy after Fe incorporation. Qualitatively, the birefringence of the dispersion arises from the collective alignment of the suspended nanoflakes in the presence of a magnetic field. The greater the magnetic anisotropy of the Fe-VMT nanoflakes, the more aligned the nanoflakes become relative to the magnetic field, resulting in a more ordered dispersion and a stronger birefringence. Quantitatively, the relationship between magnetic anisotropy and the Cotton–Mouton coefficient $C={\displaystyle \frac{∆n^p\phi ∆\chi }{15k_{B}T\lambda }}$ demonstrates a linear dependence of the Cotton–Mouton coefficient on the magnetic anisotropy $\mathsf{\Delta }\mathsf{\chi }$, the difference in magnetic susceptibility between different field orientations. Thus, an increased magnetic sensitivity of the dispersion and a larger Cotton–Mouton coefficient can be expected with the observed increasement in magnetic anisotropy.

3. Methods

3.1. VMT and Fe-VMT Samples

VMT and Fe-VMT membranes. Raw vermiculite dispersions were produced from the thermally expanded vermiculite (Sigma Aldrich, St. Louis, MA, USA) via a two-step ion exchange method. 50 mg of vermiculite granules were added to 100 mL saturated NaCl solution and stirred under refluxing at 100 °C for 12 h to replace the interlayer cations (Mg²⁺) with Na⁺. The solution was then filtered out, and the collected vermiculite flakes were repeatedly washed with DI water and ethanol to remove any residual salt. Sodium exchanged bulk vermiculite was then dispersed in 1 M LiCl solution and refluxed for 24 h followed by filtration and extensive wash with water and ethanol. The suspensions containing lithium vermiculite flakes can then be obtained and were sonicated in water for 20 min in order to exfoliate them into monolayer Li-Ver flakes and subsequently centrifuged at 3000 rpm to remove any bulk residues left in the solution. The vermiculite membrane of thickness around 2 µm were prepared by vacuum filtration of the raw vermiculite dispersion through alumina membrane filters (0.2 µm pore size and a diameter of 25 mm). The Fe-vermiculite membranes are prepared by immersing the pristine vermiculite membrane in FeCl₃ for a designed amount of time, e.g., 0.01 M for 4 h.

VMT and Fe-VMT dispersion. Fe-vermiculite dispersions were prepared by redisperse the Fe-VMT membrane in water through ultrasonic process under 750 W for 10 min using VCX (SONICS, Newtown, CT, USA). To obtain pristine vermiculite samples for property measurements, we used the Li-VMT membrane fabricated above and redispersed the membrane in water through the similar ultrasonic process under 750 W for 10 min using VCX (SONICS) such that the as-fabricated vermiculite and Fe-vermiculite samples have similar morphology for comparing magneto-optical properties. The weight percentage of the flakes in dispersion is determined by directly measuring the weight of the solid residue, after drying the drop casted dispersion onto a silicon wafer, using high-precision balances (Mettler Toledo XPE 26, Greifensee, Switzerland).

3.2. Morphological and Structural Characterizations

The morphological characteristics of the materials were investigated by AFM (Bruker Dimension FastScan, Billerica, MA, USA) and SEM (Thermal Fisher Apreo 2, Eindhoven, The Netherlands). Their detailed structural and compositional characteristics were investigated by transmission electron microscopy (TEM, Thermal Fisher Talos, Eindhoven, The Netherlands, operated at 200 kV), equipped with X-ray energy dispersive spectroscopy (EDS) and aberration-corrected scanning transmission electron microscopy (STEM, Thermal Fisher FEI Themis, Eindhoven, The Netherlands).

3.3. Magneto-Optical Measurements

A quartz cuvette with a 10 mm optical path was used as a container of the 2D VMT and Fe-VMT dispersion. The cuvette was placed in the center between two poles of a magnet with variable field strengths. Orthogonal polarizers (GL10-A, Thorlabs, Newton, NJ, USA) were placed in the optical path perpendicular to the magnetic field direction, and the angle between them was 45°. A 650 nm laser was used in the quantitative characterization of magneto-optical measurements. The polarization of transmitted light was detected by a polarimeter (PAX1000, Thorlabs), that directly reads the azimuth $\theta$ and the ellipticity $\eta$, from which we calculate the phase retardation by $\delta =\arctan \left(\tan \eta \tan \theta \right)+\arctan \left(\tan \eta /\tan \theta \right)$.

3.4. Magnetization Measurements

The magnetization of the VMT and Fe-VMT membranes was measured using a commercial superconducting quantum interference magnetometer device (SQUID, MPMS-3) from Quantum Design, San Diego, CA, USA. To fit into the MPMS-3 sample chamber, the laminated samples were initially cut into circular or square shapes with typical size of 3~4 mm using a ceramic blade. For in-plane field measurements, the sample was mounted onto the flat surface of a semicircular cross-sectional quartz paddle, which was secured by wrapping a small piece of low-magnetic Kapton tape around it. For out-of-plane field measurements, the sample was placed inside a brass half-tube sample holder, with its plane aligned perpendicular to the holder’s axis. To secure the sample position, two clear quartz rods, tightly clamped by the brass tube, were employed to brace the sample. All sample holders and quartz rods were used as Quantum Design supplied to ensure low and uniform magnetic signature. Throughout the sample handling process, strict precautions were taken to prevent magnetic contamination, such as the use of nonmagnetic tweezers, scissors and blades. To eliminate remanent magnetization, the isothermal magnetization curves (M vs. H) were always collected following a zero-field cooling from 300 K to the target temperature, typically 1.8 K, to minimize background effects. The magnetic background from the sample holders, Kapton tape, rod braces, etc., was carefully measured under the same experimental conditions used for the sample measurements and was subtracted from the data prior to analysis. In our measurements, the magnetic background contribution was typically below 1.5% for in-plane measurements and below 17% for out-of-plane measurements, ensuring reliable data analysis after background subtraction.

4. Conclusions

In summary, we provided a novel approach to modify the structure and properties of 2D materials’ dispersion. The procedure combines the techniques on self-assembly, ion exchange and dispersing of 2D materials, which are widely used in liquid exfoliation of 2D materials. We applied such procedure to 2D vermiculites and successfully incorporated magnetic ions into the interlayer spaces of the crystals while they are stably dispersed in water. Remarkably, we found that the incorporation of Fe ions results in a largely enhanced CM coefficient of the dispersion, which is attributed to the enhanced magnetization anisotropy in the material. Moreover, thanks to the diversity and versatility of 2D materials, we envision that further materials engineering could be integrated to design the related liquid-crystal devices towards target applications. These findings demonstrate magnetic ion exchange as an effective approach to enhance field-responsive properties of 2D materials, allowing future high-value applications based on low-cost minerals.