Single-Atom Cobalt-Doped 2D Graphene: Electronic Design for Multifunctional Applications in Environmental Remediation and Energy Storage
Abstract
1. Introduction
2. Results and Discussion
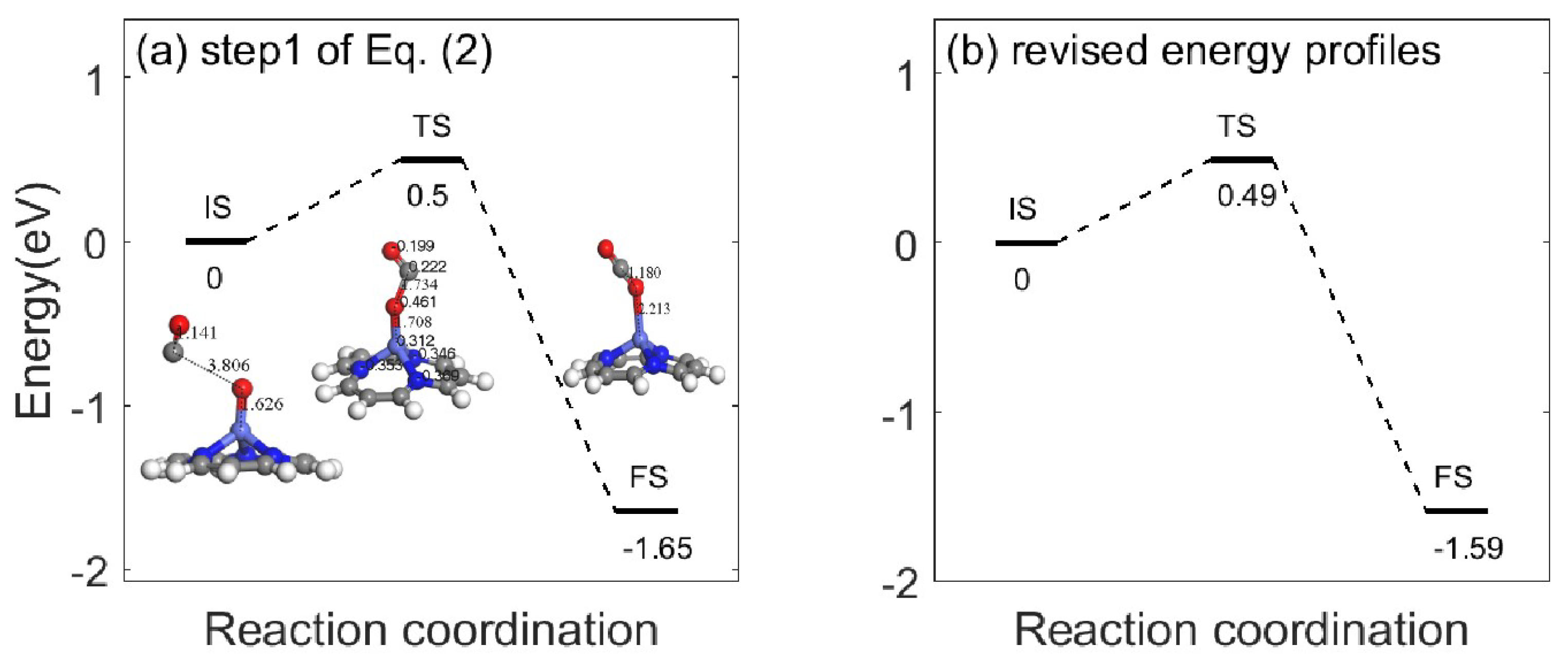
2.1. Catalytic Design for Environmental Remediation
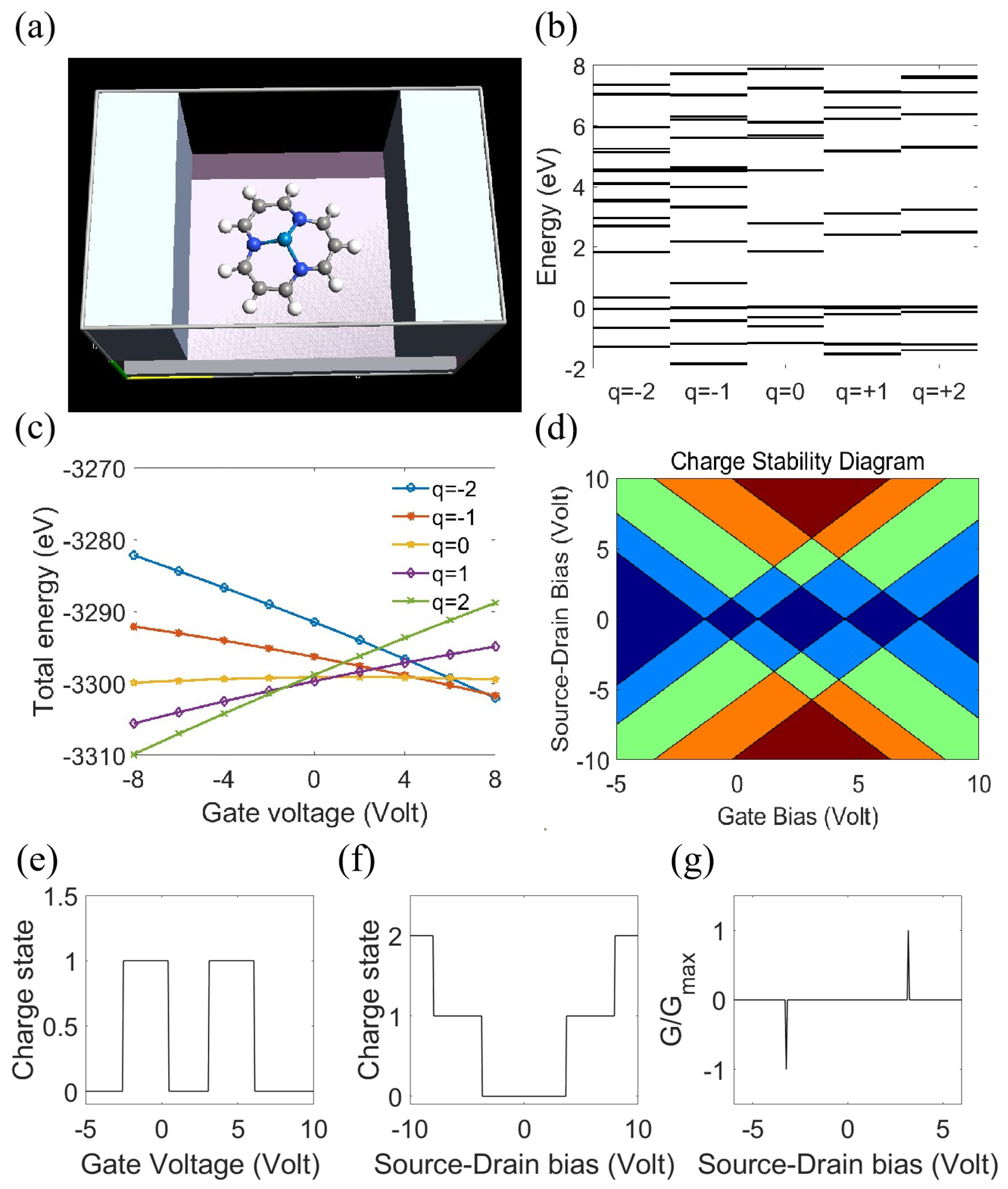
2.2. Single-Electron Phenomena in Defective 2D Graphene
2.3. Catalytic Design for Environmental Remediation
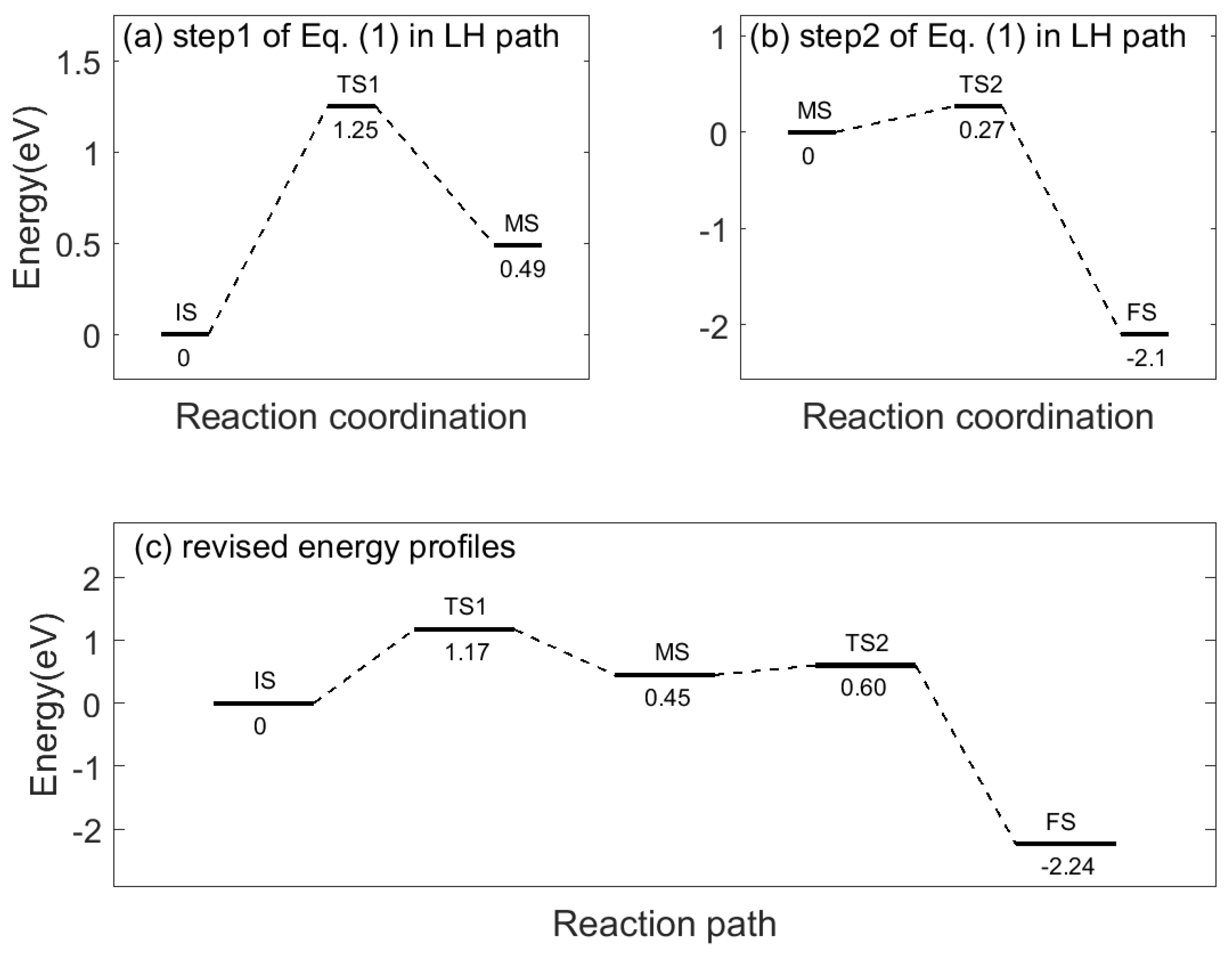
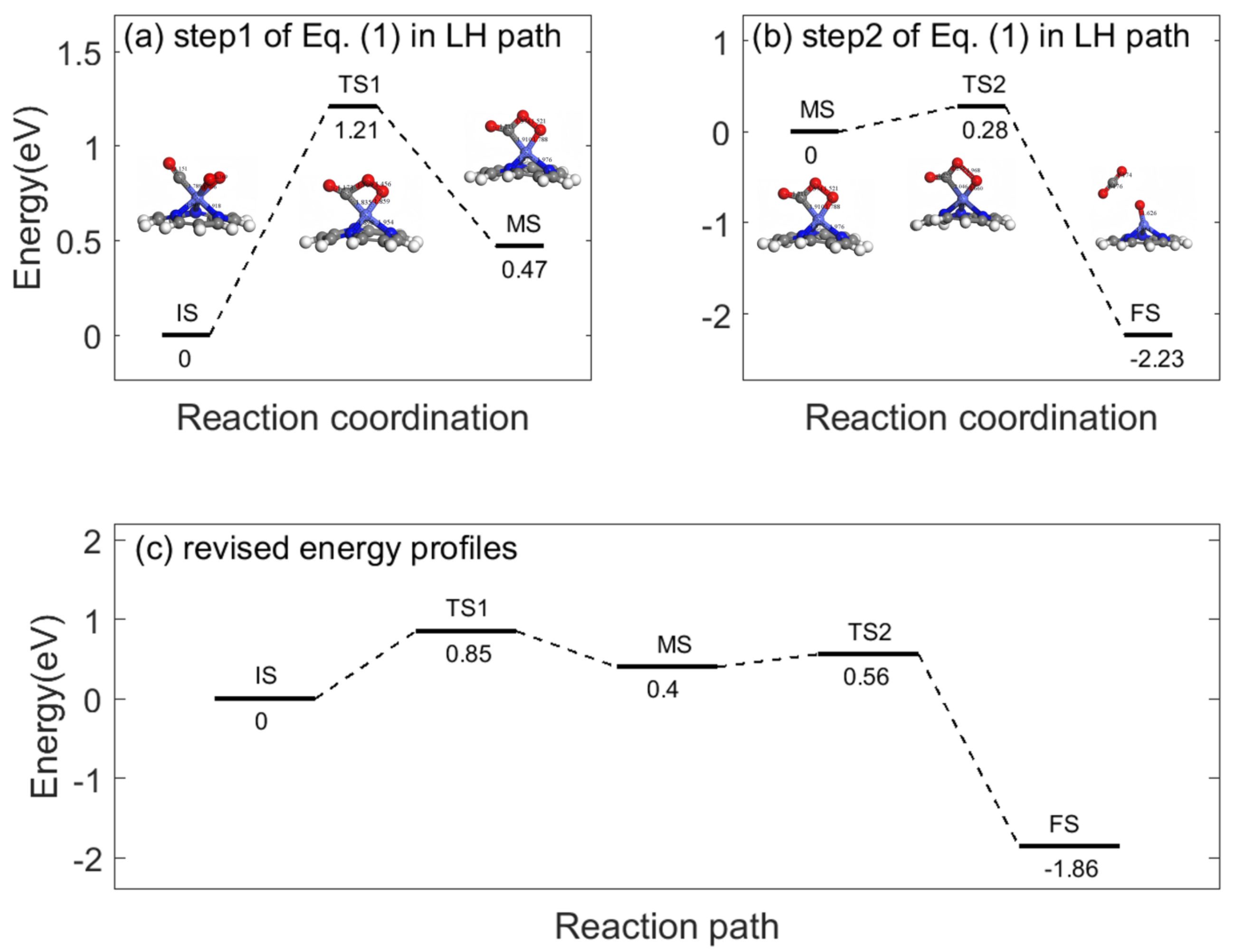
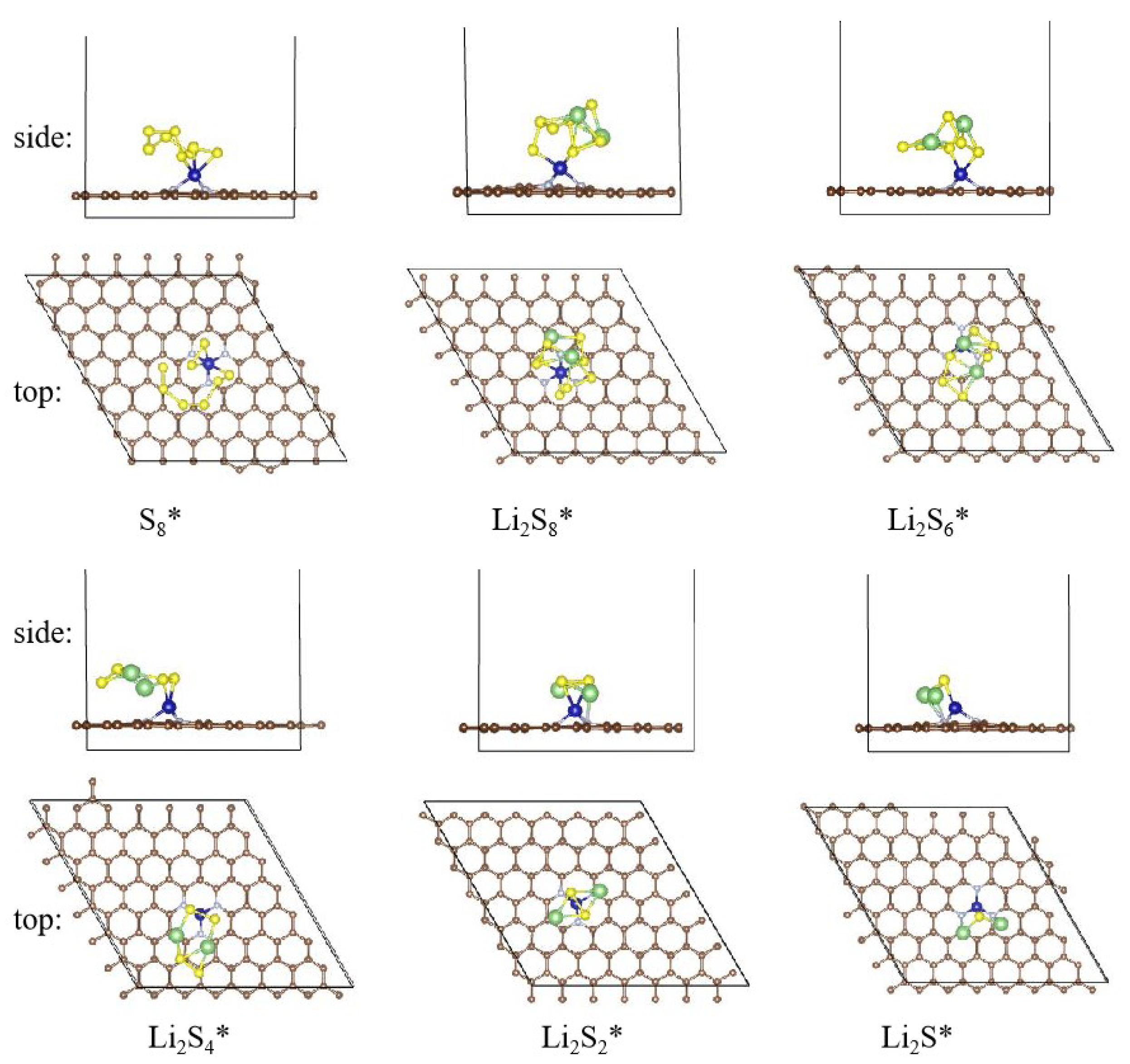
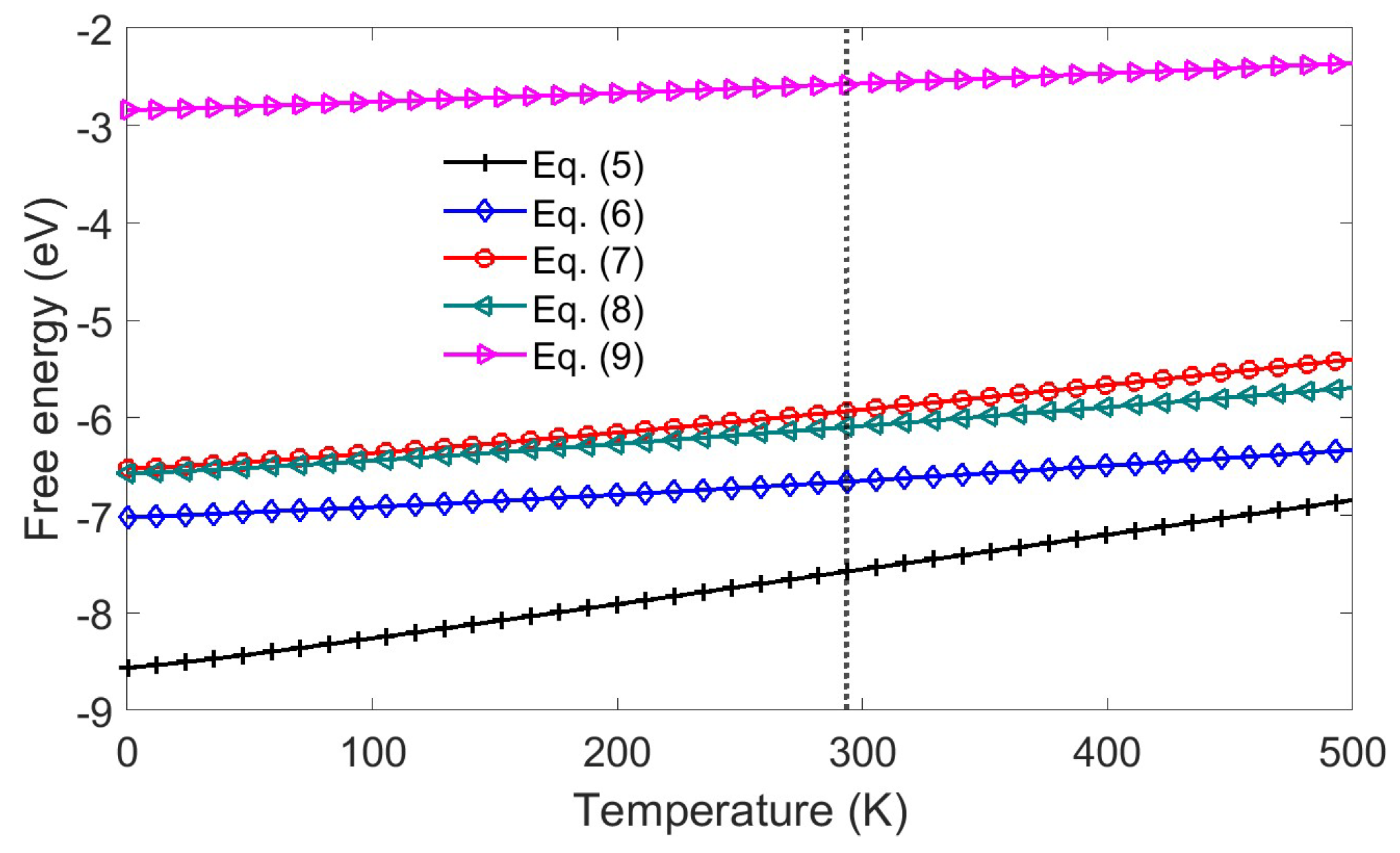
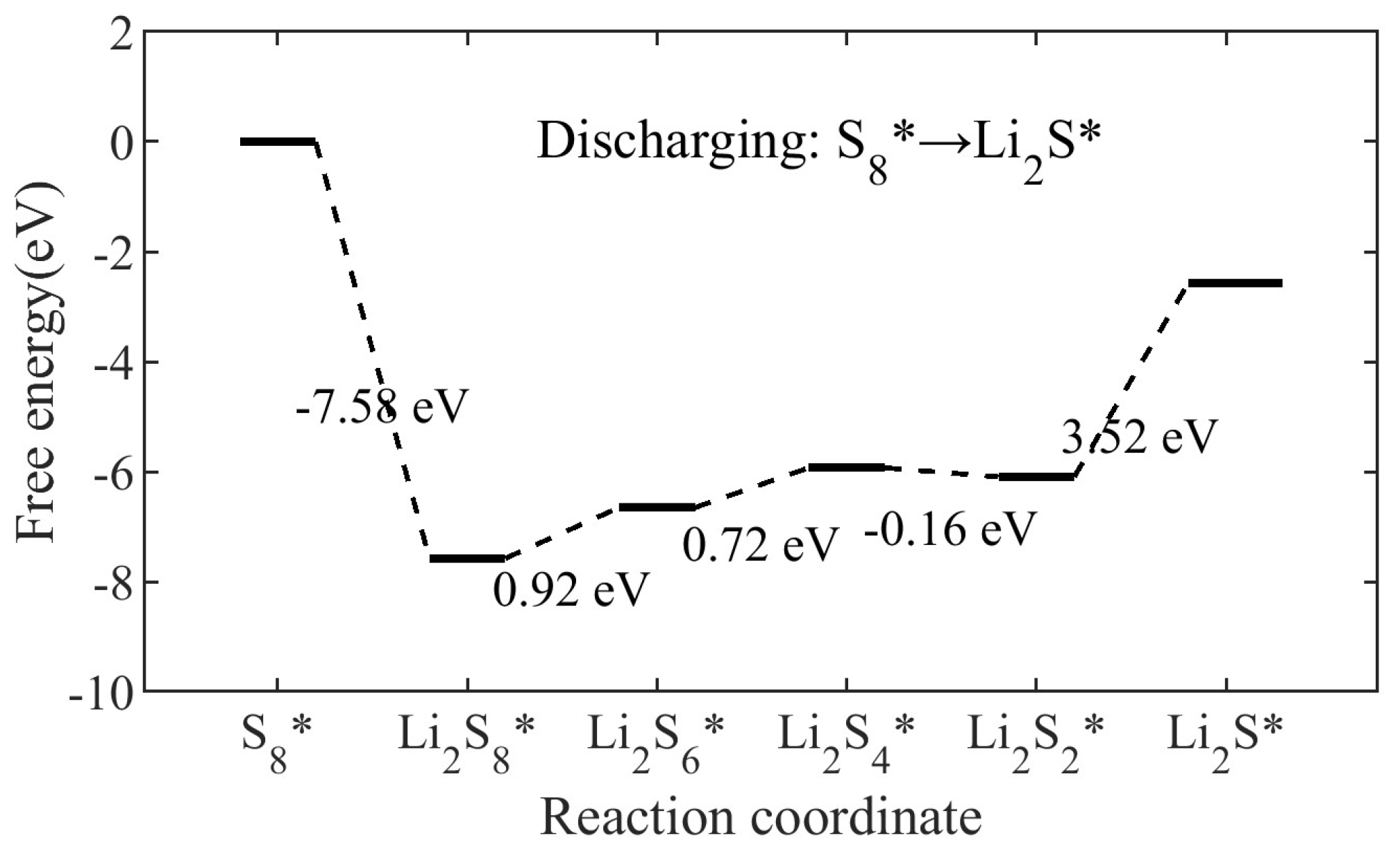
2.4. Stepwise Polysulfide Conversion Catalyzed by Atomic Cobalt Centers
3. Materials and Methods
3.1. Model Systems and Computation Details
3.1.1. Molecular Cluster Models (for CO Oxidation, SET, and Molecular Sensing)
3.1.2. Periodic Model (for Li-S Battery Applications)
3.2. Exchange-Correlation Functional and Basis Set
3.3. Convergence Parameters and Transition State Search
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Electronic Structures Analysis
Appendix A.1. PDOS Analysis
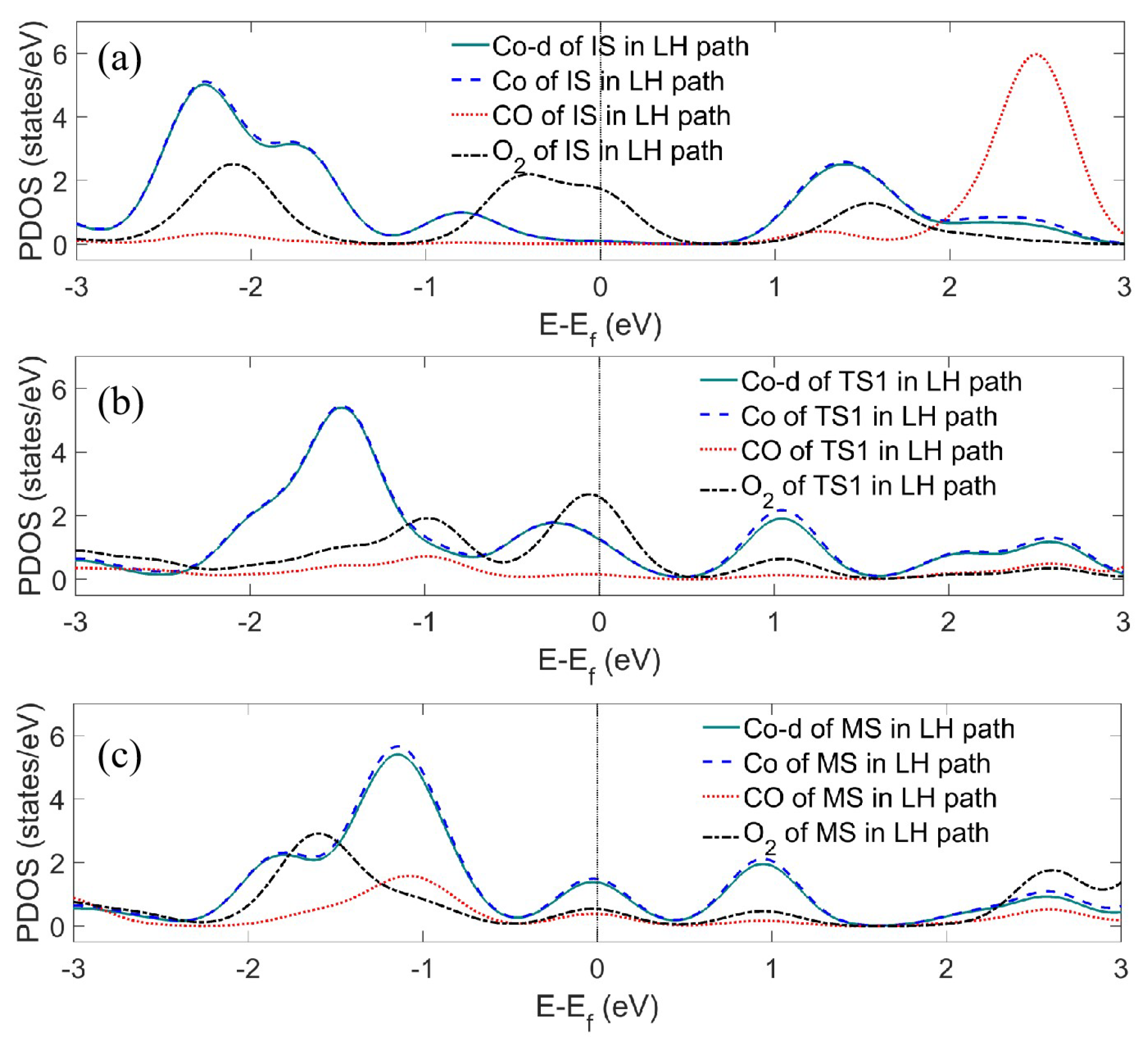


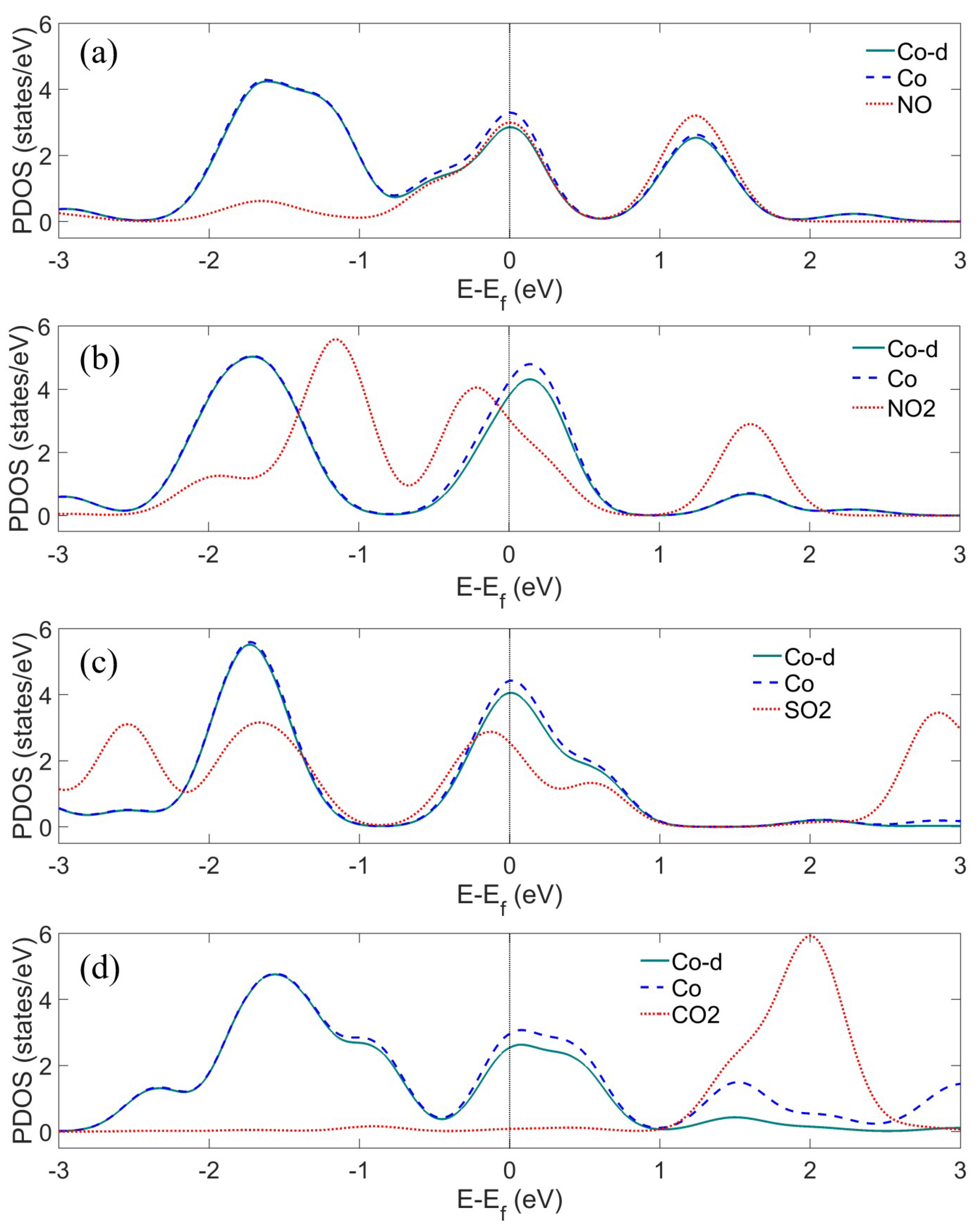
Appendix A.2. DFT-D Correction
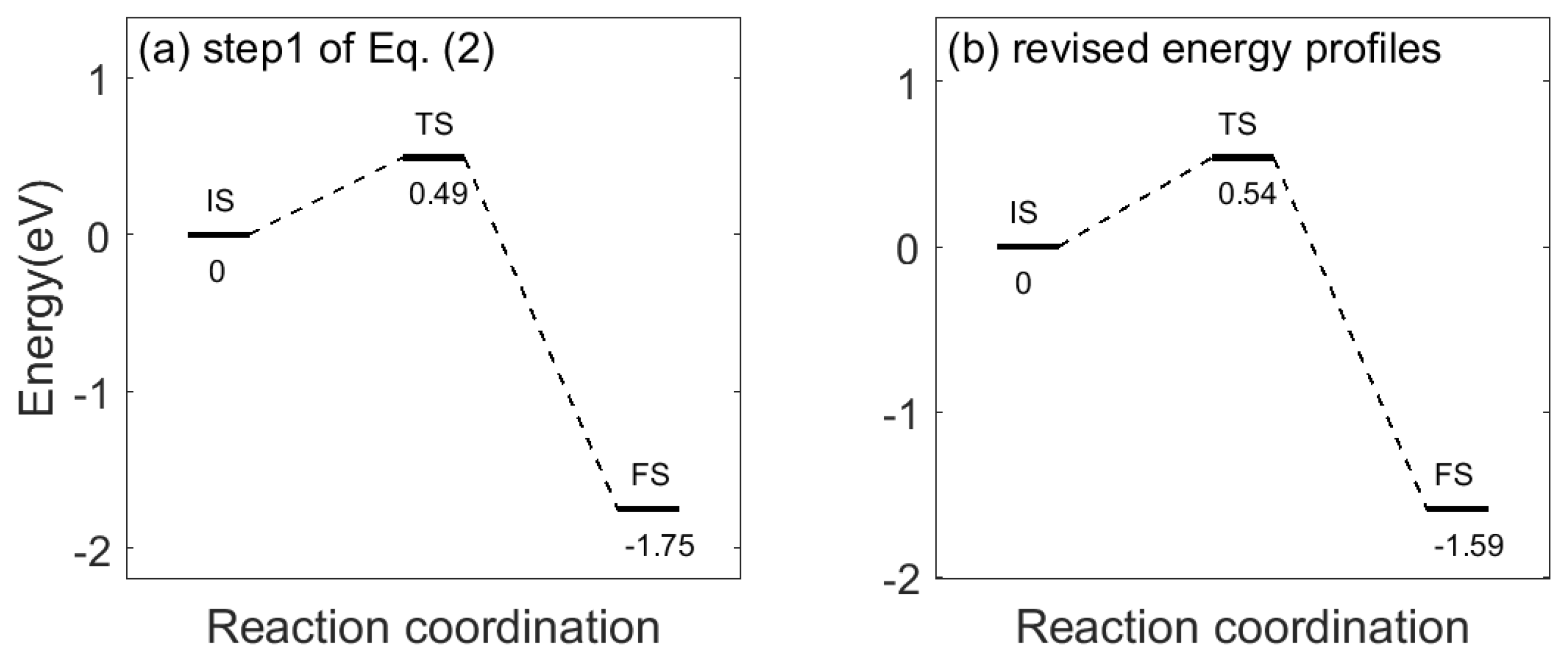
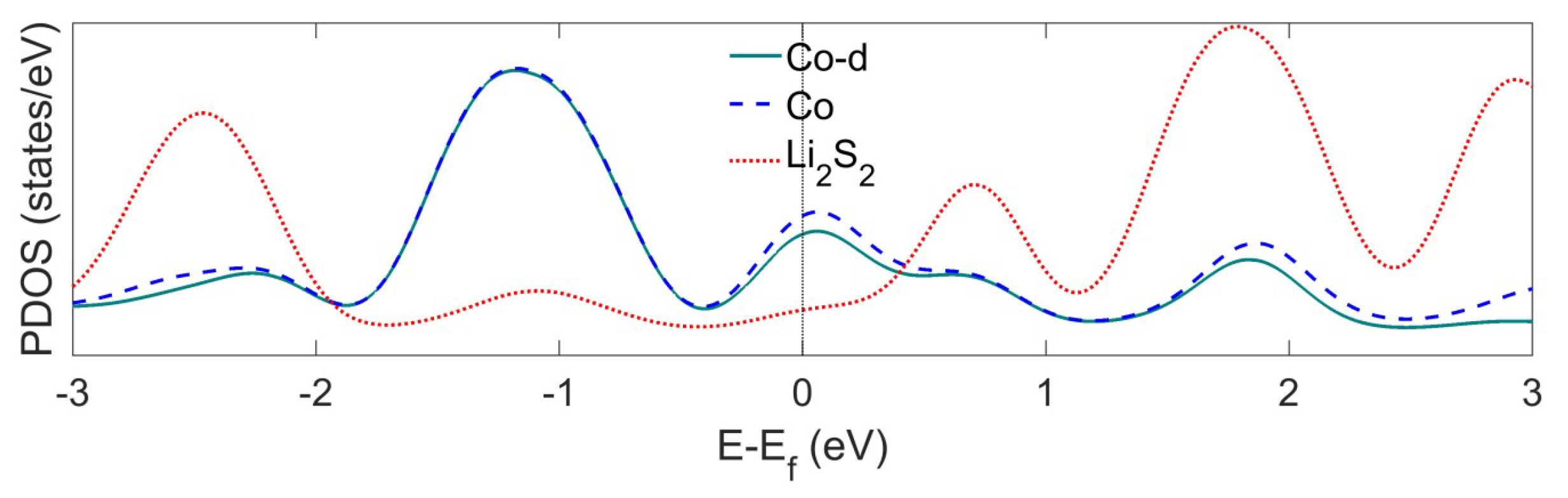
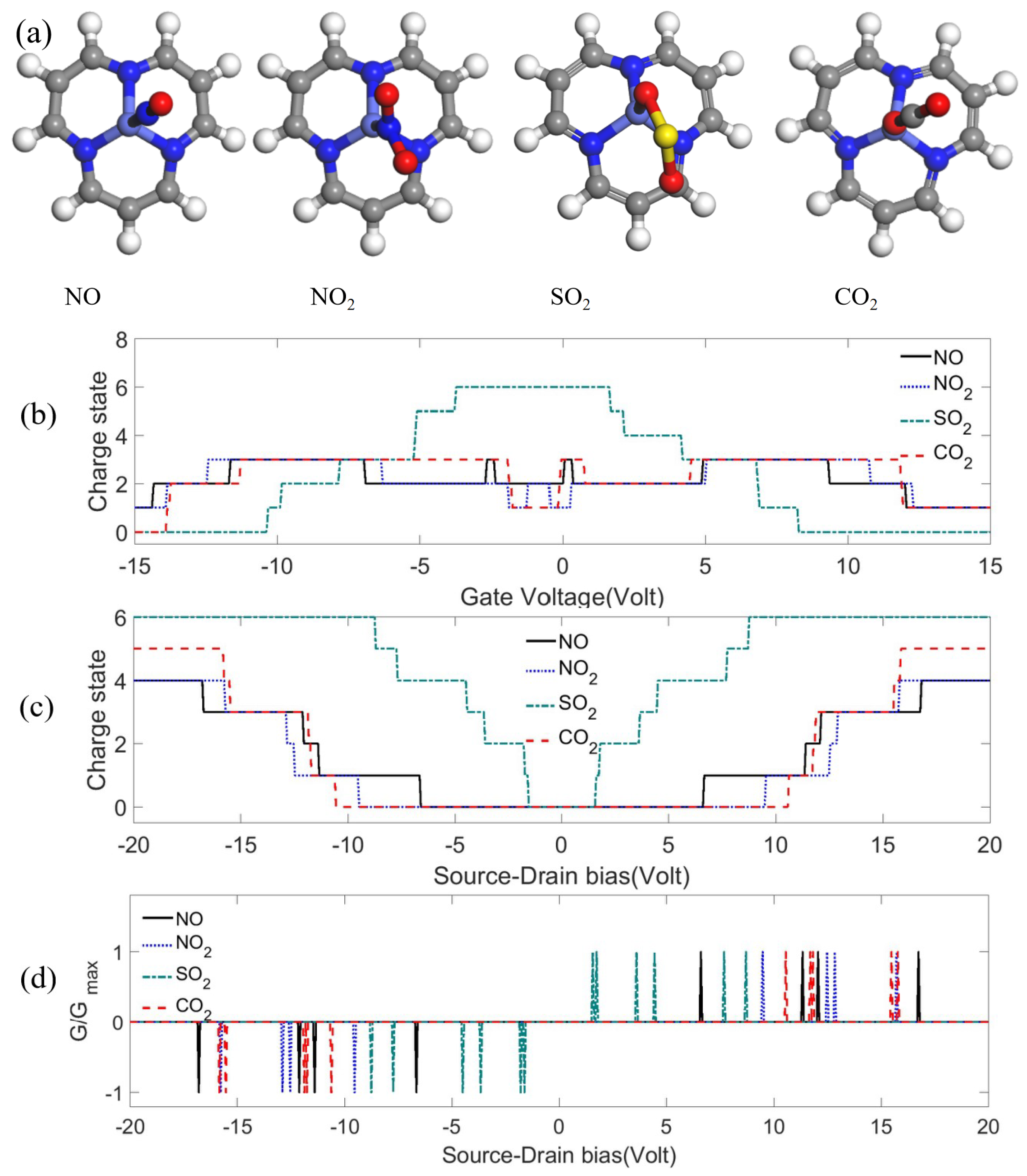
Appendix B. Sensing
Appendix B.1. Charge Transfer Mechanism
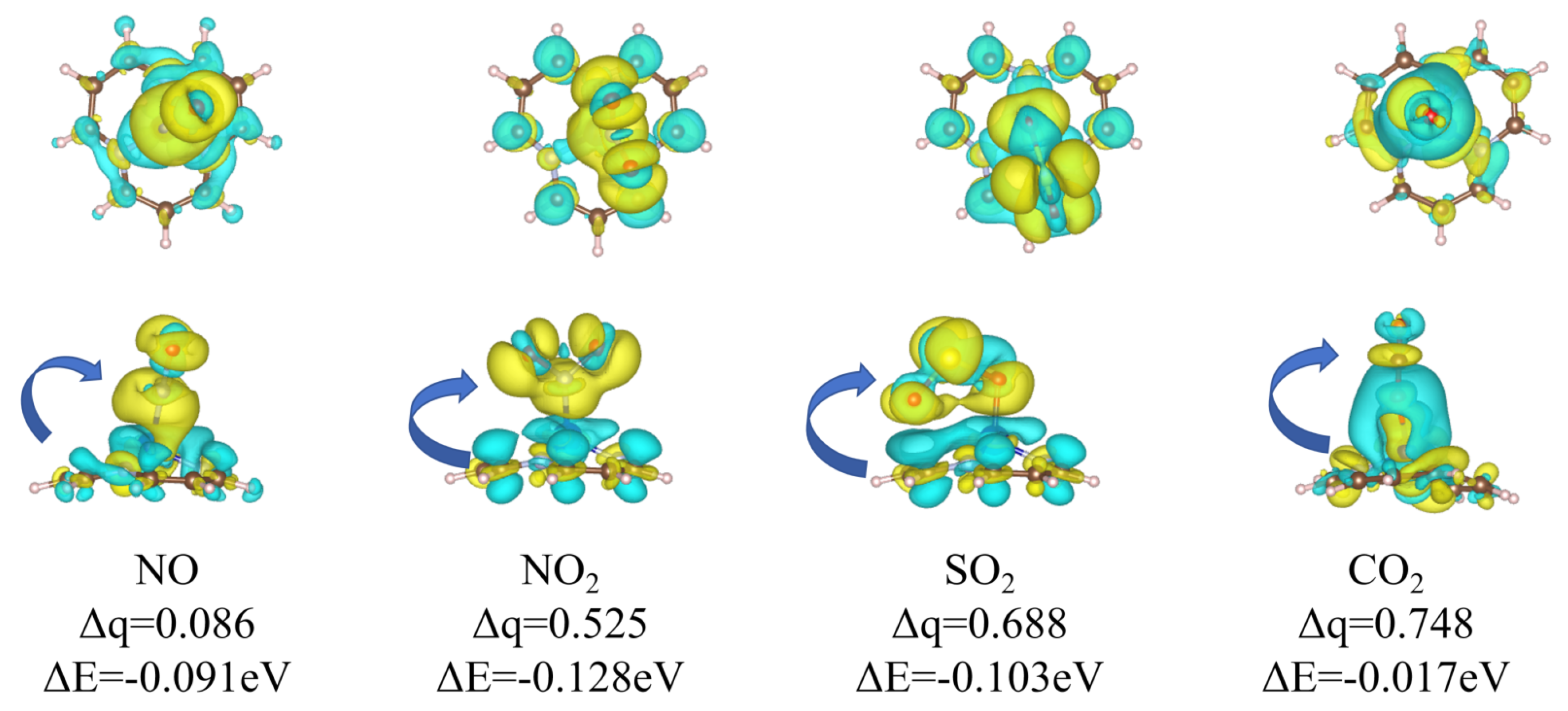
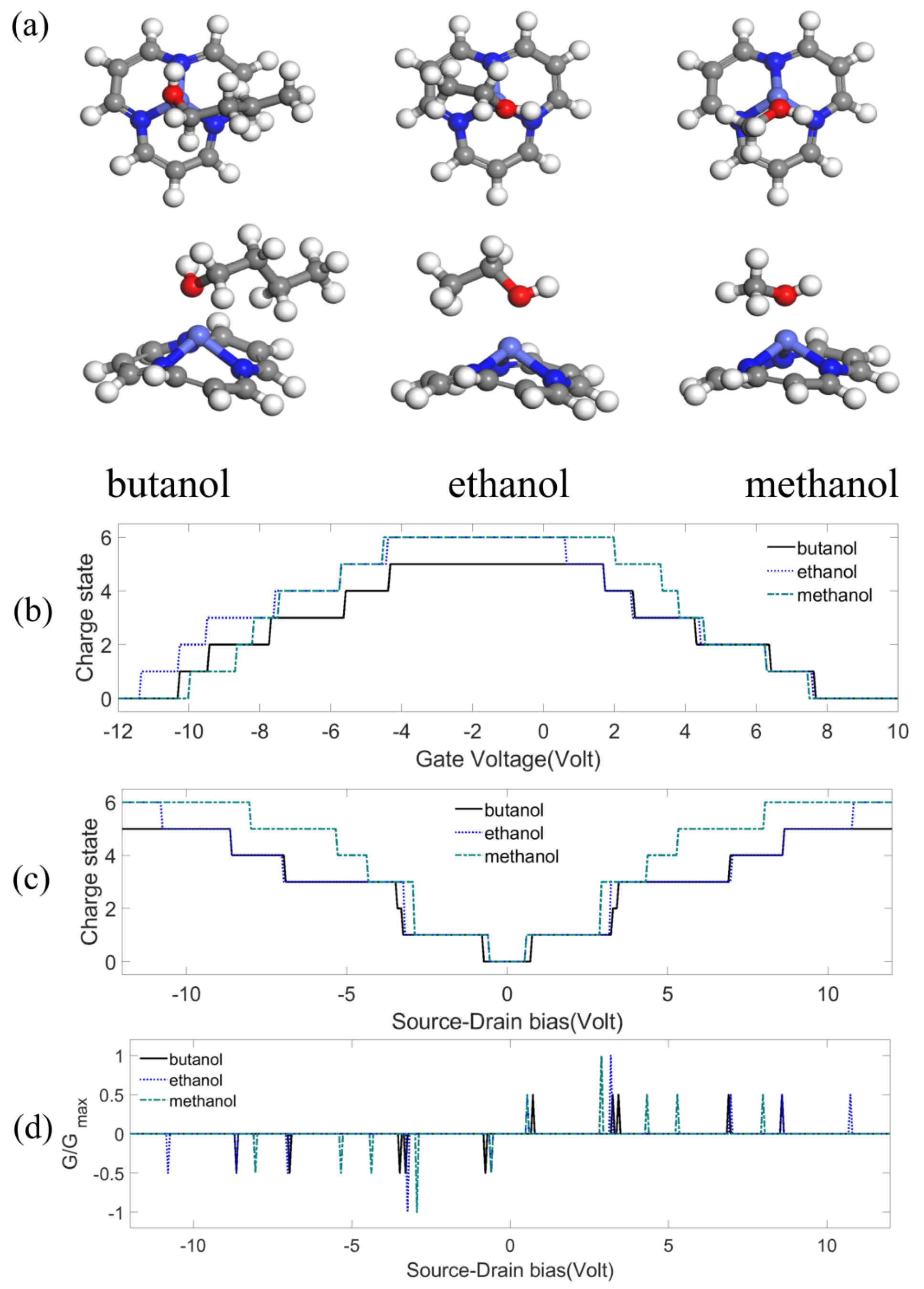
Appendix B.2. Detection of Hydrocarbon Radicals
References
- Yang, X.-F.; Wang, A.; Qiao, B.; Li, J.; Liu, J.; Zhang, T. Single-atom catalysts: A new frontier in heterogeneous catalysis. Accounts Chem. Res. 2013, 46, 1740–1748. [Google Scholar] [CrossRef] [PubMed]
- Gambardella, P.; Rusponi, S.; Veronese, M.; Dhesi, S.S.; Grazioli, C.; Dallmeyer, A.; Cabria, I.; Zeller, R.; Dederichs, P.H.; Kern, K.; et al. Giant magnetic anisotropy of single cobalt atoms and nanoparticles. Science 2003, 300, 1130–1133. [Google Scholar] [CrossRef] [PubMed]
- Ipadeola, A.K.; Chitt, M.; Abdelgawad, A.; Eid, K.; Abdullah, A.M. Graphene-based catalysts for carbon monoxide oxidation: Experimental and theoretical insights. Int. J. Hydrogen Energy 2023, 48, 17434–17467. [Google Scholar] [CrossRef]
- Park, J.; Pasupathy, A.N.; Goldsmith, J.I. Coulomb blockade and the Kondo effect in single-atom transistors. Nature 2002, 417, 722–725. [Google Scholar] [CrossRef]
- Rani, S.; Ray, S.J. Detection of gas molecule using C3N island single electron transistor. Carbon 2019, 144, 235–240. [Google Scholar] [CrossRef]
- Shabeeb, M.; Maity, S. Computational investigation on adsorption and activation of atmospheric pollutants co, no and so on small cobalt clusters. Chem. Phys. 2024, 582, 112291. [Google Scholar] [CrossRef]
- Wang, F.; Li, J.; Zhao, J.; Yang, Y.; Su, C.; Zhong, Y.L.; Yang, Q.H.; Lu, J. Single-atom electrocatalysts for lithium sulfur batteries: Progress, opportunities, and challenges. ACS Mater. Lett. 2020, 2, 1450–1463. [Google Scholar] [CrossRef]
- Ozols, K.; Jang, Y.S.; Cramer, N. Chiral cyclopentadienyl cobalt(iii) complexes enable highly enantioselective 3d-metal-catalyzed c-h functionalizations. J. Am. Chem. Soc. 2019, 141, 5675–5680. [Google Scholar] [CrossRef]
- Cao, L.; Luo, Q.; Liu, W.; Lin, Y.; Liu, X.; Cao, Y.; Zhang, W.; Wu, Y.; Yang, J.; Yao, T.; et al. Identification of single-atom active sites in carbon-based cobalt catalysts during electrocatalytic hydrogen evolution. Nat. Catal. 2019, 2, 134–141. [Google Scholar] [CrossRef]
- Hood, D.M.; Johnson, R.A.; Carpenter, A.E.; Younker, J.M.; Vinyard, D.J.; Stanley, G.G. Highly active cationic cobalt(ii) hydroformylation catalysts. Science 2020, 367, 542–548. [Google Scholar] [CrossRef]
- MacNeil, C.S.; Mendelsohn, L.N.; Pabst, T.P.; Hierlmeier, G.; Chirik, P.J. Alcohol synthesis by cobalt-catalyzed visible-light-driven reductive hydroformylation. J. Am. Chem. Soc. 2022, 144, 19219–19224. [Google Scholar] [CrossRef]
- Delolo, F.G.; Yang, J.; Neumann, H.; Dos Santos, E.N.; Gusevskaya, E.V.; Beller, M. Cobalt-catalyzed hydroformylation under mild conditions in the presence of phosphine oxides. ACS Sustain. Chem. Eng. 2021, 9, 5148–5154. [Google Scholar] [CrossRef]
- Hebrard, F.; Kalck, P. Cobalt-catalyzed hydroformylation of alkenes: Generation and recycling of the carbonyl species, and catalytic cycle. Chem. Rev. 2009, 109, 4272–4282. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Kubis, C.; Franke, R. Hydroformylation catalyzed by unmodified cobalt carbonyl under mild conditions. Science 2022, 377, 1223–1227. [Google Scholar] [CrossRef] [PubMed]
- Gao, K.; Yoshikai, N. Low-valent cobalt catalysis: New opportunities for c-h functionalization. Accounts Chem. Res. 2014, 47, 1208–1219. [Google Scholar] [CrossRef]
- Nakanowatari, S.; Mei, R.; Feldt, M.; Ackermann, L. Cobalt(iii)-catalyzed hydroarylation of allenes via c-h activation. ACS Catal. 2017, 7, 2511–2515. [Google Scholar] [CrossRef]
- Oliveira, J.C.; Dhawa, U.; Ackermann, L. Insights into the mechanism of low-valent cobalt-catalyzed c-h activation. ACS Catal. 2021, 11, 1505–1515. [Google Scholar] [CrossRef]
- Li, T.; Shen, C.; Sun, Y.; Zhang, J.; Xiang, P.; Lu, X.; Zhong, G. Cobalt-catalyzed olefinic c-h alkenylation/alkylation switched by carbonyl groups. Org. Lett. 2019, 21, 7772–7777. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, Z.; Yang, Z. Single non-noble-metal cobalt atom stabilized by pyridinic vacancy graphene: An efficient catalyst for co oxidation. J. Mol. Catal. A Chem. 2016, 417, 28–35. [Google Scholar] [CrossRef]
- Hu, W.; Wang, C.; Tan, H.; Duan, H.; Li, G.; Li, N.; Ji, Q.; Lu, Y.; Wang, Y.; Sun, Z.; et al. Embedding atomic cobalt into graphene lattices to activate room-temperature ferromagnetism. Nat. Commun. 2021, 12, 1854. [Google Scholar] [CrossRef]
- Gallagher, C.; Siddiqui, W.; Arnold, T.; Cheng, C.; Su, E.; Zhao, Q. Benchmarking a Molecular Flake Model on the Road to Programmable Graphene-Based Single-Atom Catalysts. J. Phys. Chem. C 2024, 128, 2876–2883. [Google Scholar] [CrossRef]
- Graf, H.; Vancea, J.; Hoffmann, H. Single-electron tunneling at room temperature in cobalt nanoparticles. Appl. Phys. Lett. 2002, 80, 1264–1266. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Z.; Xi, S.; Zhao, X.; Sun, T.; Li, J.; Yu, W.; Xu, H.; Herng, T.S.; Hai, X.; et al. Tuning the spin density of cobalt single-atom catalysts for efficient oxygen evolution. ACS Nano 2021, 15, 7105–7113. [Google Scholar] [CrossRef]
- Wu, D.; Tan, Z.; Feng, X.; Anderson, W.A.; Li, Q. Regeneration of cobalt complexes by thermal decomposition and acid treatment for no absorption. Chem. Eng. J. 2017, 315, 233–242. [Google Scholar] [CrossRef]
- Shen, Y.; Deng, J.; Impeng, S.; Li, S.; Yan, T.; Zhang, J.; Shi, L.; Zhang, D. Boosting toluene combustion by engineering co-o strength in cobalt oxide catalysts. Environ. Sci. Technol. 2020, 54, 10342–10350. [Google Scholar] [CrossRef] [PubMed]
- Bessell, S. Support effects in cobalt-based fischer-tropsch catalysis. Appl. Catal. A Gen. 1993, 96, 253–268. [Google Scholar] [CrossRef]
- Bruce, P.G.; Freunberger, S.A.; Hardwick, L.J.; Tarascon, J.M. Li–O2 and Li–S batteries with high energy storage. Nat. Mater. 2012, 11, 19–29. [Google Scholar] [CrossRef]
- Manthiram, A.; Fu, Y.; Su, Y.S. Challenges and prospects of lithium-sulfur batteries. Accounts Chem. Res. 2013, 46, 1125–1134. [Google Scholar] [CrossRef]
- Yin, H.; He, J.; Xiao, B.; Zhou, M.; Wang, W.; Joao, C.; Chen, Z.; Hou, Z.; Zhang, T.; Yu, Z. Advances and prospects of g-C3N4 in lithium-sulfur batteries. Nano Res. Energy 2024, 3, e9120138. [Google Scholar] [CrossRef]
- Feng, S.; Zhong, H.; Song, J.; Zhu, C.; Dong, P.; Shi, Q.; Liu, D.; Li, J.; Chang, Y.C.; Beckman, S.P.; et al. Catalytic activity of co-x (x = s, p, o) and its dependency on nanostructure/chemical composition in lithium-sulfur batteries. ACS Appl. Energy Mater. 2018, 1, 7014–7021. [Google Scholar] [CrossRef]
- Gu, Z.; Cheng, C.; Yan, T.; Liu, G.; Jiang, J.; Mao, J.; Dai, K.; Li, J.; Wu, J.; Zhang, L. Synergistic effect of Co3Fe7 alloy and n-doped hollow carbon spheres with high activity and stability for high-performance lithium-sulfur batteries. Nano Energy 2021, 86, 106111. [Google Scholar] [CrossRef]
- Huang, T.; Sun, Y.; Wu, J.; Jin, J.; Wei, C.; Shi, Z.; Wang, M.; Cai, J.; An, X.T.; Wang, P.; et al. A dual-functional fibrous skeleton implanted with single-atomic co-nxdispersions for longevous li-s full batteries. ACS Nano 2021, 15, 14105–14115. [Google Scholar] [CrossRef]
- Sun, X.; Qiu, Y.; Jiang, B.; Chen, Z.; Zhao, C.; Zhou, H.; Yang, L.; Fan, L.; Zhang, Y.; Zhang, N. Isolated fe-co heteronuclear diatomic sites as efficient bifunctional catalysts for high-performance lithium-sulfur batteries. Nat. Commun. 2023, 14, 291. [Google Scholar] [CrossRef]
- Yang, C.; Li, Y.; Peng, W.; Zhang, F.; Fan, X. In situ n-doped CoS2 anchored on mxene toward an efficient bifunctional catalyst for enhanced lithium-sulfur batteries. Chem. Eng. J. 2022, 427, 131792. [Google Scholar] [CrossRef]
- Li, Y.; Wu, J.; Zhang, B.; Wang, W.; Zhang, G.; Seh, Z.W.; Zhang, N.; Sun, J.; Huang, L.; Jiang, J.; et al. Fast conversion and controlled deposition of lithium (poly)sulfides in lithium-sulfur batteries using high-loading cobalt single atoms. Energy Storage Mater. 2020, 30, 250–259. [Google Scholar] [CrossRef]
- Wang, Y.; Chu, F.; Zeng, J.; Wang, Q.; Naren, T.; Li, Y.; Cheng, Y.; Lei, Y.; Wu, F. Single atom catalysts for fuel cells and rechargeable batteries: Principles, advances, and opportunities. ACS Nano 2021, 15, 210–239. [Google Scholar] [CrossRef]
- Liu, X.; Sui, Y.; Duan, T.; Meng, C.; Han, Y. Monodisperse pt atoms anchored on n-doped graphene as efficient catalysts for co oxidation: A first-principles investigation. Catal. Sci. Technol. 2015, 5, 1658–1667. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, Z.; Yu, G.; Chen, W.; Chen, Z. Co catalytic oxidation on iron-embedded graphene: Computational quest for low-cost nanocatalysts. J. Phys. Chem. C 2010, 114, 6250–6254. [Google Scholar] [CrossRef]
- Therrien, A.J.; Hensley, A.J.R.; Marcinkowski, M.D.; Zhang, R.; Lucci, F.R.; Coughlin, B.; Schilling, A.C.; McEwen, J.S.; Sykes, E.C.H. An atomic-scale view of single-site Pt catalysis for low-temperature CO oxidation. Nat. Catal. 2018, 1, 192–198. [Google Scholar] [CrossRef]
- Tang, Y.; Chen, W.; Zhou, J.; Chai, H.; Li, Y.; Cui, Y.; Feng, Z.; Dai, X. Mechanistic insight into the selective catalytic oxidation for no and co on co-doping graphene sheet: A theoretical study. Fuel 2019, 253, 1531–1544. [Google Scholar] [CrossRef]
- Stokbro, K. First-principles modeling of molecular single-electron transistors. J. Phys. Chem. C 2010, 114, 20461–20465. [Google Scholar] [CrossRef]
- Khademhosseini, V.; Dideban, D.; Ahmadi, M.T.; Ismail, R.; Heidari, H. Impact of hydrogen adsorption on the performance of a single electron transistor utilizing fullerene quantum dots. ECS J. Solid State Sci. Technol. 2018, 7, M191–M194. [Google Scholar] [CrossRef]
- Pronin, I.A.; Plugin, I.A.; Kolosov, D.A.; Karmanov, A.A.; Yakushova, N.D.; Varezhnikov, A.S.; Komolov, A.S.; Lazneva, E.F.; Koroleva, A.V.; Moshnikov, V.A.; et al. Sol-gel derived zno film as a gas sensor: Influence of uv processing versus a thermal annealing. Sens. Actuators A Phys. 2024, 377, 115707. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, Z.; Xu, Z.; Li, B.; Yang, S. rGO/In2O3 heterostructures based gas sensor for efficient ppb-level n-butanol detection. J. Alloys Compd. 2024, 986, 174154. [Google Scholar] [CrossRef]
- Pardeshi, N.M.; Ghuge, R.S.; Birla, P.N.; Chauhan, R.; Bhalekar, S.P.; Shinde, M.D.; Sivalingam, Y.; Kale, R.D.; Rane, S.B. Reduced graphene oxide@bimodal TiO2 nanocomposites as an efficacious console for room temperature n-butanol gas sensing. ACS Appl. Electron. Mater. 2024, 6, 4805–4818. [Google Scholar] [CrossRef]
- Song, M.K.; Cairns, E.J.; Zhang, Y. Lithium/sulfur batteries with high specific energy: Old challenges and new opportunities. Nanoscale 2013, 5, 2186–2204. [Google Scholar] [CrossRef]
- Nørskov, J.K.; Rossmeisl, J.; Logadottir, A.; Lindqvist, L.; Kitchin, J.R.; Bligaard, T.; Jónsson, H. Origin of the overpotential for oxygen reduction at a fuel-cell cathode. J. Phys. Chem. B 2004, 108, 17886–17892. [Google Scholar] [CrossRef] [PubMed]
- Shen, C.; Xie, J.; Zhang, M.; Andrei, P.; Zheng, J.P.; Hendrickson, M.; Plichta, E.J. A li-li2s4 battery with improved discharge capacity and cycle life at low electrolyte/sulfur ratios. J. Power Sources 2019, 414, 412–419. [Google Scholar] [CrossRef]
- Zhang, H.; Xin, S.; Li, J.; Cui, H.; Liu, Y.; Yang, Y.; Wang, M. Synergistic regulation of polysulfides immobilization and conversion by MOF-derived CoP-HNC nanocages for high-performance lithium-sulfur batteries. Nano Energy 2021, 85, 106011. [Google Scholar] [CrossRef]
- Molavi, R.; Safaiee, R.; Sheikhi, M.H. Oxygen adsorption properties of small cobalt oxide clusters: Application feasibility as oxygen gas sensors. Phys. Chem. Chem. Phys. 2020, 22, 14889–14899. [Google Scholar] [CrossRef] [PubMed]
- Molavi, R.; Safaiee, R.; Sheikhi, M.H.; Hassani, N. Theoretical perspective on co oxidation over small cobalt oxide clusters. Chem. Phys. Lett. 2021, 767, 138361. [Google Scholar] [CrossRef]
- Huang, Z.; Qu, J.; Peng, X.; Liu, W.; Zhang, K.; Wei, X.; Zhong, J. Quantum confinement in graphene quantum dots. Phys. Status Solidi Rapid Res. Lett. 2014, 8, 436–440. [Google Scholar] [CrossRef]
- Zayed, A.O.H.; Daud, M.N.; Zain, S.M. Global structural optimization and growth mechanism of cobalt oxide nanoclusters by genetic algorithm with spin-polarized dft. J. Alloys Compd. 2017, 695, 2513–2518. [Google Scholar] [CrossRef]
- Xie, Y.; Dong, F.; Heinbuch, S.; Rocca, J.J.; Bernstein, E.R. Oxidation reactions on neutral cobalt oxide clusters: Experimental and theoretical studies. Phys. Chem. Chem. Phys. 2010, 12, 947–959. [Google Scholar] [CrossRef]
- Johnson, G.E.; Reveles, J.U.; Reilly, N.M.; Tyo, E.C.; Khanna, S.N.; Castleman, A.W. Influence of stoichiometry and charge state on the structure and reactivity of cobalt oxide clusters with co. J. Phys. Chem. A 2008, 112, 11330–11340. [Google Scholar] [CrossRef]
- Li, M.R.; Chen, J.; Wang, G.C. Reaction mechanism of ethanol on model cobalt catalysts: Dft calculations. J. Phys. Chem. C 2016, 120, 14198–14208. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Zhang, Y.; Li, C.; Deng, L.; Song, B.; Bo, M.; Yao, C.; Lu, H.; Long, G. Single-Atom Cobalt-Doped 2D Graphene: Electronic Design for Multifunctional Applications in Environmental Remediation and Energy Storage. Inorganics 2025, 13, 312. https://doi.org/10.3390/inorganics13100312
Huang Z, Zhang Y, Li C, Deng L, Song B, Bo M, Yao C, Lu H, Long G. Single-Atom Cobalt-Doped 2D Graphene: Electronic Design for Multifunctional Applications in Environmental Remediation and Energy Storage. Inorganics. 2025; 13(10):312. https://doi.org/10.3390/inorganics13100312
Chicago/Turabian StyleHuang, Zhongkai, Yue Zhang, Chunjiang Li, Liang Deng, Bo Song, Maolin Bo, Chuang Yao, Haolin Lu, and Guankui Long. 2025. "Single-Atom Cobalt-Doped 2D Graphene: Electronic Design for Multifunctional Applications in Environmental Remediation and Energy Storage" Inorganics 13, no. 10: 312. https://doi.org/10.3390/inorganics13100312
APA StyleHuang, Z., Zhang, Y., Li, C., Deng, L., Song, B., Bo, M., Yao, C., Lu, H., & Long, G. (2025). Single-Atom Cobalt-Doped 2D Graphene: Electronic Design for Multifunctional Applications in Environmental Remediation and Energy Storage. Inorganics, 13(10), 312. https://doi.org/10.3390/inorganics13100312







