Machine-Guided Design of Oxidation-Resistant Superconductors for Quantum Information Applications
Abstract
1. Introduction
2. Methods
3. Results and Discussion
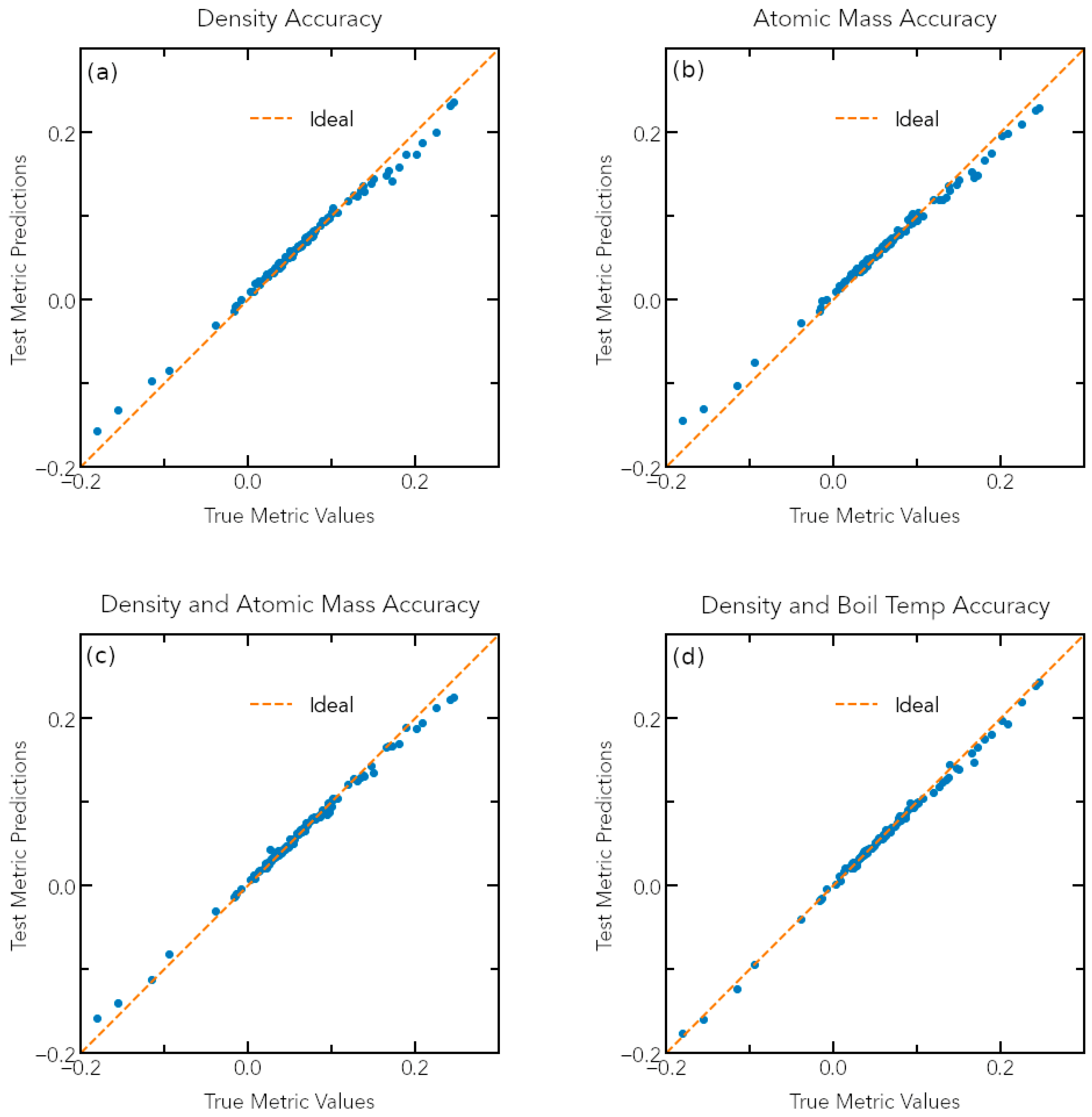
3.1. Defining and Testing an Oxidation Metric
3.2. Predicting the Oxidation Metric from Elemental Compositions
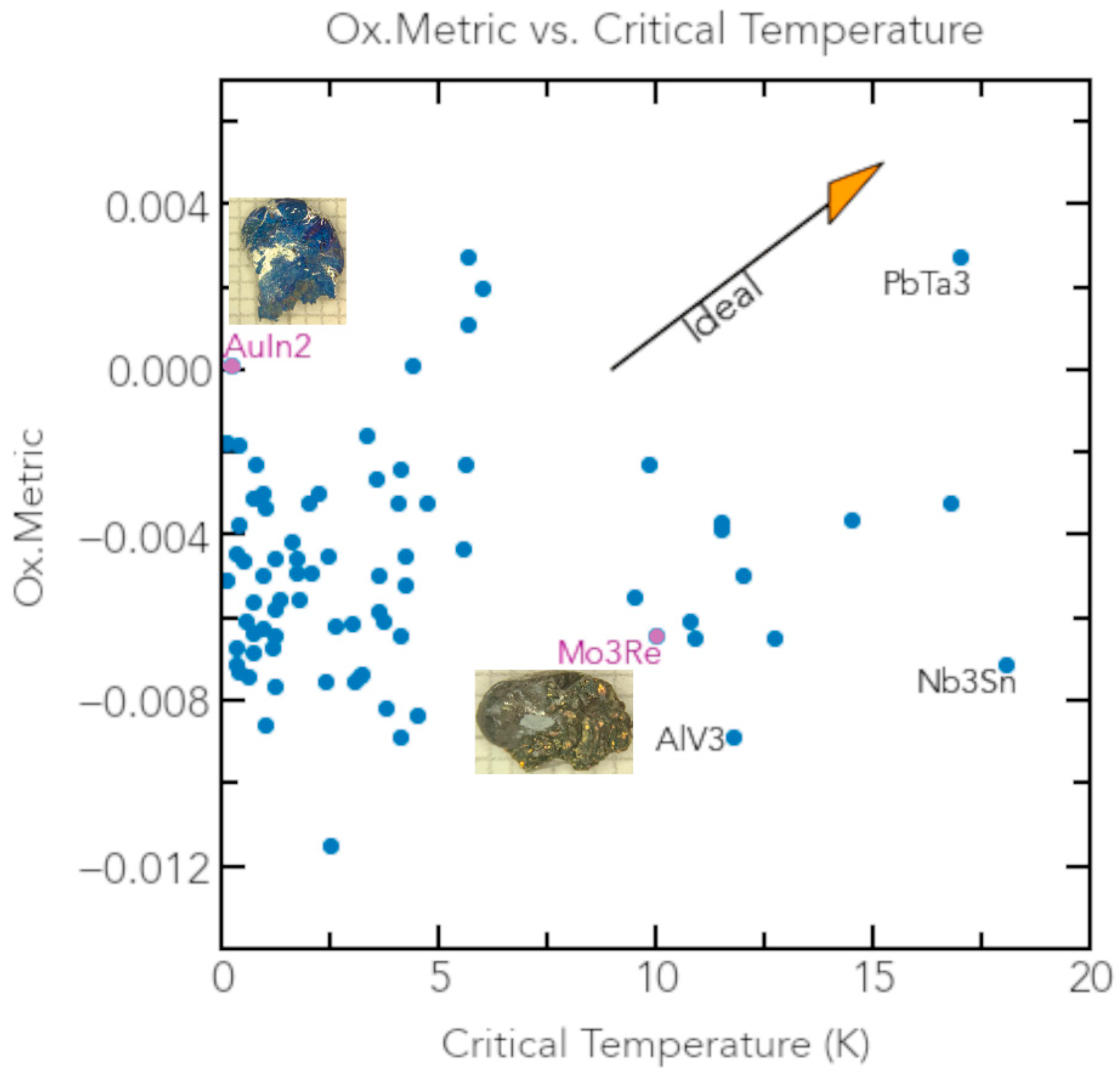
3.3. Candidate Superconductors to Enhance QISE
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Degen, C.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
- Thomas-Peter, N.; Smith, B.J.; Datta, A.; Zhang, L.; Dorner, U.; Walmsley, I. Real-World Quantum Sensors: Evaluating Resources for Precision Measurement. Phys. Rev. Lett. 2011, 107, 113603. [Google Scholar] [CrossRef]
- Kimble, H.J. The quantum internet. Nature 2008, 453, 1023–1030. [Google Scholar] [CrossRef]
- Stevenson, P.; Phenicie, C.M.; Gray, I.; Horvath, S.P.; Welinski, S.; Ferrenti, A.M.; Ferrier, A.; Goldner, P.; Das, S.; Ramesh, R.; et al. Erbium-implanted materials for quantum communication applications. Phys. Rev. B 2022, 105, 224106. [Google Scholar] [CrossRef]
- Lauk, N.; Sinclair, N.; Barzanjeh, S.; Covey, J.P.; Saffman, M.; Spiropulu, M.; Simon, C. Perspectives on quantum transduction. Quantum Sci. Technol. 2020, 5, 020501. [Google Scholar] [CrossRef]
- Rakher, M.T.; Ma, L.; Slattery, O.; Tang, X.; Srinivasan, K. Quantum transduction of telecommunications-band single photons from a quantum dot by frequency upconversion. Nat. Photonics 2010, 4, 786–791. [Google Scholar] [CrossRef]
- Dowling, J.P.; Milburn, G.J. Quantum technology: The second quantum revolution. Philos. Trans. R. Soc. A 2003, 361, 1227. [Google Scholar] [CrossRef]
- de Leon, N.P.; Itoh, K.M.; Kim, D.; Mehta, K.K.; Northup, T.E.; Paik, H.; Palmer, B.S.; Samarth, N.; Sangtawesin, S.; Steuerman, D.W. Materials challenges and opportunities for quantum computing hardware. Science 2021, 372, abb2823. [Google Scholar] [CrossRef]
- Ferrenti, A.M.; de Leon, N.P.; Thompson, J.D.; Cava, R.J. Identifying candidate hosts for quantum defects via data mining. Npj Comput. Mater. 2020, 6, 126. [Google Scholar] [CrossRef]
- Kanai, S.; Heremans, F.J.; Seo, H.; Wolfowicz, G.; Anderson, C.P.; Sullivan, S.E.; Onizhuk, M.; Galli, G.; Awschalom, D.D.; Ohno, H. Generalized scaling of spin qubit coherence in over 12,000 host materials. Proc. Nat. Acad. Sci. USA 2022, 119, e2121808119. [Google Scholar] [CrossRef]
- Sinha, M.; Pearson, T.J.; Reeder, T.R.; Vivanco, H.K.; Freedman, D.E.; Phelan, W.A.; McQueen, T.M. Introduction of spin centers in single crystals of Ba2CaWO6-d. Phys. Rev. Mater. 2019, 3, 125002. [Google Scholar] [CrossRef]
- Wolfowicz, G.; Heremans, F.J.; Anderson, C.P.; Kanai, S.; Seo, H.; Gali, A.; Galli, G.; Awschalom, D.D. Quantum guidelines for solid-state spin defects. Nat. Rev. Mater. 2021, 6, 906–925. [Google Scholar] [CrossRef]
- Place, A.P.M.; Rodgers, L.V.H.; Mundada, P.; Smitham, B.M.; Fitzpatrick, M.; Leng, Z.; Premkumar, A.; Bryon, J.; Vrajitoarea, A.; Sussman, S.; et al. New material platform for superconducting transmon qubits with coherence times exceeding 0.3 milliseconds. Nat. Commun. 2021, 12, 1779. [Google Scholar] [CrossRef] [PubMed]
- Mooij, J.E.; Orlando, T.P.; Levitov, L.; Tian, L.; van der Wal, C.H.; Lloyd, S. Josephson Persistent-Current Qubit. Science 1999, 285, 1036–1039. [Google Scholar] [CrossRef]
- Webster, J.G.; Il’ichev, E.; Oelsner, G. Superconducting Qubits. In Wiley Encyclopedia of Electrical and Electronics Engineering; Webster, J.G., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2023. [Google Scholar] [CrossRef]
- Patel, V.; Chen, W.; Pottorf, S.; Lukens, J. A fast turn-around time process for fabrication of qubit circuits. IEEE Trans. Appl. Supercond. 2005, 15, 117–120. [Google Scholar] [CrossRef]
- McLellan, R.A.; Dutta, A.; Zhou, C.; Jia, Y.; Weiland, C.; Gui, X.; Place, A.P.M.; Crowley, K.D.; Le, X.H.; Madhavan, T.; et al. Chemical profiles of the oxides on tantalum in state of the art superconducting qubits. arXiv 2023, arXiv:2301.04567. [Google Scholar]
- Crowley, K.D.; Shumiya, N.; McLellan, R.; Dutta, A.; Place, A.; Bland, M.; Chang, R.; Umbarkar, E.; Gang, Y.; Le, H.; et al. Optimizing Designs and Materials for Transmon Qubits. Bull. Am. Phys. Soc. 2023, Q75.4. Available online: https://meetings.aps.org/Meeting/MAR23/Session/Q75.4 (accessed on 25 January 2023).
- Wang, C.; Li, X.; Xu, H.; Li, Z.; Wang, J.; Yang, Z.; Mi, Z.; Liang, X.; Su, T.; Yang, C.; et al. Towards practical quantum computers: Transmon qubit with a lifetime approaching 0.5 milliseconds. Npj Quantum Inf. 2022, 8, 3. [Google Scholar] [CrossRef]
- Canfield, P.C. Still alluring and hard to predict at 100. Nat. Mater. 2011, 10, 259–261. [Google Scholar] [CrossRef]
- Sun, L.; Cava, R.J. High-entropy alloy superconductors: Status, opportunities, and challenges. Phys. Rev. Mater. 2019, 3, 090301. [Google Scholar] [CrossRef]
- Xie, Y.; Artymowicz, D.M.; Lopes, P.P.; Aiello, A.; Wang, D.; Hart, J.L.; Anber, E.; Taheri, M.L.; Zhuang, H.; Newman, R.C.; et al. A percolation theory for designing corrosion-resistant alloys. Nat. Mater. 2021, 20, 789–793. [Google Scholar] [CrossRef]
- Frankel, G.S. Pitting Corrosion of Metals: A Review of the Critical Factors. J. Electrochem. Soc. 1998, 145, 2186. [Google Scholar] [CrossRef]
- Witcomb, M.J. Oxidation of thin molybdenum-rhenium foils. J. Less Common Met. 1975, 41, 45–57. [Google Scholar] [CrossRef]
- Sims, C.T.; Craighead, C.M.; Jaffee, R.I. Physical and Mechanical Properties of Rhenium. JOM 1955, 7, 168–179. [Google Scholar] [CrossRef]
- Navrotsky, A. Progress and new directions in high temperature calorimetry revisited. Phys. Chem. Miner. 1997, 24, 222–241. [Google Scholar] [CrossRef]
- Stevanovic, V.; Lany, S.; Zhang, X.; Zunger, A. Correcting density functional theory for accurate predictions of compound enthalpies of formation: Fitted elemental-phase reference energies. Phys. Rev. B 2012, 85, 115104. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Ghemawat, S.; Irving, G.; Isard, M.; Kudlur, M.; et al. TensorFlow: A System for Large-Scale Machine Learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Designs and Implementation, Savannah, GA, USA, 2–4 November 2016. [Google Scholar]
- Stanford, C. Periodic-Table-JSON. Available online: https://github.com/Bowserinator/Periodic-Table-JSON/blob/master/PeriodicTableCSV.csv (accessed on 15 August 2022).
- Rumble, J.R. (Ed.) CRC Handbook of Chemistry and Physics, 103rd ed.; Internet Version 2022; RC Press/Taylor & Francis: Boca Raton, FL, USA, 2022; Available online: https://hbcp.chemnetbase.com/faces/contents/ContentsSearch.xhtml (accessed on 6 December 2022).
- Roscher, R.; Bohn, B.; Duarte, M.F.; Garcke, J. Explainable Machine Learning for Scientific Insights and Discoveries. IEEE Access 2020, 8, 42200–42216. [Google Scholar] [CrossRef]
- Zhong, X.; Gallagher, B.; Liu, S.; Kailkhura, B.; Hiszpanski, A.; Han, T.Y.-J. Explainable machine learning in materials science. Npj Comput. Mater. 2022, 8, 204. [Google Scholar] [CrossRef]
- Pankratov, A.L.; Revin, L.S.; Gordeeva, A.V.; Yablokov, A.A.; Kuzmin, L.S.; Il’Ichev, E. Towards a microwave single-photon counter for searching axions. Npj Quantum. Inf. 2022, 8, 61. [Google Scholar] [CrossRef]
- Lubsanov, V.; Gurtovoi, V.; Semenov, A.; Glushkov, E.; Antonov, V.; Astafiev, O. Materials for a broadband microwave superconducting single photon detector. Supercond. Sci. Technol. 2022, 35, 105013. [Google Scholar] [CrossRef]
- Kong, S.; Guevarra, D.; Gomes, C.P.; Gregoire, J.M. Materials representation and transfer learning for multi-property prediction. Appl. Phys. Rev. 2021, 8, 021409. [Google Scholar] [CrossRef]
- Pogue, E.A.; New, A.; McElroy, K.; Le, N.Q.; Pekala, M.J.; McCue, I.; Gienger, E.; Domenico, J.; Hedrick, E.; McQueen, T.M.; et al. Closed-loop machine learning for discovery of novel superconductors. arXiv 2022, arXiv:2212.11855. [Google Scholar]
- Honrao, S.J.; Yang, X.; Radhakrishnan, B.; Kuwata, S.; Komatsu, H.; Ohma, A.; Sierhuis, M.; Lawson, J.W. Discovery of novel Li SSE and anode coatings using interpretable machine learning and high-throughput multi-property screening. Sci. Rep. 2021, 11, 16484. [Google Scholar] [CrossRef] [PubMed]


| Compound | Metric | Oxide (mg/mm2) | |
|---|---|---|---|
| Set 1 | AlPt | 0.2017 | |
| AlNi | 0.1298 | ||
| Set 2 | Ni3Sn2 | 0.0769 | |
| Mn3Sn | −0.1057 | ||
| Set 3 | AlCuPt2 | 0.2372 | |
| MnSnAu | −0.1872 | ||
| Set 4 | YAlPd2 | −0.2570 | |
| YAl2Pd5 | 0.2235 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koppel, C.; Wilfong, B.; Iwanicki, A.; Hedrick, E.; Berry, T.; McQueen, T.M. Machine-Guided Design of Oxidation-Resistant Superconductors for Quantum Information Applications. Inorganics 2023, 11, 117. https://doi.org/10.3390/inorganics11030117
Koppel C, Wilfong B, Iwanicki A, Hedrick E, Berry T, McQueen TM. Machine-Guided Design of Oxidation-Resistant Superconductors for Quantum Information Applications. Inorganics. 2023; 11(3):117. https://doi.org/10.3390/inorganics11030117
Chicago/Turabian StyleKoppel, Carson, Brandon Wilfong, Allana Iwanicki, Elizabeth Hedrick, Tanya Berry, and Tyrel M. McQueen. 2023. "Machine-Guided Design of Oxidation-Resistant Superconductors for Quantum Information Applications" Inorganics 11, no. 3: 117. https://doi.org/10.3390/inorganics11030117
APA StyleKoppel, C., Wilfong, B., Iwanicki, A., Hedrick, E., Berry, T., & McQueen, T. M. (2023). Machine-Guided Design of Oxidation-Resistant Superconductors for Quantum Information Applications. Inorganics, 11(3), 117. https://doi.org/10.3390/inorganics11030117





