Abstract
In this study, we report the successful growth of single crystals of a magnetic Weyl semimetal candidate NdAlGe with the space group I41md. The crystals were grown using a floating-zone technique, which used five laser diodes, with a total power of 2 kW, as the heat source. To ensure that the molten zone was stably formed during the growth, we employed a bell-shaped distribution profile of the vertical irradiation intensity. After the nominal powder, crushed from an arc-melted ingot, was shaped under hydrostatic pressure, we sintered the feed and seed rods in an Ar atmosphere under ultra-low oxygen partial pressure (<10−26 atm) generated by an oxygen pump made of yttria-stabilized zirconia heated at 873 K. Single crystals of NdAlGe were successfully grown to a length of 50 mm. The grown crystals showed magnetic order in bulk at 13.5 K. The fundamental physical properties were characterized by magnetic susceptibility, magnetization, specific heat, thermal expansion, and electrical resistivity measurements. This study demonstrates that the magnetic order induces anisotropic magnetoelasticity, magneto-entropy, and charge transport in NdAlGe.
1. Introduction
Weyl semimetals have been rapidly advanced as a topologically nontrivial phase of matter. As the low-energy, excited quasiparticles are characterized by relativistic fermions, the electronic structures yield exotic physical phenomena such as Fermi arcs and chiral anomaly [1,2,3,4,5]. The topological Weyl semimetals can be realized when either the spatial inversion or time-reversal symmetry is broken. As well as these semimetals, magnetic topological materials have attracted much attention because the interplay between their magnetic correlations and topological electronic structures can provide rich physical properties. Novel magnetoresistance, anomalous Hall and Nernst effects, axion insulator, and chiral domain walls have been experimentally revealed in several materials [6,7,8,9]. Establishing a fundamental framework of magnetic Weyl semimetals is a demand for the next generation of spintronics applications, such as high-density and high-speed memory devices, and quantum information technology, because development of these technologies is based on the intrinsic physical properties of the Weyl semimetals [10].
The RAlT family (R: lanthanides, T: Si, Ge) with the space group I41md (No. 109) has been considered to be a candidate material in a new class of magnetic topological semimetals, because the system breaks both the spatial inversion and time-reversal symmetries [11]. The crystal structure of RAlT is shown in Figure 1. As theoretically predicted [12], the reports of topological magnetic order [13,14], topological Hall effect [15], anomalous Hall and Nernst effects [16,17,18], unusual quantum oscillatory effect [14,19,20], possible axial gauge fields [17], domain wall chirality [21], and Fermi arcs [22] have revealed that RAlT can offer rich electromagnetic properties. Since these properties can be tuned by exchanging the rare-earth elements (R) and T [17], this motivates us to systematically explore the relationship between the topology and magnetism in the RAlT family.
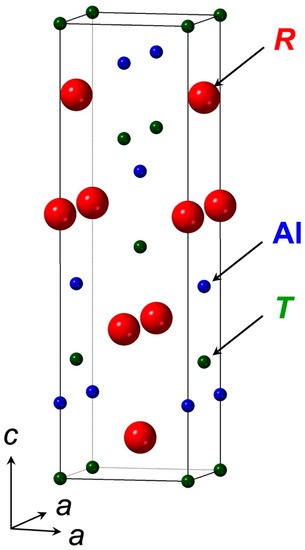
Figure 1.
Crystal structure of a magnetic Weyl semimetal candidate RAlT (R: rare earth element, T: Si, Ge), with the space group I41md (No. 109).
Thus far, a series of flux-grown crystals of RAl(Si,Ge) with R = Ce, Pr, Nd, and Sm, has been investigated [11,14,16,17,18,19,21,22,23], whereas floating-zone crystals have been examined only in CeAlGe and PrAlGe [11,15,17]. The floating-zone method offers two main advantages: (1) it minimizes the contamination level during the growth process, (2) it can obtain large crystals in cm size [24,25,26]. This enables us to deepen our knowledge of the materials through several experimental probes of the same batch of crystals. In this paper, we present the successful growth of NdAlGe crystals with the length of 50 mm by the floating-zone method, adopting laser diodes as the heat source. We demonstrate the fundamental physical properties of NdAlGe, focusing on its anisotropic response with magnetic order at 13.5 K.
2. Materials and Methods
2.1. Crystal Growth by the Floating-Zone Method
Crystal growth by using the floating-zone method is mainly composed of a polycrystalline feed-rod, molten zone, and a seed/grown crystal. As these components never touch any other part of the apparatus (including the quartz tube) throughout the growth, the growing crystal is protected from accidental contamination of any kind of impurity [24,25,26]. However, as the molten zone is fragilely supported only at the edges of the feed and seed rods, it is easily destabilized. Maintaining a stable molten zone requires great care and the optimizing of many parameters, such as the heat power required to melt the rods, the feed/seed speed, the gas atmosphere, and the applied pressure. In this study, the NdAlGe growth was kept stable by employing a laser diode as the heat source, and preparing a feed/seed rod: the latter has been successfully applied to oxides in previous studies [27]. These two stabilization techniques are described in detail below.
2.2. Laser Floating-Zone Technique
The recently developed laser-based floating-zone technique has opened a new window for crystal growth, because the laser diode enables the growth of materials that have not been obtained under optical halogen/xenon lamps connected to an infrared image furnace, which is used as the conventional heat source [28]. The laser emission can sharply define the focal point of melting, forming a narrower molten zone than can be achieved by radiation from lamps reflected at the elliptical mirrors of an image furnace [29]. Consequently, the laser-heated molten zone is homogeneous and tolerates a steeper temperature gradient at the boundary between the molten zone and the grown crystal. Most recently, the distribution profile of the vertical irradiation intensity along the length of the rod has progressed from flat to bell-shaped, where the original flat horizontal profile was maintained along the radical direction of the rod (see Figure 2 of [30]). The new bell-shaped distribution is a significant advance because it relaxes the thermal stress in the grown crystals. The modified temperature gradient imposed by the bell-shaped distribution prevents the as-grown crystals from cracking. Crystals grown under the original flat laser profile are frequently cracked by the too-sharp temperature gradient developed at the boundary [30]. Thus, modern laser technology has dramatically advanced the crystal growth field in recent years [29,30,31]. We grew single-crystalline NdAlGe using a laser diode floating-zone furnace, in which five laser diodes produce a vertical bell-shaped distribution around the focal point.
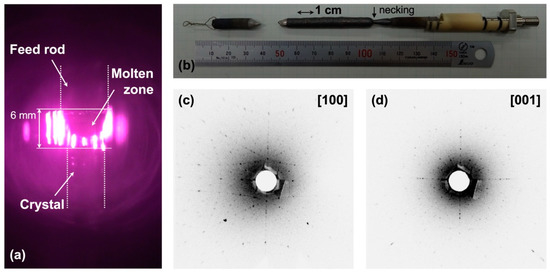
Figure 2.
(a) Picture of crystal growth of NdAlGe using a laser diode heated floating-zone furnace. Dotted white lines outline the rod and grown crystal for clarity. (b) Photograph of the grown NdAlGe crystal showing the necking formed at the beginning of the growth; (c) and (d) back-scattered Laue photographs along the [100] and [001] axes, respectively.
2.3. Preparation of Feed and Seed Rods
The floating-zone technique has grown intermetallic compounds, as well as oxides and chalcogenides [28,29,30,31,32,33,34,35]. Feed rod preparation is an important procedure for the entire growth process because the quality of the feed rods strongly affects the stability of the molten zone. In particular, the feed rods must be well-shaped, and mechanically robust with uniform density and composition [36]. The rods for intermetallic alloys have been conventionally shaped by melting the starting materials in an arc furnace or a radio-frequency induction-heating furnace. However, these methods may introduce cracks inside the resultant rods, and the cracks prevent a stable form of the molten zone during the crystal growth. An alternative advanced method has been reported, consisting of designing a modified radio-frequency induction-heating furnace [36].
We prepared a polycrystalline feed rod of NdAlGe by the following process. First, we prepared polycrystalline ingots of NdAlGe with a nominal composition via arc-melting under an Ar atmosphere (Techno Search Corp., SE-11399). The button-shaped ingot was turned over and melted several times to ensure homogeneity. The arc-melted ingots were subsequently powdered using an agate mortar and pestle. The powder with a typical weight of 18 g was packed into a tubular rubber balloon for shaping into a cylindrical rod. The powder-filled balloon was pressed under hydrostatic pressure at 40 MPa for 5 min. Here, to avoid the contamination from the as-purchased balloon of which surfaces were coated with a fine powder, we carefully cleaned both the inner and outer surfaces of the balloon before filling the NdAlGe powder, as experienced from the growth of ruthenates [27]. After their removal from the balloon, the uniform-shaped rods were sintered at 1123 K for 24 h in a tube furnace under an Ar gas flowing at 3 L/min. The Ar gas was regenerated using an oxygen pump made of yttria-stabilized zirconia heated at 873 K and circulated under an ultra-low oxygen partial pressure of less than 10−26 atm (Canon Machinery Inc., ULOCE-530) [37]. Finally, the sintered rod with a typical diameter of 6 mm was cut into two unequal parts. The longer part, with a length of 80 mm, was designated as the feed rod and the shorter part, with a length of 30 mm, was used as the seed. High-quality ruthenates were previously grown by a similar procedure [27,38,39,40,41,42,43]. This process obtained homogeneous rods with a minimal contamination risk; consequently, a series of ruthenate crystals was successfully grown under stable conditions, with no accidental cracks to the rods during irradiation in the furnace [27,39,41,42,43]. We note that the procedure can be applied to that for the growth of intermetallic alloys.
2.4. Crystal Growth
Both the feed and seed rods were set into a laser diode floating-zone furnace equipped with five 400 W GaAs-based laser heads with a wavelength of 940 nm (L-FZ 2000, Quantum Design Japan). Here, the bell-shaped distribution profile of the vertical irradiation intensity was optimized. The feed rod was suspended from a hock (made of platinum) on the upper shaft using molybdenum wire, and the seed rod was set in an alumina holder on the lower shaft. Since the growth area of the furnace was separated by a quartz tube from the outside, we could select the desired atmosphere and pressure of the gas during the crystal growth. For the growth of NdAlGe, we used a gas mixture of Ar (96%) and H2 (4%). As the laser power was smoothly increased, the bottom end of the rod started to melt. The molten rod was then connected to the top of the seed rod. The growth started with necking because a polycrystalline rod was used as the seed. Once the necking was complete, the molten zone was stabilized at both feed and seed speeds of 5 mm/h in the Ar-H2 gas mixture at 0.4 MPa and with a flow rate of 1 L/min. Applying the pressure to 0.4 MPa was in order to attempt the suppression of the evaporation during the growth. The feed and seed were rotated at 10 rpm in opposite directions to homogenize the molten liquid. The molten zone remained stable until the end of the growth without any cracking or other accidental issues arising from the sintered rods prepared by the above procedure.
2.5. Characterization
The phase purity of the crushed single crystals was checked using power X-ray diffraction under Cu Kα radiation (MiniFlex600, Rigaku) at room temperature. To cut the grown crystals along their principle crystallographic axes (the a and c axes), the orientations of the crystals were checked by a back-scattered X-ray Laue diffraction technique. The composition of the grown crystal was determined using inductively coupled plasma optical emission spectrometry (ICP-OES).
The bulk physical properties were measured down to 2 K using the options of the Physical Property Measurement System (Dynacool, Quantum Design). The temperature dependence of the magnetic susceptibility was measured in a magnetic field (H) of 0.01 T under zero-field-cooled (ZFC) and field-cooled (FC) conditions: that is, by cooling the sample before and after applying a static magnetic field, respectively. The isothermal magnetization (M) was measured between −9 and 9 T. The temperature dependence of the specific heat (CP) was measured by a relaxation method. The thermal expansion was measured by a capacitive-based technique with a temperature sweep of 0.1 K/min. In the thermal expansion measurements, we used a fused quartz dilatometer cell because fused quartz has the weakest temperature dependence among the known thermally expansive materials [44]. The magnetic entropy change (ΔSM) of H//a and H//c was determined using the thermodynamic Maxwell relation, [45], obtained from the temperature dependence of the magnetization up to 9 T under the FC process. The magnetic susceptibility, magnetization, specific heat, and thermal expansion measurements were measured on the same sample with dimensions of 2.0 mm after cutting and polishing along the a and c axes. The electrical resistivity was measured by the standard four-probe AC method, after spot-welding electrical contacts on the rectangular-shaped crystals. We also examined measurements of the a-axis resistivity of the crystals in a top-loaded dilution fridge.
3. Results and Discussion
3.1. Crystal Growth
Figure 2a shows a photo of the crystal growth of NdAlGe. The bell-shaped distribution, created by the five laser diodes, focused on the molten zone with a length of 6 mm. The rod was not cracked by the laser emission during the growth. As seen in Figure 2b, crystals with a length of 50 mm were grown under stable conditions. Additionally, there were no signs on the surface of the grown crystals that the molten liquid was dropped during the growth, suggesting that the growth was performed under stable temperature control. Figure 3 displays the powder diffraction pattern of a partially crushed crystal. All peaks were well indexed to the space group I41md [11] and no impurity phases were detected. The lattice parameters were deduced as a = 0.42245(13) nm, and c = 1.4576(6) nm, consistent with previous reports on polycrystals [46] and flux-grown crystals [23]. Figure 2c,d show the back-scattered Laue photographs of the grown crystal along the [100] and [001] directions, respectively. Clear and sharp spots from the bulk crystal confirmed that a large single crystal was obtained. From the ICP-OES results, the molar ratio of the grown crystal was determined as Nd: Al: Ge = 1.00: 0.93: 0.98. The ratio was identical along the crystal rods within the experimental error, suggesting the grown crystal is homogeneous. The aluminum deficiency reflects the evaporation of aluminum during the growth. The evaporated powder was deposited on the inside surface of the quartz tube.
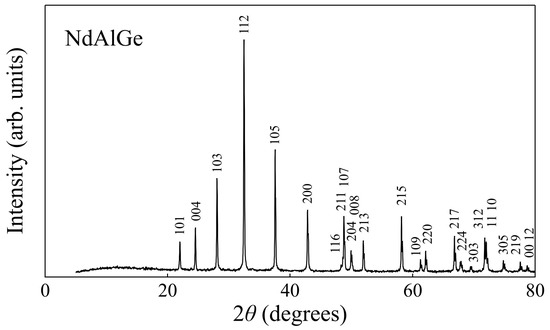
Figure 3.
Powder X-ray diffraction pattern showing the indices of crushed NdAlGe crystal (Cu Kα radiation at room temperature).
3.2. Bulk Properties of the Grown Crystal
The temperature dependences of the magnetic susceptibility (M/H) were measured in a field of 0.01 T. The results along the a and c axes are presented in Figure 4a,b, respectively. A clear magnetic transition (TM) appears at 13.5 K in both field directions. The transition temperature of our floating-zone crystal exceeded that of the flux-grown crystals [23]. Here, TM defines the temperature at which clear hysteresis occurs between the ZFC and FC processes. Such hysteresis can be attributed to pinning of the magnetic domains below the magnetic ordering temperature. We also observe a large anisotropy of the magnetic susceptibility below TM between H//a and H//c, as seen in the flux-grown crystal [23]. Figure 4c,d plot the temperature dependence of the inverse magnetic susceptibility (M/H)−1 along the a and c axes, respectively. The black lines in the figures are the fits to the Curie–Weiss law, , where kB, NA, μB are the Boltzmann constant, Avogadro’s number, and the Bohr magneton, respectively. From the fits between 100 and 300 K, the effective magnetic moments (μeff) in the paramagnetic region were μeff = 3.57 μB and 3.66 μB under H//a and H//c, respectively. These values are very close to the theoretical value of the free Nd3+ with a total angular momentum of J = 9/2, which corresponds to μeff = 3.62 μB. The results suggest a well-localized nature of the 4f electrons. The small temperature-independent term χ0, which typically represents Pauli paramagnetic and Larmor diamagnetic contributions, was 8.14 × 10−4 (4.82 × 10−4) emu/mol for H//a (H//c). The Weiss temperatures under H//a and H//c were obtained as θP = −4.4 K and +11.4 K, respectively. Here, the negative and positive θP indicate an antiferromagnetic correlation and ferromagnetic coupling, respectively.
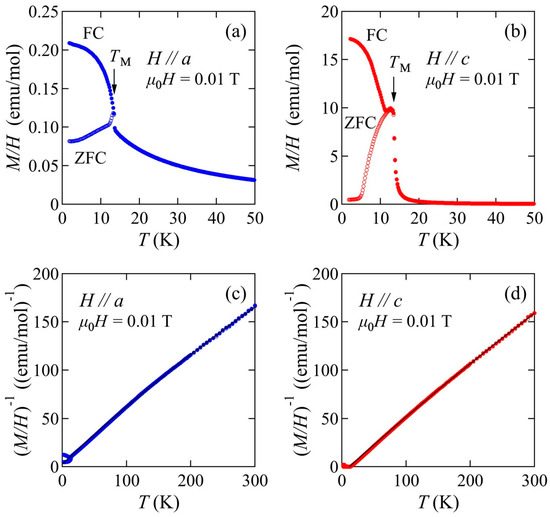
Figure 4.
Temperature dependences of the magnetic susceptibility of NdAlGe under the field along (a) H//a and (b) H//c. Measurements were performed under zero-field-cooled (open circles) and field-cooled (closed circles) processes at 0.01 T. Inverse magnetic susceptibility as a function of temperature under (c) H//a, and (d) H//c. Solid black lines are fits to the Curie–Weiss law between 100 and 300 K.
The anisotropy of the magnetic property was observed by the isothermal magnetization at 2 K under H//a and H//c up to 9 T (Figure 5a). Figure 5b enlarges the low-field region to emphasize the obvious hysteresis under H//c. The overall behavior is similar to that observed in flux-grown crystals, in which measurements were performed up to 30 T [23]. The magnetization under H//c shows a clear hysteresis with a remnant magnetization and a small coercive field of 0.07 T, indicating magnetic order with a spontaneous magnetization. In contrast, the a-axis magnetization shows no clear hysteresis and is nearly 100 times smaller than the c-axis magnetization at 0.3 T. The a-axis magnetization is linear in H up to 2 T and slightly deviates upwards at higher field. The strong anisotropy suggests that NdAlGe has an Ising-like magnetism with the c axis being the easy axis.
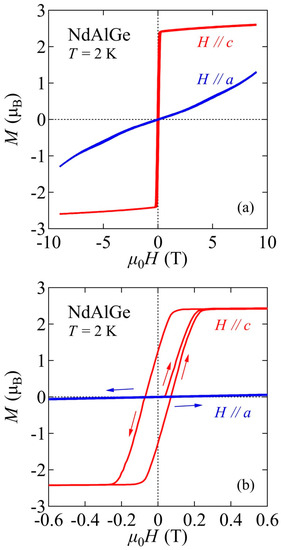
Figure 5.
(a) Isothermal magnetization of NdAlGe at 2 K under H//a, and H//c between –9 and +9 T. (b) Zoom-in of the low-field region between –0.6 and +0.6 T to emphasize the hysteresis under H//c.
Figure 6a,b plot the isothermal magnetization of NdAlGe under H//a, and H//c, respectively, at several temperatures across the TM. These data were taken after field cooling. Under H//c, the rapid increase in magnetization at low fields was suppressed as the temperature increased. The remnant magnetization disappeared at TM. Under H//a, the upward behavior observed at 2 K was suppressed as the temperature was raised.
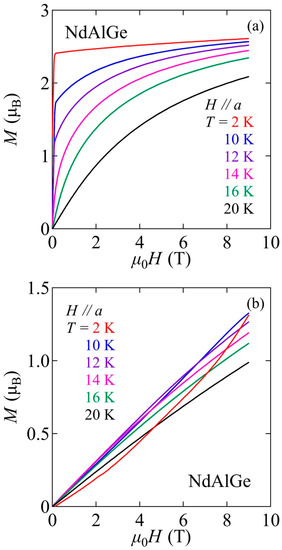
Figure 6.
Isothermal magnetization curves of NdAlGe under (a) H//a, and (b) H//c at temperatures below and above the transition temperature at 13.5 K. The data were taken under the field-cooled process.
Figure 7a shows the temperature dependence of the specific heat (CP) without field. We can see a well-defined lambda-type anomaly, as seen in the sister materials RAl(Ge,Si) [14,18]. A second-ordered-like transition temperature at 13.5 K, defined as the midpoint of the jump, corresponds accurately to the onset of the magnetic transition at TM observed in the magnetic susceptibility measurements. Judging from the result, the observed phase transition in NdAlGe occurs in bulk. We mention that only a single peak with a sharp transition width of less than 0.4 K is seen; no other transitions were detectable at our experimental resolution down to 2 K. Figure 7b plots the temperature dependence of the specific heat divided by temperature (CP/T). The ΔCP/T jumped by 0.69 J/mol K2 at TM.
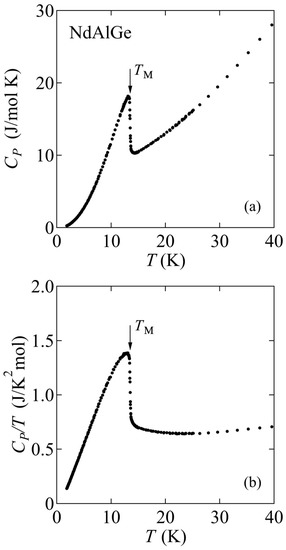
Figure 7.
(a) Temperature dependence of specific heat (CP) of NdAlGe under zero field. (b) Specific heat divided by temperature (CP/T) plotted against temperature.
Thermodynamic phase transitions can be detected through thermal expansion experiments, which provide the directional information along the independent crystallographic axes [47]. In contrast, specific heat measurements probe the overall information on phase transitions, as shown in Figure 7. Figure 8a shows the linear thermal expansions , where the index i refers to the a and c axes, as functions of temperature. The inset shows the temperature-dependent up to 300 K. Both and show a clear kink (not a discontinuous jump) at TM = 13.5 K, suggesting a second-ordered phase transition. Moreover, the results are highly anisotropic: on cooling, the thermal expansions along the a and c axes increase and decrease below TM, respectively. This result is possibly attributable to the anisotropic magnetic correlations of this material, as discussed for NdAlSi [14]. Figure 8b presents the temperature dependence of the linear thermal expansion coefficient along the a and c axes. Also shown is the volume expansion coefficient αv deduced as 2αa + αc, considering the tetragonal crystal symmetry of this material. Anomalies in both αa and αc correspond to the magnetic transition temperature at TM, suggesting a strong magnetoelastic coupling in NdAlGe.
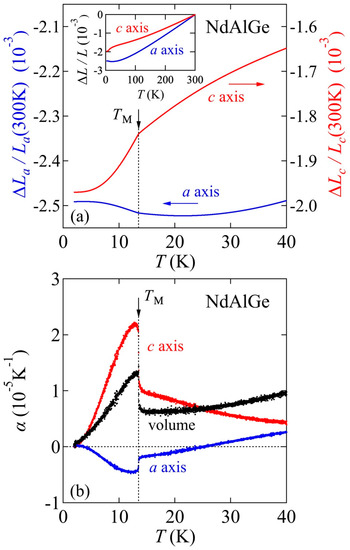
Figure 8.
(a) Temperature dependences of (a) thermal expansion and (b) linear thermal expansion coefficient along the a and c axes. Indexed by i. The volume expansion coefficient αv, obtained as 2αa + αc considering the tetragonal crystal symmetry of NdAlGe, is also shown.
For a second-ordered phase transition, the uniaxial and hydrostatic pressure dependence of the magnetic transition temperature can be determined by the Ehrenfest relation [47] , where Vm = 3.92 × 10−5 m3/mol is the molar volume, Δ(CP/T) defines the jump in the specific heat divided by the temperature (CP/T) (Figure 7b), and Δαi is the jump in the thermal expansion coefficient at TM (Figure 8b). Using our experimental results with Δ(CP/T) = 0.69 J/mol K2, Δαa = −2.2 × 10−6 K−1, and Δαc = +1.2 × 10−5 K−1, we obtained = −0.13 K/GPa, and = +0.68 K/GPa under the uniaxial pressure along the a and c axes, respectively. This result suggests that uniaxial pressure along the c axis stabilizes the magnetic ordered state, whereas that along the a axis suppresses this state. In addition, the hydrostatic pressure dependence of the magnetic transition temperature was obtained as +0.42 K/GPa. The obtained hydrostatic pressure dependence on TM in NdAlGe is close to that in the sister compounds CeAlGe, and CeAlSi with +0.64 K/GPa, and +0.62 K/GPa, respectively, and the signs of all dependencies are positive although the magnetically easy axis in these Ce-based materials reportedly aligns perpendicular to the c axis. [20,21]. The same trend of was seen in a substitution study of PrAl(Ge1-xSix); specifically, the magnetic ordered temperature monotonically increased with shrinkage as Si was substituted for Ge [18].
The magnetocaloric effect, which determines the correlation between the ordered magnetism and entropy, is worth exploring in magnetic materials. The magnetocaloric effect is a consequence of temperature change (heating or cooling) in a magnetic material under adiabatic conditions when an external magnetic field is applied and removed [48]. The efficiency of the magnetocaloric effect can be evaluated through the magnetic entropy change ΔSM, defined as the entropy difference between the magnetized material (S(H)) and demagnetized material (S(0). Formally, ΔSM = S(H)–S(0) [45]. The magnetocaloric effect is usually examined in ferromagnetic materials because such materials should, in principle, gain larger ΔSM through the demagnetized and magnetized process than non-ferromagnetic materials [49,50,51]. Although evaluating the ΔSM of NdAlGe with Ising-like magnetization under H//c (Figure 5a) is an interesting proposition, the ΔSM of Nd-containing materials are rarely considered because the magnetic moments of materials containing light rare-earth elements are smaller than those of other magnetocaloric materials containing heavy rare-earth elements such as Ho, Gd or transition metal Fe [49,50,51].
To evaluate the ΔSM of NdAlGe, we first show the temperature dependences of the magnetization (M vs. T) of NdAlGe under H//a and H//c (Figure 9a,b, respectively), under various magnetic fields up to 9 T. These measurements were performed under the FC process. Figure 9c,d present the magnetic entropy changes (ΔSM) as functions of temperature under H//a, and H//c, respectively, for various fields up to 9 T. Here, the ΔSM was evaluated from the above-mentioned Maxwell relation. Under H//c, the ΔSM shows a single minimum around TM. The negative magnetic entropy change indicates that the entropy was released/gained under magnetization/demagnetization in NdAlGe. When the field was changed from zero to 5 and 9 T, the ΔSM values were −4.2 and −5.7 J/K mol, respectively. The value at 5 T was comparable to that in a series of ternary systems summarized in a review article [52], which focused mainly on materials containing heavy rare-earth elements. In contrast, the ΔSM under H//a peaked at low temperatures and became negative at higher temperatures. Similar sign-changing behavior is seen in Ni-Mn-Sn alloys [53]. When the field changed to 9 T, the minimum value of ΔSM under H//a was −1.3 J/K mol. The positive and negative behavior of ΔSM under H//a, and the smaller values than under H//c might reflect the anisotropic magnetic coupling.
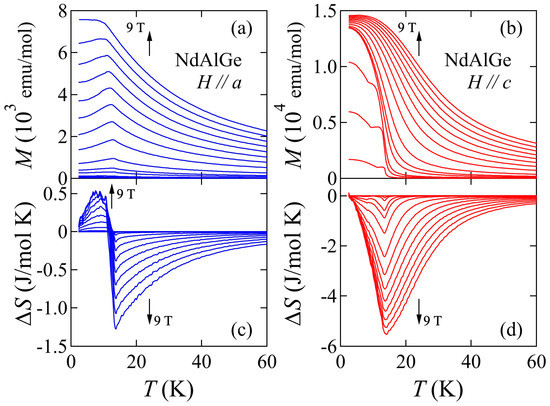
Figure 9.
Temperature dependence of magnetization of NdAlGe for (a) H//a and (b) H//c under the field-cooled process. The applied magnetic fields are 0.01, 0.05, 0.1, 0.3, 0.5, 1, 2, 3, 4, 5, 6, 7, 8, and 9 T. The magnetic entropy change ΔSM as a function of temperature for (c) H//a, and (d) H//c.
The floating-zone technique obtained the large-sized NdAlGe crystals in which we could investigate the directional electrical charge transport properties. Figure 10a presents the temperature dependences of the electrical resistivities ρa and ρc as the current flow along the a and c axes, respectively. Figure 10b enlarges the low temperature region. Both ρa and ρc exhibit metallic behaviors with sublinear temperature dependence at a high temperature. We also mention that the resistive behavior in ρa was identical along the radial direction in the grown crystal, suggesting there were homogeneous crystals in the ingot. The residual resistivity ratios (RRRs) were approximately 1.5 and 1.4, respectively. Comparable RRRs were reported in floating-zone crystals CeAlGe and PrAlGe, in which the materials were almost stoichiometric [11,17]. We also mention that the RRRs in our crystals were lower than those seen in the flux-grown crystals [14,16,18,21]. The resistive anisotropy of NdAlGe (ρc/ρa~2) was almost temperature-independent in the paramagnetic region (above TM), but the behaviors of ρa and ρc contrasted below TM; specifically, ρa and ρc were suppressed and enhanced below TM, respectively. In typical magnetic materials, in general, spin scattering and/or reconstruction of the Brillouin zone can influence the scattering rate of the conducting carriers when the system enters the ordered state [54,55]. Suppression of the scattering rate by spin scattering is frequently seen in the magnetic materials, for example, in the ferromagnetic oxide SrRuO3 [42]. Meanwhile, Brillouin zone reconstruction may enhance the resistivity, as observed in a pressure-induced antiferromagnetic ordered state in FeSe [56]. In NdAlGe, the upturn seen in ρc is possibly attributable to a reconstructed zone, whereas the downturn in ρa below TM might be dominated by suppression of the spin scattering.
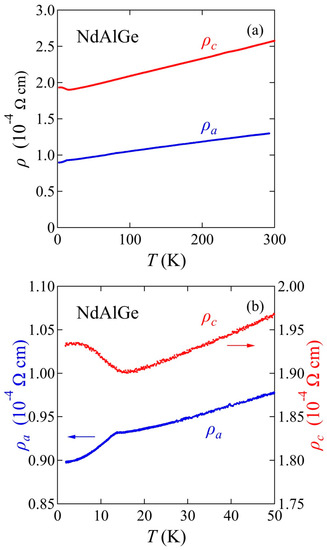
Figure 10.
(a) Temperature dependence of electrical resistivities ρa, and ρc under the current flow along the a axis and c axes, respectively. (b) Low temperature resistivities for capturing the anisotropic behavior below the transition temperature.
4. Summary
In summary, we successfully grew single crystals of a magnetic Weyl semimetal candidate NdAlGe using the laser diode heated floating-zone technique. Five laser diodes produced a bell-shaped distribution profile of vertical irradiation intensity. After the nominal powder, crushed from an arc-melted ingot, was shaped under hydrostatic pressure, we sintered the feed and seed rods under Ar gas at ultra-low oxygen partial pressure (<10−26 atm). The crystals were grown under the stable conditions of the molten zone without any cracks on the rods. We finally obtained a large-sized crystal with a length of 50 mm. When examined with bulk-sensitive probes, the grown crystals showed magnetic order at 13.5 K. The ordered state presented Ising-like behavior. The magnetic entropy largely changed when a magnetic field was applied along the easy axis (the c axis). The linear thermal expansion also confirmed anisotropic responses at the magnetic transition temperature. Applying the thermodynamic Ehrenfest relation based on our experimental data, we revealed the anisotropic uniaxial pressure dependence of the magnetic transition temperature. The hydrostatic pressure dependence on the magnetic transition temperature in NdAlGe was positively signed, as observed in sister materials of NdAlGe. Anisotropic charge transport below the ordered temperature probably originates from the scattering mechanism.
Author Contributions
N.K. and T.T. conceived the project. N.K. grew and characterized the crystals. T.K., M.H. and H.Y. performed the ICP-OES. S.U. joined the discussion and contributed to the manuscript preparation. wrote the manuscript with input from all coauthors. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by a KAKENHI Grants-in-Aids for Scientific Research (Grant Nos. 17H06136, 18K0475, 21H01033, and 22K19093), and a Core-to-Core Program (No. JPJSCCA20170002) from the Japan Society for the Promotion of Science (JSPS), and a JST-Mirai Program (Grant No. JPMJMI18A3).
Data Availability Statement
The data supporting the findings of this study are available from the corresponding authors upon reasonable request.
Acknowledgments
We acknowledge Yoshio Kaneko for fruitful advice about the laser floating-zone furnace, and Takeshi Shimada, Noritaka Kimura, John McArthur, Naohiro Kaga, Yuta Maegawa, Tohru Nagasawa, and Nobuyuki Ochiai for technical support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, Z.; Zhang, S.-C. Chiral Anomaly, Charge Density Waves, and Axion Strings from Weyl Semimetals. Phys. Rev. B 2013, 87, 161107. [Google Scholar] [CrossRef]
- Burkov, A.A. Topological Semimetals. Nat. Mater. 2016, 15, 1145. [Google Scholar] [CrossRef] [PubMed]
- Yan, B.; Felser, C. Topological Materials: Weyl Semimetals. Annu. Rev. Condens. Matter Phys. 2017, 8, 337. [Google Scholar] [CrossRef]
- Armitage, N.P.; Mele, E.J.; Vishwanath, A. Weyl and Dirac Semimetals in Three-Dimensional Solids. Rev. Mod. Phys. 2018, 90, 015001. [Google Scholar] [CrossRef]
- Nagaosa, N.; Morimoto, T.; Tokura, Y. Transport, Magnetic and Optical Properties of Weyl Materials. Nat. Rev. Mater. 2020, 5, 621. [Google Scholar] [CrossRef]
- Otrokov, M.M.; Klimovskikh, I.I.; Bentmann, H.; Estyunin, D.; Zeugner, A.; Aliev, Z.S.; Gaß, S.; Wolter, A.U.B.; Koroleva, A.V.; Shikin, A.M.; et al. Prediction and Observation of an Antiferromagnetic Topological Insulator. Nature 2019, 576, 416. [Google Scholar] [CrossRef]
- Rienks, E.D.L.; Wimmer, S.; Sánchez-Barriga, J.; Caha, O.; Mandal, P.S.; Růžička, J.; Ney, A.; Steiner, H.; Volobuev, V.V.; Groiss, H.; et al. Large Magnetic Gap at the Dirac Point in Bi2Te3/MnBi2Te4 Heterostructures. Nature 2019, 576, 423. [Google Scholar] [CrossRef]
- Bernevig, B.A.; Felser, C.; Beidenkopf, H. Progress and Prospects in Magnetic Topological Materials. Nature 2022, 603, 41. [Google Scholar] [CrossRef]
- He, Q.L.; Hughes, T.L.; Armitage, N.P.; Tokura, Y.; Wang, K.L. Topological Spintronics and Magnetoelectronics. Nat. Mater. 2022, 21, 15. [Google Scholar] [CrossRef]
- Giustino, F.; Lee, J.H.; Trier, F.; Bibes, M.; Winter, S.M.; Valentí, R.; Son, Y.-W.; Taillefer, L.; Heil, C.; Figueroa, A.I.; et al. The 2021 Quantum Materials Roadmap. J. Phys. Mater. 2020, 3, 042006. [Google Scholar] [CrossRef]
- Puphal, P.; Mielke, C.; Kumar, N.; Soh, Y.; Shang, T.; Medarde, M.; White, J.S.; Pomjakushina, E. Bulk Single-Crystal Growth of the Theoretically Predicted Magnetic Weyl Semimetals RAlGe (R = Pr, Ce). Phys. Rev. Mater. 2019, 3, 024204. [Google Scholar] [CrossRef]
- Chang, G.; Singh, B.; Xu, S.-Y.; Bian, G.; Huang, S.-M.; Hsu, C.-H.; Belopolski, I.; Alidoust, N.; Sanchez, D.S.; Zheng, H.; et al. Magnetic and Noncentrosymmetric Weyl Fermion Semimetals in the RAlGe Family of Compounds (R = Rare Earth). Phys. Rev. B 2018, 97, 041104. [Google Scholar] [CrossRef]
- Yao, X.; Verma, R.; Graf, D.E.; Yang, H.Y.; Bahrami, F.; Zhang, R.; Aczel, A.A.; Subedi, S.; Torchinsky, D.H.; Sun, J.; et al. Topological Spiral Magnetism in the Weyl Semimetal SmAlSi. arXiv 2022, arXiv:2206.05121. [Google Scholar]
- Gaudet, J.; Yang, H.-Y.; Baidya, S.; Lu, B.; Xu, G.; Zhao, Y.; Rodriguez-Rivera, J.A.; Hoffmann, C.M.; Graf, D.E.; Torchinsky, D.H.; et al. Weyl-Mediated Helical Magnetism in NdAlSi. Nat. Mater. 2021, 20, 1650. [Google Scholar] [CrossRef]
- Puphal, P.; Pomjakushin, V.; Kanazawa, N.; Ukleev, V.; Gawryluk, D.J.; Ma, J.; Naamneh, M.; Plumb, N.C.; Keller, L.; Cubitt, R.; et al. Topological Magnetic Phase in the Candidate Weyl Semimetal CeAlGe. Phys. Rev. Lett. 2020, 124, 017202. [Google Scholar] [CrossRef]
- Meng, B.; Wu, H.; Qiu, Y.; Wang, C.; Liu, Y.; Xia, Z.; Yuan, S.; Chang, H.; Tian, Z. Large Anomalous Hall Effect in Ferromagnetic Weyl Semimetal Candidate PrAlGe. APL Mater. 2019, 7, 051110. [Google Scholar] [CrossRef]
- Destraz, D.; Das, L.; Tsirkin, S.S.; Xu, Y.; Neupert, T.; Chang, J.; Schilling, A.; Grushin, A.G.; Kohlbrecher, J.; Keller, L.; et al. Magnetism and Anomalous Transport in the Weyl Semimetal PrAlGe: Possible Route to Axial Gauge Fields. NPJ Quantum Mater. 2020, 5, 5. [Google Scholar] [CrossRef]
- Yang, H.-Y.; Singh, B.; Lu, B.; Huang, C.-Y.; Bahrami, F.; Chiu, W.-C.; Graf, D.; Huang, S.-M.; Wang, B.; Lin, H.; et al. Transition from Intrinsic to Extrinsic Anomalous Hall Effect in the Ferromagnetic Weyl Semimetal PrAlGe1-xSix. APL Mater. 2020, 8, 011111. [Google Scholar] [CrossRef]
- Wang, J.-F.; Dong, Q.X.; Huang, Y.F.; Wang, Z.S.; Guo, Z.P.; Wang, Z.J.; Ren, Z.A.; Li, G.; Sun, P.J.; Dai, X.; et al. Temperature Dependent Quantum Oscillations at a Constant Magnetic Field in a Magnetic Weyl Semimetal. arXiv 2022, arXiv:2201.06412, 06412. [Google Scholar]
- Piva, M.M.; Souza, J.C.; Brousseau-Couture, V.; Pakuszewski, K.R.; John, J.K.; Adriano, C.; Côté, M.; Pagliuso, P.G.; Nicklas, M. Tuning the Nontrivial Topological Properties of the Weyl Semimetal CeAlSi. arXiv 2021, arXiv:2111.05742, 05742. [Google Scholar]
- He, X.; Li, Y.; Zeng, H.; Zhu, Z.; Cao, C.; Luo, Y. Pressure Tuning Domain-Wall Chirality in Noncentrosymmetric Magnetic Weyl Semimetal CeAlGe. arXiv 2022, arXiv:2207.08442. [Google Scholar]
- Sanchez, D.S.; Chang, G.; Belopolski, I.; Lu, H.; Yin, J.-X.; Alidoust, N.; Xu, X.; Cochran, T.A.; Zhang, X.; Bian, Y.; et al. Observation of Weyl Fermions in a Magnetic Non-centrosymmetric Crystal. Nat. Commun. 2020, 11, 3356. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Liu, W.; Rahman, A.U.; Meng, F.; Ling, L.; Xi, C.; Tong, W.; Bai, Y.; Tian, Z.; Zhong, Y.; et al. Field-Induced Tricritical Phenomenon and Magnetic Structures in Magnetic Weyl Semimetal Candidate NdAlGe. New J. Phys. 2022, 24, 013010. [Google Scholar] [CrossRef]
- Schmehr, J.L.; Wilson, S.D. Active Crystal Growth Techniques for Quantum Materials. Annu. Rev. Mater. Res. 2017, 47, 153. [Google Scholar] [CrossRef]
- Basov, D.N.; Averitt, R.D.; Hsieh, D. Towards Properties on Demand in Quantum Materials. Nat. Mater. 2017, 16, 1077. [Google Scholar] [CrossRef]
- Samarth, N. Quantum Materials Discovery from a Synthesis Perspective. Nat. Mater. 2017, 16, 1068. [Google Scholar] [CrossRef]
- Bobowski, J.S.; Kikugawa, N.; Miyoshi, T.; Suwa, H.; Xu, H.-S.; Yonezawa, S.; Sokolov, D.A.; Mackenzie, A.P.; Maeno, Y. Improved Single-Crystal Growth of Sr2RuO4. Condens. Matter 2019, 4, 6. [Google Scholar] [CrossRef]
- Ito, T.; Ushiyama, T.; Yanagisawa, Y.; Tomioka, Y.; Shindo, I.; Yanase, A. Laser-Diode-Heated Floating Zone (LDFZ) Method Appropriate to Crystal Growth of Incongruently Melting Materials. J. Cryst. Growth 2013, 363, 264. [Google Scholar] [CrossRef]
- Rey-García, F.; Ibáñez, R.; Angurel, L.A.; Costa, F.M.; de la Fuente, G.F. Laser Floating Zone Growth: Overview, Singular Materials, Broad Applications, and Future Perspectives. Crystals 2020, 11, 38. [Google Scholar] [CrossRef]
- Kaneko, Y.; Tokura, Y. Floating Zone Furnace Equipped with a High Power Laser of 1 kW Composed of Five Smart Beams. J. Cryst. Growth 2020, 533, 125435. [Google Scholar] [CrossRef]
- Admasu, A.S.; Vavilapalli, D.S. The Laser-Diode Heated Floating Zone Method for Automated Optimal Synthesis of Refractory Oxides and Alloys. arXiv 2021, arXiv:2103.05587. [Google Scholar]
- Neubauer, A.; Jonietz, F.; Meven, M.; Georgii, R.; Brandl, G.; Behr, G.; Böni, P.; Pfleiderer, C. Optical Floating Zone Growth of High-Quality Cu2MnAl Single Crystals. Nucl. Instrum. Methods Phys. Res. A 2012, 688, 66. [Google Scholar] [CrossRef]
- Brunt, D.; Hatnean, M.C.; Petrenko, O.A.; Lees, M.R.; Balakrishnan, G. Single-Crystal Growth of Metallic Rare-Earth Tetraborides by the Floating-Zone Technique. Crystals 2019, 9, 211. [Google Scholar] [CrossRef]
- Amigó, M.L.; Maljuk, A.; Manna, K.; Stahl, Q.; Felser, C.; Hess, C.; Wolter, A.U.B.; Geck, J.; Seiro, S.; Büchner, B. Laser-Assisted Floating Zone Growth of BaFe2S3 Large-Sized Ferromagnetic-Impurity-Free Single Crystals. Crystals 2021, 11, 758. [Google Scholar] [CrossRef]
- Sinha, M.; Vivanco, H.K.; Wan, C.; Siegler, M.A.; Stewart, V.J.; Pogue, E.A.; Pressley, L.A.; Berry, T.; Wang, Z.; Johnson, I.; et al. Twisting of 2D Kagomé Sheets in Layered Intermetallics. ACS Cent. Sci. 2021, 7, 1381. [Google Scholar] [CrossRef] [PubMed]
- Bauer, A.; Neubauer, A.; Münzer, W.; Regnat, A.; Benka, G.; Meven, M.; Pedersen, B.; Pfleiderer, C. Ultra-High Vacuum Compatible Induction-Heated Rod Casting Furnace. Rev. Sci. Instrum. 2016, 87, 063909. [Google Scholar] [CrossRef]
- Nagai, I.; Shirakawa, N.; Ikeda, S.-I.; Iwasaki, R.; Nishimura, H.; Kosaka, M. Highest Conductivity Oxide SrMoO3 Grown by a Floating-Zone Method under Ultralow Oxygen Partial Pressure. Appl. Phys. Lett. 2005, 87, 024105. [Google Scholar] [CrossRef]
- Mao, Z.Q.; Maeno, Y.; Fukazawa, H. Crystal Growth of Sr2RuO4. Mater. Res. Bull. 2000, 35, 1813. [Google Scholar] [CrossRef]
- Perry, R.S.; Maeno, Y. Systematic Approach to the Growth of High-Quality Single Crystals of Sr3Ru2O7. J. Cryst. Growth 2004, 271, 134. [Google Scholar] [CrossRef]
- Zhou, M.; Hooper, J.; Fobes, D.; Mao, Z.Q.; Golub, V.; O’Connor, C.J. Electronic and Magnetic Properties of Triple-Layered Ruthenate Sr4Ru3O10 Single Crystals Grown by a Floating-Zone Method. Mater. Res. Bull. 2005, 40, 942. [Google Scholar] [CrossRef]
- Kikugawa, N.; Balicas, L.; Mackenzie, A.P. Physical Properties of Single-Crystalline CaRuO3 Grown by a Floating-Zone Method. J. Phys. Soc. Jpn. 2009, 78, 014701. [Google Scholar] [CrossRef]
- Kikugawa, N.; Baumbach, R.; Brooks, J.S.; Terashima, T.; Uji, S.; Maeno, Y. Single-Crystal Growth of a Perovskite Ruthenate SrRuO3 by the Floating-Zone Method. Cryst. Growth Des. 2015, 15, 5573. [Google Scholar] [CrossRef]
- Kikugawa, N.; Sokolov, D.A.; Nagasawa, T.; Mackenzie, A.P. Single-Crystal Growth of Sr2RuO4 by the Floating-Zone Method Using an Infrared Image Furnace with Improved Halogen Lamps. Crystals 2021, 11, 392. [Google Scholar] [CrossRef]
- Martien, D.; Williamsen, M.; Spagna, S.; Black, R.; DaPron, T.; Hogan, T.; Snow, D. An Ultrasensitive Differential Capacitive Dilatometer. IEEE Trans. Magn. 2019, 55, 1. [Google Scholar] [CrossRef]
- Gschneidner, K.A.; Pecharsky, V.K. Magnetocaloric Materials. Annu. Rev. Mater. Sci. 2000, 30, 387. [Google Scholar] [CrossRef]
- Wang, T.; Guo, Y.; Wang, C.; Yang, S. Correlation between Non-centrosymmetic Structure and Magnetic Properties in Weyl Semimetal NdAlGe. Solid State Commun. 2020, 321, 114041. [Google Scholar] [CrossRef]
- Barron, T.H.K.; White, G.K. Heat Capacity and Thermal Expansion at Low Temperatures; Kluwer Academic/Plenum: New York, NY, USA, 1999. [Google Scholar]
- Tishin, A.M. Magnetocaloric Effect: From Theory to Practice, in Encyclopedia of Materials: Science and Technology; Buschow, K.H.J., Cahn, R.W., Flemings, M.C., Ilschner, B., Kramer, E.J., Mahajan, S., Veyssière, P., Eds.; Elsevier: Oxford, UK, 2001; pp. 5035–5041. [Google Scholar]
- Patra, M.; Majumdar, S.; Giri, S.; Xiao, Y.; Chatterji, T. Magnetic, Magnetocaloric and Magnetoresistive Properties of Cubic Laves Phase HoAl2 Single Crystal. J. Phys. Condens. Matter 2014, 26, 046004. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. Giant Magnetocaloric Effect in Gd5(Si2Ge2). Phys. Rev. Lett. 1997, 78, 4494. [Google Scholar] [CrossRef]
- Fujieda, S.; Fujita, A.; Fukamichi, K. Large Magnetocaloric Effect in La(FexSi1-x)13 Itinerant-Electron Metamagnetic Compounds. Appl. Phys. Lett. 2002, 81, 1276. [Google Scholar] [CrossRef]
- Gupta, S.; Suresh, K.G. Review on Magnetic and Related Properties of RTX Compounds. J. Alloys Compd. 2015, 618, 562. [Google Scholar] [CrossRef]
- Krenke, T.; Duman, E.; Acet, M.; Wassermann, E.F.; Moya, X.; Mañosa, L.; Planes, A. Inverse Magnetocaloric Effect in Ferromagnetic Ni-Mn-Sn Alloys. Nat. Mater. 2005, 4, 450. [Google Scholar] [CrossRef] [PubMed]
- Van Peski-Tinbergen, T.; Dekker, A.J. Spin-Dependent Scattering and Resistivity of Magnetic Metals and Alloys. Physica 1963, 29, 917. [Google Scholar] [CrossRef]
- Maki, S.; Adachi, K. Antiferromagnetism and Weak Ferromagnetism of Disordered Bcc Cr-Mn Alloys. J. Phys. Soc. Jpn. 1979, 46, 1131. [Google Scholar] [CrossRef]
- Terashima, T.; Kikugawa, N.; Kasahara, S.; Watashige, T.; Shibauchi, T.; Matsuda, Y.; Wolf, T.; Böhmer, A.E.; Hardy, F.; Meingast, C.; et al. Pressure-Induced Antiferromagnetic Transition and Phase Diagram in FeSe. J. Phys. Soc. Jpn. 2015, 84, 063701. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).