High-Sensitivity Fiber Fault Detection Method Using Feedback-Delay Signature of a Modulated Semiconductor Laser
Abstract
:1. Introduction
2. Methods
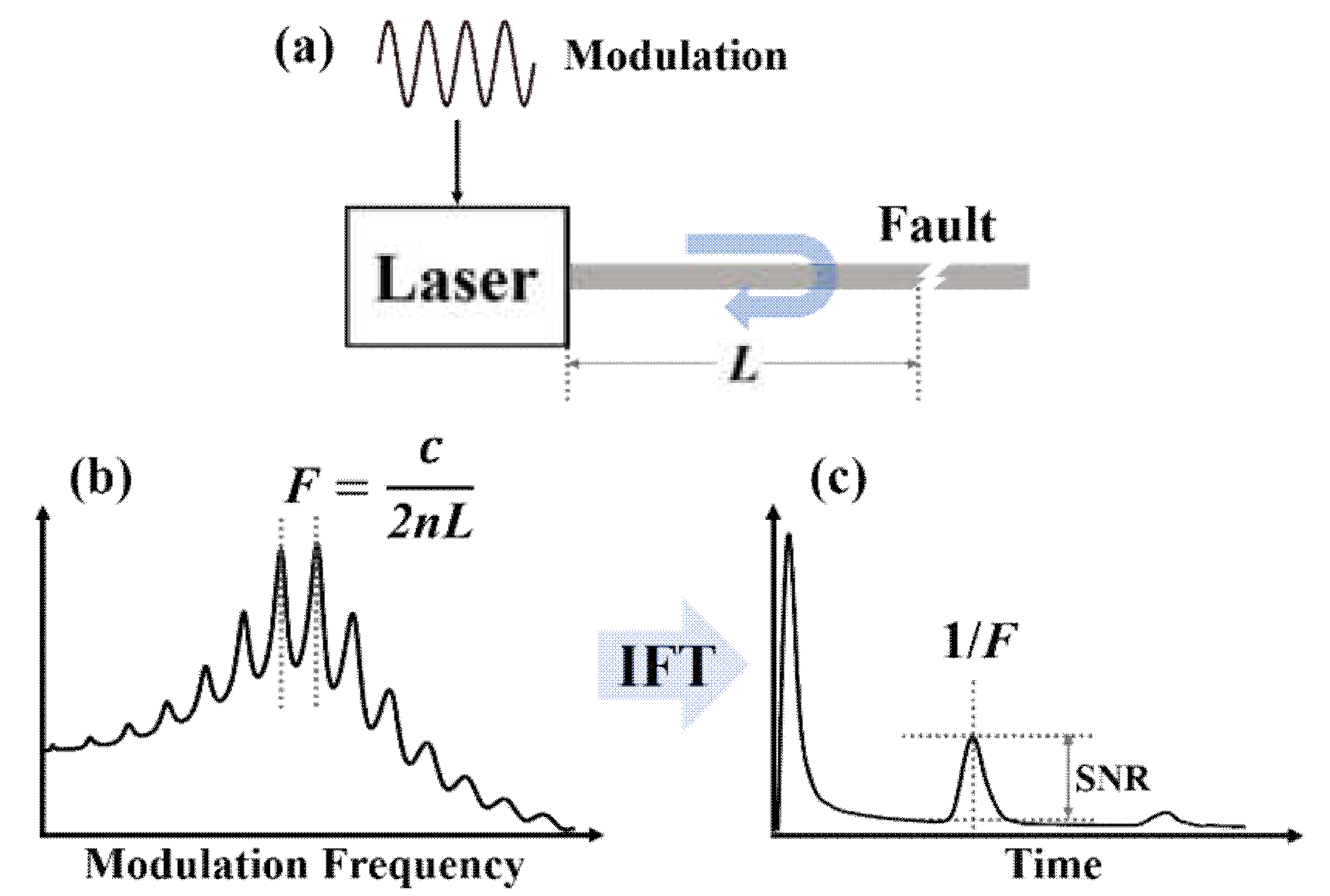
2.1. Principle
2.2. Theoretical Model
3. Results
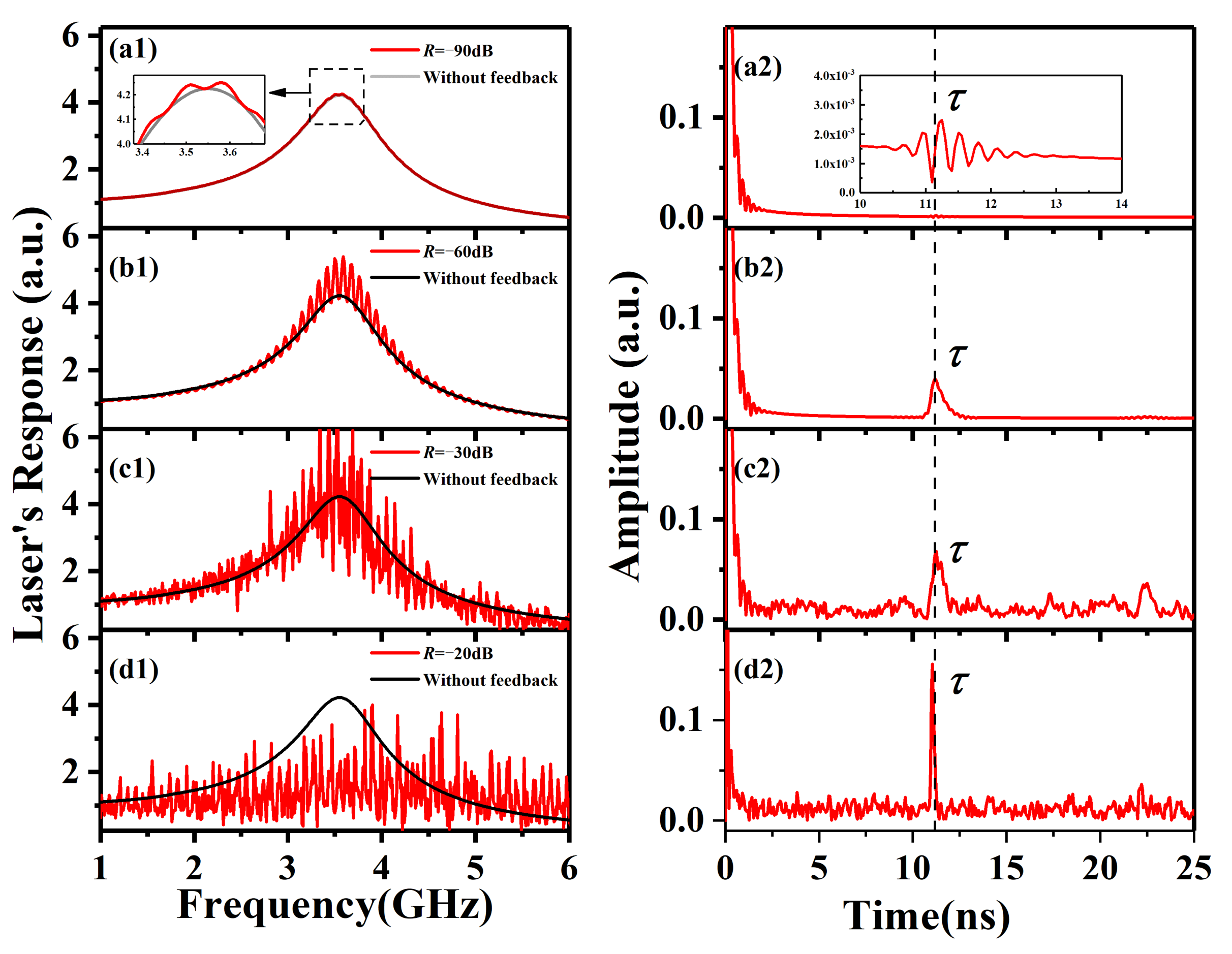
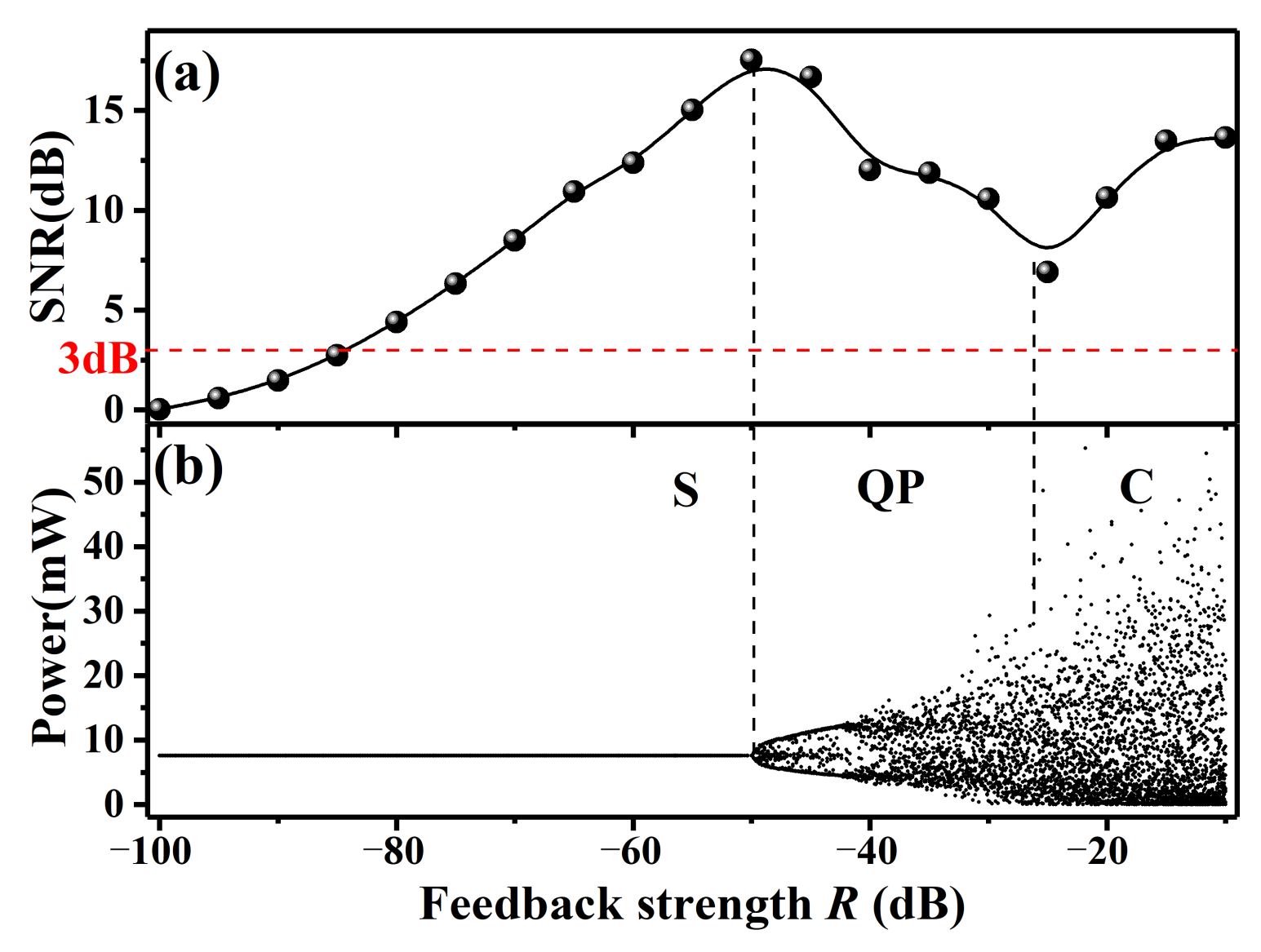
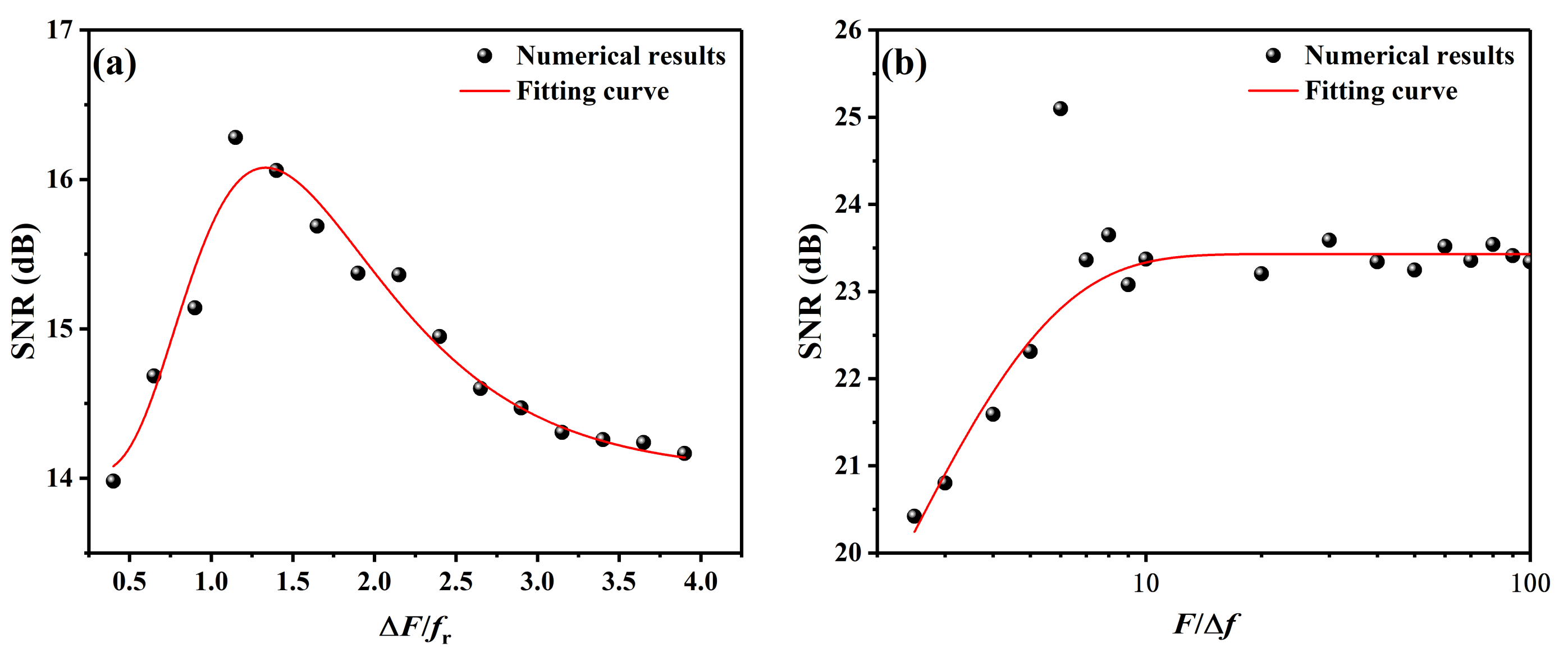
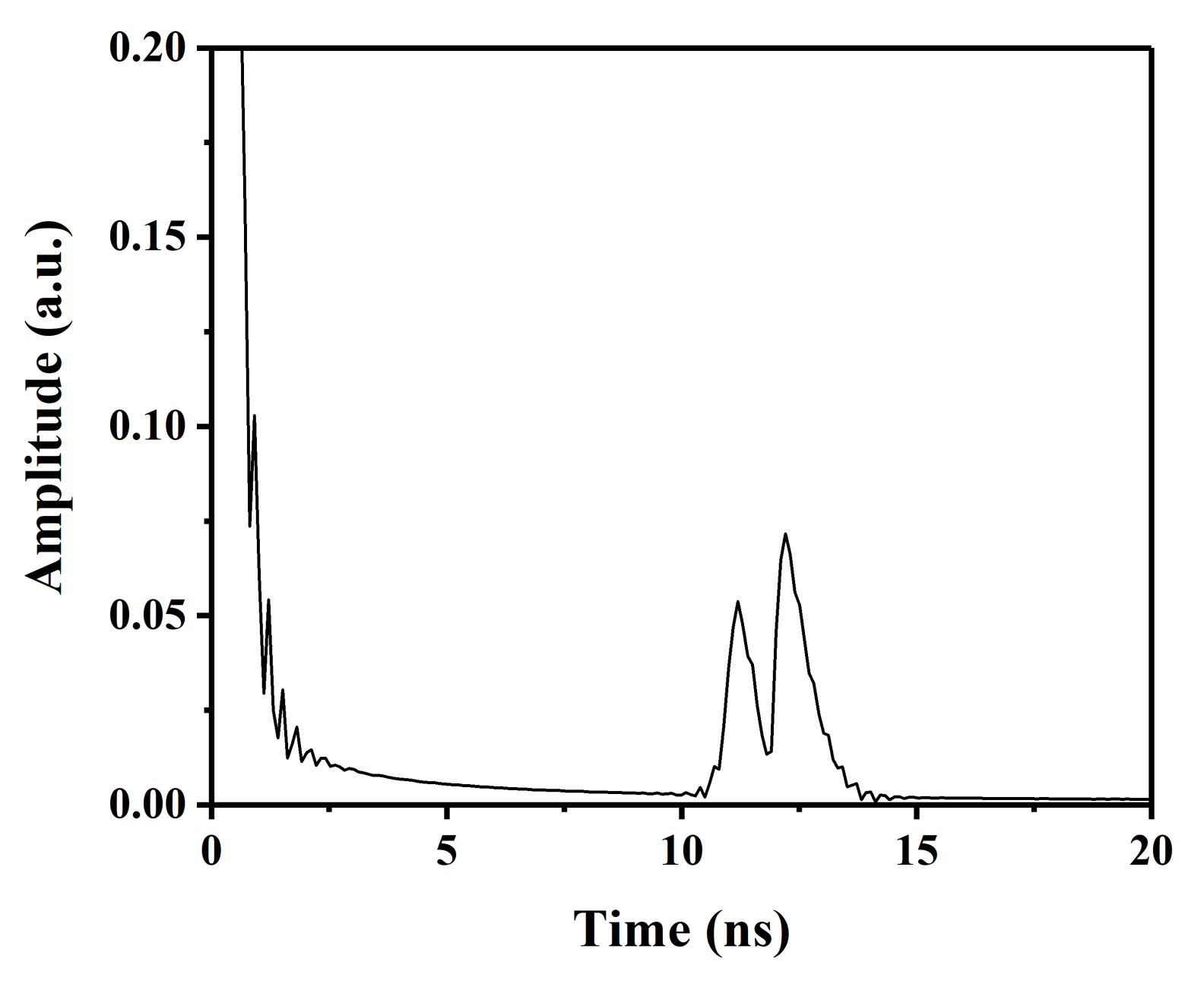
3.1. Sensitivity
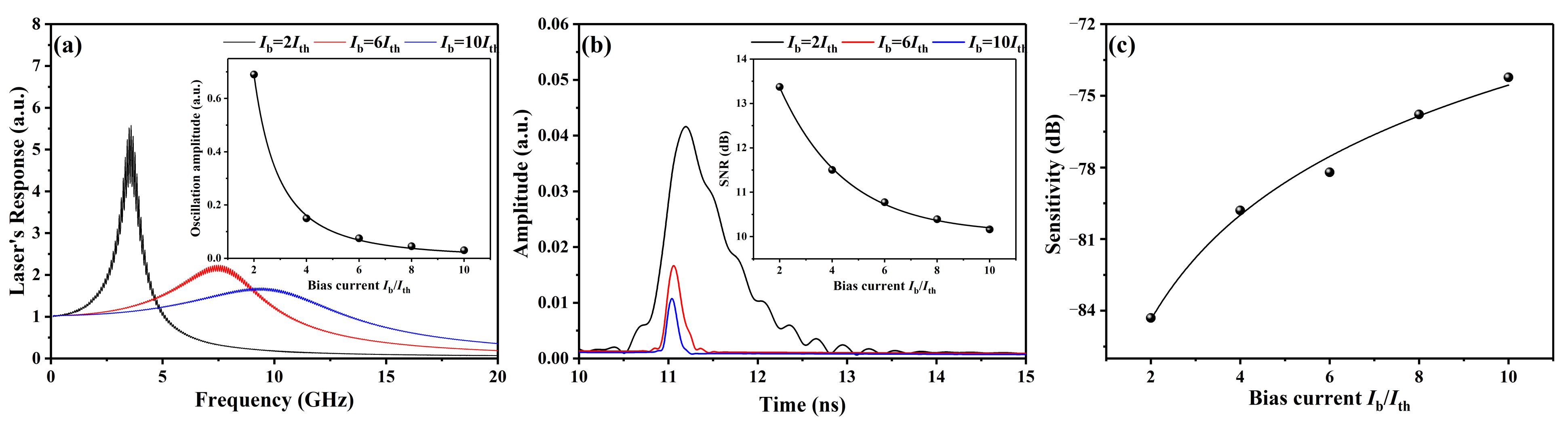
3.2. Sensitivity Improvement Potential
3.3. Modulation Parameters
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- International Telecommunication Union. G.9804.1: Higher Speed Passive Optical Networks-Requirements, 1st ed.; International Telecommunication Union: Geneva, Switzerland, 2019. [Google Scholar]
- Barnoski, M.K.; Rourke, M.D.; Jensen, S.M.; Melville, R.T. Optical time domain reflectometer. Appl. Opt. 1977, 16, 2375. [Google Scholar] [CrossRef] [PubMed]
- Jones, M.D. Using simplex codes to improve OTDR sensitivity. IEEE Photon. Technol. Lett. 1993, 5, 822. [Google Scholar] [CrossRef]
- Xiao, L.; Cheng, X.; Xu, Z.; Huang, Q. Lengthened simplex codes with complementary correlation for faulty branch detection in TDM-PON. IEEE Photon. Technol. Lett. 2013, 25, 2315. [Google Scholar] [CrossRef]
- Lee, D.; Yoon, H.; Kim, P.; Park, J.; Kim, N.Y.; Park, N. SNR enhancement of OTDR using biorthogonal codes and generalized inverses. IEEE Photon. Technol. Lett. 2004, 17, 163. [Google Scholar]
- Liao, R.; Tang, M.; Zhao, C.; Wu, H.; Fu, S.; Liu, D.; Shum, P.P. Harnessing oversampling in correlation-coded OTDR. Opt. Express 2019, 27, 1693. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Jiang, J.; Liu, K.; Wang, S.; Ma, Z.; Ding, Z.; Xu, T.; Liu, T. Coherent OTDR using flexible all-digital orthogonal phase code pulse for distributed sensing. IEEE Access 2020, 8, 85395. [Google Scholar] [CrossRef]
- Sahu, P.K.; Gowre, S.C.; Mahapatra, S. Optical time-domain reflectometer performance improvement using complementary correlated Prometheus orthonormal sequence. IET Optoelectron. 2008, 2, 128. [Google Scholar] [CrossRef]
- Zoboli, M.; Bassi, P. High spatial resolution OTDR attenuation measurements by a correlation technique. Appl. Opt. 1983, 22, 3680. [Google Scholar] [CrossRef]
- Nazarathy, M.; Newton, S.A.; Giffard, R.P.; Moberly, D.S.; Sischka, F.; Trutna, W.R.; Foster, S. Real-time long range complementary correlation optical time domain reflectometer. J. Lightwave Technol. 1989, 7, 24. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, B.; Wang, A. Chaotic correlation optical time domain reflectometer utilizing laser diode. IEEE Photon. Technol. Lett. 2008, 20, 1636. [Google Scholar] [CrossRef]
- Wang, Z.N.; Fan, M.Q.; Zhang, L.; Wu, H.; Churkin, D.V.; Li, Y.; Qian, X.Y.; Rao, Y.J. Long-range and high-precision correlation optical time-domain reflectometry utilizing an all-fiber chaotic source. Opt. Express 2015, 23, 15514. [Google Scholar] [CrossRef] [PubMed]
- Eraerds, P.; Legré, M.; Zhang, J.; Zbinden, H.; Gisin, N. Photon counting OTDR: Advantages and limitations. J. Lightwave Technol. 2010, 28, 952. [Google Scholar] [CrossRef] [Green Version]
- Koyamada, Y.; Nakamoto, H. High performance single mode OTDR using coherent detection and fibre amplifier. Electron. Lett. 1990, 26, 573. [Google Scholar] [CrossRef]
- Yuksel, K.; Wuilpart, M.; Moeyaert, V.; Mégret, P. Optical frequency domain reflectometry: A review. In Proceedings of the 2009 11th International Conference on Transparent Optical Networks, Ponta Delgada, Portugal, 28 June–2 July 2009. [Google Scholar]
- Arbel, D.; Eyal, A. Dynamic optical frequency domain reflectometry. Opt. Express 2014, 22, 8823. [Google Scholar] [CrossRef]
- Martins-Filho, J.F.; Bastos-Filho, C.J.A.; Carvalho, M.T.; Sundheimer, M.L.; Gomes, A.S.L. Dual-wavelength (1050 nm + 1550 nm) pumped thulium doped fiber amplifier characterization by optical frequency-domain reflectometer. IEEE Photon. Technol. Lett. 2003, 15, 24. [Google Scholar] [CrossRef]
- Froggatt, M.E.; Gifford, D.K.; Kreger, S.; Wolfe, M.; Soller, B.J. Characterization of polarization-maintaining fiber using high-sensitivity optical frequency-domain reflectometer. J. Lightwave Technol. 2006, 24, 4149. [Google Scholar] [CrossRef]
- De Groot, P.J.; Gallatin, G.M.; Macomber, S.H. Ranging and velocimetry signal generation in a backscatter-modulated laser diode. Appl. Opt. 1988, 27, 4475. [Google Scholar] [CrossRef]
- Keeley, J.; Bertling, K.; Rubino, P.L.; Lim, Y.L.; Taimre, T.; Qi, X.; Kundu, I.; Li, L.H.; Indjin, D.; Rakić, A.D.; et al. Detection sensitivity of laser feedback interferometry using a terahertz quantum cascade laser. Opt. Lett. 2019, 44, 3314. [Google Scholar] [CrossRef]
- Gouaux, F.; Servagent, N.; Bosch, T. Absolute distance measurement with an optical feedback interferometer. Appl. Opt. 1998, 37, 6684. [Google Scholar] [CrossRef]
- De Groot, P.J. A review of selected topics in interferometric optical metrology. Rep. Prog. Phys. 2019, 82, 056101. [Google Scholar] [CrossRef]
- Rontani, D.; Locquet, A.; Sciamanna, M.; Citrin, D.S. Loss of time-delay signature in the chaotic output of a semiconductor laser with optical feedback. Opt. Lett. 2007, 32, 2960. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, T.; Li, Q.; Bao, X.; Hu, M. Time-delay signature concealment in chaotic secure communication system combining optical intensity with phase feedback. Opt. Commun. 2020, 475, 126042. [Google Scholar] [CrossRef]
- Xue, C.; Jiang, N.; Lv, Y.; Wang, C.; Lin, S.; Qiu, K. Security-enhanced chaos communication with time-delay signature suppression and phase encryption. Opt. Lett. 2016, 41, 3690. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Wang, L.; Guo, Y.; Wang, Y.; Wang, A. Key space enhancement of optical chaos secure communication: Chirped FBG feedback semiconductor laser. Opt. Express 2019, 27, 3065. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Wang, A.; Wang, L.; Jia, Z.; Guo, Y.; Gao, Z.; Yan, L.; Qin, Y.; Wang, Y. 0.75 Gbit/s high-speed classical key distribution with mode-shift keying chaos synchronization of Fabry–Perot lasers. Light Sci. Appl. 2021, 10, 172. [Google Scholar] [CrossRef]
- Zhao, T.; Han, H.; Zhang, J.; Liu, X.; Chang, X.; Wang, A.; Wang, Y. Precise fault location in TDM-PON by utilizing chaotic laser subject to optical feedback. IEEE Photonics J. 2015, 7, 6803909. [Google Scholar] [CrossRef]
- Rontani, D.; Locquet, A.; Sciamanna, M.; Citrin, D.S.; Ortin, S. Time-delay identification in a chaotic semiconductor laser with optical feedback: A dynamical point of view. IEEE J. Quantum Electron. 2009, 45, 1879. [Google Scholar] [CrossRef]
- Wu, J.; Xia, G.; Cao, L.; Wu, Z. Experimental investigations on the external cavity time signature in chaotic output of an incoherent optical feedback external cavity semiconductor laser. Opt. Commun. 2009, 282, 3153. [Google Scholar] [CrossRef]
- Tkach, R.W.; Chraplyvy, A.R. Regimes of feedback effects in 1.5-m distributed feedback lasers. J. Lightwave Technol. 1986, 4, 1655. [Google Scholar] [CrossRef]
- Helms, J.; Petermann, K. Microwave modulation characteristics of semiconductor lasers with optical feedback. Electron. Lett. 1989, 25, 1369. [Google Scholar] [CrossRef]
- Acket, G.; Lenstra, D.; Den Boef, A.; Verbeek, B. The influence of feedback intensity on longitudinal mode properties and optical noise in index-guided semiconductor lasers. IEEE J. Quantum Electron. 1984, 20, 1163. [Google Scholar] [CrossRef]
- Zhu, N.; Shi, Z.; Zhang, Z.; Zang, Y.; Zou, C.; Zhao, Z.; Liu, Y.; Li, W. Directly Modulated Semiconductor Lasers. IEEE J. Sel. Top. Quantum Electron. 2017, 24, 1. [Google Scholar] [CrossRef]
- Ivanov, H.; Leitgeb, E.; Pezzei, P.; Freiberger, G. Experimental characterization of SNSPD receiver technology for deep space FSO under laboratory testbed conditions. Optik 2019, 195, 163101. [Google Scholar] [CrossRef]
- Urban, P.; Amaral, G.; Von der Weid, J. Fiber Monitoring Using a Sub-Carrier Band in a Sub-Carrier Multiplexed Radio-Over-Fiber Transmission System for Applications in Analog Mobile Fronthaul. J. Lightwave Technol. 2016, 34, 3118. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Z.; Zhao, T.; Wang, Y.; Wang, A. High-Sensitivity Fiber Fault Detection Method Using Feedback-Delay Signature of a Modulated Semiconductor Laser. Photonics 2022, 9, 454. https://doi.org/10.3390/photonics9070454
Shi Z, Zhao T, Wang Y, Wang A. High-Sensitivity Fiber Fault Detection Method Using Feedback-Delay Signature of a Modulated Semiconductor Laser. Photonics. 2022; 9(7):454. https://doi.org/10.3390/photonics9070454
Chicago/Turabian StyleShi, Zixiong, Tong Zhao, Yuncai Wang, and Anbang Wang. 2022. "High-Sensitivity Fiber Fault Detection Method Using Feedback-Delay Signature of a Modulated Semiconductor Laser" Photonics 9, no. 7: 454. https://doi.org/10.3390/photonics9070454
APA StyleShi, Z., Zhao, T., Wang, Y., & Wang, A. (2022). High-Sensitivity Fiber Fault Detection Method Using Feedback-Delay Signature of a Modulated Semiconductor Laser. Photonics, 9(7), 454. https://doi.org/10.3390/photonics9070454




