Next Article in Journal
Photonic Bandgaps of One-Dimensional Photonic Crystals Containing Anisotropic Chiral Metamaterials
Next Article in Special Issue
High-Sensitivity Fiber Fault Detection Method Using Feedback-Delay Signature of a Modulated Semiconductor Laser
Previous Article in Journal
An Ultra-Broadband Design of TM-Pass/TE-Stop Polarizer Based on Multistage Bragg Gratings
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Photonics
Volume 9
Issue 6
10.3390/photonics9060410
photonics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Communication

Nonlinear Dynamics of Mid-Infrared Interband Cascade Lasers Subject to Variable-Aperture Optical Feedback

by
Maorong Zhao
1,2,3,
Guangqiong Xia
1,2,
Ke Yang
4,5,
Shuman Liu
4,5,
Junqi Liu
4,5,
Qiupin Wang
1,2,
Jianglong Liu
1,2 and
Zhengmao Wu
1,2,*
1
School of Physical Science and Technology, Southwest University, Chongqing 400715, China
2
Chongqing Key Laboratory of Micro & Nano Structure Optoelectronics, Southwest University, Chongqing 400715, China
3
School of Information, Southwest Petroleum University, Nanchong 637001, China
4
Key Laboratory of Semiconductor Materials Science, Beijing Key Laboratory of Low Dimensional Semiconductor Materials and Devices, Institute of Semiconductors, Chinese Academy of Sciences, P.O. Box 912, Beijing 100083, China
5
Center of Materials Science and Optoelectronics Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
*
Author to whom correspondence should be addressed.
Photonics 2022, 9(6), 410; https://doi.org/10.3390/photonics9060410
Submission received: 17 May 2022 / Revised: 8 June 2022 / Accepted: 9 June 2022 / Published: 10 June 2022
(This article belongs to the Special Issue Advancements in Semiconductor Lasers)
Browse Figures
Versions Notes

Abstract

:
In this work, we experimentally investigate the nonlinear dynamics of an interband cascade laser (ICL) under variable-aperture optical feedback implemented by a gold mirror combining with a ring-actuated iris diaphragm (RAID). By continuously varying the diameter of RAID (DR), the evolution of the dynamical state of ICL with the aperture of the optical feedback can be inspected. The characteristics of each dynamical state are characterized by time series, power spectra, phase portraits, and Lyapunov exponents. The results show that, with the decrease of DR, the dynamical state of the ICL under variable-aperture optical feedback presents an evolution from complex, simple to stable. Diverse dynamical states including period one state (P1), period two state (P2), multi-period state (MP), quasi-period state (QP), low-frequency fluctuation (LFF), chaotic state (C), and hyperchaos have been observed. Through mapping the evolution of dynamical states with DR for the ICL biased at different currents, different evolved routes of the dynamical states are revealed.

1. Introduction

Interband cascade laser (ICL) is a kind of important mid-infrared semiconductor lasers, where the advantages of interband optical transition from quantum well lasers (QWLs) and the electron transport via the cascading stages from quantum cascade lasers (QCLs) are combined in the ICL [1,2]. Unlike ordinary QCLs, ICL is based on the interband transition of type-II quantum wells for emitting light, and its carrier lifetime is on the order of sub-nanoseconds [2,3,4]. ICL typically has five to ten cascading gain stages in its active region for enhancing the total gain. The power consumption of ICL is 1–2 orders of magnitude lower than that of mid-infrared QCL, allowing for battery-powered operation [5,6]. GaSb-based ICLs can oscillate within a wavelength range from 3 μm to 6 μm [2,3], while InAs-based ICLs can oscillate at a wavelength beyond 10 μm [7]. As a result, ICLs can be used for gas sensing [8,9] and free-space optical (FSO) communication [10] due to the unique mid-infrared spectral range.
Previous research has demonstrated that near-infrared semiconductor lasers exhibit a variety of dynamical states under external perturbations including optical injection, optical feedback, or optoelectronic feedback [11,12,13,14,15,16,17], which is of particular interest in many applications, including photonic microwave signal generation [18,19,20], random bit generation [21,22], secure communications [23,24], high performance radar, and lidar [25,26,27], as well as photonic reservoir computing [28]. For mid-infrared QCLs, related theoretical and experimental investigations on the nonlinear dynamics and their applications have been explored, and the results demonstrate that, compared with near-infrared semiconductor lasers, QCLs are less sensitive to optical feedback [29,30]. Under some special operation conditions, optical feedback QCLs can exhibit low-frequency fluctuations [31,32]. As for mid-infrared ICLs, relevant theoretical investigation predicts that an ICL under optical feedback can exhibit chaotic state [33], which has been experimentally demonstrated very recently [34].
For near-infrared semiconductor laser, the optical feedback with variable feedback ratio is relatively easy to be implemented by combining a mirror with a neutral density filter (NDF). However, for mid-infrared waveband, currently commercial NDF cannot provide continuously variable attenuation rate. Therefore, in order to build a feedback system with continuous change of feedback strength, the feedback loop based on polaroid has been proposed and demonstrated in mid-infrared external cavity QCLs [29,30,31,32] and ICLs [34]. Through changing the polarized state of the feedback light, the feedback ratio can be adjusted.
In this work, we propose a novel scheme to establish a feedback loop implemented via a ring-actuated iris diaphragm (RAID) combining with a mirror. Through varying the diameter (DR) of RAID, the aperture of feedback beam can be adjusted. As a result, we investigate the nonlinear dynamics of an ICL via the time series, power spectra, phase portraits, and Lyapunov exponents. Moreover, the dynamical state evolution of the ICL with DR is also explored.

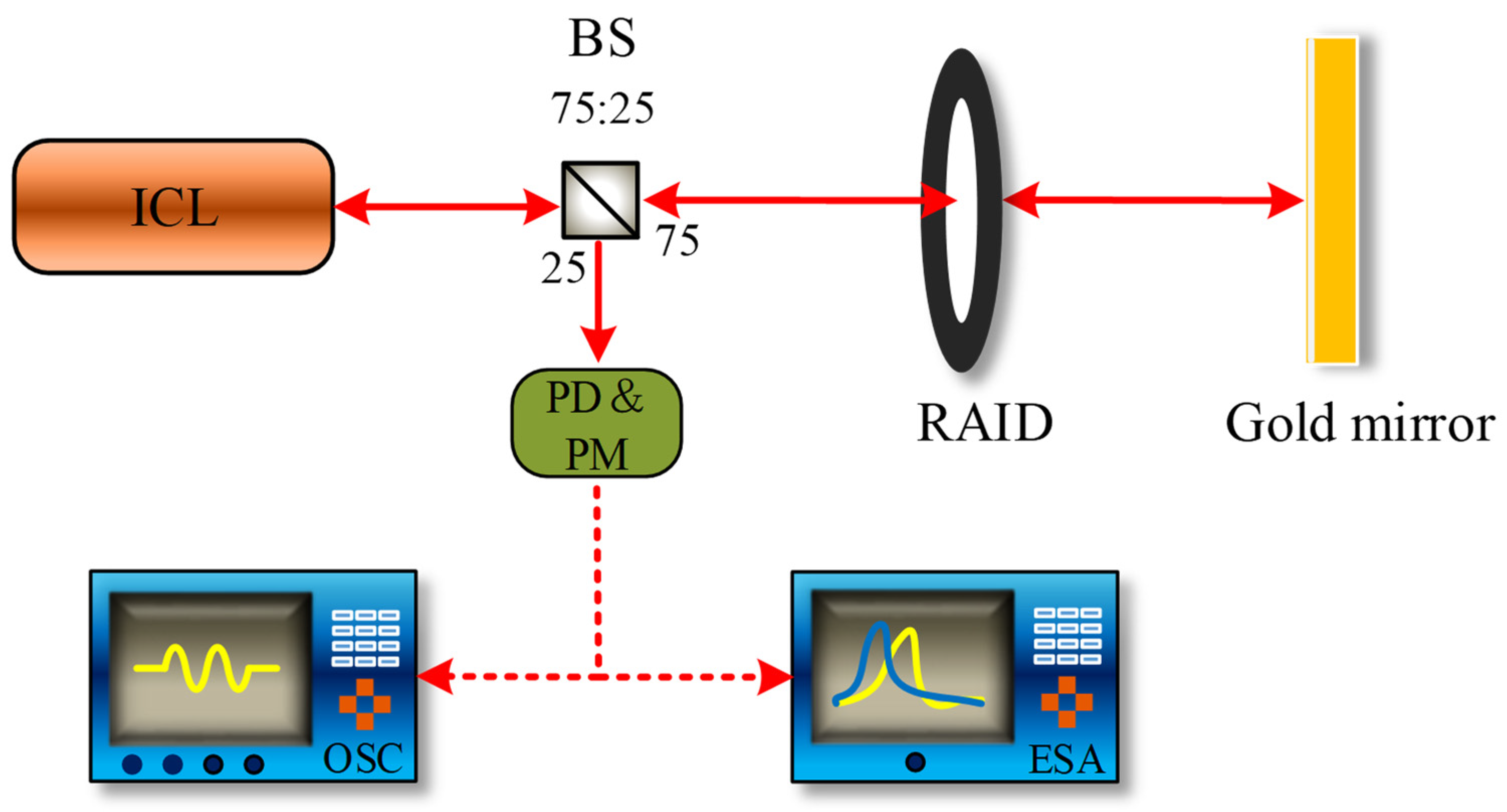
2. Experimental Setup

Figure 1 shows the schematic diagram of the experimental setup. The interband cascade laser (ICL) utilized in this experiment is a Fabry–Perot laser operating at the wave band of 3.3 μm, which is grown on GaSb substrate by solid source molecular beam epitaxy. The ICL is composed of five cascading stages of W-shaped active regions formed by InAs/GaInSb type-II quantum wells, and two cleavage planes form the resonant cavity. The ridge width and cavity length of the ICL are 20 µm and 2.0 mm, respectively. The purpose of such a relatively broad area laser structure is to obtain high power. An aspheric lens is encapsulated in the laser to collimate the emission light. The ICL is driven by a high stability and low-noise current-temperature controller (ILX-Lightwave, LDC-3724C). During the total experimental processes, the temperature is stabilized at 20.15 °C. The laser beam output from the ICL is divided into two parts by a 75:25 beam splitter (BS). The 75%-part is reflected by a plane gold mirror and then fed back to the ICL. The gold mirror is placed 21.6 cm away from the ICL. A ring-actuated iris diaphragm (RAID) is added into the feedback loop for adjusting the aperture of optical feedback, and its diameter (DR) can be adjusted from 1.0 to 8.0 mm. The 25%-part is converted into electronic signal by a fast HgCdTe photodetector (PD, Vigo PVI-4TE-5, 525 MHz bandwidth), and then is sent to the detected system. The time series and electrical spectra are recorded by a digital oscilloscope with a sampling rate of 20 GS/s (OSC, Agilent DSO9254A with 2.5 GHz bandwidth) and an electrical spectrum analyzer (ESA, Agilent E4407B with 26.5 GHz bandwidth), respectively.

3. Results

Figure 2 shows the measured power-current characteristic of the ICL at free-running (blue) and subject to variable-aperture optical feedback under DR = 4.0 mm (red). Here, the output power of the ICL is monitored by a power meter (PM) at the 25% output port of BS. As shown in this diagram, the free-running ICL exhibits a threshold current Ith of 74.50 mA. After introducing variable-aperture optical feedback under DR = 4.0 mm, the threshold current is decreased to 64.80 mA, and, meanwhile, the output power is significantly enhanced. Further experimental results show that the power-current characteristic of the ICL is not affected by the variation of DR under the case that DR is beyond 3.7 mm. In other words, under this experimental condition the size of the optical beam is about 3.7 mm. Therefore, the red curve in Figure 2 also corresponds to the case that the RAID is removed. In the following discussion, the value of DR is set to no more than 3.7 mm.
First, we fix the bias current at a relatively low level (I = 86.00 mA) and inspect the dynamical states of the ICL under variable-aperture optical feedback. Figure 3 displays the time series (first column), power spectra (second column), and corresponding phase portraits (third column) for some typical dynamical states of the ICL subject to variable-aperture optical feedback under different DR. For DR = 3.7 mm, as mentioned above, the feedback optical beam does not be limited by the RAID. Under this case, a slowly-varying envelope can be observed from the time series (in Figure 3(a1)), two or more incommensurate frequencies exist in the power spectrum (in Figure 3(b1)), and the phase portrait (in Figure 3(c1)) is characterized by a torus. Thus, this dynamical state of the ICL corresponds to a quasi-periodic state (QP). For DR = 3.0 mm (as shown in Figure 3(a2,b2,c2)), the time series behaves as a periodic oscillation whose fundamental frequency is about 259.4 MHz from the power spectrum, and the phase portrait shows a limited cycle feature. Therefore, it can be judged that the ICL operates at a period one state (P1). For DR = 2.6 mm (as shown in Figure 3(a3,b2,c3)), two peak intensities in the time series can be clearly observed, both sub-harmonic frequency (about 127.4 MHz) and fundamental frequency (about 256.4 MHz) appear in the power spectrum, and the corresponding phase portrait possesses two loops that are intertwined together. All these features mean that the dynamical state of the ICL is a period two state (P2). For DR = 2.3 mm (as shown in Figure 3(a4,b4,c4)), random intensity oscillation can be seen from the time series, the corresponding power spectrum covers a broad frequency range, and the phase portrait shows a widely scattered distribution over a large area. As a result, the ICL exhibits a chaotic state (C). Finally, for DR = 1.0 mm, which is the minimum diameter of the RAID, the time series (Figure 3(a5)) has some tiny fluctuations, mainly caused by the system noise. Accordingly, the power spectrum (Figure 3(b5)) almost coincides with the noise floor, and the phase portrait (Figure 3(c5)) shrinks as a small spot. Therefore, the dynamical state of the ICL is a stable state (S). In short, an evolution route of QP-P1-P2-C-S is presented under I = 86.00 mA through gradually decreasing DR, and the reason may be explained as follows. After introducing a RAID into the feedback loop, the edge portion of the beam beyond the diameter of RAID will be blocked. For a relatively large value of DR, the fundamental transverse mode is almost unlimited and can be fed back into the ICL. However, the higher-order transverse mode is limited by the RAID, which results in a decrease in the feedback. As a result, with the decrease in DR, the fundamental transverse mode can be driven into a more complex dynamical state. However, if DR is decreased below the size of fundamental transverse mode, the feedback strength of the fundamental transverse mode will be weakened with the decrease of DR, and then the ICL will operate at a steady state for too small DR.
Next, we fix the bias current at a relatively high level (I = 96.00 mA) and examine the influence of DR on the dynamical states of the ICL, and the corresponding results are presented in Figure 4. For DR = 3.7 mm (Figure 4(a1,b1,c1)), similar dynamical characteristics with Figure 3(a1,b1,c1) can be observed, and the dynamical state is QP. When DR is decreased to 3.3 mm (Figure 4(a2,b2,c2)), the dynamical state of the ICL is P1 with a fundamental frequency of 239.9 MHz. Further decreasing DR to 2.8 mm (Figure 4(a3,b3,c3)), the dynamical features of the ICL are similar to that in Figure 3(a3,b3,c3), both the fundamental frequency (about 237.9 MHz) and its sub-harmonic frequency (about 118.9 MHz) present clearly in the power spectrum, and then the dynamics can be identified as P2. For DR = 2.7 mm (Figure 4(a4,b4,c4)), the time series shows multiple different peaks, multiple frequency components appear upon the power spectrum, and the phase portrait shows the overlap alternation of multiple loops. Therefore, the ICL presents a multi-period state (MP). For DR = 2.5 mm (Figure 4(a5,b5,c5)), the time series fluctuates dramatically, the corresponding power spectrum continuously covers a broad frequency range, and the phase portrait shows a widely scattered distribution over a large area. Under these circumstances, it can be determined that the ICL operates at a chaotic state (C). Furthermore, if DR is decreased to 1.6 mm (Figure 4(a6,b6,c6)), the time series exhibits a sudden power dropout with a following gradual power recovery. In addition, the time series raises the low-frequency noise for frequency below about 20 MHz in the power spectrum, and the phase portrait shows a cluster sited around −0.13 to 0.06 V. All these features indicate that the ICL exhibits a low-frequency fluctuation (LFF). In further decreasing DR to 1.0 mm (Figure 4(a7,b7,c7)), the ICL shows an S state. In a word, with the decrease of DR from 3.7 mm to 1.0 mm, the ICL shows rich nonlinear dynamical states followed a route of QP-P1-P2-MP-C-LFF-S.
The largest Lyapunov exponent (LLE), which describes the divergence rate of nearby attractor trajectories, is an effective method to determine the dynamical state [35,36]. A chaotic state at least possesses one positive Lyapunov exponent [37,38]. Based on the time series, we have calculated the evolution of LLE with DR under I = 96.00 mA, and the results are given in Figure 5a. As shown in Figure 5a, when DR is decreased from 3.7 mm to 2.6 mm, the ICL exhibits different states of QP-P1-P2-MP, and the values of LLE are nearly zero. When further decreasing DR, the ICL is driven into C state, and the LLE arrives at its maximum value of 1.69 ns−1 under DR = 2.5 mm For the case that DR is decreased from 2.3 mm to 1.6 mm, the ICL exhibits LFF, and the LLEs are 0.93 ns−1, 0.52 ns−1, respectively. Figure 5b shows the corresponding Lyapunov exponent spectrum when the LLE arrives at the maximum value of 1.69 ns−1. From this diagram, it can be seen that five largest Lyapunov exponents are 1.62, 0.94, 0.37, −0.06, and −0.61 ns−1. As a result, there exist three positive Lyapunov exponents, which demonstrates that the output of ICL is hyperchaos [39].
The above results reveal that the bias current I and the diameter DR of RAID are two key parameters to seriously affect the dynamical state of the ICL. Finally, a two-dimensional map of the dynamical evolutions of the ICL under variable-aperture optical feedback in the parameter space of I and DR is integrated in Figure 6, where the bias current varies from 80.00 mA to 96.00 mA with a step of 2.00 mA and the diameter of RAID is varied from 1.0 to 3.7 mm. From this diagram, one can see that a large bias current is helpful for that the ICL presents rich nonlinear dynamical states. For the ICL biased at 80.00 mA, the dynamical states only involve P1 and stable state. If the bias current of ICL is increased to 86.00 mA, with the continuous decrease of DR, the ICL can be entered into C state via a route of QP-P1-P2-C. 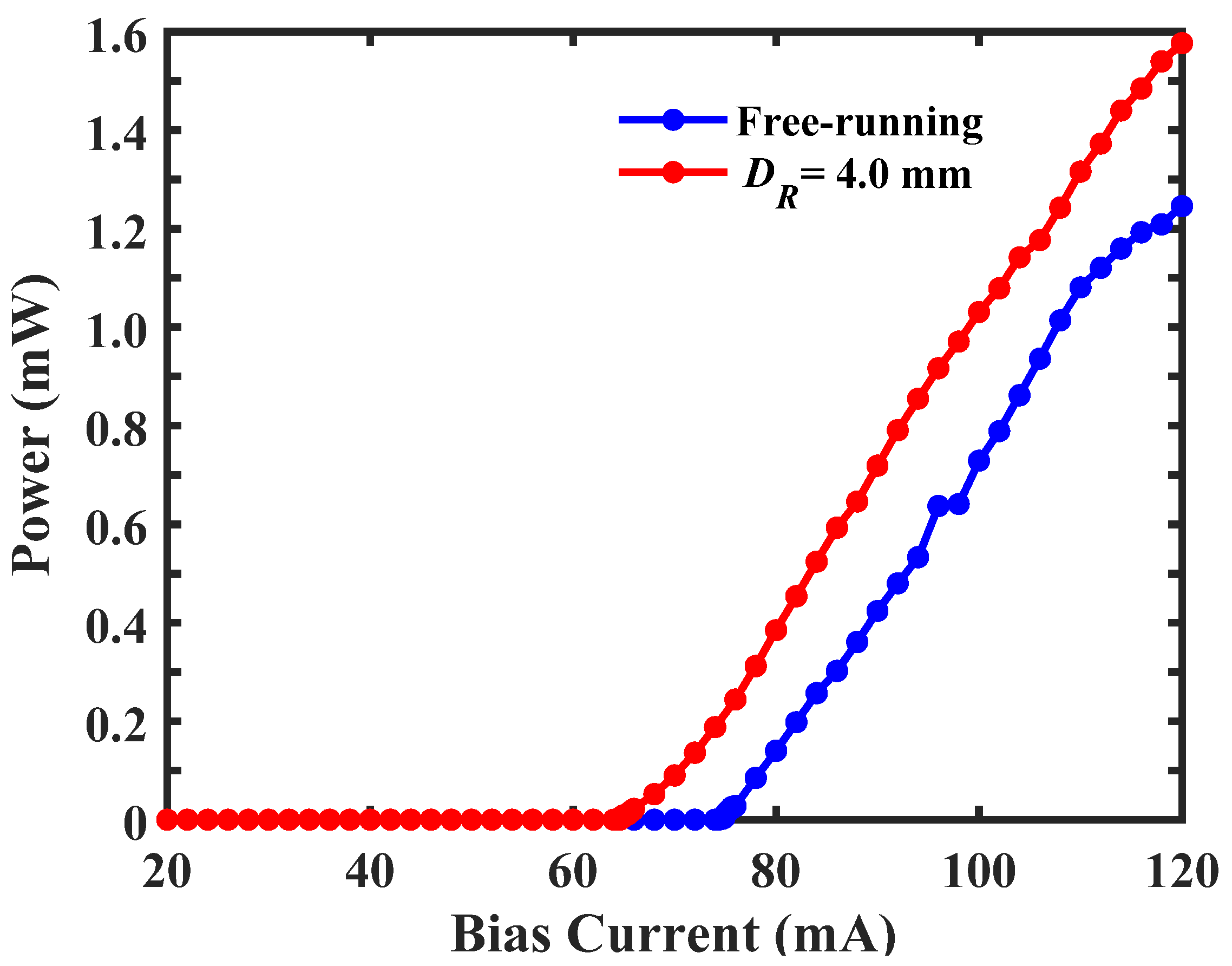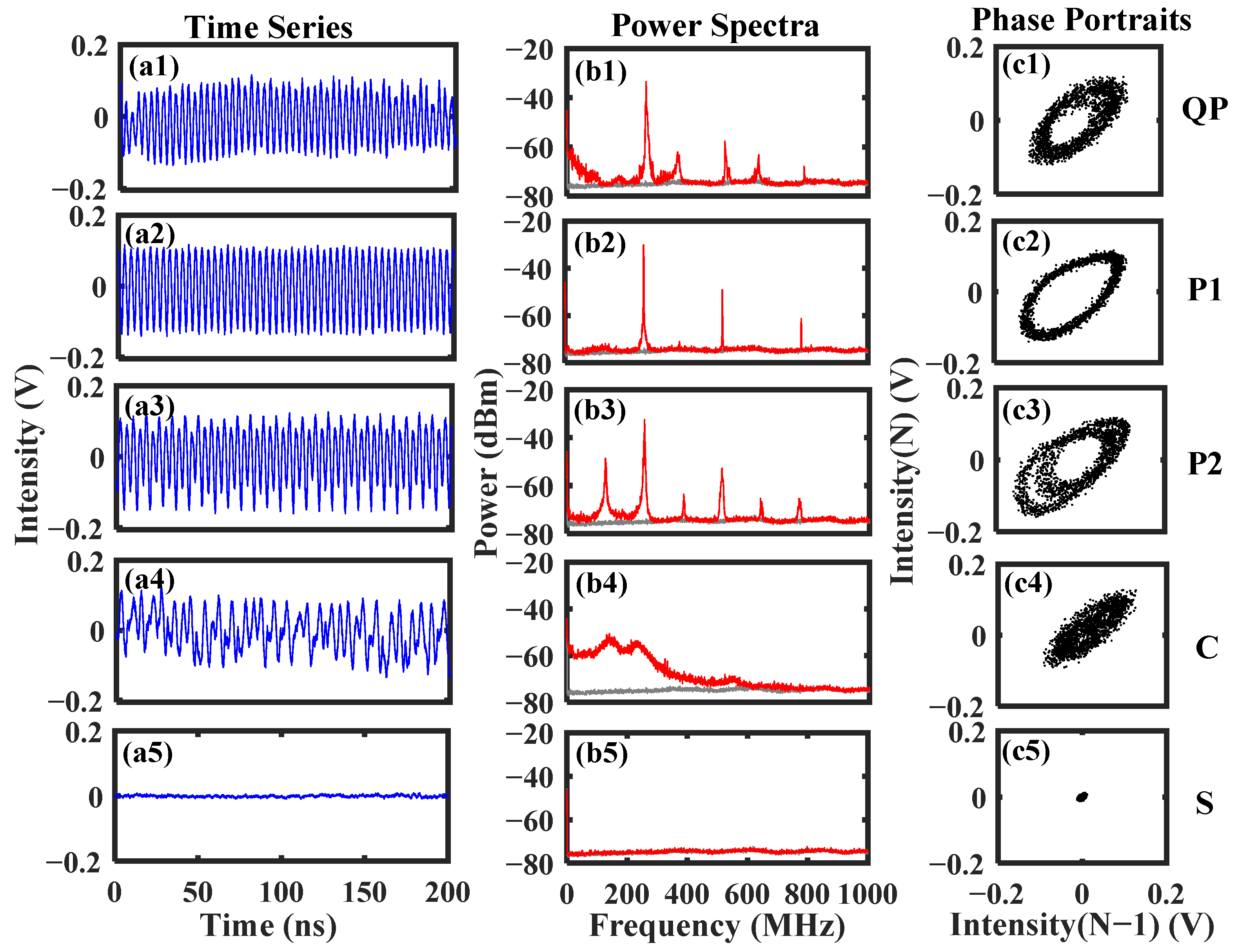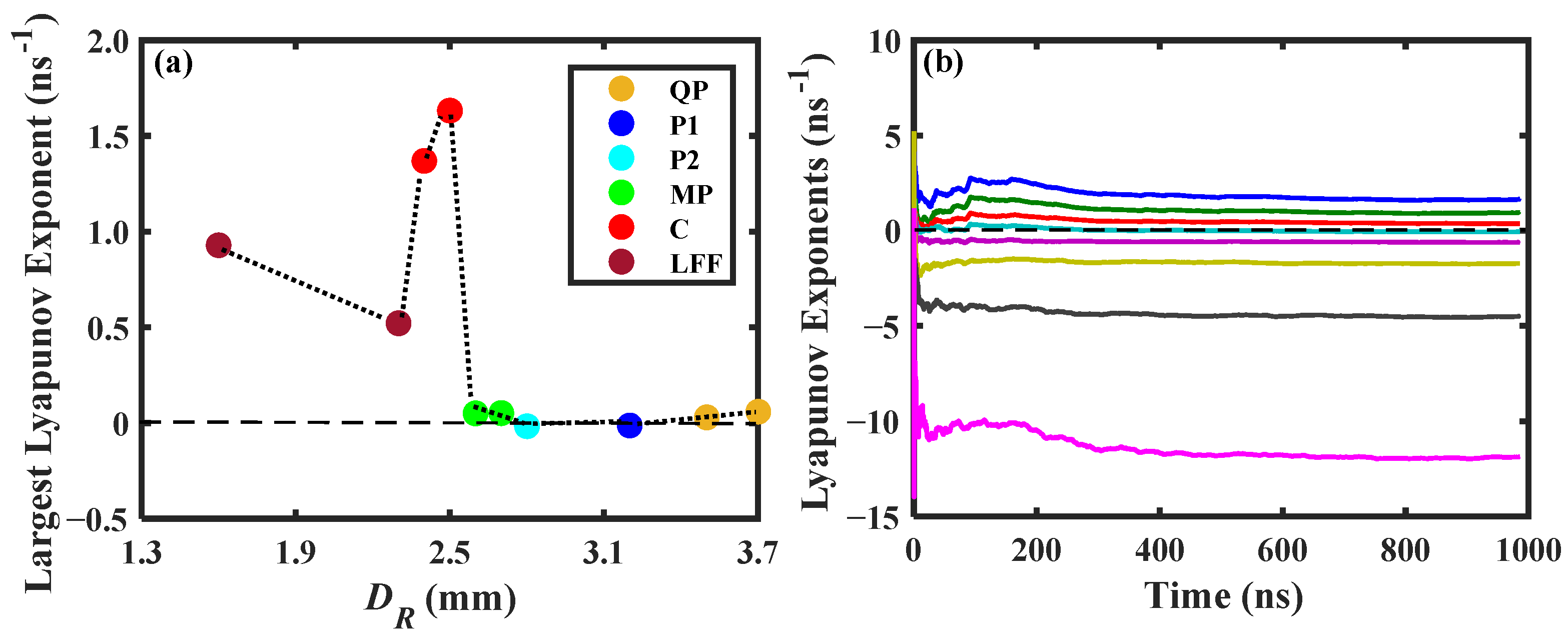For a larger bias current of the ICL, the evolution of dynamical state with DR follows a route of QP-P1-P2-MP-C-LFF-S.

4. Discussion

In this work, based on a ring-actuated iris diaphragm (RAID) combining with a mirror, a novel feedback scheme is proposed for driving an ICL into different dynamical states, which have application prospects in free-space optical communication and sensing, optical generation of microwave, radar and lidar, etc. For such a feedback scheme, the variation of feedback strength is realized through changing the transverse field distribution implemented by adjusting the aperture of RAID. Therefore, compared to the feedback loop based on polarizers [29,30,31,32,34], such a feedback scheme is more simple and easily implemented.
Additionally, as proved in Ref. [40], the beam shaping with optical feedback in QCLs is a flexible solution to obtain high-quality mid-infrared sources by controlling the filamentation. Due to a similar principle, it can be predicted that through introducing such a feedback scheme into ICLs, high-quality mid-infrared sources can also be obtained. As a result, we will pay attention to this issue in our further research.

5. Conclusions

In summary, the nonlinear dynamics of an interband cascade laser (ICL) under variable-aperture optical feedback are experimentally investigated, where the variable-aperture optical feedback is implemented by a gold mirror combining with a ring-actuated iris diaphragm (RAID). Via the time series, power spectra, phase portraits, and largest Lyapunov exponent (LLE), the dynamical states of the ICL under variable-aperture optical feedback can be determined, and various dynamical states, including period one state (P1), period two state (P2), multi-period state (MP), quasi-period state (QP), low-frequency fluctuation (LFF), chaotic state (C), and hyperchaos, have been observed. Through mapping the dynamical states in a parameter space of the bias current (I) of ICL and the diameter (DR) of RAID, different evolution routes of dynamical state are revealed. Due to the unique virtue of relatively easy implementation, we hope that this work can offer an effective way to control ICL operating at an expected dynamical state for some special scenarios.

Author Contributions

Conceptualization, M.Z. and G.X.; methodology, M.Z.; validation, M.Z., G.X. and Z.W.; investigation, M.Z. and K.Y.; resources, G.X., S.L. and J.L. (Junqi Liu); data curation, Q.W. and J.L. (Jianglong Liu); writing—original draft preparation, M.Z.; writing—review and editing, G.X. and Z.W.; visualization, M.Z.; supervision, Z.W.; project administration, G.X. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by National Natural Science Foundation of China (61875167, 61790583 and 61835011) and Bureau of Science and Technology of Nanchong City (19SXHZ0021).

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Meyer, J.; Bewley, W.; Canedy, C.; Kim, C.; Kim, M.; Merritt, C.; Vurgaftman, I. The interband cascade lasers. Photonics 2020, 7, 75. [Google Scholar] [CrossRef]
  2. Ning, C.; Yu, T.; Liu, S.M.; Zhang, J.C.; Wang, L.J.; Liu, J.Q.; Zhuo, N.; Zhai, S.Q.; Li, Y.; Liu, F.Q. Interband cascade lasers with short electron injector. Chin. Opt. Lett. 2022, 20, 022501. [Google Scholar] [CrossRef]
  3. Vurgaftman, I.; Bewley, W.W.; Canedy, C.L.; Kim, C.S.; Kim, M.; Merritt, C.D.; Abell, J.; Meyer, J.R. Interband cascade lasers with low threshold powers and high output powers. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 1200210. [Google Scholar] [CrossRef]
  4. Didier, P.; Spitz, O.; Cerutti, L.; Diaz-Thomas, D.A.; Baranov, A.N.; Carras, M.; Grillot, F. Relative intensity noise and intrinsic properties of RF mounted interband cascade laser. Appl. Phys. Lett. 2021, 119, 171107. [Google Scholar] [CrossRef]
  5. Vurgaftman, I.; Bewley, W.W.; Canedy, C.L.; Kim, C.S.; Kim, M.; Merritt, C.D.; Abell, J.; Lindle, J.R.; Meyer, J.R. Rebalancing of internally generated carriers for mid-infrared interband cascade lasers with very low power consumption. Nat. Commun. 2011, 2, 585. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  6. Bradshaw, J.L.; Yang, R.Q.; Bruno, J.D.; Pham, J.T.; Wortman, D.E. High-efficiency interband cascade lasers with peak power exceeding 4 W/facet. Appl. Phys. Lett. 1999, 75, 2362–2364. [Google Scholar] [CrossRef]
  7. Tian, Z.; Li, L.; Ye, H.; Yang, R.Q.; Mishima, T.D.; Santos, M.B.; Johnson, M.B. InAs-based interband cascade lasers with emission wavelength at 10.4 μm. Electron. Lett. 2012, 48, 113–114. [Google Scholar] [CrossRef]
  8. Liu, Z.W.; Zheng, C.T.; Chen, C.; Li, Y.F.; Xie, H.T.; Ren, Q.; Wang, Y.D.; Tittel, F.K. ICL-based mid-infrared carbon dioxide sensor system for deep-sea natural gas hydrate exploration. Opt. Express 2019, 27, 5598–5609. [Google Scholar] [CrossRef]
  9. Dong, L.; Li, C.G.; Sanchez, N.P.; Gluszek, A.K.; Griffin, R.J.; Tittel, F.K. Compact CH4 sensor system based on a continuous-wave, low power consumption, room temperature interband cascade laser. Appl. Phys. Lett. 2016, 108, 011106. [Google Scholar] [CrossRef] [Green Version]
  10. Soibel, A.; Wright, M.W.; Farr, W.H.; Keo, S.A.; Hill, C.J.; Yang, R.Q.; Liu, H.C. Midinfrared interband cascade laser for free space optical communication. IEEE Photonics Technol. Lett. 2010, 22, 121–123. [Google Scholar] [CrossRef]
  11. Petermann, K. External optical feedback phenomena in semiconductor-lasers. IEEE J. Sel. Top. Quantum Electron. 1995, 1, 480–489. [Google Scholar] [CrossRef]
  12. Hwang, S.K.; Liu, J.M. Dynamical characteristics of an optically injected semiconductor laser. Opt. Commun. 2000, 183, 195–205. [Google Scholar] [CrossRef]
  13. Gatare, I.; Sciamanna, M.; Buesa, J.; Thienpont, H.; Panajotov, K. Nonlinear dynamics accompanying polarization switching in vertical-cavity surface-emitting lasers with orthogonal optical injection. Appl. Phys. Lett. 2006, 88, 101106. [Google Scholar] [CrossRef]
  14. Hong, Y.H.; Spencer, P.S.; Shore, K.A. Wideband chaos with time-delay concealment in vertical-cavity surface-emitting lasers with optical feedback and injection. IEEE J. Quantum Electron. 2014, 50, 236–242. [Google Scholar] [CrossRef]
  15. Zhong, Z.Q.; Wu, Z.M.; Xia, G.Q. Experimental investigation on the time-delay signature of chaotic output from a 1550 nm VCSEL subject to FBG feedback. Photon. Res. 2017, 5, 6–10. [Google Scholar] [CrossRef]
  16. Chen, J.J.; Li, C.X.; Mu, X.L.; Li, L.F.; Duan, Y.N. Time-delay signature suppression of polarization-resolved wideband chaos in VCSELs with dual-path chaotic optical injections. Appl. Opt. 2020, 59, 7217–7224. [Google Scholar] [CrossRef]
  17. Zhao, A.; Jiang, N.; Zhang, Y.Q.; Peng, J.F.; Liu, S.Q.; Qiu, K.; Deng, M.L.; Zhang, Q.W. Semiconductor laser-based multi-channel wideband chaos generation using optoelectronic hybrid feedback and parallel filtering. J. Lightwave Technol. 2022, 40, 751–761. [Google Scholar] [CrossRef]
  18. Chan, S.C.; Liu, J.M. Tunable narrow-linewidth photonic microwave generation using semiconductor laser dynamics. IEEE J. Sel. Top. Quantum Electron. 2004, 10, 1025–1032. [Google Scholar] [CrossRef] [Green Version]
  19. Qi, X.Q.; Liu, J.M. Photonic microwave applications of the dynamics of semiconductor lasers. IEEE J. Sel. Top. Quantum Electron. 2011, 17, 1198–1211. [Google Scholar] [CrossRef]
  20. Huang, Y.; Zhou, P.; Li, N.Q. Broad tunable photonic microwave generation in an optically pumped spin-VCSEL with optical feedback stabilization. Opt. Lett. 2021, 46, 3147–3150. [Google Scholar] [CrossRef]
  21. Uchida, A.; Amano, K.; Inoue, M.; Hirano, K.; Naito, S.; Someya, H.; Oowada, I.; Kurashige, T.; Shiki, M.; Yoshimori, S.; et al. Fast physical random bit generation with chaotic semiconductor lasers. Nat. Photonics 2008, 2, 728–732. [Google Scholar] [CrossRef]
  22. Reidler, I.; Aviad, Y.; Rosenbluh, M.; Kanter, I. Ultrahigh-speed random number generation based on a chaotic semiconductor laser. Phys. Rev. Lett. 2009, 103, 024102. [Google Scholar] [CrossRef] [PubMed]
  23. Argyris, A.; Syvridis, D.; Larger, L.; Annovazzi-Lodi, V.; Colet, P.; Fischer, I.; Garcia-Ojalvo, J.; Mirasso, C.R.; Pesquera, L.; Shore, K.A. Chaos-based communications at high bit rates using commercial fibre-optic links. Nature 2005, 438, 343–346. [Google Scholar] [CrossRef] [PubMed]
  24. Wu, J.G.; Wu, Z.M.; Tang, X.; Fan, L.; Deng, W.; Xia, G.Q. Experimental demonstration of LD-based bidirectional fiber-optic chaos communication. IEEE Photonics Technol. Lett. 2013, 25, 587–590. [Google Scholar] [CrossRef]
  25. Lin, F.Y.; Liu, J.M. Diverse waveform generation using semiconductor lasers for radar and microwave applications. IEEE J. Quantum Electron. 2004, 40, 682–689. [Google Scholar] [CrossRef]
  26. Lin, F.Y.; Liu, J.M. Chaotic lidar. IEEE J. Sel. Top. Quantum Electron. 2004, 10, 991–997. [Google Scholar] [CrossRef]
  27. Zhong, D.Z.; Xu, G.L.; Luo, W.; Xiao, Z.Z. Real-time multi-target ranging based on chaotic polarization laser radars in the driveresponse VCSELs. Opt. Express 2017, 25, 21684–21704. [Google Scholar] [CrossRef]
  28. Chen, Y.P.; Yi, L.L.; Ke, J.X.; Yang, Z.; Yang, Y.P.; Huang, L.Y.; Zhuge, Q.B.; Hu, W.S. Reservoir computing system with double optoelectronic feedback loops. Opt. Express 2019, 27, 27431–27440. [Google Scholar] [CrossRef]
  29. Zhao, B.B.; Wang, X.G.; Zhang, J.C.; Wang, C. Relative intensity noise of a mid-infrared quantum cascade laser: Insensitivity to optical feedback. Opt. Express 2019, 27, 26639–26647. [Google Scholar] [CrossRef]
  30. Zhao, B.B.; Wang, X.G.; Wang, C. Strong optical feedback stabilized quantum cascade laser. ACS Photonics 2020, 7, 1255–1261. [Google Scholar] [CrossRef]
  31. Jumpertz, L.; Schires, K.; Carras, M.; Sciamanna, M.; Grillot, F. Chaotic light at mid-infrared wavelength. Light Sci. Appl. 2016, 5, e16088. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  32. Spitz, O.; Wu, J.G.; Carras, M.; Wong, C.W.; Grillot, F. Low-frequency fluctuations of a mid-infrared quantum cascade laser operating at cryogenic temperatures. Laser Phys. Lett. 2018, 15, 116201. [Google Scholar] [CrossRef] [Green Version]
  33. Han, H.; Cheng, X.M.; Jia, Z.W.; Shore, K.A. Nonlinear dynamics of interband cascade laser subjected to optical feedback. Photonics 2021, 8, 366. [Google Scholar] [CrossRef]
  34. Deng, Y.; Fan, Z.F.; Zhao, B.B.; Wang, X.G.; Zhao, S.Y.; Wu, J.G.; Grillot, F.; Wang, C. Mid-infrared hyperchaos of interband cascade lasers. Light Sci. Appl. 2022, 11, 7. [Google Scholar] [CrossRef]
  35. Wolf, A. Wolf Lyapunov Exponent Estimation from a Time Series. MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/48084-wolf-lyapunov-exponent-estimation-from-a-time-series (accessed on 10 January 2022).
  36. Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time-series. Phys. D 1985, 16, 285–317. [Google Scholar] [CrossRef] [Green Version]
  37. Ott, E. Chaos in Dynamical Systems; Cambridge University: Cambridge, UK, 2002. [Google Scholar]
  38. Sprott, J.C. Chaos and Time-Series Analysis; Oxford University: New York, NY, USA, 2003. [Google Scholar]
  39. Matsumoto, T.; Chua, L.O.; Kobayashi, K. Hyperchaos: Laboratory experiment and numerical confirmation. IEEE Trans. Circuits Syst. 1986, 33, 1143–1147. [Google Scholar] [CrossRef]
  40. Ferre, S.; Jumpertz, L.; Carras, M.; Ferreira, R.; Grillot, F. Beam shaping in high-power broad-area quantum cascade lasers using optical feedback. Sci. Rep. 2017, 7, 44284. [Google Scholar] [CrossRef] [Green Version]
Photonics 09 00410 g001 550
Figure 1. Schematic diagram of the experimental setup. ICL: Interband cascade laser, BS: Beam splitter, RAID: Ring-actuated iris diaphragm, PM: Power meter, PD: Photodetector, OSC: Oscilloscope, ESA: Electrical spectrum analyzer. Solid line: optical path, dashed line: microwave path.
Figure 1. Schematic diagram of the experimental setup. ICL: Interband cascade laser, BS: Beam splitter, RAID: Ring-actuated iris diaphragm, PM: Power meter, PD: Photodetector, OSC: Oscilloscope, ESA: Electrical spectrum analyzer. Solid line: optical path, dashed line: microwave path.
Photonics 09 00410 g001
Photonics 09 00410 g002 550
Figure 2. Power–current characteristic of the ICL at free-running (blue) and subject to variable-aperture optical feedback under DR = 4.0 mm (red).
Figure 2. Power–current characteristic of the ICL at free-running (blue) and subject to variable-aperture optical feedback under DR = 4.0 mm (red).
Photonics 09 00410 g002
Photonics 09 00410 g003 550
Figure 3. Time series (a1–a5), power spectra (b1–b5), and corresponding phase portraits (c1–c5) for some typical dynamical states of the ICL biased at I = 86.00 mA under variable-aperture optical feedback with DR of 3.7 mm (row 1), 3.0 mm (row 2), 2.6 mm (row 3), 2.3 mm (row 4), and 1.0 mm (row 5). The gray lines in the power spectra denote the noise floor. QP: quasi-period state; P1: period one state; P2: period two state; C: chaotic state; S: stable state.
Figure 3. Time series (a1–a5), power spectra (b1–b5), and corresponding phase portraits (c1–c5) for some typical dynamical states of the ICL biased at I = 86.00 mA under variable-aperture optical feedback with DR of 3.7 mm (row 1), 3.0 mm (row 2), 2.6 mm (row 3), 2.3 mm (row 4), and 1.0 mm (row 5). The gray lines in the power spectra denote the noise floor. QP: quasi-period state; P1: period one state; P2: period two state; C: chaotic state; S: stable state.
Photonics 09 00410 g003
Photonics 09 00410 g004 550
Figure 4. Time series (a1–a5), power spectra (b1–b5), and corresponding phase portraits (c1–b5) for some typical dynamical states of the ICL biased at I = 96.00 mA subject to variable-aperture optical feedback with DR of 3.7 mm (row 1), 3.3 mm (row 2), 2.8 mm (row 3), 2.7 mm (row 4), 2.5 mm (row 5), 1.6 mm (row 6), and 1.0 mm (row 7). The gray lines in the power spectra denote the noise floor. MP: multi-period state; LFF: low-frequency fluctuation.
Figure 4. Time series (a1–a5), power spectra (b1–b5), and corresponding phase portraits (c1–b5) for some typical dynamical states of the ICL biased at I = 96.00 mA subject to variable-aperture optical feedback with DR of 3.7 mm (row 1), 3.3 mm (row 2), 2.8 mm (row 3), 2.7 mm (row 4), 2.5 mm (row 5), 1.6 mm (row 6), and 1.0 mm (row 7). The gray lines in the power spectra denote the noise floor. MP: multi-period state; LFF: low-frequency fluctuation.
Photonics 09 00410 g004
Photonics 09 00410 g005 550
Figure 5. (a) Largest Lyapunov exponent as a function of DR under the ICL biased at I = 96.00 mA, and (b) Lyapunov exponent spectrum of the chaotic output obtained under DR = 2.5 mm. For the calculated spectrum, the curves converge to values 1.62 ns−1,0.94 ns−1, 0.37 ns−1, −0.06 ns−1, −0.61 ns−1, −1.75 ns−1, −4.53 ns−1, and −11.89 ns−1 from the top down.
Figure 5. (a) Largest Lyapunov exponent as a function of DR under the ICL biased at I = 96.00 mA, and (b) Lyapunov exponent spectrum of the chaotic output obtained under DR = 2.5 mm. For the calculated spectrum, the curves converge to values 1.62 ns−1,0.94 ns−1, 0.37 ns−1, −0.06 ns−1, −0.61 ns−1, −1.75 ns−1, −4.53 ns−1, and −11.89 ns−1 from the top down.
Photonics 09 00410 g005
Photonics 09 00410 g006 550
Figure 6. Mapping of the dynamical states of the ICL under variable-aperture optical feedback in the parameter space of I and DR. Different color blocks correspond to different dynamical states.
Figure 6. Mapping of the dynamical states of the ICL under variable-aperture optical feedback in the parameter space of I and DR. Different color blocks correspond to different dynamical states.
Photonics 09 00410 g006
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Zhao, M.; Xia, G.; Yang, K.; Liu, S.; Liu, J.; Wang, Q.; Liu, J.; Wu, Z. Nonlinear Dynamics of Mid-Infrared Interband Cascade Lasers Subject to Variable-Aperture Optical Feedback. Photonics 2022, 9, 410. https://doi.org/10.3390/photonics9060410

AMA Style

Zhao M, Xia G, Yang K, Liu S, Liu J, Wang Q, Liu J, Wu Z. Nonlinear Dynamics of Mid-Infrared Interband Cascade Lasers Subject to Variable-Aperture Optical Feedback. Photonics. 2022; 9(6):410. https://doi.org/10.3390/photonics9060410

Chicago/Turabian Style

Zhao, Maorong, Guangqiong Xia, Ke Yang, Shuman Liu, Junqi Liu, Qiupin Wang, Jianglong Liu, and Zhengmao Wu. 2022. "Nonlinear Dynamics of Mid-Infrared Interband Cascade Lasers Subject to Variable-Aperture Optical Feedback" Photonics 9, no. 6: 410. https://doi.org/10.3390/photonics9060410

APA Style

Zhao, M., Xia, G., Yang, K., Liu, S., Liu, J., Wang, Q., Liu, J., & Wu, Z. (2022). Nonlinear Dynamics of Mid-Infrared Interband Cascade Lasers Subject to Variable-Aperture Optical Feedback. Photonics, 9(6), 410. https://doi.org/10.3390/photonics9060410

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop