Laser Ion Acceleration in a Near Critical Density Trap

Abstract

In order to accelerate ions by a laser, we go back to the original and the fundamental idea of how longitudinal field structure generation can be carried out in an ionized media and how particles may be trapped by the created wakefield. The latter condition is characterized by the phase velocity of the longitudinal structure v_ph be equal to the particle trapping width v_tr. Since the trapping width is inversely proportional to the square-root of the mass of the accelerated particles, this width is much shorter for ions than for electrons. Thus, our dictum for laser ion acceleration is to impose a near critical density trap to decelerate laser group velocity, v_g and subsequently to generate longitudinal wakefield to be able to trap ions under the condition of v_tr = v_ph. We demonstrate this concept by PIC simulation and find that this method is effective, and the efficiency of laser ion acceleration is enhanced by a couple of orders of magnitude toward unity.

1. Introduction and History

The utilization of the collective force that resides in plasma was first put forward by V. Veksler in 1956 [1]. The plasma was chosen for two reasons: (A) plasma does not break down as it is already ionized; (B) the forces mediated by plasma are long-range and can interact with many particles. Norman Rostoker was a pioneer who started to utilize an electron beam to accelerate ions (e.g., [2,3,4]). Another early experiment [5] had a relatively thick metallic foil causing the sheath formation that did not propagate with ions, which limited ion acceleration process. In Habs’s team work [6,7] the target thickness has been designed sufficiently thin so that the irradiating laser can form penetration enough to (a) cause the ponderomotive fields and (b) that ponderomotive fields propagate with the ions. The condition to realize this (a) and (b) have been established, which is called the coherent acceleration of ions by laser (CAIL) condition:

$$\sigma =a_0$$

(1)

where $a_0$ is the normalized vector potential of the laser while the normalization of the target thickness is $\sigma =\frac{n_e}{n_c}\frac{d}{{\lambda }_L}$, where $n_e$ is the target density, $n_c$ is the critical density, $d$ is the target thickness, and laser wavelength, ${\lambda }_L$.

Habs’s group likened the CAIL regime to a bullet train “Shinkansen”. In order to pick up the much heavier ions (likened to “passengers”), it was argued that the laser (or its ponderomotive force) induced electrostatic accelerating structure or wake (“Shinkansen locomotive”) must become nearly stationary as it approaches the “station” before to pick up the “passengers”. Thus, we formulate the target in such a way so as to slow down the group velocity of the laser pulse to near 0 ($v_{gr}\to 0$) before the laser interacts with the thin foil.

The goal of this paper is to establish the laser group velocity $v_{gr}\to 0$ in front of the target. The photon group velocity in plasma is governed by

$$v_g=c\sqrt{1-\frac{{\omega }_{pe}^2}{{\omega }^2}}=c\sqrt{1-\frac{n_e}{\gamma n_c}},$$

(2)

where, ${\omega }_{pe}$ and $\omega$ are the plasma and the laser frequency respectively, $\gamma =\sqrt{1+\frac{a_0^2}{2}}$ is relativistic factor. In this paper we assume the weakly relativistic case $a_0\approx 1$. The phase velocity of the accelerating structure speed also equal to the group velocity of the photons [8]. Two regimes are defined in Equation (1) by the ratio of the plasma and critical density: over-dense regime ($n_e>n_c$) with laser not propagating and under-dense regime ($n_e<n_c$) with laser propagating. Thus, the plasma density can be adjusted to slow down the laser group velocity. This technique has been suggested [9] to slow down the laser group velocity to enhance proton acceleration.

In this paper we propose and show a scheme whereas the laser pulse is trapped in a region of less than or close to the critical density, this region is followed by the usual over dense target. It is important to resurrect the concept of trapping velocity and its role in accelerating ions with the laser-driven waves. The trapping velocity was first introduced by O’Neil (1965), among a series of nonlinear wave interaction studies of large (or finite amplitude) plasma waves [10,11]. The trapping velocity is given [12] by

$$v_{tr}=\sqrt{\frac{eE}{mk}},$$

(3)

where E is the electrostatic field in the plasma, m is the mass of the particles that are to be trapped, and k is the wavenumber of the electrostatic wave. If the particle velocity v is less than v_tr, that particle is trapped in a closed elliptical orbit of the equipotential contour orbit of the phase space [12]. If v > v_tr, on the other hand, particles execute untrapped open (and nearly straight) orbit. Thus, in order for a particle to gain substantial energy, it is must be trapped, i.e., v < v_tr. Laser excites a growing wakefield which drives increasing trapping velocity, $v_{tr}.$ Particles with velocity, $v$, that satisfy the condition

$$\left|v_{\varphi }-v\right| < v_{tr}$$

(4)

can be trapped, where $v_{\varphi }$ is the electrostatic wave phase velocity. At saturation, Equation (4) can be written as

$$v_{\varphi }=v_{tr},$$

(5)

indicating the wakefield became large to trap bulk particles with $v\approx 0$ (or $v$ much smaller compared with speed of light). With $v_{\varphi }$~c and $k={\omega }_p/c$, Equation (5) can be used to obtain the Tajima-Dawson field $E_{TD}=m{\omega }_{p}c/e$ [13] with $v_{tr}$ given in Equation (3). This also tells us that for effective ion acceleration, we have to make the phase velocity of the electrostatic wave (or thus the group velocity of the laser) 50 times smaller than the case for electrons. This is the motivation that for effective ion acceleration (and trapping), we need to choose the electron density near (or at) the critical density, reflective of Equation (2).

Because of the near critical density, the wake (or the plasma electrostatic accelerating structure) can now be able to trap ions and begin to increase their velocities. This allows ions to be moving with the often much faster electronic wake eventually. In this configuration trapped laser pulse converts almost all of its energy into particle energy.

In this paper we suggest a strategy to design the density of the pre-target plasma to decelerate and trap the laser photon to achieve a high efficiency laser-to-ion conversion. This is achieved by a laser-created resonator with a high reflectivity inside the pre-target region. The resulting trap-mirror configuration is akin to a to the flying mirror [14,15,16].

We perform parameter scan using 1D3V simulations to arrive at an optimized parameter regime; this is the main goal of Section 2. In Section 3 we examine the detailed evolution of the laser and plasma under this condition. Section 4 extends the 1D study to 2D by simulation the 1D best case scenario in 2D.

2. Far Increased Efficiency of Ion Acceleration by the Trap

We explore the above concept and theoretical expectation by carrying a series of particle in cell (PIC) simulations using the explicit 1D3V EPOCH code [17]. An extensive campaign (several hundred runs) to determine the optimal target yielded results shown in

Table 1. Summary of the most successful runs based on laser-to-proton energy efficiency conversion. Parameter varied are in columns 2–8 are shown in Figure 1. The last two rows display the extreme cases of tailor region only and foil-only.

Run #	${\mathit{L}}_{\mathbf{1}}$	${\mathit{L}}_{\mathbf{2}}$	${\mathit{L}}_{\mathbf{3}}$	${\mathit{n}}_{\mathit{e}\mathbf{1}}$	${\mathit{n}}_{\mathit{e}\mathbf{2}}$	${\mathit{n}}_{\mathit{e}\mathbf{3}}$	Foil Thickness [nm]	Pulse Length $\mathbf{\left[}{\mathit{T}}_{\mathit{L}}\mathbf{\right]}$	Sigma	Effi. [%]
35	0.7	1.4	0.3	0.9	0.8	0.95	320	5	3.2	75
	0.7	1.4	0.3	0.45	0.4	0.43	320	5	3.2	6.2
	0.8	2.8	0.3	0.9	0.8	0.95	320	5	3.2	65
	0.5	0.5	0.15	0.9	0.8	0.95	320	5		4.5
	0.8	1.0	0.3	0.9	0.8	0.95	320	5		57
186	0.7	1.4	0.3	0.9	0.8	0.95	320	16		5.1
184	0.7	1.4	0.3	0.9	0.8	0.95	320	4		71.0
	0.7	1.4	0.3	0.9	0.8	0.95	320	8		42
233	0.2	1.4	0.6	0.9	0.8	0.95	320	8		4.4
34	0.7	1.4	0.3	0.9	0.8	0.95	160	5	1.6	70.1
48	0.7	1.4	0.3	0.95	0.8	0.9	640	5	6.4	59.9
Tailor only	0.7	1.4	0.3	0.95	0.8	0.9	0	5	0	38
Foil only	-	-	-	-	-	-	320	5	3.2	0.5

for a fixed laser $a_0=1$. The density profile to provide the laser pulse trapping prior to the target and their designations are shown in Figure 1 with the pre-foil region divided into 3 segments with varying density. Each run in the campaign has been simulated using a domain [−20, 20] $\mathsf{\mu }\mathrm{m}$ resolved with 10,000 grids resulting with a skin depth $c/{\omega }_{pe}$ resolved with 25 grids, where we assumed electron density, $n_e=10n_c$. To reduce noise, we used the fifth order particle weighing and 5000 particles per grid.

The first row in Table 1 shows the most successful run, yielding the highest proton conversion efficiency of 75%. In contrast, for the foil target alone—without the photon slowdown in the pre-foil—the efficiency is 0.5% (the bottom row of the Table 1). This case shows that the thickness of the typical thin foil 320 nm (we model here the electrons are pre-ionized) is far too greater than the thickness of the collisionless skin depth $c/{\omega }_{pe}$. This makes the lack of laser field penetration into the thin foil. This leads to poor acceleration efficiency. (We note that more realistic cases lead to some alternative developments. For example, the laser may have a pre-pulse, which pre-ionizes part of the electrons in the thin foil.) Under this idealized thin foil laser-foil interaction, we show the most of the laser power is reflected due to the condition of $c/{\omega }_{pe}$ << d (Figure 2).

Another run may be the case where we have no thin foil and institute only the pre-foil density tailoring (PFDT) alone. In this case, we observe the efficiency at 38% in the second from the last line in Table 1. In Table 1 we show various numerical combinations of the PFDT and the thin foil. Upon combination of the foil and PFDT, the proton conversion efficiency increases to 75%.

3. Excited Trapped Waves

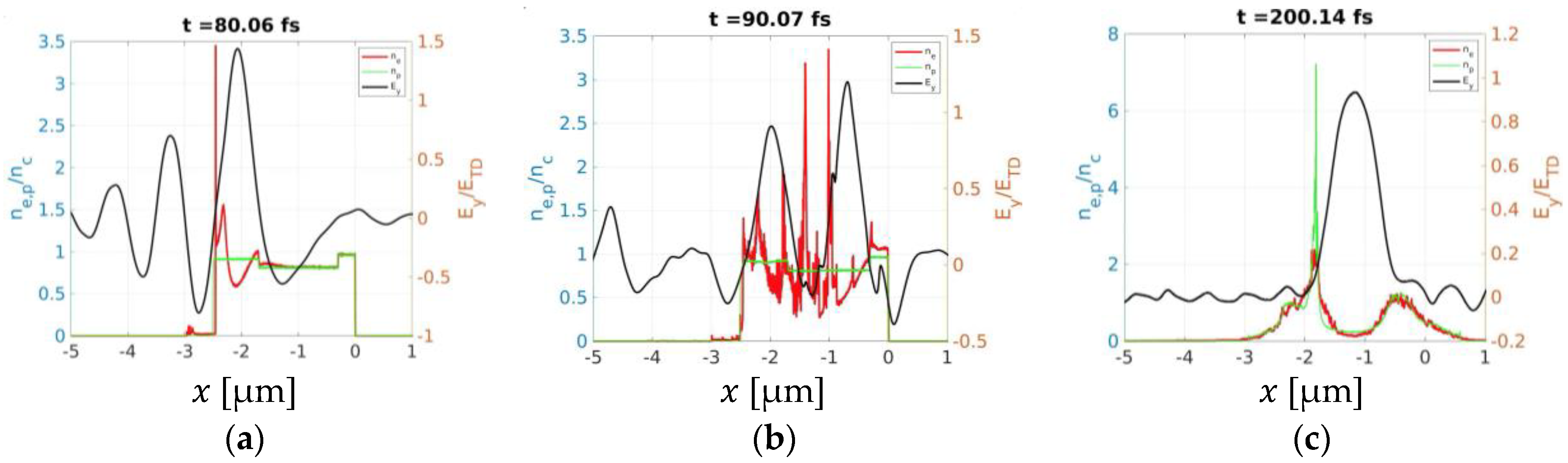
In Figure 2 we track the evolution of the laser pulse interaction with the foil only; the laser transverse field is black, longitudinal electric field is blue, electron and proton densities are red and green respectively. The laser enters the computational domain at t = 0 from the left, and reaches the foil at a normal incidence at 33.4 fs, as shown in Figure 1. Figure 1 shows the full laser wave packet as a Gaussian irradiating 320 nm thick foil composed of hydrogen plasma at density $n_e=10n_c$. In Figure 2b, at 53.4 fs, half of the laser wave packet interacted with the foil compressing the electrons (red) into the foil up to the skin depth ($c/{\omega }_{pe}$). Lastly, Figure 2c, at 70.1 fs, shows the full wave pocket reflect and reverse the direction of propagation. Since the thickness of the foil is much greater than the skin depth, very little of the laser field has transmitted. However, we can see the longitudinal electric field (blue) set up at the backside of the foil indicating electrons have penetrated the foil and created the accelerating field. Overall, since the laser-plasma interaction duration is short, the conversion efficiency from the laser to the particles is very low ~0.5%. The photon group velocity, $v_g=0,$ has achieved our objective, however, immediately reaccelerated to the speed of light.

Lengthening of the laser-plasma interaction is accomplished by introduction of a subcritical region ($n_e<n_c$) in front of the over dense foil as shown in Figure 1 which reduces the photon group velocity well below the speed of light. The density is specifically tailored to allow the laser pulse trapping by dividing the region into 3 segments, i.e., without the over dense foil. In this scenario, the laser pulse impinges from left and the peak intensity arrives at 75.1 fs. The evolution of the laser pulse and the electron and proton density in the underdense tailor region is shown in Figure 3. The laser dispersion relation in vacuum for the laser carrier (i.e., the central frequency of the laser) is, of course, the well-known $\omega =k c$, where $\omega$ is the frequency of the carrier of the laser, $k$ is the wavenumber. When the laser pulse enters the near critical density trap, the dispersion relation changes to accommodate the plasma frequency ${\omega }_p$ that is close to the laser frequency $\omega$. In the trap region the dispersion relation of the photon is ${\omega }^2={\omega }_p^2+k_t^2{c}^2$, since the laser frequency is conserved, we obtain

$$k_t=\sqrt{k^2-\frac{{\omega }_p^2}{c^2}}.$$

(6)

Because the trap density is near critical by our design, the wavenumber of the trap $k_t$ is much smaller than the vacuum laser wavelength, i.e., the wavelength is expanded as it can. The description leading to Equation (6) provides a credible explanation of the laser entering stationary underdense target, however, it fails to capture the long-time laser behavior within the trapped region.

Figure 3a shows the target after the laser pulse entrance. The laser pulse ponderomotive force strongly modifies the local electron density while the ion density remains unperturbed since proton respond on ~$1/{\omega }_{pi}$ times. Indeed, this first stage is akin to laser wakefield acceleration. However, in the next stage the strongly perturbed electron density exceeds the critical density and forms a flying mirror [14,15,16] that causes the laser pulse breaking up and trapping as shown in Figure 3b. At this stage the laser pulse entered the plasma region, however, the proton density remains unperturbed. The laser pulse trapping is achieved within a resonator with a high reflectivity that has an over-critical density on both ends and a sub-critical density in the middle shown in Figure 3c together with the highly perturbed proton density. Overall, the efficiency conversion is 38%. However, a large portion of the laser energy is transmitted.

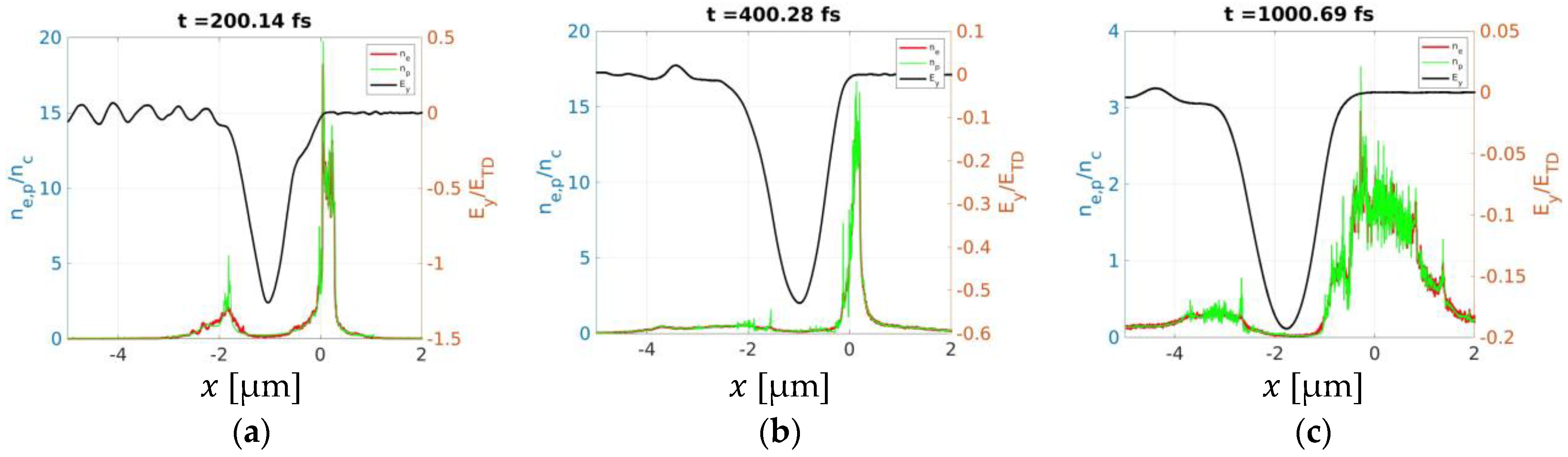
To suppress the laser energy transmission through the target, we introduce the overdense foil behind segment 3 shown in Figure 1. The laser-plasma evolution is similar to the case with tailor region only but with very little transmission shown in Figure 4a. Due to this unique configuration of laser pulse trapping, a half-cycle pulse is created in front of the foil for long times; Figure 4b shows the pulse at 1 ps with 20% of the peak transverse electric retained, and Figure 4c shows retention of almost 10% at 2 ps. Once such a long wavelength mode (even a subcyclic mode) is established, it exerts ponderomotive forces on the plasma. Because the group velocity is very small, as required in Equation (5), the ponderomotive force is effective in establishing an electrostatic longitudinal wave with small phase velocity that is equal to or less than the trapping width even for ions, i.e., accelerating not only electrons but also ions. This explains the enhanced efficiency of laser energy conversion into ions, once ions catch up with electron acceleration, most of the electron energy is now converted into ions (because they acquire the similar velocities and the large ion-to-electron mass ratio). Furthermore, this is accompanied by the trapped laser pulse expelling plasma electrons and ions, thus forming a depressed plasma density where the large amplitude laser is located with small $k_t$ conveyed in Figure 4. The eigenmode is not only trapped but also modifies the trapping region by ejecting plasma to provide a deeper well and guide for trapping. The mode period preserves the initial laser pulse period $T_L=3.3$ fs.

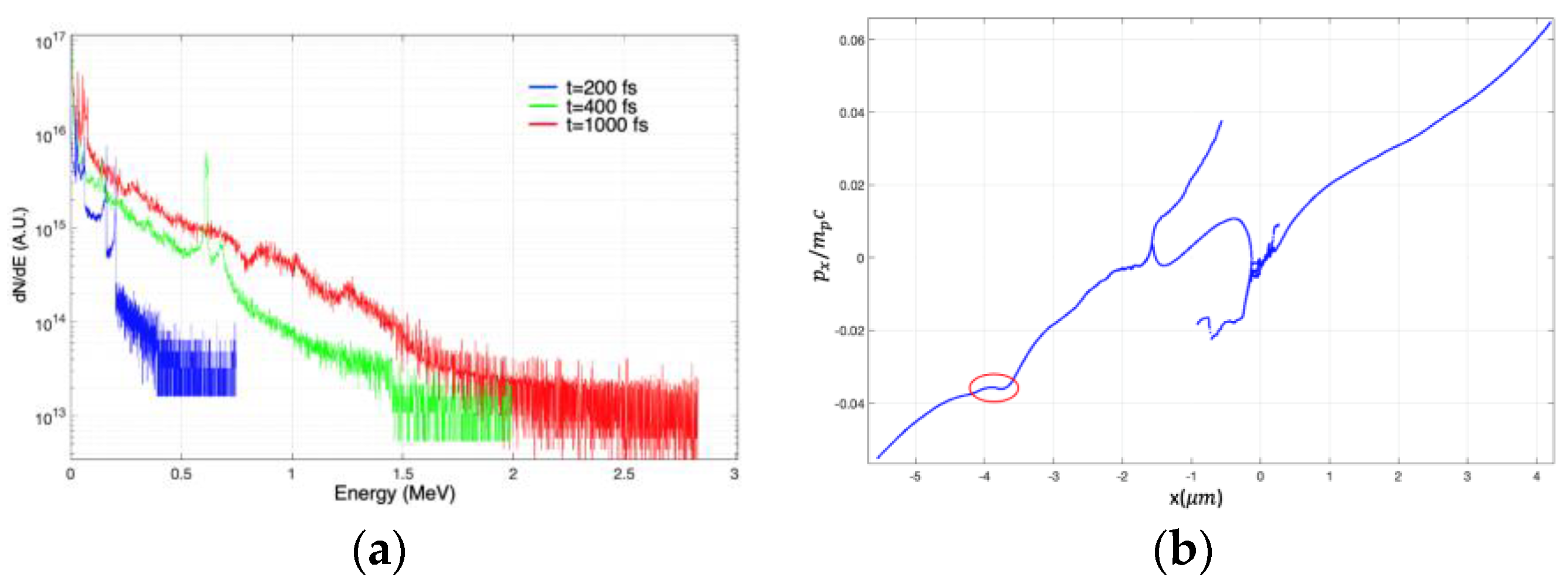
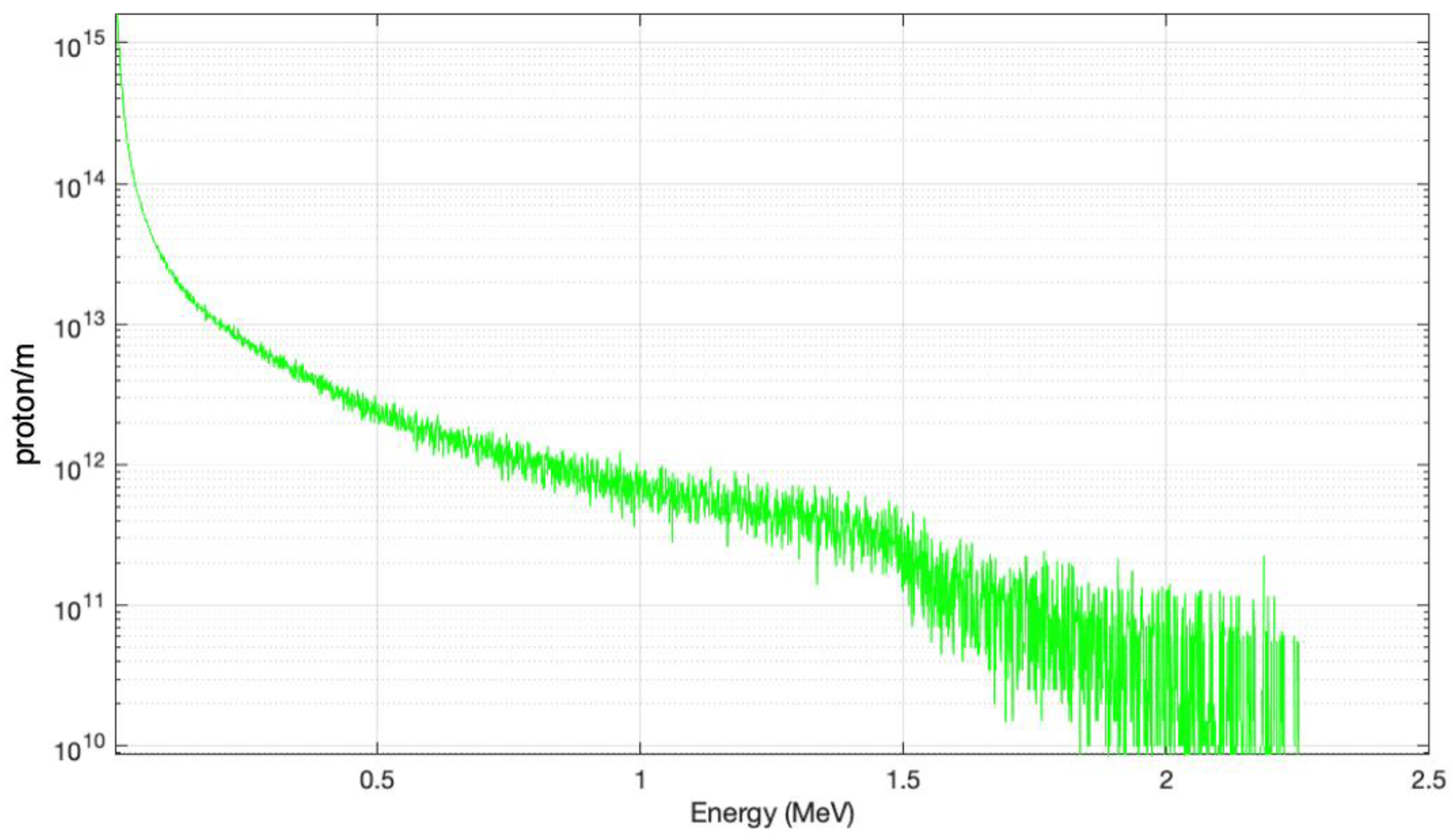
The proton energy spectrum is shown in Figure 5a for three different times corresponding to time slices shown in Figure 4. The earlier time spectra exhibit quasi-monoenergetic features at t = 400 fs protons with energy around 0.6 MeV coalesce into a beam indicating trapped protons. This feature is also depicted (red ellipse) in the phase space plot of Figure 5b is located at the leading edge of the plasma expanding to the left.

However, proton trapping is observed in the later stages as well. e.g., Figure 6 shows the proton phase plot at t = 1668 fs with the electrostatic potential color map plotted on the bottom. The potential exhibits many peaks and valleys with the trapping region located around −4 $\mathsf{\mu }\mathrm{m}$, the inset shows the zoomed in portion of the trapped region demonstrating the protons are confined and accelerated by the potential. The electrostatic potential has been derived from the electron and proton density and Poisson equation. The centroid of the trapped region is moving to the left with energy 47 keV which compares well to $p_x=-0.01 m_{p}c$.

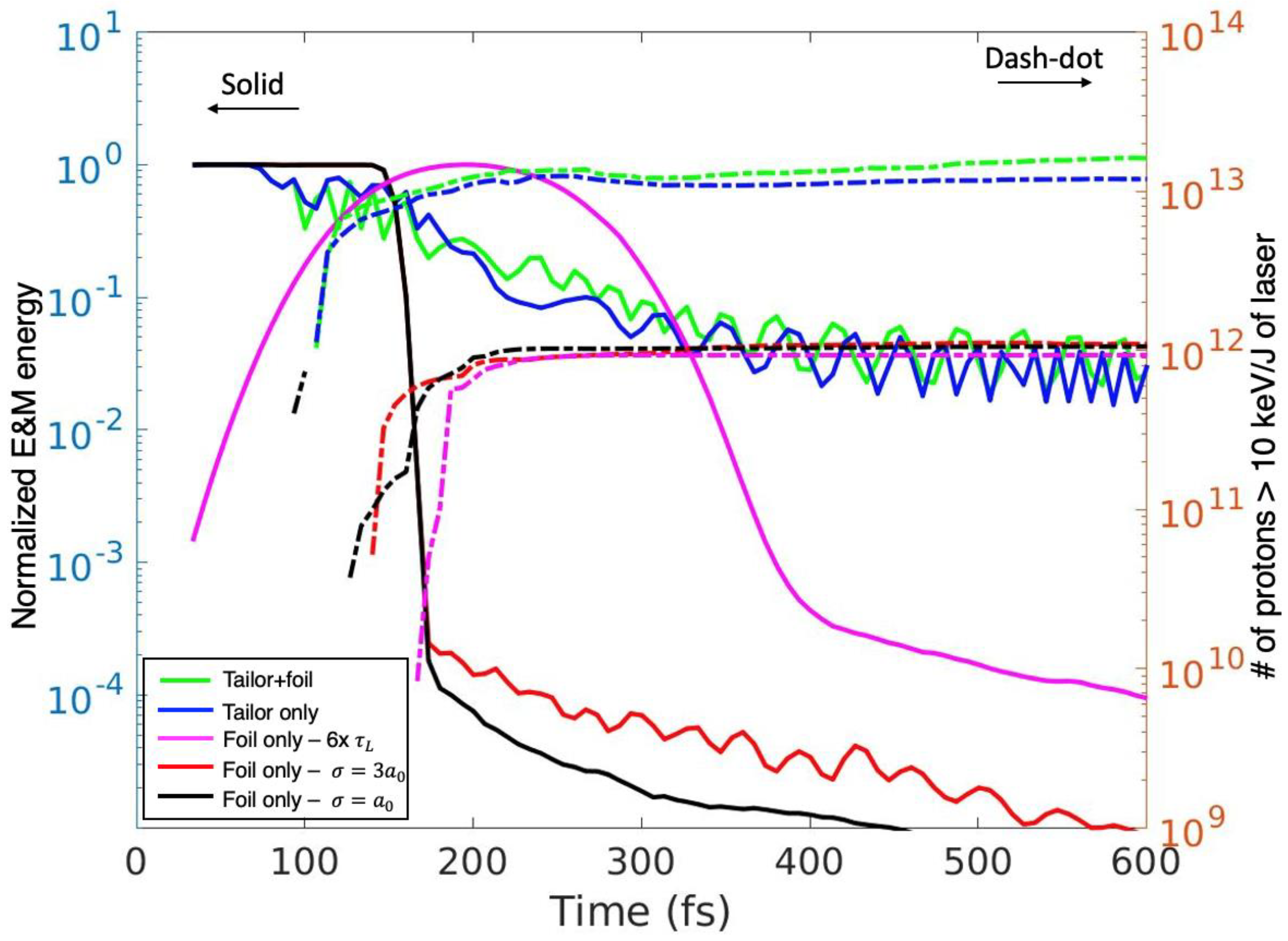
To obtain a comparison between the various cases, we plot the total electromagnetic energy in the computational domain (solid) and the number of protons exceeding 10 keV normalized to laser energy, $Y_p$, (dash-dot) vs. time in Figure 7. We can observe that for the case of foil only the electromagnetic energy in the computational domain disappears on a time scale of the laser pulse return trip upon reflection from the overdense foil. Interestingly, for the case of 6 times longer pulse (magenta) the $Y_p$ is the same as for the shorter laser pulse (${\tau }_L=5T_L$) cases and foil only. In contrast, for the cases of tailor only (blue) and tailor + foil (green) the stored energy in the electromagnetic fields is retained for much longer duration, consequently $Y_p$ is greatly enhanced.

The trapping region allows the laser pulse to enter into a unique entity of half cycled pulse for a long time. The amplitude of this half cycle laser is very high, as the laser pulse is now collapsed on top of each other to form the narrow condensation of the laser trapping. Features of coherent sub-cyclic photon formation by itself must be of interest to the ultrafast photonics in general and attosecond laser science in particular [18]. There might be additional nonlinear plasma interaction when the stationary trap of a large amplitude plasma waves in the density trap [19].

We believe that the enhanced (or acquired) high level of coherent phase space structure (which we call in a general language as “structure formation” and coherent structure at it) of electrons and in particular that of ions are quite remarkable. In earlier works [20,21], Rau et al. remarked that sub-cyclic laser can make more coherent particle acceleration and its phase space structure. We, in fact, observe such a highly coherent phase space structures in our simulations. We have yet to learn how significant such highly coherent structural formation might result into new phenomena and physics.

4. Filamentation in 2D

We have carried out a 2D3V PIC simulation studies, guided by the extensive 1D simulation insights. A linearly polarized laser with ${\tau }_L=5 T_L$ pulse length is injected through the left boundary onto the target of special tailored ionized hydrogen plasma (again pre-ionized plasma is a rough but good approximation to the high intensity laser irradiation with $a_0=1$, which necessitates immediate above-field ionization). The longitudinal density profile cross section is same as shown in Figure 1 for the 1D case with transverse extend of $\pm 15 \mathsf{\mu }\mathrm{m}$. The computational domain of 40 × 40${ \mathsf{\mu }\mathrm{m}}^2$ is used and grid of 4000 × 2000 is applied with 40 particles per species per cell with 17 million particles per species. The laser focal length is $19 \mathsf{\mu }\mathrm{m}$ thus the laser is focused $1 \mathsf{\mu }\mathrm{m}$ in front of the foil, i.e., in the middle of the tailor region. The beam has a Gaussian profile $\exp \left(-y^2/w_0^2\right)$ with $w_0=4 \mathsf{\mu }\mathrm{m}$ focal spot.

The 2D energy spectrum is shown in Figure 8 at t = 1000 fs with the evolution of the proton and electron density highlighted in Figure 9. A proton conversion efficiency of 38% is achieved for this tailor profile, and furthermore an efficiency of 55% is reached for the electrons. This is somewhat a reduction from the more ideal 1D results we cited above. We will follow with further studies and optimizations in future, however for the purpose of this paper, the foil only case with $3a_0=\sigma$ results in efficiency of 0.5% and maximum proton energy of 0.05 MeV.

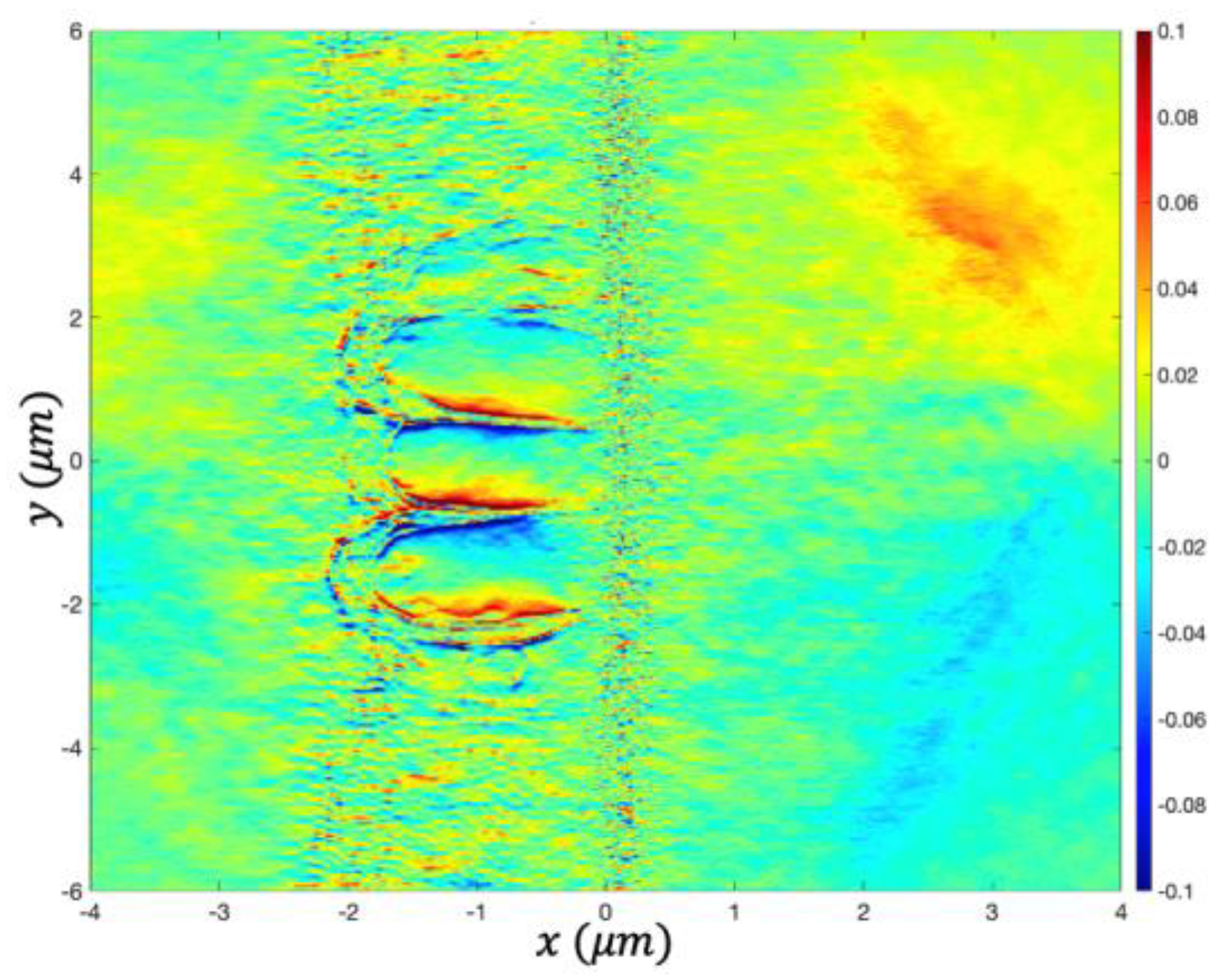
The transverse electric field applies the ponderomotive force in 2D and is thus somewhat diminished from the 1D case as shown in Figure 10 at t = 400 fs. The maximum $E_y$ in the 1D case was 0.5, in contrast the maximum field for the 2D case is 0.2.

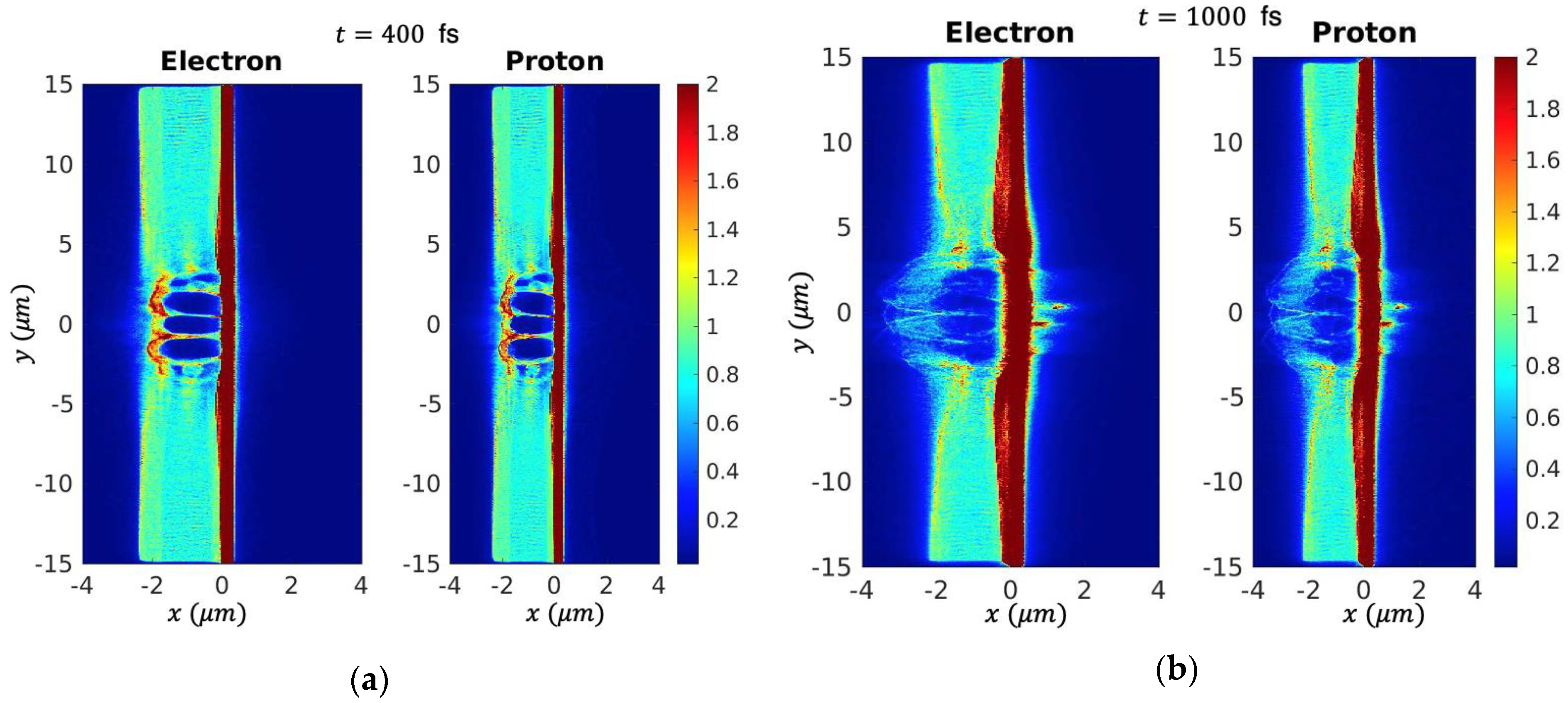
The electron and proton densities are shown in Figure 9. At t = 400 fs both electron and proton densities develop a density bubble similar to the density depression in the 1D case. This bubble is an indication of laser pulse trapping in the near critical density tailor region. Since both the proton and the electron exhibit the bubble, we can conclude that the protons are following electrons closely even at the later stages as shown in Figure 9b at t = 1000 fs. The laser pulse upon interaction with the tailor region undergoes strongly non-linear interaction similar to Figure 3b, thus it is remarkable that out of this chaos the plasma developes a well-organized structure shown in Figure 9.

5. Discussions

With the development of nanomaterial [22,23,24,25] and their adoption into many fields, we believe that the near-critical region proposed in this paper can be artificially grown using carbon nanotubes (CNT), carbon nano foams or other carbon allotropes. Indeed, this idea has been simulated [9,26,27]. Nanomaterials can be grown to precisely tailor density by setting the substrate structure, for example, the design of the precise profile of the critical or near critical density is within our capabilities.

We also observe that the laser that is trapped shows a marked coherence. In particular, as shown in Figure 4, we observe subcyclic laser pulse generated in side of the trap. We could design to make subcyclic laser pulse and condensation of entrant non-subcyclic laser pulse may be done by adopting out density trap strategy. Such a scheme may also help as a technique to generate subcyclic laser pulses. Rau et al. also mentioned that the use of subcyclic laser pulse is helpful to create more coherent wakefield acceleration than the case with longer laser pulse length [20,21]. Also, such creation of an intense laser subcyclic fields may be a useful technique to lend a path of intense subcyclic laser pulse generation field [18,28].

A potential application of the ion acceleration with a weakly relativistic laser presented here is a neutron generation through the deuterium and tritium fusion. Such neutrons have a large scope of applications ranging from neutron imaging to the incineration of spent nuclear fuel [29]. We thus look forward to the application of the present laser ion acceleration with the density trap to the transmutation of the spent nuclear waste by having efficient and effective ion acceleration and its driven neutrons may be of interest [30,31,32,33,34,35,36]. Since the present acceleration technique is (relatively) simple, compact, and controllable (via the laser operation), its application to the purpose of transmutator may be promising and operationally attractive [36]. It may be multiple of small ion accelerators that are attached to the vessel of the transmutator. This may be far different from a large and high energy (several 100 MeV or even GeV) accelerator [31]. We now have a candidate for high efficiency ion acceleration in a tiny accelerator for such a purpose.

In addition, low energy application (compared with high energy physics) of such a trap to nuclear physics may be of interest. For example, in a nuclear physics domain ions from our method may explore by simple and abundant ions from the present method, to help increase luminosity or other issues in possible experiments to test recent topic in nuclear physics experiments such as the one by [37,38].

6. Conclusions

We have demonstrated by simulations the concept of near critical density trap to effectively trap laser pulse and accelerate ions with efficiency of up to 75%. The mechanism is to make the laser group velocity sufficiently small so that the phase velocity of the induced electrostatic wave (wakefield) is also made substantially reduced. The smallness of the group velocity (“Shinkansen (bullet) train” (laser pulse)) is to pick up heavy ions (“passengers”). Once laser pulse is trapped, this process continues till most of the trapped laser pulse energy is used up to convert its energy into ion energy. This is the reason why ion acceleration is made very efficient. The increase of the efficiency from the cases without the density trap to the ones with it is a spectacular jump from sub 1% efficiency to over 70%. Further investigation will include laser irradiation of a mixture of carbon and hydrogen, as well as a more realistic portrayal of CNT.