Supporting Quadric Method for Designing Freeform Mirrors That Generate Prescribed Near-Field Irradiance Distributions
Abstract
1. Introduction
2. Methods
2.1. Problem Statement
2.2. Envelope Representation of the Mirror Surface
2.3. Supporting Quadric Method
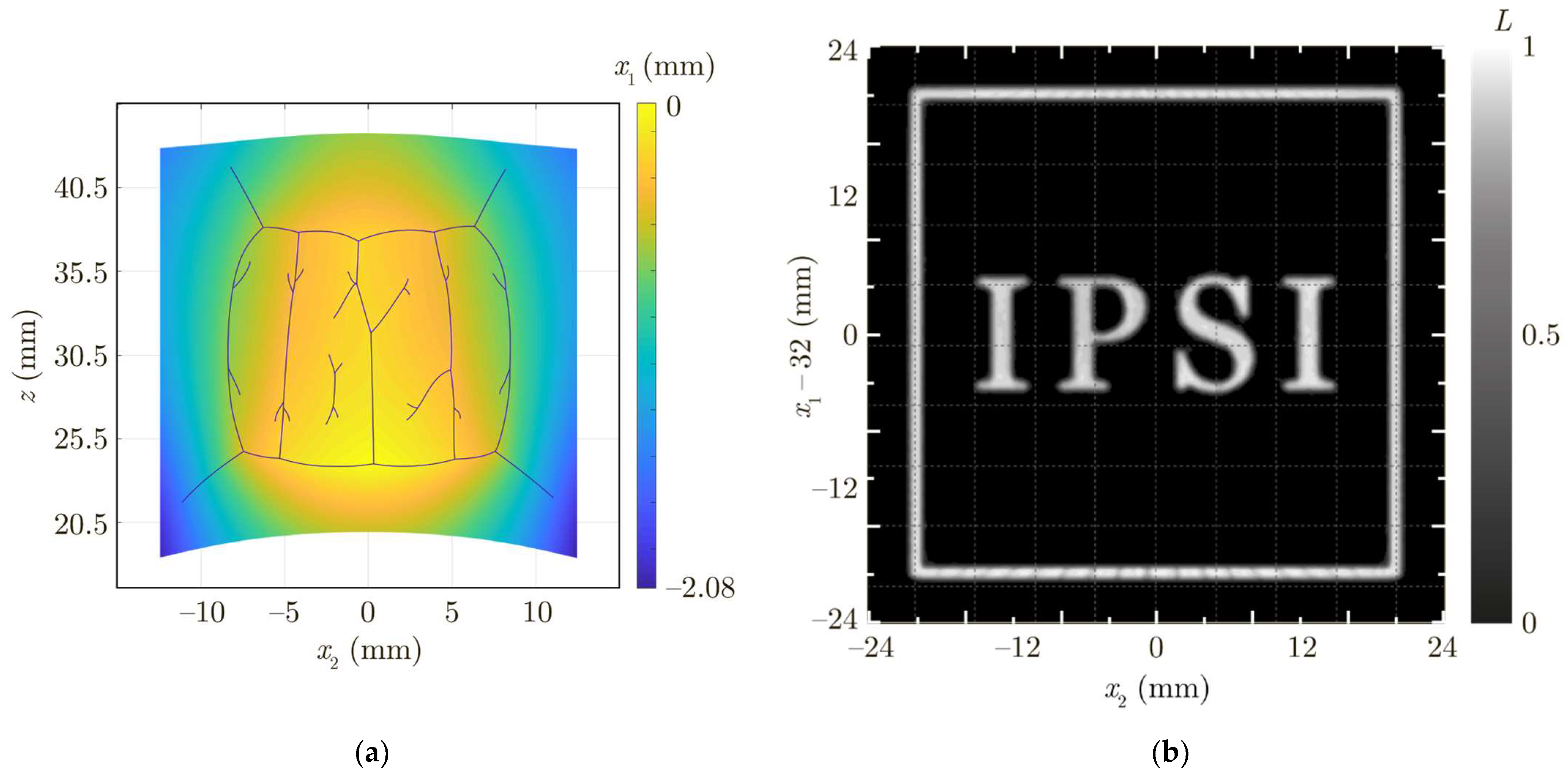
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, R.; Feng, Z.; Zheng, Z.; Liang, R.; Benítez, P.; Miñano, J.C.; Duerr, F. Design of freeform illumination optics. Laser Photon. Rev. 2020, 12, 1700310. [Google Scholar] [CrossRef]
- Ries, H.; Muschaweck, J. Tailored freeform optical surfaces. J. Opt. Soc. Am. A 2002, 19, 590–595. [Google Scholar] [CrossRef]
- Wu, R.; Xu, L.; Liu, P.; Zhang, Y.; Zheng, Z.; Li, H.; Liu, X. Freeform illumination design: A nonlinear boundary problem for the elliptic Monge–Ampére equation. Opt. Lett. 2013, 38, 229–231. [Google Scholar] [CrossRef]
- Wu, R.; Zhang, Y.; Sulman, M.M.; Zheng, Z.; Benítez, P.; Miñano, J.C. Initial design with L2 Monge-Kantorovich theory for the Monge–Ampère equation method in freeform surface illumination design. Opt. Express 2014, 22, 16161–16177. [Google Scholar] [CrossRef]
- Wu, R.; Chang, S.; Zheng, Z.; Zhao, L.; Liu, X. Formulating the design of two freeform lens surfaces for point-like light sources. Opt. Lett. 2018, 43, 1619–1622. [Google Scholar] [CrossRef]
- Brix, K.; Hafizogullari, Y.; Platen, A. Designing illumination lenses and mirrors by the numerical solution of Monge–Ampère equations. J. Opt. Soc. Am. A 2015, 32, 2227–2236. [Google Scholar] [CrossRef]
- Brix, K.; Hafizogullari, Y.; Platen, A. Solving the Monge–Ampère equations for the inverse reflector problem. Math. Model. Methods Appl. Sci. 2015, 25, 803–837. [Google Scholar] [CrossRef]
- Prins, C.R.; ten Thije Boonkkamp, J.H.M.; van Roosmalen, J.; IJzerman, W.L.; Tukker, T.W. A Monge–Ampère-solver for free-form reflector design. SIAM J. Sci. Comput. 2014, 36, B640–B660. [Google Scholar] [CrossRef][Green Version]
- Shen, F.; Yang, L.; Hu, G.; Ding, Z.; She, J.; Zhang, Y.; Wu, R. Freeform and precise irradiance tailoring in arbitrarily oriented planes. Opt. Express 2021, 29, 42844–42854. [Google Scholar] [CrossRef]
- Bösel, C.; Gross, H. Ray mapping approach for the efficient design of continuous freeform surfaces. Opt. Express 2016, 24, 14271–14282. [Google Scholar] [CrossRef] [PubMed]
- Doskolovich, L.L.; Bykov, D.A.; Mingazov, A.A.; Bezus, E.A. Optimal mass transportation and linear assignment problems in the design of freeform refractive optical elements generating far-field irradiance distributions. Opt. Express 2019, 27, 13083–13097. [Google Scholar] [CrossRef]
- Doskolovich, L.L.; Bykov, D.A.; Andreev, E.S.; Byzov, E.V.; Moiseev, M.A.; Bezus, E.A.; Kazanskiy, N.L. Design and fabrication of freeform mirrors generating prescribed far-field irradiance distributions. Appl. Opt. 2020, 59, 5006–5012. [Google Scholar] [CrossRef] [PubMed]
- Bykov, D.A.; Doskolovich, L.L.; Bezus, E.A. Multiscale approach and linear assignment problem in designing mirrors generating far-field irradiance distributions. Opt. Lett. 2020, 45, 3549–3552. [Google Scholar] [CrossRef]
- Doskolovich, L.L.; Bykov, D.A.; Andreev, E.S.; Bezus, E.A.; Oliker, V. Designing double freeform surfaces for collimated beam shaping with optimal mass transportation and linear assignment problems. Opt. Express 2018, 26, 24602–24613. [Google Scholar] [CrossRef] [PubMed]
- Caffarelli, L.; Kochengin, S.; Oliker, V. On the numerical solution of the problem of reflector design with given far-field scattering data. Contemp. Math. 1999, 226, 13–32. [Google Scholar]
- Kochengin, S.; Oliker, V. Computational algorithms for constructing reflectors. Comput. Vis. Sci. 2003, 6, 15–21. [Google Scholar] [CrossRef]
- Oliker, V. Mathematical aspects of design of beam shaping surfaces in geometrical optics. In Trends in Nonlinear Analysis; Kirkilionis, M., Krömker, S., Rannacher, R., Tomi, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 193–224. [Google Scholar]
- Fournier, F.R.; Cassarly, W.J.; Rolland, J.P. Fast freeform reflector generation using source-target maps. Opt. Express 2010, 18, 5295–5304. [Google Scholar] [CrossRef]
- Michaelis, D.; Schreiber, P.; Brauer, A. Cartesian oval representation of freeform optics in illumination systems. Opt. Lett. 2011, 36, 918–920. [Google Scholar] [CrossRef]
- Oliker, V. Controlling light with freeform multifocal lens designed with supporting quadric method (SQM). Opt. Express 2017, 25, A58–A72. [Google Scholar] [CrossRef]
- Doskolovich, L.L.; Moiseev, M.A.; Bezus, E.A.; Oliker, V. On the use of the supporting quadric method in the problem of the light field eikonal calculation. Opt. Express 2015, 23, 19605–19617. [Google Scholar] [CrossRef]
- Mingazov, A.A.; Bykov, D.A.; Bezus, E.A.; Doskolovich, L.L. On the use of the supporting quadric method in the problem of designing double freeform surfaces for collimated beam shaping. Opt. Express 2020, 28, 22642–22657. [Google Scholar] [CrossRef] [PubMed]
- Glimm, T.; Oliker, V. Optical design of single reflector systems and the Monge-Kantorovich mass transfer problem. J. Math. Sci. 2003, 117, 4096–4108. [Google Scholar] [CrossRef]
- Wang, X.-J. On design of a reflector antenna II. Calc. Var. Partial. Differ. Equ. 2004, 20, 329–341. [Google Scholar] [CrossRef]
- Glimm, T.; Oliker, V. Optical design of two-reflector systems, the Monge-Kantorovich mass transfer problem and Fermat’s principle. Indiana Univ. Math. J. 2004, 53, 1255–1277. [Google Scholar] [CrossRef][Green Version]
- Doskolovich, L.L.; Mingazov, A.A.; Byzov, E.V.; Skidanov, R.V.; Ganchevskaya, S.V.; Bykov, D.A.; Bezus, E.A.; Podlipnov, V.V.; Porfirev, A.P.; Kazanskiy, N.L. Hybrid design of diffractive optical elements for optical beam shaping. Opt. Express 2021, 29, 31875–31890. [Google Scholar] [CrossRef]
- Doskolovich, L.L.; Andreev, E.S.; Kharitonov, S.I.; Kazansky, N.L. Reconstruction of an optical surface from a given source-target map. J. Opt. Soc. Am. A 2016, 33, 1504–1508. [Google Scholar] [CrossRef]
- Zalgaller, V.A. The Theory of Envelopes; Nauka: Moscow, Russia, 1975. [Google Scholar]
- Bykov, D.A.; Doskolovich, L.L.; Mingazov, A.A.; Bezus, E.A. Optimal mass transportation problem in the design of freeform optical elements generating far-field irradiance distributions for plane incident beam. Appl. Opt. 2019, 58, 9131–9140. [Google Scholar] [CrossRef]
- Glimm, T. A rigorous analysis using optimal transport theory for a two-reflector design problem with a point source. Inverse Probl. 2010, 26, 045001. [Google Scholar] [CrossRef]
- Doskolovich, L.L.; Mingazov, A.A.; Bykov, D.A.; Andreev, E.S.; Bezus, E.A. Variational approach to calculation of light field eikonal function for illuminating a prescribed region. Opt. Express 2017, 25, 26378–26392. [Google Scholar] [CrossRef]
- Tracepro, Illumination and Non-Imaging Optical Design & Analysis Tool. Available online: https://lambdares.com/tracepro/ (accessed on 29 December 2021).



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doskolovich, L.L.; Byzov, E.V.; Mingazov, A.A.; Karapetian, G.J.; Smorodin, V.I.; Kazanskiy, N.L.; Bykov, D.A.; Bezus, E.A. Supporting Quadric Method for Designing Freeform Mirrors That Generate Prescribed Near-Field Irradiance Distributions. Photonics 2022, 9, 118. https://doi.org/10.3390/photonics9020118
Doskolovich LL, Byzov EV, Mingazov AA, Karapetian GJ, Smorodin VI, Kazanskiy NL, Bykov DA, Bezus EA. Supporting Quadric Method for Designing Freeform Mirrors That Generate Prescribed Near-Field Irradiance Distributions. Photonics. 2022; 9(2):118. https://doi.org/10.3390/photonics9020118
Chicago/Turabian StyleDoskolovich, Leonid L., Egor V. Byzov, Albert A. Mingazov, Gor J. Karapetian, Vitalii I. Smorodin, Nikolay L. Kazanskiy, Dmitry A. Bykov, and Evgeni A. Bezus. 2022. "Supporting Quadric Method for Designing Freeform Mirrors That Generate Prescribed Near-Field Irradiance Distributions" Photonics 9, no. 2: 118. https://doi.org/10.3390/photonics9020118
APA StyleDoskolovich, L. L., Byzov, E. V., Mingazov, A. A., Karapetian, G. J., Smorodin, V. I., Kazanskiy, N. L., Bykov, D. A., & Bezus, E. A. (2022). Supporting Quadric Method for Designing Freeform Mirrors That Generate Prescribed Near-Field Irradiance Distributions. Photonics, 9(2), 118. https://doi.org/10.3390/photonics9020118






