Abstract
Theoretical modelling has been used to calculate the holographic recording beam angles required in air (at any recording wavelength) to produce a Volume Holographic Optical Element (VHOE) for any defined input and output beam angles. The approach is used to facilitate the design and fabrication of diffractive coupling elements through a holographic process that avoids the use of coupling prisms during recording and will help in the design of recording arrangements that better suit the mass production of low-cost elements, especially those designed for non-normal incidence. In this study, the recording angles needed for a range of recording wavelengths were explored for VHOE couplers designed for input angles (in air) ranging from 0° to −55°. Then, in order to validate the model, holographic recording in Bayfol HX 200 photopolymer at 532 nm was used to fabricate photopolymer VHOE couplers for 633 nm light (−45° input angle in air). Bragg curves obtained experimentally for different probe wavelengths (403 nm, 532 nm and 633 nm) confirm the recording of the desired grating structures to a precision of ±1°, and coupling is demonstrated at 633 nm with a diffraction efficiency of up to 72%. Furthermore, the model is used to identify the origins of some weaker spurious gratings observed alongside the expected ones.
Keywords:
holography; coupler; waveguide; non-normal incidence; Bayfol; volume holography; spurious gratings; HOE; VHOE; diffraction 1. Introduction
Holographic optical elements (HOEs) are holograms whose purpose is to replicate the function of optical components, such as mirrors, lenses, etc., by diffracting light. HOEs have the potential for high efficiency, have tuneable angular and wavelength selectivity and are relatively low-cost to produce. A key advantage is that, being thin and lightweight, they are well suited to compact systems and films or coatings, but they also have restricted chromatic and angular bandwidths. Volume HOEs have been developed for a broad range of applications, including data storage [1,2,3], optical communication [4,5,6,7,8] and others [9,10], but two of the most active research areas in recent years have been augmented reality displays and solar concentrators.
Augmented reality (AR) displays combine a digital image with the real-world view [11]; head-up displays (HUDs) and head-mounted displays (HMDs) have typical fields of view (FOVs) of 30° and 45°, respectively [12]. HOEs have been used as part or all of the optical system. For example, Li et al. created a holographic augmented reality display using a mirror-lens HOE [13], and Piao et al. fabricated full-colour HOEs to replace both the couple-in and couple-out optics in a head-mounted display [14], whereas in [15], which involved a waveguide-based system, a prism was used as an in-coupler, and a reflective hologram was used as an out-coupler. Diffraction efficiencies of 25% were achieved from three exposures at RGB wavelengths. Zhang et al. proposed and experimentally demonstrated a holographic waveguide display system with a planar hologram as an in-coupler and a volume hologram as an out-coupler to correct the chromatic dispersion and increase the efficiency of the waveguide display [16]. In [17], an integrated waveguide display system consisting of an infrared volume holographic grating (IVHG) and a visible-light grating was recorded on the same waveguide. The IVHG was used for eye tracking, and the visible grating was used for the augmented reality display. Gu et al. developed a laminated composite polarized volume grating (LCOM-PVG) with a reflective PVG that was left-circularly polarised and with another reflective PVG that was right-circularly polarised to increase the angular bandwidth [18]. Shen et al. have recently implemented an RGB display using coupler VHOEs [19].
VHOEs have also long been considered an attractive option for use in conjunction with photovoltaic (PV) devices in solar energy collection, more recently in spectrum-splitting holographic solar concentrators and multiplexed systems [20,21,22,23,24]. Muller et al. developed a holographic system for daylighting, solar shading and PV power generation. They installed laminated glass with HOEs in three terraced houses in Stuttgart. In winter, relatively little solar radiation was used to heat the room, and in the rest of the seasons, it was used for heat, light and the generation of electricity [25]. VHOEs can act as deflectors and/or concentrators, increasing the solar collection angle of the PV cell and improving efficiency and/or lowering costs [26]. Prism Solar Technology recently patented solar concentrator systems using transmission and reflection HOEs ([27,28]).
These VHOEs can be fabricated in lightweight polymer films via the light-induced refractive index modulation of the photosensitive layers, which occurs due to the polymerisation and diffusion of monomers within the layer [29,30]. Some of the parameters that affect the final diffraction efficiency of VHOEs are the layer thickness, the exposure intensity and energy used, the ratio between the energies of the object and reference beams, the dark reaction time (time between recording and curing) and the spatial frequency [30,31,32].
Coupler HOEs have a broad range of applications since they are designed to deflect light that would otherwise be transmitted through a film or layer and trap it through total internal reflection.
The most straightforward way to holographically record any diffractive optical element is to use recording beams with a wavelength identical to the wavelength at which the coupler will function. In that case, recording wavefronts identical to the intended input and output wavefronts can be used. They interfere to create the photonic structure required to convert the desired input to the desired output (as well as the reverse). However, for coupler elements, this presents a particular challenge, since one of the beams is, by definition, trapped within the medium. Arranging the two recording beams to enter the medium and overlap appropriately, therefore, requires the use of prisms and index matching [33]. While this is readily achievable in a laboratory setting, it poses much larger challenges in mass production, mainly because of the need to avoid an air gap, and is not suitable for any kind of non-contact master-copying automated production method.
An alternative approach is to determine the slant and spatial frequency of the grating needed to diffract the input beam appropriately at the desired wavelength and then use a different recording wavelength to record that structure. With careful design, this approach can exploit the change in the Bragg angle with the wavelength so that the desired structure can be holographically recorded at beam angles that do not require the use of prisms. Several researchers have demonstrated this approach with success [24,34,35], usually for situations where one of the beams is required to be normally incident, which reduces the design complexity.
Gallego et al. [36] recently demonstrated this approach for couplers designed for use at 633 nm; they carried out holographic recording at green wavelengths and pointed out that different combinations of spatial frequency and slant can be used to achieve coupling in the final device. The authors demonstrate three examples, two with normal incidence and one with slightly off-normal incidence. They demonstrate the approach in three different materials that are more or less suited to different combinations of slant and spatial frequency.
To the best of our knowledge, to date, no systematic modelling has been carried out for the holographic recording of couplers of non-normally incident light, with a view to exploit this approach for a wide range of incidence angles.
Many authors have published on the subject of modelling volume-phase gratings, holograms and holographic optical elements [37,38,39], and the relationship of the grating diffraction efficiency to the grating spacing, thickness, refractive index modulation, angle of incidence and wavelength has long been understood. On this basis, sophisticated models for predicting the diffraction behaviour of grating structures have been developed, and excellent agreement was demonstrated between theory and the experimental results of diffraction analysis across a very wide range of angles of incidence [40], although additional spurious gratings were noted in the experimental data. More recent work [41] modelled both the angle of incidence and wavelength simultaneously, allowing the visualisation of a large number of the main characteristics of a particular grating structure through a single angular-spectral map and a comparison with a similar map based on experimentally obtained data. Spurious gratings were again noted. A number of authors have also modelled the chemical and physical processes within different recording materials that produce the desired photonic structure [42,43,44,45] as well as specific material issues, for example, shrinkage, in order to quantitatively assess the detuning effect this causes and enable compensation through design [46]. Finally, there has been extensive application-specific modelling. Some examples include the modelling of rays directed towards a solar cell [47], optimal grating characteristics for sensor design [48] and colour combining for a waveguide display [49].
In the current work, however, the main interest is in modelling the grating characteristics (spatial period and slant angle) needed to provide a specific functionality at a specific wavelength and translating that into recording beam angles for a given recording wavelength. For this type of modelling, a key work is the paper by Close [50], which extended work by Latta [51] to develop a design approach that uses straightforward ray tracing to define the slant and fringe spacing in the designed HOE based on the angular change in direction needed at each location in the element. Although Bragg selectivity and the photosensitive material’s response are key elements in developing a functioning HOE with high efficiency over a suitable range of spatial frequencies, for the design of the optical arrangement for holographic recording, only the spatial frequency and slant need to be considered, as these are the parameters that are directly determined by the optical recording arrangement. Once these parameters are set, the material choice and exposure time and energy can be used to control efficiency, selectivity, etc.
This paper presents a simple but flexible model to systematically determine the holographic recording arrangements needed to produce diffractive optical elements designed for any input and output beam angles. It facilitates the design of recording arrangements at wavelengths different from the operating wavelength to record structures that would otherwise be challenging or impossible to record (at the operating wavelength). It allows an at-a-glance assessment of the range of recording wavelengths that will be practical for that particular element and compensation for the effect of large beam angles on pattern contrast. While the equations comprising the model are well known, the use of systematic modelling for the design of coupler elements (spatial frequency, slant angle and recording beam angles) that have distinct recording and operation wavelengths has not been reported elsewhere to the best of our knowledge.
This work offers a clear and straightforward protocol for use in fabricating angle- and/or wavelength-specific HOE coupler waveguides for any application. Coupler-waveguide elements are chosen as an interesting example to explore in this instance because it is not possible to simply holographically record them at the same wavelength at which they will function. In this paper, the accuracy of the theoretical model is validated via the design, fabrication and characterisation of holographic coupler elements. In the experimental work, HOE couplers were recorded at 532 nm using a commercially available (Covestro’s HX200) photopolymer material [52]. Efficient coupling (72%) at the intended input angle is demonstrated for a 633 nm beam at non-normal incidence
A wide-angle Bragg diffraction analysis of the recorded coupling element’s structures was carried out in red (the chosen coupling wavelength), green and blue, and the peak positions were compared with the theoretically predicted values. In addition, the model was used to identify the source of some spurious gratings caused by back reflections, further validating the usefulness of the model.
2. Modelling and Design
2.1. Identification of HOE Parameters for Desired Input and Output Angles
The ability of a HOE to redirect an incident beam of a specified wavelength at a desired angle depends primarily on two grating parameters: the spatial period and slant angle of the grating fringes. A primary objective of this simple model is to allow a user to compute the required spatial period and slant angle combination that will enable the redirection of an incident beam from its initial angle (i.e., model input angle, θ1) to another desired angle (i.e., model output angle, θ2).
In the simplest case, the desired HOE structure is a uniform volume diffraction grating characterised by a single spatial period and fringe slant angle, which obeys Bragg’s law:
where n is the refractive index of the medium, Λ is the grating period, θB is the Bragg angle within that medium, λ is the wavelength of the light in air, and m is the order of diffraction. The spatial frequency is given by 1/Λ.
2nΛsin(θB) = mλ
The first step is to calculate the required grating spatial period, Λ. As can be seen in Figure 1, the required Bragg angle, θB, for the volume diffraction grating is given by
since this is the angle through which an incident beam will be diffracted when it interacts with the grating. Thus, for any incident beam of a specified wavelength, knowing the material refractive index (n), we can use Equation (1) to determine the value of the grating spatial period, Λ, that is required for any specified values of θ1 and θ2.
2θB = (θ2 − θ1)
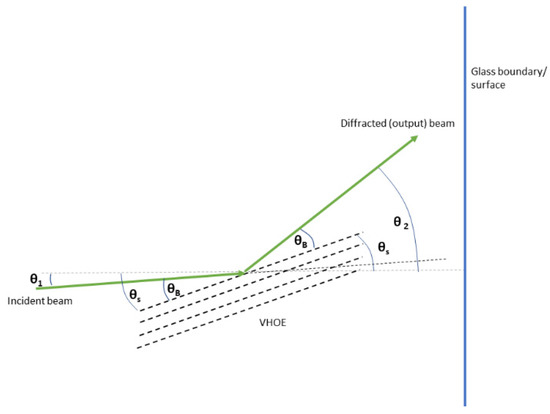
Figure 1.
General relation of slant angle with incident angle, Bragg angle and diffraction angle (all angles are within the medium).
Next, the required slant angle must be determined, which defines the orientation of the fringes relative to the material boundaries. θS is used to define the angle the grating planes make with the normal of the glass surface. In order to produce a specific diffracted beam forming angle θ2 with the normal from a beam incident at angle θ1, the planes of the grating need to be oriented correctly at a slant of θS, where
θS = (θ2 + θ1)/2.
2.2. Calculation of the Appropriate Recording Beam Angles for a Range of Recording Wavelengths
Having defined the required HOE structure (within the medium) in terms of the slant angle and spatial period, it is now possible to explore the range of holographic recording arrangements that could produce that slant and spatial period inside a photosensitive medium by using different combinations of recording wavelengths and recording angles. Holographic recording is achieved by overlapping two coherent beams to produce an interference pattern that has the required spatial period and slant. If the incident wavelength and the recording wavelength match, then the recording beam angles will be exactly θ1 and θ2, as above. The slant angle required defines the plane that bisects the two recording beams, and their position on either side of that plane is dictated by the required grating spacing. Equation (1) is again used, but this time with the wavelength and spacing fixed so that the required recording angle can be determined. Knowing the plane around which the two beams must be centred, we can then calculate the exact recording angles needed for that recording wavelength, first inside the medium and then the equivalent angles in air. Graphing the recording beam angles in air allows assessments to be made at a glance on the practicality of making that structure using any particular recording wavelength. This is especially true where there is no angle in air that can produce the required beam inside the medium, as is often the case with couplers.
A flowchart illustrating the various steps of the model is shown in Figure 2. Using the Bragg equation (Equation (1)) with the desired input and output beam directions and including refraction effects at the boundaries of the medium, the model calculates the corresponding recording beam angles (in air) that are required to produce the HOE structure needed for any recording wavelength. Yellow boxes indicate that the beam angles are in air, and blue boxes indicate beam angles inside the medium with the specified refractive index (1 in all results shown here). After specifying the desired input and output beam angles in air (0° is taken to be along the normal of the front surface), the input and output angles inside the medium are calculated using Snell’s law. Then, the grating spatial period and spatial frequency are calculated for the desired wavelength using the method described in Section 2.1 above.

Figure 2.
Flowchart showing how the recording angles are calculated using the model.
It should be borne in mind that for volume gratings, Bragg’s law (Equation (1)) only determines the incident and diffracted beam angles that give the maximum diffraction. For beams that deviate from this, Kogelnik’s Coupled Wave Theory (KCWT) [53] can be used to determine the relative efficiency in the case that just one diffracted order propagates. Another aspect of the design is matching the selectivity to a desired application. For example, a high spatial frequency and thick gratings are preferable for applications involving RGB wavelength multiplexing in order to ensure minimised crosstalk, whereas the opposite is true in solar collection, where high efficiency over the broadest possible angular and wavelength ranges is key. In this particular study, we focus on controlling the direction of the on-Bragg beam. Future work will address the control of the angular and wavelength bandwidth around the Bragg maxima.
2.3. Calculation of the Appropriate Recording Beam Angles for Fabrication of Couplers
In order to achieve the total internal reflection (TIR) of the output beam in a typical glass or polymer medium, the incident beam angle at the internal boundary must be greater than the critical angle (e.g., 41.6° for a medium refractive index of 1.5). In this study, in order to achieve TIR and the coupling of light inside the medium, we specified the desired output angle of the HOE coupler device to be 45° inside the medium, but any angle greater than the critical angle would also successfully trap light (as shown in Figure 3). The model in Section 2.2 was then used to compute the grating geometries (spatial period and slant angle) and recording beam conditions (recording wavelength and beam angles) required to produce a HOE with an output beam angle of 45° inside the medium.
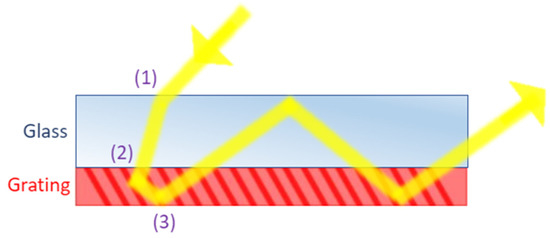
Figure 3.
Principle of operation of a HOE coupler: (1) an incident light beam enters the glass layer and is refracted; (2) the beam then enters the refractive-index-matched diffraction grating and is diffracted by the grating at an angle greater than the critical angle for the medium; (3) the beam is totally internally reflected and ‘coupled’ along the length of the device.
Figure 4a shows the recording angles required for four HOEs designed for four different input beam angles (0°, −35°, −45° and −55° in air) for operation at 633 nm wavelength and an output angle of +45° inside the medium. The curves show the recording angles needed to holographically record the required structures at a range of wavelengths. The two recording beams that need to interfere are shown in a single colour for each HOE. As would be expected, at some recording wavelengths, there is no second beam, indicating that it is not possible to achieve the required angle in air (without the use of prisms). It is possible to examine the graph and quickly decide on the recording wavelengths that will have achievable recording angles, bearing in mind practical difficulties with reflection losses and obliquity at very high angles, as well as any particular material considerations, such as the avoidance of very high slant angles. Figure 4b shows the linear variation in the slant angle inside the medium along with the four different incidence angles in air.
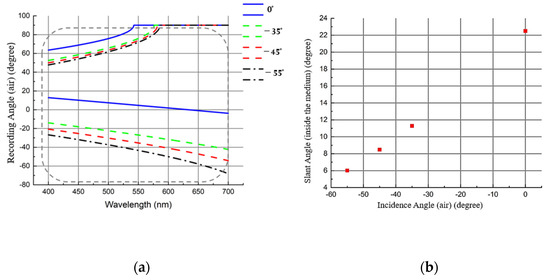
Figure 4.
(a) Recording angles for both recording beams (in air) vs. recording wavelengths for four HOE couplers designed for 633 nm with incident angles (in air) of 0°, −35°, −45° and −55° (the dotted box shows the practically achievable angles). (b) Slant angle for each of the four HOE couplers. In all cases, the diffraction angle is such that the 633 nm beam is incident internally at +45° and thus is totally internally reflected.
For subsequent studies, we chose an input beam angle of −45° in air. To produce the desired +45° output angle in the medium for a specified wavelength of 633 nm, the required slant angle is 8.5°, and the required spatial frequency is 2823 lines/mm. HOE couplers matching these parameters were experimentally fabricated; the calculated recording angles for recording this HOE at 532 nm are −69.5° and 33.5° outside the medium. The total interbeam angle is 103° outside the medium. Figure 5 shows an example of a coupler designed for use at 633 nm, holographically recorded by the interference of two green laser beams. In order to combat the losses due to high angles of incidence, the obliquity factor is considered in the design. The losses due to Fresnel reflection at the air–photopolymer interface are also considered in the model.
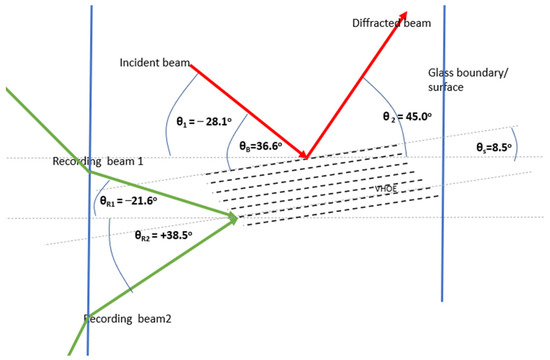
Figure 5.
Recording beams of 532 nm (green arrows) needed for a grating designed to work as a coupler for 633 nm, and the incident and diffracted beams (red arrows) for operation at 633 nm. All angles shown are inside the medium.
2.4. Modelling the Two Incident Angles at Which Bragg Diffraction Peaks Appear for a Range of Input Beam Wavelengths
To characterise the performance of the couplers, their diffraction efficiency was measured over a range of incident angles. In order to facilitate data analysis, the model was also adapted so that it can predict the incident angles at which the Bragg diffraction peaks will appear for a range of input beam wavelengths. Characterisation at three separate wavelengths (red, green and blue) allows for a more complete analysis of the recorded structures. The red and green wavelengths are chosen to be equal to the recording (532 nm) and operating (633 nm) wavelengths, and the blue wavelength (405 nm) provides an independent measurement at a third probe wavelength. In this version, the recording arrangement and wavelength are the inputs, and the model calculates the expected Bragg peak positions using the steps outlined in Figure 6. Since the photonic structures are designed to work as couplers for a wavelength of 633 nm, only one diffraction angle is present at 633 nm. Since the required spatial frequency and slant angle are defined in the design stage, a simpler version of the model could input these parameters and simply calculate the changed Bragg angle at the new wavelength and, combining this with the (unchanging) slant angle, calculate the Bragg peak positions for that wavelength. However, to achieve wider applicability and allow for the calculation of peak positions for unintended (spurious) gratings, as well as the designed grating, it was decided to have recording beam angles and wavelength as the specified inputs for this model and include a step where the spatial frequency and slant are calculated directly.

Figure 6.
Flowchart to find the Bragg angles for different wavelengths.
Figure 7a shows the calculated angle of incidence for maximum Bragg diffraction (in air) from the recorded grating structure modelled (slant angle = 8.5° (inside the medium); grating SF = 2823 lines/mm). This is plotted as a function of the incident beam wavelength over the visible range. The red, green and blue rectangles highlight the regions that correspond to the probe beams used for experimental tests: 633 nm, 532 nm and 403 nm, respectively. It is worth noting that while two incident angles are expected to cause Bragg diffraction peaks at the blue and green wavelengths, for red, the appropriate incident angle for the second peak exceeds 90 degrees in air, and only one main diffraction peak is expected. This is because the element has been designed to function as a coupler at this wavelength.
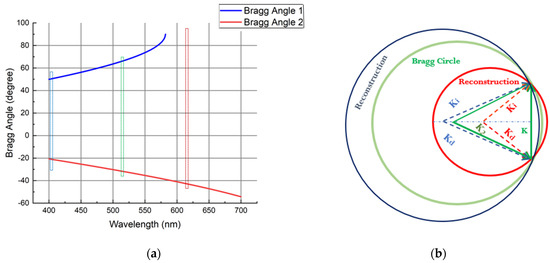
Figure 7.
(a) Expected incident beam angles for maximum Bragg diffraction as a function of wavelength for the coupler HOE (designed for input angle −45° in air and output angle 45° in the medium (633 nm)). (b) Bragg circle diagram for the coupler at 633 nm, 532 nm and 405 nm.
Figure 7b shows a Bragg circle diagram for different wavelengths. The grating vector (K) associated with the incident beam (Ki) and the diffracted beam (Kd) is shown in red. The relation among them is given by
Kd − Ki = K
In other words, the difference between Ki and Kd is satisfied by K(=2π/Λ).
3. Fabrication of VHOEs—Materials and Method
3.1. Fabrication of VHOEs
Following the identification of the recording beam angles required to produce holographic couplers with the desired input and beam diffraction angles using the theoretical model, a set of coupler devices were then fabricated in order to test the theoretical model. A commercially available Bayfol HX 200 photopolymer (purchased from Geola Digital UAB, Lithuania) film was used, which is sensitive to red, green and blue wavelengths [52]. The Bayfol HX 200 layer has a thickness of 16 ± 2 µm, and a refractive index modulation greater than 0.03 can be achieved. To ensure sufficient stability during holographic recording, the Bayfol HX 200 film was adhered to a glass slide. Holographic recording was conducted using a two-beam interferometric geometry, as shown in Figure 8a. Briefly, a single 532 nm beam from a (Hubner Photonics Cobolt SambaTM 1500 532 nm) laser was directed through a half-wave plate, spatially filtered and collimated before its division by a beam-splitter cube. Using a two-mirror arrangement, the two recording beams were redirected to overlap at the photosensitive layer at the desired recording beam angles (in air) of −33.5° and 69.5° and a total interbeam angle of 103° (in air). The laser beam intensity was monitored using an optical power meter (Newport, model 843-R), and data were transferred to a computer. The holographic recording exposure time was controlled via an electronic shutter. The total exposure energy (mJ/cm2) is estimated from Intensity (mW/cm2) x Exposure time (s). The coupler diffraction efficiency is calculated as the percentage of the available light intensity that is diverted into TIR-trapped light within the glass medium.
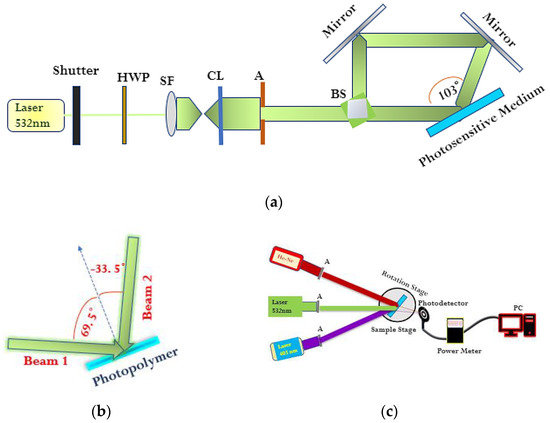
Figure 8.
(a) Recording setup. (b) Recording beam angles of incidence on the photopolymer. (c) Reconstruction setup.
The influence of the recording conditions (recording intensity and exposure energy) on the efficiency of the coupler devices fabricated in the Bayfol HX 200 film was investigated, and the results are presented in Section 4.1. It is important to restate that obliquity and Fresnel reflection losses were accounted for in all calculations of the total recording intensity. Table 1 below shows the computed intensities that are required in beam 1 and beam 2 in order to yield the total intensity desired inside the film/medium.

Table 1.
Recording intensities for the beams incident on the photopolymer calculated to compensate for reflection losses and obliquity at the recording angles for a HOE designed for −45° incidence in air diffracted to a +45° angle inside the medium (for a 633 nm operating wavelength) for a 1:1 beam ratio inside the medium.
3.2. Characterisation of VHOE Performance
A separate multi-wavelength reconstruction setup, shown in Figure 8c, was then used to analyse the holographic coupler performance and measure the diffraction efficiency at three separate wavelengths: 403 nm, 532 nm and 633 nm. In this setup, the fabricated holographic coupler was positioned on an electronically controlled rotational stage (Newport ESP300). The coupler was probed sequentially by each of the three probe wavelengths; before taking each measurement corresponding to a probe beam of a different wavelength, it was ensured that when the probe beam is normal to the sample, the reading on the rotation stage corresponded to 0 degrees; in each case, the intensity of the transmitted beam was measured, and the percentage transmitted in the zero-order beam was calculated based on the initial intensity transmitted through glass, which is taken as 100% transmission and equivalent to 0% diffraction into any other beam. The coupler diffraction efficiency (CDE) is calculated using the following method:
By rotating the coupler via the stage, these wide-angle transmission efficiency scans were obtained at each wavelength. This allowed for the identification and positional measurement of the reconstructed diffraction peaks, and the results are presented in Section 4.2. At each wavelength, a full angular scan was also completed with a glass slide to allow the estimation of reflection losses. The approximate diffraction efficiency of the coupler is estimated by taking the difference between the percentage transmission at that angle in the absence of a grating and the percentage transmission with the grating in place as a ratio to the percentage transmission at that angle in the absence of a grating.
4. Experimental Results
4.1. Optimisation of the Holographic Recording Conditions for Couplers
Using the recording arrangement shown above, couplers were recorded holographically with 532 nm light for a range of exposure conditions, and their diffraction efficiencies were measured (see Section 3 above). Figure 9a shows the coupler diffraction efficiency at 633 nm for three different sets of samples recorded with 532 nm and total intensities inside the medium of 2 mW/cm2, 3 mW/cm2 and 4 mW/cm2 (Table 1). The variation in the coupler diffraction efficiency with exposure energy is shown in Figure 9b.
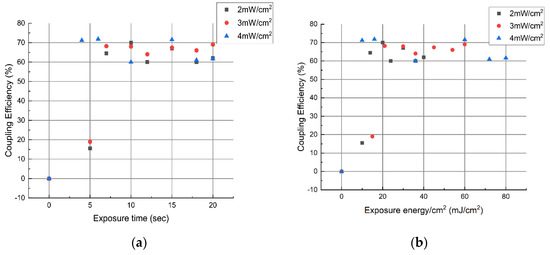
Figure 9.
(a) Coupler diffraction efficiency vs. exposure time. (b) Coupler diffraction efficiency vs. exposure energy.
From Figure 9a,b, we can conclude that highly efficient couplers are readily achievable in a range of exposure conditions. The minimum exposure energy required for efficiency above 60% appears to be approximately 10–15 mJ/cm2, which is compatible with mass production requirements. Efficiency > 70% was achieved with approximately 6 s of exposure at 4 mW/cm2. At longer times and higher exposure energies, the data are quite scattered but broadly in the 60–70% range and not significantly increased or decreased by further exposure. We expect that this is due to the well-designed maximum refractive index modulation and thickness for these HX200 photopolymer layers. The repeatability of specific efficiency values may be improved by the more precise control of exposure energy in the recording system.
4.2. Multi-Wavelength Angular Characterisation of the Fabricated Couplers
In order to examine the diffraction behaviour of the recorded photonic structure in more detail, wide-angle zero-order Bragg curves were measured for three different probe wavelengths. Figure 10a–c present Bragg curves for a particular example of one of the couplers recorded as described above. In this case, the total recording intensity is 4 mW/cm2, the exposure time is 6 s, and the probe wavelengths are 633 nm, 532 nm and 403 nm, respectively. Figure 10d presents the background with a simple glass slide for the above-mentioned wavelengths. It should be noted that for Figure 10a,b, an FFT filter (with points of window = 5 units) was used to smooth the curve. Similar remarks apply to the backgrounds of 633 nm and 532 nm, as shown in Figure 10d.
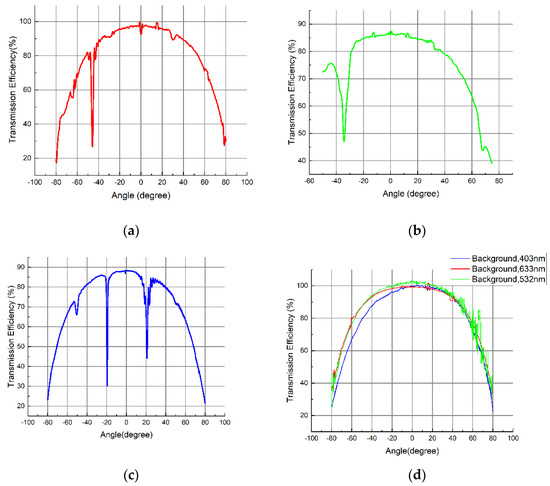
Figure 10.
Transmission efficiency versus angle of incidence for the HOE coupler when probed with wavelengths of (a) 633 nm, (b) 532 nm and (c) 403 nm (d). Background measurements made for the same range of angles at all three wavelengths with a glass slide in place of the HOE.
5. Discussion
There are a number of observations that can be made from the data shown above relating to the expected diffraction maxima/minima and validation of the model, the diffraction efficiency of the recorded structure and the observation of additional diffraction peaks/spurious grating structures.
5.1. Bragg Angles for the Recorded Structure at the Three Probe Wavelengths
Table 2 compares the expected peak positions with the measured peak positions for three different probing wavelengths. The expected angular position for the Bragg diffraction of light of 633 nm wavelength (the design wavelength in air) is −45°, representing the angle at which the incident light is diffracted. No second diffraction peak is expected to be observed in Figure 10a because the scan is performed by varying the incidence angle in air; at this wavelength, the HOE functions as a coupler, and therefore, the second angle of incidence that would produce strong diffraction is impossible to access from outside the air–glass boundary. When probed at 532 nm, as shown in Figure 10b, the photonic structure acts as an ordinary slanted diffraction grating, and the angles are close to the recording angles, confirming that the expected grating was recorded. Finally, for scans completed with 403 nm, as shown in Figure 10c, diffraction is expected (in air) (see Section 2) at −20.9° and +50.3°. Diffraction is observed very close to both of these angles; however, the results are somewhat obscured by strong diffraction from an additional unintended grating that diffracts particularly strongly in blue. This is discussed below.

Table 2.
The model-predicted angles (in air) and measured angles (in air) for all three different wavelengths.
The diffraction peaks are within ±1° (in air) of the expected values, but the exact position of the peak that should be at 69.5° for 532 nm is difficult to determine, as the percentage of light transmitted at that angle is lower. The experimental error in setting the recording beam angles is estimated at ±0.2°, while the error in setting the photopolymer layer in the holder for recording is estimated at ±0.3°, and the error that arises in estimating the position of maximum diffraction on the angular scans is estimated at approximately ±0.1°. In this context, and bearing in mind that there will inevitably be some material issues contributing, the experimental data are considered to be very well matched to the model, validating the approach. The maximum coupling efficiency at the design wavelength of 72% is achieved by the coupler recorded with a total intensity of 4 mW/cm2 and an exposure time of 6s, as shown in Figure 10a.
5.2. Spurious Gratings and Additional Diffraction Peaks
Although the above provides validation of the model insofar as the expected diffraction maxima are all present and are (within a margin of error) observed at the angles the model predicts, some diffraction efficiencies are lower than expected, and a number of ‘unexpected’ diffraction maxima are observed without an obvious connection in their positions at different wavelengths. The efficiency of the spurious peaks is not particularly repeatable in the different recordings, but the angles at which they occur are repeated in many samples. This is to be expected since the extent to which unwanted gratings (due to back reflections) are recorded will vary with exposure conditions, but the angle at which they are observed should be consistent. Figure 11 is an example in which most of the recurring spurious peaks are particularly dominant (2 mW/cm2 couplers) and easy to see. A simple comparison of the Bragg scans at different wavelengths does not point to a single recorded structure causing the unexpected diffraction maxima. For example, two small ‘peaks’ observed ±30° (in air) on either side of normal incidence in most of the data taken at 633 nm might indicate a non-slanted transmission grating with a spatial frequency of approximately 2426 lines/mm (Figure 11), and one would expect to observe similar symmetrical peaks in the other two scans (405 nm and 532 nm) at appropriately smaller diffraction angles. However, these are not observed. In the green scans, we observe the expected peaks (in air) at around −33° and +69° (corresponding to the recording beams) but also smaller peaks at +33° and (just visible) −69° (Figure 8), and in blue, the unexpected peaks (in air) are observed at −50.4° and +20.9°.
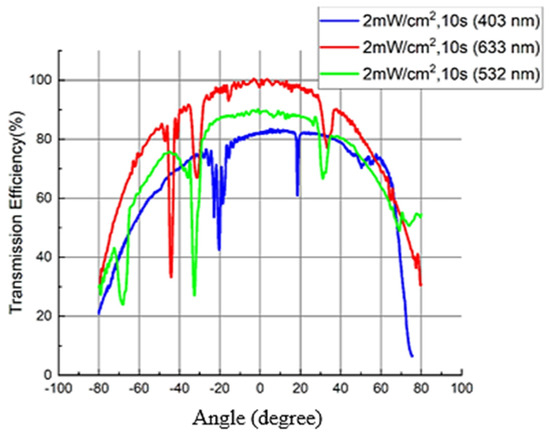
Figure 11.
An example of a recording with particularly strong spurious gratings scanned at three wavelengths: 405 nm, 532 nm and 633 nm.
Using the model, the structures that could arise from potential reflections occurring during recording were analysed.
- The back reflection of the two primary recording beams interfering with one another (creates a transmission grating with the same spatial frequency as the intended coupler but with opposite slant, the beams have similar intensities, so a high-contrast pattern is recorded);
- The back reflection of each beam interfering with that beam (creates two non-slanted reflection gratings, presumably quite weak due to the poor beam ratio);
- The back reflection from each beam interfering with the opposite main recording beam (creates two slanted reflection gratings, presumably quite weak due to the poor beam ratio).
The very strong diffraction around +20° (in air) noted in the blue scans and the +33° (in air) and the (just visible) −69° (in air) diffractions observed in the green scans all correspond to the strong grating formed by the back reflections of the two main recording beams. The equivalent single diffraction peak that might have been expected at +45° (in air) at 633 nm was not observed, however.
In the 633 nm scan, two small peaks, symmetrical around 0°, appear close to the ±33° (in air) that the model predicts for diffraction from the structure caused by the interference of the recording beam (−69.5°) (in air) with itself (Figure 12b). The same structure causes diffraction at ±69° at 532 nm, which is observed as a broadening of the 69° peak. An additional structure that corresponds to the interference of the recording beam (−33.5°) (in air) with itself (Figure 12c) may well be present, but, from the set of wavelengths tested here, it would only be observable at 532 nm and coincides with the expected peak at that wavelength. This may be responsible for the broadened/non-standard peak shape observed here. Table 3 shows the detail analysis of the spurious peak positions for three different wavelengths
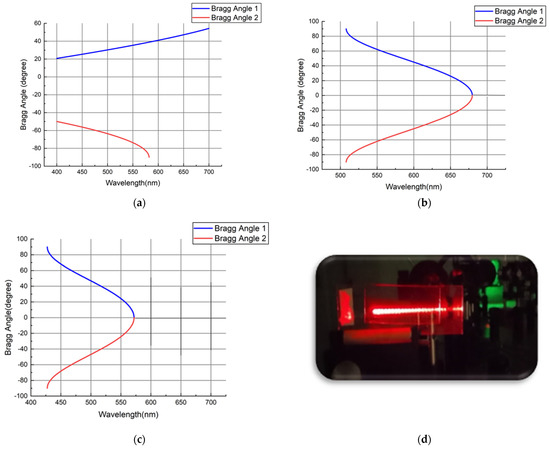
Figure 12.
Expected angles for maximum Bragg diffraction vs. wavelength due to (a) interference of the reflection of the recording beams with each other, (b) interference of recording beam (−69.5°) with itself and (c) interference of recording beam (33.5°) with itself. (d) Photo of 633 nm laser being coupled into a microscope slide via the coupler HOE.

Table 3.
The expected positions of the spurious peaks (in air) and measured positions of the spurious peaks (in air) for all three different wavelengths. Not Applicable (NA) means angles are imaginary in air.
There are additional, weaker interferences, which have also been thoroughly analysed by the model; however, since the main additional features observed can be explained by the above, we have not presented them here.
6. Conclusions
A theoretical model that enables the identification of suitable recording angles for volume holographic optical couplers has been described. This model was then used to aid the fabrication of VHOE couplers for operation at 633 nm using a recording wavelength of 532 nm.
The model has several advantages: it generates data on the required beam angles across all possible recording wavelengths and facilitates the design of a suitable holographic recording arrangement in free space, avoiding the use of coupling prisms; it allows all input and output angle options to be explored so that the user can easily determine under which conditions and at which wavelengths the recording angles would be suitable to work without prisms; and it includes a simple beam ratio calculator to help compensate for the very large obliquity factor and Fresnel reflections at large recording beam angles. This is especially useful when the interfering beams have very different angles of incidence on the recording medium.
Different recording intensities and exposure times for the fabrication of high-efficiency couplers were investigated. Three different sets of total intensities inside the medium were considered: 2 mW/cm2, 3 mW/cm2 and 4 mW/cm2. The maximum coupling efficiency of 72% is achieved for a total intensity of 4 mW/cm2 and an exposure time of 6 s. This compares well with the diffraction efficiency results achieved by other authors for coupling elements; for example, Gallego et al. [36] obtained an efficiency higher than 70% with penta/hexa-acrylate-based polymer with dispersed nematic liquid crystal molecules, PDLC, having a thickness of 40 microns and a spatial frequency of 2000 lines/mm.
Three different wavelengths were used for probing the recorded elements, and angular agreement with the desired value within ±1° was achieved at all three wavelengths. Spurious grating peaks were observed, and the model was further used to determine the origin of such peaks. Potentially, such HOE couplers can be used in various applications, such as augmented reality displays, solar collectors and compact photonic devices.
Author Contributions
S.M., V.T. and I.N. developed the initial concept; S.M. and D.C. (Dipanjan Chakraborty) obtained the funding for the project from Technological University Dublin Research Scholarship programme; S.M. led the project; S.M., D.C. (Dervil Cody) and D.C. (Dipanjan Chakraborty) contributed to the experimental plan for this manuscript and provided supervision; S.M. developed the model, and D.C. (Dipanjan Chakraborty) implemented it in MATLAB. D.C. (Dipanjan Chakraborty) carried out the majority of the experimental work with help from R.G., S.A. and S.M. S.M., D.C. (Dervil Cody) and D.C. (Dipanjan Chakraborty) contributed to the data analysis; D.C. (Dipanjan Chakraborty) produced most of the figures; D.C. (Dipanjan Chakraborty) wrote the initial manuscript draft. All authors have read and agreed to the published version of the manuscript.
Funding
Dipanjan Chakraborty is funded by the Technological University Dublin Research Scholarship programme. Rosen Georgiev and Suzanne Martin received funding from Enterprise Ireland and the European Union’s Horizon 2021 Research and Innovation Programme under the Marie Skłodowska-Curie grant agreement No. 847402. The authors thank FOCAS, TU Dublin, for the technical facilities and administrative support provided.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ashley, J.; Bernal, M.-P.; Burr, G.W.; Coufal, H.; Guenther, H.; Hoffnagle, J.A.; Jefferson, C.M.; Marcus, B.; Macfarlane, R.M.; Shelby, R.M.; et al. Holographic data storage technology. IBM J. Res. Dev. 2000, 44, 341–368. [Google Scholar] [CrossRef]
- Dhar, L.; Hill, A.; Curtis, K.; Wilson, W.; Ayres, M. Holographic Data Storage: From Theory to Practical Systems; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Li, J.; Hu, P.; Jin, J.; Wang, J.; Liu, J.; Wu, J.; Lin, X.; Tan, X. Highly sensitive photopolymer for holographic data storage. Opt. Express 2022, 30, 40599–40610. [Google Scholar] [CrossRef] [PubMed]
- Miller, J.M.; de Beaucoudrey, N.; Chavel, P.; Turunen, J.; Cambril, E. Design and fabrication of binary slanted surface-relief gratings for a planar optical interconnection. Appl. Opt. 1997, 36, 5717–5727. [Google Scholar] [CrossRef] [PubMed]
- Soares, O. Holographic coupler for fiber optics. Opt. Eng. 1981, 20, 740–745. [Google Scholar] [CrossRef]
- Singh, A.K.; Yadav, A.; Khan, A.A.; Roy, S.; Yadav, H.L. Design and analysis of holographic optical elements for their use as couplers with appreciable efficiency at different optical transmission windows. Optik 2022, 261, 169184. [Google Scholar] [CrossRef]
- He, C.; Neild, A.; Helmerson, K.; Cincotta, S.; Zuk, J.; Armstrong, J. Dual-aperture hologram receiver for visible light communications. Opt. Commun. 2021, 490, 126943. [Google Scholar] [CrossRef]
- Shimizu, S.; Okamoto, A.; Mizukawa, F.; Ogawa, K.; Tomita, A.; Takahata, T.; Shinada, S.; Wada, N. Volume holographic spatial mode demultiplexer with a dual-wavelength method. Appl. Opt. 2018, 57, 146–153. [Google Scholar] [CrossRef]
- Zhang, Y.; Fan, H.; Poon, T.-C. Optical image processing using acousto-optic modulators as programmable volume holograms: A review. Chin. Opt. Lett. 2022, 20, 021101. [Google Scholar] [CrossRef]
- Alcaraz, P.E.; Nero, G.; Blanche, P.-A. Bandwidth optimization for the Advanced Volume Holographic Filter. Opt. Express 2022, 30, 576–587. [Google Scholar] [CrossRef]
- Park, J.-H.; Lee, B. Holographic techniques for augmented reality and virtual reality near-eye displays. Light Adv. Manuf. 2022, 3, 1–14. [Google Scholar] [CrossRef]
- Putilin, A.; Morozov, A.; Kopenkin, S.; Dubynin, S.; Borodin, Y.P. Holographic waveguide periscopes in augmented reality displays. Opt. Spectrosc. 2020, 128, 1828–1836. [Google Scholar] [CrossRef]
- Li, G.; Lee, D.; Jeong, Y.; Cho, J.; Lee, B. Holographic display for see-through augmented reality using mirror-lens holographic optical element. Opt. Lett. 2016, 41, 2486–2489. [Google Scholar] [CrossRef] [PubMed]
- Piao, J.-A.; Li, G.; Piao, M.-L.; Kim, N. Full Color Holographic Optical Element Fabrication for Waveguide-type Head Mounted Display Using Photopolymer. J. Opt. Soc. Korea 2013, 17, 242–248. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, J.; Wang, Y. A high-efficiency holographic waveguide display system with a prism in-coupler. J. Soc. Inf. Disp. 2013, 21, 524–528. [Google Scholar] [CrossRef]
- Zhang, N.; Liu, J.; Han, J.; Li, X.; Yang, F.; Wang, X.; Hu, B.; Wang, Y. Improved holographic waveguide display system. Appl. Opt. 2015, 54, 3645–3649. [Google Scholar] [CrossRef]
- Lv, Z.; Liu, J.; Xiao, J.; Kuang, Y. Integrated holographic waveguide display system with a common optical path for visible and infrared light. Opt. Express 2018, 26, 32802–32811. [Google Scholar] [CrossRef] [PubMed]
- Gu, Y.; Weng, Y.; Wei, R.; Shen, Z.; Wang, C.; Zhang, L.; Zhang, Y. Holographic waveguide display with large field of view and high light efficiency based on polarized volume holographic grating. IEEE Photonics J. 2021, 14, 1–7. [Google Scholar] [CrossRef]
- Shen, Z.; Wang, Z.; Weng, Y.; Zhang, Y. 15.2: Design and Realization of Full-Color VHG Holographic Waveguide Display. In SID Symposium Digest of Technical Papers, Proceedings of the International Conference on Display Technology (ICDT) 2022, Fuzhou, China, 9–12 July 2022; Shen, Z., Wang, C., Weng, Y., Zhang, Y., Eds.; Wiley Online Library: Hoboken, NJ, USA, 2022. [Google Scholar]
- Collados, M.V.; Chemisana, D.; Atencia, J. Holographic solar energy systems: The role of optical elements. Renew. Sustain. Energy Rev. 2016, 59, 130–140. [Google Scholar] [CrossRef]
- Kostuk, R.K.; Rosenberg, G. Analysis and design of holographic solar concentrators. In High and Low Concentration for Solar Electric Applications III, Proceedings of the SOLAR ENERGY + APPLICATIONS, San Diego, CA, USA, 10–14 August 2008; Kostuk, R.K., Rosenberg, G., Eds.; SPIE: Bellingham, WA, USA, 2008. [Google Scholar]
- Naydenova, I.; Akbari, H.; Dalton, C.; Yahya, M.; Ilyas, S.M.; Wei, C.P.T.; Toal, V.; Martin, S. Photopolymer Holographic Optical Elements for Application in Solar Energy Concentrators. Holography-Basic Principles and Contemporary Applications; Mihaylova, E., Ed.; InTech: London, UK, 2013. [Google Scholar]
- Zhang, D.; Gordon, M.; Russo, J.M.; Vorndran, S.D.; Kostuk, R.K. Spectrum-splitting photovoltaic system using transmission holographic lenses. J. Photonics Energy 2013, 3, 034597. [Google Scholar] [CrossRef]
- Ferrara, M.A.; Bianco, G.; Borbone, F.; Centore, R.; Striano, V.; Coppola, G. Volume holographic optical elements as solar concentrators. In Holographic Materials and Optical Systems; IntechOpen: London, UK, 2017; pp. 27–50. [Google Scholar]
- Müller, H. Application of holographic optical elements in buildings for various purposes like daylighting, solar shading and photovoltaic power generation. Renew. Energy 1994, 5, 935–941. [Google Scholar] [CrossRef]
- Neipp, C.; Taleb, S.I.; Francés, J.; Fernández, R.; Puerto, D.; Calzado, E.M.; Gallego, S.; Beléndez, A. Analysis of the Imaging Characteristics of Holographic Waveguides Recorded in Photopolymers. Polymers 2020, 12, 1485. [Google Scholar] [CrossRef]
- Aspnes, E.D.; Castillo-Aguilella, J.E.; Courreges, R.D.; Hauser, P.S.; Stewart, K.R. Non-latitude and vertically mounted solar energy concentrators. U.S. Patent US20130312811A1, 28 November 2013. [Google Scholar]
- Aspnes, E.D.; Castillo-Aguilella, J.E.; Courreges, R.D.; Hauser, P.S.; Stewart, K.R. Solar energy concentrator with multiplexed diffraction gratings. U.S. Patent US20130319524A1, 5 December 2013. [Google Scholar]
- Kao, H.; Ma, J.; Wang, C.; Wu, T.; Su, P. Crosstalk-Reduced Double-Layer Half-Divided Volume Holographic Concentrator for Solar Energy Concentration. Sensors 2020, 20, 6903. [Google Scholar] [CrossRef] [PubMed]
- Huang, Q.; Ashley, P.R. Holographic Bragg grating input–output couplers for polymer waveguides at an 850-nm wavelength. Appl. Opt. 1997, 36, 1198–1203. [Google Scholar] [CrossRef]
- Wang, C.; Ma, J.; Kao, H.; Wu, T.; Su, P. Wide-Band High Concentration-Ratio Volume-Holographic Grating for Solar Concentration. Sensors 2020, 20, 6080. [Google Scholar] [CrossRef] [PubMed]
- Ludman, J.E. Holographic solar concentrator. Appl. Opt. 1982, 21, 3057–3058. [Google Scholar] [CrossRef] [PubMed]
- Bigler, C.M.; Blanche, P.-A.; Sarma, K. Holographic waveguide heads-up display for longitudinal image magnification and pupil expansion. Appl. Opt. 2018, 57, 2007–2013. [Google Scholar] [CrossRef] [PubMed]
- Stoeva, P.; Mikulchyk, T.; Rogers, B.; Oubaha, M.; Martin, S.; Ferrara, M.A.; Coppola, G.; Naydenova, I. Development of volume holographic optical element for application in wound healing monitoring. In Proceedings of the Photonics Ireland, Virtual Conference, 14–16 June 2021. [Google Scholar]
- Toal, V.; Whelan, M.; Volcan, A.; Naydenova, I.; Martin, S. Replay at optical communications wavelengths of holographic gratings recorded in the visible. In Proceedings of the SPIE, Varna, Bulgaria, 21–25 May 2005. [Google Scholar]
- Fernández, R.; Bleda, S.; Gallego, S.; Neipp, C.; Márquez, A.; Tomita, Y.; Pascual, I.; Beléndez, A. Holographic waveguides in photopolymers. Opt. Express 2019, 27, 827–840. [Google Scholar] [CrossRef]
- Kogelnik, H. Coupled wave theory for thick hologram gratings. Bell Syst. Tech. J. 1969, 48, 2909–2947. [Google Scholar] [CrossRef]
- Moharam, M.; Gaylord, T. Rigorous coupled-wave analysis of planar-grating diffraction. JOSA 1981, 71, 811–818. [Google Scholar] [CrossRef]
- Gaylord, T.K.; Moharam, M. Analysis and applications of optical diffraction by gratings. Proc. IEEE 1985, 73, 894–937. [Google Scholar] [CrossRef]
- Syms, R.; Solymar, L. Planar volume phase holograms formed in bleached photographic emulsions. Appl. Opt. 1983, 22, 1479–1496. [Google Scholar] [CrossRef] [PubMed]
- Vojtsek, P.; Kveton, M.; Richter, I. Complex method for angular-spectral analysis of volume phase diffraction gratings recorded in photopolymers. J. Eur. Opt. Soc. 2016, 11, 16009. [Google Scholar] [CrossRef]
- Mackey, D.; O’Reilly, P.; Naydenova, I. Theoretical modeling of the effect of polymer chain immobilization rates on holographic recording in photopolymers. JOSA A 2016, 33, 920–929. [Google Scholar] [CrossRef] [PubMed]
- Zhao, G.; Mouroulis, P. Diffusion model of hologram formation in dry photopolymer materials. J. Mod. Opt. 1994, 41, 1929–1939. [Google Scholar] [CrossRef]
- Sheridan, J.T.; Lawrence, J.R. Nonlocal-response diffusion model of holographic recording in photopolymer. JOSA A 2000, 17, 1108–1114. [Google Scholar] [CrossRef] [PubMed]
- Babeva, T.; Naydenova, I.; Mackey, D.; Martin, S.; Toal, V. Two-way diffusion model for short-exposure holographic grating formation in acrylamide-based photopolymer. JOSA B 2010, 27, 197–203. [Google Scholar] [CrossRef]
- Heifetz, A.; Shen, J.T.; Tsang, S.C.; Pati, G.S.; Lee, J.-K.; Shahriar, M. Angular directivity of diffracted wave in Bragg-mismatched readout of volume holographic gratings. In Proceedings of the Frontiers in Optics, San Jose, CA, USA, 16–20 September 2007; Optica Publishing Group: Washington, DC, USA, 2007. [Google Scholar]
- Bañares-Palacios, P.; Álvarez-Álvarez, S.; Marín-Sáez, J.; Collados, M.-V.; Chemisana, D.; Atencia, J. Broadband behavior of transmission volume holographic optical elements for solar concentration. Opt. Express 2015, 23, A671–A681. [Google Scholar] [CrossRef]
- Cody, D.; Naydenova, I. Theoretical modeling and deign of photonic structures in zeolite nanocomposites for gas sensing. Part I: Surface relief gratings. JOSA A 2017, 34, 2110–2119. [Google Scholar] [CrossRef]
- Guo, J.; Tu, Y.; Yang, L.; Wang, L.; Wang, B. Design of a multiplexing grating for color holographic waveguide. Opt. Eng. 2015, 54, 125105. [Google Scholar] [CrossRef]
- Close, D. Holographic optical elements. Opt. Eng. 1975, 14, 408–419. [Google Scholar] [CrossRef]
- Latta, J.N. Computer-based analysis of hologram imagery and aberrations. I. Hologram types and their nonchromatic aberrations. Appl. Opt. 1971, 10, 599–608. [Google Scholar] [CrossRef] [PubMed]
- Bruder, F.-K.; Fäcke, T.; Rölle, T. The chemistry and physics of Bayfol® HX film holographic photopolymer. Polymers 2017, 9, 472. [Google Scholar] [CrossRef] [PubMed]
- Kogelnik, H. Coupled wave theory for thick hologram gratings. In Landmark Papers On Photorefractive Nonlinear Optics; World Scientific: Singapore, 1995; pp. 133–171. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).