Modelling of Plasma Temperatures and Densities in Laser Ablation Plumes of Different Metals
Abstract
1. Introduction
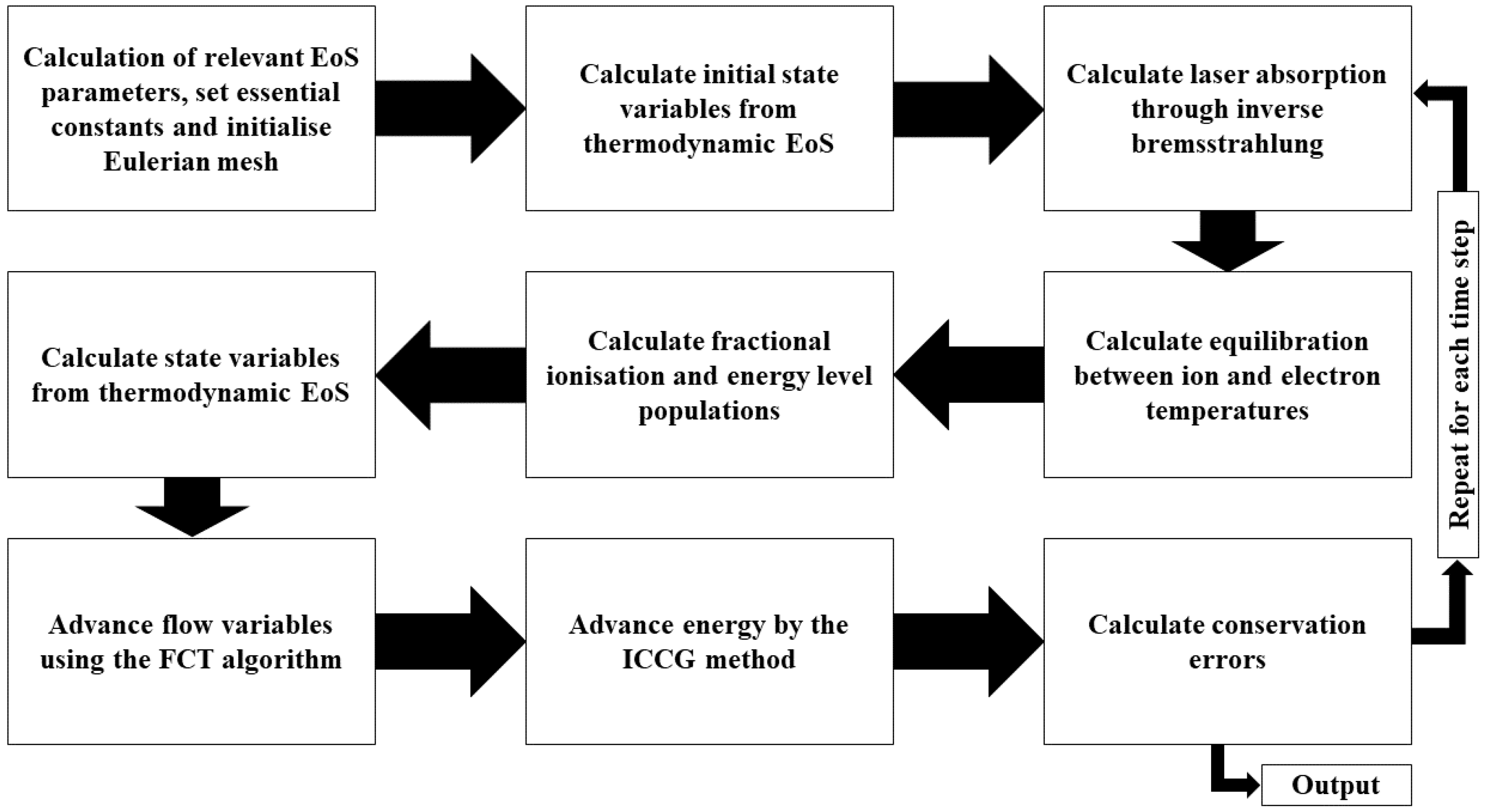
2. Methodology
3. Results & Discussion
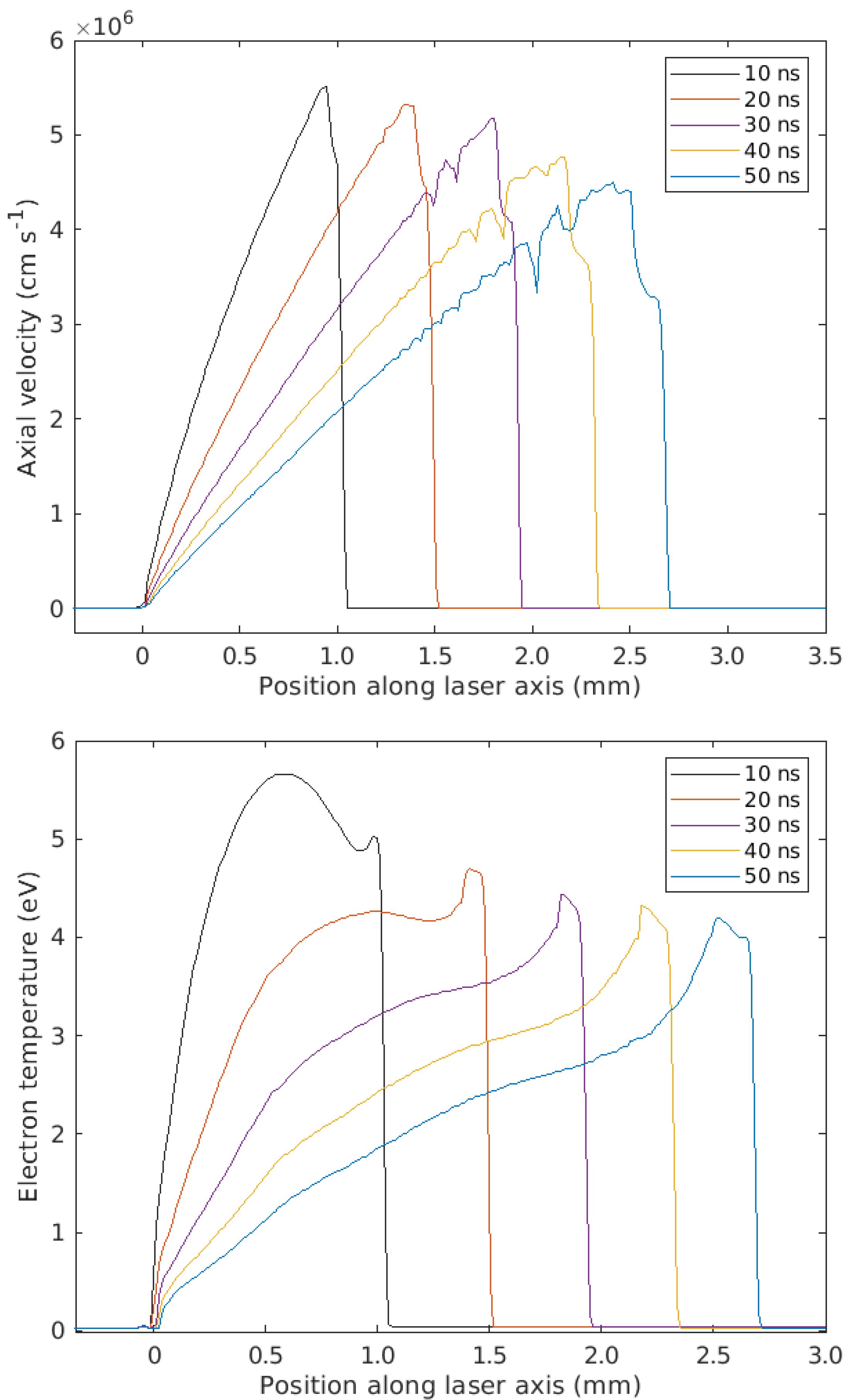
3.1. Laser Ablation of Titanium
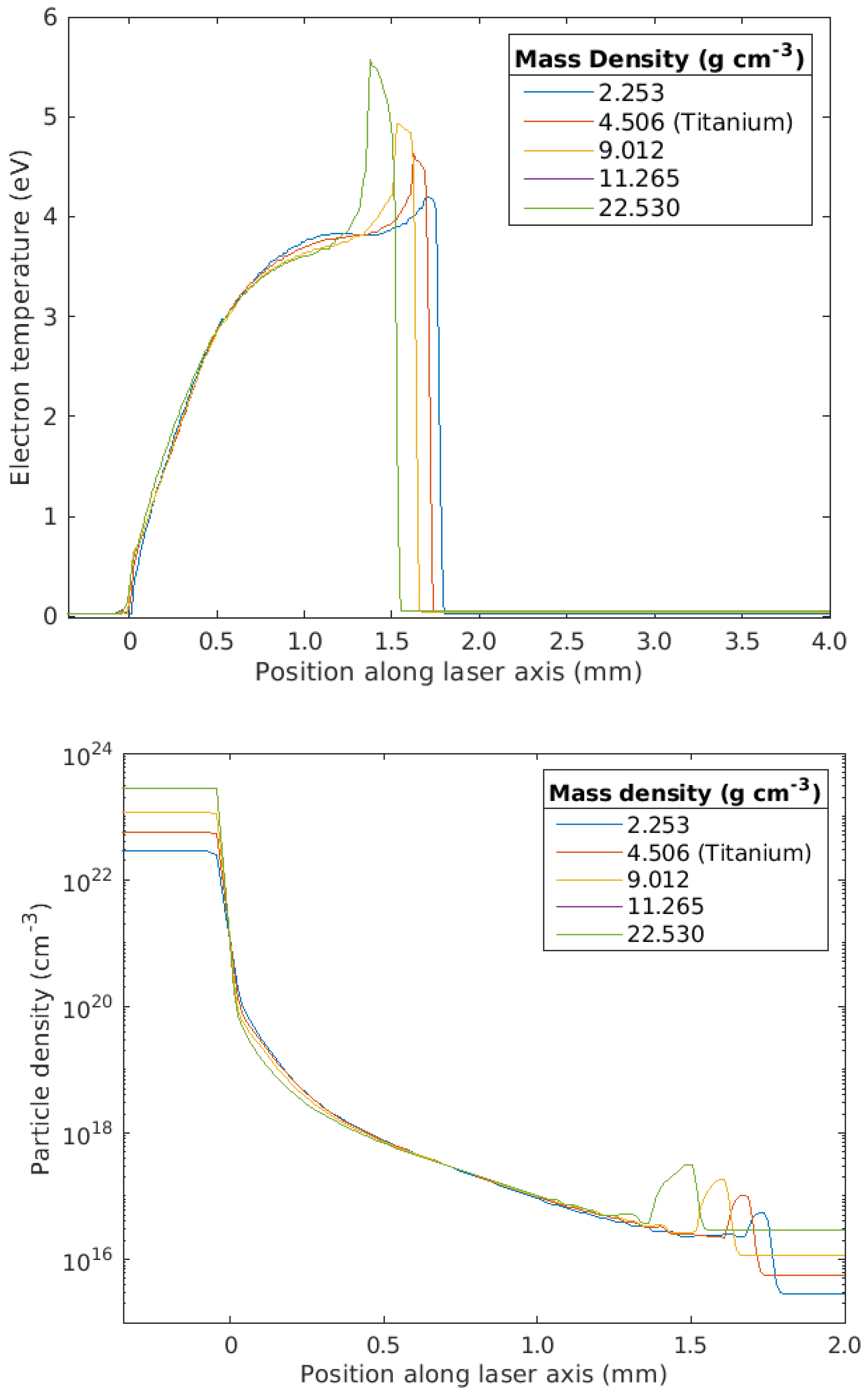
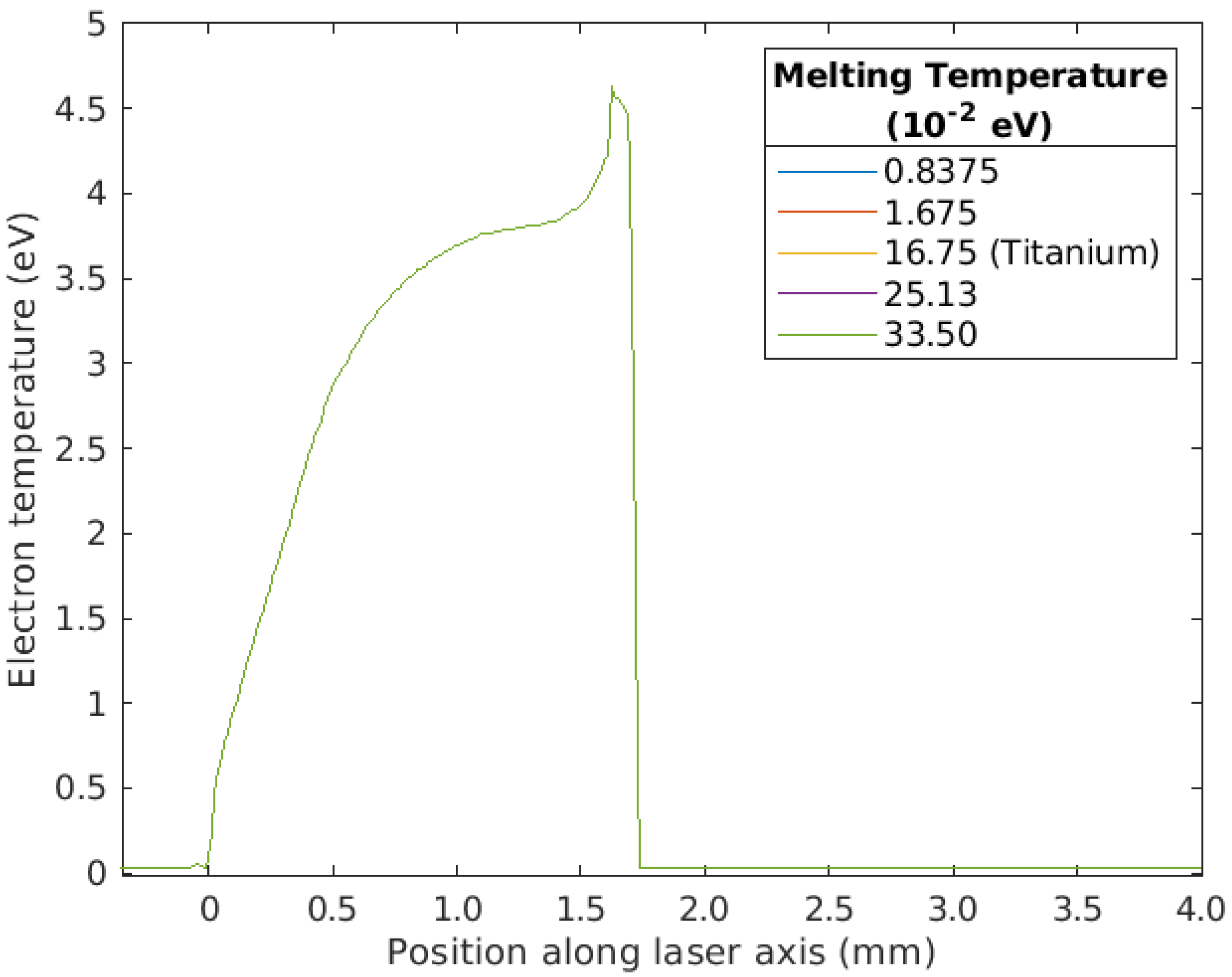
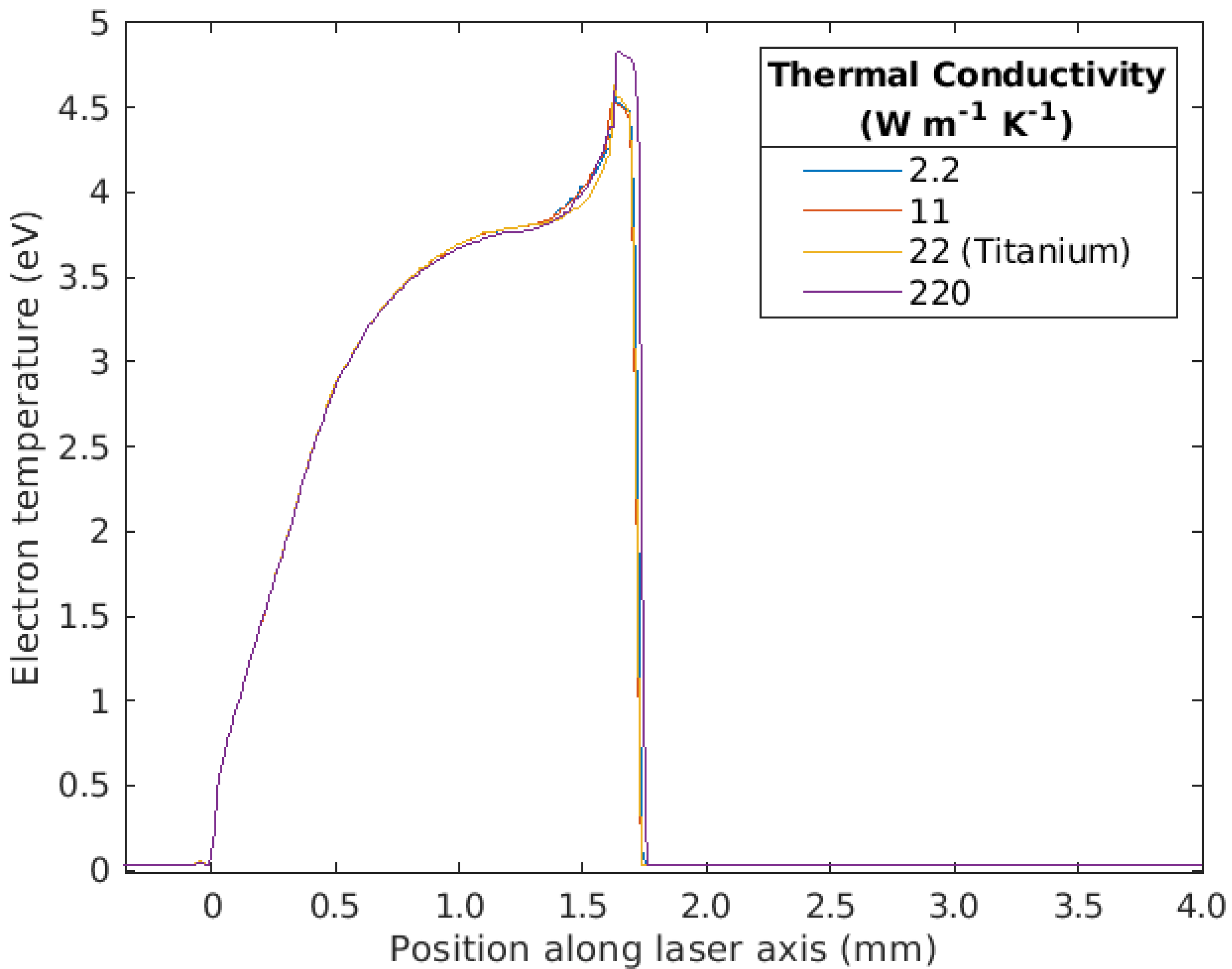
3.2. Investigating the Effects of Material Properties on Titanium Plasma Plumes
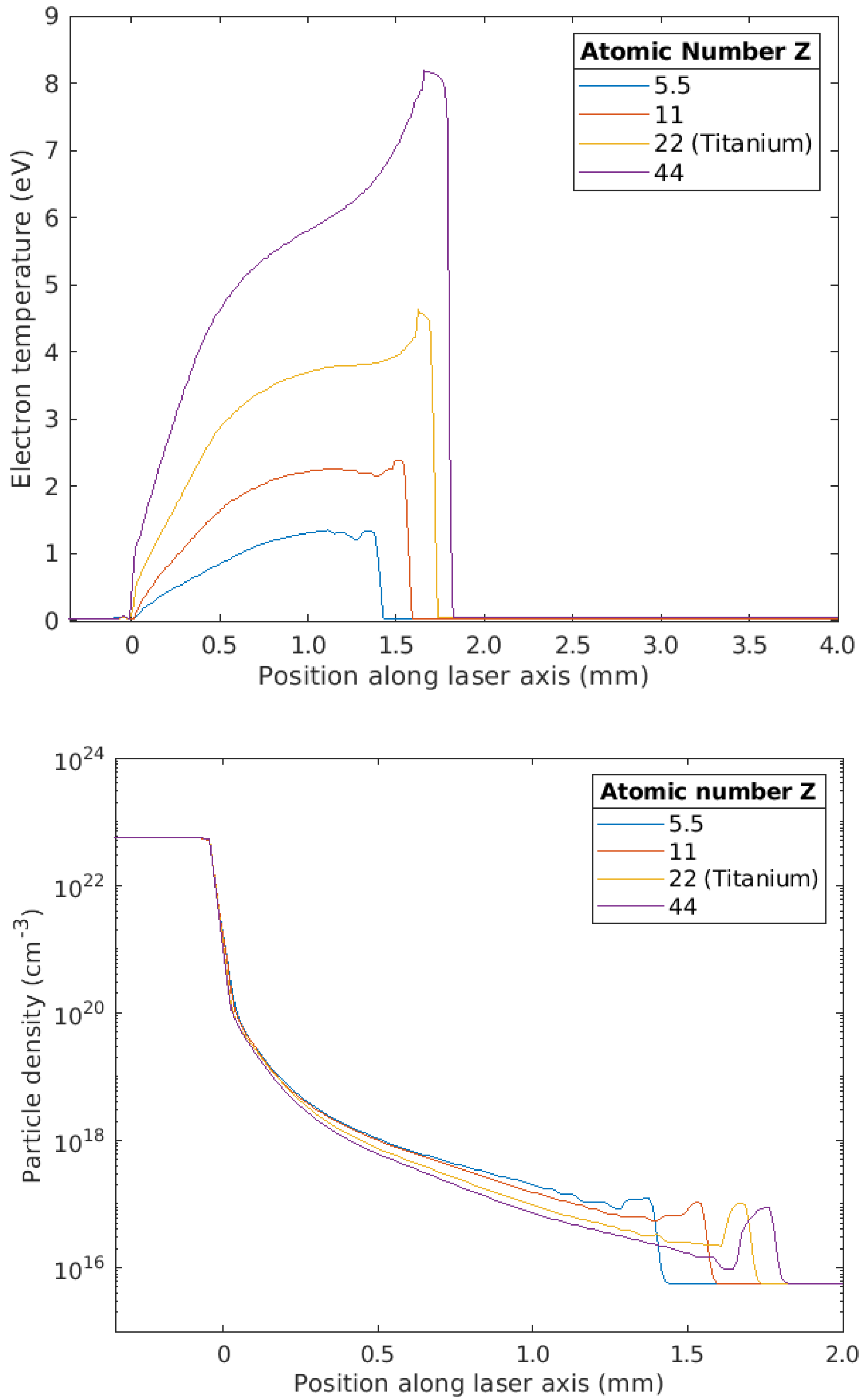
3.3. Comparison of Plasma Plumes from Different Materials
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Becker, W.F. Metal nanoparticles generated by laser ablation. Nanostructured Mater. 1998, 10, 853–863. [Google Scholar] [CrossRef]
- Darwood, R.J. Randomized clinical trial comparing endovenous laser ablation with surgery for the treatment of primary great saphenous varicose veins. Br. J. Surg. 2008, 95, 294–301. [Google Scholar] [CrossRef] [PubMed]
- Vertes, A. Laser Ionization Mass Analysis; Vertes, A., Gijbels, R., Adams, F., Eds.; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Radziemski, L.J. Laser-Induced Plasmas and Applications; Radziemski, L.J., Cremers, D.A., Eds.; Wiley: New York, NY, USA, 1989. [Google Scholar]
- Rajendiran, S.; Rossall, A.K.; Gibson, A.; Wagenaars, E. Modelling of laser ablation and reactive oxygen plasmas for pulsed laser deposition of zinc oxide. Surf. Coat. Technol. 2014, 260, 417–423. [Google Scholar] [CrossRef]
- Ashfold, M.N.; Claeyssens, F.; Fuge, G.M.; Henley, S.J. Pulsed laser ablation and deposition of thin films. Chem. Soc. Rev. 2003, 33, 23–31. [Google Scholar] [CrossRef] [PubMed]
- Autrique, D.; Alexiades, V.; Khanal, H. Hydrodynamic modelling of ns-laser ablation. Electron. J. Differ. Equat. 2013, 20. Available online: https://commons.erau.edu/cgi/viewcontent.cgi?article=1902&context=publication (accessed on 1 December 2022).
- Chen, Z.; Bogaerts, A. Laser ablation of Cu and plume expansion into 1 atm ambient gas. J. Appl. Phys. 2005, 97, 063305. [Google Scholar] [CrossRef]
- Sivakumaran, V.; Joshi, H.C.; Singh, R.K.; Kumar, A. Optical time of flight studies of lithium plasma in double pulse laser ablation: Evidence of inverse bremsstrahlung absorption. Phys. Plasmas 2014, 21, 063110. [Google Scholar] [CrossRef]
- Clair, G.; L’Hermite, D. 1D modelling of nanosecond laser ablation of copper samples in argon at P = 1 atm with a wavelength of 532 nm. J. Appl. Phys. 2011, 110, 083307. [Google Scholar] [CrossRef]
- Jeschke, H.O.; Garcia, M.E.; Lenzner, M.; Bonse, J.; Krüger, J.; Kautek, W. Laser ablation thresholds of silicon for different pulse durations: Theory and experiment. Appl. Surf. Sci. 2002, 197–198, 839–844. [Google Scholar] [CrossRef]
- Roberts, D.E.; du Plesis, A.; Botha, L.R. Femtosecond laser ablation of silver foil with single and double pulses. Appl. Surf. Sci. 2010, 256, 1784–1792. [Google Scholar] [CrossRef]
- Qaisar, M.S.; Pert, G.J. Laser ablation of Mg, Cu and Pb using infrared and ultraviolet low-fluence lasers. J. Appl. Phys. 2003, 94, 1468. [Google Scholar] [CrossRef]
- Honda, K.; Fujishima, A. Electrochemical photolysis of water at a semiconductor electrode. Nature 1972, 238, 37–38. [Google Scholar]
- Rajendiran, S.; Meehan, D.; Wagenaars, E. Plasma-enhanced pulsed laser deposition of copper and zinc oxide thin films. AIP Adv. 2020, 10, 065323. [Google Scholar] [CrossRef]
- Fortunato, E.; Barquinha, P.; Martins, R. Oxide semiconductor thin-film transistors: A review of recent advances. Adv. Mater. 2012, 24, 2495. [Google Scholar] [CrossRef] [PubMed]
- Wong, T.K.; Zhuk, S.; Masudy-Panah, S.; Dalapati, G.K. Current status and future prospects of copper oxide heterojunction solar cells. Materials 2020, 9, 271. [Google Scholar] [CrossRef]
- Özgür, Ü.; Alivov, Y.I.; Liu, C.; Teke, A.; Reshchikov, M. A comprehensive review of ZnO materials and devices. J. Appl. Phys. 2005, 98, 041301. [Google Scholar]
- Kumar, R.; Kumar, G.; Al-Dossary, O.; Umar, A. ZnO nanostructured thin films: Depositions, properties and applications—A review. Mater. Express 2015, 5, 3. [Google Scholar] [CrossRef]
- Pert, G.J. Models of laser-plasma ablation. J. Plasma Phys. 1986, 35, 43–74. [Google Scholar] [CrossRef]
- Pert, G.J. Models of laser-plasma ablation Part 2—Steady-state theory: Self-regulating flow. J. Plasma Phys. 1986, 36, 415–446. [Google Scholar] [CrossRef]
- Pert, G.J. Models of laser-plasma ablation Part 3—Steady-state theory: Deflagration flow. J. Plasma Phys. 1988, 39, 241–276. [Google Scholar] [CrossRef]
- Pert, G.J. Two-dimensional hydrodynamic models of laser-produced plasmas. J. Plasma Phys. 1989, 41, 263–280. [Google Scholar] [CrossRef]
- Liu, H.; Ashfold, M.N.; Meehan, D.N.; Wagenaars, E. Wavelength-dependent variations of the electron characteristics in laser-induced plasmas: A combined hydrodynamic and adiabatic expansion modelling and time-gated, optical emission imaging study. J. Appl. Phys. 2019, 125, 083304. [Google Scholar] [CrossRef]
- Boris, J.P.; Book, D.L. Flux-corrected transport. I. SHASTA, a fluid transport algorithm that works. J. Comp. Phys. 1987, 11, 38–69. [Google Scholar] [CrossRef]
- Thompson, S.L. Improvements in the Chart-D Radiation-Hydrodynamic Code I: Analytic Equations of State, Sandia Labs Report. 1970, SC-RR-70-28. Available online: https://www.osti.gov/biblio/4125539 (accessed on 1 December 2022).
- Latter, R. Temperature behavior of the Thomas-Fermi statistical model for atoms. Phys. Rev. 1955, 11, 1854. [Google Scholar] [CrossRef]
- Kershaw, D.S. The incomplete Cholesky—Conjugate gradient method for the iterative solution of systems of linear equations. J. Comp. Phys. 1978, 26, 43–65. [Google Scholar] [CrossRef]
- Pert, G.J. Inverse bremsstrahlung absorption in large radiation fields during binary collisions-classical theory. II. Integrated rate coefficients for Coulomb collisions. J. Phys. A Math. Gen. 1976, 9, 463–471. [Google Scholar] [CrossRef]
- Pert, G.J. Inverse bremsstrahlung absorption in large radiation fields during binary collisions-classical theory. II(b). summed rate coefficients for Coulomb collisions. J. Phys. A Math. Gen. 1976, 9, 1797–1800. [Google Scholar] [CrossRef]
- Hermann, J.; Grojo, D.; Axente, E.; Craciun, V. Local thermodynamic equilibrium in a laser-induced plasma evidenced by blackbody radiation. Spectrochim. Acta Part B 2018, 144, 82–86. [Google Scholar] [CrossRef]
- Cristoforetti, G.; Lorenzetti, G.; Legnaioli, S.; Palleschi, V. Investigation on the role of air in the dynamical evolution and thermodynamic state of a laser-induced aluminium plasma by spatial- and time-resolved spectroscopy. Spectrochim. Acta Part B 2010, 65, 787–796. [Google Scholar] [CrossRef]
- Royal Society of Chemistry. Periodic Table. Available online: Rsc.org/periodic-table (accessed on 1 December 2022).
- Zhang, J.; Zhao, Y.; Hixson, R.S.; Gray, G.T., III; Wang, L.; Utsumi, W.; Hiroyuki, S.; Takanori, H. Thermal equations of state for titanium obtained by high pressure—Temperature diffraction studies. Phys. Rev. B. 2008, 78, 054119. [Google Scholar] [CrossRef]
- Katahara, K.W. Pressure derivatives of the elastic moduli of niobium and tantalum. J. Appl. Phys. 1976, 47, 434–439. [Google Scholar] [CrossRef]
- Kerley, G.I. Equations of State for Titanium and Ti6A14V Alloy; Sandia Report; Sandia National Laboratories: Albuquerque, NM, USA, 2003. [Google Scholar]
- Greeff, C.W.; Johnson, J.D. New Sesame Equation of State for Tantalum; Los Alamos Report; Los Alamos National Lab.: Santa Fe, NM, USA, 2000; Volume 78, p. LA-13681-MS. [Google Scholar]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Desai, P.D. Thermodynamic properties of Aluminium. Int. J. Thermophys. 1987, 8, 621–638. [Google Scholar] [CrossRef]
- Arblaster, J.W. Thermodynamic Properties of Gold. J. Phase Equilib. Diffus. 2016, 37, 229–245. [Google Scholar] [CrossRef]
- McCreary, J.R.; Thorn, R.J. Enthalpy of sublimation of Zinc and Cadmium. J. Chem. Phys. 1969, 50, 3725. [Google Scholar] [CrossRef]
- Arblaster, J.W. Thermodynamic Properties of Copper. J. Phase Equilib. Diffus. 2015, 36, 422–444. [Google Scholar] [CrossRef]
- Desai, P.D. Thermodynamic Properties of Titanium. Int. J. Thermophys. 1987, 8, 781–794. [Google Scholar] [CrossRef]
- Arblaster, J.W. Thermodynamic Properties of Tantalum. J. Phase Equilib. Diffus. 2018, 39, 255–272. [Google Scholar] [CrossRef]
- Properties of Chemical Elements. Available online: Material-properties.org/properties-of-chemical-elements/ (accessed on 1 December 2022).



| Chart-D Variable | Aluminium, Al | Gold, Au | Zinc, Zn | Copper, Cu | Titanium, Ti | Tantalum, Ta |
|---|---|---|---|---|---|---|
| Mass density () | 2.700 [33] | 19.30 [33] | 7.140 [33] | 8.940 [33] | 4.506 [33] | 16.40 [33] |
| Bulk modulus () | [33] | [33] | [33] | [33] | [34] | [35] |
| Gruneisen coefficient | 2.060 [26] | 3.054 [26] | 1.390 [26] | 2.020 [26] | 1.184 [36] | 1.590 [37] |
| Debye temperature () | [38] | [38] | [38] | [38] | [38] | [38] |
| Enthalpy of sublimation ( ) | [39] | [40] | [41] | [42] | [43] | [44] |
| Melting temperature () | [33] | [33] | [33] | [33] | [33] | [33] |
| Thermal conductivity coefficient ( ) | [45] | [45] | [45] | [45] | [45] | [45] |
| Atomic number | 13 | 79 | 30 | 29 | 22 | 73 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hill, M.; Wagenaars, E. Modelling of Plasma Temperatures and Densities in Laser Ablation Plumes of Different Metals. Photonics 2022, 9, 937. https://doi.org/10.3390/photonics9120937
Hill M, Wagenaars E. Modelling of Plasma Temperatures and Densities in Laser Ablation Plumes of Different Metals. Photonics. 2022; 9(12):937. https://doi.org/10.3390/photonics9120937
Chicago/Turabian StyleHill, Matthew, and Erik Wagenaars. 2022. "Modelling of Plasma Temperatures and Densities in Laser Ablation Plumes of Different Metals" Photonics 9, no. 12: 937. https://doi.org/10.3390/photonics9120937
APA StyleHill, M., & Wagenaars, E. (2022). Modelling of Plasma Temperatures and Densities in Laser Ablation Plumes of Different Metals. Photonics, 9(12), 937. https://doi.org/10.3390/photonics9120937






