An Experimental and Numerical Study of the Impact of Ambient Light of SiPMs in VLC Receivers
Abstract
1. Introduction
2. Experimental Procedure and Monte Carlo Simulation of SiPMs
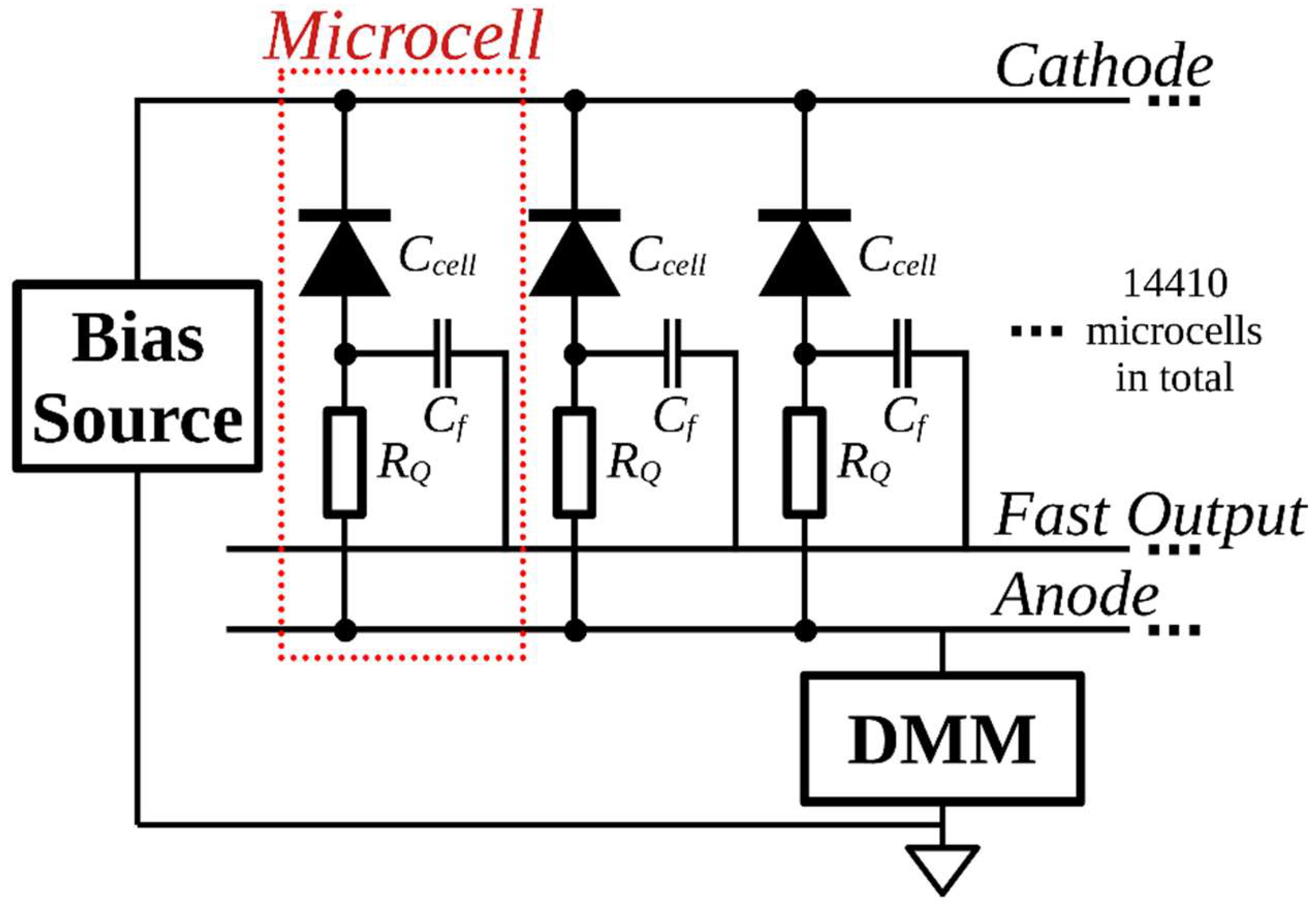
2.1. Description of SiPMs and Their Response to Light
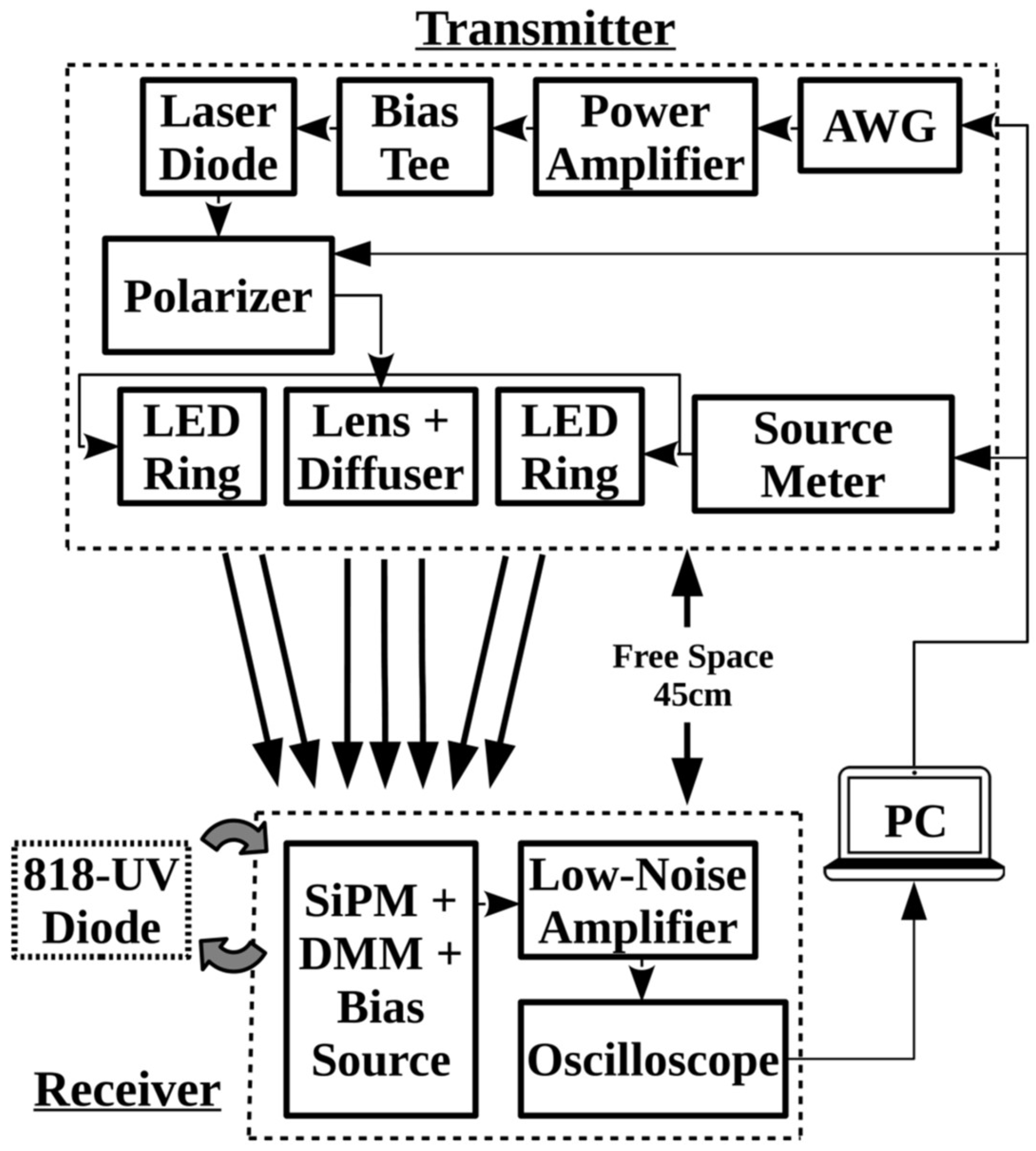
2.2. Experimental Procedure
2.3. Monte Carlo Simulation of an SiPM
3. Results
3.1. Photon Detection Efficiency Measurement
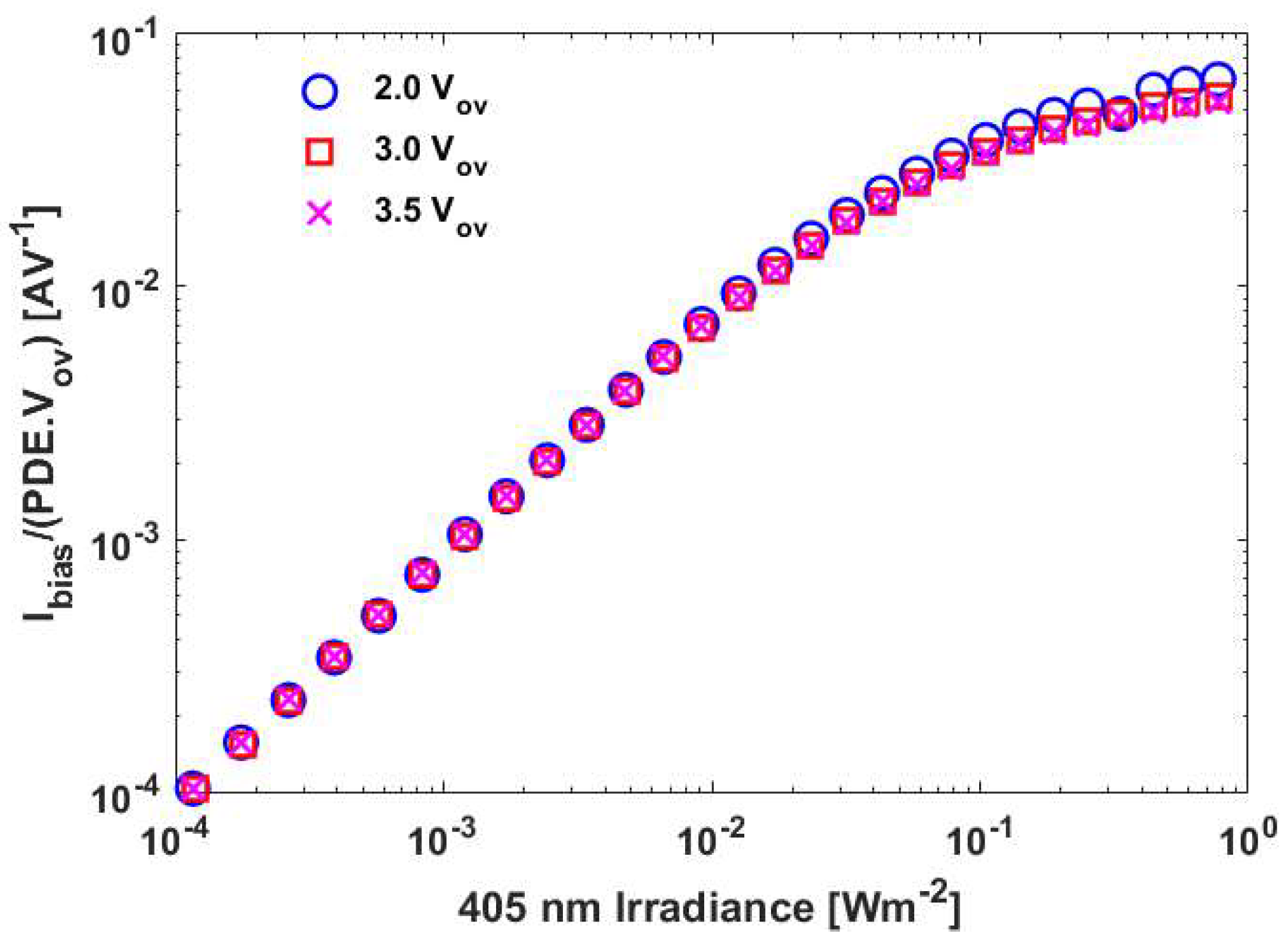
3.2. Measured Bias Current
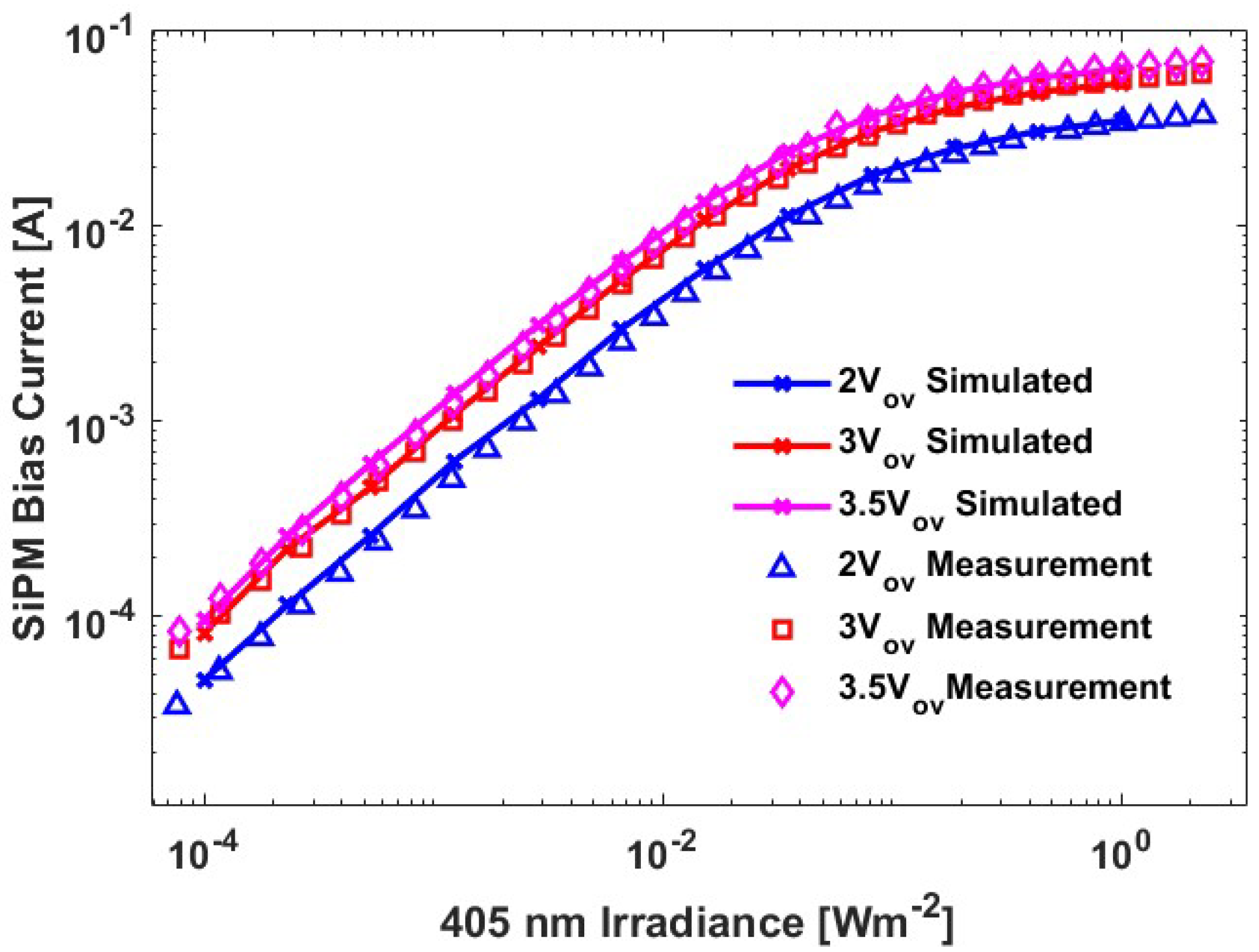
3.3. Comparison of Measured and Simulated Bias Currents
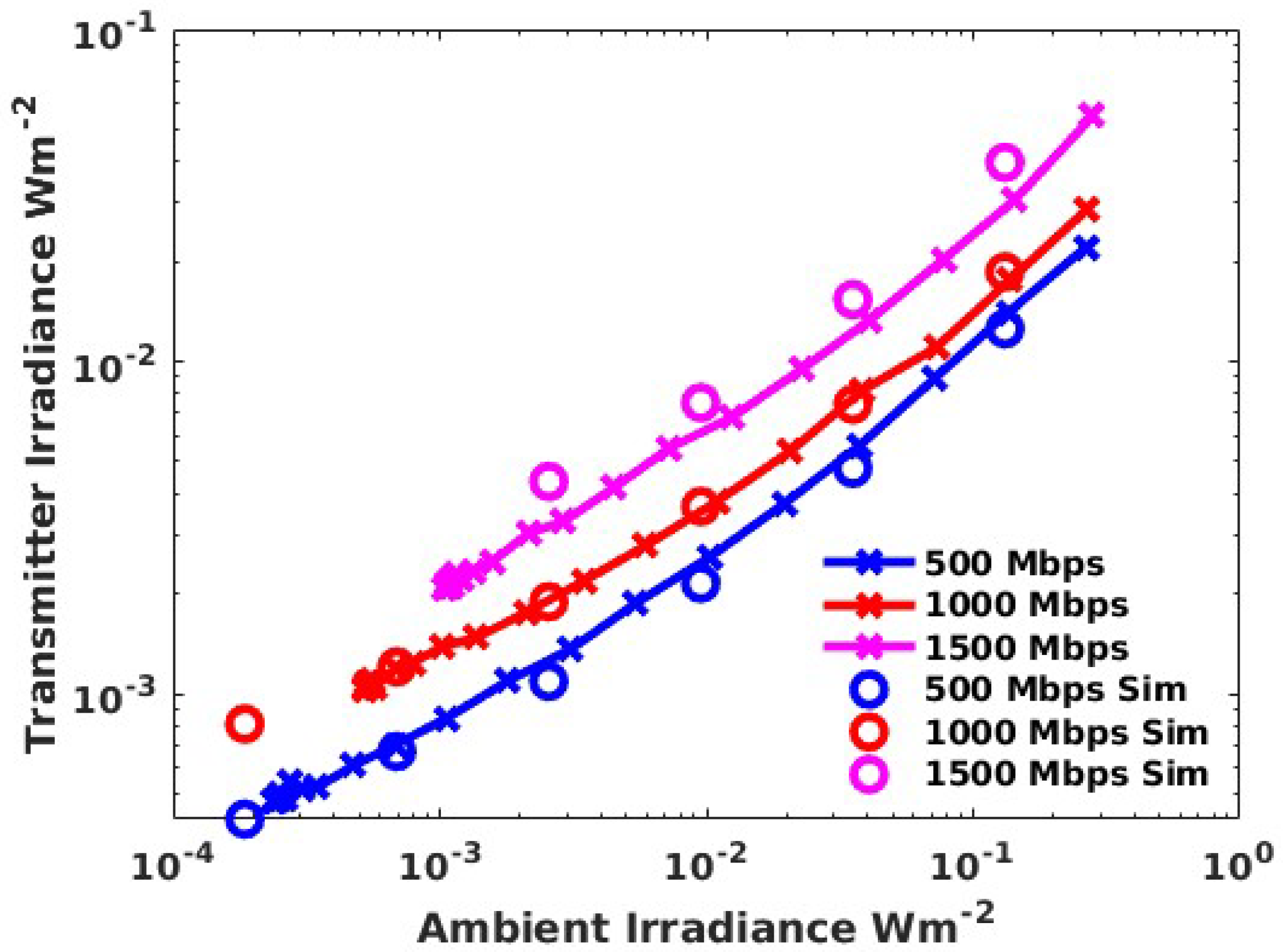
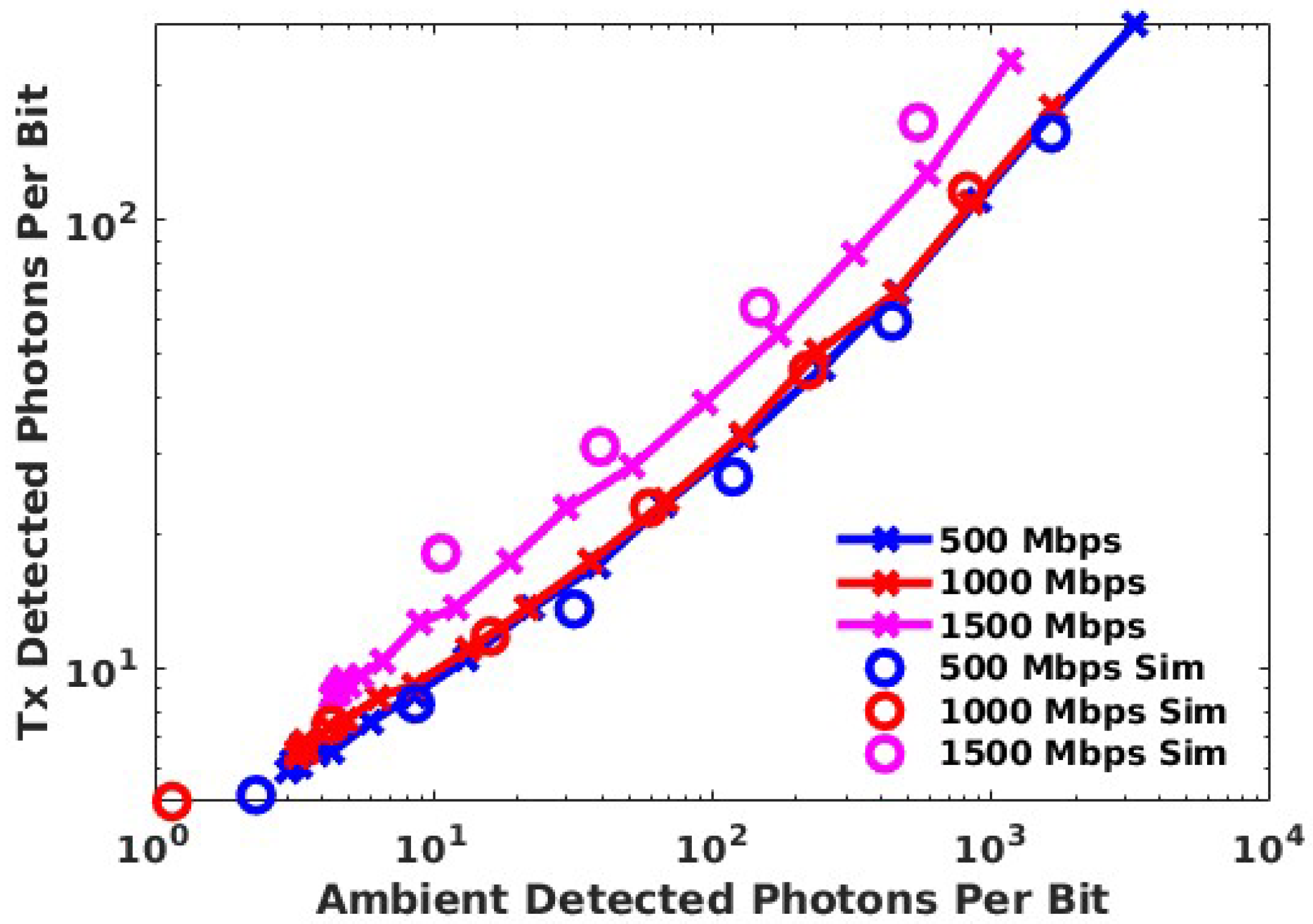
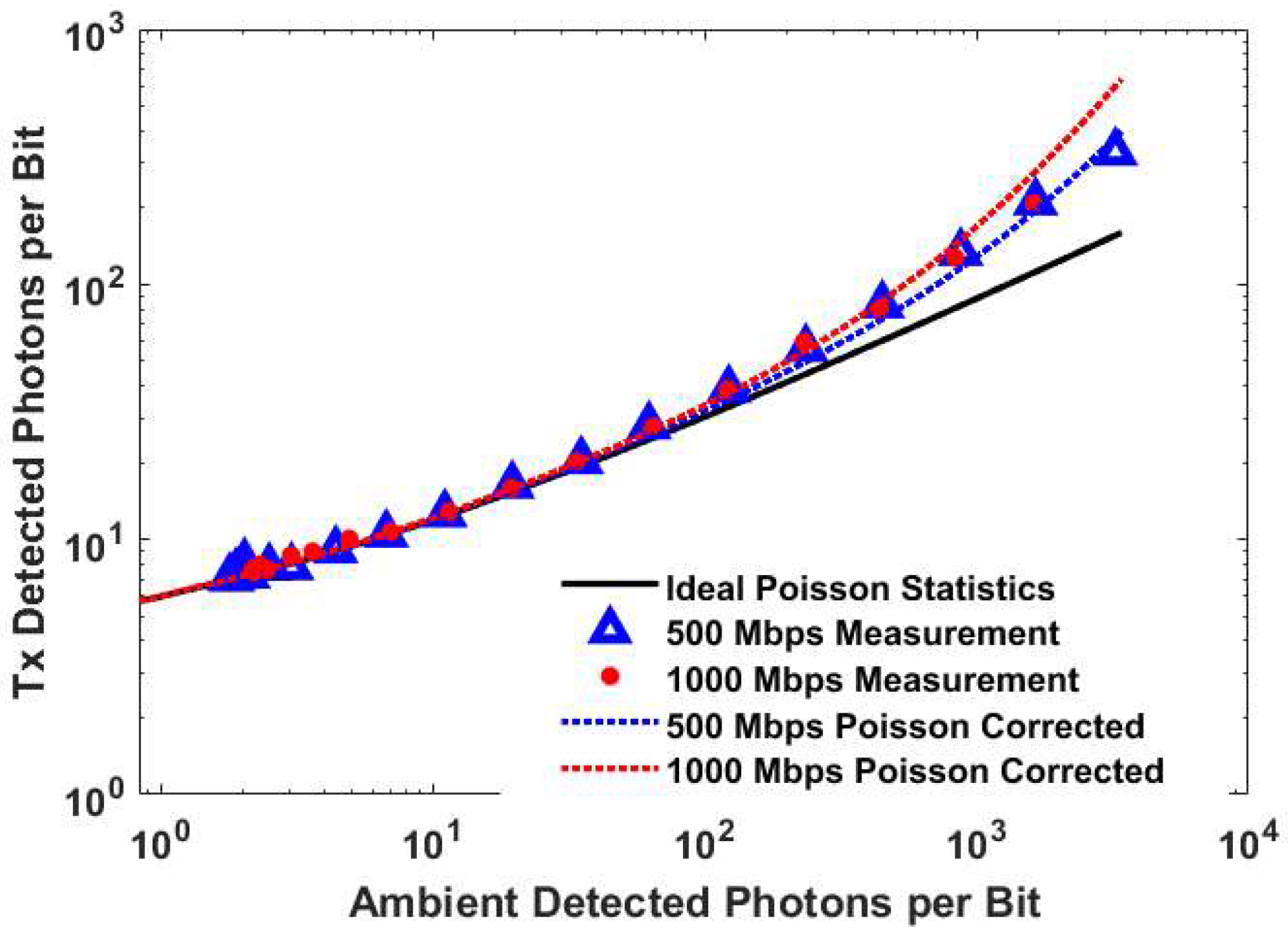
3.4. Data Transmission Experiments in Ambient Light
4. Discussion
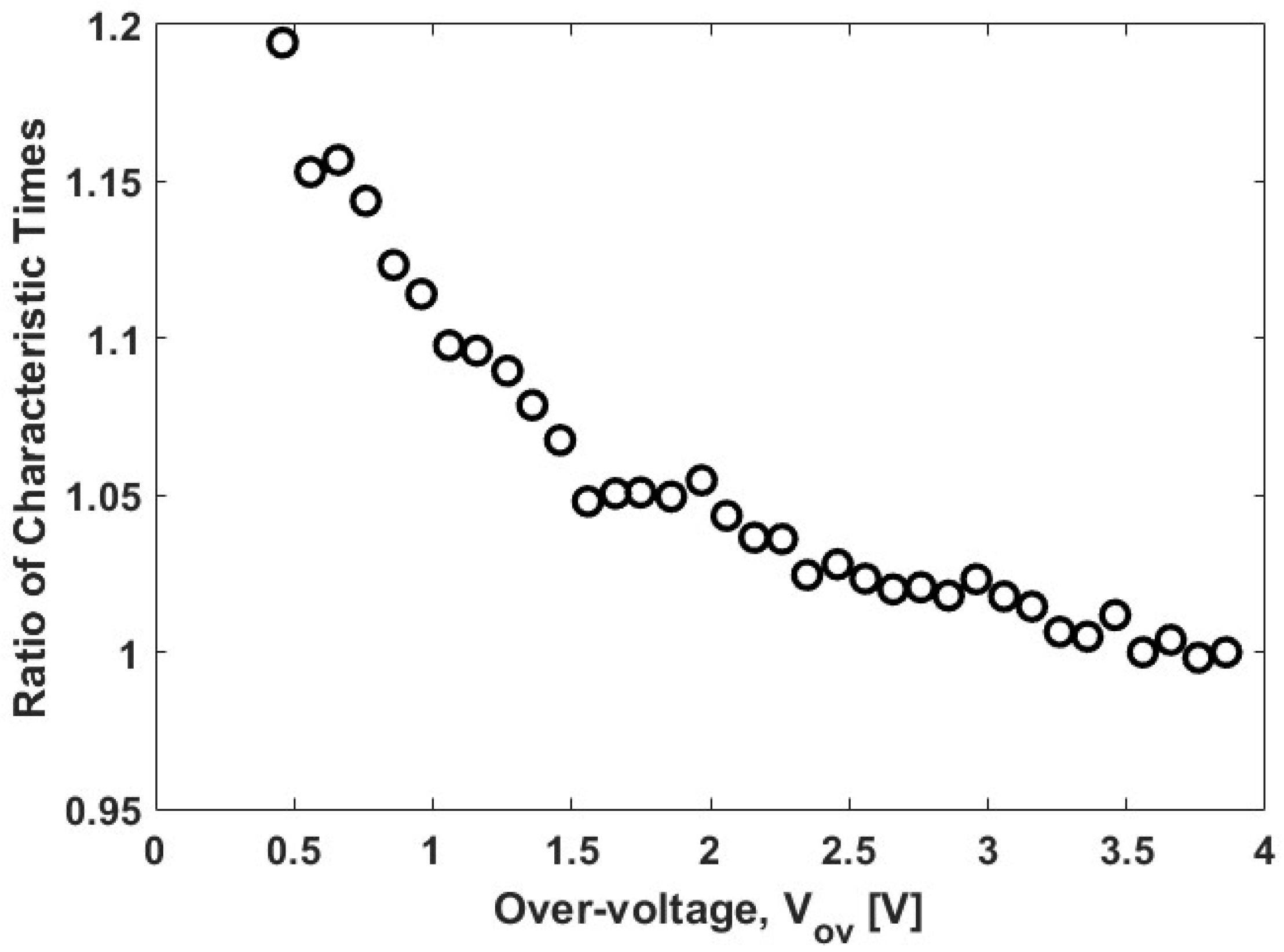
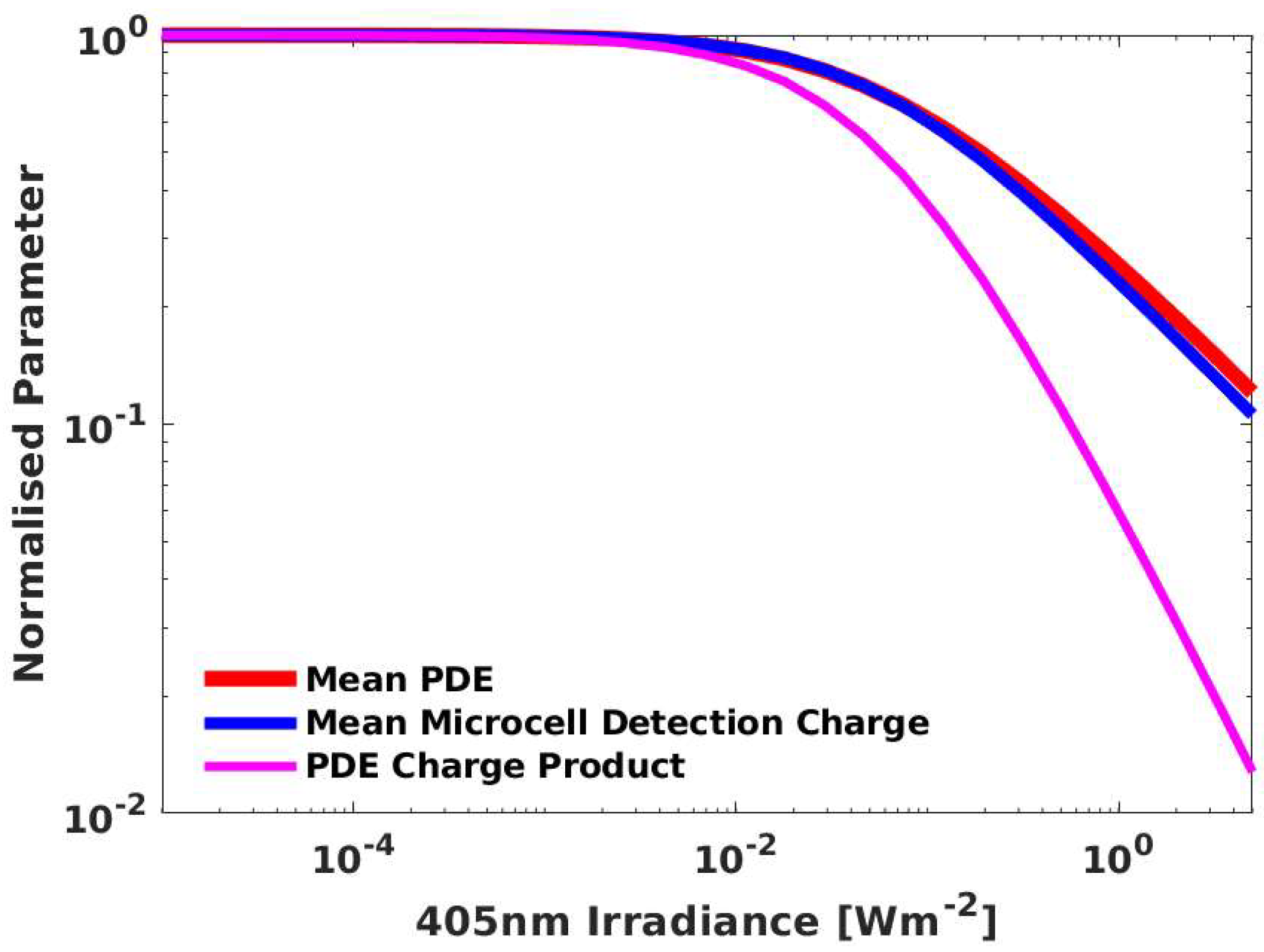
4.1. The Origins of the SiPMs Non-Linearity
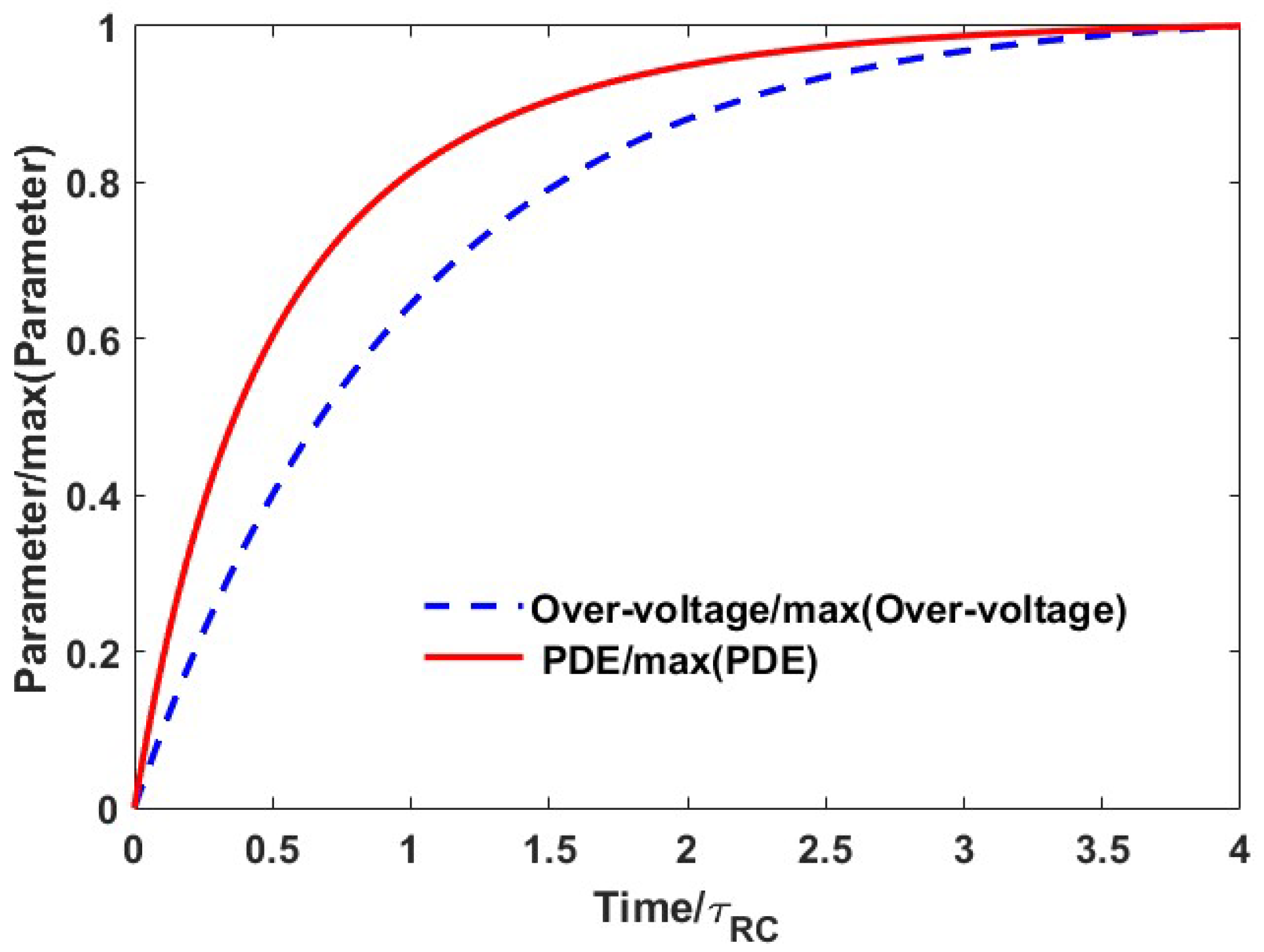
4.2. A Simple Method of Estimating the Maximum Count Rate
4.3. A Simple Method of Predicting the Impact of Ambient Light
4.4. Selecting Optical Filters for Operation in Ambient Light
4.5. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Haas, H.; Elmirghani, J.; White, I. Optical Wireless Communication. Philos. Trans. R. Soc. A 2020, 378, 20200051. [Google Scholar] [CrossRef] [PubMed]
- Khalighi, M.-A.; Hamza, T.; Bourennane, S.; Leon, P.; Opderbecke, J. Underwater Wireless Optical Communications Using Silicon Photo-Multipliers. IEEE Photon. J. 2017, 9, 1–10. [Google Scholar] [CrossRef]
- Leon, P.; Roland, F.; Brignone, L.; Opderbecke, J.; Greer, J.; Khalighi, M.A.; Hamza, T.; Bourennane, S.; Bigand, M. A new underwater optical modem based on highly sensitive Silicon Photomultipliers. In Proceedings of the OCEANS 2017, Aberdeen, UK, 19–22 June 2017. [Google Scholar] [CrossRef]
- Zhang, L.; Chitnis, D.; Chun, H.; Rajbhandari, S.; Faulkner, G.; O’Brien, D.; Collins, S. A Comparison of APD- and SPAD-Based Receivers for Visible Light Communications. J. Light. Technol. 2018, 36, 2435–2442. [Google Scholar] [CrossRef]
- Ahmed, Z.; Zhang, L.; Faulkner, G.; O’Brien, D.; Collins, S. A Shot-Noise Limited 420 Mbps Visible Light Communication System using Commercial Off-the-Shelf Silicon Photomultiplier (SiPM). In Proceedings of the 2019 IEEE International Conference on Communications Workshops (ICC Workshops), Shanghai, China, 20–24 May 2019. [Google Scholar]
- Ahmed, Z.; Singh, R.; Ali, W.; Faulkner, G.; O’Brien, D.; Collins, S. A SiPM-Based VLC Receiver for Gigabit Communication Using OOK Modulation. IEEE Photonics Technol. Lett. 2020, 32, 317–320. [Google Scholar] [CrossRef]
- Zhang, L.; Tang, X.; Sun, C.; Chen, Z.; Li, Z.; Wang, H.; Jiang, R.; Shi, W.; Zhang, A. Over 10 attenuation length gigabits per second underwater wireless optical communication using a silicon photomultiplier (SiPM) based receiver. Opt. Express 2020, 28, 24968. [Google Scholar] [CrossRef] [PubMed]
- Khalighi, M.A.; Akhouayri, H.; Hranilovic, S. Silicon-Photomultiplier-Based Underwater Wireless Optical Communication Using Pulse-Amplitude Modulation. IEEE J. Ocean. Eng. 2019, 45, 1611–1621. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, L.; Sun, C.; Chen, Z.; Wang, H.; Jiang, R.; Li, Z.; Shi, W.; Zhang, A. Underwater Wireless Optical Communication Based on DPSK Modulation and Silicon Photomultiplier. IEEE Access 2020, 8, 204676–204683. [Google Scholar] [CrossRef]
- Matthews, W.; Ahmed, Z.; Ali, W.; Collins, S. A 3.45 Gigabits/s SiPM-Based OOK VLC Receiver. IEEE Photonics Technol. Lett. 2021, 33, 487–490. [Google Scholar] [CrossRef]
- Ali, W.; Faulkner, G.; Ahmed, Z.; Matthews, W.; Collins, S. Giga-Bit Transmission Between an Eye-Safe Transmitter and Wide Field-of-View SiPM Receiver. IEEE Access 2021, 9, 154225–154236. [Google Scholar] [CrossRef]
- Li, Y.; Hua, Y.; Henderson, R.K.; Chitnis, D. A Photon Limited SiPM Based Receiver for Internet of Things. In Proceedings of the 2021 Asia Communications and Photonics Conference (ACP), Shanghai, China, 24–27 October 2021. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, R.; Tang, X.; Chen, Z.; Chen, J.; Wang, H. A Simplified Post Equalizer for Mitigating the Nonlinear Distortion in SiPM Based OFDM-VLC System. IEEE Photon. J. 2021, 14, 1–7. [Google Scholar] [CrossRef]
- Huang, S.; Chen, C.; Bian, R.; Haas, H.; Safari, M. 5 Gbps Optical Wireless Communication using Commercial SPAD Array Receivers. Opt. Lett. 2022, 47, 2294–2297. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Chitnis, D. A real-time SiPM based receiver for FSO communication. In Proceedings of the Next-Generation Optical Communication: Components, Sub-Systems, and Systems XI, San Francisco, CA, USA, 3 March 2022. [Google Scholar]
- Matthews, W.; Collins, S. The negative impact of anode resistance on SiPMs as VLC receivers. In Proceedings of the 2022 17th Conference on Ph. D Research in Microelectronics and Electronics (PRIME), Sardinia, Italy, 12–15 June 2022. [Google Scholar] [CrossRef]
- Acerbi, F.; Gundacker, S. Understanding and simulating SiPMs. In Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment; Elsevier: Amsterdam, The Netherlands, 2019; Volume 926, pp. 16–35. [Google Scholar]
- Gnecchi, S.; Dutton, N.A.W.; Parmesan, L.; Rae, B.R.; McLeod, S.J.; Pellegrini, S.; Grant, L.A.; Henderson, R.K. A Simulation Model for Digital Silicon Photomultipliers. IEEE Trans. Nucl. Sci. 2016, 63, 1343–1350. [Google Scholar] [CrossRef][Green Version]
- He, C.; Ahmed, Z.; Collins, S. Signal Pre-Equalization in a Silicon Photomultiplier-Based Optical OFDM System. IEEE Access 2021, 9, 23344–23356. [Google Scholar] [CrossRef]
- Huang, S.; Safari, M. Hybrid SPAD/PD Receiver for Reliable Free-Space Optical Communication. IEEE Open J. Commun. Soc. 2020, 1, 1364–1373. [Google Scholar] [CrossRef]
- Huang, S.; Safari, S. SPAD-Based Optical Wireless Communication With Signal Pre-Distortion and Noise Normalization. IEEE Trans. Commun. 2022, 70, 2593–2605. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, R.; Tang, X.; Chen, Z.; Li, Z.; Chen, J. Performance Estimation and Selection Guideline of SiPM Chip within SiPM-Based OFDM-OWC System. Photonics 2022, 9, 637. [Google Scholar] [CrossRef]
- Hinrichs, M.; Berenguer, P.W.; Hilt, J.; Hellwig, P.; Schulz, D.; Paraskevopoulos, A.; Bober, K.L.; Freund, R.; Jungnickel, V. A Physical Layer for Low Power Optical Wireless Communications. IEEE Trans. Green Commun. Netw. 2020, 5, 4–17. [Google Scholar] [CrossRef]
- Otte, A.N.; Garcia, D.; Nguyen, T.; Purushotham, D. Characterization of three high efficiency and blue sensitive silicon photomultipliers. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2017, 846, 106–125. [Google Scholar] [CrossRef]
- Onsemi.com 2022. Introduction to the Silicon Photomultiplier (SiPM) AND977O/D. Available online: https://www.onsemi.com/pub/Collateral/AND9770-D.PDF (accessed on 8 November 2022).
- Onsemi.com. 2020. J-Series SiPM Sensors Datasheet. Available online: https://www.onsemi.com/pub/Collateral/MICROJ-SERIES-D.PDF (accessed on 20 June 2022).
- He, C.; Lim, Y. Silicon Photomultiplier (SiPM) Selection and Parameter Analysis in Visible Light Communications. In Proceedings of the 31st Wireless and Optical Communications Conference (WOCC), Shenzhen, China, 11–12 August 2022. [Google Scholar] [CrossRef]


| Parameter | 30020 |
|---|---|
| Number of microcells | 14,410 |
| Microcells active area diameter (µm) | 20 |
| Fill factor (%) | 62 |
| Recharge/recovery time constant (ns) | 15 |
| Dark Count Rate (MHz) | 1.2 (@ 5 Vov) |
| Fast output pulse width (ns) | 1.4 |
| Parameter | 30020 |
|---|---|
| SiPM Area (mm2) | 9 |
| Number of microcells | 14,410 |
| Vbreakdown (V) | 24.5 |
| Vchar (V) | 2.03 V |
| Maximum Photon Detection Efficiency at 405 nm | 0.46 |
| Recharge RC time constant (ns) | 30.8 |
| Microcell Capacitance (fF) | 46 |
| Full width at half maximum offset output pulse width (ns) | 1.4 |
| Simulation time step (s) | Maximum of (bit time)/20 and 0.05 ns |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matthews, W.; Collins, S. An Experimental and Numerical Study of the Impact of Ambient Light of SiPMs in VLC Receivers. Photonics 2022, 9, 888. https://doi.org/10.3390/photonics9120888
Matthews W, Collins S. An Experimental and Numerical Study of the Impact of Ambient Light of SiPMs in VLC Receivers. Photonics. 2022; 9(12):888. https://doi.org/10.3390/photonics9120888
Chicago/Turabian StyleMatthews, William, and Steve Collins. 2022. "An Experimental and Numerical Study of the Impact of Ambient Light of SiPMs in VLC Receivers" Photonics 9, no. 12: 888. https://doi.org/10.3390/photonics9120888
APA StyleMatthews, W., & Collins, S. (2022). An Experimental and Numerical Study of the Impact of Ambient Light of SiPMs in VLC Receivers. Photonics, 9(12), 888. https://doi.org/10.3390/photonics9120888




