Abstract
Mercury vacancies, acting as double acceptors, are the dominant point defects in ternary HgCdTe alloys. Though HgCdTe is one of the leading materials in infrared optoelectronics, the energy spectra of the vacancies are still a matter of some debate. This work investigated the rates at which holes are captured to a singly ionized mercury vacancy via acoustic phonon emission in narrow-gap Hg1−xCdxTe with technologically relevant x~0.22. Combined with the calculated rates of intracenter transitions, the data allow one to predict the most pronounced optical transitions in the emission spectrum of a double-charged acceptor. The results are sustained by the photoluminescence spectroscopy in the terahertz domain, allowing one to identify the emission band that is related to neutral vacancies.
1. Introduction
Ternary Hg1−xCdxTe (MCT) alloys have been studied for more than five decades due to their paramount importance in mid-infrared detection [,]. MCT alloys feature the possibility of changing the band gap by selecting the composition: from 1.6 eV in pure CdTe to 0 in a ternary alloy with less than 16.5% of Cd. This fundamental property makes MCT alloys of interest for far-infrared optoelectronics []. One of the main problems in the development of interband detectors and long-wavelength emitters is the decrease in the carrier lifetimes due to the so-called Shockley–Reed–Hall (SRH) recombination that takes place via impurity-defect centers.
The most common MCT defect is mercury vacancy, arising due to a weak chemical bond between mercury and tellurium. The mercury vacancy is a doubly charged or double acceptor. Such an acceptor can be found in three charge states: a neutral A20 center with which two holes are bound, a singly ionized A2−1 center with which one hole is bound and, finally, a fully ionized A2−2 center free of holes. Despite the fact that mercury vacancies are always formed in Hg1−xCdxTe, their energy spectrum is still insufficiently studied. A relative consensus has been reached that the vacancy is a double acceptor and its minimum ionization energy is about 10 meV for x~0.2 [,,] and 14 meV for x~0.3 [,,].
Determining the energy spectrum of the vacancies is of considerable interest, since they can play a significant role in SRH recombination. Usually, the excess carriers are captured to the impurity-defect centers by a non-radiative process in which electrons and holes transfer their energy to phonons. However, when some optical transitions have a significant matrix element, they can also make a discernable contribution to the capture process. Thus, the SRH process may turn out to be partially radiative. Such “radiative” capture was observed in a number of semiconductors and low-dimensional heterostructures by far-infrared photoluminescence (PL) studies [,].
Terahertz (THz) PL associated with acceptor states in bulk MCT epitaxial layers and HgTe/CdHgTe heterostructures with quantum wells has been reported in papers [,]. Two bands in the PL spectra were found near the photon energies of 10 meV and 20 meV. The distinctive feature of these below-bandgap PL bands is that they do not shift to the short-wavelength region as temperature rises, while the lines of interband transitions are driven by the bandgap increase with temperature.
The acceptor states in MCT epitaxial layers and HgTe/CdHgTe heterostructures with p-type conductivity were also studied by photoconductivity (PC) measurements [,] in the THz domain. The PC spectra exhibited bands near 10 meV and 20 meV that were associated with the photoexcitation of neutral and singly ionized mercury vacancies, respectively. The shape of these PC bands and their quenching with temperature indicated that they are mainly formed due to the photothermal ionization of the vacancy, i.e., an optical transition to a shallow excited state followed by thermal excitation into the valence band continuum [].
In turn, the PL studies in Ref. [] were carried out for an n-type structure in which all acceptor centers were completely ionized. Thus, all mercury vacancies in the absence of illumination were in the A2−2 charge state. In this case, A2−1 centers, which provide the PL at the longest wavelengths, appeared in non-equilibrium conditions due to the excess holes being captured from the valence band to A2–2 mercury vacancies.
Thus, PL spectroscopy in THz region allows for the study of residual acceptors in the material with n-type conductivity in which there can be no PC due to acceptor ionization. It should also be noted that in photothermal ionization spectroscopy, the amplitudes of the PC lines reflect the probability of the thermal ionization from the corresponding excited states of the acceptor. Therefore, they can be quite small for the transitions involving deep excited states. The amplitude of PL lines is controlled by (i) the population of the excited states from which the transition to the ground state occurs and (ii) the probabilities of the radiative and non-radiative mechanisms for the hole transition to the final state.
The aim of this work was to estimate the rates of the non-radiative capture of holes to the localized states of a singly ionized mercury vacancy (A2−1 center) as well as the rates of the intracenter transitions for the A20 center that is formed due to such capture. Aside from interpreting the PL spectra associated with mercury vacancies, the results may be of interest for modeling the carrier trapping on impurity-defect centers in MCT structures during SRH recombination.
2. Calculation Methods
We applied Fermi’s golden rule to calculate the possibility of hole transitions to various states of Hg vacancies during phonon emission. As the ionization energy of a neutral Hg vacancy (11 meV []) is lower than the energy of a transversal optical phonon (~15 meV []), only acoustic phonons can be involved in the hole capture by a singly charged center and in the non-radiative intracenter transitions of a neutral vacancy.
Phonons cause atom displacements and thereby distort the ideal periodic potential of the lattice. We denote such a correction to the crystal potential as δV. This δV potential can be split into an electrostatic macrofield and a deformation microfield that becomes zero when averaging over a volume greatly larger than the lattice cell volume: []. The macrofield only occurs in polar semiconductors in which atom displacements can induce polarization. Carrier interaction with the acoustic phonons via the macrofield is called the piezoacoustic carrier–phonon interaction, while interaction via the microfield is called the deformative–acoustic interaction. In polar semiconductors, the former interaction is usually of more importance; for instance, in GaAs, the carrier mobility at temperatures T > 100 K is controlled by piezoacoustic scattering, while deformative–acoustic interaction is of minor importance []. Therefore, it is natural to anticipate piezoacoustic interaction to dominate the deformative one during intracenter transitions and hole transitions from the valence band to the vacancies in HgCdTe.
Let us find the electrostatic potential that occurs when the crystal is deformed. As there are no external charges, , so one can define potential:
where P is the polarization density caused by the atom displacement in the phonon field. For the harmonic phonon wave:
For acoustic phonons, the polarization density depends on the inhomogeneity of the atom displacement in the phonon field, described by the deformation tensor: , where ξ is the atom displacement vector in the phonon field and are coordinates with indexes i, j = 1,2,3.
The displacement vector may be written as:
where M is the total mass of atoms in the elementary cell (net masses of Hg and Te atoms), is a unit vector of polarization, is the phonon wave amplitude, is the phonon wave vector, is the phonon frequency, V is the volume of the sample, and is the lattice constant of Hg1−xCdxTe ternary alloy, which is a liner interpolation between HgTe (6.46 Å) and CdTe (6.48 Å) lattice constants [].
The phonon frequency can be written as , where is the speed of sound. The latter is estimated from the dispersion curves for longitudinal and transverse acoustic phonons in HgTe and CdTe from refs. [,]. For HgTe-like phonons, the speed is 723 m/s and 1987 m/s for transverse and longitudinal phonons, respectively; for CdTe-like phonons, the speed is 1376 m/s and 2522 m/s, respectively. We used the spherical approximation (assuming the phonon dispersion law to be isotropic) as in the calculation of the acceptor wave functions.
The energies of the transverse acoustic phonons do not exceed 2.26 meV [] and 4.3 meV [] for HgTe-like and CdTe-like phonons, respectively. For the longitudinal acoustic phonons, these energies are 10.56 meV [] and 13.4 meV []. This factor limits the kinetic energy of carriers involved in the transitions to localized states via acoustic phonon emission. The energy should not exceed , where is the phonon limit energy and is the ionization energy of the state to which the carrier transits. Thus, the longitudinal phonons make the main contribution to the hole transitions to deeper states, while for shallower states, the contribution of the transverse phonons is also significant.
When the atom displacement is small compared to the lattice constant, the strain tensor also turns out to be small, and the polarization density linearly depends on this tensor (the polarization density can be expanded into a series leaving only a linear term):
where are the components of the piezomodule tensor. For cubic symmetry, the piezomodule tensor can be written as , if j ≠ m ≠ l. The piezomodules are zero if at least two indexes are equal. Finally, the equation for the electrostatic potential becomes:
and in the case of cubic symmetry:
where and are the creation and destruction operators for phonons, respectively. In our case, one should keep in (5) only the component proportional to the creation operator during the phonon emission. As given in Ref. [], the components of the piezomodule tensor can be found to be = . According to Ref. [], coefficient can be estimated by the order of magnitude as , where e is the elementary charge. Using (6), it is possible to calculate the probability of phonon emission per unit time during the hole transition between the states of the acceptor:
where is the number of phonons and ,, are the wave functions and energies of the initial and final states of Hg vacancy, respectively. We took into account only the processes with spontaneous phonon emission ( = 0), which gives us a lower estimate for the transition probabilities.
The hole capture frequency (inverse capture time) from a continuous spectrum can be obtained from the expression (6) by integrating over the states of a continuous spectrum, taking into account the hole distribution law:
The thermalization time of the free carrier distribution is much shorter than the carrier lifetime in the valence band, which reaches several microseconds at low temperatures []. Therefore, one can assume carrier distribution f to be quasi-equilibrium:
Here, kB is the Boltzmann constant, T is temperature, and μ is quasi-Fermi-level, which depends on the free hole concentration p in the valence band and temperature, according to
where mh denotes the heavy hole effective mass. The calculated Fermi energy was used to compute the frequency of hole capture from the valence band, according to (8). The frequency of transitions between the localized states is equal to the probability of transitions per unit time between such states:
Note that for mercury vacancies, the observed ionization energies deviate from the results of calculations in the framework of the effective mass approximation [,]. Therefore, we calculated the hole energies and wave functions with the central cell potential (CCP) added to the acceptor field, as described in detail in Ref. [].
3. Materials and Measurement Methods
The structure under study was grown by molecular beam epitaxy on a semi-insulating GaAs(013) substrate. Buffer layers of ZnTe (50 nm thick) and CdTe (5 µm thick) were grown before the main part of the structure with x = 0.22. The structure was not deliberately doped; however, the concentration of residual donors, determined via the measurements of the Hall effect at T = 77 K, was no less than 2 × 1014 cm–3.
The PL spectra were obtained under continuous excitation at a wavelength of 808 nm using the step-scan mode of a Bruker Vertex 80v spectrometer. A silicon bolometer was used as the detector. The measurement technique is described in detail in Ref. [].
The sample was mounted in a closed cycle cryostat, hermetically coupled to the spectrometer. Thus, the absorption of THz radiation by the atmospheric air was completely excluded. To cut off the radiation of the exciting laser, we used filters made of black polyethylene with no features in the spectral range of measurements. Mylar films of various thicknesses were used as beam splitters to expand the attainable spectral range from the long-wavelength side to quanta energies of 0.5 meV so that the long-wavelength boundary of the PL spectrum was accurately determined. As a result, the experimental setup allowed us to explore the THz region from 0.12 THz to 4 THz.
The photoconductivity measurements were performed in the same spectral range using globar as the radiation source. The spectral resolution was set to 0.5 meV. Strip contacts were deposited on the sample surface near its edges. The bias voltage of ~1V was applied to the samples that had a typical size of 5 × 4 mm2. The sample was mounted in an Oxford Instruments «OptistatCF» flow cryostat, which was installed into the spectrometer so that the sample was placed in the focus of the radiation beam.
4. Results and Discussion
4.1. The Rates of Hole Capture to the Localized Vacancy States
To analyze the experimental data given below, we first calculated the energy spectrum for the neutral mercury vacancy in Hg0.78Cd0.22Te (the second column in Table 1). As mentioned above, mercury vacancy is a double acceptor and a neutral center is formed when two holes are bound to the vacancy. For such a center, the energy of the two-particle state falls into the continuous spectrum unless one of the holes occupies the ground state []. Therefore, the states in Table 1 are denoted as single-particle states for the second hole (while the first hole is always in the 1Γ8 + state). The fourth column in Table 1 shows the matrix elements for the intracenter optical transitions. The transitions with large matrix elements should be well-pronounced in spectroscopic studies. The energy spectrum and the matrix elements were calculated analogously to that in [] in which one can find the details of the calculation procedure.

Table 1.
The calculated characteristics of the ground s-like and excited odd p-like (to which the optical transitions from the ground state are allowed) states of the neutral mercury vacancies in Hg0.78Cd0.22Te. W is the frequency of hole capture from the valence band to the state at T = 4.2 K and free hole concentration p = 5 × 1014 cm−3. Ei is the ionization energy of the state, E is the energy of the transition from the ground state, and |M|2 is the square of the matrix element of the optical transition from the ground state. Ei*, E*, |M*|2 are similar values for a singly charged acceptor with the same binding energy as the neutral mercury vacancy. The CCP parameters for calculating the states of a double acceptor were taken from [] and the CCP parameters for a singly charged acceptor were chosen so that the ionization energy is equal to 11.0 meV. The bold type for 1Γ7 – and 3Γ7 – states highlights a large matrix element of the optical transition to the ground state.
Table 1 also presents the calculated hole capture rates that correspond to the different states of the vacancy (via acoustic phonon emission). The values of capture rates W in Table 1 were yielded using (8), with the distribution function given by (9). The Fermi-level for (9) was determined from (10) for p = 5 × 1014 cm–3. The carrier lifetimes measured in [,] allow one to estimate that this non-equilibrium concentration corresponds to the pumping intensity of ~10 mW/cm2, which is the minimum excitation level that allowed for the observation of PL with a tenable signal-to-noise ratio.
The capture rate rapidly increases as the state becomes shallower. The transition times to the shallow excited states (3Γ8 – and with lower ionization energy, see Table 1) are no more than 120 ps for a non-equilibrium hole concentration of 5 × 1014 cm–3. The transition times decrease for higher concentrations. Therefore, free holes are rapidly captured onto the shallow localized states and leave the valence band, as established in the cascade capture model []. In this case, the vacancy-related PL should be formed by the transitions to or between relatively deep localized states.
As can be seen in Table 1, the hole capture to the ground state has a negligible rate compared to the frequency of transitions to the shallow excited states. This can be naturally explained by the fact that the ionization energies of the deep states (11.1 meV and 7.01 meV, see Table 1) are comparable with the maximum acoustic phonon energies (10.56 meV and 13.4 meV). As a result, only phonons with large wave vectors can participate in the capture. The wavelength of such a phonon is much smaller than the localization scale of the acceptor state wave function and the matrix element of the non-radiative transition turns out to be small.
4.2. The Photoluminescence and Photoconductivity Vacancy-Related Spectra
Figure 1 shows the PL and PC spectra of the bulk Hg0.78Cd0.22Te epitaxial layer in the THz domain. The bandgap of the structure is about 85 meV; therefore, the interband PL line is not shown and the PL spectrum is related to the vacancies. Figure 1 confirms that the PL spectrum drops at low quanta energies due to extremely fast non-radiative transitions to the shallow vacancy states, as discussed above. The PL spectrum has two maxima corresponding to photon energies of about 7.2 meV and 10.4 meV (features A and B). The spectral position of feature B is in positive agreement with the maximum of the PC spectrum of the p-type sample obtained from the same structure upon annealing that increases the concentration of mercury vacancies.
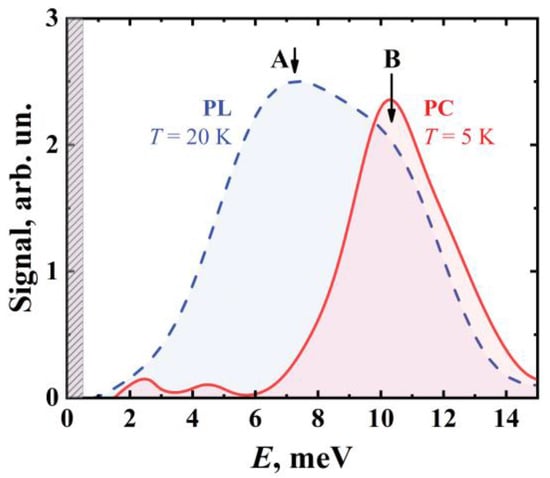
Figure 1.
THz PL spectrum of a bulk n-type Hg0.78Cd0.22Te epitaxial layer upon excitation with an intensity of 10 mW/cm2 and the PC spectrum of the p-type Hg0.78Cd0.22Te layer. The temperatures at which measurements were taken are indicated in the figure. The arrows indicate the features of the PL spectrum. The gray area indicates the long-wavelength limit of the beamsplitter exploited in the PL study.
The energy position of feature B (10.4 meV) corresponds well to the energy of the hole transition from the 3Γ7 – state to the ground state of the neutral mercury vacancy (1Γ8 +), which has a relatively large matrix element (Table 1). However, unlike the single-line PC spectrum, two features are clearly present in the PL band in Figure 1. The position of feature A in the PL spectrum is close to the energies of the 2Γ8 − → 1Γ8 + and 1Γ7 − → 1Γ8 + transitions (Table 2). The radiative transition 1Γ7 − → 1Γ8 + has the largest matrix element and corresponds to the so-called D-line of the typical impurity absorption spectrum in a p-type semiconductor []. This transition is not pronounced in the PC spectrum, apparently due to the fact that its final state is rather deep (the binding energy is 3.07 meV, see Table 1), which leads to a low probability of thermal ionization at T = 5 K. It was not possible to “activate” this transition in the PC spectrum by increasing the temperature because a rise in temperature increases free hole density and leads to the rapid quenching of the PC signal []. On the other hand, to be observable in the PL spectrum, the acceptor states should effectively accumulate the non-equilibrium carriers, i.e., the transitions to these states should be faster than the transitions from them.

Table 2.
Calculated energies (E) and frequencies of transitions between the lower states of a neutral mercury vacancy upon emission of an acoustic phonon in the Hg0.78Cd0.22Te ternary alloy. The ionization energies (Ei) of the initial states of the transitions are also indicated.
4.3. Non-Radiative Intracenter Transitions of the Vacancy
To reveal the balance between hole filling and leaving the relevant energy levels, we calculated the frequencies of hole transitions between the localized states of a neutral mercury vacancy with the emission of acoustic phonons. The results are presented in Table 2. The frequencies in Table 2 were calculated using (11) and (7) with the wave functions and energies of mercury states analogously calculated as in [].
In Table 1 and Table 2, one can notice that 2Γ8 − state is filled with holes either by the direct capture from the continuum at a frequency of 135 μs−1 or by the transitions from the 1Γ7 − state (ionization energy 3.07 meV, see Table 1) with a frequency of 560 μs−1 (Table 2). Note that holes populate the 1Γ7 − state quite rapidly by transitions from the continuum with a frequency of 620 μs−1. The 2Γ8 − state is depopulated with a frequency of 12 µs−1 due to transitions to the ground state and with a frequency of 100 µs−1 upon the transition to the lower excited state with an ionization energy of 7.01 meV. Thus, the 2Γ8 − state can accumulate holes favoring their optical transitions to the ground state. The 1Γ7 − state should accumulate holes to a lesser extent; however, due to the largest matrix element of the 1Γ7 − → 1Γ8 + optical transition, a significant contribution to the PL spectrum can be expected from it as well. Thus, the “strong” transitions 2Γ8 − → 1Γ8 + and 1Γ7 − → 1Γ8 + form the main PL maximum in the range of 7–8 meV (Figure 1).
The 3Γ7 − state (ionization energy 0.42 meV, see Table 1) is rapidly filled with holes from the valence band and the non-radiative transitions of holes from this level to the deeper states turn out to be slow compared to the hole capture to the shallower states from the continuum. This is due to the fact that the 3Γ7 − state is formed mainly by the light hole wave functions, while the underlying levels are formed by the wave functions of heavy holes []. Therefore, transitions to the latter states from the 3Γ7 − state appear to be quasi-forbidden. Thus, holes accrue at the 3Γ7 − level, creating favorable conditions for observing the 3Γ7 − → 1Γ8 + transition in the PL spectrum as well.
Note that the observed pattern of optical transitions is an independent confirmation that the observed PL line should be associated with the double acceptor. To illustrate this, Table 1 also shows the calculated transition energies for a singly charged acceptor. By selecting an appropriate CCP, one can obtain the same ionization energy as for a neutral mercury vacancy. However, the CCP only significantly changes the energy of the ground state []. Therefore, the difference between the energy of 3Γ7 − → 1Γ8 + transition and the energy of the 1Γ7 − → 1Γ8 + transition is determined by whether the acceptor is a singly charged one or a double one in a greater degree than by variations in the CCP parameters. In the case of a singly charged acceptor, the D-line should correspond to a transition energy of 9.3 meV, which does not agree with the structure of the PL spectrum in Figure 1. Thus, the spectral distance between these transitions weakly depends on the central cell potential and therefore can be used to identify that the PL band is related to a double acceptor and not to a singly charged one.
THz spectroscopy is probably the most direct method to analyze acceptor impurities, which are technologically relevant due to the well-known problem of p-type doping in MCT. In this respect, the results of this work offer a useful method for decoupling the relevant spectral features (e.g., resulting from the intentional doping) from the bands related to double-charged vacancies, since mercury vacancies are always present in MCT material.
5. Conclusions
In conclusion, the calculated frequencies of non-radiative hole transitions revealed the states of the neutral mercury vacancy in HgCdTe that can accumulate the non-equilibrium holes. In conjunction with the calculated matrix elements for the optical transitions to the same states, the results of this work were validated by the PL spectrum associated with the neutralization of the mercury vacancy in HgCdTe ternary alloys. In contrast with PC spectra, the PL studies make it possible to detect at least two intracenter transitions with a large matrix element, offering a tool to identify the two-particle states of a neutral vacancy.
Author Contributions
Conceptualization, D.V.K. and V.V.R.; methodology, D.V.K., V.V.R. and A.V.I.; software, D.V.K.; validation, V.V.U., K.A.M. and A.A.R.; formal analysis, D.V.K., V.V.R. and A.V.I.; investigation, V.V.U. and A.A.R.; resources, N.N.M. and S.A.D.; data curation, D.V.K., V.V.R. and A.V.I.; writing—original draft preparation, D.V.K. and V.V.R.; writing—review and editing, A.V.I.; visualization, D.V.K., V.V.R., K.A.M. and A.V.I.; supervision, S.V.M. and V.I.G.; project administration, S.V.M. and V.I.G.; funding acquisition, S.V.M. and V.I.G. All authors have read and agreed to the published version of the manuscript.
Funding
The PL and PC measurements were supported by the Russian Science Foundation (grant #22-12-00298) and the calculations of frequencies for non-radiative transitions were supported by Russian Foundation for Basic Research (grant #21-52-12020).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kopytko, M.; Rogalski, A. New insights into the ultimate performance of HgCdTe photodiodes. Sens. Actuators A Phys. 2022, 339, 113511. [Google Scholar] [CrossRef]
- Kopytko, M.; Sobieski, J.; Gawron, W.; Martyniuk, P. Study of HgCdTe (100) and HgCdTe (111)B Heterostructures Grown by MOCVD and Their Potential Application to APDs Operating in the IR Range up to 8 µm. Sensors 2022, 22, 924. [Google Scholar] [CrossRef] [PubMed]
- Ruffenach, S.; Kadykov, A.; Rumyantsev, V.V.; Torres, J.; Coquillat, D.; But, D.; Krishtopenko, S.; Consejo, C.; Knap, W.; Winnerl, S.; et al. HgCdTe-based heterostructures for terahertz photonics. APL Mater. 2017, 5, 035503. [Google Scholar] [CrossRef]
- Gemain, F.; Robin, I.C.; De Vita, M.; Brochen, S.; Lusson, A. Identification of the double acceptor levels of the mercury vacancies in HgCdTe. Appl. Phys. Lett. 2011, 98, 131901. [Google Scholar] [CrossRef]
- Li, B.; Gui, Y.; Chen, Z.; Ye, H.; Chu, J.; Wang, S.; Ji, R.; He, L. Study of impurity states in p-type Hg1−xCdxTe using far-infrared spectroscopy. Appl. Phys. Lett. 1998, 73, 1538. [Google Scholar] [CrossRef]
- Sasaki, T.; Oda, N.; Kawano, M.; Sone, S.; Kanno, T.; Saga, M. Mercury annealing effect on the electrical properties of HgCdTe grown by molecular beam epitaxy. J. Cryst. Growth 1992, 117, 222. [Google Scholar] [CrossRef]
- Mynbaev, K.D.; Zablotsky, S.V.; Shilyaev, A.V.; Bazhenov, N.L.; Yakushev, M.V.; Marin, D.V.; Varavin, V.S.; Dvoretsky, S.A. Defects in Mercury-Cadmium Telluride Heteroepitaxial Structures Grown by Molecular-Beam Epitaxy on Silicon Substrates. Semiconductors 2016, 50, 208. [Google Scholar] [CrossRef]
- Shao, J.; Lü, X.; Guo, S.; Lu, W.; Chen, L.; Wei, Y.; Yang, J.; He, L.; Chu, J. Impurity levels and bandedge electronic structure in as-grown arsenic-doped HgCdTe by infrared photoreflectance spectroscopy. Phys. Rev. B 2009, 80, 155125. [Google Scholar] [CrossRef]
- Zhang, X.; Shao, J.; Chen, L.; Lü, X.; Guo, S.; He, L.; Chu, J. Infrared photoluminescence of arsenic-doped HgCdTe in a wide temperature range of up to 290 K. J. Appl. Phys. 2011, 110, 043503. [Google Scholar] [CrossRef]
- Andrianov, A.V.; Zakhar’in, A.O.; Ivanov, Y.L.; Kipa, M.S. Terahertz impurity luminescence under the interband photoexcitation of semiconductors. JETP Lett. 2010, 91, 96–99. [Google Scholar] [CrossRef]
- Firsov, D.A.; Vorobjev, L.E.; Panevin, V.Y.; Sofronov, A.N.; Balagula, R.M.; Makhov, I.S.; Kozlov, D.V.; Vasil’Ev, A.P. Terahertz radiation associated with impurity electron transitions in quantum wells at optical and electrical pumping. Semiconductors. 2015, 49, 28–32. [Google Scholar] [CrossRef]
- Kozlov, D.V.; Rumyantsev, V.V.; Kadykov, A.M.; Fadeev, M.A.; Kulikov, N.S.; Utochkin, V.V.; Mikhailov, N.N.; Dvoretskii, S.A.; Gavrilenko, V.I.; Hubers, H.-W.; et al. Features of Photoluminescence of Double Acceptors in HgTe/CdHgTe Heterostructures with Quantum Wells in a Terahertz Range. JETP Lett. 2019, 109, 657–662. [Google Scholar] [CrossRef]
- Kozlov, D.V.; Rumyantsev, V.V.; Morozov, S.V.; Kadykov, A.M.; Fadeev, M.A.; Zholudev, M.S.; Varavin, V.S.; Mikhailov, N.N.; Dvoretskii, S.A.; Gavrilenko, V.I.; et al. Terahertz Photoluminescence of Double Acceptors in Bulky Epitaxial HgCdTe Layers and HgTe/CdHgTe Structures with Quantum Wells. J. Exp. Theor. Phys. 2018, 127, 1125–1129. [Google Scholar] [CrossRef]
- Rumyantsev, V.V.; Kozlov, D.V.; Morozov, S.V.; Fadeev, M.A.; Kadykov, A.M.; Teppe, F.; Varavin, V.S.; Yakushev, M.V.; Mikhailov, N.N.; A Dvoretskii, S.; et al. Terahertz photoconductivity of double acceptors in narrow gap HgCdTe epitaxial films grown by molecular beam epitaxy on GaAs(013) and Si(013) substrates. Semicond. Sci. Technol. 2017, 32, 095007. [Google Scholar] [CrossRef]
- Nikolaev, I.D.; Uaman Svetikova, T.A.; Rumyantsev, V.V.; Zholudev, M.S.; Kozlov, D.V.; Morozov, S.V.; Dvoretsky, S.A.; Mikhailov, N.N.; Gavrilenko, V.I.; Ikonnikov, A.V. Probing States of a Double Acceptor in CdHgTe Heterostructures via Optical Gating. JETP Lett. 2020, 111, 575–581. [Google Scholar] [CrossRef]
- Kozlov, D.V.; Uaman Svetikova, T.A.; Ikonnikov, A.V.; Rumyantsev, V.V.; Razova, A.A.; Zholudev, M.S.; Mikhailov, N.N.; Dvoretskii, S.A.; Gavrilenko, V.I.; Morozov, S.V. Photothermal Ionization Spectroscopy of Mercury Vacancies in HgCdTe Epitaxial Films. JETP Lett. 2021, 113, 402–408. [Google Scholar] [CrossRef]
- Talwar, D.N.; Vandevyver, M. Vibrational properties of HgCdTe system. J. Appl. Phys. 1984, 56, 1601. [Google Scholar] [CrossRef]
- Gantmakher, V.F.; Levinson, Y.B. Carrier Scattering in Metals and Semiconductors; Science, Russian Federation: Moscow, Russia, 1984; 352p. [Google Scholar]
- Stillman, G.E.; Wolfe, C.M.; Dimmock, J.O. Hall coefficient factor for polar mode scattering in n-type GaAs. J. Phys. Chem. Solids 1970, 31, 1199–1204. [Google Scholar] [CrossRef]
- Novik, E.G.; Pfeuffer-Jeschke, A.; Jungwirth, T.; Latussek, V.; Becker, C.R.; Landwehr, G.; Buhmann, H.; Molenkamp, L.W. Band structure of semimagnetic Hg1−yMnyTe quantum wells. Phys. Rev. B 2005, 72, 035321. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Kushwaha, S.S. Lattice dynamics of ZnTe, CdTe, GaP, and InP. Can. J. Phys. 1980, 58, 351. [Google Scholar] [CrossRef]
- Kepa, H.; Giebultowicz, T.; Buras, B.; Lebech, B.; Claußen, K. A Neutron Scattering Study of Lattice Dynamics of HgTe and HgSe. Phys. Scr. 1982, 25, 807–809. [Google Scholar] [CrossRef]
- Rumyantsev, V.V.; Ikonnikov, A.V.; Antonov, A.V.; Morozov, S.V.; Zholudev, M.S.; Spirin, K.E.; Gavrilenko, V.I.; Dvoretskii, S.A.; Mikhailov, N.N. Specific features of the spectra and relaxation kinetics of long-wavelength photoconductivity in narrow-gap HgCdTe epitaxial films and heterostructures with quantum wells. Semiconductors 2013, 47, 1438–1441. [Google Scholar] [CrossRef]
- Morozov, S.V.; Rumyantsev, V.V.; Antonov, A.V.; Maremyanin, K.V.; Kudryavtsev, K.E.; Krasilnikova, L.V.; Mikhailov, N.N.; Dvoretskii, S.A.; Gavrilenko, V.I. Efficient long wavelength interband photoluminescence from HgCdTe epitaxial films at wavelengths up to 26 μm. Appl. Phys. Lett. 2014, 104, 072102. [Google Scholar] [CrossRef]
- Bethe, H.A.; Salpeter, E.E. Quantum Mechanics of One-and-Two-Electron Atoms; Berlin: Springer, Germany, 1957; 368p. [Google Scholar]
- Abakumov, V.N.; Perel, V.I.; Yassievich, I.N. Nonradiative Recombination in Semiconductors; Elsevier: Amsterdam, The Netherlands, 1991; pp. 191–197. [Google Scholar]
- Murzin, V.N. Submillimeter Spectroscopy of Collective and Bound Carrier States in Semiconductors; Science, Russian Federation: Moscow, Russia, 1985; 264p. [Google Scholar]
- Zholudev, M.S.; Rumyantsev, V.V.; Morozov, S.V. Calculation of Bound and Resonant Levels of Acceptors in Narrow-Gap CdHgTe Solid Solutions. JETP Lett. 2022, 116, 313–318. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).