Quantum Speed Limit for a Moving Qubit inside a Leaky Cavity
Abstract
1. Introduction
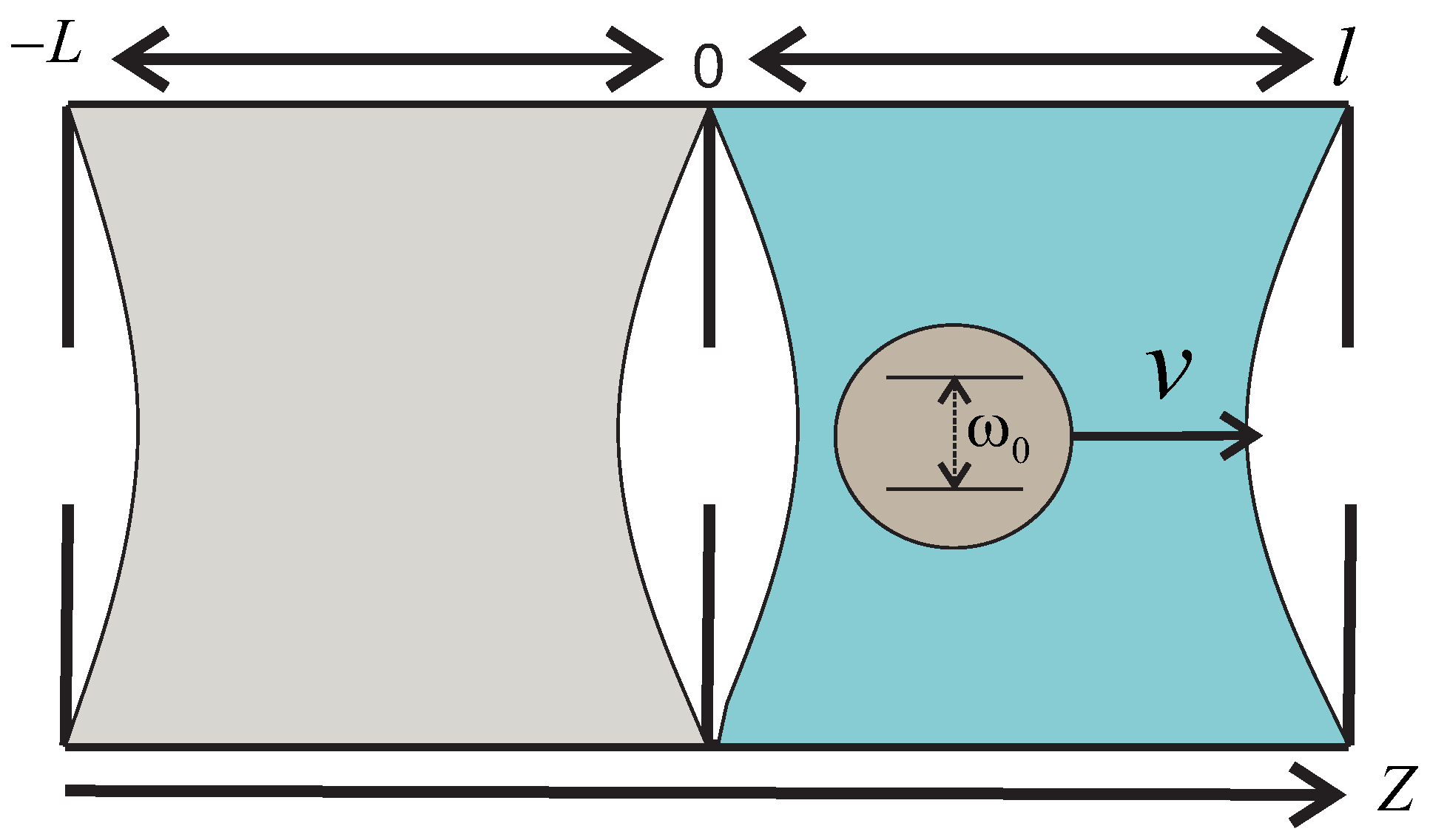
2. Moving Qubit inside a Leaky Cavity
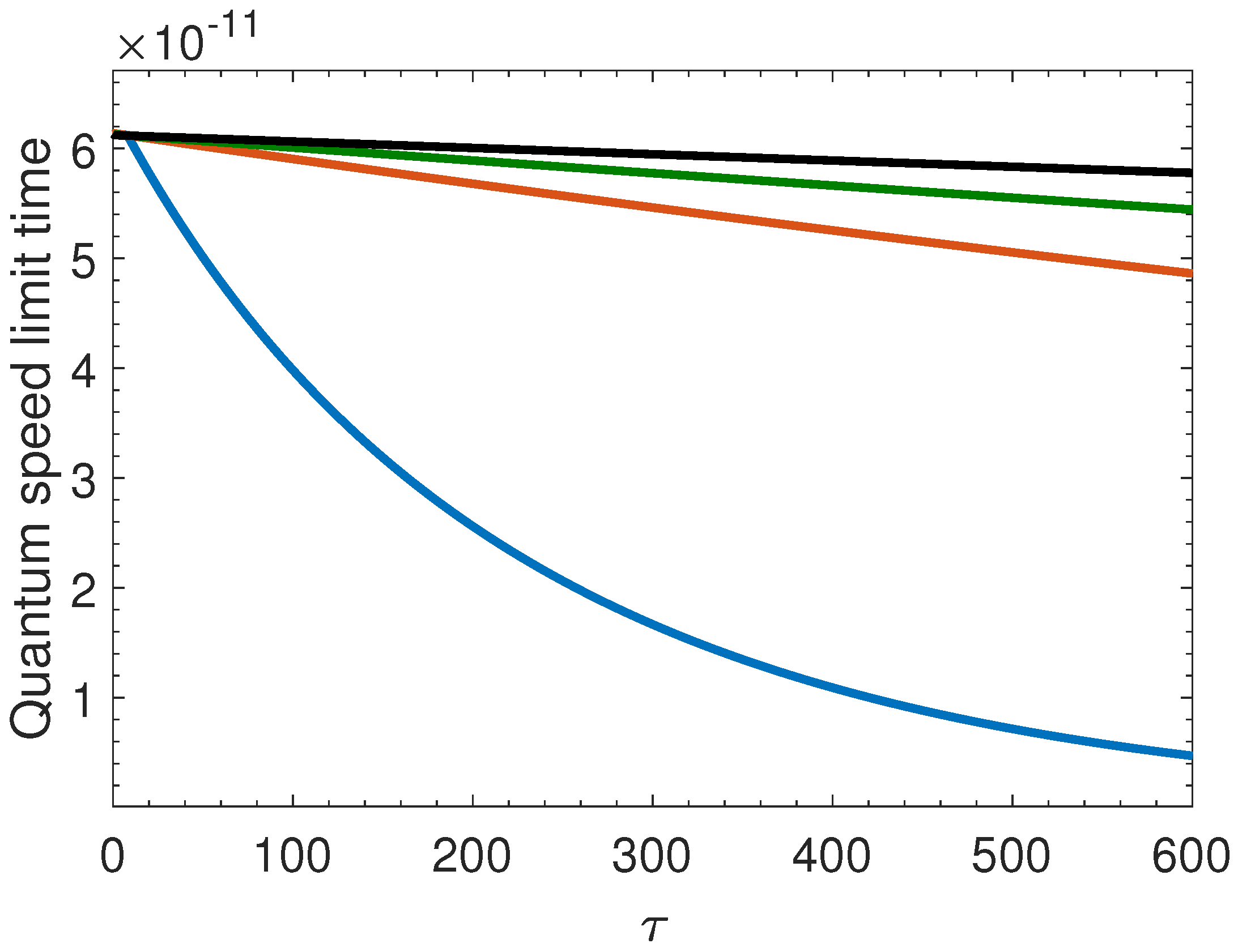
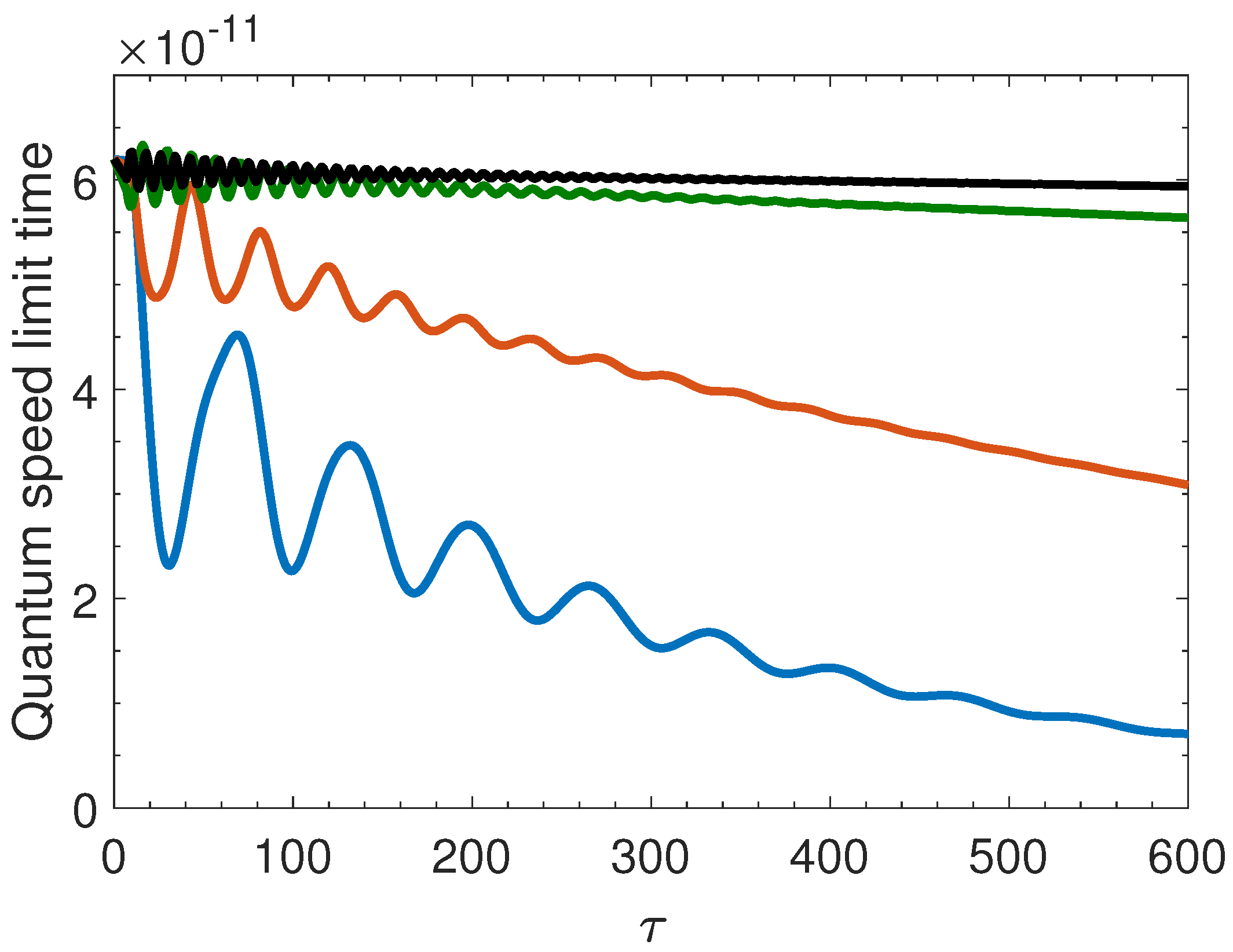
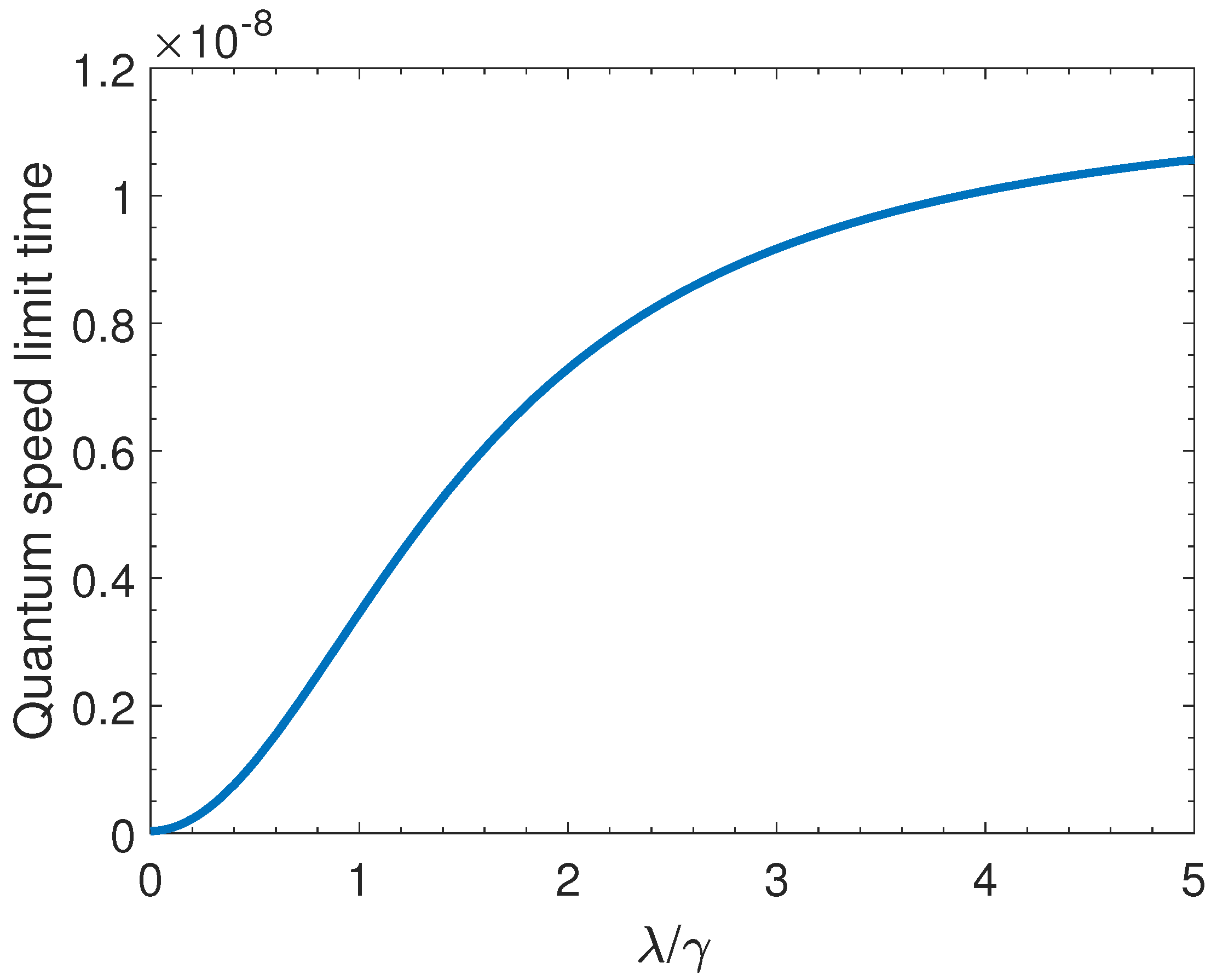
3. QSL Time for the Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| QSL | Quantum speed limit |
| MT | Mandelstam and Tamm |
| ML | Margolus and Levitin |
| QST | Quantum state tomography |
References
- Bekenstein, J.D. Energy cost of information transfer. Phys. Rev. Lett. 1981, 46, 623. [Google Scholar] [CrossRef]
- Giovanetti, V.; Lloyd, S.; Maccone, L. Advances in quantum metrology. Nat. Photonics 2011, 5, 222. [Google Scholar] [CrossRef]
- Lloyd, S. Computational capacity of the Universe. Phys. Rev. Lett. 2002, 88, 237901. [Google Scholar] [CrossRef] [PubMed]
- Caneva, T.; Murphy, M.; Calarco, T.; Fazio, R.; Montangero, S.; Giovannetti, V.; Santoro, G.E. Optimal control at the quantum speed limit. Phys. Rev. Lett. 2009, 103, 240501. [Google Scholar] [CrossRef] [PubMed]
- Uhlmann, A. An energy dispersion estimate. Phys. Lett. A 1992, 161, 329. [Google Scholar] [CrossRef]
- Pfeifer, P. How fast can a quantum state change with time? Phys. Rev. Lett. 1993, 70, 3365. [Google Scholar] [CrossRef]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum limits to dynamical evolution. Phys. Rev. A 2003, 67, 052109. [Google Scholar] [CrossRef]
- Pfeifer, P.; Fröhlich, J. Generalized time-energy uncertainty relations and bounds on lifetimes of resonances. Rev. Mod. Phys. 1995, 67, 759. [Google Scholar] [CrossRef]
- Chau, H.F. Tight upper bound of the maximum speed of evolution of a quantum state. Phys. Rev. A 2010, 81, 062133. [Google Scholar] [CrossRef]
- Deffner, S.; Lutz, E. Energy–time uncertainty relation for driven quantum systems. J. Phys. A Math. Theor. 2013, 46, 335302. [Google Scholar] [CrossRef]
- Mandelstam, L.; Tamm, I. Quantum speed limits: From Heisenberg’s uncertainty principle to optimal quantum control. J. Phys. (USSR) 1945, 9, 249. [Google Scholar]
- Margolus, N.; Levitin, L.B. The maximum speed of dynamical evolution. Physica D 1998, 120, 188. [Google Scholar] [CrossRef]
- Levitin, L.B.; Toffoli, T. Fundamental limit on the rate of quantum dynamics: The unified bound is tight. Phys. Rev. Lett. 2009, 103, 160502. [Google Scholar] [CrossRef] [PubMed]
- Davies, E.B. Quantum Theory of Open Systems; Academic Press: London, UK, 1976. [Google Scholar]
- Alicki, R.; Lendi, K. Quantum Dynamical Semigroups and Applications; Springer: Berlin, Germany, 1987. [Google Scholar]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Fogarty, T.; Deffner, S.; Busch, T.; Campbell, S. Orthogonality catastrophe as a consequence of the quantum speed limit. Phys. Rev. Lett. 2020, 124, 110601. [Google Scholar] [CrossRef] [PubMed]
- Puebla, R.; Deffner, S.; Campbell, S. Kibble-Zurek scaling in quantum speed limits for shortcuts to adiabaticity. Phys. Rev. Res. 2020, 2, 032020. [Google Scholar] [CrossRef]
- Poggi, P.M. Análisis de cotas inferiores para tiempos de control y su relación con el límite de velocidades cuántico. Anales AFA 2020, 31, 29. [Google Scholar] [CrossRef]
- Campaioli, F.; Sloan, W.; Modi, K.; Pollock, F.A. Algorithm for solving unconstrained unitary quantum brachistochrone problems. Phys. Rev. A 2019, 100, 062328. [Google Scholar] [CrossRef]
- Pires, D.P.; Cianciaruso, M.; Celeri, L.C.; Adesso, G.; Soares-Pinto, D.O. Generalized geometric quantum speed limits. Phys. Rev. X 2016, 6, 021031. [Google Scholar] [CrossRef]
- Taddei, M.M.; Escher, B.M.; Davidovich, L.; De Matos Filho, R.L. Quantum speed limit for physical processes. Phys. Rev. Lett. 2013, 110, 050402. [Google Scholar] [CrossRef]
- del Campo, A.; Egusquiza, I.L.; Plenio, M.B.; Huelga, S.F. Quantum speed limits in open system dynamics. Phys. Rev. Lett. 2013, 110, 050403. [Google Scholar] [CrossRef]
- Deffner, S.; Lutz, E. Quantum speed limit for non-Markovian dynamics. Phys. Rev. Lett. 2013, 111, 010402. [Google Scholar] [CrossRef]
- Sun, Z.; Liu, J.; Ma, J.; Wang, X. Quantum speed limits in open systems: Non-Markovian dynamics without rotating-wave approximation. Sci. Rep. 2015, 5, 8444. [Google Scholar] [CrossRef]
- Mondal, D.; Datta, C.; Sazim, S. Quantum coherence sets the quantum speed limit for mixed states. Phys. Lett. A 2016, 380, 689. [Google Scholar] [CrossRef]
- Jones, P.J.; Kok, P. Geometric derivation of the quantum speed limit. Phys. Rev. A 2010, 82, 022107. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Han, W.; Xia, Y.J.; Cao, J.P.; Fan, H. Quantum speed limit for arbitrary initial states. Sci. Rep. 2014, 4, 4890. [Google Scholar] [CrossRef] [PubMed]
- Mirkin, N.; Toscano, F.; Wisniacki, D.A. Quantum-speed-limit bounds in an open quantum evolution. Phys. Rev. A 2016, 94, 052125. [Google Scholar] [CrossRef]
- Uzdin, R.; Kosloff, R. Speed limits in Liouville space for open quantum systems. EPL 2016, 115, 40003. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, Y.; Luo, S. Quantum speed limit for qubit systems: Exact results. Phys. Lett. A 2018, 382, 2599. [Google Scholar] [CrossRef]
- Teittinen, J.; Lyyra, H.; Maniscalco, S. There is no general connection between the quantum speed limit and non-Markovianity. New J. Phys. 2019, 21, 123041. [Google Scholar] [CrossRef]
- Ektesabi, A.; Behzadi, N.; Faizi, E. Improved bound for quantum-speed-limit time in open quantum systems by introducing an alternative fidelity. Phys. Rev. A 2017, 95, 022115. [Google Scholar] [CrossRef]
- Cai, X.; Zheng, Y. Quantum dynamical speedup in a nonequilibrium environment. Phys. Rev. A 2017, 95, 052104. [Google Scholar] [CrossRef]
- Deffner, S. Geometric quantum speed limits: A case for Wigner phase space. New J. Phys. 2017, 19, 103018. [Google Scholar] [CrossRef]
- Wu, S.X.; Yu, C.S. Quantum speed limit for a mixed initial state. Phys. Rev. A 2018, 98, 042132. [Google Scholar] [CrossRef]
- Funo, K.; Shiraishi, N.; Saito, K. Speed limit for open quantum systems. New J. Phys. 2019, 21, 013006. [Google Scholar] [CrossRef]
- Brody, D.C.; Longstaff, B. Evolution speed of open quantum dynamics. Phys. Rev. Res. 2019, 1, 033127. [Google Scholar] [CrossRef]
- Campaioli, F.; Pollock, F.A.; Modi, K. Tight, robust, and feasible quantum speed limits for open dynamics. Quantum 2019, 3, 168. [Google Scholar] [CrossRef]
- Van Vu, T.; Hasegawa, Y. Geometrical bounds of the irreversibility in Markovian systems. Phys. Rev. Lett. 2021, 126, 010601. [Google Scholar] [CrossRef]
- Campaioli, F.; Yu, C.S.; Pollock, F.A.; Modi, K. Resource speed limits: Maximal rate of resource variation. New J. Phys. 2022, 24, 065001. [Google Scholar] [CrossRef]
- Bagheri Harouni, M. Quantum speed limit time and entanglement in a non-Markovian evolution of spin qubits of coupled quantum dots. Chin. Phys. B 2020, 29, 124203. [Google Scholar] [CrossRef]
- Bagheri Harouni, M. Influences of spin-orbit interaction on quantum speed limit and entanglement of spin qubits in coupled quantum dots. Chin. Phys. B 2021, 30, 090301. [Google Scholar] [CrossRef]
- Dehdashti, S.; Yasar, F.; Bagheri Harouni, M.; Mahdifar, A.; Mirza, B. Quantum speed limit in the thermal spin-boson system with and without tunneling term. Quant. Inf. Process. 2020, 19, 308. [Google Scholar] [CrossRef]
- Awasthi, N.; Joshi, D.K.; Sachdev, S. Variation of quantum speed limit under Markovian and non-Markovian noisy environment. Laser Phys. Lett. 2022, 19, 035201. [Google Scholar] [CrossRef]
- Awasthi, N.; Joshi, D.K.; Sachdev, S. Dynamics of quantum speed limit time for correlated and uncorrelated noise channels. Int. J. Theor. Phys. 2022, 61, 123. [Google Scholar] [CrossRef]
- Lan, K.; Xie, S.; Cai, X. Geometric quantum speed limits for Markovian dynamics in open quantum systems. New J. Phys. 2022, 24, 055003. [Google Scholar] [CrossRef]
- Haseli, S.; Salimi, S.; Dolatkhah, H.; Khorashad, A.S. Quantum speed limit time in the presence of disturbance. Mod. Phys. Lett. A 2021, 36, 2150009. [Google Scholar] [CrossRef]
- Mortezapour, A.; Borji, M.A.; Park, D.; Franco, R.L. Non-Markovianity and coherence of a moving qubit inside a leaky cavity. Open Syst. Inf. Dyn. 2017, 24, 1740006. [Google Scholar] [CrossRef]
- Mortezapour, A.; Borji, M.A.; Franco, R.L. Protecting entanglement by adjusting the velocities of moving qubits inside non-Markovian environments. Laser Phys. Lett. 2017, 14, 055201. [Google Scholar] [CrossRef]
- Calajo, G.; Rabl, P. Strong coupling between moving atoms and slow-light Cherenkov photons. Phys. Rev. A 2017, 95, 043824. [Google Scholar] [CrossRef]
- Garcia, L.A.; Felicetti, S.; Rico, E.; Solano, E.; Sabin, C. Entanglement of superconducting qubits via acceleration radiation. Sci. Rep. 2017, 7, 657. [Google Scholar] [CrossRef]
- Felicetti, S.; Sabin, C.; Fuentes, I.; Lamata, L.; Romero, G.; Solano, E. Relativistic motion with superconducting qubits. Phys. Rev. B 2015, 92, 064501. [Google Scholar] [CrossRef]
- Moustos, D.; Anastopoulos, C. Non-Markovian time evolution of an accelerated qubit. Phys. Rev. D 2017, 95, 025020. [Google Scholar] [CrossRef]
- Lang, R.; Scully, M.O.; Lamb, W.E. Why is the laser line so narrow? A theory of single-quasimode laser operation. Phys. Rev. A 1973, 7, 1788. [Google Scholar] [CrossRef]
- Gea-Banacloche, J.; Lu, N.; Pedrotti, L.M.; Prasad, S.; Scully, M.O.; Wodkiewicz, K. Treatment of the spectrum of squeezing based on the modes of the universe. I. Theory and a physical picture. Phys. Rev. A 1990, 41, 369. [Google Scholar] [CrossRef] [PubMed]
- Leonardi, C.; Vaglica, A. Non-markovian dynamics and spectrum of a moving atom strongly coupled to the field in a damped cavity. Opt. Commun. 1993, 97, 130. [Google Scholar] [CrossRef]
- Franco, R.L.; Bellomo, B.; Maniscalco, S.; Compagno, G. Dynamics of quantum correlations in two-qubit systems within non-Markovian environments. Int. J. Mod. Phys. B 2013, 27, 1345053. [Google Scholar] [CrossRef]
- Bellomo, B.; Franco, R.L.; Compagno, G. Non-Markovian effects on the dynamics of entanglement. Phys. Rev. Lett. 2007, 99, 160502. [Google Scholar] [CrossRef]
- Rivas, A.; Huelga, S.F. Open Quantum Systems; Springer: Berlin, Germany, 2012. [Google Scholar]
- Daffer, S.; Wodkiewicz, K.; Cresser, J.D.; Mclver, J.K. Depolarizing channel as a completely positive map with memory. Phys. Rev. A 2004, 70, 010304(R). [Google Scholar] [CrossRef]
- Breuer, H.P.; Laine, E.M.; Piilo, J.; Vacchini, B. Colloquium: Non-Markovian dynamics in open quantum systems. Rev. Mod. Phys. 2016, 88, 021002. [Google Scholar] [CrossRef]
- Czerwinski, A. Dynamics of open quantum systems—Markovian semigroups and beyond. Symmetry 2022, 14, 1752. [Google Scholar] [CrossRef]
- Czerwinski, A. Entanglement dynamics governed by time-dependent quantum generators. Axioms 2022, 11, 589. [Google Scholar] [CrossRef]
- Benabdallah, F.; Rahman, A.U.; Haddadi, S.; Daoud, M. Long-time protection of thermal correlations in a hybrid-spin system under random telegraph noise. Phys. Rev. E 2022, 106, 034122. [Google Scholar] [CrossRef] [PubMed]
- Ahansaz, B.; Ektesabi, A. Quantum speedup, non-Markovianity and formation of bound state. Sci. Rep. 2019, 9, 14946. [Google Scholar] [CrossRef] [PubMed]
- Schirmer, S.G.; Fu, H.; Solomon, A.I. Complete controllability of quantum systems. Phys. Rev. A 2001, 63, 063410. [Google Scholar] [CrossRef]
- Wu, S.L.; Ma, W. Trajectory tracking for non-Markovian quantum systems. Phys. Rev. A 2022, 105, 012204. [Google Scholar] [CrossRef]
- Song, Y.J.; Kuang, L.M. Controlling decoherence speed limit of a single impurity atom in a Bose–Einstein-condensate reservoir. Ann. Phys. (Berlin) 2019, 531, 1800423. [Google Scholar] [CrossRef]
- Song, Y.J.; Tan, Q.S.; Kuang, L.M. Control quantum evolution speed of a single dephasing qubit for arbitrary initial states via periodic dynamical decoupling pulses. Sci. Rep. 2017, 7, 43654. [Google Scholar] [CrossRef]
- Song, Y.J.; Kuang, L.M.; Tan, Q.S. Quantum speedup of uncoupled multiqubit open system via dynamical decoupling pulses. Quant. Inf. Process. 2016, 15, 2325. [Google Scholar] [CrossRef]
- Silberfarb, A.; Jessen, P.S.; Deutsch, I.H. Quantum state reconstruction via continuous measurement. Phys. Rev. Lett. 2005, 95, 030402. [Google Scholar] [CrossRef]
- Merkel, S.T.; Riofrío, C.A.; Flammia, S.T.; Deutsch, I.H. Random unitary maps for quantum state reconstruction. Phys. Rev. A 2010, 81, 032126. [Google Scholar] [CrossRef]
- Czerwinski, A. Quantum state tomography with informationally complete POVMs generated in the time domain. Quantum Inf. Process. 2021, 20, 105. [Google Scholar] [CrossRef]
- Czerwinski, A. Quantum tomography of entangled qubits by time-resolved single-photon counting with time-continuous measurements. Quantum Inf. Process. 2022, 21, 332. [Google Scholar] [CrossRef]
- Numata, K.; Kemery, A.; Camp, J. Thermal-noise limit in the frequency stabilization of lasers with rigid cavities. Phys. Rev. Lett. 2004, 93, 250602. [Google Scholar] [CrossRef] [PubMed]
- Xu, G.; Jiao, D.; Chen, L.; Zhang, L.; Dong, R.; Liu, T.; Wang, J. Thermal noise in cubic optical cavities. Photonics 2021, 8, 261. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hadipour, M.; Haseli, S.; Dolatkhah, H.; Haddadi, S.; Czerwinski, A. Quantum Speed Limit for a Moving Qubit inside a Leaky Cavity. Photonics 2022, 9, 875. https://doi.org/10.3390/photonics9110875
Hadipour M, Haseli S, Dolatkhah H, Haddadi S, Czerwinski A. Quantum Speed Limit for a Moving Qubit inside a Leaky Cavity. Photonics. 2022; 9(11):875. https://doi.org/10.3390/photonics9110875
Chicago/Turabian StyleHadipour, Maryam, Soroush Haseli, Hazhir Dolatkhah, Saeed Haddadi, and Artur Czerwinski. 2022. "Quantum Speed Limit for a Moving Qubit inside a Leaky Cavity" Photonics 9, no. 11: 875. https://doi.org/10.3390/photonics9110875
APA StyleHadipour, M., Haseli, S., Dolatkhah, H., Haddadi, S., & Czerwinski, A. (2022). Quantum Speed Limit for a Moving Qubit inside a Leaky Cavity. Photonics, 9(11), 875. https://doi.org/10.3390/photonics9110875






