Abstract
We propose a new quantum state reconstruction method that combines ideas from compressed sensing, non-convex optimization, and acceleration methods. The algorithm, called Momentum-Inspired Factored Gradient Descent (MiFGD), extends the applicability of quantum tomography for larger systems. Despite being a non-convex method, MiFGD converges provably close to the true density matrix at an accelerated linear rate asymptotically in the absence of experimental and statistical noise, under common assumptions. With this manuscript, we present the method, prove its convergence property and provide the Frobenius norm bound guarantees with respect to the true density matrix. From a practical point of view, we benchmark the algorithm performance with respect to other existing methods, in both synthetic and real (noisy) experiments, performed on the IBM’s quantum processing unit. We find that the proposed algorithm performs orders of magnitude faster than the state-of-the-art approaches, with similar or better accuracy. In both synthetic and real experiments, we observed accurate and robust reconstruction, despite the presence of experimental and statistical noise in the tomographic data. Finally, we provide a ready-to-use code for state tomography of multi-qubit systems.
1. Introduction
Quantum tomography is one of the main procedures to identify the nature of imperfections and deviations in quantum processing unit (QPU) implementations [1,2]. Generally, quantum tomography is composed of two main parts: (i) measuring the quantum system, and (ii) analyzing the measurement data to obtain an estimate of the density matrix (in the case of state tomography [1]), or of the quantum process (in the case of process tomography [3]). In this manuscript, we focus on the state tomography.
Quantum tomography is generally considered as a non-scalable protocol [4], as the number of free parameters that define quantum states and processes scale exponentially with the number of subsystems. In particular, quantum state tomography (QST) suffers from two bottlenecks. The first concerns about the large amount of data one needs to collect to perform tomography; the second concerns about numerically searching in an exponentially increasing space for a density matrix that is consistent with the data.
There have been various approaches to improve the scalability of QST, in terms of the amount of data required [5,6,7]. To address the data collection bottleneck, prior information about the unknown quantum state is often assumed. For example, in compressed sensing QST [4,8], the density matrix of the quantum system is assumed to be low-rank. In neural network QST [9,10,11], the wave-functions are often assumed to be real and positive, confining the landscape of quantum states (To handle more complex wave-functions, neural network approaches require a proper re-parameterization of the Restricted Boltzmann machines [9]). The prior information considered in these cases is that they are characterized by structured quantum states [9] (Such assumptions are often the reason behind accurate solutions of neural network QST in high-dimensional spaces.) Ref. [9] considers also the case of a completely unstructured case and test the limitation of this technique, which does not perform as expected, due to lack of any exploitable structure). Similarly, in matrix-product-state tomography [12,13], one assumes that the quantum state can be represented with low bond-dimension matrix-product state.
To address the computational bottleneck, several works introduce sophisticated numerical methods to improve the efficiency of QST. In particular, variants of gradient-based convex solvers—e.g., [14,15,16,17]—have been tested on synthetic scenarios [17]. The problem is that, achieving these results often requires utilizing special-purpose hardwares, such as Graphics Processing Units (GPUs), on top of carefully designing a proper distributed system [18]. Thus, going beyond current capabilities requires novel methods that can efficiently search in the space of density matrices under more realistic scenarios. Importantly, such numerical methods should come with rigorous guarantees on their convergence and performance.
The setup we consider here is the estimation of an n-qubit state, under the prior assumption that the state is close to a pure state, and thus its density matrix is of low-rank. This assumption is justified by the state-of-the-art experiments, where the aim is to manipulate the pure states with unitary maps. From a theoretical perspective, the low-rank assumption implies that we can use compressed sensing techniques [19], which allow the recovery of the density matrix from relatively fewer measurement data [20,21].
Indeed, compressed sensing QST is widely used for estimating highly-pure quantum states; e.g., [4,22,23,24]. However, compressed sensing QST usually relies on convex optimization for the estimation [8], which limits the applicability to relatively small system sizes [4] (In particular, convex solvers over low-rank structures utilize the nuclear norm over matrices. This assumes calculating all eigenvalues of such matrices per iteration, which has cubic complexity ). On the other hand, non-convex optimization approaches could preform much faster than their convex counterparts [25]. Although non-convex optimization typically lacks convergence guarantees, it was recently shown that one can formulate the compressed sensing QST as a non-convex problem, and solve it with rigorous convergence guarantees (under certain but generic conditions), allowing the state estimation of larger system sizes [26].
Following the non-convex path, we introduce a new algorithm to the toolbox of QST—the Momentum-Inspired Factored Gradient Descent (MiFGD). Our approach combines the ideas from compressed sensing, non-convex optimization, and acceleration/momentum techniques to scale QST beyond the current capabilities. MiFGD includes acceleration motions per iteration, meaning that it uses two previous iterates to update the next estimate; see Section 2 for details. The intuition is that if the k-th and -th estimates were pointing to the correct direction, then both information should be useful to determine the -th estimate. Of course such approach requires an additional estimate to be stored—yet, we show both theoretically and experimentally that momentum results in faster estimation. We emphasize that the analysis becomes non-trivially challenging due to the inclusion of two previous iterates.
The contributions of the paper are summarized as follows:
- (i)
- We prove that the non-convex MiFGD algorithm asymptotically enjoys an accelerated linear convergence rate in terms of the iterate distance, in the noiseless measurement data case and under common assumptions.
- (ii)
- We provide QST results using the real measurement data from IBM’s quantum computers up to 8-qubits, contributing to recent efforts on testing QST algorithms in real quantum data [22]. Our synthetic examples scale up to 12-qubits effortlessly, leaving the space for an efficient and hardware-aware implementation open for future work.
- (iii)
- We show through extensive empirical evaluations that MiFGD allows faster estimation of quantum states compared to the state-of-the-art convex and non-convex algorithms, including recent deep learning approaches [9,10,11,27], even in the presence of statistical noise in the measurement data.
- (iv)
- We further increase the efficiency of MiFGD by extending its implementation to utilize parallel execution over the shared and distributed memory systems. We experimentally showcase the scalability of our approach, which is particularly critical for the estimation of larger quantum system.
- (v)
- We provide the implementation of our approach at https://github.com/gidiko/MiFGD (accessed on 18 January 2023), which is compatible with the open-source software Qiskit [28].
The rest of this manuscript is organized as follows. In Section 2, we set up the problem in detail, and present our proposed method: MiFGD. Then, we detail the experimental set up in Section 3, followed by the results in Section 4. Finally, we discuss related and future works with concluding remarks in Section 5.
2. Methods
2.1. Problem Setup
We consider the estimation of a low-rank density matrix on an n-qubit Hilbert space with dimension , through the following -norm reconstruction objective:
Here, is the measurement data (observations) (Specific description on how y is generated and what it represents will follow), and is the linear sensing map, where . The sensing map relates the density matrix to (expected, noiseless) observations through the Born rule: , where are matrices closely related to the measured observable or the POVM elements of appropriate dimensions.
The objective function in Equation (1) has two constraints: the positive semi-definite constraint: and the low-rank constraint: . The former is a convex constraint, whereas the latter is a non-convex one, rendering Equation (1) to be a non-convex optimization problem (Convex optimization problem requires both the objective function as well as the constraints to be convex). Following compressed sensing QST results [8], the unit trace constraint (which should be satisfied by any density matrix by definition) can be disregarded, without affecting the precision of the final estimate.
A pivotal assumption to apply compressed sensing results is that the linear sensing map should satisfy the restricted isometry property, which we recall below.
Definition 1
(Restricted Isometry Property (RIP) [29]). A linear operator satisfies the RIP on rank-r matrices with the RIP constant , if the following holds with high probability for any rank-r matrix :
Such maps (almost) preserve the Frobenius norm of low-rank matrices, and, as an extension, of low-rank Hermitian matrices. The intuition behind RIP is that the operator behaves almost as a bijection between the subspaces and for low-rank matrices.
Following recent works [26], instead of solving Equation (1), we propose to solve a factorized version of it:
where denotes the adjoint of U, and is re-parametrized with . The motivation for this reformulation is two-folds. First, by representing the dimensional density matrix with (the outer product of) its dimensional low-rank factors U, the search space for the density matrix (that is consistent with the measurement data) significantly reduces, given that . Second, via the reformulation both the PSD constraint and the low-rank constraint are automatically satisfied, transforming the constrained optimization problem in Equation (1) to the unconstrained optimization problem in Equation (3). An important implication is that, to solve Equation (3), one can bypass the projection step onto the PSD and low-rank subspace, which requires a sigular value decomposition (SVD) of the estimate of the density matrix on every iteration. This is prohibitively expensive when the dimension is large, which is the case for even moderate number of qubits n. As such, working in the factored space was shown to improve time and space complexities [26,30,31,32,33,34].
A common approach to solve a factored objective as in Equation (3) is to use gradient descent [35] on the parameter U, with iterates as follows (We assume the case where . If this does not hold, the theory still holds by carrying around instead of just , after proper scaling):
Here, is the k-th iterate, and the operator is the adjoint of , defined as , for . The hyperparameter is the step size. This algorithm has been studied in [25,32,34,36,37,38]. We will refer to the above iteration as the factored gradient descent (FGD) algorithm, as in [30]. In what follows, we will introduce our proposed method, the MiFGD algorithm: momentum-inspired factored gradient descent.
2.2. The MiFGD Algorithm
The MiFGD algorithm is a two-step variant of FGD, which iterates as follows:
Here, is a rectangular matrix (with the same dimension as ) that accumulates the “momentum” of the iterates [39]. is the momentum parameter that weighs the amount of mixture of the previous estimate and the current to generate . The above iteration is an adaptation of Nesterov’s accelerated first-order method for convex problems [40]. We borrow this momentum formulation, and study how the choice of the momentum parameter affects the overall performance in non-convex problem formulations, such as Equation (3). We note that the theory and algorithmic configurations in [40] do not generalize to non-convex problems, which is one of the contributions of this work. Albeit being a non-convex problem, we show that MiFGD asymptotically converges at an accelerated linear rate around a neighborhood of the optimal value, akin to convex optimization results [40].
An important observation is that the factorization is not unique. For instance, suppose that is an optimal solution for Equation (3); then, for any rotation matrix satisfying , the matrix is also optimal for Equation (3) (To see this, observe that ). To resolve this ambiguity, we use the distance between a pair of matrices as the minimum distance up to rotations, where . In words, we want to track how close an estimate U is to , up to the minimizing rotation matrix.
Algorithm 1 contains the details of the MiFGD. As Problem (3) is non-convex, the initialization plays an important role in achieving global convergence. The initial point is either randomly initialized [36,41,42], or set according to Lemma 4 in [26]:
where is the projection onto the set of PSD matrices, is the RIP constant from Definition 1, and is the gradient of evaluated at all-zero matrix. Since computing the RIP constant is NP-hard, in practice we compute through , where ; see Theorem 1 below for details.
| Algorithm 1 Momentum-Inspired Factored Gradient Descent (MiFGD). |
Input: (sensing map), y (measurement data), r (rank), and (momentum parameter). Set randomly or as in Equation (8). Set . Set as in Equation (9). for
do end for Output:
|
Compared to randomly selecting , the initialization scheme in Equation (8) involves a gradient and a top-r eigenvalue computations. Yet, Equation (8) provides a more informed initial point, as it is based on the data , which could lead to convergence in fewer iterations in practice, and satisfies the initialization condition of Theorem 1 for small enough (Based on our experiments, in practice, both initializations are applicable and useful).
For the step size in Algorithm 1, it is set to the following based on our theoretical analysis (c.f., Lemma A6):
where . Similarly to the above, in practice we replace the RIP constant with . The step size remains constant at every iteration, and requires only two top-eigenvalue computations to obtain the spectral norms and . These computations can be efficiently implemented by any off-the-shelf eigenvalue solver, such as the Power Method or the Lanczos method [43].
2.3. Theoretical Guarantees of the MiFGD Algorithm
We now present the formal convergence theorem, where under certain conditions, MiFGD asymptotically achieves an accelerated linear rate.
Theorem 1
(Accelerated asymptotic convergence rate). Assume that satisfies the RIP in Definition 1 with the constant . Initialize such that
where is the (inverse) condition number of , is the condition number of ρ with , and is the i-th singular value of ρ. Set the step size η such that
and the momentum parameter for user-defined . Then, for the (noiseless) measurement data with rank the output of the MiFGD in Algorithm 1 satisfies the following: for any , there exist constants and such that, for all k,
where . That is, the MiFGD asymptotically enjoys an accelerated linear convergence rate in iterate distances up to a constant proportional to the momentum parameter μ.
Theorem 1 can be interpreted as follows. The right hand side of Equation (10) depends on the initial distance akin to convex optimization results, where asymptotically appear as the contraction factor. In contrast, the contraction factor of vanilla FGD [26] is of the order .
The main assumption is that the sensing map satisfies RIP. This assumption implies that the condition number of f depends on the RIP constants such that since the eigenvalues of the Hessian of f, i.e., , lie between and (when restricted to low-rank matrices) (In this sense, the RIP assumption plays the similar role to assuming f is -strongly convex and L-smooth (when restricted to low-rank matrices)). Such assumption has become standard in the optimization and the signal processing community [19,25,29]. Hence, MiFGD has better dependency on the (inverse) condition number of f compared to FGD. Such improvement of the dependency on the condition number is referred to as “acceleration” in the convex optimization literature [44,45]. Thus, assuming that the initial points and are close enough to the optimum as stated in the theorem, MiFGD decreases its distance to at an accelerated linear rate, up to an “error” level that depends on the momentum parameter , which is bounded by .
Theorem 1 requires a strong assumption on the momentum parameter , which depends on quantities that might not be known a priori for general problems. However, we note that for the special case of QST, we know these quantities exactly: r is the rank of density matrix—thus, for pure states ; is the (rank-restricted) condition number of the density matrix —for pure states, ; and finally, is the condition number of the sensing map, and satisfies: given the constraint . This analysis leads to a momentum value (This is the numerical value of we use in experiments in Section 4). However, as we show in both real and synthetic experiments in Section 4 (and further in Appendix A), the theory is conservative; much larger values of lead to fast, stable, and improved performance. Finally, the bound on the condition number in Theorem 1 is not strict, and comes out of the analysis we follow; we point the reader to similar assumptions made where is assumed to be constant: [46].
The detailed proof of Theorem 1 is provided in Appendix B. The proof differs from state of the art proofs for non-accelerated factored gradient descent: due to the inclusion of the memory term, three different terms——need to be handled simultaneously. Further, the proof differs from other recent proofs on non-convex, but non-factored, gradient descent methods, as in [47]: the distance metric over rotations , where includes estimates from two steps in history, is not amenable to simple triangle inequality bounds. As a result, a careful analysis is required, including the design of two-dimensional dynamical systems, where we characterize and bound the eigenvalues of a contraction matrix.
3. Experimental Setup
3.1. Density Matrices and Quantum Circuits
In our numerical and real experiments, we have considered (different subsets of) the following n-qubit pure quantum states (The content in this subsection is implemented in the states.py component of our complementary software package: https://github.com/gidiko/MiFGD (accessed on 18 January 2023)):
- The (generalized) GHZ state:
- The (generalized) GHZ-minus state:
- The Hadamard state:
- A random state .
We have implemented these states (on the IBM quantum simulator and/or the IBM’s QPU) using the following circuits. The GHZ state is generated by applying the Hadamard gate to one of the qubits, and then applying CNOT gates between this qubit (as a control) and the remaining qubits (as targets). The GHZ-minus state is generated by applying the X gate to one of the qubits (e.g., the first qubit) and the Hadamard gate to the remaining qubits, followed by applying CNOT gates between the first qubit (as a target) and the other qubits (as controls). Finally, we apply the Hadamard gate to all of the qubits. The Hadamard state is a separable state, and is generated by applying the Hadamard gate to all of the qubits. The random state is generated by a random quantum gate selection: In particular, for a given circuit depth, we uniformly select among generic single-qubit rotation gates with 3 Euler angles, and controlled-X gates, for every step in the circuit sequence. For the rotation gates, the qubits involved are selected uniformly at random, as well as the angles from the range . For the controlled-X gates, the source and target qubits are also selected uniformly at random.
We generically denote the density matrix that correspond to pure state as . For clarity, we will drop the bra-ket notation when we refer to , , and . While the density matrices of the and are sparse in the basis, the density matrix of state is fully-dense in this basis, and the sparsity of the density matrix that of may be different form one state to another.
3.2. Measuring Quantum States
The quantum measurement model. In our experiments (both synthetic and real), we measure the qubits in the Pauli basis (This is the non-commutative analogue of the Fourier basis, for the case of sparse vectors [19,48]). A Pauli basis measurement on an n-qubit system has possible outcomes. The Pauli basis measurement is uniquely defined by the measurement setting. A Pauli measurement is a string of n letters such that for all . Note that there are at most distinct Pauli strings. To define the Pauli basis measurement associated with a given measurement string , we first define the the following three bases on :
These are the eigenbases of the single-qubit Pauli operators, , and , whose matrix representations are given by:
Given a Pauli setting , the Pauli basis measurement is defined by the projectors:
where ℓ denotes the bit string . Since there are distinct Pauli measurement settings, there are the same number of possible Pauli basis measurements.
Technically, this set forms a positive operator-valued measure (POVM). The projectors that form are the measurement outcomes (or POVM elements) and the probability to obtain an outcome –when the state of the system is – is given by the Born rule: .
The RIP and expectation values of Pauli observables. Starting with the requirements of our algorithm, the sensing map we consider is comprised of a collection of matrices , such that . We denote the vector by y.
When no prior information about the quantum state is assumed, to ensure its (robust) recovery, one must choose a set m sensing matrices , so that of them are linearly independent. One example of such choice is the POVM elements of the Pauli basis measurements.
Yet, when it is known that the state-to-be-reconstructed is of low-rank, theory on low-rank recovery problems suggests that could just be “incoherent” enough with respect to [20], so that recovery is possible from a limited set of measurements, i.e., with . In particular, it is known [4,20,21] that if the sensing matrices correspond to random Pauli monomials, then ’s are sufficient for a successful recovery of , using convex solvers for Equation (1) (The main difference between [4,20] and [21] is that the former guarantees recovery for almost all choices of random Pauli monomials, while the latter proves that there exists a universal set of Pauli monomials that guarantees successful recovery).
A Pauli monomial is an operator in the set , that is, an n-fold tensor product of single-qubit Pauli operators (including the identity operator). For convenience we re-label the single-qubit Pauli operators as , and , so that we can also write with for all . These results [4,20,21] are feasible since the Pauli-monomial-based sensing map obeys the RIP property, as in Definition 1 (In particular, the RIP is satisfied for the sensing mechanisms that obeys , . Further, the case considered in [21] holds for a slightly larger set than the set of rank-r density matrices: for all such that ). For the remainder of this manuscript, we will use the term “Pauli expectation value” to denote .
From Pauli basis measurements to Pauli expectation values. While the theory for compressed sensing was proven for Pauli expectation values, in real QPUs, experimental data is obtained from Pauli basis measurements. Therefore, to make sure we are respecting the compressed sensing requirements on the sensing map, we follow this protocol:
- (i)
- We sample or Pauli monomials uniformly over with , where represents the percentage of measurements out of full tomography.
- (ii)
- For every monomial, , in the generated set, we identify an experimental setting that corresponds to the monomial. There, qubits, for which their Pauli operator in is the identity operator, are measured, without loss of generality, in the basis. For example, for and , we identify the measurement setting .
- (iii)
- We measure the quantum state in the Pauli basis that corresponds to , and record the outcomes.
To connect the measurement outcomes to the expectation value of the Pauli monomial, we use the relation:
where is a mapping that takes a bit string ℓ and returns a new bit string (of the same size) such that for all k’s for which (that is, the locations of the identity operators in ), and is the parity of the bit string .
3.3. Algorithmic Setup
In our implementation, we explore a number of control parameters, including the maximum number of iterations maxiters, the step size , the relative error from successive state iterates reltol, the momentum parameter , the percentage of the complete set of measurements (i.e., over all possible Pauli monomials) measpc, and the seed. In the sequel experiments we set , , and , unless stated differently. Regarding acceleration, when acceleration is muted; we experiment over the range of values when investigating the acceleration effect, beyond the theoretically suggested . In order to explore the dependence of our approach on the number of measurements available, measpc varies over the set of ; seed is used for differentiating repeating runs with all other parameters kept fixed (maxiters is num_iterations in the code; also reltol is relative_error_tolerance, measpc is complete_measurements_percentage).
Denoting the estimate of by MiFGD, we report on outputs including:
- The evolution with respect to the distance between and : , for various ’s.
- The number of iterations to reach to for various ’s.
- The fidelity of , defined as (for rank-1 ), as a function of the acceleration parameter in the default set.
In our plots, we sweep over our default set of measpc values, repeat 5 times for each individual setup, varying supplied seed, and depict their 25-, 50- and 75-percentiles.
3.4. Experimental Setup on Quantum Processing Unit (QPU)
We show empirical results on 6- and 8-qubit real data, obtained on the 20-qubit IBM QPU ibmq_boeblingen. The layout/connectivity of the device is shown in Figure 1. The 6-qubit data was from qubits , and the 8-qubit data was from . The coherence times are , and coherence times are . The circuit for generating 6-qubit and 8-qubit GHZ states are shown in Figure 1. The typical two qubit gate errors measured from randomized benchmarking (RB) for relevant qubits are summarized in Table 1.
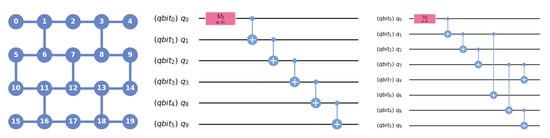
Figure 1.
Left panel: Layout connectivity of IBM backend ibmq_boeblingen;Middle and right panels: Circuits used to generate 6-qubit state (left) and 8-qubit GHZ state (right). refers to the quantum registers used in qiskit, and q corresponds to qubits on the real device.

Table 1.
Two qubit error rates for the relevant gates used in generating 6-qubit and 8-qubit GHZ states on ibmq_boeblingen.
The QST circuits were generated using the tomography module in qiskit-ignis (https://github.com/Qiskit/qiskit-ignis (accessed on 18 January 2023)). For complete QST of a n-qubits state circuits are needed. The result of each circuit is averaged over 8192, 4096 or 2048, for different n-qubit scenarios. To mitigate for readout errors, we prepare and measure all of the computational basis states in the computation basis to construct a calibration matrix C. C has dimension by , where each column vector corresponds to the measured outcome of a prepared basis state. In the ideal case of no readout error, C is an identity matrix. We use C to correct for the measured outcomes of the experiment by minimizing the function:
Here and are the measured and calibrated outputs, respectively. The minimization problem is then formulated as a convex optimization problem and solved by quadratic programming using the package cvxopt [49].
4. Results
4.1. MiFGD on 6- and 8-Qubit Real Quantum Data
We realize two types of quantum states on IBM QPUs, parameterized by the number of qubits n for each case: the and the circuits. We collected measurements over all possible Pauli settings by repeating the experiment for each setting a number of times: these are the number of shots for each setting. The (circuit, number of shots) measurement configurations from IBM Quantum devices are summarized in Table 2.

Table 2.
QPU settings.
In Appendix A, we provide target error list plots for the evolution of for reconstructing all the settings in Table 2, both for real data and for simulated scenarios. Further, we provide plots that relate the effect of momentum acceleration on the final fidelity observed for these cases. For clarity, in Figure 2, we summarize the efficiency of momentum acceleration, by showing the reconstruction error only for the following settings: , , , and . In the plots, corresponds to the FGD algorithm in [30], corresponds to the value obtained through our theory, while we use to study the acceleration effect. For , per our theory, we follow the rule for ; see also Section 2 for details (For this application, , , and by construction; we also approximated , which, for user-defined , results in . Note that smaller values result into a smaller radius of the convergence region; however, more pessimistic values result into small , with no practical effect in accelerating the algorithm). Note that, in most of the cases, the curve corresponding to is hidden behind the curve corresponding to . We run each QST experiment for 5 times for random initializations. We record the evolution of the error at each step, and stop when the relative error of successive iterates gets smaller than or the number of iterations exceeds (whichever happens first). To implement , we follow the description given in Equation (11) with .
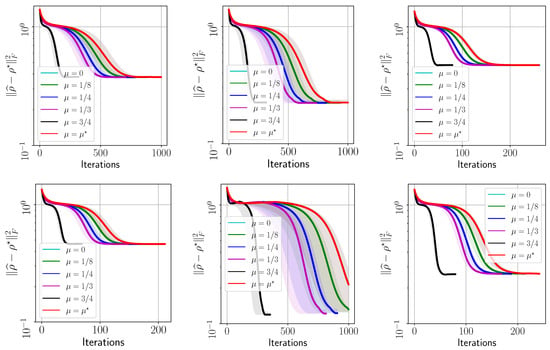
Figure 2.
Target error list plots versus method iterations using real IBM QPU data. Top-left: with 2048 shots; Top-middle: with 8192 shots; Top-right: with 2048 shots; Bottom-left: with 4096 shots/copies of ; Bottom-middle: with 8192 shots; Bottom-right: with 4096 shots. All cases have . Shaded area denotes standard deviation around the mean over repeated runs in all cases.
To highlight the level of noise existing in real quantum data, in Figure 3, we repeat the same setting using the QASM simulator in qiskit-aer. This is a parallel, high performance quantum circuit simulator written in C++ that can support a variety of realistic circuit level noise models.
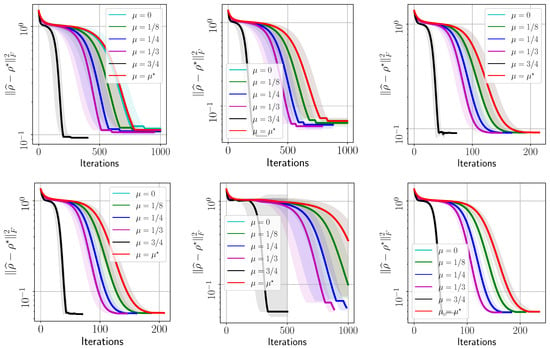
Figure 3.
Target error list plots versus method iteration using synthetic IBM’s quantum simulator data. Top-left: with 2048 shots; Top-middle: with 8192 shots; Top-right: with 2048 shots; Bottom-left: with 4096 shots; Bottom-middle: with 8192 shots; Bottom-right: with 4096 shots. All cases have . Shaded area denotes standard deviation around the mean over repeated runs in all cases.
Figure 2 summarizes the performance of our proposal on different , and for different values on real IBM QPU data. All plots show the evolution of across iterations, featuring a steep dive to convergence for the largest value of we tested: we report that we also tested , which shows only slight worse performances than . Figure 2 highlights the universality of our approach: its performance is oblivious to the quantum state reconstructed, as long as it satisfies purity or it is close to a pure state. Our method does not require any additional structure assumptions in the quantum state.
To highlight the effect of real noise on the performance of MiFGD, we further plot its performance on the same settings but using measurements coming from an idealized quantum simulator. Figure 3 considers the exact same settings as in Figure 2. It is obvious that MiFGD can achieve better reconstruction performance when data are less erroneous. This also highlights that, in real noisy scenarios, the radius of the convergence region of MiFGD around is controlled mostly by the the noise level, rather than by the inclusion of momentum acceleration.
Finally, in Figure 4, we depict the fidelity of achieved using MiFGD, defined as , versus various values and for different circuits . Shaded area denotes standard deviation around the mean over repeated runs in all cases. The plots show the significant gap in performance when using real quantum data versus using synthetic simulated data within a controlled environment.
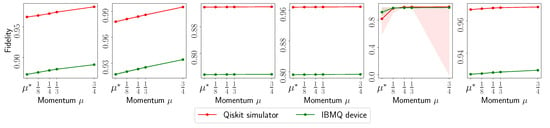
Figure 4.
Fidelity list plots where we depict the fidelity of to . From left to right: (i) with 2048 shots; (ii) with 8192 shots; (iii) with 2048 shots; (iv) with 4096 shots; (v) with 8192 shots; (vi) with 4096 shots. All cases have . Shaded area denotes standard deviation around the mean over repeated runs in all cases.
4.2. Performance Comparison with Full Tomography Methods in Qiskit
We compare the MiFGD with publicly available implementations for QST reconstruction. Two common techniques for QST, included in the qiskit-ignis distribution [28], are: (i) the CVXPY fitter method, that uses the CVXPY convex optimization package [50,51]; and (ii) the lstsq method, that uses least-squares fitting [52]. Both methods solve the full tomography problem (In [8], it was sown that the minimization program (13) yields a robust estimation of low-rank states in the compressed sensing. Thus, one can use CVXPY fitter method to solve Equation (13) with Pauli expectation value to obtain a robust reconstruction of ) according to the following expression:
We note that MiFGD is not restricted to “tall” U scenarios to encode PSD and rank constraints: even without rank constraints, one could still exploit the matrix decomposition to avoid the PSD projection, , where . For the lstsq fitter method, the putative estimate is rescaled using the method proposed in [52]. For CVXPY, the convex constraint makes the optimization problem a semidefinite programming (SDP) instance. By default, CVXPY calls the SCS solver that can handle all problems (including SDPs) [53,54]. Further comparison results with matrix factorization techniques from the machine learning community is provided in the Appendix for .
The settings we consider for full tomography are the following: , and quantum states (for ). We focus on fidelity of reconstruction and computation timings performance between , and . We use 100% of the measurements. We experimented with states simulated in QASM and measured taking 2048 shots. For MiFGD, we set , , and stopping criterion/tolerance . All experiments are run on a Macbook Pro with 2.3 GHz Quad-Core Intel Core i7CPU and 32GB RAM.
The results are shown in Figure 5; higher-dimensional cases are provided in Table 3. Some notable remarks: (i) For small-scale scenarios (), CVXPY and lstsq attain almost perfect fidelity, while being comparable or faster than MiFGD. (ii) The difference in performance becomes apparent from and on: while MiFGD attains 98% fidelity in <5 s, CVXPY and lstsq require up to hundreds of seconds to find a good solution. (iii) Finally, while MiFGD gets to high-fidelity solutions in seconds for , CVXPY and lstsq methods could not finish tomography as their memory usage exceeded the system’s available memory.
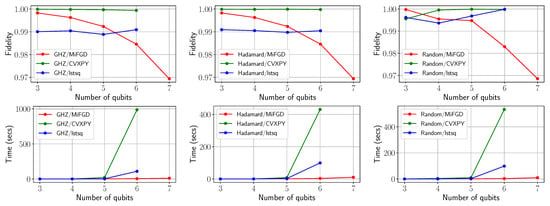
Figure 5.
Fidelity versus time plots using synthetic IBM’s quantum simulator data. Left panel: for ; Middle panel: for ; Right panel: for .

Table 3.
Fidelity of reconstruction and computation timings using 100% of the complete measurements. Rows correspond to combinations of number of qubits (7∼8), synthetic circuit, and tomographic method (MiFGD, Qiskit’s lstsq and CVXPY fitters. 2048 shots per measurement circuit. For MiFGD, , , . All experiments are run on a 13” Macbook Pro with 2.3 GHz Quad-Core Intel Core i7 CPU and 32 GB RAM.
It is noteworthy that the reported fidelities for MiFGD are the fidelities at the last iteration, before the stopping criterion is activated, or the maximum number of iterations is exceeded. However, the reported fidelity is not necessarily the best one during the whole execution: for all cases, we observe that MiFGD finds intermediate solutions with fidelity >99%. Though, it is not realistic to assume that the iteration with the best fidelity is known a priori, and this is the reason we report only the final iteration fidelity.
4.3. Performance Comparison of MiFGD with Neural-Network Quantum State Tomography
We compare the performance of MiFGD with neural network approaches. Per [9,10,11,27], we model a quantum state with a two-layer Restricted Boltzmann Machine (RBM). RBMs are stochastic neural networks, where each layer contains a number of binary stochastic variables: the size of the visible layer corresponds to the number of input qubits, while the size of the hidden layer is a hyperparameter controlling the representation error. We experiment with three types of RBMs for reconstructing either the positive-real wave function, the complex wave function, or the density matrix of the quantum state. In the first two cases the state is assumed pure while in the last, general mixed quantum states can be represented. We leverage the implementation in QuCumber [10], PositiveRealWaveFunction (PRWF), ComplexWaveFunction (CWF), and DensityMatrix (DM), respectively.
We reconstruct , and quantum states (for ), by training PRWF, CWF, and DM neural networks (We utilize GPU (NVidia GeForce GTX 1080 TI,11GB RAM) for faster training of the neural networks) with measurements collected by the QASM Simulator.
For our setting, we consider measpc = 50% and shots = 2048. The set of measurements is presented to the RBM implementation, along with the target positive-real wave function (for PRWF), complex wavefunction (for CWF) or the target density matrix (for DM) in a suitable format for training. We train Hadamard and Random states with 20 epochs, and GHZ state with 100 epochs (We experimented higher number of epochs (up to 500) for all cases, but after the reported number of epochs, Qucumber methods did not improve, if not worsened). We set the number of hidden variables (and also of additional auxilliary variables for DM) to be equal to the number of input variables n and we use 100 data points for both the positive and the negative phase of the gradient (as per the recommendation for the defaults). We choose contrastive divergence steps and fixed the learning rate to 10 (per hyperparameter tuning). Lastly, we limit the fitting time of Qucumber methods (excluding data preparation time) to be three hours. To compare to the RBM results, we run MiFGD with , , and using measpc = 50%, keeping previously chosen values for all other hyperparameters.
We report the fidelity of the reconstruction as a function of elapsed training time for in Figure 6 for PRWF, CWF, and DM. We observe that for all cases, Qucumber methods are orders of magnitude slower than MiFGD. E.g., for , for all three states, CWF and DM did not finish a single epoch in 3 h, while MiFG achieves high fidelity in less than 30 s. For the and , reaching reasonable fidelities is significantly slower for both CWF and DM, while PRWF hardly improves its performance throughout the training. For the GHZ case, CWF and DM also shows non-monotonic behaviors: even after a few thousands of seconds, fidelities have not “stabilized”, while PRWF stabilizes in very low fidelities. In comparison MiFGD is several orders of magnitude faster than both CWF and DM and fidelity smoothly increases to comparable or higher values. Further, in Table 4, we report final fidelities (within the 3 h time window), and reported times.
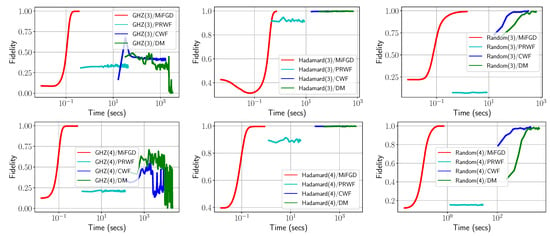
Figure 6.
Fidelity versus time plots on MiFGD, PRWF, CWF, and DM, using synthetic IBM’s quantum simulator data. Left panel: for ; Middle panel: for ; Right panel: for .

Table 4.
Fidelity of reconstruction and computation timings using and . Rows correspond to combinations of number of qubits (3∼8), final fidelity within the 3 h time limit, and computation time. For MiFGD, , , . For FGD, , . “N/A” indicates that the method could not complete a single epoch in 3 h training time limit, and thus could not provide any fidelity result. All experiments are run on a NVidia GeForce GTX 1080 TI, 11 GB RAM.
4.4. The Effect of Parallelization
We study the effect of parallelization in running MiFGD. We parallelize the iteration step across a number of processes, that can be either distributed and network connected, or sharing memory in a multicore environment. Our approach is based on Message Passing Interface (MPI) specification [55], which is the lingua franca for interprocess communication in high performance parallel and supercomputing applications. A MPI implementation provides facilities for launching processes organized in a virtual topology and highly tuned primitives for point-to-point and collective communication between them.
We assign to each process a subset of the measurement labels consumed by the parallel computation. At each step, a process first computes the local gradient-based corrections due only to its assigned Pauli monomials and corresponding measurements. These local gradient-based corrections will then (i) need to be communicated, so that they can be added, and (ii) finally, their sum will be shared across all processes to produce a global update for U for next step. We accomplish this structure in MPI using MPI_Allreduce collective communication primitive with MPI_SUM as its reduction operator: the underlying implementation will ensure minimum communication complexity for the operation (e.g., steps for p processes organized in a communication ring) and thus maximum performance (This communication pattern can alternatively be realized in two stages, as naturally suggested in its structure: (i) first invoke MPI’s MPI_Reduce primitive, with MPI_SUM as its reduction operator, which results in the element-wise accumulation of local corrections (vector sum) at a single, designated root process, and (ii) finally, send a “copy” of this sum from root process to each process participating in the parallel computation (broadcasting); MPI_Bcast primitive can be utilized for this latter stage. However, MPI_Allreduce is typically faster, since its actual implementation is not constrained by the requirement to have the sum available at a specific, root process, at an intermediate time point - as the two-stage approach implies). We leverage mpi4py [56] bindings to issue MPI calls in our parallel Python code.
We conducted our parallel experiments on a server equipped with 4 × E7-4850 v2 CPUs @ 2.30GHz (48/96 physical/virtual cores), 256 GB RAM, using shared memory multiprocessing over multiple cores. We experimented with states simulated in QASM and measured taking 8192 shots; parallel MiFGD runs with default parameters and using all measurements (measpc = 100%). Reported times are wall-clock computation time. These exclude initialization time for all processes to load Pauli monomials and measurements: we here target parallelizing computation proper in MiFGD.
In our first round of experiments, we investigate the scalability of our approach. We vary the number p of parallel processes (), collect timings for reconstructing , and states and report speedups we gain from MiFGD in Figure 7 Left. We observe that the benefits of parallelization are pronounced for bigger problems (here: qubits) and maximum scalability results when we use all physical cores (48 in our platform).
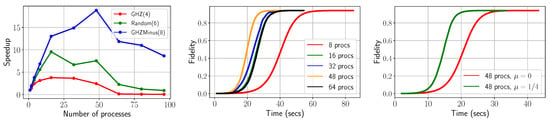
Figure 7.
Left panel: Scalability of our approach as we vary the number p of parallel processes. Middle panel: Fidelity function versus time consumed for different number of processes p. Right panel: The effect of momentum for a fixed scenario with state, , and varying momentum from to .
Further, we move to larger problems ( qubits: reporting on reconstructing state) and focus on the effect parallelization to achieving a given level of fidelity in reconstruction. In Figure 7 Middle, we illustrate the fidelity as a function of the time spent in the iteration loop of MiFGD for (): we observe the smooth path to convergence in all p counts which again minimizes compute time for . Note that in this case we use measpc = 10% and .
Finally, in Figure 7 Right, we fix the number of processes to , in order to minimize compute time and increase the percentage of used measurements to of the total available for . We vary the acceleration parameter, (no acceleration) to and confirm that we indeed get faster convergence times in the latter case while the fidelity value remains the same (i.e., coinciding upper plateau value in the plots). We can also compare with the previous fidelity versus time plot, where the same but half the measurements are consumed: more measurements translate to faster convergence times (plateau is reached roughly faster; compare the green line with the yellow line in the previous plot).
5. Conclusions and Discussions
We have introduced the MiFGD algorithm for the factorized form of the low-rank QST problems. We proved that, under certain assumptions on the problem parameters, MiFGD converges linearly to a neighborhood of the optimal solution, whose size depends on the momentum parameter , while using acceleration motions in a non-convex setting. We demonstrate empirically, using both simulated and real data, that MiFGD outperforms non-accelerated methods on both the original problem domain and the factorized space, contributing to recent efforts on testing QST algorithms in real quantum data [22]. These results expand on existing work in the literature illustrating the promise of factorized methods for certain low-rank matrix problems. Finally, we provide a publicly available implementation of our approach, compatible to the open-source software Qiskit [28], where we further exploit parallel computations in MiFGD by extending its implementation to enable efficient, parallel execution over shared and distributed memory systems.
Despite our theory does not apply to the Pauli basis measurement directly (i.e., using randomly selected Pauli bases , does not lead to the -norm RIP), using the data from random Pauli basis measurements directly could provide excellent tomographic reconstruction with MiFGD. Preliminary results suggest that only random Pauli bases should be taken for a reconstruction, with the same level of accuracy as with expectation values of random Pauli matrices. We leave the analysis of our algorithm in this case for future work, along with detailed experiments.
Related Work
Matrix sensing. The problem of low-rank matrix reconstruction from few samples was first studied within the paradigm of convex optimization, using the nuclear norm minimization [29,57,58]. The use of non-convex approaches for low-rank matrix recovery—by imposing rank-constraints—has been proposed in [59,60,61]. In all these works, the convex and non-convex algorithms involve a full, or at least a truncated, singular value decomposition (SVD) per algorithm iteration. Since SVD can be prohibitive, these methods are limited to relatively small system sizes.
Momentum acceleration methods are used regularly in the convex setting, as well as in machine learning practical scenarios [62,63,64,65,66,67]. While momentum acceleration was previously studied in non-convex programming setups, it mostly involve non-convex constraints with a convex objective function [47,61,68,69]; and generic non-convex settings but only considering with the question of whether momentum acceleration leads to fast convergence to a saddle point or to a local minimum, rather than to a global optimum [45,70,71,72].
The factorized version for semi-definite programming was popularized in [73]. Effectively the factorization of a the set of PSD matrices to a product of rectangular matrices results in a non-convex setting. This approach have been heavily studied recently, due to computational and space complexity advantages [25,26,30,31,32,33,34,36,37,38,41,74,75,76]. None of the works above consider the inclusion and analysis of momentum. Moreover, the Procrustes Flow approach [32,34] uses certain initializations techniques, and thus relies on multiple SVD computations. Our approach on the other hand uses a single, unique, top-r SVD computation. Comparison results beyond QST are provided in the appendix.
Compressed sensing QST using non-convex optimization. There are only few works that study non-convex optimization in the context of compressed sensing QST. The authors of [16] propose a hybrid algorithm that (i) starts with a conjugate-gradient (CG) algorithm in the factored space, in order to get initial rapid descent, and (ii) switch over to accelerated first-order methods in the original space, provided one can determine the switch-over point cheaply. Using the multinomial maximum likelihood objective, in the initial CG phase, the Hessian of the objective is computed per iteration (i.e., a matrix), along with its eigenvalue decomposition. Such an operation is costly, even for moderate values of qubit number n, and heuristics are proposed for its completion. From a theoretical perspective, [16] provide no convergence or convergence rate guarantees.
From a different perspective, [77] relies on spectrum estimation techniques [78,79] and the Empirical Young Diagram algorithm [80,81] to prove that copies suffice to obtain an estimate that satisfies ; however, to the best of our knowledge, there is no concrete implementation of this technique to compare with respect to scalability.
Ref. [82] proposes an efficient quantum tomography protocol by determining the permutationally invariant part of the quantum state. The authors determine the minimal number of local measurement settings, which scales quadratically with the number of qubits. The paper determines which quantities have to be measured in order to get the smallest uncertainty possible. See [83] for a more recent work on permutationally invariant tomography. The method has been tested in a six-qubit experiment in [84].
Ref. [22] presented an experimental implementation of compressed sensing QST of a qubit system, where only 127 Pauli basis measurements are available. To achieve recovery in practice, the authors proposed a computationally efficient estimator, based on gradient descent method in the factorized space. The authors of [22] focus on the experimental efficiency of the method, and provide no specific results on the optimization efficiency, neither convergence guarantees of the algorithm. Further, there is no available implementation publicly available.
Similar to [22], Ref. [26] also proposes a non-convex projected gradient decent algorithm that works on the factorized space in the QST setting. The authors prove a rigorous convergence analysis and show that, under proper initialization and step-size, the algorithm is guaranteed to converge to the global minimum of the problem, thus ensuring a provable tomography procedure. Our results extend these results by including acceleration techniques in the factorized space. The key contribution of our work is proving convergence of the proposed algorithm in a linear rate to the global minimum of the problem, under common assumptions. Proving our results required developing a whole set of new techniques, which are not based on a mere extension of existing results.
Compressed sensing QST using convex optimization. The original formulation of compressed sensing QST [4] is based on convex optimization methods, solving the trace-norm minimization, to obtain an estimation of the low-rank state. It was later shown [8] that essentially any convex optimization program can be used to robustly estimate the state. In general, there are two drawbacks in using convex optimization optimization in QST. Firstly, as the dimension of density matrices grow exponentially in the number of qubits, the search space in convex optimization grows exponentially in the number of qubits. Secondly, the optimization requires projection onto the PSD cone at every iteration, which becomes exponentially hard in the number of qubits. We avoid these two drawbacks by working in the factorized space. Using this factorization results in a search space that is substantially smaller than its convex counterpart, and moreover, in a single use of top-r SVD during the entire execution algorithm. Bypassing these drawbacks, together with accelerating motions, allows us to estimate quantum states of larger qubit systems than state-of-the-art algorithms.
Full QST using non-convex optimization. The use of non-convex algorithms in QST was studied in the context of full tomography as well. By “full tomography” we refer to the situation where an informationally complete measurement is performed, so that the input data to the algorithm is of size . The exponential scaling of the data size restrict the applicability of full tomography to relatively small system sizes. In this setting non-convex algorithms which work in the factored space were studied [85,86,87,88,89]. Except of the work [88], we are not aware of theoretical results on the convergence of the proposed algorithm due to the presence of spurious local minima. The authors of [88] characterize the local vs. the global behavior of the objective function under the factorization and discuss how existing methods fail due to improper stopping criteria or due to the lack of algorithmic convergence results. Their work highlights the lack of rigorous convergence results of non-convex algorithms used in full quantum state tomography. There is no available implementation publicly available for these methods as well.
Full QST using convex optimization. Despite the non-scalability of full QST, and the limitation of convex optimization, a lot of research was devoted to this topic. Here, we mention only a few notable results that extend the applicability of full QST using specific techniques in convex optimization. Ref [52] shows that for given measurement schemes the solution for the maximum likelihood is given by a linear inversion scheme, followed by a projection onto the set of density matrices. More recently, the authors of [18] used a combination of the techniques of [52] with the sparsity of the Pauli matrices and the use of GPUs to perform a full QST of 14 qubits. While pushing the limit of full QST using convex optimization, obtaining full tomographic experimental data for more than a dozen qubits is significantly time-intensive. Moreover, this approach is highly centralized, in comparison to our approach that can be distributed. Using the sparsity pattern property of the Pauli matrices and GPUs is an excellent candidate approach to further enhance the performance of non-convex compressed sensing QST.
QST using neural networks. Deep neural networks are ubiquitous, with many applications to science and industry. Recently, [9,10,11,27] show how machine learning and neural networks can be used to perform QST, driven by experimental data. The neural network architecture used is based on restricted Boltzmann machines (RBMs) [90], which feature a visible and a hidden layer of stochastic binary neurons, fully connected with weighted edges. Test cases considered include reconstruction of W state, magnetic observables of local Hamiltonians, the unitary dynamics induced by Hamiltonian evolution. Comparison results are provided in the Main Results section. Alternative approaches include conditional generative adversarial networks (CGANs) [91,92]: in this case, two dueling neural networks, a generator and a discriminator, learn to generate and identify multi-modal models from data.
QST for Matrix Product States (MPS). This is the case of highly structured quantum states where the state is well-approximated by a MPS of low bond dimension [12,13]. The idea behind this approach is, in order to overcome exponential bottlenecks in the general QST case, we require highly structured subsets of states, similar to the assumptions made in compressed sensing QST. MPS QST is considered an alternative approach to reduce the computational and storage complexity of QST.
Direct fidelity estimation. Rather than focusing on entrywise estimation of density matrices, the direct fidelity estimation procedure focuses on checking how close is the state of the system to a target state, where closeness is quantified by the fidelity metric. Classic techniques require up to number of samples, where denotes the accuracy of the fidelity term, when considering a general quantum state [93,94], but can be reduced to almost dimensionality-free number of samples for specific cases, such as stabilizer states [95,96,97]. Shadow tomography is considered as an alternative and generalization of this technique [98,99]; however, as noted in [94], the procedure in [98,99] requires exponentially long quantum circuits that act collectively on all the copies of the unknown state stored in a quantum memory, and thus has not been implemented fully on real quantum machines. A recent neural network-based implementation of such indirect QST learning methods is provided here [100].
The work in [93,94], goes beyond simple fidelity estimation, and utilizes random single qubit rotations to learn a minimal sketch of the unknown quantum state by which one that can predict arbitrary linear function of the state. Such methods constitute a favorable alternative to QST as they do not require number of samples that scale polynomially with the dimension; however, this, in turn, implies that these methods cannot be used in general to estimate the density matrix itself.
Author Contributions
Conceptualization, A.K. (Amir Kalev) and A.K. (Anastasios Kyrillidis); methodology, J.L.K. and A.K. (Anastasios Kyrillidis); software, J.L.K. and G.K.; formal analysis, J.L.K. and A.K. (Anastasios Kyrillidis); investigation, J.L.K., G.K., A.K. (Amir Kalev) and A.K. (Anastasios Kyrillidis); data curation, K.X.W. and G.K.; writing—original draft preparation, J.L.K. and A.K. (Anastasios Kyrillidis); writing—review and editing, J.L.K., G.K., A.K. (Amir Kalev) and A.K. (Anastasios Kyrillidis); visualization, J.L.K. and G.K.; supervision, A.K. (Amir Kalev) and A.K. (Anastasios Kyrillidis); project administration, A.K. (Anastasios Kyrillidis); funding acquisition, A.K. (Amir Kalev) and A.K. (Anastasios Kyrillidis). All authors have read and agreed to the published version of the manuscript.
Funding
Anastasios Kyrillidis and Amir Kalev acknowledge funding by the NSF (CCF-1907936).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The empirical results were obtained via synthetic and real experiments; the algorithm’s implementation is available at https://github.com/gidiko/MiFGD (accessed on 18 January 2023).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Additional Experiments
Appendix A.1. IBM Quantum System Experiments: GHZ—(6) Circuit, 2048 Shots
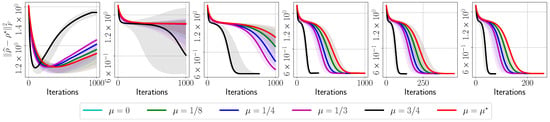
Figure A1.
Target error list plots for reconstructing circuit using real measurements from IBM Quantum system experiments.
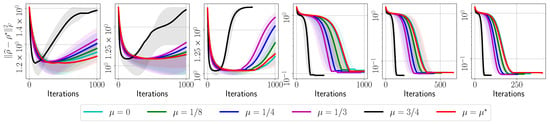
Figure A2.
Target error list plots for reconstructing circuit using synthetic measurements from IBM’s quantum simulator.
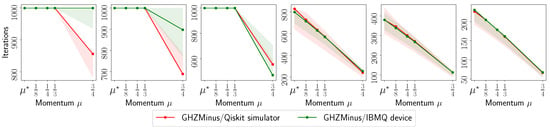
Figure A3.
Convergence iteration plots for reconstructing circuit using using real measurements from IBM Quantum system experiments and synthetic measurements from Qiskit simulation experiments.
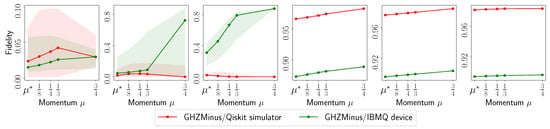
Figure A4.
Fidelity list plots for reconstructing circuit using using real measurements from IBM Quantum system experiments and synthetic measurements from Qiskit simulation experiments.
Appendix A.2. IBM Quantum System Experiments: GHZ—(8) Circuit, 2048 Shots
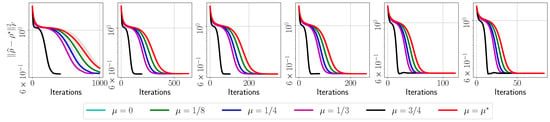
Figure A5.
Target error list plots for reconstructing circuit using real measurements from IBM Quantum system experiments.
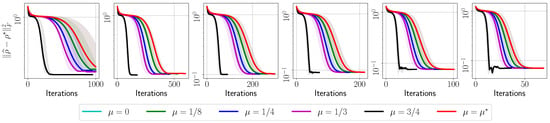
Figure A6.
Target error list plots for reconstructing circuit using synthetic measurements from IBM’s quantum simulator.
Figure A7.
Convergence iteration plots for reconstructing circuit using using real measurements from IBM Quantum system experiments and synthetic measurements from Qiskit simulation experiments.
Figure A8.
Fidelity list plots for reconstructing circuit using using real measurements from IBM Quantum system experiments and synthetic measurements from Qiskit simulation experiments.
Appendix A.3. IBM Quantum System Experiments: GHZ—(8) Circuit, 4096 Shots
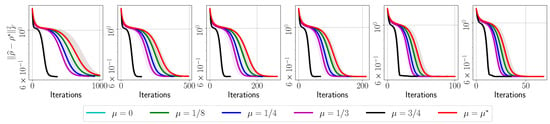
Figure A9.
Target error list plots for reconstructing circuit using real measurements from IBM Quantum system experiments.
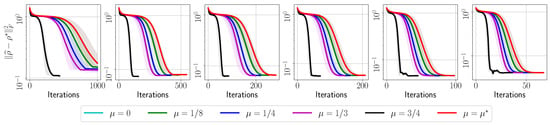
Figure A10.
Target error list plots for reconstructing circuit using synthetic measurements from IBM’s quantum simulator.
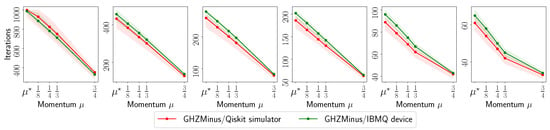
Figure A11.
Convergence iteration plots for reconstructing circuit using using real measurements from IBM Quantum system experiments and synthetic measurements from Qiskit simulation experiments.

Figure A12.
Fidelity list plots for reconstructing circuit using using real measurements from IBM Quantum system experiments and synthetic measurements from Qiskit simulation experiments.
Appendix A.4. IBM Quantum System Experiments: Hadamard(6) Circuit, 8192 Shots
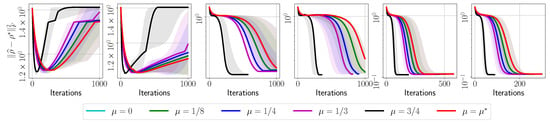
Figure A13.
Target error list plots for reconstructing circuit using real measurements from IBM Quantum system experiments.
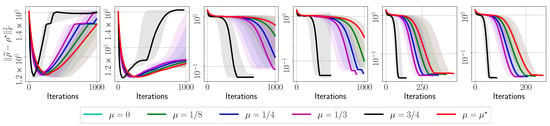
Figure A14.
Target error list plots for reconstructing circuit using synthetic measurements from IBM’s quantum simulator.
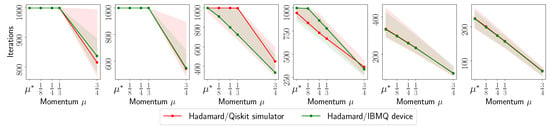
Figure A15.
Convergence iteration plots for reconstructing circuit using using real measurements from IBM Quantum system experiments and synthetic measurements from Qiskit simulation.
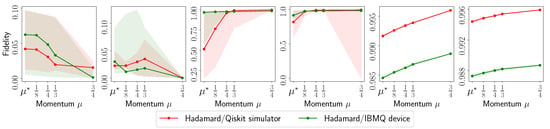
Figure A16.
Fidelity list plots for reconstructing circuit using using real measurements from IBM Quantum system experiments and synthetic measurements from Qiskit simulation experiments.
Appendix A.5. IBM Quantum System Experiments: Hadamard(8) Circuit, 4096 Shots
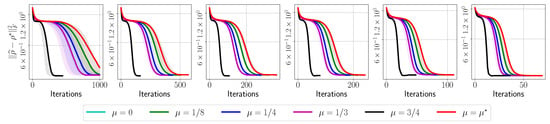
Figure A17.
Target error list plots for reconstructing circuit using real measurements from IBM Quantum system experiments.
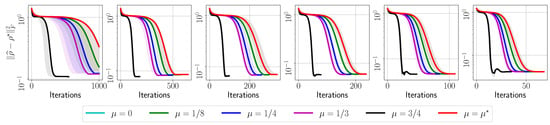
Figure A18.
Target error list plots for reconstructing circuit using synthetic measurements from IBM’s quantum simulator.
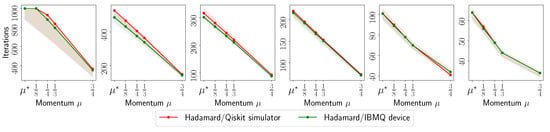
Figure A19.
Convergence iteration plots for reconstructing circuit using using real measurements from IBM Quantum system experiments and synthetic measurements from Qiskit simulation.
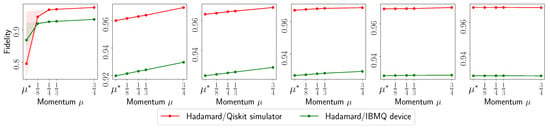
Figure A20.
Fidelity list plots for reconstructing circuit using using real measurements from IBM Quantum system experiments and synthetic measurements from Qiskit simulation experiments.
Appendix A.6. Synthetic Experiments for n = 12
We compare MiFGD with (i) the Matrix ALPS framework [61], a state of the art projected gradient descent algorithm, and an optimized version of matrix iterative hard thresholding, operating on the full matrix variable , with adaptive step size (we note that this algorithm has outperformed most of the schemes that work on the original space ; see [61]); (ii) the plain Procrustes Flow/FGD algorithm [25,26,32], where we use the step size as reported in [25], since the later has reported better performance than vanilla Procrustes Flow. We note that the Procrustes Flow/FGD algorithm is similar to our algorithm without acceleration. Further, the original Procrustes Flow/FGD algorithm relies on performing many iterations in the original space as an initialization scheme, which is often prohibitive as the problem dimensions grow. Both for our algorithm and the plain Procrustes Flow/FGD scheme, we use random initialization.
To properly compare the algorithms in the above list, we pre-select a common set of problem parameters. We fix the dimension (equivalent to qubits), and the rank of the optimal matrix to be (equivalent to a mixed quantum state reconstruction). Similar behavior has been observed for other values of r, and are omitted. We fix the number of observables m to be , where . In all algorithms, we fix the maximum number of iterations to 4000, and we use the same stopping criterion: . For the implementation of , we have used the momentum parameter , as well as the theoretical value.
The procedure to generate synthetically the data is as follows: The observations y are set to for some noise vector w; while the theory holds for the noiseless case, we show empirically that noisy cases are robustly handled by the same algorithm. We use permuted and subsampled noiselets for the linear operator [101]. The optimal matrix is generated as the multiplication of a tall matrix such that , and , without loss of generality. The entries of are drawn i.i.d. from a Gaussian distribution with zero mean and unit variance. In the noisy case, w has the same dimensions with y, its entries are drawn from a zero mean Gaussian distribution with norm . The random initialization is defined as drawn i.i.d. from a Gaussian distribution with zero mean and unit variance.
The results are shown in Figure A21. Some notable remarks: (i) While factorization techniques might take more iterations to converge compared to non-factorized algorithms, the per iteration time complexity is much less, such that overall, factorized gradient descent converges more quickly in terms of total execution time. (ii) Our proposed algorithm, even under the restrictive assumptions on acceleration parameter μ, performs better than the non-accelerated factored gradient descent algorithms, such as Procrustes Flow. (iii) Our theory is conservative: using a much larger we obtain a faster convergence; the proof for less strict assumptions for is an interesting future direction. In all cases, our findings illustrate the effectiveness of the proposed schemes on different problem configurations.
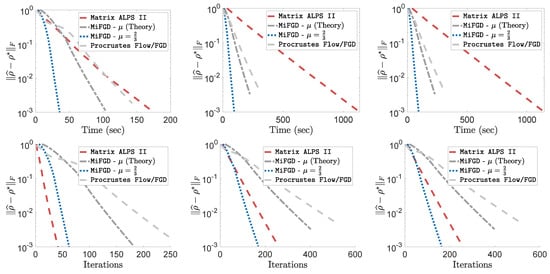
Figure A21.
Synthetic example results on low-rank matrix sensing in higher dimensions (equivalent to qubits). Top row: Convergence behavior vs. time elapsed. Bottom row: Convergence behavior vs. number of iterations. Left panel: , noiseless case; Center panel: , noiseless case; Right panel: , noisy case, .
Appendix A.7. Asymptotic Complexity Comparison of lstsq, CVXPY, and MiFGD
We first note that lstsq can be only applied to the case we have a full tomographic set of measurements; this makes lstsq algorithm inapplicable in the compressed sensing scenario, where the number of measurements can be significantly reduced. Yet, we make the comparison by providing information-theoretically complete set of measurements to lstsq and CVXPY, as well as to MiFGD, to highlight the efficiency of our proposed method, even in the scenario that is not exactly intended in our work. Given this, we compare in detail the asymptotic scailing of MiFGD with lstsq and CVXPY below:
- lstsq is based on the computation of eigenvalues/eigenvector pairs (among other steps) of a matrix of size equal to the density matrix we want to reconstruct. Based on our notation, the density matrices are denoted as with dimensions . Here, n is the number of qubits in the quantum system. Standard libraries for eigenvalue/eigenvector calculations, like LAPACK, reduce a Hermitian matrix to tridiagonal form using the Householder method, which takes overall a computational complexity. The other steps in the lstsq procedure either take constant time, or complexity. Thus, the actual run-time of an implementation depends on the eigensystem solver that is being used.
- CVXPY is distributed with the open source solvers; for the case of SDP instances, CVXPY utilizes the Splitting Conic Solver (SCS) (https://github.com/cvxgrp/scs (accessed on 18 January 2023)), a general numerical optimization package for solving large-scale convex cone problems. SCS applies Douglas-Rachford splitting to a homogeneous embedding of the quadratic cone program. Based on the PSD constraint, this again involves the computation of eigenvalues/eigenvector pairs (among other steps) of a matrix of size equal to the density matrix we want to reconstruct. This takes overall a computational complexity, not including the other steps performed within the SCS solver. This is an iterative algorithm that requires such complexity per iteration. Douglas-Rachford splitting methods enjoy convergence rate in general [53,102,103]. This leads to a rough overall iteration complexity (This is an optimistic complexity bound since we have skipped several details within the Douglas-Rachford implementation of CVXPY).
- For MiFGD, and for sufficiently small momentum value, we require iterations to get close to the optimal value. Per iteration, MiFGD does not involve any expensive eigensystem solvers, but relies only on matrix-matrix and matrix-vector multiplications. In particular, the main computational complexity per iteration origins from the iteration:Here, for all k. Observe that where each element is computed independently. For an index , requires complexity, and thus computing requires complexity, overall. By definition the adjoing operation satisfies: ; thus, the operation is still dominated by complexity. Finally, we perform one more matrix-matrix multiplication with , which results into an additional complexity. The rest of the operations involve adding matrices, which does not dominate the overall complexity. Combining the iteration complexity with the per-iteration computational complexity, MiFGD has a complexity.
Combining the above, we summarize the following complexities:
Observe that (i) MiFGD has the best dependence on the number of qubits and the ambient dimension of the problem, ; (ii) MiFGD applies to cases that lstsq is inapplicable; (iii) MiFGD has a better iteration complexity than other iterative algorithms, while has a better polynomial dependency on .
Appendix B. Detailed Proof of Theorem 1
For notational brevity, we first denote , , and . Let us start with the following equality. For as the minimizer of , we have:
The proof focuses on how to bound the last part on the right-hand side. By the definition of , we get:
Observe the following:
By Lemmata A7 and A8, we have:
Next, we use the following lemma:
Lemma A1
([32] (Lemma 5.4)). For any , the following holds:
From Lemma A1, the quantity satisfies:
which, in our main recursion, results in:
where is due to Lemma A6, and is due to the definition of .
Under the assumptions that , for user-defined, and , the main constants in our proof so far simplify to:
by Corollary A3. Thus:
and our recursion becomes:
Finally, we have
where is by the definition of for , which is one of our assumptions as explained above. Combining the above in our main inequality, we obtain:
Taking square root on both sides, we obtain:
Let us define . Using the definitions and , we get
where follows from steps similar to those in Lemma A5. Further observe that
which leads to:
Including two subsequent iterations in a single two-dimensional first-order system, we get the following characterization:
Now, let . Then, we can write the above relation as
where we denote the “contraction matrix” by A. Observe that A has non-negative values. Unfolding the above recursion for k iterations, we obtain:
Taking norms on both sides, we get
where is by triangle inequality, and is by submultiplicativity of matrix norms.
To bound Equation (A6), we will use spectral analysis. We first recall the definition of the spectral radius of a matrix M:
where is the set of all eigenvalues of M. We then use the following lemma:
Lemma A2
(Lemma 11 in [104]). Given a matrix M and , there exists a matrix norm such that
We further use the Gelfand’s formula:
Lemma A3
(Theorem 12 in [104]). Given any matrix norm , the following holds:
The proofs for the above lemmata can be found in [104]. Using Lemmas A2 and A3, we have that for any , there exists such that
Further, let Then, we have
Therefore, asymptotically, the convergence rate is where is the spectral radius of the contraction matrix A. We thus compute below. Since A is a matrix, its eigenvalues are:
where follows since every term in is positive.
To show an accelerated convergence rate, we want the above eigenvalue (which determines the convergence rate) to be bounded by (This is akin to the notion of acceleration and optimal method (for certain function classes) from convex optimization literature, where the condition number appears inside the term. For details, see [39,44]). To show this, first note that this term is bounded above as follows:
where (i) is by the conventional bound on momentum: , and (ii) is by the relation for . Therefore, to show an accelerated rate of convergence, we want the following relation to hold:
Recalling our definition of , the problem boils down to choosing the right step size such that the above inequality on in Equation (A9) is satisfied. With simple algebra, we can show the following lower bound on :
Finally, the argument inside the term of has to be non-negative, yielding the following upper bound on :
Combining two inequalities, and noting that the term is bounded above by 1, we arrive at the following bound on :
In sum, for the specific satisfying Equation (A10), we have shown that
Above bound translates Equation (A8) into:
Without loss of generality, we can take the Euclidean norm from the above (By the equivalence of norms [105], can absorb additional constants), which yields:
Re-substituting , and using the same initialization for and , we get:
where in the equality, with slight abuse of notation, we absorbed factor to , and similarly absorbed the last term such that This concludes the proof for Theorem 1.
Supporting Lemmata
In this subsection, we present a series of lemmata, used for the proof of Theorem 1.
Lemma A4.
Let and , such that for some , where , , for , and . Then:
Proof.
By the fact and using Weyl’s inequality for perturbation of singular values [106] (Theorem 3.3.16), we have:
Then,
Similarly:
In the above, we used the fact that , for all i, and the fact that , for . □
Lemma A5.
Let , and , such that and, where , and , for , and . Set the momentum parameter as , for user-defined. Then,
Proof.
Let and . By the definition of the distance function:
where is due to the fact that . We keep in the expression, but we use it for clarity for the rest of the proof. □
Corollary A1.
Let and , such that for some , and . Then:
Given that , we get:
Proof.
The proof follows similar motions as in Lemma A4. □
Corollary A2.
Under the same assumptions of Lemma A4 and Corollary A1, and given the assumptions on μ, we have:
Proof.
The proof is easily derived based on the quantities from Lemma A4 and Corollary A1. □
Corollary A3.
Let and , such that for some , and . Define . Then:
where . for .
Proof.
The proof uses the definition of the condition number and the results from Lemma A4 and and Corollary A1. □
Lemma A6.
Consider the following three step sizes:
Here, is the initial point, is the current point, is the optimal solution, and denotes a basis of the column space of Z. Then, under the assumptions that , and , and assuming , for the user-defined parameter , we have:
Proof.
The assumptions of the lemma are identical to that of Corollary A2. Thus, we have: , , and We focus on the inequality . Observe that:
where is due to smoothness via RIP constants of the objective and the fact . For the first two terms on the right-hand side, where is the minimizing rotation matrix for Z, we obtain:
where is due to the relation of and derived above, is due to Lemma A5. Similarly:
Using these above, we obtain:
Thus:
Similarly, one gets .
For the relation between and , we will prove here the lower bound; similar motions lead to the upper bound also. By definition, and using the relations in Corollary A2, we get:
For the gradient term, we observe:
where is due to , is due to the restricted smoothness assumption and the RIP, is due to the bounds above on , is due to the bounds on , w.r.t. , as well as the bound on .
Thus, in the inequality above, we get:
Similarly, one can show that . □
Lemma A7.
Let , and , such that and, where , and , for , and . By Lemma A5, the above imply also that: . Then, under RIP assumptions of the mapping , we have:
where
and .
Proof.
First, denote . Then:
Note that follows from the fact , for a matrix Q that spans the row space of , and follows from , for PSD matrix B (Von Neumann’s trace inequality [107]). For the transformation in , we use that fact that the row space of , , is a subset of , as is a linear combination of U and .
To bound the first term in Equation (A12), we observe:
where is due to the definition of .
To bound term A, we observe that or . This results into bounding A as follows:
Combining the above inequalities, we obtain:
where follows from , is due to Corollary A3, bounding , where by Lemma A5, is due to , and by Corollary A1, is due to the fact
and is due to Corollary A1.
Next, we bound the second term in Equation (A12):
where follows from and , is due to smoothness of f and the RIP constants, follows from [25] (Lemma 18), for , follows from substituting above, and observing that and .
Combining the above we get:
where . □
Lemma A8.
Under identical assumptions with Lemma A7, the following inequality holds:
Proof.
By smoothness assumption of the objective, based on the RIP assumption, we have:
due to the optimality , for any . Also, by the restricted strong convexity with RIP, we get:
Adding the two inequalities, we obtain:
To proceed we observe:
where is due to the fact , for a basis matrix whose columns span the column space of Z; also, I is the identity matrix whose dimension is apparent from the context. Thus:
and, hence,
Define Then, using the definition of , we know that , and thus:
Going back to the main recursion and using the above expression for , we have:
where is due to the symmetry of the objective; is due to Cauchy-Schwarz inequality and the fact:
where is due to , and the last inequality comes from the definition of the and its upper bound; is due to the upper bound on above; is due to ; is due to . The above lead to the desiderata:
□
References
- Altepeter, J.B.; James, D.F.; Kwiat, P.G. 4 qubit quantum state tomography. In Quantum State Estimation; Springer: Berlin/Heidelberg, Germany, 2004; pp. 113–145. [Google Scholar]
- Eisert, J.; Hangleiter, D.; Walk, N.; Roth, I.; Markham, D.; Parekh, R.; Chabaud, U.; Kashefi, E. Quantum certification and benchmarking. arXiv 2019, arXiv:1910.06343. [Google Scholar] [CrossRef]
- Mohseni, M.; Rezakhani, A.; Lidar, D. Quantum-process tomography: Resource analysis of different strategies. Phys. Rev. A 2008, 77, 032322. [Google Scholar] [CrossRef]
- Gross, D.; Liu, Y.K.; Flammia, S.; Becker, S.; Eisert, J. Quantum state tomography via compressed sensing. Phys. Rev. Lett. 2010, 105, 150401. [Google Scholar] [CrossRef] [PubMed]
- Vogel, K.; Risken, H. Determination of quasiprobability distributions in terms of probability distributions for the rotated quadrature phase. Phys. Rev. A 1989, 40, 2847. [Google Scholar] [CrossRef]
- Ježek, M.; Fiurášek, J.; Hradil, Z. Quantum inference of states and processes. Phys. Rev. A 2003, 68, 012305. [Google Scholar] [CrossRef]
- Banaszek, K.; Cramer, M.; Gross, D. Focus on quantum tomography. New J. Phys. 2013, 15, 125020. [Google Scholar] [CrossRef]
- Kalev, A.; Kosut, R.; Deutsch, I. Quantum tomography protocols with positivity are compressed sensing protocols. NPJ Quantum Inf. 2015, 1, 15018. [Google Scholar] [CrossRef]
- Torlai, G.; Mazzola, G.; Carrasquilla, J.; Troyer, M.; Melko, R.; Carleo, G. Neural-network quantum state tomography. Nat. Phys. 2018, 14, 447–450. [Google Scholar] [CrossRef]
- Beach, M.J.; De Vlugt, I.; Golubeva, A.; Huembeli, P.; Kulchytskyy, B.; Luo, X.; Melko, R.G.; Merali, E.; Torlai, G. QuCumber: Wavefunction reconstruction with neural networks. SciPost Phys. 2019, 7, 009. [Google Scholar] [CrossRef]
- Torlai, G.; Melko, R. Machine-Learning Quantum States in the NISQ Era. Annu. Rev. Condens. Matter Phys. 2020, 11, 325–344. [Google Scholar] [CrossRef]
- Cramer, M.; Plenio, M.B.; Flammia, S.T.; Somma, R.; Gross, D.; Bartlett, S.D.; Landon-Cardinal, O.; Poulin, D.; Liu, Y.K. Efficient quantum state tomography. Nat. Comm. 2010, 1, 149. [Google Scholar] [CrossRef] [PubMed]
- Lanyon, B.; Maier, C.; Holzäpfel, M.; Baumgratz, T.; Hempel, C.; Jurcevic, P.; Dhand, I.; Buyskikh, A.; Daley, A.; Cramer, M.; et al. Efficient tomography of a quantum many-body system. Nat. Phys. 2017, 13, 1158–1162. [Google Scholar] [CrossRef]
- Gonçalves, D.; Gomes-Ruggiero, M.; Lavor, C. A projected gradient method for optimization over density matrices. Optim. Methods Softw. 2016, 31, 328–341. [Google Scholar] [CrossRef]
- Bolduc, E.; Knee, G.; Gauger, E.; Leach, J. Projected gradient descent algorithms for quantum state tomography. NPJ Quantum Inf. 2017, 3, 44. [Google Scholar] [CrossRef]
- Shang, J.; Zhang, Z.; Ng, H.K. Superfast maximum-likelihood reconstruction for quantum tomography. Phys. Rev. A 2017, 95, 062336. [Google Scholar] [CrossRef]
- Hu, Z.; Li, K.; Cong, S.; Tang, Y. Reconstructing Pure 14-Qubit Quantum States in Three Hours Using Compressive Sensing. IFAC-PapersOnLine 2019, 52, 188–193. [Google Scholar] [CrossRef]
- Hou, Z.; Zhong, H.S.; Tian, Y.; Dong, D.; Qi, B.; Li, L.; Wang, Y.; Nori, F.; Xiang, G.Y.; Li, C.F.; et al. Full reconstruction of a 14-qubit state within four hours. New J. Phys. 2016, 18, 083036. [Google Scholar] [CrossRef]
- Candes, E.; Tao, T. Near-optimal signal recovery from random projections: Universal encoding strategies? IEEE Trans. Inf. Theory 2006, 52, 5406–5425. [Google Scholar] [CrossRef]
- Gross, D. Recovering low-rank matrices from few coefficients in any basis. IEEE Trans. Inf. Theory 2011, 57, 1548–1566. [Google Scholar] [CrossRef]
- Liu, Y.K. Universal low-rank matrix recovery from Pauli measurements. In Proceedings of the Advances in Neural Information Processing Systems, Granada, Spain, 12–15 December 2011; pp. 1638–1646. [Google Scholar]
- Riofrío, C.; Gross, D.; Flammia, S.; Monz, T.; Nigg, D.; Blatt, R.; Eisert, J. Experimental quantum compressed sensing for a seven-qubit system. Nat. Commun. 2017, 8, 15305. [Google Scholar] [CrossRef]
- Kliesch, M.; Kueng, R.; Eisert, J.; Gross, D. Guaranteed recovery of quantum processes from few measurements. Quantum 2019, 3, 171. [Google Scholar] [CrossRef]
- Flammia, S.T.; Gross, D.; Liu, Y.K.; Eisert, J. Quantum tomography via compressed sensing: Error bounds, sample complexity and efficient estimators. New J. Phys. 2012, 14, 095022. [Google Scholar] [CrossRef]
- Bhojanapalli, S.; Kyrillidis, A.; Sanghavi, S. Dropping convexity for faster semi-definite optimization. In Proceedings of the Conference on Learning Theory, New York, NY, USA, 23–26 June 2016; pp. 530–582. [Google Scholar]
- Kyrillidis, A.; Kalev, A.; Park, D.; Bhojanapalli, S.; Caramanis, C.; Sanghavi, S. Provable compressed sensing quantum state tomography via non-convex methods. NPJ Quantum Inf. 2018, 4, 36. [Google Scholar] [CrossRef]
- Gao, X.; Duan, L.M. Efficient representation of quantum many-body states with deep neural networks. Nat. Commun. 2017, 8, 1–6. [Google Scholar] [CrossRef]
- tA v, A.; Anis, M.S.; Mitchell, A.; Abraham, H.; AduOffei; Agarwal, R.; Agliardi, G.; Aharoni, M.; Ajith, V.; Akhalwaya, I.Y.; et al. Qiskit: An Open-Source Framework for Quantum Computing. 2021. Available online: https://zenodo.org/record/7591922#.Y9zUYK1BxPY (accessed on 18 January 2023).
- Recht, B.; Fazel, M.; Parrilo, P.A. Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. SIAM Rev. 2010, 52, 471–501. [Google Scholar] [CrossRef]
- Park, D.; Kyrillidis, A.; Caramanis, C.; Sanghavi, S. Finding low-rank solutions to matrix problems, efficiently and provably. arXiv 2016, arXiv:1606.03168. [Google Scholar]
- Park, D.; Kyrillidis, A.; Bhojanapalli, S.; Caramanis, C.; Sanghavi, S. Provable Burer-Monteiro factorization for a class of norm-constrained matrix problems. arXiv 2016, arXiv:1606.01316. [Google Scholar]
- Tu, S.; Boczar, R.; Simchowitz, M.; Soltanolkotabi, M.; Recht, B. Low-rank solutions of linear matrix equations via Procrustes flow. In Proceedings of the 33rd International Conference on International Conference on Machine Learning-Volume 48, New York, NY, USA, 19–24 June 2016; pp. 964–973. [Google Scholar]
- Zhao, T.; Wang, Z.; Liu, H. A nonconvex optimization framework for low rank matrix estimation. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 559–567. [Google Scholar]
- Zheng, Q.; Lafferty, J. A convergent gradient descent algorithm for rank minimization and semidefinite programming from random linear measurements. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 109–117. [Google Scholar]
- Cauchy, A. Méthode générale pour la résolution des systemes d’équations simultanées. Comp. Rend. Sci. Paris 1847, 25, 536–538. [Google Scholar]
- Park, D.; Kyrillidis, A.; Caramanis, C.; Sanghavi, S. Non-square matrix sensing without spurious local minima via the Burer-Monteiro approach. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Ft. Lauderdale, FL, USA, 20–22 April 2017; pp. 65–74. [Google Scholar]
- Ge, R.; Jin, C.; Zheng, Y. No spurious local minima in nonconvex low rank problems: A unified geometric analysis. arXiv 2017, arXiv:1704.00708. [Google Scholar]
- Hsieh, Y.P.; Kao, Y.C.; Karimi Mahabadi, R.; Alp, Y.; Kyrillidis, A.; Cevher, V. A Non-Euclidean Gradient Descent Framework for Non-Convex Matrix Factorization. IEEE Trans. Signal Process. 2018, 66, 5917–5926. [Google Scholar] [CrossRef]
- Polyak, B. Some methods of speeding up the convergence of iteration methods. USSR Comput. Math. Math. Phys. 1964, 4, 1–17. [Google Scholar] [CrossRef]
- Nesterov, Y. A method of solving a convex programming problem with convergence rate O(1k2). Sov. Math. Dokl. 1983, 27, 372–376. [Google Scholar]
- Bhojanapalli, S.; Neyshabur, B.; Srebro, N. Global optimality of local search for low rank matrix recovery. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 3873–3881. [Google Scholar]
- Stöger, D.; Soltanolkotabi, M. Small random initialization is akin to spectral learning: Optimization and generalization guarantees for overparameterized low-rank matrix reconstruction. Adv. Neural Inf. Process. Syst. 2021, 34, 23831–23843. [Google Scholar]
- Lanczos, C. An Iteration Method for the Solution of the Eigenvalue Problem of Linear Differential and Integral Operators1. J. Res. Natl. Bur. Stand. 1950, 45. [Google Scholar] [CrossRef]
- Nesterov, Y. Introductory Lectures on Convex Optimization: A Basic Course; Springer Science & Business Media: Berlin, Germany, 2013; Volume 87. [Google Scholar]
- Carmon, Y.; Duchi, J.; Hinder, O.; Sidford, A. Accelerated methods for non-convex optimization. arXiv 2016, arXiv:1611.00756. [Google Scholar]
- Li, Y.; Ma, C.; Chen, Y.; Chi, Y. Nonconvex Matrix Factorization from Rank-One Measurements. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Naha, Japan, 16–18 April 2019. [Google Scholar]
- Khanna, R.; Kyrillidis, A. IHT dies hard: Provable accelerated Iterative Hard Thresholding. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Playa Blanca, Lanzarote, Canary Islands, 9–11 April 2018; pp. 188–198. [Google Scholar]
- Rudelson, M.; Vershynin, R. On sparse reconstruction from Fourier and Gaussian measurements. Commun. Pure Appl. Math. A J. Issued Courant Inst. Math. Sci. 2008, 61, 1025–1045. [Google Scholar] [CrossRef]
- Vandenberghe, L. The CVXOPT Linear and Quadratic Cone Program Solvers. 2010. Available online: https://www.seas.ucla.edu/vandenbe/publications/coneprog.pdf (accessed on 18 January 2023).
- Diamond, S.; Boyd, S. CVXPY: A Python-embedded modeling language for convex optimization. J. Mach. Learn. Res. 2016, 17, 1–5. [Google Scholar]
- Agrawal, A.; Verschueren, R.; Diamond, S.; Boyd, S. A rewriting system for convex optimization problems. J. Control. Decis. 2018, 5, 42–60. [Google Scholar] [CrossRef]
- Smolin, J.A.; Gambetta, J.M.; Smith, G. Efficient method for computing the maximum-likelihood quantum state from measurements with additive gaussian noise. Phys. Rev. Lett. 2012, 108, 070502. [Google Scholar] [CrossRef]
- O’Donoghue, B.; Chu, E.; Parikh, N.; Boyd, S. Conic Optimization via Operator Splitting and Homogeneous Self-Dual Embedding. J. Optim. Theory Appl. 2016, 169, 1042–1068. [Google Scholar] [CrossRef]
- O’Donoghue, B.; Chu, E.; Parikh, N.; Boyd, S. SCS: Splitting Conic Solver, Version 2.1.2. 2019. Available online: https://github.com/cvxgrp/scs (accessed on 18 January 2023).
- Forum, T.M. MPI: A Message Passing Interface. In Proceedings of the 1993 ACM/IEEE Conference on Supercomputing, Portland, OR, USA, 19 November 1993; Association for Computing Machinery: New York, NY, USA, 1993; pp. 878–883. [Google Scholar] [CrossRef]
- Dalcin, L.D.; Paz, R.R.; Kler, P.A.; Cosimo, A. Parallel distributed computing using Python. Adv. Water Resour. 2011, 34, 1124–1139. [Google Scholar] [CrossRef]
- Lee, K.; Bresler, Y. Guaranteed minimum rank approximation from linear observations by nuclear norm minimization with an ellipsoidal constraint. arXiv 2009, arXiv:0903.4742. [Google Scholar]
- Liu, Z.; Vandenberghe, L. Interior-point method for nuclear norm approximation with application to system identification. SIAM J. Matrix Anal. Appl. 2009, 31, 1235–1256. [Google Scholar] [CrossRef]
- Jain, P.; Meka, R.; Dhillon, I.S. Guaranteed rank minimization via singular value projection. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 6–9 December 2010; pp. 937–945. [Google Scholar]
- Lee, K.; Bresler, Y. Admira: Atomic decomposition for minimum rank approximation. IEEE Trans. Inf. Theory 2010, 56, 4402–4416. [Google Scholar] [CrossRef]
- Kyrillidis, A.; Cevher, V. Matrix recipes for hard thresholding methods. J. Math. Imaging Vis. 2014, 48, 235–265. [Google Scholar] [CrossRef]
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Tieleman, T.; Hinton, G. Lecture 6.5-RMSPro: Divide the gradient by a running average of its recent magnitude. COURSERA Neural Netw. Mach. Learn. 2012, 4, 26–31. [Google Scholar]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- O’Donoghue, B.; Candes, E. Adaptive restart for accelerated gradient schemes. Found. Comput. Math. 2015, 15, 715–732. [Google Scholar] [CrossRef]
- Bubeck, S.; Lee, Y.T.; Singh, M. A geometric alternative to Nesterov’s accelerated gradient descent. arXiv 2015, arXiv:1506.08187. [Google Scholar]
- Goh, G. Why Momentum Really Works. Distill 2017, 2, e6. [Google Scholar] [CrossRef]
- Kyrillidis, A.; Cevher, V. Recipes on hard thresholding methods. In Proceedings of the Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), San Juan, PR, USA, 13–16 December 2011; pp. 353–356. [Google Scholar]
- Xu, P.; He, B.; De Sa, C.; Mitliagkas, I.; Re, C. Accelerated stochastic power iteration. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Playa Blanca, Lanzarote, Canary Islands, 9–11 April 2018; pp. 58–67. [Google Scholar]
- Ghadimi, S.; Lan, G. Stochastic first-and zeroth-order methods for nonconvex stochastic programming. SIAM J. Optim. 2013, 23, 2341–2368. [Google Scholar] [CrossRef]
- Lee, J.; Simchowitz, M.; Jordan, M.; Recht, B. Gradient descent only converges to minimizers. In Proceedings of the Conference on Learning Theory, New York, NY, USA, 23–26 June 2016; pp. 1246–1257. [Google Scholar]
- Agarwal, N.; Allen-Zhu, Z.; Bullins, B.; Hazan, E.; Ma, T. Finding approximate local minima for nonconvex optimization in linear time. arXiv 2016, arXiv:1611.01146. [Google Scholar]
- Burer, S.; Monteiro, R.D. A nonlinear programming algorithm for solving semidefinite programs via low-rank factorization. Math. Program. 2003, 95, 329–357. [Google Scholar] [CrossRef]
- Jain, P.; Dhillon, I.S. Provable inductive matrix completion. arXiv 2013, arXiv:1306.0626. [Google Scholar]
- Chen, Y.; Wainwright, M.J. Fast low-rank estimation by projected gradient descent: General statistical and algorithmic guarantees. arXiv 2015, arXiv:1509.03025. [Google Scholar]
- Sun, R.; Luo, Z.Q. Guaranteed matrix completion via non-convex factorization. IEEE Trans. Inf. Theory 2016, 62, 6535–6579. [Google Scholar] [CrossRef]
- O’Donnell, R.; Wright, J. Efficient quantum tomography. In Proceedings of the Forty-Eighth Annual ACM Symposium on Theory of Computing, Cambridge, MA, USA, 19–21 June 2016; pp. 899–912. [Google Scholar]
- Hayashi, M.; Matsumoto, K. Quantum universal variable-length source coding. Phys. Rev. A 2002, 66, 022311. [Google Scholar] [CrossRef]
- Christandl, M.; Mitchison, G. The spectra of quantum states and the Kronecker coefficients of the symmetric group. Commun. Math. Phys. 2006, 261, 789–797. [Google Scholar] [CrossRef]
- Alicki, R.; Rudnicki, S.; Sadowski, S. Symmetry properties of product states for the system of N n-level atoms. J. Math. Phys. 1988, 29, 1158–1162. [Google Scholar] [CrossRef]
- Keyl, M.; Werner, R.F. Estimating the spectrum of a density operator. In Asymptotic Theory of Quantum Statistical Inference: Selected Papers; World Scientific: Singapore, 2005; pp. 458–467. [Google Scholar]
- Tóth, G.; Wieczorek, W.; Gross, D.; Krischek, R.; Schwemmer, C.; Weinfurter, H. Permutationally invariant quantum tomography. Phys. Rev. Lett. 2010, 105, 250403. [Google Scholar] [CrossRef] [PubMed]
- Moroder, T.; Hyllus, P.; Tóth, G.; Schwemmer, C.; Niggebaum, A.; Gaile, S.; Gühne, O.; Weinfurter, H. Permutationally invariant state reconstruction. New J. Phys. 2012, 14, 105001. [Google Scholar] [CrossRef]
- Schwemmer, C.; Tóth, G.; Niggebaum, A.; Moroder, T.; Gross, D.; Gühne, O.; Weinfurter, H. Experimental comparison of efficient tomography schemes for a six-qubit state. Phys. Rev. Lett. 2014, 113, 040503. [Google Scholar] [CrossRef] [PubMed]
- Banaszek, K.; D’Ariano, G.M.; Paris, M.G.A.; Sacchi, M.F. Maximum-likelihood estimation of the density matrix. Phys. Rev. A 1999, 61, 010304. [Google Scholar] [CrossRef]
- Paris, M.; D’Ariano, G.; Sacchi, M. Maximum-likelihood method in quantum estimation. In Proceedings of the AIP Conference Proceedings; 2001; Volume 568, pp. 456–467. [Google Scholar]
- Řeháček, J.; Hradil, Z.; Knill, E.; Lvovsky, A.I. Diluted maximum-likelihood algorithm for quantum tomography. Phys. Rev. A 2007, 75, 042108. [Google Scholar] [CrossRef]
- Gonçalves, D.; Gomes-Ruggiero, M.; Lavor, C.; Farias, O.J.; Ribeiro, P. Local solutions of maximum likelihood estimation in quantum state tomography. Quantum Inf. Comput. 2012, 12, 775–790. [Google Scholar] [CrossRef]
- Teo, Y.S.; Řeháček, J.; Hradil, Z. Informationally incomplete quantum tomography. Quantum Meas. Quantum Metrol. 2013, 1, 57–83. [Google Scholar] [CrossRef]
- Sutskever, I.; Hinton, G.E.; Taylor, G.W. The recurrent temporal restricted boltzmann machine. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 7–10 December 2009; pp. 1601–1608. [Google Scholar]
- Ahmed, S.; Muñoz, C.S.; Nori, F.; Kockum, A. Quantum state tomography with conditional generative adversarial networks. arXiv 2020, arXiv:2008.03240. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, S.; Muñoz, C.; Nori, F.; Kockum, A. Classification and reconstruction of optical quantum states with deep neural networks. arXiv 2020, arXiv:2012.02185. [Google Scholar] [CrossRef]
- Paini, M.; Kalev, A.; Padilha, D.; Ruck, B. Estimating expectation values using approximate quantum states. Quantum 2021, 5, 413. [Google Scholar] [CrossRef]
- Huang, H.Y.; Kueng, R.; Preskill, J. Predicting Many Properties of a Quantum System from Very Few Measurements. arXiv 2020, arXiv:2002.08953. [Google Scholar] [CrossRef]
- Flammia, S.T.; Liu, Y.K. Direct fidelity estimation from few Pauli measurements. Phys. Rev. Lett. 2011, 106, 230501. [Google Scholar] [CrossRef] [PubMed]
- da Silva, M.P.; Landon-Cardinal, O.; Poulin, D. Practical characterization of quantum devices without tomography. Phys. Rev. Lett. 2011, 107, 210404. [Google Scholar] [CrossRef] [PubMed]
- Kalev, A.; Kyrillidis, A.; Linke, N.M. Validating and certifying stabilizer states. Phys. Rev. A 2019, 99, 042337. [Google Scholar] [CrossRef]
- Aaronson, S. Shadow tomography of quantum states. In Proceedings of the 50th Annual ACM SIGACT Symposium on Theory of Computing, Los Angeles, CA, USA, 25–29 June 2018; pp. 325–338. [Google Scholar]
- Aaronson, S.; Rothblum, G.N. Gentle measurement of quantum states and differential privacy. In Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, Phoenix, AZ, USA, 23–26 June 2019; pp. 322–333. [Google Scholar]
- Smith, A.; Gray, J.; Kim, M. Efficient Approximate Quantum State Tomography with Basis Dependent Neural-Networks. arXiv 2020, arXiv:2009.07601. [Google Scholar]
- Waters, A.E.; Sankaranarayanan, A.C.; Baraniuk, R. SpaRCS: Recovering low-rank and sparse matrices from compressive measurements. In Proceedings of the Advances in Neural Information Processing Systems, Granada, Spain, 12–14 December 2011; pp. 1089–1097. [Google Scholar]
- He, B.; Yuan, X. On the convergence rate of Douglas–Rachford operator splitting method. Math. Program. 2015, 153, 715–722. [Google Scholar] [CrossRef]
- O’Donoghue, B. Operator Splitting for a Homogeneous Embedding of the Linear Complementarity Problem. SIAM J. Optim. 2021, 31, 1999–2023. [Google Scholar] [CrossRef]
- Foucart, S. Matrix Norms and Spectral Radii. 2012. Available online: https://www.math.drexel.edu/~foucart/TeachingFiles/F12/M504Lect6.pdf (accessed on 18 January 2023).
- Johnson, S.G. Notes on the Equivalence of Norms. 2012. Available online: https://math.mit.edu/~stevenj/18.335/norm-equivalence.pdf (accessed on 18 January 2023).
- Horn, R.; Johnson, C. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Mirsky, L. A trace inequality of John von Neumann. Monatshefte Math. 1975, 79, 303–306. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).