Design and Application of Phase-Only Diffractive Optical Element Based on Non-Iterative Method
Abstract
:1. Introduction
2. Design Method
2.1. Phase Gradient Calculation
2.2. Gradient Integration Methods
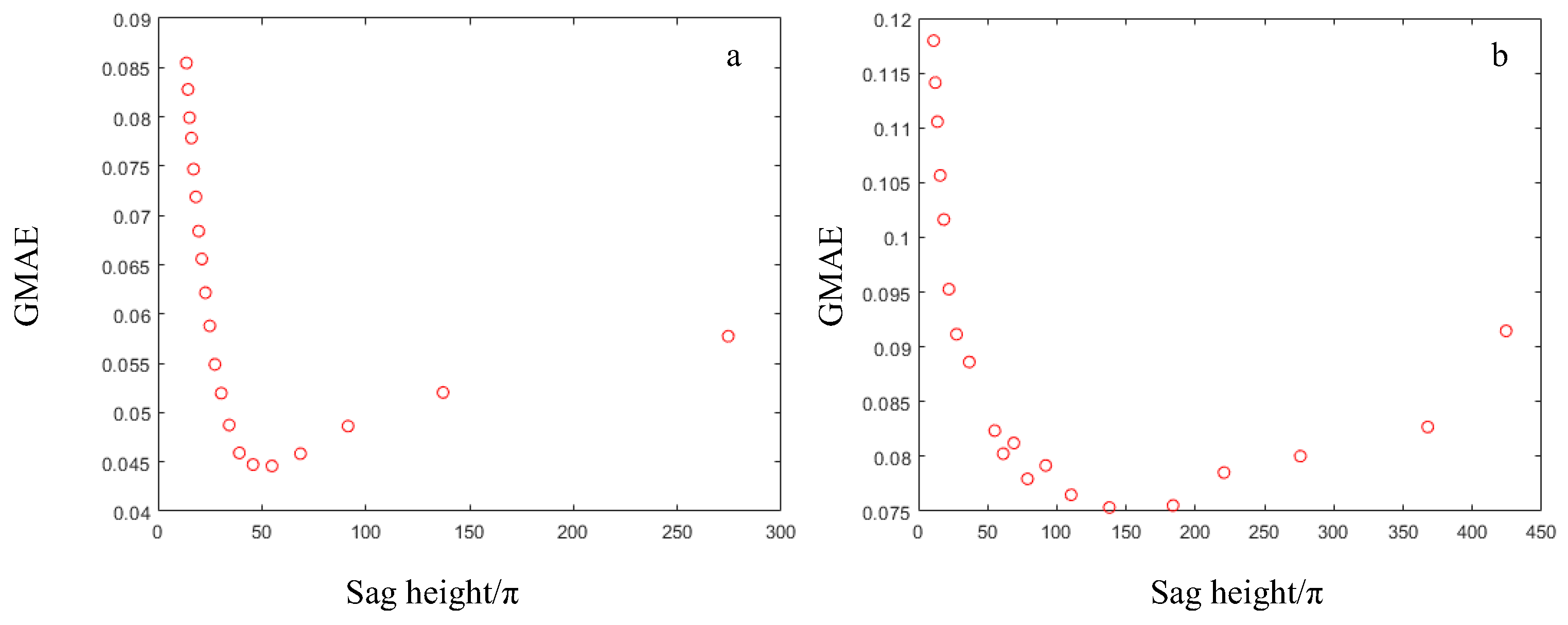
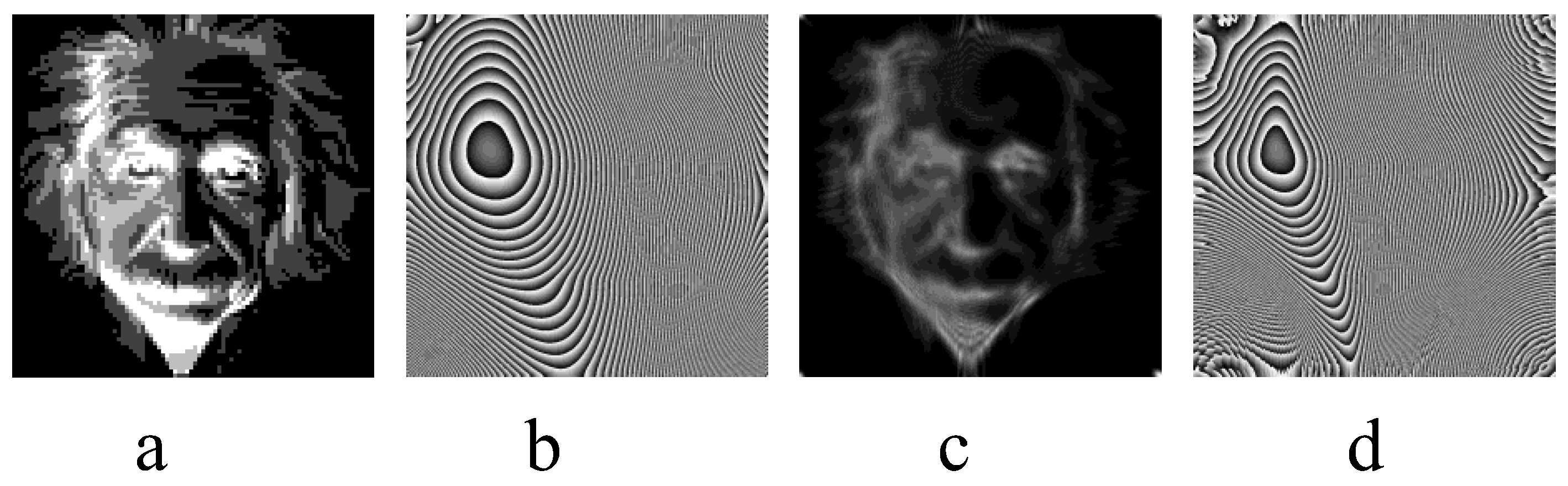
3. Design Examples
3.1. Uniform Illumination
3.2. Non-Uniform Illumination Focusing
3.3. Illumination Experiment Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, Z.; Sui, X.; Jin, G.; Cao, L. Progress in virtual reality and augmented reality based on holographic display. Appl. Opt. 2019, 58, A74–A81. [Google Scholar] [CrossRef] [PubMed]
- Wu, R.; Xu, L.; Liu, P.; Zhang, Y.; Zheng, Z.; Li, H.; Liu, X. Freeform illumination design: A nonlinear boundary problem for the elliptic Monge–Ampère equation. Opt. Lett. 2013, 38, 229–231. [Google Scholar] [CrossRef] [PubMed]
- Simpson, N.B.; Dholakia, K.; Allen, L.; Padgett, M.J. Mechanical equivalence of spin and orbital angular momentum of light: An optical spanner. Opt. Lett. 1997, 22, 52–54. [Google Scholar] [CrossRef] [PubMed]
- Padgett, M.; Bowman, R. Tweezers with a twist. Nat. Photonics 2011, 5, 343–348. [Google Scholar] [CrossRef]
- Hell, S.W.; Wichmann, J. Breaking the diffraction resolution limit by stimulated emission: Stimulated-emission-depletion fluorescence microscopy. Opt. Lett. 1994, 19, 780–782. [Google Scholar] [CrossRef] [PubMed]
- Tsang, P.W.M. Computer-Generated Phase-Only Holograms for 3D Displays: A Matlab Approach; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Chang, C.; Xia, J.; Yang, L.; Lei, W.; Yang, Z.; Chen, J. Speckle-suppressed phase-only holographic three-dimensional display based on double-constraint Gerchberg–Saxton algorithm. Appl. Opt. 2015, 54, 6994–7001. [Google Scholar] [CrossRef] [PubMed]
- Pang, H.; Wang, J.; Zhang, M.; Cao, A.; Shi, L.; Deng, Q. Non-iterative phase-only Fourier hologram generation with high image quality. Opt. Express 2017, 25, 14323–14333. [Google Scholar] [CrossRef] [PubMed]
- Wu, R.; Liu, P.; Zhang, Y.; Zheng, Z.; Li, H.; Liu, X. A mathematical model of the single freeform surface design for collimated beam shaping. Opt. Express 2013, 21, 20974–20989. [Google Scholar] [CrossRef] [PubMed]
- Caffarelli, L.A.; Kochengin, S.A.; Oliker, V.I. On the numerical solution of the problem of reflector design with given far-field scattering data. Ser. Contemp. Appl. Math. 1999, 226, 13–32. [Google Scholar]
- Michaelis, D.; Schreiber, P.; Bräuer, A. Cartesian oval representation of freeform optics in illumination systems. Opt. Lett. 2011, 36, 918–920. [Google Scholar] [CrossRef] [PubMed]
- Doskolovich, L.L.; Moiseev, M.A.; Bezus, E.A.; Oliker, V. On the use of the supporting quadric method in the problem of the light field eikonal calculation. Opt. Express 2015, 23, 19605–19617. [Google Scholar] [CrossRef] [PubMed]
- Doskolovich, L.L.; Mingazov, A.A.; Bykov, D.A.; Andreev, E.S.; Bezus, E.A. Variational approach to calculation of light field eikonal function for illuminating a prescribed region. Opt. Express 2017, 25, 26378–26392. [Google Scholar] [CrossRef] [PubMed]
- Bykov, D.A.; Doskolovich, L.L.; Mingazov, A.A.; Bezus, E.A.; Kazanskiy, N.L. Linear assignment problem in the design of freeform refractive optical elements generating prescribed irradiance distributions. Opt. Express 2018, 26, 27812–27825. [Google Scholar] [CrossRef] [PubMed]
- Doskolovich, L.L.; Mingazov, A.A.; Byzov, E.V.; Skidanov, R.V.; Ganchevskaya, S.V.; Bykov, D.A.; Bezus, E.A.; Podlipnov, V.V.; Porfirev, A.P.; Kazanskiy, N.L. Hybrid design of diffractive optical elements for optical beam shaping. Opt. Express 2021, 29, 31875–31890. [Google Scholar] [CrossRef] [PubMed]
- Southwell, W.H. Wave-front estimation from wave-front slope measurements. J. Opt. Soc. Am. 1980, 70, 998–1006. [Google Scholar] [CrossRef]
- Li, G.; Li, Y.; Liu, K.; Ma, X.; Wang, H. Improving wavefront reconstruction accuracy by using integration equations with higher-order truncation errors in the Southwell geometry. J. Opt. Soc. Am. A 2013, 30, 1448–1459. [Google Scholar] [CrossRef] [PubMed]
- Tong, K.; Zheng, Y.; Zhang, Z.; Zhao, X.; Zhang, B.; Song, L.; Wang, L.; Wang, C.; Wu, P. Model of radial basis functions based on surface slope for optical freeform surfaces. Opt. Express 2018, 26, 14010–14023. [Google Scholar] [CrossRef] [PubMed]
- Mochi, I.; Goldberg, K.A. Modal wavefront reconstruction from its gradient. Appl. Opt. 2015, 54, 3780–3785. [Google Scholar] [CrossRef]
- Zhang, G.J.; Zhang, M.; Zhao, Y. Wave front control with SLM and simulation of light wave diffraction. Opt. Express 2018, 26, 33543–33564. [Google Scholar]







| SNR | MAE | RNew1 | RNew2 | RMSE | |
|---|---|---|---|---|---|
| R_0.02 | 1.6444 | 0.0380 | −0.1276 | 0.3793 | 0.1552 |
| R_0.05 | 1.4472 | 0.0432 | 0.4933 | 0.5595 | 0.1101 |
| CIST_0.02 | 1.6748 | 0.1526 | −0.2070 | 0.4083 | 0.2991 |
| CIST_0.05 | 1.8275 | 0.1398 | 0.1212 | 0.4805 | 0.2626 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, K.; Zhang, G. Design and Application of Phase-Only Diffractive Optical Element Based on Non-Iterative Method. Photonics 2022, 9, 874. https://doi.org/10.3390/photonics9110874
Shi K, Zhang G. Design and Application of Phase-Only Diffractive Optical Element Based on Non-Iterative Method. Photonics. 2022; 9(11):874. https://doi.org/10.3390/photonics9110874
Chicago/Turabian StyleShi, Kuo, and Gongjian Zhang. 2022. "Design and Application of Phase-Only Diffractive Optical Element Based on Non-Iterative Method" Photonics 9, no. 11: 874. https://doi.org/10.3390/photonics9110874
APA StyleShi, K., & Zhang, G. (2022). Design and Application of Phase-Only Diffractive Optical Element Based on Non-Iterative Method. Photonics, 9(11), 874. https://doi.org/10.3390/photonics9110874





